10 Κεφάλαιο: Μοντέλα με μια Ποσοτική Ανεξάρτητη Μεταβλητή

10.1 Χρήση Ποσοτικής Ανεξάρτητης Μεταβλητής σε ένα Μοντέλο

Η μεταβλητή Height2Group είναι ποιοτική. Το μοντέλο με ανεξάρτητη μεταβλητή τη Height2Group ονομάζεται μοντέλο ομάδων, καθώς στηρίζεται στους μέσους όρους των ομάδων για να προβλέψει το μήκος του αντίχειρα σε κάθε ομάδα (στην προκειμένη περίπτωση, «κοντοί» και «ψηλοί» φοιτητές).

Ωστόσο, δεν είναι όλα τα μοντέλα αυτού του τύπου. Όταν η ανεξάρτητη μεταβλητή είναι ποσοτική, απαιτείται μια διαφορετική προσέγγιση. Τα μοντέλα που περιλαμβάνουν ποσοτικές ανεξάρτητες μεταβλητές ονομάζονται συνήθως μοντέλα παλινδρόμησης (regression models).

Το Μοντέλο του Ύψους (`Height`)

Μια ποσοτική μεταβλητή από το σύνολο δεδομένων Fingers, η οποία ενδέχεται να εξηγεί μέρος της μεταβλητότητας στο μήκος του αντίχειρα (Thumb), είναι η Height — το ύψος φοιτητή ή φοιτήτριας. (Σημείωση: η μεταβλητή Height μετριέται σε εκατοστά, ενώ η Thumb σε χιλιοστά.)

Σε προηγούμενο κεφάλαιο δημιουργήσαμε ένα διάγραμμα διασποράς που αναπαριστά τη σχέση μεταξύ των μεταβλητών Thumb και Height. Το επαναλαμβάνουμε παρακάτω:

gf_point(Thumb ~ Height, data = Fingers)

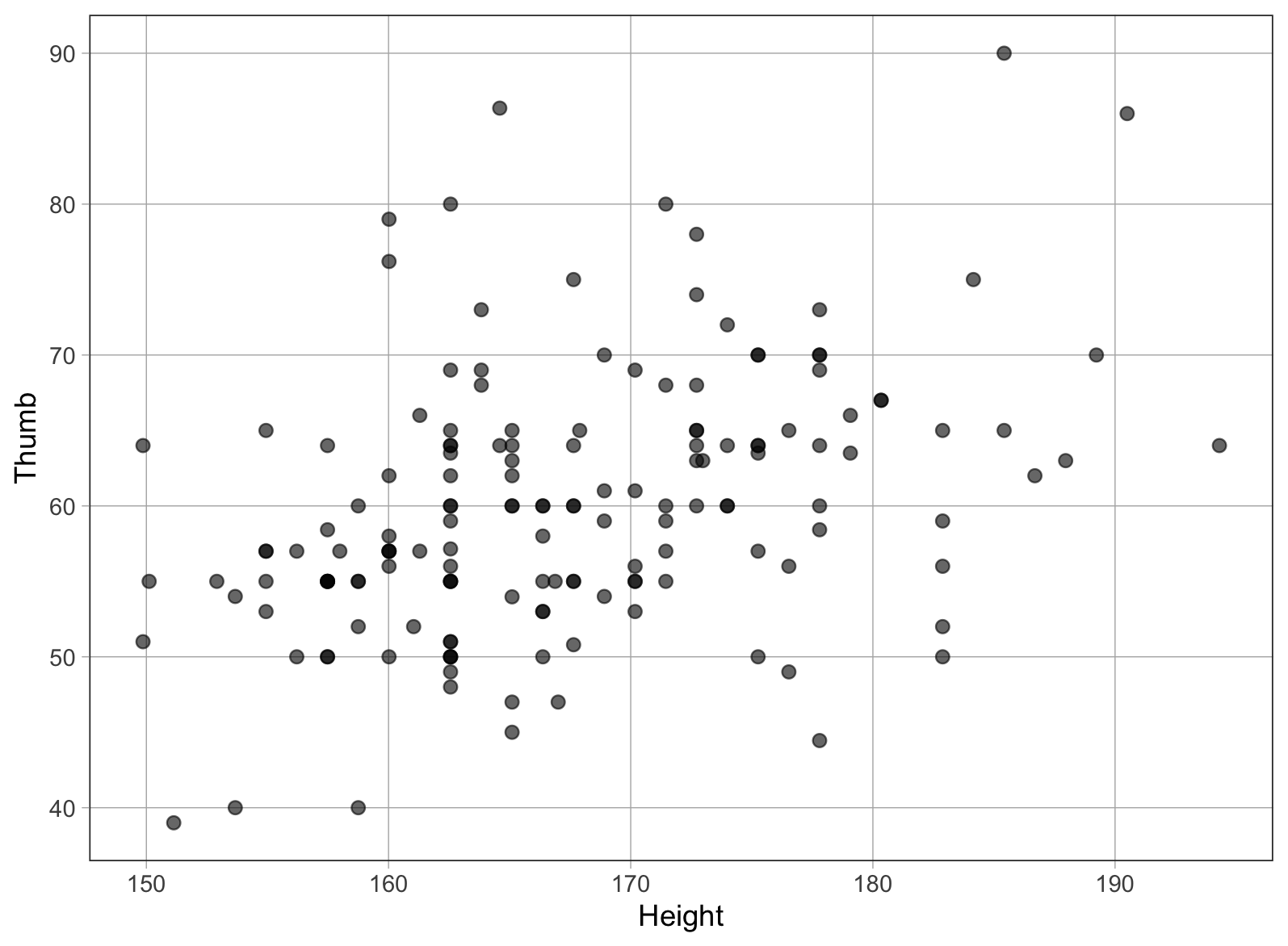
Όπως φαίνεται, αν γνωρίζουμε το ύψος ενός ατόμου μπορούμε να κάνουμε πιο ακριβή πρόβλεψη για το μήκος του αντίχειρά του σε σχέση με το να μην είχαμε αυτή την πληροφορία. Τα ψηλότερα άτομα τείνουν να έχουν μεγαλύτερους αντίχειρες, ενώ τα κοντύτερα μικρότερους. Πρόκειται για μια θετική συσχέτιση, καθώς η αύξηση της μιας μεταβλητής συνοδεύεται από αύξηση της άλλης.

Αν θέλουμε να κάνουμε συγκεκριμένες προβλέψεις και να συγκρίνουμε ποσοτικά το μοντέλο της Height με άλλα μοντέλα, πρέπει να το μετατρέψουμε σε στατιστικό μοντέλο, όπως κάναμε και με το μοντέλο της Height2Group. Αυτή τη φορά, όμως, δεν μπορούμε να βασιστούμε σε μέσους όρους ομάδων — γιατί δεν υπάρχουν ομάδες! Αντί για αυτό, θα χρησιμοποιήσουμε μια ευθεία γραμμή, γνωστή ως ευθεία παλινδρόμησης (regression line), για να κάνουμε τις προβλέψεις.

Η ευθεία παλινδρόμησης είναι ο απλούστερος τρόπος να περιγράψουμε τη σχέση μεταξύ δύο ποσοτικών μεταβλητών. Στο παρακάτω διάγραμμα έχουμε προσθέσει την ευθεία παλινδρόμησης. Η γραμμή αυτή δείχνει την τιμή πρόβλεψης του μήκους αντίχειρα ενός οποιουδήποτε ατόμου με βάση το ύψος του.

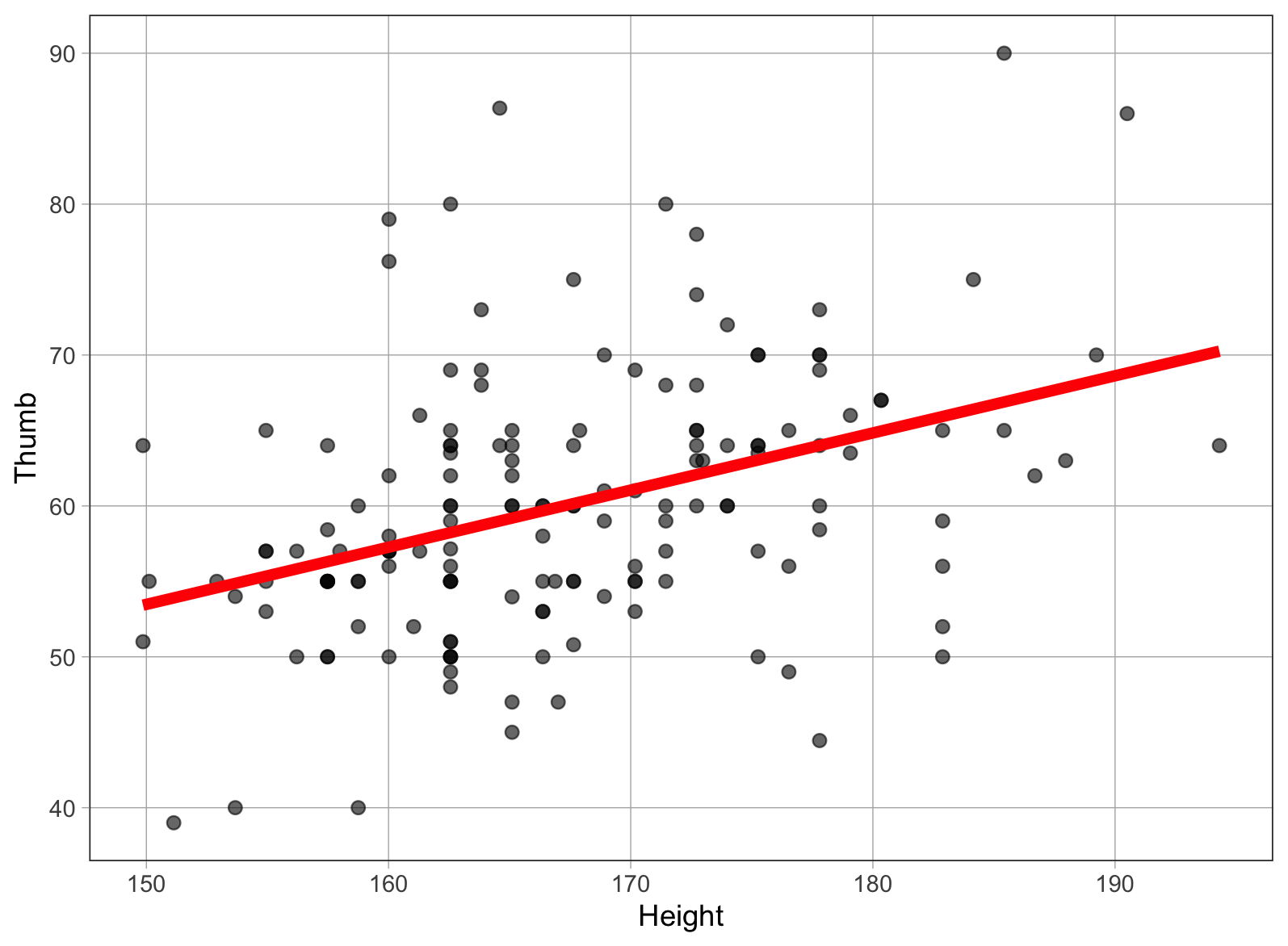
Θα δούμε στη συνέχεια πώς να προσαρμόζουμε ένα μοντέλο παλινδρόμησης με την R — δηλαδή πώς να βρίσκουμε τη μοναδική αυτή ευθεία που περιγράφει με τον καλύτερο δυνατό τρόπο τη σχέση μεταξύ δύο μεταβλητών. Πριν το κάνουμε αυτό, αξίζει να τονίσουμε ότι η ευθεία παλινδρόμησης δεν είναι μια τυχαία ευθεία, όπως ακριβώς ο μέσος όρος δεν είναι ένας τυχαίος αριθμός.

Όπως οι μέσοι όροι των ομάδων είναι εκείνες οι τιμές που ελαχιστοποιούν το άθροισμα τετραγώνων των υπολοίπων σε ένα μοντέλο ομάδων, έτσι και η ευθεία παλινδρόμησης είναι η μοναδική ευθεία — ορισμένη από την κλίση της και το σημείο τομής της με τον άξονα y — για την οποία τα υπόλοιπα είναι ισορροπημένα και το άθροισμα τετραγώνων των υπολοίπων ελαχιστοποιείται.

Ας δούμε πιο αναλυτικά τι σημαίνει αυτό.

Προβλέψεις από το Μοντέλο της `Height`

Για να προσαρμόσουμε το μοντέλο παλινδρόμησης με ανεξάρτητη μεταβλητή το ύψος (Height) θα χρησιμοποιήσουμε τη συνάρτηση lm() με τον ίδιο τρόπο όπως και στα μοντέλα ομάδων. Δεν χρειάζεται να δηλώσουμε στη R ότι πρόκειται για μοντέλο παλινδρόμησης — θα το αναγνωρίσει αυτόματα, επειδή η ανεξάρτητη μεταβλητή είναι ποσοτική.

Δίνεται παρακάτω η εντολή για την προσαρμογή του μοντέλου δύο ομάδων με την Height2Group ως ανεξάρτητη μεταβλητή:

lm(Thumb ~ Height2Group, data = Fingers)

Πώς θα την τροποποιήσουμε αν θέλουμε να χρησιμοποιήσουμε την Height αντί της Height2Group για να εξηγήσουμε τη μεταβλητότητα στην Thumb;

lm(Height ~ Height2Group, data = Fingers)lm(Thumb ~ Height, data = Fingers)lm(Thumb ~ Height2Group, data = Height)lm(Height ~ Thumb, data = Fingers)

Επεξήγηση

Σωστή απάντηση: Β - lm(Thumb ~ Height, data = Fingers)

Δομή της συνάρτησης lm():

lm(Y ~ X, data = dataset)

Όπου:

Y = Εξαρτημένη μεταβλητή
X = Ανεξάρτητη μεταβλητή
dataset = Το όνομα του πλαισίου δεδομένων

Η σύνταξη διαβάζεται ως:

«Μοντελοποίησε την Y ως συνάρτηση της X χρησιμοποιώντας δεδομένα από το dataset.»

Τι αλλάζει στο ερώτημα;

Αρχικό μοντέλο:

lm(Thumb ~ Height2Group, data = Fingers)

Εξαρτημένη (Y): Thumb (μήκος αντίχειρα)
Ανεξάρτητη (X): Height2Group (ποιοτική: short/tall)
Πλαίσιο δεδομένων: Fingers

Νέο μοντέλο (ζητούμενο):

lm(Thumb ~ Height, data = Fingers)

Εξαρτημένη (Y): Thumb (ίδια! ✓)
Ανεξάρτητη (X): Height (ποσοτική/συνεχής μεταβλητή)
Δεδομένα: Fingers (ίδιο! ✓)

Τι αλλάζει: Μόνο η ανεξάρτητη μεταβλητή (από Height2Group σε Height)

Τι παραμένει ίδιο: - Η εξαρτημένη μεταβλητή (Thumb)

Το πλαίσιο δεδομένων (Fingers)

Διαφορά μεταξύ Height2Group και Height

Height2Group (ποιοτική μεταβλητή):

Τύπος: Factor με 2 επίπεδα (short, tall)
Μοντέλο: $\text{Thumb}_i = b_0 + b_1 \times \text{Height2Group}_{\text{tall},i}$
Ερμηνεία: Διαφορά μέσων όρων μεταξύ ομάδων

Height (ποσοτική μεταβλητή):

Τύπος: Αριθμητική μεταβλητή (numeric)
Τιμές: Ύψος σε cm (π.χ., 165, 170, 175, …)
Μοντέλο: $\text{Thumb}_i = b_0 + b_1 \times \text{Height}_i$

Γιατί οι άλλες είναι λάθος;

Α. lm(Height ~ Height2Group, data = Fingers) - ΛΑΘΟΣ

Αυτό αντιστρέφει την εξαρτημένη και ανεξάρτητη μεταβλητή
Μοντελοποιεί την Height (ύψος) ως εξαρτημένη
Χρησιμοποιεί την Height2Group ως ανεξάρτητη

Τι μοντελοποιεί:

«Πρόβλεψη του ύψους από την ομάδα ύψους»

Το ζητούμενο:

«Πρόβλεψη του μήκους αντίχειρα από το ύψος»

Σύγκριση:

Στοιχείο	Επιλογή Α	Ζητούμενο
Εξαρτημένη (Y)	Height ✗	Thumb ✓
Ανεξάρτητη (X)	Height2Group	Height
Πλαίσιο δεδομένων	Fingers ✓	Fingers ✓

Γ. lm(Thumb ~ Height2Group, data = Height) - ΛΑΘΟΣ

Αυτό αλλάζει το πλαίσιο δεδομένων από Fingers σε Height
Το Height δεν είναι πλαίσιο δεδομένων - είναι μεταβλητή!
Θα προκαλέσει σφάλμα στην R:

lm(Thumb ~ Height2Group, data = Height)
# Error: object 'Height' not found
# (Εκτός αν υπάρχει πλαίσιο δεδομένων με όνομα "Height")

Σύγχυση:

Height (μεταβλητή) ≠ Fingers (πλαίσιο δεδομένων)
Το data = χρειάζεται το όνομα του πλαισίου δεδομένων, όχι μεταβλητής

Δ. lm(Height ~ Thumb, data = Fingers) - ΛΑΘΟΣ

Αυτό αντιστρέφει πλήρως το μοντέλο
Μοντελοποιεί την Height ως εξαρτημένη
Χρησιμοποιεί την Thumb ως ανεξάρτητη

Τι μοντελοποιεί:

«Πρόβλεψη του ύψους από το μήκος αντίχειρα»

Το ζητούμενο:

«Πρόβλεψη του μήκους αντίχειρα από το ύψος»

Σύγκριση:

Στοιχείο	Επιλογή Δ	Ζητούμενο
Εξαρτημένη (Y)	Height ✗	Thumb ✓
Ανεξάρτητη (X)	Thumb ✗	Height ✓
Πλαίσιο δεδομένων	Fingers ✓	Fingers ✓

Συμπέρασμα

Για να αλλάξουμε από Height2Group σε Height:

Αντικαθιστούμε μόνο την ανεξάρτητη μεταβλητή (δεξιά του ~)

Σωστή απάντηση:

lm(Thumb ~ Height, data = Fingers)

Γιατί:

✓ Η Thumb παραμένει η εξαρτημένη - αυτό που προβλέπουμε

✓ Η Height γίνεται η νέα ανεξάρτητη - αντί για την Height2Group

✓ Το Fingers παραμένει το σύνολο δεδομένων

Χρησιμοποιήστε το παρακάτω πλαίσιο κώδικα για να προσαρμόσετε το μοντέλο της Height με τη συνάρτηση lm() και αποθηκεύστε το αποτέλεσμα σε ένα αντικείμενο με όνομα Height_model. Έπειτα, προσθέστε κώδικα που θα δημιουργεί τις τιμές πρόβλεψης του μοντέλου και θα τις αποθηκεύει ως νέα στήλη στο πλαίσιο δεδομένων Fingers. (Υπόδειξη: χρησιμοποιήστε τη συνάρτηση predict() για να δημιουργήσετε τις προβλέψεις.)

  Thumb  Height Height_predict
1 66.00 179.070       64.48330
2 64.00 164.592       59.00056
3 56.00 162.560       58.23105
4 58.42 177.800       64.00235
5 74.00 172.720       62.07859
6 60.00 172.720       62.07859

Ας εξετάσουμε τις τιμές πρόβλεψης του μοντέλου της Height (παραπάνω).

Με ποιον τρόπο αυτές οι τιμές πρόβλεψης διαφέρουν από τις τιμές πρόβλεψης που παράγει το μοντέλο της Height2Group;

Εκτελέσαμε τον παρακάτω κώδικα για να προβάλλουμε στο αρχικό διάγραμμα διασποράς τις τιμές πρόβλεψης του μοντέλου της Height. Οι τιμές πρόβλεψης εμφανίζονται με κόκκινους κύκλους, κάτι που επιτύχαμε προσθέτοντας τα κατάλληλα ορίσματα για το σχήμα και το χρώμα στη συνάρτηση gf_point().

Fingers$prediction <- predict(Height_model)
gf_point(Thumb ~ Height, data = Fingers) %>%
gf_point(prediction ~ Height, shape = 1, size = 3, color = "firebrick")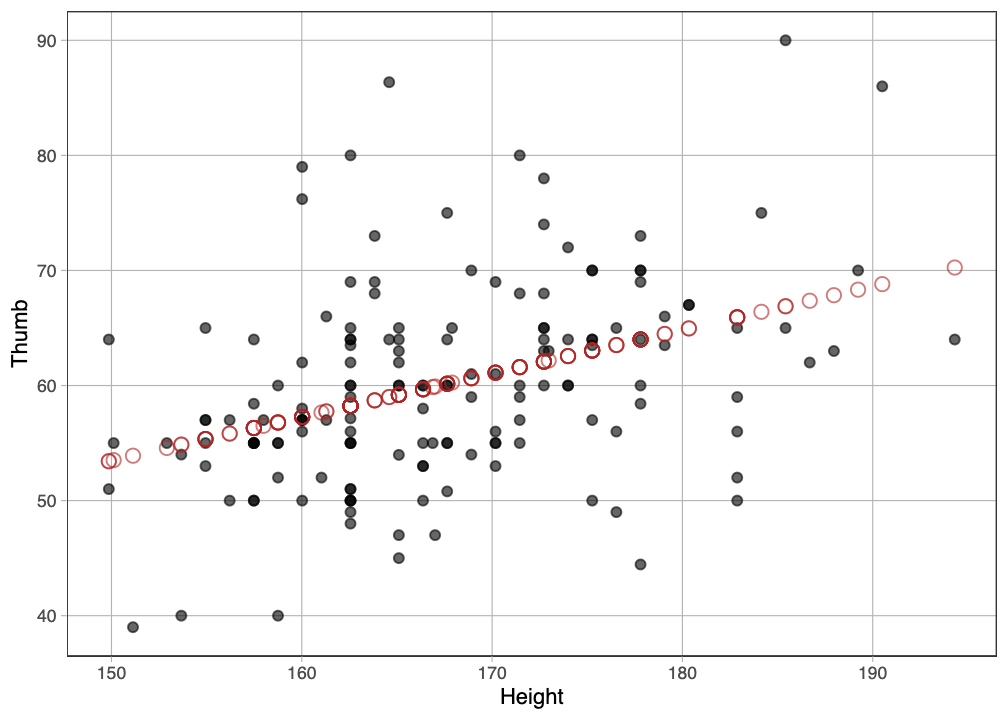

Κάθε τιμή της μεταβλητής Height (π.χ. 162.56, 172.72, 177.8) στο σύνολο δεδομένων αντιστοιχεί σε μια μοναδική τιμή πρόβλεψης του μοντέλου — που αναπαρίσταται με κόκκινο κύκλο. Παρατηρήστε ότι όλες οι προβλέψεις σχηματίζουν μια ευθεία γραμμή. Αυτό δεν είναι τυχαίο! Συμβαίνει επειδή οι προβλέψεις προέρχονται από την ευθεία παλινδρόμησης που προσαρμόστηκε στα δεδομένα μέσω της lm().

Αν προσθέσουμε τη συνάρτηση gf_model() στο διάγραμμα διασποράς, η καλύτερα προσαρμοσμένη ευθεία του μοντέλου θα συμπέσει ακριβώς με τις τιμές πρόβλεψης (τους κόκκινους κύκλους).

gf_point(Thumb ~ Height, data = Fingers) %>%
gf_point(prediction ~ Height, shape = 1, size = 3, color = "firebrick") %>%
gf_model(Height_model, color = "red")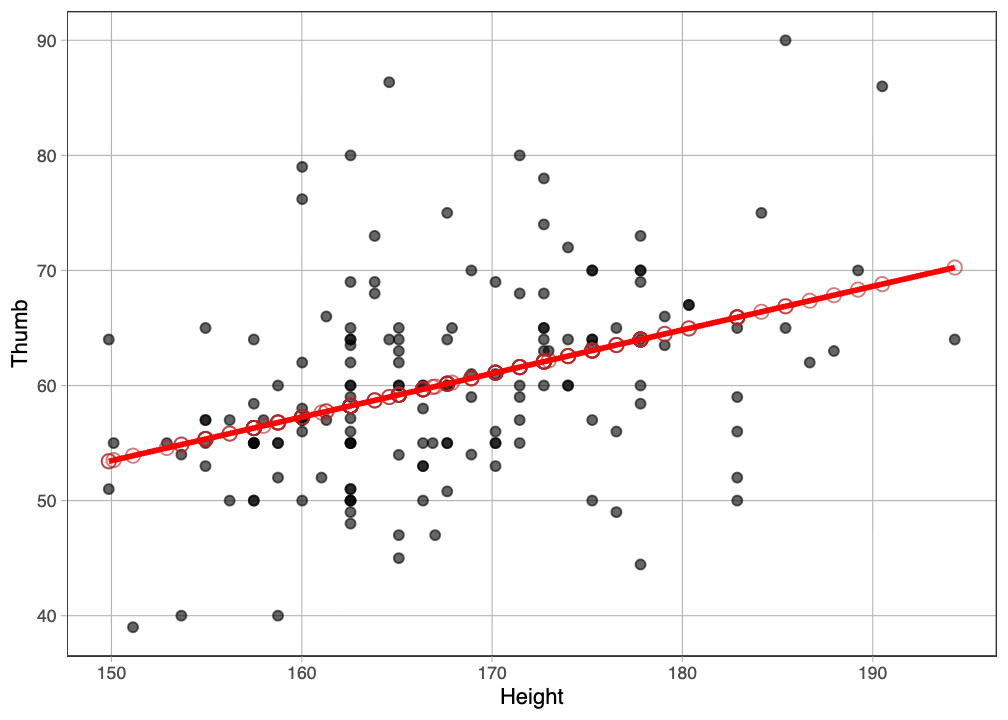

Σημειώστε ότι υπάρχουν δύο βασικοί τρόποι για να προβάλετε ένα μοντέλο παλινδρόμησης σε ένα διάγραμμα διασποράς. Ο πρώτος τρόπος είναι με τη χρήση της συνάρτησης gf_model(), η οποία απαιτεί να καθορίσουμε ρητά το μοντέλο που θέλουμε να εμφανίσουμε στο διάγραμμα (π.χ. gf_model(Height_model)). Το πλεονέκτημα της gf_model() είναι ότι μπορεί να χρησιμοποιηθεί τόσο για μοντέλα ομάδων όσο και για μοντέλα παλινδρόμησης.

Ο δεύτερος τρόπος είναι να προσθέσουμε τη συνάρτηση gf_lm() στο διάγραμμα διασποράς. Αυτή η συνάρτηση δεν χρειάζεται να της δοθεί κάποιο μοντέλο — το υπολογίζει αυτόματα με βάση τα δεδομένα του διαγράμματος. Ωστόσο, μπορεί να χρησιμοποιηθεί μόνο για μοντέλα παλινδρόμησης.

10.2 Προσδιορισμός του Μοντέλου της `Height` με τη Σημειογραφία του GLM

Ας δούμε πώς μπορούμε να περιγράψουμε ένα μοντέλο παλινδρόμησης όταν η ανεξάρτητη μεταβλητή είναι ποσοτική (όπως η Height):

\[Y_i = b_0 + b_1X_i + e_i\]

Μπορούμε τώρα να συγκρίνουμε αυτήν την εξίσωση με εκείνη που χρησιμοποιήσαμε στο προηγούμενο κεφάλαιο, όταν το μοντέλο αφορούσε δύο ομάδες (όπως στην περίπτωση της Height2Group):

\[Y_i = b_0 + b_1X_i + e_i\]

Ποια είναι η διαφορά στη σημειογραφία του GLM ανάμεσα σε αυτά τα δύο μοντέλα;

Παρατηρούμε ότι η εξίσωση είναι ίδια και στις δύο περιπτώσεις. Αυτή η ομοιότητα δεν είναι τυχαία· αποτελεί βασικό χαρακτηριστικό του Γενικού Γραμμικού Μοντέλου (General Linear Model).

Το GLM παρέχει ένα ενιαίο μαθηματικό πλαίσιο που μπορεί να περιγράψει τόσο μοντέλα με ποιοτικές ανεξάρτητες μεταβλητές (όπως ομάδες ή κατηγορίες) όσο και μοντέλα με ποσοτικές μεταβλητές (όπως μετρήσεις ή τιμές). Αυτό το καθιστά ένα ευέλικτο και ισχυρό εργαλείο για την ανάλυση δεδομένων σε πολλές διαφορετικές περιπτώσεις.

Αν και και τα δύο μοντέλα εκφράζονται με την ίδια εξίσωση, η ερμηνεία της διαφέρει ανάλογα με το είδος της ανεξάρτητης μεταβλητής και το πλαίσιο στο οποίο εφαρμόζεται.

Όπως είδαμε, και τα δύο μοντέλα, Height2Group και Height, μπορούν να αναπαρασταθούν με την ίδια εξίσωση του GLM: $Y_i = b_0 + b_1X_i + e_i$.

Ποιο μέρος της εξίσωσης αντιπροσωπεύει την εξαρτημένη μεταβλητή (Thumb) και στα δύο μοντέλα;

$Y_i$$X_i$$e_i$

Επεξήγηση

Σωστή απάντηση: Α — Το $Y_i$ αντιπροσωπεύει την εξαρτημένη μεταβλητή και στα δύο μοντέλα.

Ανάλυση της σημειογραφίας του GLM

Στο Γενικό Γραμμικό Μοντέλο (GLM), η εξίσωση $Y_i = b_0 + b_1X_i + e_i$ περιλαμβάνει τα εξής στοιχεία:

$Y_i$: Η εξαρτημένη μεταβλητή — αυτό που προσπαθούμε να προβλέψουμε ή να εξηγήσουμε
$X_i$: Η ανεξάρτητη μεταβλητή — αυτό που χρησιμοποιούμε για την πρόβλεψη
$b_0$: Ο σταθερός όρος (intercept) — η τιμή του $Y_i$ όταν $X_i = 0$
$b_1$: Ο συντελεστής κλίσης (slope) — η μεταβολή στο $Y_i$ για κάθε μονάδα αύξησης του $X_i$
$e_i$: Το σφάλμα — η διαφορά μεταξύ της παρατηρούμενης τιμής και της τιμής πρόβλεψης

Εφαρμογή στα δύο μοντέλα

Και στα δύο μοντέλα (Height2Group και Height), η μεταβλητή Thumb είναι η εξαρτημένη μεταβλητή:

Μοντέλο της Height2Group: Προβλέπουμε το μήκος αντίχειρα ($Y_i$) με βάση την ομάδα ύψους (short/tall)
Μοντέλο της Height: Προβλέπουμε το μήκος αντίχειρα ($Y_i$) με βάση το συνεχές ύψος

Και στις δύο περιπτώσεις, η Thumb αναπαρίσταται από το $Y_i$ στην εξίσωση.

Γιατί οι άλλες επιλογές είναι λάθος

Β. «$X_i$» — ΛΑΘΟΣ

Το $X_i$ αντιπροσωπεύει την ανεξάρτητη μεταβλητή.
Στο μοντέλο της Height2Group, το $X_i$ είναι η ομάδα ύψους (short/tall).
Στο μοντέλο της Height, το $X_i$ είναι το συνεχές ύψος.
Δεν είναι η εξαρτημένη μεταβλητή που προσπαθούμε να προβλέψουμε.

Γ. «$e_i$» — ΛΑΘΟΣ

Το $e_i$ αντιπροσωπεύει το σφάλμα ή το υπόλοιπο (residual).
Είναι η διαφορά μεταξύ της πραγματικής τιμής της Thumb και της τιμής πρόβλεψης από το μοντέλο.
Δηλαδή: $e_i = Y_i - \hat{Y}_i$ (παρατηρούμενη τιμή μείον τιμή πρόβλεψης).
Δεν είναι η εξαρτημένη μεταβλητή αλλά η απόκλιση από την πρόβλεψη.

Συμπέρασμα

Το $Y_i$ είναι πάντα η εξαρτημένη μεταβλητή σε ένα GLM.
Στα δύο μοντέλα, το $Y_i$ αντιπροσωπεύει το μήκος του αντίχειρα για κάθε παρατήρηση $i$.
Το $X_i$ είναι η ανεξάρτητη μεταβλητή (Height ή Height2Group).
Το $e_i$ είναι το σφάλμα πρόβλεψης.

Συνοπτικά: Το $Y_i$ αναπαριστά την εξαρτημένη μεταβλητή (Thumb) και στα δύο μοντέλα. Είναι η μεταβλητή που προσπαθούμε να προβλέψουμε χρησιμοποιώντας τις ανεξάρτητες μεταβλητές.

Ποιο μέρος της εξίσωσης αντιπροσωπεύει το σφάλμα (που ονομάζεται και υπόλοιπο) και στα δύο μοντέλα;

$Y_i$$X_i$$e_i$

Επεξήγηση

Σωστή απάντηση: Γ — Το $e_i$ αντιπροσωπεύει το σφάλμα ή το υπόλοιπο (residual) και στα δύο μοντέλα.

Τι είναι το $e_i$

Στο Γενικό Γραμμικό Μοντέλο (GLM), το $e_i$ αντιπροσωπεύει:

Το σφάλμα πρόβλεψης
Το υπόλοιπο ή κατάλοιπο
Τη διαφορά μεταξύ της πραγματικής τιμής και της τιμής πρόβλεψης

Γιατί υπάρχει το σφάλμα $e_i$

Το μοντέλο δεν μπορεί να προβλέψει τέλεια τις τιμές της εξαρτημένης μεταβλητής επειδή:

Υπάρχει φυσική μεταβλητότητα στα δεδομένα
Άλλοι παράγοντες (που δεν περιλαμβάνονται στο μοντέλο) επηρεάζουν το αποτέλεσμα
Υπάρχει σφάλμα μέτρησης

Για παράδειγμα, στο μοντέλο πρόβλεψης της Thumb:

Δύο άτομα με το ίδιο ύψος μπορεί να έχουν διαφορετικό μήκος αντίχειρα
Το $e_i$ καταγράφει αυτή τη διαφορά για κάθε παρατήρηση $i$

Παράδειγμα

Έστω ότι για ένα άτομο:

Πραγματικό μήκος αντίχειρα: $Y_i = 58$ mm
Τιμή πρόβλεψης του μήκους από το μοντέλο: $\hat{Y}_i = 60$ mm
Υπόλοιπο: $e_i = 58 - 60 = -2$ mm

Το αρνητικό υπόλοιπο σημαίνει ότι το μοντέλο υπερεκτίμησε το μήκος του αντίχειρα κατά 2 mm.

Γιατί οι άλλες επιλογές είναι λάθος

Α. «$Y_i$» — ΛΑΘΟΣ

Το $Y_i$ είναι η εξαρτημένη μεταβλητή.
Αντιπροσωπεύει την πραγματική, παρατηρούμενη τιμή του μήκους αντίχειρα.
Δεν είναι το σφάλμα αλλά η τιμή που προσπαθούμε να προβλέψουμε.

Β. «$X_i$» — ΛΑΘΟΣ

Το $X_i$ είναι η ανεξάρτητη μεταβλητή.
Αντιπροσωπεύει το ύψος (Height) ή την ομάδα ύψους (Height2Group).
Δεν είναι το σφάλμα αλλά η μεταβλητή που χρησιμοποιούμε για την πρόβλεψη.

Συμπέρασμα

Το $e_i$ αντιπροσωπεύει το σφάλμα ή το υπόλοιπο στο GLM.
Είναι η διαφορά μεταξύ της παρατηρούμενης τιμής $Y_i$ και της τιμής πρόβλεψης $\hat{Y}_i$.
Καταγράφει την απόκλιση των δεδομένων από τις προβλέψεις του μοντέλου.

Συνοπτικά: Το $e_i$ είναι το σφάλμα/υπόλοιπο που αντιπροσωπεύει τη διαφορά μεταξύ της πραγματικής τιμής και της τιμής πρόβλεψης. Δείχνει πόσο «αστοχεί» το μοντέλο για κάθε παρατήρηση.

Ποιο μέρος της εξίσωσης αντιπροσωπεύει την ανεξάρτητη μεταβλητή (είτε Height είτε Height2Group);

$Y_i$$X_i$$e_i$

Επεξήγηση

Σωστή απάντηση: Β — Το $X_i$ αντιπροσωπεύει την ανεξάρτητη μεταβλητή και στα δύο μοντέλα.

Τι είναι το $X_i$

Στο Γενικό Γραμμικό Μοντέλο (GLM), το $X_i$ αντιπροσωπεύει:

Την ανεξάρτητη μεταβλητή Είναι η μεταβλητή που χρησιμοποιούμε για να εξηγήσουμε ή να προβλέψουμε τις τιμές της εξαρτημένης μεταβλητής $Y_i$.

Εφαρμογή στα δύο μοντέλα

Και στα δύο μοντέλα, το $X_i$ αντιπροσωπεύει μια μεταβλητή που σχετίζεται με το ύψος:

1. Μοντέλο της Height:

$X_i$ = το ύψος του ατόμου $i$ σε εκατοστά (συνεχής μεταβλητή)
Παράδειγμα: $X_1 = 165$ cm, $X_2 = 180$ cm, κ.λπ.

2. Μοντέλο της Height2Group:

$X_i$ = ψευδομεταβλητή (dummy variable) για την ομάδα ύψους
$X_i = 0$ αν το άτομο ανήκει στην ομάδα short
$X_i = 1$ αν το άτομο ανήκει στην ομάδα tall

Πώς λειτουργεί το $X_i$ στο μοντέλο

Στην εξίσωση $Y_i = b_0 + b_1X_i + e_i$:

Το $X_i$ πολλαπλασιάζεται με τον συντελεστή $b_1$
Όσο μεγαλύτερη είναι η τιμή του $X_i$, τόσο περισσότερο επηρεάζει την πρόβλεψη του $Y_i$
Η σχέση μεταξύ $X_i$ και $Y_i$ καθορίζεται από το πρόσημο και το μέγεθος του $b_1$

Γιατί οι άλλες επιλογές είναι λάθος

Α. «$Y_i$» — ΛΑΘΟΣ

Το $Y_i$ είναι η εξαρτημένη μεταβλητή.
Αντιπροσωπεύει το μήκος του αντίχειρα.
Είναι αυτό που προσπαθούμε να εξηγήσουμε, όχι η ανεξάρτητη μεταβλητή.

Γ. «$e_i$» — ΛΑΘΟΣ

Το $e_i$ είναι το σφάλμα ή το υπόλοιπο.
Αντιπροσωπεύει τη διαφορά μεταξύ της παρατηρούμενης και της τιμής πρόβλεψης.
Δεν είναι ανεξάρτητη μεταβλητή αλλά η απόκλιση από το μοντέλο.

Συμπέρασμα

Το $X_i$ αντιπροσωπεύει την ανεξάρτητη μεταβλητή στο GLM.
Στο μοντέλο της Height, το $X_i$ είναι το συνεχές ύψος.
Στο μοντέλο της Height2Group, το $X_i$ είναι η ψευδομεταβλητή για την ομάδα ύψους.
Χρησιμοποιείται για να προβλέψουμε την εξαρτημένη μεταβλητή $Y_i$.

Συνοπτικά: Το $X_i$ είναι η ανεξάρτητη μεταβλητή που χρησιμοποιούμε για να προβλέψουμε το αποτέλεσμα. Στα δύο μοντέλα, το $X_i$ αντιπροσωπεύει το ύψος (είτε ως συνεχής μεταβλητή είτε ως ποιοτική).

Στο μοντέλο της Height2Group, η μεταβλητή είχε δυαδική (dummy) κωδικοποίηση, με τιμές 0 και 1. Η τιμή 1 δεν αντιπροσώπευε κάποια ποσότητα, αλλά υποδήλωνε απλώς αν το άτομο ανήκει στην ομάδα των «ψηλών» ή όχι. Αντίθετα, στο μοντέλο της Height, η μεταβλητή αντιστοιχεί στο πραγματικό μετρημένο ύψος του ατόμου (σε εκατοστά), και συνεπώς έχει ποσοτικό χαρακτήρα.

Αυτή η διαφορά στην κωδικοποίηση οδηγεί σε ελαφρώς διαφορετικές —αλλά στενά συνδεδεμένες— ερμηνείες του συντελεστή $b_1$.

Στο μοντέλο ομάδων (μοντέλο της Height2Group), ο συντελεστής $b_1$ αντιπροσωπεύει:

Τη μέση διαφορά μεταξύ των δύο ομάδωνΤην ποσότητα που προστίθεται στο $b_0$ για να πάρουμε το μέσο μήκος αντίχειρα των φοιτητών στην ομάδα tallΤην ποσότητα που προστίθεται στο $b_0$ όταν το $X_i$ είναι ίσο με 1

Επεξήγηση

Σωστή απάντηση: Όλα τα παραπάνω είναι σωστά.

Ανάλυση του μοντέλου ομάδων

Στο μοντέλο της Height2Group, η εξίσωση είναι:

\[Y_i = b_0 + b_1X_i + e_i\]

όπου:

$Y_i$ = μήκος αντίχειρα για το άτομο $i$
$X_i$ = ψευδομεταβλητή (dummy variable):
- $X_i = 0$ αν το άτομο ανήκει στην ομάδα short
- $X_i = 1$ αν το άτομο ανήκει στην ομάδα tall
$b_0$ = το μέσο μήκος αντίχειρα της ομάδας αναφοράς (short)
$b_1$ = ο συντελεστής που αντιπροσωπεύει τη διαφορά μεταξύ των ομάδων

Γιατί όλες οι απαντήσεις είναι σωστές

Α. «Η μέση διαφορά μεταξύ των δύο ομάδων» — ΣΩΣΤΟ ✓

Ο συντελεστής $b_1$ μετρά πόσο διαφέρει κατά μέσο όρο η ομάδα tall από την ομάδα short.

Για την ομάδα short ($X_i = 0$): \[\hat{Y}_i = b_0 + b_1 \times 0 = b_0\]

Για την ομάδα tall ($X_i = 1$): \[\hat{Y}_i = b_0 + b_1 \times 1 = b_0 + b_1\]

Διαφορά μεταξύ των ομάδων: \[(b_0 + b_1) - b_0 = b_1\]

Άρα, το $b_1$ είναι η μέση διαφορά μεταξύ των δύο ομάδων.

Β. «Η ποσότητα που προστίθεται στο $b_0$ για να πάρουμε το μέσο μήκος αντίχειρα της ομάδας των ψηλών φοιτητών» — ΣΩΣΤΟ ✓

Το $b_0$ είναι το μέσο μήκος αντίχειρα για την ομάδα short (ομάδα αναφοράς).

Για να υπολογίσουμε το μέσο μήκος αντίχειρα της ομάδας tall: \[\text{Μέσος αντίχειρας tall} = b_0 + b_1\]

Δηλαδή, προσθέτουμε το $b_1$ στο $b_0$ για να βρούμε το μέσο όρο της ομάδας των ψηλών.

Γ. «Η ποσότητα που προστίθεται όταν το $X_i$ είναι ίσο με 1» — ΣΩΣΤΟ ✓

Όταν $X_i = 1$ (δηλαδή το άτομο είναι ψηλό), η εξίσωση γίνεται: \[Y_i = b_0 + b_1 \times 1 + e_i = b_0 + b_1 + e_i\]

Το $b_1$ είναι η ποσότητα που προστίθεται στην πρόβλεψη όταν η ψευδομεταβλητή $X_i$ έχει τιμή 1.

Παράδειγμα με αριθμούς

Έστω ότι το μοντέλο είναι: \[Y_i = 57 + 3X_i + e_i\]

όπου:

$b_0 = 57$ mm (μέσο μήκος αντίχειρα για short)
$b_1 = 3$ mm (διαφορά μεταξύ tall και short)

Για άτομο στην short ($X_i = 0$): \[\hat{Y}_i = 57 + 3 \times 0 = 57 \text{ mm}\]

Για άτομο στην tall ($X_i = 1$): \[\hat{Y}_i = 57 + 3 \times 1 = 60 \text{ mm}\]

Παρατηρούμε ότι:

Η διαφορά μεταξύ των ομάδων είναι: $60 - 57 = 3$ mm ✓
Προσθέσαμε $b_1 = 3$ στο $b_0 = 57$ για να πάρουμε το 60 mm ✓
Όταν $X_i = 1$, προσθέτουμε την ποσότητα $b_1 = 3$ ✓

Ερμηνεία του $b_1$

Σε ένα μοντέλο με ψευδομεταβλητή, ο συντελεστής $b_1$ έχει τριπλή ερμηνεία:

Διαφορά μέσων όρων: Πόσο διαφέρουν οι δύο ομάδες κατά μέσο όρο
Ποσότητα που προστίθεται στο intercept: Τι προστίθεται στο $b_0$ για την άλλη ομάδα
Επίδραση της μεταβλητής: Τι συμβαίνει όταν $X_i$ αλλάζει από 0 σε 1

Και οι τρεις ερμηνείες είναι ισοδύναμες και σωστές.

Γενίκευση

Για οποιοδήποτε μοντέλο με ψευδομεταβλητή:

Το $b_0$ = μέσος όρος της ομάδας αναφοράς ($X_i = 0$)
Το $b_1$ = μέση διαφορά από την ομάδα αναφοράς
Το $b_0 + b_1$ = μέσος όρος της άλλης ομάδας ($X_i = 1$)

Συμπέρασμα

Ο συντελεστής $b_1$ στο μοντέλο ομάδων:

Αντιπροσωπεύει τη μέση διαφορά μεταξύ των δύο ομάδων
Είναι η ποσότητα που προστίθεται στο $b_0$ για την ομάδα tall
Ενεργοποιείται όταν $X_i = 1$ (άτομο στην ομάδα tall)

Και οι τρεις περιγραφές εκφράζουν την ίδια ιδέα με διαφορετικό τρόπο.

Συνοπτικά: Ο συντελεστής $b_1$ σε ένα μοντέλο με ψευδομεταβλητή μπορεί να ερμηνευτεί με τρεις ισοδύναμους τρόπους: ως η διαφορά μέσων όρων, ως η ποσότητα που προστίθεται στον σταθερό όρο, και ως η επίδραση όταν $X_i = 1$. Όλες οι απαντήσεις είναι σωστές!

Στο μοντέλο ομάδων (της Height2Group), το $b_1$ ήταν η ποσότητα κατά την οποία αλλάζει η τιμή πρόβλεψης του μήκους αντίχειρα όταν η Height2Grouptall αυξάνεται κατά 1 (δηλαδή, πηγαίνει από 0 σε 1). Τι νομίζετε ότι είναι το $b_1$ στο μοντέλο παλινδρόμησης (της Height);

Η τιμή πρόβλεψης του μήκους αντίχειρα όταν το ύψος = 1Η ποσότητα που προστίθεται στην τιμή πρόβλεψης του μήκους αντίχειρα όταν το ύψος αυξάνεται κατά 1 μονάδαΗ ποσότητα που πρέπει να αλλάξει η τιμή πρόβλεψης του μήκους αντίχειρα όταν η ομάδα ύψους αυξάνεται κατά 1

Επεξήγηση

Σωστή απάντηση: Β — Η ποσότητα που προστίθεται στην τιμή πρόβλεψης του μήκους αντίχειρα όταν το ύψος αυξάνεται κατά 1 μονάδα.

Αναλογία μεταξύ των μοντέλων

Και στα δύο μοντέλα, ο συντελεστής $b_1$ αντιπροσωπεύει την αλλαγή στο $Y_i$ όταν το $X_i$ αυξάνεται κατά 1 μονάδα.

Μοντέλο της Height2Group (ποιοτική μεταβλητή):

\[Y_i = b_0 + b_1X_i + e_i\]

$X_i$ = 0 (short) ή 1 (tall)
Όταν το $X_i$ αυξάνεται από 0 σε 1 (αλλαγή κατά 1 μονάδα):
- Πηγαίνουμε από την ομάδα short στην ομάδα tall
- Η πρόβλεψη αλλάζει κατά $b_1$

Μοντέλο της Height (συνεχής μεταβλητή):

\[Y_i = b_0 + b_1X_i + e_i\]

$X_i$ = ύψος σε εκατοστά (π.χ., 160, 165, 170, …)
Όταν το $X_i$ αυξάνεται κατά 1 μονάδα (π.χ. από 170 σε 171 cm):
- Το ύψος αυξάνεται κατά 1 εκατοστό
- Η πρόβλεψη αλλάζει κατά $b_1$

Η έννοια της κλίσης της ευθείας (slope)

Το $b_1$ είναι ο συντελεστής διεύθυνσης ή η κλίση της ευθείας και δείχνει:

\[b_1 = \frac{\text{Αλλαγή στο } Y}{\text{Αλλαγή στο } X} = \frac{\Delta Y}{\Delta X}\]

Για μεταβολή 1 μονάδας στην $X$: \[b_1 = \frac{\Delta Y}{1} = \Delta Y\]

Δηλαδή, το $b_1$ είναι η μεταβολή στην $Y$ όταν η $X$ αλλάζει κατά 1 μονάδα.

Παράδειγμα με αριθμούς

Έστω ότι το μοντέλο της Height είναι: \[Y_i = 20 + 0.25X_i + e_i\]

όπου:

$b_0 = 20$ mm
$b_1 = 0.25$ mm/cm

Για άτομο με ύψος 170 cm: \[\hat{Y}_i = 20 + 0.25 \times 170 = 20 + 42.5 = 62.5 \text{ mm}\]

Για άτομο με ύψος 171 cm (αύξηση κατά 1 cm): \[\hat{Y}_i = 20 + 0.25 \times 171 = 20 + 42.75 = 62.75 \text{ mm}\]

Αλλαγή στην πρόβλεψη: \[62.75 - 62.5 = 0.25 \text{ mm}\]

Άρα, όταν το ύψος αυξάνεται κατά 1 cm, η τιμή πρόβλεψης του μήκους αντίχειρα αυξάνεται κατά $b_1 = 0.25$ mm.

Γιατί οι άλλες επιλογές είναι λάθος

Α. «Η τιμή πρόβλεψης του μήκους αντίχειρα όταν το ύψος = 1» — ΛΑΘΟΣ

Αυτό περιγράφει το $b_0 + b_1 \times 1$, όχι απλώς το $b_1$.
Η τιμή πρόβλεψης του μήκους όταν $X_i = 1$ θα ήταν: $\hat{Y}_i = b_0 + b_1$
Επιπλέον, ύψος = 1 cm δεν έχει νόημα στο πλαίσιο του προβλήματος.
Το $b_1$ μόνο του δεν είναι μια πρόβλεψη αλλά μια μεταβολή.

Γ. «Η ποσότητα που πρέπει να αλλάξει η τιμή πρόβλεψης όταν η ομάδα ύψους αυξάνεται κατά 1» — ΛΑΘΟΣ

Αυτό ισχύει για το μοντέλο της Height2Group, όχι για το μοντέλο της Height.
Στο μοντέλο της Height, δεν υπάρχουν ομάδες — το ύψος είναι συνεχής μεταβλητή.
Η ερώτηση ζητά την ερμηνεία του $b_1$ στο μοντέλο της Height, όχι σε αυτό της Height2Group.

Σύγκριση των μοντέλων

Μοντέλο	Τύπος $X_i$	Ερμηνεία του $b_1$
`Height2Group`	Ψευδομεταβλητή (0/1)	Διαφορά μέσων όρων μεταξύ `tall` και `short`
`Height`	Συνεχής (cm)	Αλλαγή στο μήκος αντίχειρα ανά 1 cm αύξησης ύψους

Και στις δύο περιπτώσεις, το $b_1$ είναι η αλλαγή στο $Y$ όταν το $X$ αυξάνεται κατά 1.

Γενική αρχή

Σε οποιοδήποτε γραμμικό μοντέλο $Y_i = b_0 + b_1X_i + e_i$:

Το $b_0$ (σταθερός όρος) = η τιμή του $Y$ όταν $X = 0$
Το $b_1$ (κλίση) = η αλλαγή στο $Y$ όταν το $X$ αυξάνεται κατά 1

Αυτός ο κανόνας ισχύει ανεξάρτητα από το αν το $X$ είναι:

Ποιοτική μεταβλητή (ψευδομεταβλητή)
Ποσοτική Συνεχής μεταβλητή
Ποσοτική Διακριτή μεταβλητή

Συμπέρασμα

Στο μοντέλο της Height:

Το $b_1$ είναι η κλίση (slope) της ευθείας παλινδρόμησης
Αντιπροσωπεύει την αλλαγή στην τιμή πρόβλεψης του μήκους αντίχειρα όταν το ύψος αυξάνεται κατά 1 cm
Μας λέει πόσο αυξάνεται (ή μειώνεται αν $b_1 < 0$) ο αντίχειρας για κάθε επιπλέον εκατοστό ύψους

Συνοπτικά: Κατ’ αναλογία, όπως το $b_1$ στο μοντέλο της Height2Group δείχνει την αλλαγή όταν πηγαίνουμε από short σε tall (αλλαγή κατά 1 στο $X$), έτσι και στο μοντέλο της Height το $b_1$ δείχνει την αλλαγή όταν το ύψος αυξάνεται κατά 1 cm. Είναι η ποσότητα που προστίθεται στην τιμή πρόβλεψης ανά μονάδα αύξησης του ύψους.

Στο μοντέλο παλινδρόμησης, ο συντελεστής $b_1$ εξακολουθεί να εκφράζει μια ποσότητα που προστίθεται στον σταθερό όρο $b_0$. Πιο συγκεκριμένα, αντιπροσωπεύει τη μεταβολή που αναμένεται στη εξαρτημένη μεταβλητή για κάθε αύξηση κατά μία μονάδα της ανεξάρτητης μεταβλητής Height. Αυτός είναι ουσιαστικά ο ορισμός της κλίσης μιας ευθείας: το μέγεθος της «κατακόρυφης μεταβολής» που αντιστοιχεί σε κάθε μονάδα «οριζόντιας μεταβολής». Με άλλα λόγια, ο συντελεστής $b_1$ δείχνει πόσο αλλάζει η τιμή της Thumb για κάθε επιπλέον εκατοστό ύψους. (Σημειώστε ότι η μεταβολή αυτή μπορεί να είναι και αρνητική, αν το $b_1$ είναι αρνητικό.)

Ο συντελεστής $b_1$, λοιπόν, είναι η κλίση της ευθείας παλινδρόμησης που προσαρμόζεται καλύτερα στα δεδομένα.

Και στα δύο μοντέλα, ο συντελεστής $b_0$ αντιπροσωπεύει το σημείο τομής (intercept), δηλαδή την τιμή πρόβλεψης της εξαρτημένης μεταβλητής όταν η ανεξάρτητη μεταβλητή είναι μηδέν.

Ωστόσο, η ερμηνεία του διαφέρει:

Στο μοντέλο της Height2Group, το Height2Group = 0 σημαίνει ότι το άτομο ανήκει στην ομάδα των φοιτητών χαμηλού αναστήματος (short), δηλαδή στην ομάδα αναφοράς.
Στο μοντέλο της Height, το Height = 0 θα σήμαινε κυριολεκτικά ότι το άτομο έχει ύψος 0 εκατοστά — κάτι που προφανώς δεν έχει νόημα στην πράξη. Παρ’ όλα αυτά, το μοντέλο μπορεί μαθηματικά να υπολογίσει τιμή πρόβλεψης ακόμη και για μια τέτοια υποθετική περίπτωση.

Τι θα προέβλεπε αυτό το μοντέλο για ένα άτομο που έχει ύψος 0;

$b_0$$b_1$$b_0 + b_1$

Επεξήγηση

Σωστή απάντηση: Α — Το μοντέλο θα προέβλεπε την τιμή του $b_0$ για ένα άτομο με ύψος 0.

Ανάλυση της πρόβλεψης

Το γραμμικό μοντέλο είναι:

\[Y_i = b_0 + b_1X_i + e_i\]

Για να βρούμε την τιμή πρόβλεψης, χρησιμοποιούμε την εξίσωση χωρίς το σφάλμα:

\[\hat{Y}_i = b_0 + b_1X_i\]

Όταν το ύψος είναι 0 (δηλαδή $X_i = 0$):

\[\hat{Y}_i = b_0 + b_1 \times 0 = b_0 + 0 = b_0\]

Άρα, η πρόβλεψη του μοντέλου είναι απλώς ο σταθερός όρος $b_0$.

Τι είναι ο σταθερός όρος ($b_0$)

Το $b_0$ είναι το σημείο τομής (intercept) και αντιπροσωπεύει:

Την τιμή πρόβλεψης της $Y$ όταν όλες οι ανεξάρτητες μεταβλητές είναι 0
Το σημείο όπου η ευθεία παλινδρόμησης τέμνει τον κατακόρυφο άξονα (άξονας y)
Το “σημείο εκκίνησης” της πρόβλεψης πριν προσθέσουμε την επίδραση της $X$

Γεωμετρική ερμηνεία

Σε ένα διάγραμμα διασποράς με γραμμή παλινδρόμησης:

Ο οριζόντιος άξονας (X) είναι το ύψος
Ο κατακόρυφος άξονας (Y) είναι το μήκος αντίχειρα
Η ευθεία παλινδρόμησης τέμνει τον άξονα Y στο σημείο $(0, b_0)$
Όταν $X = 0$, είμαστε ακριβώς σε αυτό το σημείο, άρα $Y = b_0$

Παράδειγμα με αριθμούς

Έστω ότι το μοντέλο είναι: \[Y_i = 25 + 0.20X_i + e_i\]

όπου:

$b_0 = 25$ mm
$b_1 = 0.20$ mm/cm

Για άτομο με ύψος $X_i = 0$ cm: \[\hat{Y}_i = 25 + 0.20 \times 0 = 25 \text{ mm}\]

Για άτομο με ύψος $X_i = 170$ cm: \[\hat{Y}_i = 25 + 0.20 \times 170 = 25 + 34 = 59 \text{ mm}\]

Βλέπουμε ότι όταν $X = 0$, η πρόβλεψη είναι απλώς ο σταθερός όρος.

Γιατί οι άλλες επιλογές είναι λάθος

Β. «$b_1$» — ΛΑΘΟΣ

Το $b_1$ είναι ο συντελεστής κλίσης της ευθείας (slope), όχι η πρόβλεψη.
Δείχνει πόσο αλλάζει η $Y$ όταν η $X$ αυξάνεται κατά 1.
Δεν είναι η τιμή της $Y$ όταν $X = 0$. Γ. «$b_0 + b_1$» — ΛΑΘΟΣ
Αυτή η έκφραση θα ήταν η πρόβλεψη αν $X_i = 1$, όχι $X_i = 0$.
Όταν $X_i = 1$: $\hat{Y}_i = b_0 + b_1 \times 1 = b_0 + b_1$
Αλλά εδώ η ερώτηση είναι για $X_i = 0$, όχι για $X_i = 1$.
Επιπλέον, η πρόσθεση $b_0 + b_1$ δεν έχει νόημα γιατί οι δύο μεταβλητές έχουν διαφορετικές μονάδες.

Συμπέρασμα

Όταν $X_i = 0$, η πρόβλεψη του μοντέλου είναι ο σταθερός όρος $b_0$.
Αυτό ισχύει για κάθε γραμμικό μοντέλο της μορφής $Y = b_0 + b_1X$.
Το $b_0$ είναι η βασική τιμή πρόβλεψης πριν προσθέσουμε την επίδραση της ανεξάρτητης μεταβλητής.

Συνοπτικά: Όταν το ύψος είναι 0 ($X_i = 0$), η εξίσωση γίνεται $\hat{Y}_i = b_0 + b_1 \times 0 = b_0$. Ο σταθερός όρος $b_0$ είναι η πρόβλεψη του μοντέλου όταν η ανεξάρτητη μεταβλητή είναι μηδέν.

Σχέση με την Άλγεβρα

Στην άλγεβρα, μια ευθεία περιγράφεται συνήθως από την εξίσωση:

$y = \alpha x+\beta$

όπου το $\alpha$ είναι η κλίση και το $\beta$ είναι η τομή με τον άξονα $y$.

Στη στατιστική, χρησιμοποιούμε την ίδια βασική εξίσωση, αλλά αλλάζουμε λίγο τη μορφή της, ώστε ο σταθερός όρος να εμφανίζεται πρώτος $y = \beta + \alpha x$, και χρησιμοποιούμε διαφορετικά γράμματα για να αναπαραστήσουμε το σταθερό όρο και την κλίση ($b_0$ και $b_1$, αντίστοιχα).

Παρατηρήστε ότι υπάρχει ομοιότητα μεταξύ της εξίσωσης του GLM και της εξίσωσης μιας ευθείας:

\[Y_i = b_0 + b_1X_i + e_i \text{ έναντι } y = αx + β\]

1. Ποιο μέρος της εξίσωσης του GLM αντιστοιχεί στο $y$ στην εξίσωση της ευθείας;

$Y_i$$b_0$$b_1$$X_i$

Επεξήγηση

Σωστή απάντηση: Α — $Y_i$

Το $Y_i$ στο GLM αντιστοιχεί στο $y$ στην εξίσωση της ευθείας. Και τα δύο αντιπροσωπεύουν την εξαρτημένη μεταβλητή - την τιμή που προβλέπουμε ή υπολογίζουμε.

Ομοιότητες:

Και τα δύο είναι το αποτελέσμα της εξίσωσης
Και τα δύο εξαρτώνται από την τιμή του $x$ ή $X_i$
Και τα δύο μπορούν να παρασταθούν στον κατακόρυφο άξονα ενός διαγράμματος

Διαφορά: Το $Y_i$ στο GLM περιλαμβάνει επίσης το σφάλμα $e_i$, ενώ η απλή εξίσωση ευθείας δεν έχει όρο σφάλματος.

2. Ποιο μέρος της εξίσωσης του GLM αντιστοιχεί στο $\beta$ στην εξίσωση της ευθείας;

$Y_i$$b_0$$b_1$$X_i$

Επεξήγηση

Σωστή απάντηση: Β — $b_0$

Το $b_0$ στο GLM αντιστοιχεί στο $\beta$ στην εξίσωση της ευθείας. Και τα δύο αντιπροσωπεύουν το σημείο τομής - τη σταθερά της εξίσωσης.

Ομοιότητες:

Και τα δύο είναι η τιμή του $y$ ή $Y_i$ όταν $x$ ή $X_i$ είναι 0
Και τα δύο δείχνουν πού η ευθεία τέμνει τον κατακόρυφο άξονα
Και τα δύο είναι σταθερές (δεν αλλάζουν με το $x$ ή $X_i$)

Σημείωση: Στη στατιστική, το $b$ συνήθως χρησιμοποιείται για τον σταθερό όρο, ενώ στα μαθηματικά το $\beta$ είναι ο σταθερός όρος στην εξίσωση $y = \alpha x + \beta$. Στο GLM, το $b_0$ είναι πιο περιγραφικό (δείχνει ότι είναι η παράμετρος με δείκτη 0).

3. Ποιο μέρος της εξίσωσης του GLM αντιστοιχεί στο $\alpha$ στην εξίσωση της ευθείας;

$Y_i$$b_0$$b_1$$X_i$

Επεξήγηση

Σωστή απάντηση: Γ — $b_1$

Το $b_1$ στο GLM αντιστοιχεί στο $\alpha$ στην εξίσωση της ευθείας. Και τα δύο αντιπροσωπεύουν την κλίση (slope) - πόσο αλλάζει το $y$ ή $Y_i$ για κάθε μονάδα αλλαγής στο $x$ ή $X_i$.

Ομοιότητες:

Και τα δύο δείχνουν το ρυθμό μεταβολής του $y$ ως προς το $x$
Και τα δύο πολλαπλασιάζονται με την ανεξάρτητη μεταβλητή
Και τα δύο καθορίζουν την κλίση της ευθείας

Ερμηνεία:

\[\text{Κλίση} = \frac{\text{Αλλαγή στο } y}{\text{Αλλαγή στο } x} = \frac{\Delta y}{\Delta x}\]

Για μία μονάδα αύξησης στο $x$ ή $X_i$, το $y$ ή $Y_i$ αλλάζει κατά $\alpha$ ή $b_1$ μονάδες.

4. Ποιο μέρος της εξίσωσης του GLM αντιστοιχεί στο $x$ στην εξίσωση της ευθείας;

$Y_i$$b_0$$b_1$$X_i$

Επεξήγηση

Σωστή απάντηση: Δ — $X_i$

Το $X_i$ στο GLM αντιστοιχεί στο $x$ στην εξίσωση της ευθείας. Και τα δύο αντιπροσωπεύουν την ανεξάρτητη μεταβλητή - την τιμή εισόδου που χρησιμοποιούμε για να υπολογίσουμε το $y$ ή $Y_i$.

Ομοιότητες:

Και τα δύο είναι η είσοδος της εξίσωσης
Και τα δύο πολλαπλασιάζονται με την κλίση ($\alpha$ ή $b_1$)
Και τα δύο μπορούν να παρασταθούν στον οριζόντιο άξονα ενός διαγράμματος

Σημείωση: Το $i$ στο $X_i$ δείχνει ότι πρόκειται για την τιμή της παρατήρησης $i$ - στη στατιστική έχουμε πολλές παρατηρήσεις, όχι μόνο μία τιμή $x$.

5. Ποιο είναι το στοιχείο που υπάρχει στην εξίσωση του GLM αλλά ΔΕΝ υπάρχει στην απλή εξίσωση ευθείας $y = \alpha x + \beta$;

Η κλίσηΟ σταθερός όροςΟ όρος σφάλματος $e_i$Η ανεξάρτητη μεταβλητή

Επεξήγηση

Σωστή απάντηση: Γ — Ο όρος σφάλματος $e_i$

Η κύρια διαφορά μεταξύ του GLM και της απλής εξίσωσης ευθείας είναι ο όρος σφάλματος $e_i$.

Απλή εξίσωση ευθείας: \[y = \alpha x + \beta\]

Αυτή είναι μια ντετερμινιστική σχέση - για κάθε τιμή $x$, υπάρχει μία ακριβής τιμή $y$.

GLM: \[Y_i = b_0 + b_1X_i + e_i\]

Αυτή είναι μια στατιστική σχέση - αναγνωρίζει ότι υπάρχει μεταβλητότητα στα δεδομένα. Για την ίδια τιμή $X_i$, διαφορετικές παρατηρήσεις μπορεί να έχουν διαφορετικές τιμές $Y_i$.

Γιατί χρειαζόμαστε το $e_i$:

Τα πραγματικά δεδομένα δεν πέφτουν ακριβώς πάνω σε μια ευθεία
Υπάρχει φυσική μεταβλητότητα στις μετρήσεις
Άλλοι παράγοντες (που δεν περιλαμβάνονται στο μοντέλο) επηρεάζουν το αποτέλεσμα
Υπάρχει σφάλμα μέτρησης

Πίνακας με αντιστοιχίες:

GLM	Εξίσωση ευθείας	Ερμηνεία
$Y_i$	$y$	Εξαρτημένη μεταβλητή
$b_0$	$\beta$	Σταθερός όρος (Intercept)
$b_1$	$\alpha$	Κλίση (slope)
$X_i$	$x$	Ανεξάρτητη μεταβλητή
$e_i$	—	Σφάλμα/υπόλοιπο

Συμπέρασμα:

Το GLM είναι μια επέκταση της απλής εξίσωσης ευθείας που:

Χρησιμοποιεί πιο περιγραφικά σύμβολα ($b_0, b_1$ αντί για $\beta, \alpha$)
Προσθέτει δείκτες $i$ για να δείξει ότι έχουμε πολλές παρατηρήσεις
Περιλαμβάνει τον όρο σφάλματος $e_i$ για να αναγνωρίσει τη μεταβλητότητα στα δεδομένα

Συνοπτικά: Το GLM $Y_i = b_0 + b_1X_i + e_i$ είναι η στατιστική εκδοχή της εξίσωσης ευθείας $y = \alpha x + \beta$. Η βασική δομή είναι η ίδια, αλλά στο GLM προστίθεται ο όρος σφάλματος $e_i$ για να λάβει υπόψη τη μεταβλητότητα στα πραγματικά δεδομένα.

Η προσαρμογή ενός μοντέλου παλινδρόμησης είναι τελικά ζήτημα εύρεσης εκείνης της ευθείας που προσαρμόζεται καλύτερα στα δεδομένα — δηλαδή, εκείνης που ελαχιστοποιεί το άθροισμα των τετραγώνων των σφαλμάτων.

10.3 Ερμηνεία των Εκτιμήσεων Παραμέτρων σε ένα Μοντέλο Παλινδρόμησης

Προηγουμένως, χρησιμοποιήσαμε τη συνάρτηση lm() για να προσαρμόσουμε το μοντέλο του ύψους (Height) για την πρόβλεψη του μήκους αντίχειρα (Thumb) και το αποθηκεύσαμε ως Height_model:

Height_model <- lm(Thumb ~ Height, data = Fingers)

Ας εξετάσουμε τώρα τις εκτιμήσεις των παραμέτρων του μοντέλου και ας δούμε πώς μπορούμε να τις ερμηνεύσουμε. Χρησιμοποιήστε το παρακάτω παράδειγμα κώδικα για να εμφανίσετε τις εκτιμήσεις των παραμέτρων του μοντέλου του ύψους (Height model).

Call:
lm(formula = Thumb ~ Height, data = Fingers)

Coefficients:
(Intercept)       Height
    -3.3295       0.3787

Τι είναι το $-3.33$ στα παραπάνω αποτελέσματα; (Υπάρχουν περισσότερες από μία σωστές απαντήσεις.)

$b_0$$b_1$$X_i$Η κλίση μιας ευθείας παλινδρόμησηςΗ διαφορά μεταξύ δύο ομάδωνΟ σταθερός όρος (η τιμή του $Y_i$ όταν $X_i = 0$)

Επεξήγηση

Σωστές απαντήσεις: Α και ΣΤ

Το $-3.3295$ είναι ο σταθερός όρος (intercept) του μοντέλου παλινδρόμησης.

Α. «$b_0$» — ΣΩΣΤΟ ✓

Το -3.33 είναι το $b_0$ στην εξίσωση: \[Y_i = b_0 + b_1X_i + e_i\]

Από τα αποτελέσματα: \[\text{Thumb}_i = -3.33 + 0.378 \times \text{Height}_i + e_i\]

ΣΤ. «Ο σταθερός όρος (η τιμή του $Y_i$ όταν $X_i = 0$)» — ΣΩΣΤΟ ✓

Ο σταθερός όρος είναι η τιμή πρόβλεψης του μήκους αντίχειρα όταν το ύψος είναι 0.

Όταν $\text{Height} = 0$: \[\hat{\text{Thumb}} = -3.33 + 0.378 \times 0 = -3.33 \text{ mm}\]

Σημείωση: Αν και αλγεβρικά αυτός είναι ο σταθερός όρος, στην πράξη δεν έχει νόημα - κανείς δεν έχει ύψος 0 εκατοστά! Ο σταθερός όρος είναι απαραίτητος για τη μαθηματική μορφή της εξίσωσης, αλλά η ερμηνεία του έχει νόημα μόνο εντός του εύρους των παρατηρούμενων δεδομένων.

Γιατί οι άλλες επιλογές είναι λάθος

Β. «$b_1$» — ΛΑΘΟΣ

Το $b_1$ είναι ο συντελεστής κλίσης (slope), όχι ο σταθερός όρος.

Στο output: - $b_0 = -3.3295$ (Intercept) - $b_1 = 0.3787$ (Height)

Το -3.33 είναι το $b_0$, όχι το $b_1$.

Γ. «$X_i$» — ΛΑΘΟΣ

Το $X_i$ είναι η ανεξάρτητη μεταβλητή (Height), όχι μια παράμετρος του μοντέλου.

Το $X_i$ είναι δεδομένα που παρατηρούμε (π.χ., ύψος = 170 cm)
Το $b_0$ είναι μια τιμή παραμέτρου που εκτιμά το μοντέλο

Το -3.33 είναι τιμή παραμέτρου, όχι δεδομένα.

Δ. «Η κλίση μιας ευθείας παλινδρόμησης» — ΛΑΘΟΣ

Η κλίση (slope) είναι το $b_1 = 0.3787$, όχι το $b_0 = -3.33$.

Η κλίση δείχνει πόσο αλλάζει η Thumb για κάθε 1 μονάδα αύξησης στην Height
Ο σταθερός όρος είναι η τιμή εκκίνησης όταν Height = 0

Αυτές είναι δύο διαφορετικές τιμές παραμέτρου με διαφορετικές ερμηνείες.

Ε. «Η διαφορά μεταξύ δύο ομάδων» — ΛΑΘΟΣ

Αυτό θα ίσχυε αν το μοντέλο ήταν με ποιοτική ανεξάρτητη μεταβλητή (π.χ., Height2Group).

Στο μοντέλο της Height2Group:

Το $b_0$ = μέσος όρος της ομάδας αναφοράς
Το $b_1$ = διαφορά μέσων όρων μεταξύ των ομάδων

Αλλά στο τρέχον μοντέλο, η Height είναι συνεχής μεταβλητή, όχι κατηγορική. Δεν υπάρχουν ομάδες - το ύψος μετράται σε εκατοστά.

Επομένως, το -3.33 είναι ο σταθερός όρος για τη συνεχή σχέση, όχι διαφορά ομάδων.

Γεωμετρική ερμηνεία

Σε ένα διάγραμμα διασποράς:

Ο οριζόντιος άξονας (X) = Height
Ο κατακόρυφος άξονας (Y) = Thumb
Η ευθεία παλινδρόμησης έχει:
- Κλίση = 0.3787 (πόσο απότομη είναι η ευθεία)
- Intercept = -3.33 (πού τέμνει τον άξονα Y στο σημείο X = 0)

Γιατί ο σταθερός όρος είναι αρνητικός;

Η αρνητική τιμή του σταθερού όρου δεν σημαίνει ότι υπάρχουν αρνητικά μήκη αντίχειρα! Συμβαίνει επειδή:

Η ευθεία παλινδρόμησης εκτείνεται πέρα από το εύρος των δεδομένων
Κανείς δεν έχει πραγματικά ύψος κοντά στο 0
Ο σταθερός όρος είναι ένα μαθηματικό χαρακτηριστικό της εξίσωσης
Οι προβλέψεις είναι αξιόπιστες μόνο εντός του εύρους των παρατηρούμενων υψών

Πρακτική χρήση:

Ο σταθερός όρος είναι απαραίτητος για τον υπολογισμό προβλέψεων, αλλά η άμεση ερμηνεία του συχνά δεν έχει νόημα. Αυτό που έχει νόημα είναι:

Η κλίση $b_1 = 0.3787$: Πόσο αλλάζει το μήκος αντίχειρα ανά cm ύψους
Οι προβλέψεις για ρεαλιστικές τιμές ύψους (π.χ., 150-200 cm)

Συμπέρασμα

Το -3.33 είναι:

✓ Το $b_0$ (η εκτίμηση παραμέτρου)
✓ Το intercept (η τιμή του $Y$ όταν $X = 0$)
✗ ΌΧΙ η κλίση
✗ ΌΧΙ διαφορά ομάδων (γιατί η Height είναι συνεχής μεταβλητή)

Συνοπτικά: Το -3.33 είναι ο σταθερός όρος ($b_0$) του μοντέλου - η θεωρητική τιμή του μήκους αντίχειρα όταν το ύψος είναι 0. Αν και δεν έχει πρακτική ερμηνεία (κανείς δεν έχει ύψος 0), είναι απαραίτητο για την αλγεβρική μορφή της εξίσωσης παλινδρόμησης.

Τι είναι το 0.3787 στα παραπάνω αποτελέσματα; (Υπάρχουν περισσότερες από μία σωστές απαντήσεις.)

Επεξήγηση

Σωστές απαντήσεις: Β και Δ

Το 0.3787 είναι ο συντελεστής κλίσης (slope) του μοντέλου παλινδρόμησης.

Β. «$b_1$» — ΣΩΣΤΟ ✓

Το 0.3787 είναι το $b_1$ στην εξίσωση: \[Y_i = b_0 + b_1X_i + e_i\]

Από τα αποτελέσματα: \[\text{Thumb}_i = -3.3295 + 0.3787 \times \text{Height}_i + e_i\]

όπου:

$b_0 = -3.3295$ (Σταθερός όρος)
$b_1 = 0.3787$ (Height — αυτός είναι ο συντελεστής που πολλαπλασιάζει την Height)

Δ. «Η κλίση μιας ευθείας παλινδρόμησης» — ΣΩΣΤΟ ✓

Το $b_1 = 0.3787$ είναι η κλίση (slope) της ευθείας παλινδρόμησης.

Ερμηνεία: Για κάθε 1 cm αύξησης στο ύψος, το μήκος αντίχειρα αυξάνεται κατά μέσο όρο 0.3787 mm.

Αλγεβρικά: \[\text{Κλίση} = \frac{\Delta \text{Thumb}}{\Delta \text{Height}} = \frac{0.3787 \text{ mm}}{1 \text{ cm}}\]

Γιατί οι άλλες επιλογές είναι λάθος

Α. «$b_0$» — ΛΑΘΟΣ

Το $b_0$ είναι ο σταθερός όρος, όχι η κλίση.

Στα αποτελέσματα: - $b_0 = -3.3295$ (σταθερός όρος) - $b_1 = 0.3787$ (ύψος) ← Αυτό είναι το 0.3787

Το 0.3787 είναι το $b_1$, όχι το $b_0$.

Γ. «$X_i$» — ΛΑΘΟΣ

Το $X_i$ είναι η ανεξάρτητη μεταβλητή (Height), δηλαδή τα δεδομένα που έχουμε.

Το $X_i$ παίρνει διαφορετικές τιμές για κάθε άτομο (π.χ., 165 cm, 170 cm, 180 cm)
Το $b_1 = 0.3787$ είναι μια εκτίμηση παραμέτρου που εκτιμά το μοντέλο - είναι σταθερή για όλες τις παρατηρήσεις

Το 0.3787 δεν είναι μια παρατήρηση αλλά ο συντελεστής που πολλαπλασιάζει το $X_i$.

Ε. «Η διαφορά μεταξύ δύο ομάδων» — ΛΑΘΟΣ

Αυτό θα ίσχυε αν το μοντέλο είχε ποιοτική ανεξάρτητη μεταβλητή (π.χ., την Height2Group με ομάδες short/tall).

Μοντέλο με ποιοτική μεταβλητή (Height2Group): \[\text{Thumb}_i = b_0 + b_1 \times \text{Height2Grouptall}_i + e_i\]

Εδώ το $b_1$ θα ήταν η διαφορά μέσου όρου μεταξύ tall και short.

Μοντέλο με συνεχή μεταβλητή (Height): \[\text{Thumb}_i = b_0 + b_1 \times \text{Height}_i + e_i\]

Εδώ το $b_1$ είναι η κλίση - η αλλαγή στο Thumb ανά μονάδα αύξησης της Height.

Το τρέχον μοντέλο χρησιμοποιεί την συνεχή Height, όχι ομάδες, άρα το 0.3787 δεν είναι διαφορά ομάδων.

ΣΤ. «Ο σταθερός όρος (η τιμή του $Y_i$ όταν $X_i = 0$)» — ΛΑΘΟΣ

Ο σταθερός όρος είναι το $b_0 = -3.3295$, όχι το $b_1 = 0.3787$.

Σταθερός όρος ($b_0$): Η τιμή του $Y$ όταν $X = 0$
Κλίση ($b_1$): Πόσο αλλάζει το $Y$ όταν το $X$ αυξάνεται κατά 1

Αυτά είναι δύο διαφορετικές εκτιμήσεις παραμέτρων με διαφορετικές ερμηνείες.

Λεπτομερής ερμηνεία του $b_1 = 0.3787$

Το μοντέλο είναι: \[\text{Thumb}_i = -3.3295 + 0.3787 \times \text{Height}_i + e_i\]

Τι σημαίνει η κλίση 0.3787:

Για κάθε 1 cm αύξησης στο ύψος, το μήκος αντίχειρα αυξάνεται κατά μέσο όρο 0.3787 mm (περίπου 0.378 mm)
Η σχέση είναι θετική: όσο πιο ψηλό το άτομο, τόσο μεγαλύτερος ο αντίχειρας
Η σχέση είναι γραμμική: η αύξηση είναι σταθερή (0.378 mm ανά cm) σε όλο το εύρος των υψών

Παραδείγματα προβλέψεων:

Για άτομο με ύψος 160 cm: \[\hat{\text{Thumb}} = -3.33 + 0.3787 \times 160 = -3.33 + 60.59 = 57.26 \text{ mm}\]

Για άτομο με ύψος 170 cm: \[\hat{\text{Thumb}} = -3.33 + 0.3787 \times 170 = -3.33 + 64.38 = 61.05 \text{ mm}\]

Διαφορά μεταξύ των δύο προβλέψεων: \[61.05 - 57.26 = 3.79 \text{ mm} \approx 10 \times 0.378 \text{ mm}\]

Για 10 cm διαφορά στο ύψος, έχουμε περίπου 3.8 mm διαφορά στον αντίχειρα, που είναι ακριβώς $10 \times 0.3787$.

Εναλλακτική ερμηνεία:

Μπορούμε να εκφράσουμε την κλίση και ως:

Για κάθε 10 cm αύξησης στο ύψος → αύξηση 3.787 mm στον αντίχειρα
Για κάθε 1 m αύξησης στο ύψος → αύξηση 37.87 mm (3.787 cm) στον αντίχειρα

Γεωμετρική ερμηνεία

Σε ένα διάγραμμα διασποράς:

Ο οριζόντιος άξονας (X) = Height σε cm
Ο κατακόρυφος άξονας (Y) = Thumb σε mm
Η ευθεία παλινδρόμησης έχει:
- Κλίση = 0.3787 (πόσο απότομη είναι η γραμμή)
- Σταθερός όρος = -3.33 (πού τέμνει τον άξονα Y στο σημείο X = 0)

Η κλίση 0.3787 σημαίνει ότι για κάθε 1 cm που κινούμαστε δεξιά στον οριζόντιο άξονα, ανεβαίνουμε 0.378 mm στον κατακόρυφο άξονα.

Συμπέρασμα

Το 0.3787 είναι:

✓ Το $b_1$ είναι
✓ η κλίση της ευθείας παλινδρόμησης
✗ ΌΧΙ ο σταθερός όρος
✗ ΌΧΙ διαφορά ομάδων (γιατί η Height είναι συνεχής μεταβλητή)

Συνοπτικά: Το 0.3787 είναι η κλίση ($b_1$) του μοντέλου παλινδρόμησης - η αλλαγή στο μήκος αντίχειρα (σε mm) για κάθε 1 cm αύξησης στο ύψος. Η τιμή του συντελεστή εξαρτάται από τις μονάδες μέτρησης (0.378 mm), αλλά η υποκείμενη σχέση παραμένει η ίδια.

Ο σταθερός όρος (Intercept) αντιστοιχεί στο $b_0$ και ο συντελεστής της Height αντιστοιχεί στο $b_1$. Το προσαρμοσμένο μας μοντέλο μπορεί να γραφτεί ως:

\[Thumb_i = -3.33 + 0.378 \, Height_i + e_i\] Ή, ισοδύναμα, χρησιμοποιώντας τη σημειογραφία του GLM:

\[Y_i = -3.33 + 0.378 \, X_i + e_i\]

Τι θα προέβλεπε αυτό το μοντέλο ως μήκος αντίχειρα για ένα άτομο με ύψος 0; (Υπάρχουν περισσότερες από μία σωστές απαντήσεις.)

Επεξήγηση

Σωστές απαντήσεις: Α, Γ και Δ

Ανάλυση της πρόβλεψης

Το μοντέλο είναι: \[Y_i = b_0 + b_1X_i + e_i\]

Για την πρόβλεψη χρησιμοποιούμε: \[\hat{Y}_i = b_0 + b_1X_i\]

Όταν το ύψος είναι 0 (δηλαδή $X_i = 0$): \[\hat{Y}_i = b_0 + b_1 \times 0 = b_0 + 0 = b_0\]

Α. «$b_0$» — ΣΩΣΤΟ ✓

Όταν $X_i = 0$, η πρόβλεψη είναι απλώς ο σταθερός όρος $b_0$.

Από την εξίσωση: \[\hat{Y}_i = b_0 + b_1 \times 0 = b_0\]

Γ. «$b_0 + b_1(0)$» — ΣΩΣΤΟ ✓

Αυτή είναι η πλήρης μορφή της εξίσωσης πρόβλεψης όταν $X_i = 0$.

\[\hat{Y}_i = b_0 + b_1(0) = b_0 + 0 = b_0\]

Αυτή η έκφραση είναι μαθηματικά ισοδύναμη με την επιλογή Α, απλώς δείχνει ρητά τον υπολογισμό.

Δ. «-3.33» — ΣΩΣΤΟ ✓

Από τα αποτελέσματα του μοντέλου: \[b_0 = -3.3295\]

Άρα, όταν $\text{Height} = 0$: \[\hat{\text{Thumb}} = -3.3295 + 0.378 \times 0 = -3.3295 \text{ mm}\]

Αυτή είναι η αριθμητική τιμή της πρόβλεψης.

Γιατί οι άλλες επιλογές είναι λάθος

Β. «$b_1$» — ΛΑΘΟΣ

Το $b_1$ είναι η κλίση, όχι η πρόβλεψη όταν $X = 0$.

Το $b_1 = 0.378$ δείχνει πόσο αλλάζει το $Y$ όταν το $X$ αυξάνεται κατά 1
Η πρόβλεψη όταν $X = 0$ είναι το $b_0 = -3.33$, όχι το $b_1$

Ε. «0.378» — ΛΑΘΟΣ

Το 0.378 είναι η τιμή του $b_1$ (η κλίση), όχι η πρόβλεψη όταν $X = 0$.

Από τα αποτελέσματα: - Σταθερός όρος = $b_0 = -3.3295$ - Συντελεστής της Height = $b_1 = 0.378$

Η πρόβλεψη όταν Height = 0 είναι ο σταθερός όρος (-3.3295), όχι η κλίση (0.378).

ΣΤ. «$-3.3295 + 0.378$» — ΛΑΘΟΣ

Αυτή η έκφραση θα ήταν σωστή αν το ύψος ήταν 1, όχι 0.

Πρακτική σημασία

Αν και αλγεβρικά η πρόβλεψη για ύψος 0 είναι -3.33 mm, αυτό δεν έχει πρακτικό νόημα επειδή:

Κανείς δεν έχει ύψος 0 cm
Αρνητικό μήκος αντίχειρα είναι φυσικά αδύνατο
Οι προβλέψεις είναι αξιόπιστες μόνο εντός του εύρους των παρατηρούμενων δεδομένων

Ο σταθερός όρος είναι απαραίτητος για τη μαθηματική μορφή της εξίσωσης, αλλά η ερμηνεία του έχει νόημα μόνο όταν $X = 0$ βρίσκεται εντός (ή κοντά στο) εύρος των δεδομένων.

Συμπέρασμα

Όταν το ύψος είναι 0, το μοντέλο προβλέπει:

✓ $b_0$ (συμβολικά)
✓ $b_0 + b_1(0)$ (πλήρης έκφραση)
✓ $-3.33$ mm (αριθμητικά)

Και οι τρεις εκφράσεις είναι αλγεβρικά ισοδύναμες και σωστές.

Συνοπτικά: Όταν το ύψος είναι 0, η πρόβλεψη του μοντέλου είναι ο σταθερός όρος $b_0 = -3.33$ mm. Αυτό προκύπτει από την εξίσωση $\hat{Y} = b_0 + b_1 \times 0 = b_0$. Αν και μαθηματικά ορθή, αυτή η πρόβλεψη δεν έχει πρακτικό νόημα γιατί κανείς δεν έχει ύψος 0.

Η σταθερά $b_0 = -3.33$ αντιπροσωπεύει το σημείο τομής, δηλαδή την τιμή πρόβλεψης του μήκους αντίχειρα (Thumb) όταν το ύψος (Height) είναι 0.

Φυσικά, ούτε ένα ύψος 0 εκατοστών ούτε ένα μήκος αντίχειρα $-3.33$ χιλιοστών είναι ρεαλιστικά. Αυτό μας υπενθυμίζει ότι οι προβλέψεις ενός μοντέλου παλινδρόμησης δεν έχουν πάντα πρακτικό ή φυσικό νόημα. Είναι λοιπόν σημαντικό να εξετάζουμε ποιες τιμές των μεταβλητών και ποιες προβλέψεις είναι λογικές μέσα στο πλαίσιο των δεδομένων μας.

Πώς τα Μοντέλα Παλινδρόμησης Κάνουν Προβλέψεις

Μπορούμε να χρησιμοποιήσουμε το μοντέλο της Height για να προβλέψουμε το μήκος του αντίχειρα ατόμων διαφορετικού ύψους, όπως ακριβώς χρησιμοποιήσαμε το μοντέλο της Height2Group για να προβλέψουμε το μήκος του αντίχειρα για φοιτητές με χαμηλό και υψηλό ανάστημα.

Μπορούμε να γράψουμε το προσαρμοσμένο μοντέλο της Height ως εξής:

\[\text{Thumb}_i = -3.3295 + 0.378\text{Height}_i + e_i\]

Ποιο μέρος αυτής της εξίσωσης θα χρησιμοποιούσαμε για να προβλέψουμε το μήκος αντίχειρα ενός νέου άτομου;

$\text{Thumb}_i = -3.3295 + 0.378\text{Height}_i + e_i$$-3.3295 + 0.378\text{Height}_i + e_i$$-3.3295 + 0.378\text{Height}_i$

Επεξήγηση

Σωστή απάντηση: Γ — $-3.3295 + 0.378\text{Height}_i$

Γιατί χρησιμοποιούμε αυτό το μέρος της εξίσωσης;

Για να κάνουμε πρόβλεψη, χρησιμοποιούμε μόνο το ντετερμινιστικό μέρος του μοντέλου, δηλαδή το μέρος χωρίς τον όρο σφάλματος $e_i$.

Πλήρες μοντέλο: \[\text{Thumb}_i = -3.3295 + 0.378\text{Height}_i + e_i\]

Εξίσωση πρόβλεψης: \[\hat{\text{Thumb}}_i = -3.3295 + 0.378\text{Height}_i\]

Το σύμβολο $\hat{Y}$ (“Y hat”) υποδηλώνει την τιμή πρόβλεψης.

Γιατί αφαιρούμε το $e_i$;

Ο όρος σφάλματος $e_i$ αντιπροσωπεύει:

Τη μεταβλητότητα που δεν εξηγείται από το μοντέλο
Την απόκλιση της πραγματικής παρατήρησης από την πρόβλεψη
Την επίδραση άλλων παραγόντων που δεν περιλαμβάνονται στο μοντέλο

Για ένα νέο άτομο, δεν γνωρίζουμε το σφάλμα $e_i$ (γιατί δεν έχουμε ακόμα μετρήσει το πραγματικό μήκος του αντίχειρα του). Επομένως:

Δεν μπορούμε να συμπεριλάβουμε το $e_i$ στην πρόβλεψη
Χρησιμοποιούμε μόνο το συστηματικό μέρος του μοντέλου: $b_0 + b_1X_i$
Υποθέτουμε ότι κατά μέσο όρο το σφάλμα είναι 0: $E(e_i) = 0$

Γιατί οι άλλες επιλογές είναι λάθος

Α. «$\text{Thumb}_i = -3.3295 + 0.378\text{Height}_i + e_i$» — ΛΑΘΟΣ

Αυτή είναι η πλήρης εξίσωση του μοντέλου, όχι η εξίσωση πρόβλεψης.

Η εξίσωση αυτή περιγράφει τη σχέση μεταξύ των μεταβλητών για τα υπάρχοντα δεδομένα: \[\text{Thumb}_i = \underbrace{-3.3295 + 0.378\text{Height}_i}_{\text{τιμή πρόβλεψης}} + \underbrace{e_i}_{\text{απόκλιση από την πρόβλεψη}}\]

Για νέο άτομο, χρησιμοποιούμε μόνο το μέρος της πρόβλεψης: \[\hat{\text{Thumb}}_i = -3.3295 + 0.378\text{Height}_i\]

Β. «$-3.3295 + 0.378\text{Height}_i + e_i$» — ΛΑΘΟΣ

Αυτή η έκφραση περιλαμβάνει τον όρο σφάλματος $e_i$, ο οποίος δεν πρέπει να συμπεριληφθεί στην πρόβλεψη.

Γιατί όχι;

Δεν γνωρίζουμε το $e_i$ για νέο άτομο (δεν έχουμε μετρήσει ακόμα το πραγματικό μήκος αντίχειρα (Thumb)
Κατά μέσο όρο, το $e_i = 0$ (τα σφάλματα είναι τυχαία γύρω από το μηδέν)
Η πρόβλεψη βασίζεται μόνο στο συστηματικό μέρος του μοντέλου

Διαφορά μεταξύ μοντέλου και πρόβλεψης

Εξίσωση	Χρήση	Περιλαμβάνει $e_i$;
$Y_i = b_0 + b_1X_i + e_i$	Περιγραφή των δεδομένων	Ναι
$\hat{Y}_i = b_0 + b_1X_i$	Πρόβλεψη για νέα δεδομένα	Όχι

Παράδειγμα πρόβλεψης

Έστω ότι ένα νέο άτομο έχει ύψος 170 cm. Για να προβλέψουμε το μήκος του αντίχειρα του:

ΣΩΣΤΟΣ τρόπος (χρησιμοποιώντας την εξίσωση πρόβλεψης): \[\hat{\text{Thumb}} = -3.3295 + 0.378 \times 170 = -3.3295 + 64.26 = 60.93 \text{ mm}\]

ΛΑΘΟΣ τρόπος (αν συμπεριλάβουμε το $e_i$): \[\text{Thumb} = -3.3295 + 0.378 \times 170 + e_i = 60.93 + e_i\]

Αλλά τι είναι το $e_i$; Δεν το γνωρίζουμε! Το $e_i$ είναι η διαφορά μεταξύ της πραγματικής τιμής (που δεν έχουμε ακόμα) και της πρόβλεψης.

Η φύση του σφάλματος $e_i$

Το $e_i$ μπορεί να υπολογιστεί μόνο αφού έχουμε την πραγματική παρατήρηση:

Πρόβλεψη: $\hat{\text{Thumb}} = -3.3295 + 0.378 \times 170 = 60.93$ mm
Πραγματική μέτρηση: Έστω $\text{Thumb} = 62$ mm
Υπόλοιπο: $e_i = 62 - 60.93 = 1.07$ mm

Το $e_i$ είναι το υπόλοιπο (residual) - πόσο η πραγματική τιμή διαφέρει από την πρόβλεψη.

Ιδιότητες της εξίσωσης πρόβλεψης

Η εξίσωση πρόβλεψης $\hat{Y}_i = b_0 + b_1X_i$:

Δίνει την καλύτερη εκτίμηση με βάση τα διαθέσιμα δεδομένα
Είναι η τιμή με τη μικρότερη μέση τετραγωνική απόκλιση
Αντιπροσωπεύει τη μέση τιμή του $Y$ για δεδομένο $X$
Δεν περιλαμβάνει τυχαίο σφάλμα

Γραφική αναπαράσταση

Σε ένα διάγραμμα διασποράς:

Η ευθεία παλινδρόμησης $\hat{Y} = b_0 + b_1X$ είναι η γραμμή πρόβλεψης
Τα σημεία δεδομένων δεν πέφτουν ακριβώς πάνω στη γραμμή
Η κατακόρυφη απόσταση κάθε σημείου από τη γραμμή είναι το $e_i$

Όταν κάνουμε πρόβλεψη για νέο σημείο, χρησιμοποιούμε την ευθεία, όχι τις αποκλίσεις.

Συμπέρασμα

Για να προβλέψουμε το μήκος αντίχειρα ενός νέου ατόμου, χρησιμοποιούμε:

\[\hat{\text{Thumb}}_i = -3.3295 + 0.378\text{Height}_i\]

Δηλαδή, μόνο το ντετερμινιστικό μέρος του μοντέλου, χωρίς τον όρο σφάλματος $e_i$.

Βασικές αρχές:

Το $e_i$ περιγράφει την παρατηρούμενη απόκλιση στα υπάρχοντα δεδομένα
Για νέες προβλέψεις, δεν γνωρίζουμε (ούτε μπορούμε να γνωρίζουμε) το $e_i$
Η τιμή πρόβλεψης είναι ο μέσος όρος για δεδομένο $X$
Το σφάλμα έχει μέση τιμή 0

Συνοπτικά: Για πρόβλεψη χρησιμοποιούμε την εξίσωση $\hat{\text{Thumb}}_i = -3.3295 + 0.378\text{Height}_i$ χωρίς τον όρο σφάλματος $e_i$, γιατί το σφάλμα είναι άγνωστο για νέες παρατηρήσεις και έχει μέση τιμή μηδέν. Η πρόβλεψη αντιπροσωπεύει την αναμενόμενη (μέση) τιμή του μήκους αντίχειρα για δεδομένο ύψος.

Θυμηθείτε ότι το μήκος αντίχειρα (και η τιμή πρόβλεψής του) εκφράζεται σε χιλιοστά. Η τιμή -3.3295 είναι η τιμή πρόβλεψης του μήκους αντίχειρα, σε χιλιοστά, για ένα άτομο με ύψος 0 εκατοστά. Αν προεκτείνουμε τον οριζόντιο άξονα ώστε να περιλαμβάνει το 0, θα περιμέναμε η ευθεία παλινδρόμησης να τέμνει τον κατακόρυφο άξονα στο -3.3295. (Παρατηρήστε, ωστόσο, ότι στο παρακάτω διάγραμμα δεν υπάρχουν άνθρωποι με ύψος 0 εκατοστά — για προφανείς λόγους!)

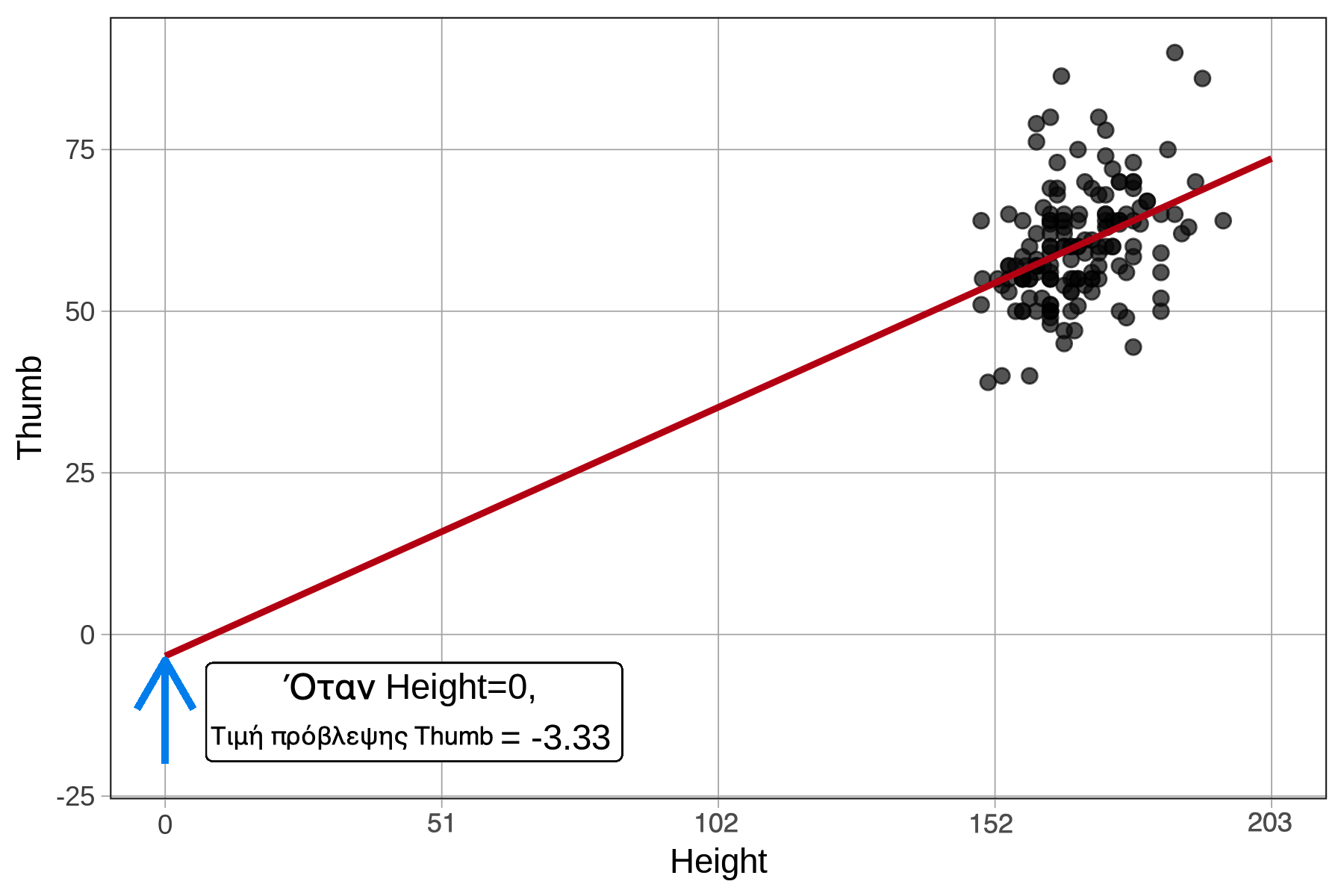
Η εκτίμηση παραμέτρου $b_1$ = 0.378 είναι η κλίση: για κάθε αύξηση κατά 1 μονάδα στο ύψος (Height), το μοντέλο μας προβλέπει αύξηση κατά 0.378 μονάδες στο μήκος του αντίχειρα (Thumb).

Το γεγονός ότι το ύψος μετριέται σε εκατοστά, ενώ το μήκος του αντίχειρα σε χιλιοστά, δεν δημιουργεί πρόβλημα· η ευθεία παλινδρόμησης είναι μια συνάρτηση (το τμήμα $b_0 +b_1X$ που δέχεται τιμές σε εκατοστά και παράγει προβλέψεις σε χιλιοστά). Αυτό σημαίνει ότι, κατά μέσο όρο, τα άτομα που είναι 1 cm ψηλότερα αναμένεται να έχουν αντίχειρες 0.378 mm μακρύτερους, σύμφωνα με το μοντέλο.

Παρακάτω παρουσιάζεται μια διαγραμματική αναπαράσταση αυτής της σχέσης:

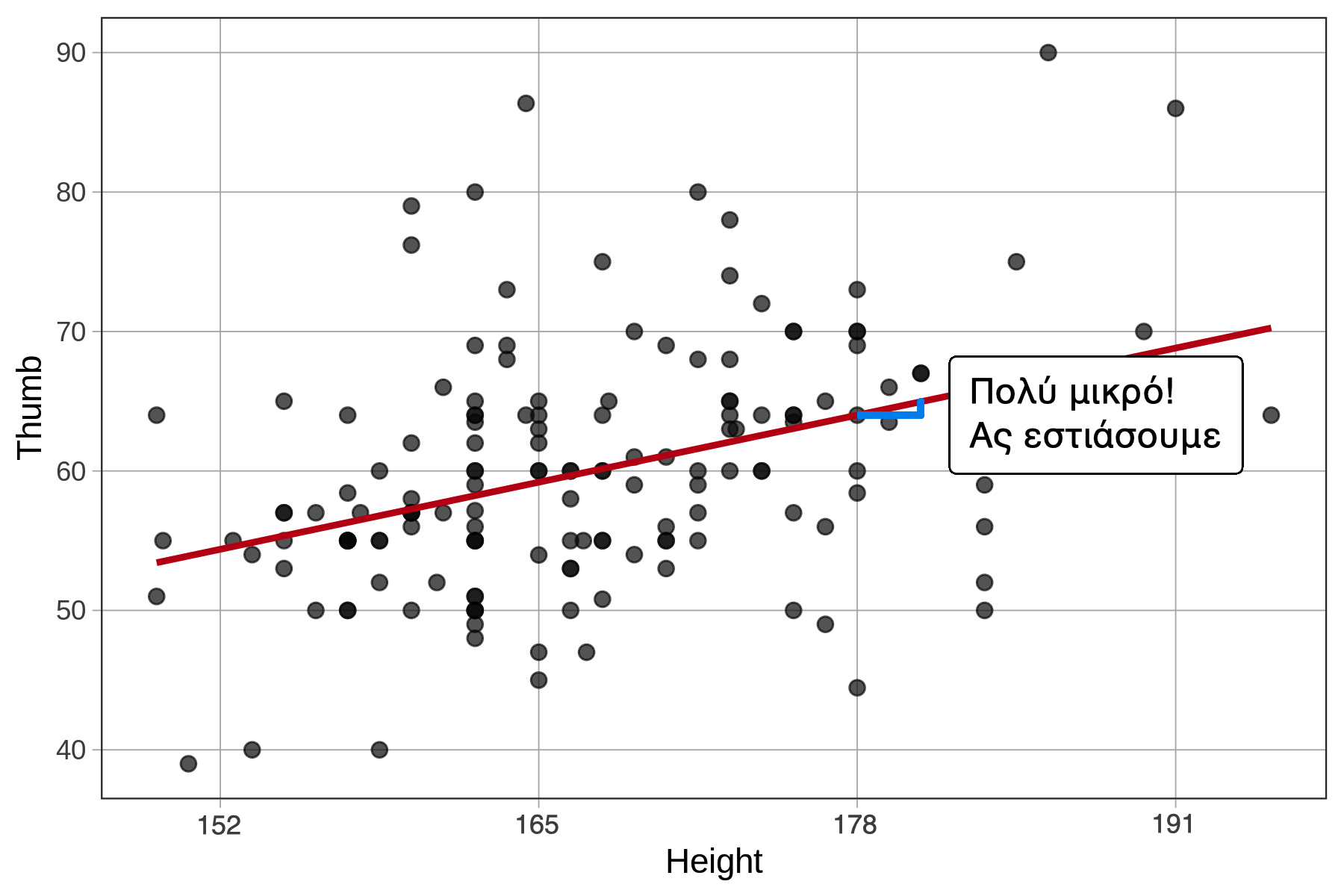Ας εστιάσουμε σε μια συγκεκριμένη περιοχή του διαγράμματος. Η τιμή πρόβλεψης του μήκους αντίχειρα ενός ατόμου με ύψος 178 εκατοστά είναι περίπου 178 $\times$ 0.378 $-$ 3.3295 = 63.95 χιλιοστά. Όταν το ύψος αυξάνεται κατά 1 cm, τότε η τιμή πρόβλεψης του μήκους αντίχειρα γίνεται 63.85 + 0.378 = 64.33 χιλιοστά.

Ποια από τις παρακάτω εκφράσεις θα δώσει την τιμή πρόβλεψης του μήκους αντίχειρα του μοντέλου για ένα άτομο με ύψος 180 cm;

$-3.3295 + 0.378(180)$$-3.3295 + 0.378 + (180)$$180 + 0.378$$180X_i$

Επεξήγηση

Σωστή απάντηση: Α — $-3.3295 + 0.378(180)$

Ανάλυση της εξίσωσης πρόβλεψης

Το μοντέλο της Height είναι: \[\hat{\text{Thumb}}_i = -3.3295 + 0.378 \times \text{Height}_i\]

Για άτομο με ύψος 180 cm, αντικαθιστούμε το $\text{Height}_i = 180$: \[\hat{\text{Thumb}} = -3.3295 + 0.378 \times 180\]

Υπολογισμός: \[\hat{\text{Thumb}} = -3.3295 + 68.04 = 64.71 \text{ mm}\]

Α. «$-3.3295 + 0.378(180)$» — ΣΩΣΤΟ ✓

Αυτή είναι η ορθή εφαρμογή της εξίσωσης πρόβλεψης.

Η γενική μορφή είναι: \[\hat{Y}_i = b_0 + b_1X_i\]

Όπου:

$b_0 = -3.3295$ (σταθερός όρος)
$b_1 = 0.378$ (κλίση)
$X_i = 180$ (ύψος σε cm)

Άρα: \[\hat{Y}_i = -3.3295 + 0.378 \times 180\]

Βήμα προς βήμα:

Πολλαπλασιάζουμε την κλίση επί το ύψος: $0.378 \times 180 = 68.04$
Προσθέτουμε τον σταθερό όρο: $-3.3295 + 68.04 = 64.71$ mm

Γιατί οι άλλες επιλογές είναι λάθος

Β. «$-3.3295 + 0.378 + (180)$» — ΛΑΘΟΣ

Αυτή η έκφραση προσθέτει όλες τις τιμές αντί να πολλαπλασιάσει την κλίση με το ύψος.

Λάθος υπολογισμός: \[-3.3295 + 0.378 + 180 = 177.048\]

Αυτό θα έδινε μήκος αντίχειρα 177 mm, που είναι παράλογο (θα ήταν 17.7 cm!).

Το σωστό:

Η κλίση πρέπει να πολλαπλασιαστεί με το ύψος, όχι απλώς να προστεθεί: \[-3.3295 + (0.378 \times 180) \neq -3.3295 + 0.378 + 180\]

Γιατί πολλαπλασιάζουμε;

Η κλίση $b_1 = 0.378$ σημαίνει “0.378 mm ανά cm ύψους”. Για 180 cm: \[0.378 \frac{\text{mm}}{\text{cm}} \times 180 \text{ cm} = 68.04 \text{ mm}\]

Γ. «$180 + 0.378$» — ΛΑΘΟΣ

Αυτή η έκφραση:

Παραλείπει τον σταθερό όρο $b_0 = -3.33$
Προσθέτει αντί να πολλαπλασιάζει
Αντιστρέφει τη σειρά των όρων

Λάθος υπολογισμός: \[180 + 0.378 = 180.378\]

Αυτό θα έδινε μήκος αντίχειρα 180.378 mm (18 cm!), που είναι εντελώς λάθος.

Το σωστό:

Πρέπει να ξεκινήσουμε με τον σταθερό όρο και να πολλαπλασιάσουμε την κλίση με το ύψος: \[-3.3295 + 0.378 \times 180\]

Δ. «$180X_i$» — ΛΑΘΟΣ

Αυτή η έκφραση δεν έχει καμία σχέση με την εξίσωση πρόβλεψης.

Προβλήματα:

Το $X_i$ είναι το ύψος (180 cm), όχι μια άλλη μεταβλητή
Παραλείπονται τόσο ο σταθερός όρος όσο και η κλίση
Ο πολλαπλασιασμός $180 \times X_i = 180 \times 180 = 32400$ δεν έχει νόημα

Σημείωση: Το $X_i$ είναι το σύμβολο για την ανεξάρτητη μεταβλητή (Height). Στην περίπτωσή μας, $X_i = 180$ cm.

Κατανόηση της δομής της εξίσωσης

Η εξίσωση γραμμικής παλινδρόμησης έχει τη μορφή: \[\hat{Y} = b_0 + b_1X\]

Στοιχεία της εξίσωσης:

$b_0$ (intercept): Σταθερά που προστίθεται
$b_1$ (κλίση): Συντελεστής που πολλαπλασιάζει το $X$
$X$ (ανεξάρτητη μεταβλητή): Η τιμή εισόδου (ύψος)

Για το μοντέλο μας:

Σύμβολο	Τιμή	Ερμηνεία
$b_0$	-3.3295	Σταθερός όρος
$b_1$	0.378	Κλίση (mm/cm)
$X$	180	Ύψος (cm)
$\hat{Y}$	?	Τιμή πρόβλεψης `Thumb` (mm)

Επαλήθευση της απάντησης

Η τιμή πρόβλεψης $\hat{\text{Thumb}} = 64.71$ mm είναι λογική;

Ύψος 180 cm είναι λίγο πάνω από το μέσο όρο
Μήκος αντίχειρα ~65 mm (6.5 cm) είναι ρεαλιστικό
Η τιμή είναι θετική (όπως αναμένεται)
Η τιμή είναι εντός λογικού εύρους (50-80 mm)

✓ Η απάντηση φαίνεται σωστή!

Συμπέρασμα

Για να προβλέψουμε το μήκος αντίχειρα ατόμου με ύψος 180 cm, χρησιμοποιούμε:

\[\hat{\text{Thumb}} = -3.3295 + 0.378(180) = 64.71 \text{ mm}\]

Βασική δομή: Σταθερός όρος + (Κλίση × Ύψος)

Συνοπτικά: Η σωστή έκφραση είναι $-3.3295 + 0.378(180)$, που ακολουθεί τη μορφή $\hat{Y} = b_0 + b_1X$. Αντικαθιστούμε το ύψος 180 cm στο $X$ και πολλαπλασιάζουμε με την κλίση 0.378, μετά προσθέτουμε τον σταθερό όρο -3.3295, για να πάρουμε την τιμή πρόβλεψης 64.71 mm.

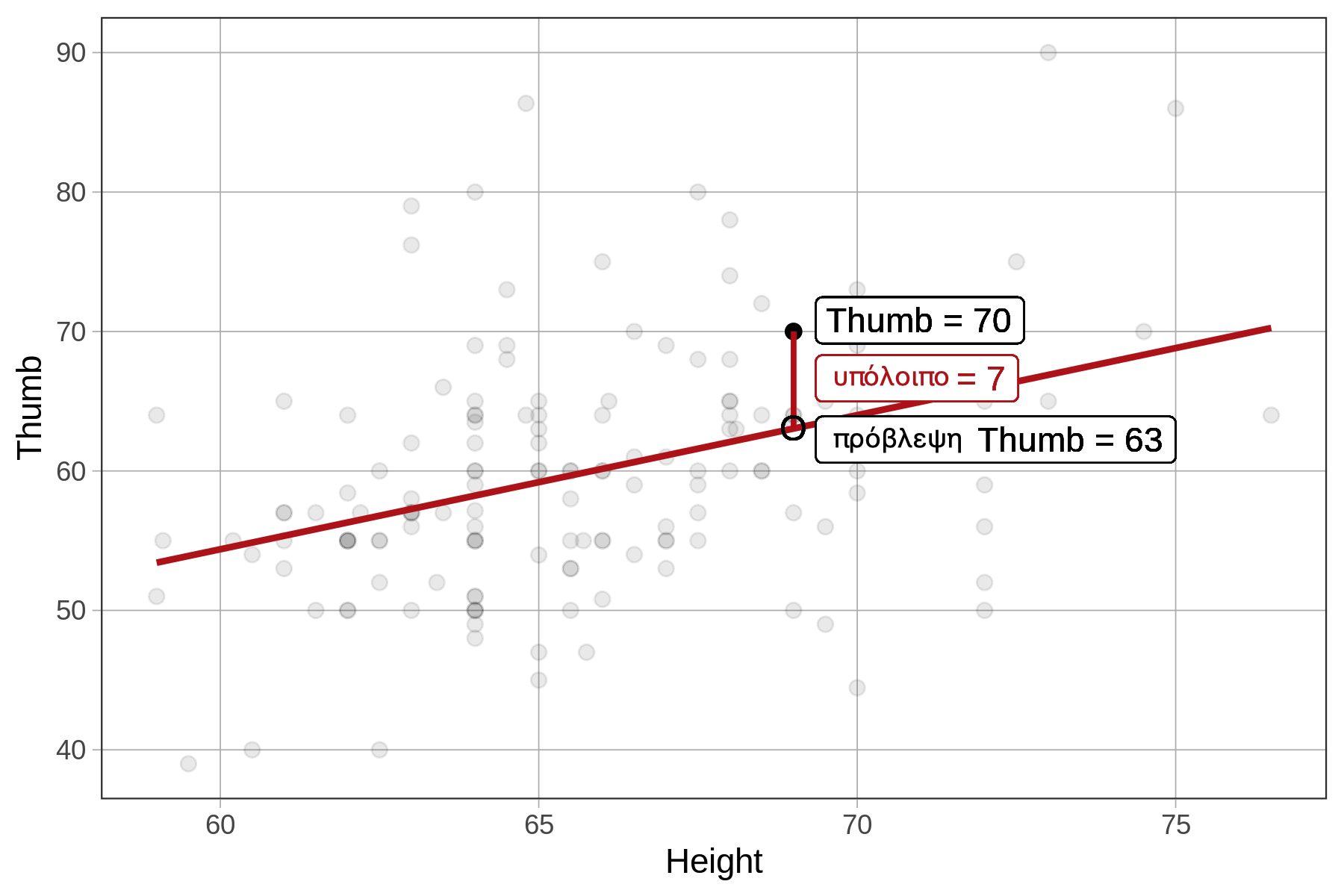
Αντίστοιχα, η τιμή πρόβλεψης του μήκους αντίχειρα ενός ατόμου με ύψος 180 εκατοστά είναι 64.71 χιλιοστά. Αυτή είναι η τιμή του μήκους αντίχειρα (Thumb) πάνω στην ευθεία παλινδρόμησης όταν το ύψος (Height) είναι 180, όπως φαίνεται στο παρακάτω διάγραμμα:

Οι Συντελεστές Παλινδρόμησης δεν είναι Συμμετρικοί

Όταν προσαρμόζουμε ένα μοντέλο παλινδρόμησης, έχει σημασία ποια μεταβλητή επιλέγουμε ως εξαρτημένη και ποια ως ανεξάρτητη. Για παράδειγμα, αν προσαρμόσουμε το μοντέλο Thumb ∼ Height, τα αποτελέσματα (σταθερός όρος και κλίση) θα διαφέρουν από εκείνα που θα προκύψουν αν προσαρμόσουμε το μοντέλο Height ∼ Thumb.

Call:
lm(formula = Thumb ~ Height, data = Fingers)

Coefficients:
(Intercept)       Height  
    -3.3295       0.3787   

Call:
lm(formula = Height ~ Thumb, data = Fingers)

Coefficients:
(Intercept)        Thumb  
   143.2327       0.4038

Ο λόγος αυτής της διαφοράς είναι ότι οι δύο μεταβλητές έχουν διαφορετικές μονάδες μέτρησης και διαφορετικές κατανομές. Αν η εξαρτημένη μεταβλητή είναι η Thumb, τότε η κλίση ($b_1$ = 0.3787) δείχνει πόσο μεταβάλλεται η τιμή πρόβλεψης του μήκους αντίχειρα (σε χιλιοστά) για κάθε αύξηση κατά 1 εκατοστό στο ύψος. Αντίθετα, αν η εξαρτημένη μεταβλητή είναι η Height, τότε η κλίση ($b_1$ = 0.4038) δείχνει πόσο μεταβάλλεται η τιμή πρόβλεψης του ύψος (σε εκατοστά) για κάθε αύξηση κατά 1 χιλιοστό στο μήκος του αντίχειρα.

Πρόκειται, επομένως, για δύο διαφορετικές σχέσεις με διαφορετική ερμηνεία, παρόλο που βασίζονται στα ίδια δεδομένα.

10.4 Σύγκριση Μοντέλων Παλινδρόμησης με Μοντέλα Ομάδων

Σύγκριση των Μοντέλων της `Height2Group` και της `Height`

Έχουμε πλέον μάθει πώς να ορίζουμε και να προσαρμόζουμε δύο διαφορετικούς τύπους μοντέλων: τα μοντέλα ομάδων (π.χ. Height2Group_model) και τα μοντέλα παλινδρόμησης (π.χ. Height_model). Ας σκεφτούμε τώρα λίγο ποιες είναι οι ομοιότητες και οι διαφορές ανάμεσα σε αυτούς τους δύο τύπους μοντέλων.

Σύμβολο	Μοντέλο Ομάδων $Y_i = b_0 + b_1 X_i + e_i$ $Thumb_i = b_0 + b_1 Height2Group_{tall,i} + e_i$	Μοντέλο Παλινδρόμησης $Y_i = b_0 + b_1 X_i + e_i$ $Thumb_i = b_0 + b_1 Height_i + e_i$
$Y_i$	Μήκος αντίχειρα του φοιτητή $i$	Μήκος αντίχειρα του φοιτητή $i$
$b_0$	Τιμή πρόβλεψης μήκους αντίχειρα όταν $Height2Group_i = 0$ (μέσο μήκος αντίχειρα για τους φοιτητές χαμηλού αναστήματος)	Τιμή πρόβλεψης μήκους αντίχειρα όταν $Height_i = 0$ (τεταγμένη τομής της γραμμής παλινδρόμησης)
$b_1$	Μεταβολή στην τιμή πρόβλεψης μήκους αντίχειρα για φοιτητές υψηλού αναστήματος (η μέση διαφορά μεταξύ των δύο ομάδων)	Μεταβολή στην τιμή πρόβλεψης μήκους αντίχειρα για κάθε αύξηση του ύψους κατά μία μονάδα (η κλίση της γραμμής παλινδρόμησης)
$X_i$	Μεταβλητή `Height2Group` του φοιτητή $i$ (κωδικοποιημένη ως 0 = όχι ψηλός, 1 = ψηλός)	Ύψος του φοιτητή $i$ (σε εκατοστά)
$e_i$	Σφάλμα πρόβλεψης για τον φοιτητή $i$	Σφάλμα πρόβλεψης για τον φοιτητή $i$

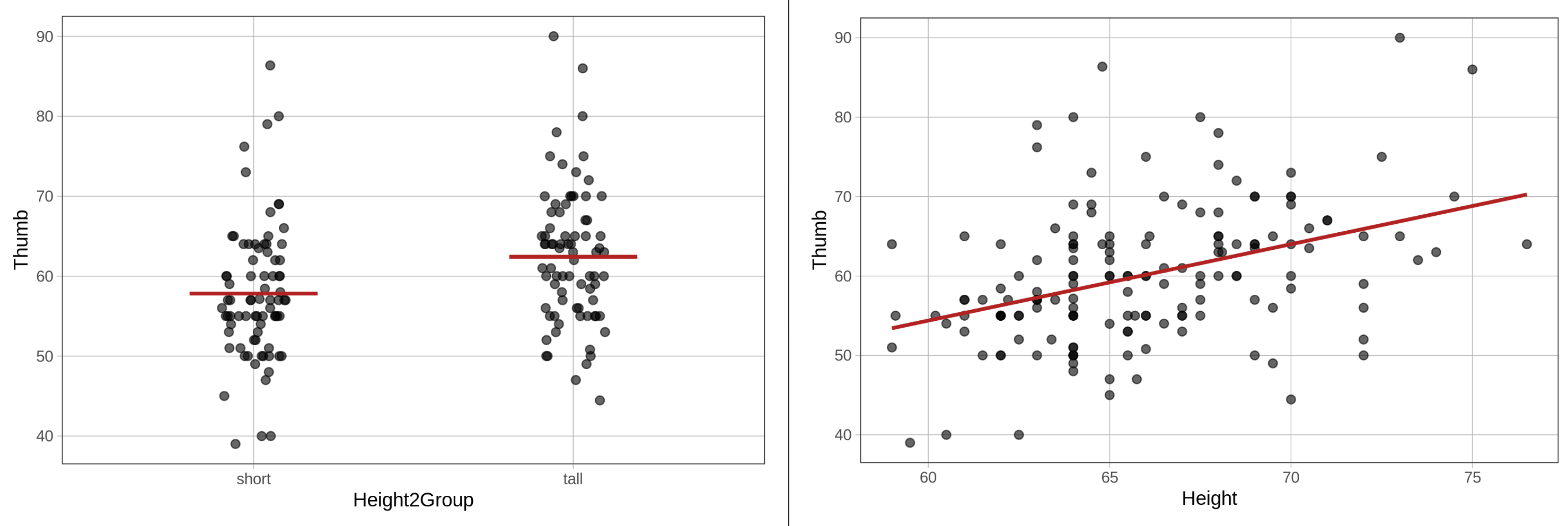
Οπτικοποίηση των Μοντέλων

Σχήμα 10.6: Μοντέλο Ομάδων (αριστερά) και Μοντέλο Παλινδρόμησης (δεξιά)

Προσαρμογή Μοντέλου Παλινδρόμησης κατά Λάθος

Αν και η R είναι αρκετά «έξυπνη» ώστε να αναγνωρίζει ποιο είδος μοντέλου πρέπει να εφαρμόσει, δεν κάνει πάντα τη σωστή επιλογή. Αν κωδικοποιήσουμε τη μεταβλητή ομάδων με αλφαριθμητικές τιμές όπως female και male ή short και tall, η R θα καταλάβει ότι η μεταβλητή είναι ποιοτική και θα προσαρμόσει ένα μοντέλο ομάδων.

Ωστόσο, αν χρησιμοποιήσουμε αριθμητική κωδικοποίηση, π.χ. 1 και 2, και ξεχάσουμε να τη δηλώσουμε ως παράγοντα (factor), τότε η R μπορεί να «μπερδευτεί» και να θεωρήσει τη μεταβλητή ποσοτική, προσαρμόζοντας έτσι ένα μοντέλο παλινδρόμησης αντί για ένα μοντέλο ομάδων.

Για παράδειγμα, προσθέσαμε μια νέα μεταβλητή στα δεδομένα Fingers, ονόματι GenderNum. Τα δεδομένα φαίνονται ως εξής:

  Thumb  Gender GenderNum
1    66   male         2
2    64 female         1
3    56 female         1
4    70   male         2
5    52 female         1
6    62   male         2

Αν παρατηρήσουμε τις μεταβλητές Gender και GenderNum, θα δούμε ότι περιέχουν την ίδια πληροφορία: οι φοιτητές 2, 3 και 5 ανήκουν στη μία ομάδα, ενώ οι φοιτητές 1, 4 και 6 στην άλλη.

Είτε προσαρμόσουμε ένα μοντέλο με τη Gender (π.χ. Gender_model) είτε με τη GenderNum (π.χ.GenderNum_model), θα περιμέναμε να προκύψουν ακριβώς τα ίδια αποτελέσματα. Ας το δοκιμάσουμε στην πράξη.

Call:
lm(formula = Thumb ~ Gender, data = Fingers)

Coefficients:
(Intercept)   Gendermale
     58.256        6.447 

Call:
lm(formula = Thumb ~ GenderNum, data = Fingers)

Coefficients:
(Intercept)    GenderNum
     51.809        6.447

Ποια εκτίμηση παραμέτρου είναι διαφορετική στο μοντέλο της Gender έναντι του μοντέλου της GenderNum;

$b_0$, η τιμή πρόβλεψης του μήκους αντίχειρα όταν $X_i = 0$$b_1$, η μεταβολή στο μήκος αντίχειρα όταν το $X_i$ αυξάνεται κατά μία μονάδα

Επεξήγηση

Σωστή απάντηση: Α - $b_0$, η τιμή πρόβλεψης του μήκους αντίχειρα όταν $X_i = 0$

Σύγκριση παραμέτρων:

Εκτίμηση παραμέτρου	Μοντέλο της `Gender`	Μοντέλο της `GenderNum`	Διαφορά;
$b_0$ (σταθερός όρος)	58.256	51.809	ΝΑΙ ✓ (διαφορετικό)
$b_1$ (κλίση)	6.447	6.447	ΟΧΙ (ίδιο)

Η μόνη διαφορά είναι το $b_0$ (σταθερός όρος)!

Κωδικοποίηση των μεταβλητών

Gender (factor):

levels(Fingers$Gender)
# [1] "female" "male"

Τύπος: Factor με 2 επίπεδα
Κωδικοποίηση στο μοντέλο:
- female = 0 (ομάδα αναφοράς, αυτόματα από την R)
- male = 1

GenderNum (numeric):

Τύπος: Αριθμητική μεταβλητή (1 ή 2)
Κωδικοποίηση:
- female = 1
- male = 2

Βασική διαφορά: Η Gender χρησιμοποιεί 0/1, ενώ η GenderNum χρησιμοποιεί 1/2. Αυτή η μετατόπιση κατά 1 μονάδα επηρεάζει τον σταθερό όρο!

Γιατί το $b_0$ διαφέρει;

Ο σταθερός όρος $b_0$ αντιπροσωπεύει την τιμή πρόβλεψης όταν $X = 0$.

Μοντέλο της Gender (κωδικοποίηση 0/1):

\[\text{Thumb}_i = 58.256 + 6.447 \times \text{Gender}_{\text{male},i}\]

Όταν $\text{Gender}_{\text{male}} = 0$ (δηλ. female): $\hat{Y} = 58.256$
Άρα το $b_0 = 58.256$ είναι ο μέσος όρος για τις γυναίκες

Μοντέλο της GenderNum (κωδικοποίηση 1/2):

\[\text{Thumb}_i = 51.809 + 6.447 \times \text{GenderNum}_i\]

Όταν $\text{GenderNum} = 0$ (υποθετική τιμή): $\hat{Y} = 51.809$
Αλλά η τιμή $\text{GenderNum} = 0$ δεν υπάρχει στα δεδομένα!
Το $b_0 = 51.809$ είναι η υποθετική τιμή που θα είχαμε αν υπήρχε $\text{GenderNum} = 0$

Επαλήθευση με τις πραγματικές προβλέψεις:

GenderNum=1 (female): $\hat{Y} = 51.809 + 6.447 \times 1 = 58.256$ ✓
GenderNum=2 (male): $\hat{Y} = 51.809 + 6.447 \times 2 = 64.703$ ✓

Οι προβλέψεις ταιριάζουν με τους μέσους όρους των ομάδων!

Μαθηματική σχέση μεταξύ των μοντέλων

Μοντέλο της Gender (0/1):

\[Y = 58.256 + 6.447 \times X_{\text{Gender}}\]

Όπου $X_{\text{`Gender`}} \in \{0, 1\}$

Μοντέλο της GenderNum (1/2):

\[Y = 51.809 + 6.447 \times X_{\text{GenderNum}}\]

Όπου $X_{\text{GenderNum}} \in \{1, 2\}$

Παρατηρήστε ότι:

\[X_{\text{GenderNum}} = X_{\text{Gender}} + 1\]

Η GenderNum είναι η Gender μετατοπισμένη κατά 1.

Αντικαθιστώντας:

\[Y = 51.809 + 6.447 \times (X_{\text{Gender}} + 1)\]

\[Y = 51.809 + 6.447 \times X_{\text{Gender}} + 6.447\]

\[Y = (51.809 + 6.447) + 6.447 \times X_{\text{Gender}}\]

\[Y = 58.256 + 6.447 \times X_{\text{Gender}}\]

Ακριβώς το μοντέλο της Gender! ✓

Γενικός τύπος:

Όταν $X_{\text{new}} = X_{\text{old}} + c$, τότε:

\[b_{0,\text{new}} = b_{0,\text{old}} - b_1 \times c\]

Στην περίπτωσή μας ($c = 1$):

\[b_{0,\text{GenderNum}} = b_{0,\text{Gender}} - 6.447 \times 1\]

\[51.809 = 58.256 - 6.447\] ✓

Γιατί το $b_1$ παραμένει ίδιο;

Το $b_1 = 6.447$ σε αμφότερα τα μοντέλα

Το $b_1$ εκφράζει τη διαφορά μεταξύ των δύο ομάδων:

mean(Thumb ~ Gender, data = Fingers)
#   female     male
# 58.25641 64.70339

# Διαφορά
64.70339 - 58.25641
# [1] 6.44698 ≈ 6.447 ✓

Αυτή η διαφορά δεν αλλάζει με την κωδικοποίηση!

Στη Gender: Από 0 σε 1 (αύξηση 1 μονάδας) → +6.447 mm
Στη GenderNum: Από 1 σε 2 (αύξηση 1 μονάδας) → +6.447 mm

Και στις δύο περιπτώσεις, μία μονάδα αύξησης αντιστοιχεί στη μετάβαση από female σε male, δηλαδή στην ίδια διαφορά.

Σύγκριση κωδικοποιήσεων

Χαρακτηριστικό	`Gender` (0/1)	`GenderNum` (1/2)	Σχόλιο
Κωδικοποίηση `female`	0	1	Διαφορά +1
Κωδικοποίηση `male`	1	2	Διαφορά +1
$b_0$	58.256	51.809	Διαφορά -6.447
$b_1$	6.447	6.447	Ίδιο
Πρόβλεψη `female`	58.256	58.256	Ίδιο ✓
Πρόβλεψη `male`	64.703	64.703	Ίδιο ✓

Παρατήρηση: Η διαφορά στο $b_0$ είναι ακριβώς $-b_1$, επειδή η κωδικοποίηση μετατοπίστηκε κατά +1.

Συμπέρασμα

Ποια εκτίμηση παραμέτρου διαφέρει;

Μόνο το $b_0$ (σταθερός όρος) είναι διαφορετικό μεταξύ των δύο μοντέλων.

Γιατί διαφέρει το $b_0$;

✓ Η Gender χρησιμοποιεί κωδικοποίηση 0/1 (female=0, male=1)

✓ Η GenderNum χρησιμοποιεί κωδικοποίηση 1/2 (female=1, male=2)

✓ Το $b_0$ αντιπροσωπεύει την πρόβλεψη όταν $X = 0$:

Στη Gender: το $X=0$ αντιστοιχεί σε female → $b_0 = 58.256$ (μέσος όρος female)
Στη GenderNum: το $X=0$ είναι υποθετική τιμή (δεν υπάρχει) → $b_0 = 51.809$

✓ Η μετατόπιση της κωδικοποίησης κατά +1 προκαλεί αλλαγή στο $b_0$ κατά $-b_1$:

\[b_{0,\text{GenderNum}} = b_{0,\text{Gender}} - b_1 = 58.256 - 6.447 = 51.809\] ✓

Γιατί ΔΕΝ διαφέρει το $b_1$;

✓ Το $b_1$ εκφράζει τη διαφορά μεταξύ των ομάδων: male - female = 6.447 mm

✓ Αυτή η διαφορά είναι ανεξάρτητη από την κωδικοποίηση

✓ Και στα δύο μοντέλα, 1 μονάδα αύξηση στο $X$ σημαίνει μετάβαση από female σε male

Τελική σύνοψη:

Στοιχείο	`Gender` (0/1)	`GenderNum` (1/2)
$b_0$	58.256	51.809 (διαφέρει κατά -6.447)
$b_1$	6.447	6.447 (ίδιο)
Προβλέψεις	Ίδιες	Ίδιες

Το $b_0$ διαφέρει επειδή η κωδικοποίηση 1/2 “μετατοπίζει” το σημείο αναφοράς κατά 1 μονάδα, αλλά τα δύο μοντέλα περιγράφουν την ίδια σχέση και δίνουν ταυτόσημες προβλέψεις!

Γιατί οι εκτιμήσεις των παραμέτρων στο μοντέλο GenderNum δεν είναι ίδιες με αυτές του μοντέλου Gender;

Επειδή η Gender είναι ποιοτική μεταβλητή (δηλαδή τύπου factor), η συνάρτηση lm() προσαρμόζει ένα μοντέλο ομάδων. Αντίθετα, όταν χρησιμοποιούμε τη GenderNum, η lm() θεωρεί ότι η αριθμητική κωδικοποίηση (1 ή 2) αντιστοιχεί σε ποσοτική μεταβλητή. Εφόσον δεν δηλώσαμε ρητά ότι η GenderNum πρέπει να αντιμετωπιστεί ως ποιοτική, η lm() προσαρμόζει μια ευθεία παλινδρόμησης αντί για ένα μοντέλο δύο ομάδων. Ως αποτέλεσμα, η ερμηνεία των εκτιμήσεων της παλινδρόμησης διαφέρει από αυτήν που θα περιμέναμε σε ένα μοντέλο ομάδων.

H κλίση ($b_1$) θα είναι αριθμητικά ίδια με εκείνη του μοντέλου δύο ομάδων, καθώς εξακολουθεί να εκφράζει τη μεταβολή στο μήκος του αντίχειρα για μια μονάδα αύξησης της ανεξάρτητης μεταβλητής.

Για τη Gender, μια μεταβολή κατά μία μονάδα σημαίνει μετάβαση από το «όχι άνδρας» ($X_i = 0$) στο «άνδρας» ($X_i = 1$).

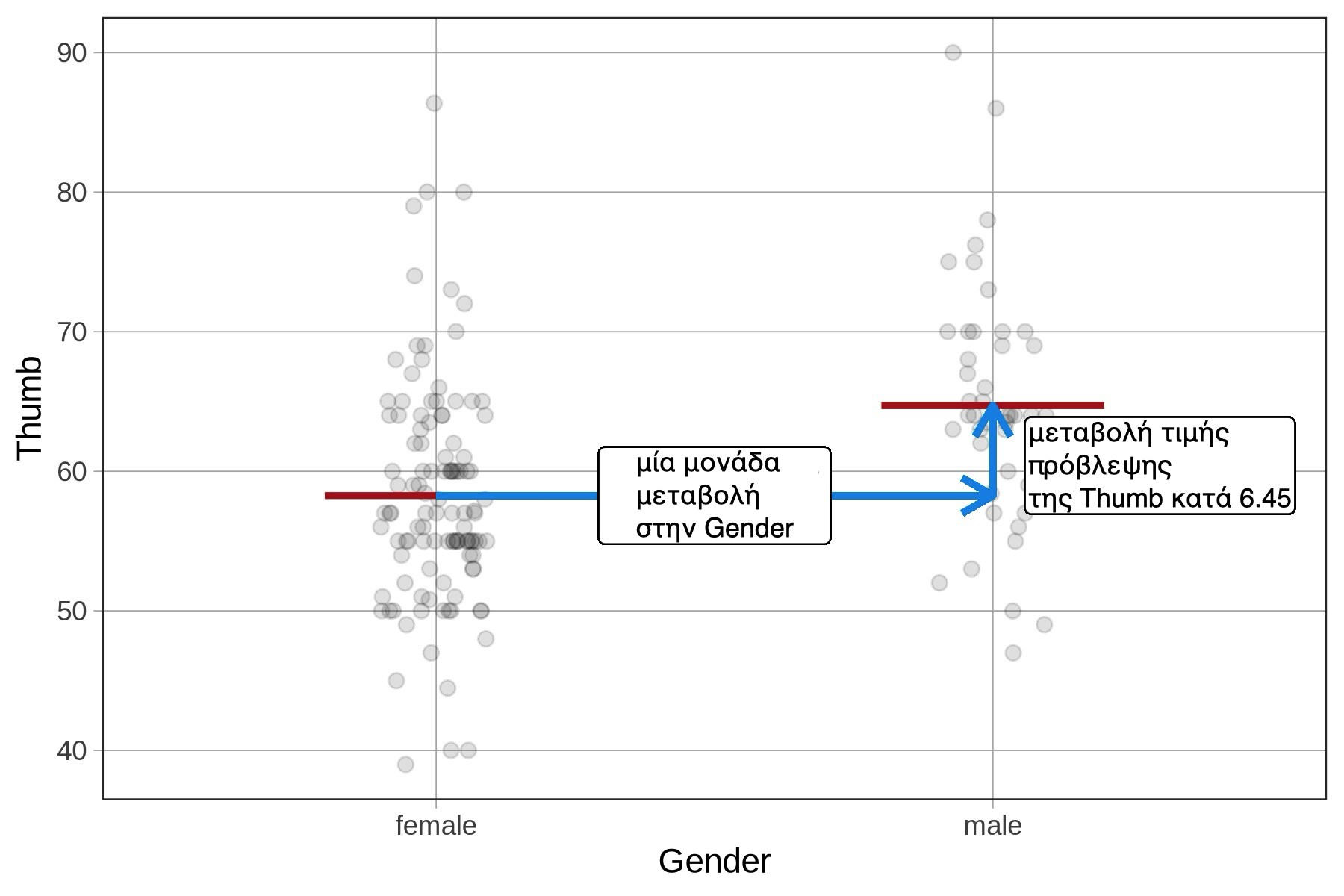b_1 του μοντέλου της Gender Για τη GenderNum, η μεταβολή από το «όχι άνδρας» ($X_i = 1$) στο «άνδρας» ($Χ_i = 2$) έχει το ίδιο νόημα, αλλά το μοντέλο την αντιμετωπίζει ως συνεχή αριθμητική μεταβολή και όχι ως μέση διαφορά ανάμεσα σε ομάδες.

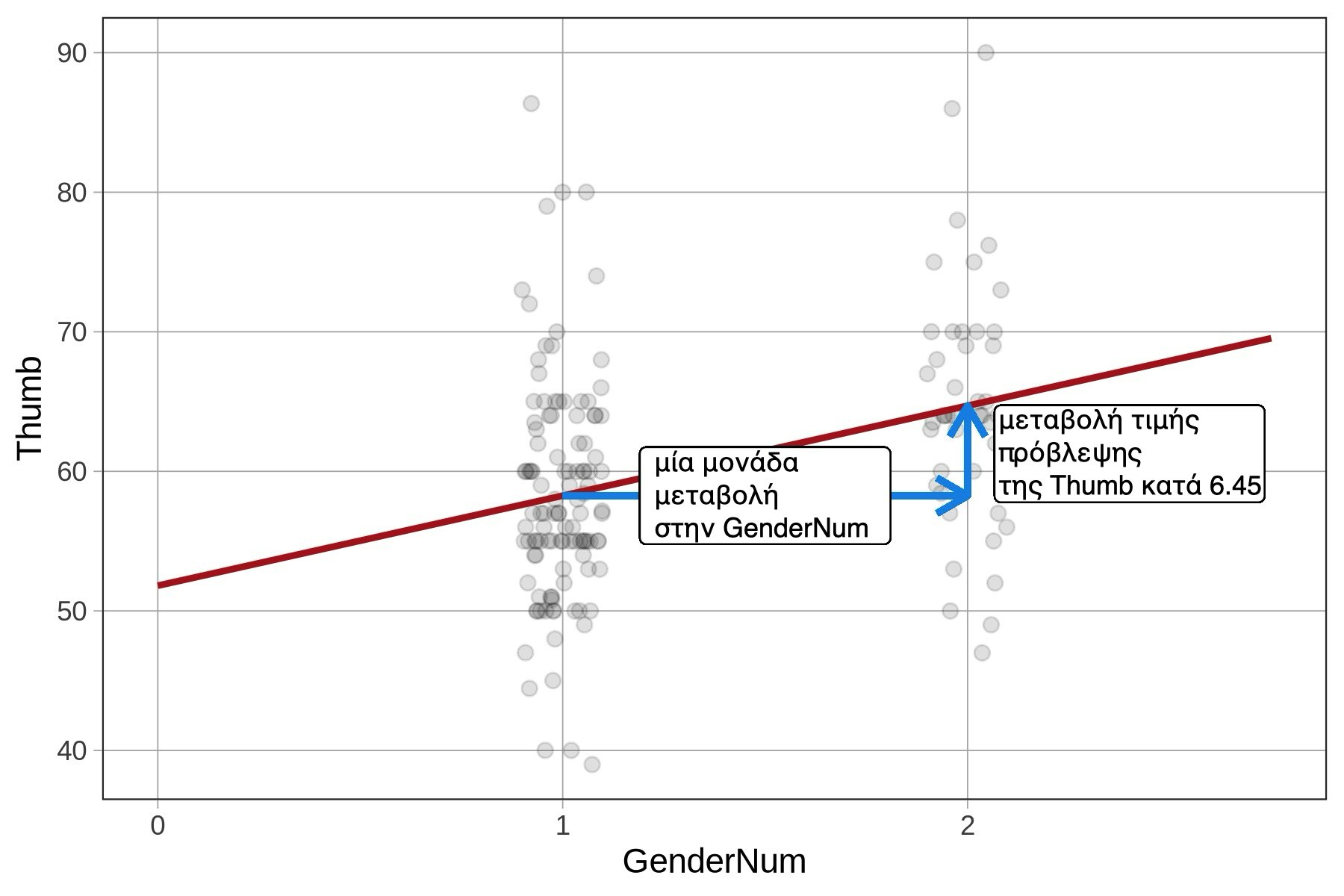
Σχήμα 10.7: $b_1$ του μοντέλου της `GenderNum`

Ωστόσο, ο σταθερός όρος ($b_0$) θα είναι διαφορετικός στο μοντέλο με τη GenderNum, όπου αντιπροσωπεύει το σημείο τομής της ευθείας παλινδρόμησης με τον άξονα y, δηλαδή την τιμή πρόβλεψης του μήκους αντίχειρα όταν η μεταβλητή έχει τιμή 0. Αυτό, βέβαια, δεν έχει νόημα όταν υπάρχουν μόνο δύο ομάδες που έχουν κωδικοποιηθεί ως 1 και 2. Σε αυτή την περίπτωση, το αποτέλεσμα είναι ανεπιθύμητο μοντέλο παλινδρόμησης που προσαρμόστηκε κατά λάθος.

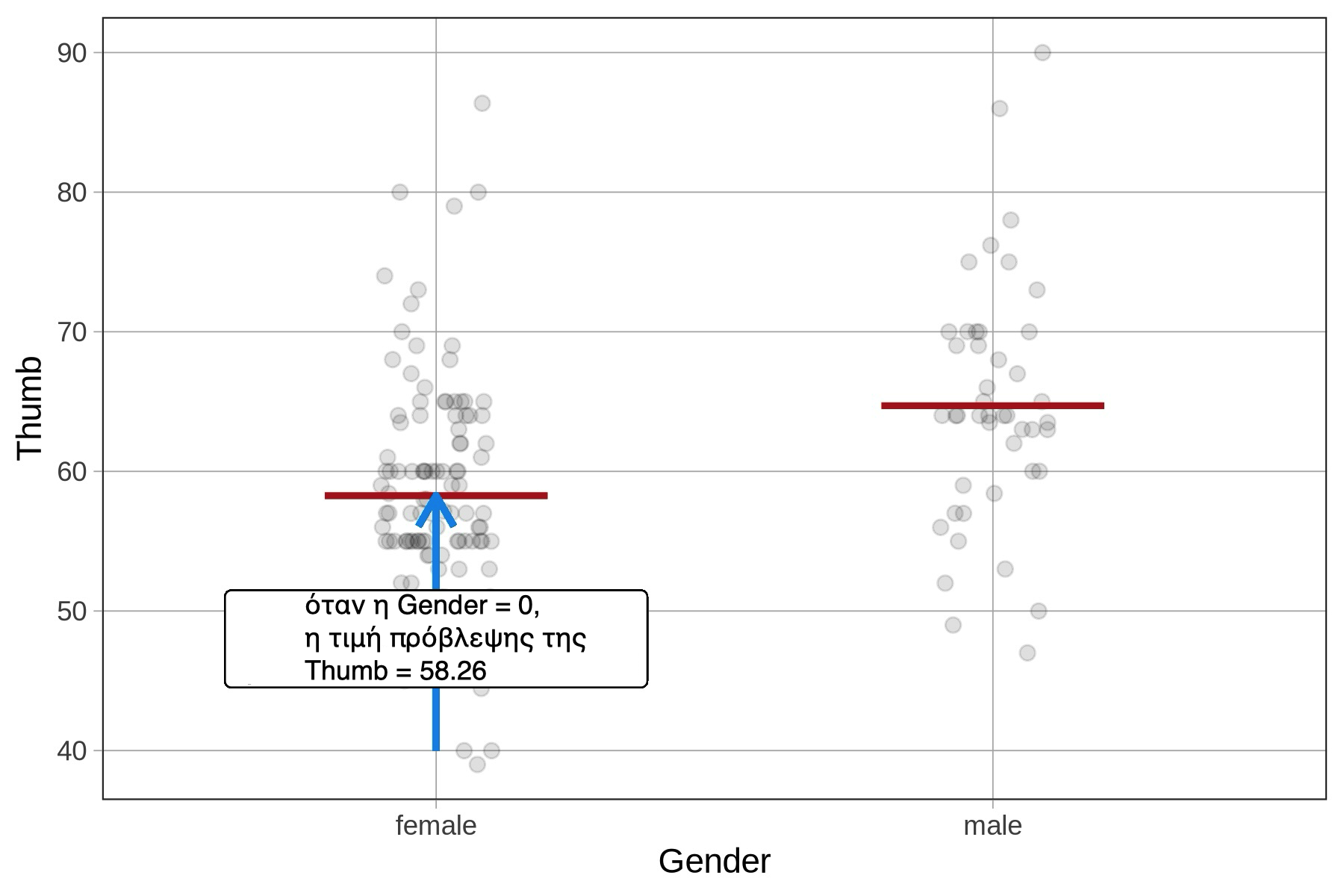
Σχήμα 10.8: $b_0$ του μοντέλου της `Gender`

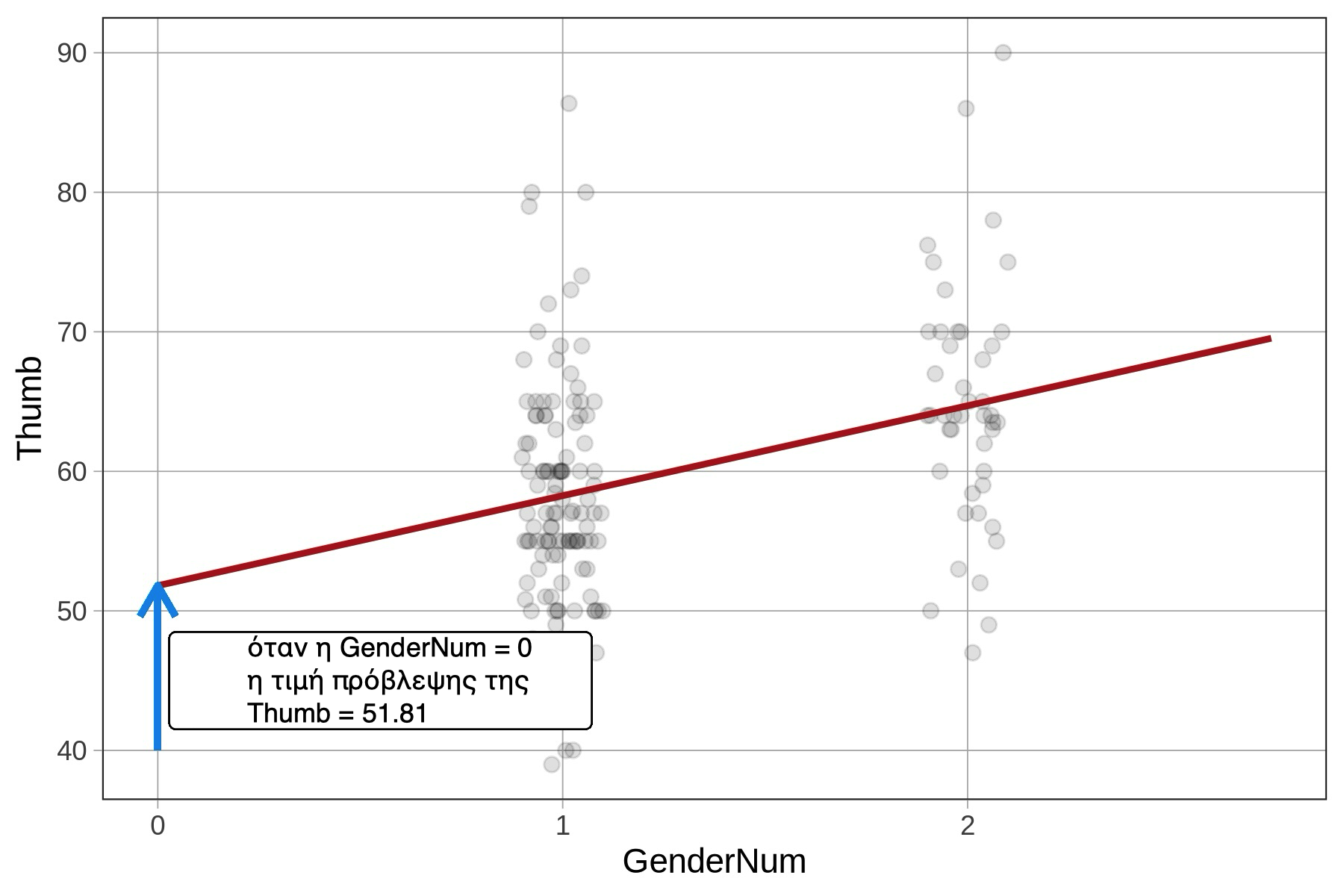
Σχήμα 10.9: $b_0$ του μοντέλου της `GenderNum`

Τι νομίζεις ότι θα συνέβαινε αν κωδικοποιούσαμε τις ομάδες της GenderNum ως 0 και 1 αντί για 1 και 2; Γιατί;

10.5 Σφάλμα από το Μοντέλο της `Height`

Ανεξάρτητα από το είδος του μοντέλου, το σφάλμα του μοντέλου (ή υπόλοιπο, residual) υπολογίζεται πάντα με τον ίδιο τρόπο για κάθε παρατήρηση:

υπόλοιπο = παρατηρούμενη τιμή - τιμή πρόβλεψης

Θυμηθείτε και την εξίσωση ΔΕΔΟΜΕΝΑ = ΜΟΝΤΕΛΟ + ΣΦΑΛΜΑ. Ποια στοιχεία αυτής της εξίσωσης αντιστοιχούν στα μέρη της παραπάνω σχέσης;

Για τα μοντέλα παλινδρόμησης, η τιμή πρόβλεψης της $Y_i$ βρίσκεται επάνω στην ευθεία παλινδρόμησης. Συνεπώς, το σφάλμα (υπόλοιπο) υπολογίζεται ως η κατακόρυφη απόσταση μεταξύ της πραγματικής τιμής μιας παρατήρησης στον άξονα $Y$ (την εξαρτημένη μεταβλητή) και της αντίστοιχης τιμής πρόβλεψης που δίνει η ευθεία παλινδρόμησης.

Στο παρακάτω διάγραμμα επισημαίνονται έξι παρατηρήσεις (σημεία με μαύρο χρώμα) και τα αντίστοιχα υπόλοιπά τους (οι κάθετες γραμμές με κόκκινο χρώμα) από το μοντέλο παλινδρόμησης της Height.

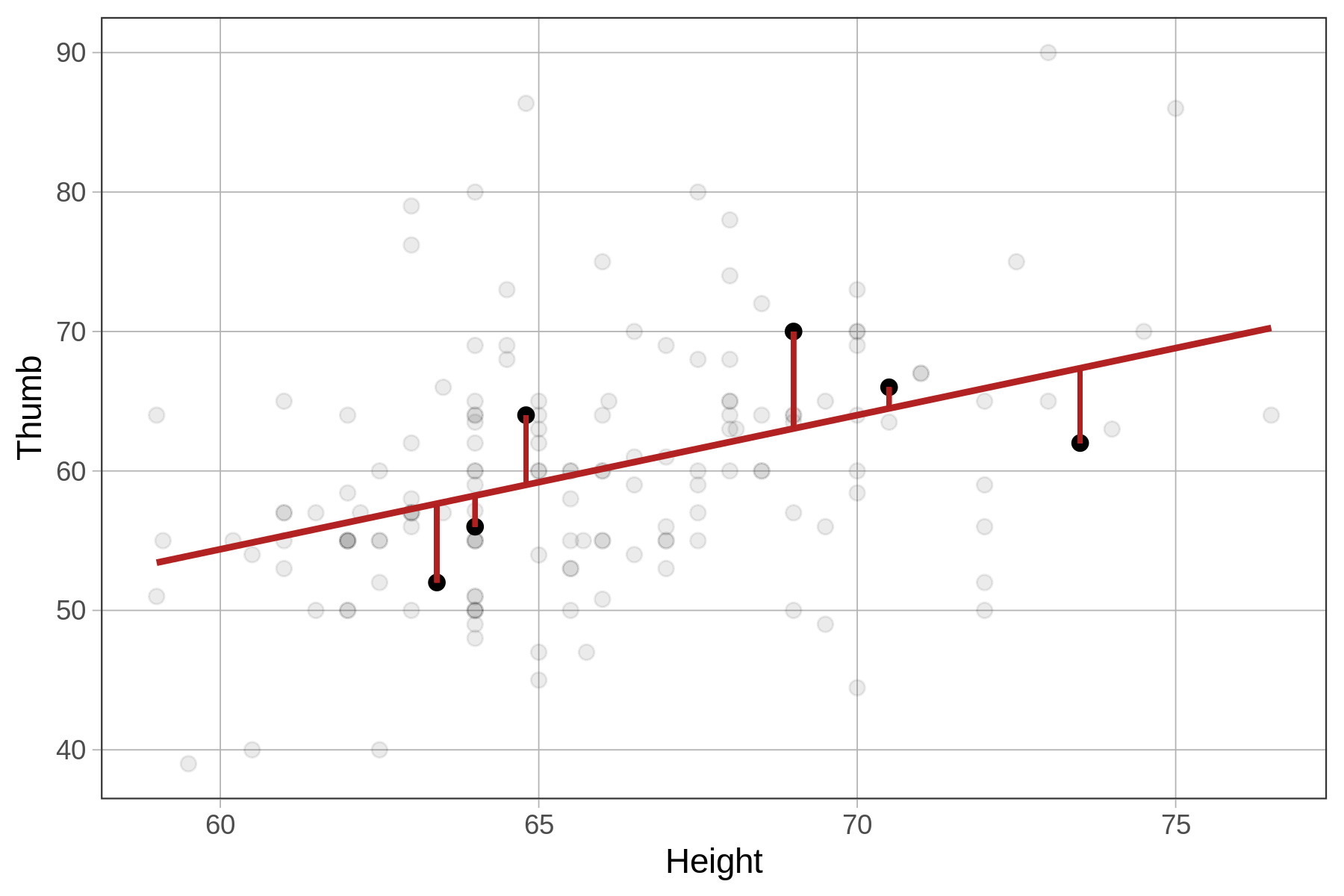Σημειώστε ότι μια αρνητική τιμή υπολοίπου (που βρίσκεται κάτω από την ευθεία παλινδρόμησης) σημαίνει ότι η παρατηρούμενη τιμή του μήκους αντίχειρα (Thumb) είναι μικρότερη από την τιμή πρόβλεψης του μήκους αντίχειρα, με βάση το ύψος του φοιτητή.

Τι σημαίνει μια θετικη τιμή υπολοίπου;

Τα υπόλοιπα από το μοντέλο της Height αντιπροσωπεύουν τη μεταβλητότητα του μήκους αντίχειρα (Thumb) που υπολείπεται αφού αφαιρεθεί το μέρος που μπορεί να εξηγηθεί από το ύψος.

Για παράδειγμα, ας εξετάσουμε ένα συγκεκριμένο φοιτητή (που εμφανίζεται στο παρακάτω διάγραμμα) με μήκος αντίχειρα 70 mm. Ένα υπόλοιπο ίσο με 7 σημαίνει ότι ο αντίχειρας του φοιτητή είναι 7 mm μακρύτερος από αυτόν που θα είχε προβλεφθεί από το μοντέλο με βάση το ύψος του.

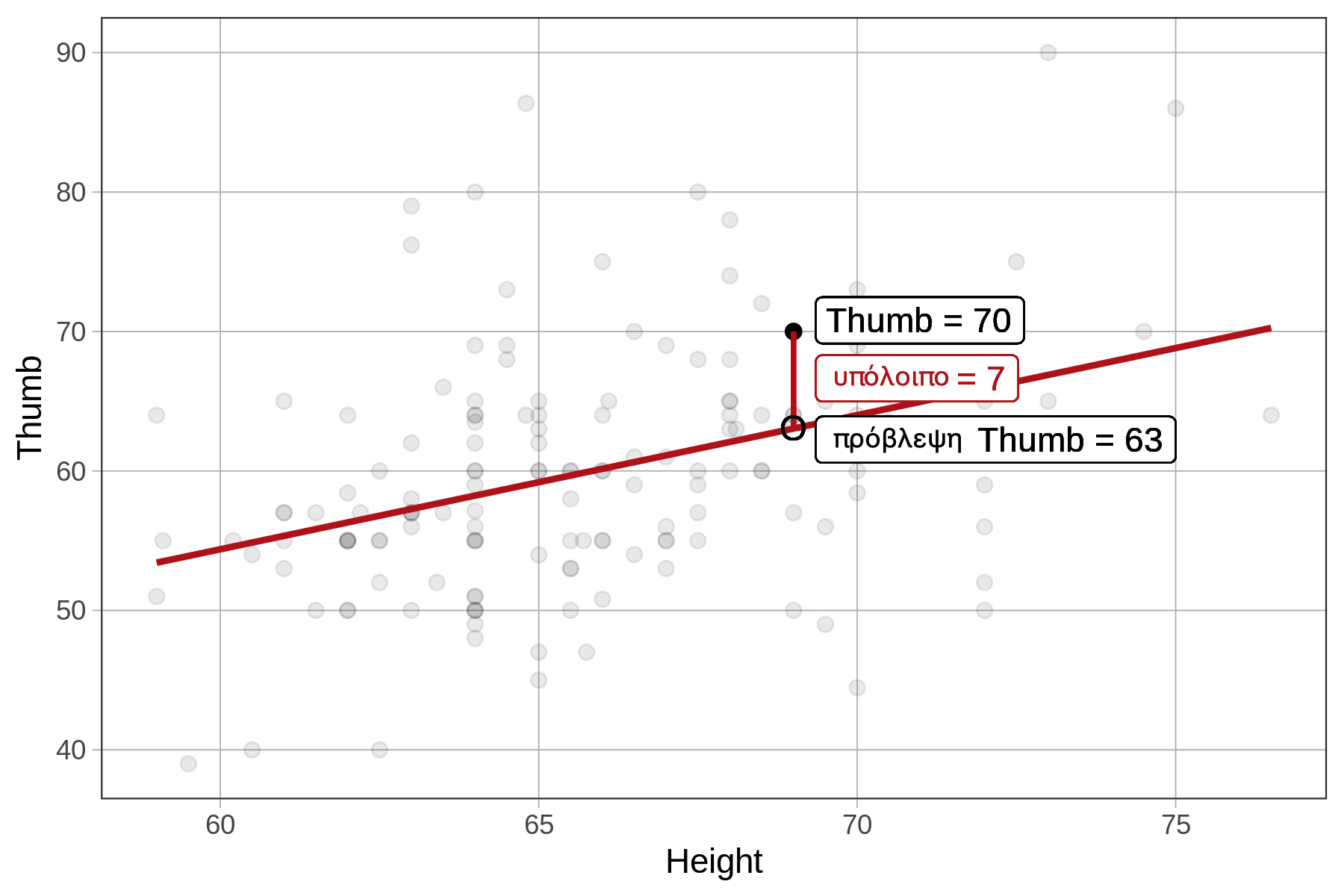
Με άλλα λόγια, μπορούμε να πούμε ότι, λαμβάνοντας υπόψη την επίδραση του ύψους (controlling for Height), ο αντίχειρας αυτού του φοιτητή είναι 7 mm μακρύτερος από το αναμενόμενο.

Ένα θετικό υπόλοιπο δείχνει ότι ο αντίχειρας είναι μακρύτερος από το αναμενόμενο για ένα άτομο αυτού του ύψους, ενώ ένα αρνητικό υπόλοιπο δείχνει ότι είναι κοντύτερος από το αναμενόμενο.

Αυτά τα υπόλοιπα μπορεί να μας οδηγήσουν στο ερώτημα: ποιοι άλλοι παράγοντες, πέρα από το ύψος θα μπορούσαν να εξηγήσουν αυτές τις διαφορές;

Άθροισμα Τετραγώνων Σφαλμάτων (`SS Error`) για το Μοντέλο του Ύψους

Όπως και στα άλλα μοντέλα που έχουμε δει (π.χ. το κενό μοντέλο και το μοντέλο ομάδων), η μετρική που χρησιμοποιούμε για να ποσοτικοποιήσουμε το συνολικό σφάλμα του μοντέλου της Height είναι το άθροισμα τετραγώνων των υπολοίπων (Sum of Squared Errors, ή SS Error).

Το SS Error υπολογίζεται από τα υπόλοιπα με τον ίδιο τρόπο όπως και στο μοντέλο ομάδων — δηλαδή, υψώνοντας κάθε υπόλοιπο στο τετράγωνο και στη συνέχεια αθροίζοντάς τα όλα (βλ. παρακάτω διάγραμμα).

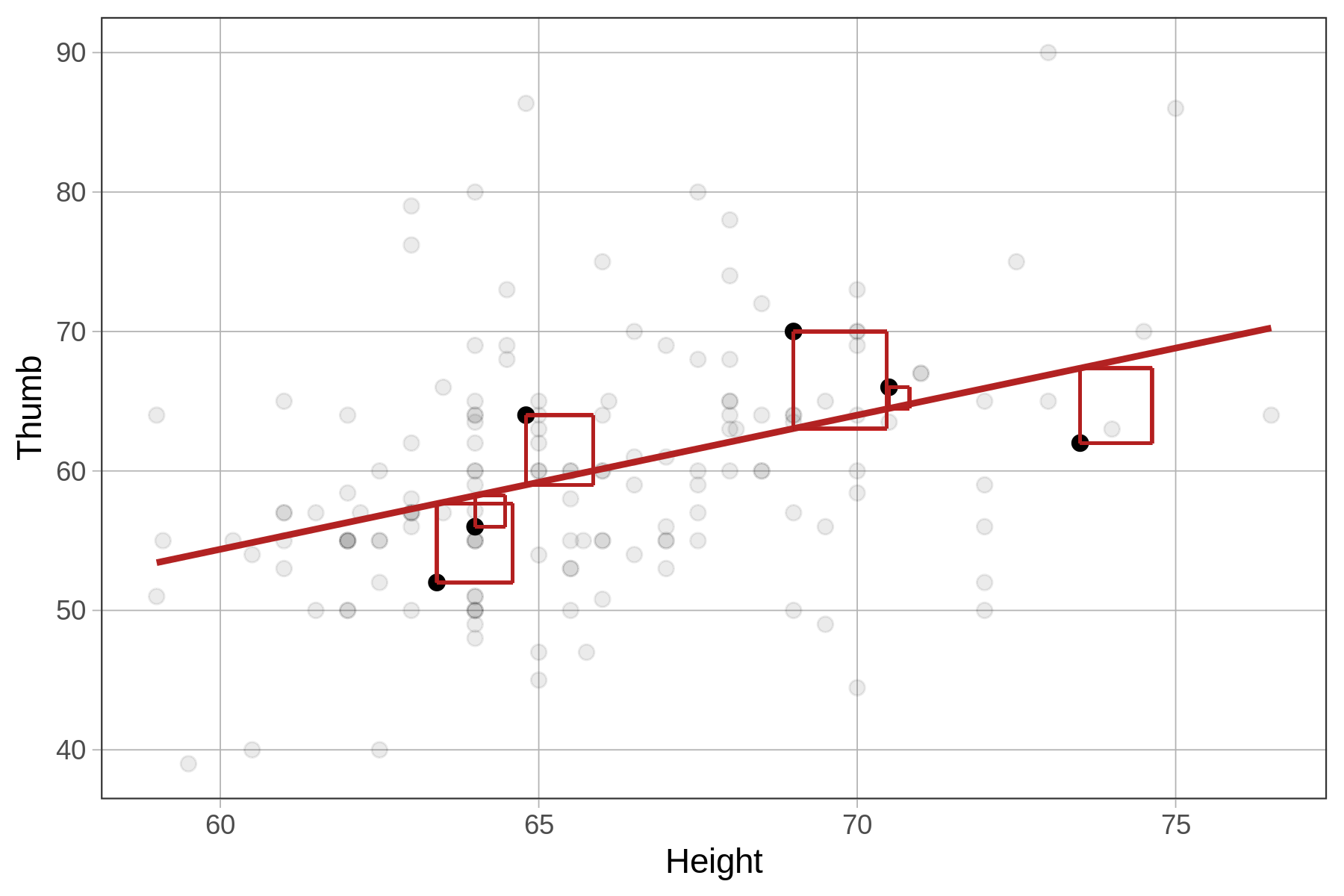
Να συγκρίνετε το άθροισμα τετραγώνων των υπολοίπων από το κενό μοντέλο (SS Total - SST) και το μοντέλο του ύψους (SS Error - SSE) για τις έξι παρατηρήσεις που φαίνονται στα παρακάτω διαγράμματα.

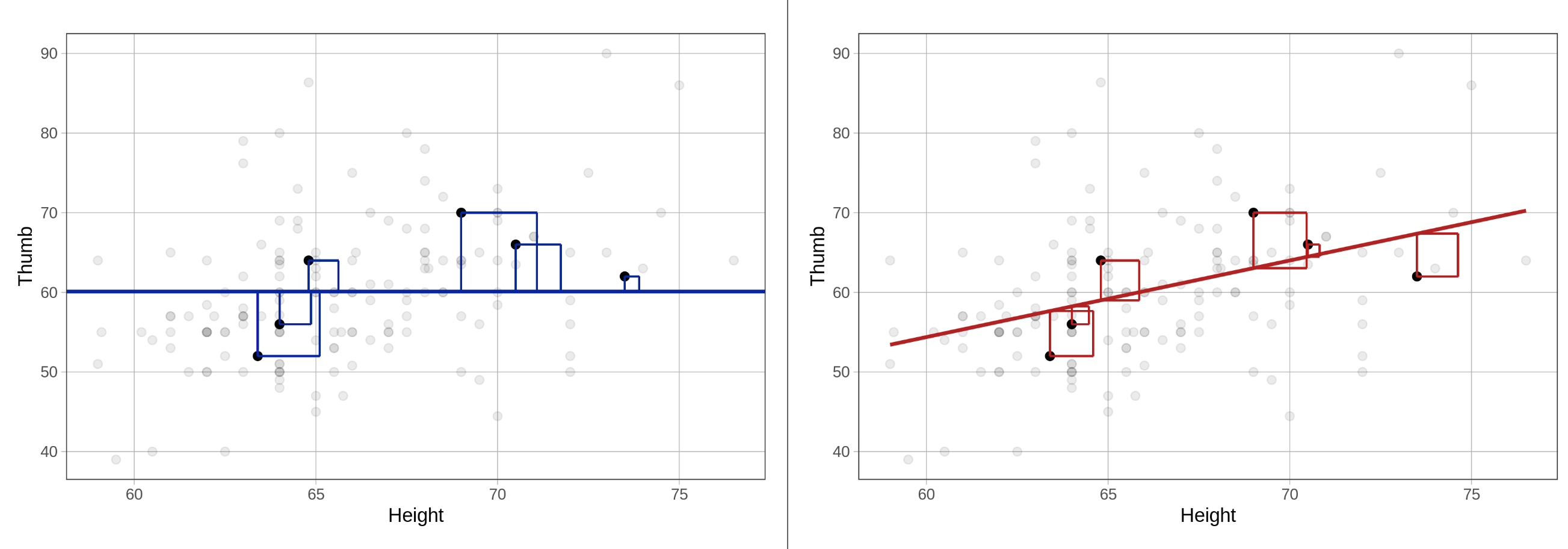
`SS Total`, Άθροισμα Τετραγώνων των Υπολοίπων από το κενό μοντέλο (αριστερά) και `SS Error`, Άθροισμα Τετραγώνων των Υπολοίπων από το μοντέλο της `Height` (δεξιά)

Με βάση τα τετραγωνισμένα υπόλοιπα για αυτές τις 6 παρατηρήσεις, ποιο μοντέλο πιστεύετε ότι θα είχε μικρότερο άθροισμα τετραγώνων των υπολοίπων; Με άλλα λόγια, σε ποιο μοντέλο, κατά μέσο όρο, είναι τα τετράγωνα μικρότερα;

Το SS Error (SSE) φαίνεται μικρότερο για το μοντέλο του ύψουςΤο SS Total (SST) φαίνεται μικρότερο για το κενό μοντέλο

Επεξήγηση

Σωστή απάντηση: Α — Το SSE φαίνεται μικρότερο για το μοντέλο του ύψους

Κατανόηση των όρων

Πρώτα, ας ξεκαθαρίσουμε την ορολογία:

SSE (Άθροισμα Τετραγώνων των Υπολοίπων ή των Σφαλμάτων):

Το άθροισμα των τετραγωνισμένων υπολοίπων για ένα συγκεκριμένο μοντέλο
Μετρά πόσο οι παρατηρήσεις αποκλίνουν από τις προβλέψεις του μοντέλου
Όσο μικρότερο το SSE, τόσο καλύτερα προβλέπει το μοντέλο

\[\text{SSE} = \sum_{i=1}^{n} (Y_i - \hat{Y}_i)^2\]

όπου: - $Y_i$ = παρατηρούμενη τιμή - $\hat{Y}_i$ = τιμή πρόβλεψης από το μοντέλο - $(Y_i - \hat{Y}_i)$ = υπόλοιπο (residual)

SST (Συνολικό Άθροισμα Τετραγώνων):

Το άθροισμα των τετραγωνισμένων αποκλίσεων από τον γενικό μέσο όρο
Μετρά τη συνολική μεταβλητότητα στα δεδομένα
Αναφέρεται στο κενό μοντέλο (empty model) που προβλέπει απλώς το μέσο όρο

\[\text{SST} = \sum_{i=1}^{n} (Y_i - \bar{Y})^2\]

όπου:

$\bar{Y}$ = μέσος όρος του $Y$
$(Y_i - \bar{Y})$ = απόκλιση από τον μέσο όρο

Σύγκριση μοντέλων

Κενό μοντέλο (Empty Model): \[\hat{Y}_i = \bar{Y}\]

Προβλέπει την ίδια τιμή (το μέσο όρο) για όλες τις παρατηρήσεις
Δεν χρησιμοποιεί καμία ανεξάρτητη μεταβλητή
Το σφάλμα του είναι το SST

Μοντέλο της Height: \[\hat{Y}_i = b_0 + b_1 \times \text{Height}_i\]

Προβλέπει διαφορετικές τιμές ανάλογα με το ύψος κάθε ατόμου
Χρησιμοποιεί την Height ως ανεξάρτητη μεταβλητή
Το σφάλμα του είναι το SSE

Γιατί το SSE είναι μικρότερο από το SST;

Το μοντέλο της Height πρέπει να έχει μικρότερο ή ίσο SSE από το κενό μοντέλο, επειδή:

Εξηγεί μέρος της μεταβλητότητας: Η μεταβλητή Height εξηγεί γιατί μερικά άτομα έχουν μεγαλύτερους αντίχειρες
Προσαρμόζεται καλύτερα στα δεδομένα: Οι προβλέψεις είναι πιο κοντά στις πραγματικές τιμές
Μαθηματική σχέση: $\text{SSE} \leq \text{SST}$ (πάντα)

Γιατί η επιλογή Β είναι λάθος

Β. «Το SS Total (SST) φαίνεται μικρότερο για το κενό μοντέλο» — ΛΑΘΟΣ

Γενική αρχή:

\[\text{SSE (οποιοδήποτε μοντέλο)} \leq \text{SST (κενό μοντέλο)}\]

Όσο περισσότερες ανεξάρτητες μεταβλητές προσθέτουμε (που έχουν σχέση με την εξαρτημένη), τόσο περισσότερο μειώνεται το άθροισμα τετραγώνων των υπολοίπων.

Συνοπτικά: Το μοντέλο της Height έχει μικρότερο άθροισμα τετραγώνων υπολοίπων (SS Error) από το κενό μοντέλο (SS Total), γιατί χρησιμοποιεί το ύψος για να εξηγήσει μέρος της μεταβλητότητας στο μήκος του αντίχειρα. Τα υπόλοιπα (και τα τετράγωνά τους) είναι μικρότερα στο μοντέλο της Height.

Τι σημαίνει όταν ένα μοντέλο έχει μικρότερο άθροισμα τετραγώνων (SS) από το κενό μοντέλο;

Χρήση της R για τη σύγκριση των Αθροισμάτων Τετραγώνων του μοντέλου της `Height` και του κενού μοντέλου

Όπως κάναμε και με τα μοντέλα ομάδων (π.χ. το μοντέλο της Height2Group και το μοντέλο της Gender), μπορούμε να χρησιμοποιήσουμε τη συνάρτηση resid() για να πάρουμε τα υπόλοιπα από το μοντέλο της Height. Στη συνέχεια, μπορούμε να τα υψώσουμε στο τετράγωνο και να τα αθροίσουμε για να υπολογίσουμε το SS Error του μοντέλου, ως εξής:

Height_model <- lm(Thumb ~ Height, data = Fingers)
sum(resid(Height_model)^2)

Το SS Total (από το κενό μοντέλο) είναι 11880. Κάντε μια πρόβλεψη: Ποια θα είναι η σχέση του με το SS Error (από το μοντέλο της Height);

Το SSE θα είναι ίσο με το SSTΤο SSE θα είναι μεγαλύτερο από το SSTΤο SSE θα είναι μικρότερο από το SST

Επεξήγηση

Σωστή απάντηση: Γ — Το SSE θα είναι μικρότερο από το SST

Κατανόηση των όρων

SS Total (SST): Το συνολικό άθροισμα τετραγώνων (Sum of Squares Total)

Μετράει τη συνολική μεταβλητότητα στα δεδομένα
Υπολογίζεται από το κενό μοντέλο (empty model)
Το κενό μοντέλο προβλέπει το μέσο όρο για όλες τις παρατηρήσεις: $\hat{Y}_i = \bar{Y}$

\[\text{SST} = \sum_{i=1}^{n}(Y_i - \bar{Y})^2\]

SS Error (SSE): Το άθροισμα τετραγώνων των υπολοίπων ή σφαλμάτων (Sum of Squares Error)

Μετράει τη μεταβλητότητα που δεν εξηγείται από το μοντέλο
Υπολογίζεται από το μοντέλο με μια ανεξάρτητη μεταβλητή (π.χ., μοντέλο της Height)
Είναι το άθροισμα των τετραγώνων των υπολοίπων (residuals)

\[\text{SSE} = \sum_{i=1}^{n}(Y_i - \hat{Y}_i)^2\]

Γιατί το SSE είναι μικρότερο από το SST

Το μοντέλο της Height βελτιώνει τις προβλέψεις

Κενό μοντέλο:

\[\hat{Y}_i = \bar{Y} \text{ (ίδια πρόβλεψη για όλους)}\]

Προβλέπει το μέσο όρο για κάθε άτομο, ανεξάρτητα από το ύψος τους
Αγνοεί τη σχέση μεταξύ Height και Thumb
Έχει μεγάλα σφάλματα πρόβλεψης

Μοντέλο της Height: \[\hat{Y}_i = -3.33 + 0.378 \times \text{Height}_i\]

Προβλέπει διαφορετικές τιμές για κάθε άτομο, ανάλογα με το ύψος τους
Χρησιμοποιεί τη σχέση μεταξύ της Height και της Thumb
Έχει μικρότερα σφάλματα πρόβλεψης

Θεμελιώδης αρχή της παλινδρόμησης:

Ένα μοντέλο με ανεξάρτητη μεταβλητή πάντα κάνει καλύτερες προβλέψεις (ή στη χειρότερη περίπτωση τις ίδιες) από το κενό μοντέλο.

\[\text{SSE (με ανεξάρτητη μεταβλητή)} \leq \text{SST (κενό μοντέλο)}\]

Γιατί οι άλλες επιλογές είναι λάθος

Α. «Το SSE θα είναι ίσο με το SST» — ΛΑΘΟΣ

Αυτό θα ίσχυε μόνο αν το μοντέλο της Height δεν είχε καμία προβλεπτική ικανότητα.

Αν SSE = SST, τότε: \[\text{SST} - \text{SSE} = 0\]

Αυτό θα σήμαινε ότι:

Η Height δεν εξηγεί τίποτα από τη μεταβλητότητα της Thumb
Δεν υπάρχει καμία σχέση μεταξύ ύψους και μήκους αντίχειρα
Ο συντελεστής κλίσης θα ήταν $b_1 = 0$

Αλλά γνωρίζουμε ότι υπάρχει σχέση (το μοντέλο έχει $b_1 = 0.378 \neq 0$), άρα SSE < SST.

Β. «Το SSE θα είναι μεγαλύτερο από το SST» — ΛΑΘΟΣ

Αυτό είναι μαθηματικά αδύνατο.

Το SSE δεν μπορεί ποτέ να υπερβεί το SST επειδή:

Το κενό μοντέλο είναι το χειρότερο δυνατό μοντέλο
- Προβλέπει το μέσο όρο για όλους
- Δίνει το SST (μέγιστη ανεξήγητη μεταβλητότητα)
Κάθε άλλο μοντέλο βελτιώνει (ή στη χειρότερη περίπτωση είναι ίδιο με το κενό)
- Χρησιμοποιεί πληροφορία από ανεξάρτητες μεταβλητές
- Μειώνει την ανεξήγητη μεταβλητότητα

Πότε το SSE είναι κοντά στο SST;

Το SSE πλησιάζει το SST όταν:

Η ανεξάρτητη μεταβλητή έχει μικρή προβλεπτική ικανότητα
Η σχέση μεταξύ X και Y είναι αδύναμη
Το PRE ή $R^2$ θα είναι κοντά στο 0

Συμπέρασμα

Το SS Error από το μοντέλο της Height θα είναι μικρότερο από το SS Total γιατί:

Το μοντέλο της Height χρησιμοποιεί πληροφορία για να βελτιώσει τις προβλέψεις
Μέρος της μεταβλητότητας εξηγείται από τη σχέση Height-Thumb
Η ανεξήγητη μεταβλητότητα (SSE) μειώνεται > Συνοπτικά: Το SSE από το μοντέλο της Height θα είναι μικρότερο από το SST γιατί το μοντέλο της Height εξηγεί μέρος της μεταβλητότητας της Thumb. Η διαφορά SST - SSE αντιπροσωπεύει τη μεταβλητότητα που εξηγείται από το ύψος. Όσο ισχυρότερη η σχέση, τόσο μεγαλύτερη η μείωση από SST σε SSE.

Ο παρακάτω κώδικας θα υπολογίσει το SST από το κενό μοντέλο και το SSE από το μοντέλο της Height. Μπορείτε να τον εκτελέσετε για να ελέγξετε τι ισχύει σχετικά με το SSE:

[1] "SST"
11880.21

[1] "SSE"
10063.35

Το SSE (10063) είναι μικρότερο από το SST, επειδή τα υπόλοιπα είναι μικρότερα (όπως φαίνεται και στα προηγούμενα διαγράμματα από τις μικρότερες κατακόρυφες γραμμές). Το άθροισμα τετραγώνων μικρότερων υπολοίπων δίνει και μικρότερο SSE. Συνεπώς, το συνολικό σφάλμα έχει μειωθεί με αυτό το μοντέλο παλινδρόμησης.

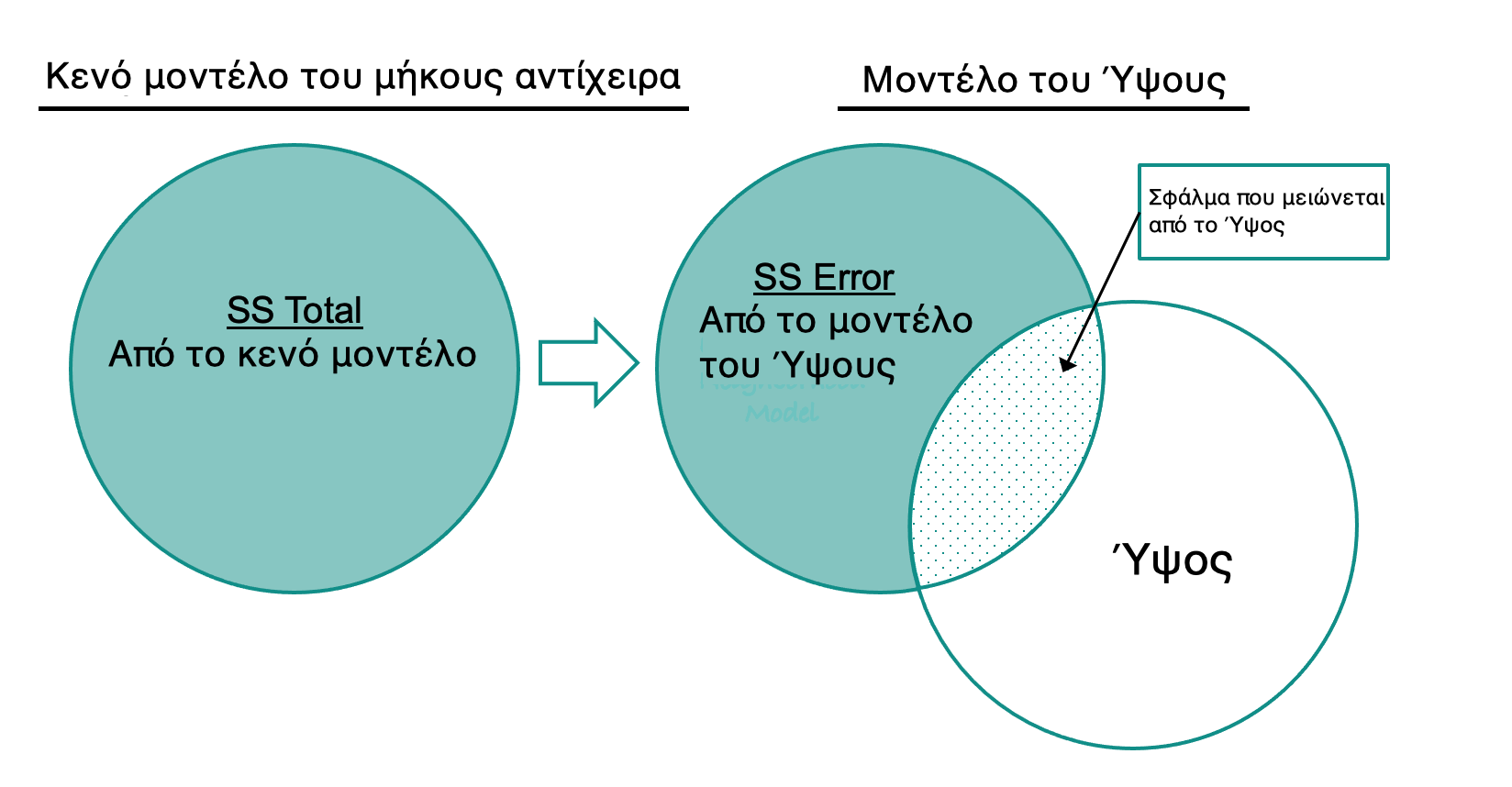
Το SSE για το μοντέλο του Ύψους είναι 10063. Ποιο μέρος του παραπάνω σχήματος αντιπροσωπεύει αυτόν τον αριθμό;

Ολόκληρος ο τιρκουάζ κύκλος (αριστερά)Το τιρκουάζ τμήμα του κύκλου στα δεξιά (SS Error από το μοντέλο του Ύψους)Η γραμμοσκιασμένη περιοχή (σφάλμα που μειώνεται από το Ύψος)Ο κύκλος στα δεξιά με την ετικέτα 'Ύψος'

Επεξήγηση

Σωστή απάντηση: Β — Το τιρκουάζ τμήμα του κύκλου στα δεξιά (SS Error από το μοντέλο του Ύψους)

Κατανόηση του διαγράμματος

Το διάγραμμα Venn δείχνει πώς το μοντέλο του Ύψους επηρεάζει τη μεταβλητότητα:

Κύκλος στα αριστερά (Κενό μοντέλο):

Ολόκληρος ο τιρκουάζ κύκλος: SST = 11880 (συνολική μεταβλητότητα)
Όλη η μεταβλητότητα είναι ανεξήγητη

Κύκλος στα δεξιά (Μοντέλο του Ύψους):

Τιρκουάζ τμήμα (που ΔΕΝ επικαλύπτεται με το Ύψος): SSE = 10063 (ανεξήγητη μεταβλητότητα)
Γραμμοσκιασμένη περιοχή (επικάλυψη): 11880 - 10063 = 1817 (εξηγούμενη μεταβλητότητα)
Δεξιός κύκλος ‘Ύψος’: Αντιπροσωπεύει την ανεξάρτητη μεταβλητή

Γιατί το τιρκουάζ τμήμα;

Το τιρκουάζ τμήμα που δεν επικαλύπτεται με τον κύκλο του Ύψους αντιπροσωπεύει τη μεταβλητότητα που:

ΔΕΝ εξηγείται από το Ύψος
Παραμένει ανεξήγητη μετά την προσθήκη του Ύψους στο μοντέλο
Αντιστοιχεί στο SS Error (SSE) = 10063

Η γραμμοσκιασμένη περιοχή (επικάλυψη):

Αντιπροσωπεύει το σφάλμα που μειώνεται όταν προσθέτουμε το Ύψος:

Αυτή είναι η μεταβλητότητα που εξηγείται από το Ύψος
1817

Το SSE για το μοντέλο του Ύψους είναι 10063. Τι σημαίνει αυτό; (Υπάρχουν περισσότερες από μία σωστές απαντήσεις.)

Το SSE για το μοντέλο του Ύψους είναι λίγο μικρότερο από ό,τι είναι για το κενό μοντέλο.Το SSE για το μοντέλο του Ύψους είναι λίγο μεγαλύτερο από ό,τι είναι για το κενό μοντέλο.Υπολογίσαμε το SSE εσφαλμένα γιατί το SSE πρέπει να ισούται με το SST.Το μοντέλο του Ύψους έχει λιγότερο ανεξήγητο σφάλμα από το κενό μοντέλο.Το μοντέλο του Ύψους εξηγεί περισσότερο από το σφάλμα σε σχέση με το κενό μοντέλο.

Επεξήγηση

Σωστές απαντήσεις: Α, Δ και Ε

Σύγκριση των μοντέλων

Μοντέλο	`SS Error`	Διαφορά
Κενό μοντέλο	`SST` = 11880	—
Ύψος	`SSE` = 10063	-1817

Μείωση του σφάλματος: \[11880 - 10063 = 1817\]

Ποσοστό μείωσης: \[\frac{1817}{11880} \times 100\% = 15.3\%\]

Το μοντέλο του Ύψους μείωσε το ανεξήγητο σφάλμα κατά περίπου 15.3% ή 1817 μονάδες.

Α. «Το SSE για το μοντέλο του Ύψους ήταν λίγο μικρότερο από ό,τι ήταν για το κενό μοντέλο» — ΣΩΣΤΟ ✓

Αυτό είναι σωστό:

Κενό μοντέλο: SSE = SST = 11880
Μοντέλο Ύψους: SSE = 10063
Διαφορά: 11880 - 10063 = 1817

Το SSE μειώθηκε κατά 1817 μονάδες, που είναι περίπου 15% του αρχικού σφάλματος.

Σημείωση: Το “λίγο” είναι σχετικό - η μείωση 15% μπορεί να θεωρηθεί “λίγο” ή “μέτρια” ανάλογα με το πλαίσιο.

Δ. «Το μοντέλο του Ύψους έχει λιγότερο ανεξήγητο σφάλμα από το κενό μοντέλο» — ΣΩΣΤΟ ✓

Αυτό είναι απόλυτα σωστό και ισοδύναμο με την επιλογή Α.

Κενό μοντέλο:

Ανεξήγητο σφάλμα = 11880 (όλη η μεταβλητότητα είναι ανεξήγητη)

Μοντέλο Ύψους:

Ανεξήγητο σφάλμα = 10063 (μέρος της μεταβλητότητας εξηγείται από το Ύψος)

Το μοντέλο του Ύψους έχει λιγότερο ανεξήγητο σφάλμα γιατί χρησιμοποιεί την πληροφορία του ύψους για να βελτιώσει τις προβλέψεις.

Ε. «Το μοντέλο του Ύψους εξηγεί περισσότερο από το σφάλμα σε σχέση με το κενό μοντέλο» — ΣΩΣΤΟ ✓

Αυτό είναι επίσης σωστό.

Κενό μοντέλο:

Δεν εξηγεί: SSE = 11880

Μοντέλο Ύψους: - Εξηγεί: 1817 (χρησιμοποιεί το Ύψος)

Δεν εξηγεί: SSE = 10063

Το μοντέλο του Ύψους εξηγεί 1817 μονάδες μεταβλητότητας που το κενό μοντέλο δεν εξηγούσε.

Οπτική αναπαράσταση στο διάγραμμα:

Κύκλος στα αριστερά (κενό μοντέλο): Όλη η περιοχή είναι τιρκουάζ = SST = 11880
Κύκλος στα δεξιά (μοντέλο του Ύψους):
- Τιρκουάζ τμήμα (εκτός επικάλυψης) = SSE = 10063
- Γραμμοσκιασμένη Περιοχή (επικάλυψη) = 1817

Το βέλος δείχνει τη μετάβαση: μέρος του ανεξήγητου σφάλματος (1817) γίνεται εξηγούμενη μεταβλητότητα.

Γιατί οι άλλες επιλογές είναι λάθος

Β. «Το SSE για το μοντέλο του Ύψους ήταν λίγο μεγαλύτερο από ό,τι ήταν για το κενό μοντέλο» — ΛΑΘΟΣ

Αυτό είναι εντελώς λάθος και αντίθετο με την πραγματικότητα.

Κενό: SSE = 11880
Ύψους: SSE = 10063
10063 < 11880 (όχι μεγαλύτερο!)

Το SSE μειώθηκε, δεν αυξήθηκε. Το διάγραμμα το δείχνει καθαρά: το τιρκουάζ τμήμα του κύκλου στα δεξιά είναι μικρότερο από τον πλήρη κύκλο στα αριστερά.

Γ. «Υπολογίσαμε το SSE εσφαλμένα γιατί το SSE πρέπει να ισούται με το SST» — ΛΑΘΟΣ

Αυτό είναι λάθος. Το SSE δεν πρέπει να ισούται με το SST.

Πότε SSE = SST;

Το SSE ισούται με το SST μόνο στο κενό μοντέλο (ή σε μοντέλο χωρίς προβλεπτική ικανότητα).

Στην περίπτωσή μας:

\[10063 = 11880 - 1817\]

Αυτό είναι απόλυτα σωστό. Το γεγονός ότι SSE < SST σημαίνει ότι το μοντέλο λειτουργεί!

Το διάγραμμα το επιβεβαιώνει: Η γραμμοσκιασμένη περιοχή (1817) δείχνει ότι μέρος της μεταβλητότητας εξηγείται.

Το μοντέλο του Ύψους εξηγεί 15.3% της μεταβλητότητας στο μήκος αντίχειρα.

Ερμηνεία:

Το ύψος είναι ένας στατιστικά σημαντικός προβλεπτικός παράγοντας
Αλλά εξηγεί μόνο ένα μικρό μέρος της μεταβλητότητας
Υπάρχουν άλλοι παράγοντες που επηρεάζουν το μήκος αντίχειρα (84.7% παραμένει ανεξήγητο)

Πρακτική σημασία

Το γεγονός ότι SSE = 10063 < SST = 11880 σημαίνει:

Το μοντέλο του Ύψους είναι χρήσιμο
- Βελτιώνει τις προβλέψεις σε σχέση με το κενό μοντέλο
- Το ύψος έχει στατιστικά σημαντική σχέση με το μήκος αντίχειρα
Υπάρχει περιθώριο βελτίωσης
- Το 84.7% της μεταβλητότητας παραμένει ανεξήγητο
- Θα μπορούσαμε να προσθέσουμε άλλες μεταβλητές (π.χ., φύλο, ηλικία, γενετικούς παράγοντες)
Το μοντέλο δεν είναι τέλειο
- Οι προβλέψεις θα έχουν σφάλματα
- Δεν μπορούμε να προβλέψουμε με 100% ακρίβεια

Συμπέρασμα

Το SSE = 10063 σημαίνει ότι:

✓ Το SSE είναι μικρότερο από το SST (11880)
✓ Το μοντέλο του Ύψους έχει λιγότερο ανεξήγητο σφάλμα από το κενό
✓ Το μοντέλο του Ύψους εξηγεί περισσότερο από το κενό (1817)
✗ ΌΧΙ το SSE δεν είναι μεγαλύτερο
✗ ΌΧΙ ο υπολογισμός δεν είναι λάθος - το SSE δεν πρέπει να ισούται με το SST

Συνοπτικά: Το SSE = 10063 αντιπροσωπεύεται από το τιρκουάζ τμήμα που δεν επικαλύπτεται με τον κύκλο του Ύψους στα δεξιά. Είναι μικρότερο από το SST = 11880, πράγμα που σημαίνει ότι το μοντέλο του Ύψους λειτουργεί. Η γραμμοσκιασμένη περιοχή (1817) δείχνει τη μεταβλητότητα που εξηγείται από το ύψος - περίπου 15.3% της συνολικής μεταβλητότητας.

Σύγκριση της Ευθείας Παλινδρόμησης με το Μέσο Όρο

Θυμηθείτε ότι ο μέσος όρος είναι το κέντρο μιας μονομεταβλητής κατανομής. Αποτελεί το σημείο ισορροπίας της κατανομής, όπου τα υπόλοιπα είναι τέλεια ισορροπημένα πάνω και κάτω από την τιμή του μέσου όρου. Με παρόμοιο τρόπο, η ευθεία παλινδρόμησης είναι το κέντρο μιας διμεταβλητής κατανομής μεταξύ δύο ποσοτικών μεταβλητών. Όπως το άθροισμα των υπολοίπων γύρω από το μέσο όρο ισούται με 0, έτσι και το άθροισμα των υπολοίπων γύρω από την ευθεία παλινδρόμησης ισούται επίσης με 0.

Μια ακόμα ενδιαφέρουσα σχέση μεταξύ μέσου όρου και ευθείας παλινδρόμησης είναι ότι η καλύτερα προσαρμοσμένη ευθεία παλινδρόμησης πάντα περνάει από το σημείο των μέσων όρων (point of means), δηλαδή το σημείο που αντιστοιχεί στο μέσο όρο και των δύο μεταβλητών. Έτσι, αν το ύψος ενός ατόμου είναι ακριβώς στο μέσο όρο, η τιμή πρόβλεψης του μήκους αντίχειρα θα είναι επίσης ακριβώς στο μέσο όρο.

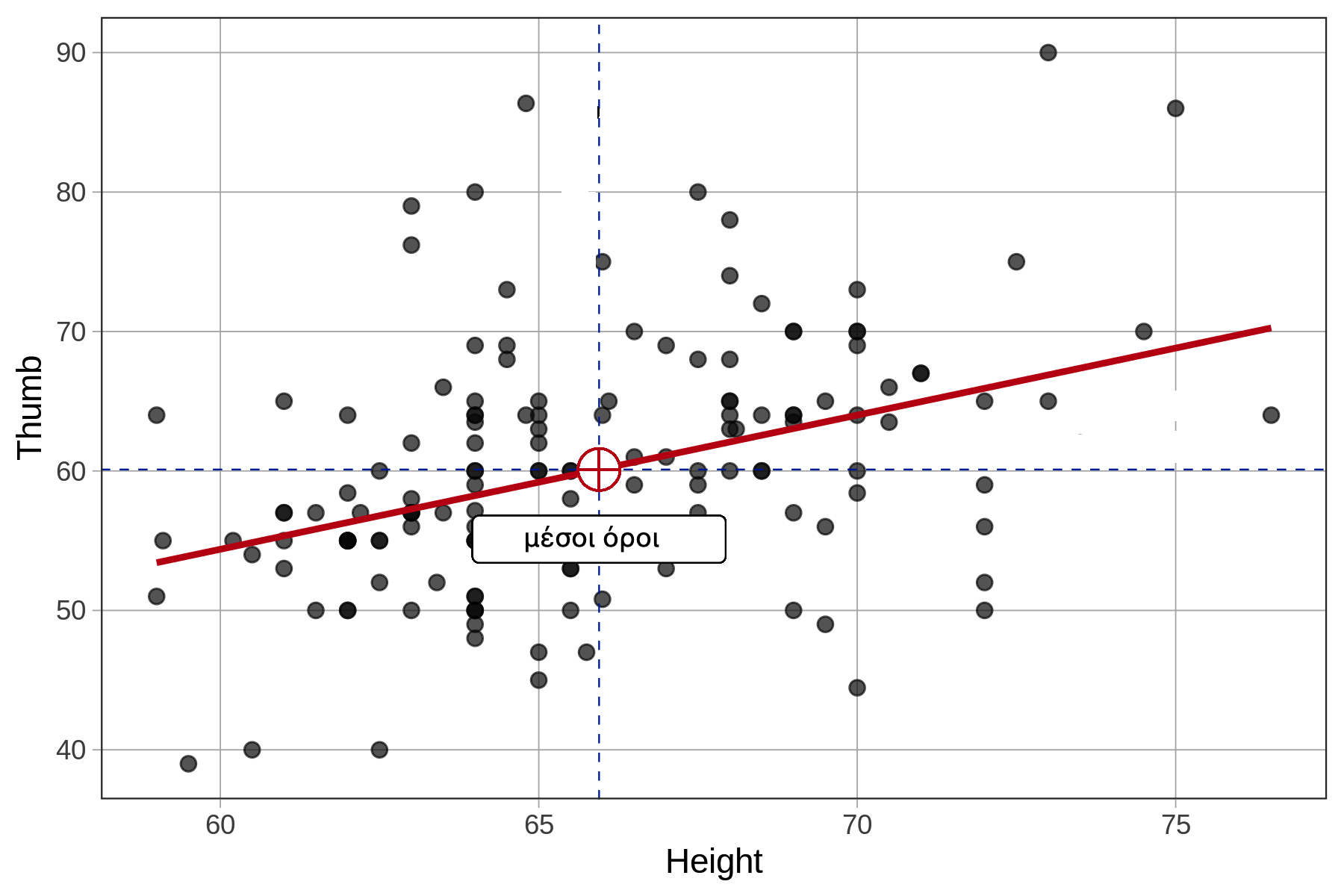
Τέλος, όπως ο μέσος όρος είναι το σημείο στη μονομεταβλητή κατανομή όπου το SS Error είναι ελάχιστο, το ίδιο ισχύει και για τα σφάλματα γύρω από την ευθεία παλινδρόμησης. Το άθροισμα τετραγώνων των αποκλίσεων των παρατηρούμενων τιμών είναι το μικρότερο δυνατό γύρω από την ευθεία που προσαρμόζεται καλύτερα στα δεδομένα.

10.6 Αθροίσματα Τετραγώνων στον πίνακα ANOVA

Τέλος, ας χρησιμοποιήσουμε τον πίνακα ANOVA για να αξιολογήσουμε πόσο καλά προσαρμόζεται το μοντέλο του ύψους στα δεδομένα. Το αντικείμενο Height_model έχει αποθηκευτεί στο παρακάτω παράδειγμα κώδικα. Χρησιμοποιήστε τη συνάρτηση supernova() για να δημιουργήσετε τον πίνακα ANOVA.

Παρακάτω εμφανίζεται ο πίνακας ANOVA για το Height_model, μαζί με εκείνον που δημιουργήσαμε νωρίτερα για το Height2Group_model.

Το μοντέλο της Height

Analysis of Variance Table (Type III SS)
Model: Thumb ~ Height

                               SS  df       MS      F    PRE     p
----- --------------- | --------- --- -------- ------ ------ -----
Model (error reduced) |  1816.862   1 1816.862 27.984 0.1529 .0000
Error (from model)    | 10063.349 155   64.925
----- --------------- | --------- --- -------- ------ ------ -----
Total (empty model)   | 11880.211 156   76.155

Το μοντέλο της Height2Group

Analysis of Variance Table (Type III SS)
Model: Thumb ~ Height2Group

                               SS  df      MS      F    PRE     p
----- --------------- | --------- --- ------- ------ ------ -----
Model (error reduced) |   830.880   1 830.880 11.656 0.0699 .0008
Error (from model)    | 11049.331 155  71.286
----- --------------- | --------- --- ------- ------ ------ -----
Total (empty model)   | 11880.211 156  76.155

Ποια είναι η εξαρτημένη μεταβλητή στο μοντέλο της Height2Group;

Height (Ύψος)Groups (Ομάδες)Gender (Φύλο)Thumb (Μήκος αντίχειρα)

Επεξήγηση

Σωστή απάντηση: Δ — Thumb (Μήκος αντίχειρα)

Από τον πίνακα ANOVA βλέπουμε:

Model: Thumb ~ Height2Group

Αυτό σημαίνει:

Εξαρτημένη μεταβλητή: Thumb (μήκος αντίχειρα)
Ανεξάρτητη μεταβλητή: Height2Group (ομάδα ύψους)

Το σύμβολο ~ διαβάζεται ως “προβλέπεται από” ή “εξαρτάται από”.

Η εξαρτημένη μεταβλητή είναι πάντα αυτό που προσπαθούμε να προβλέψουμε ή να εξηγήσουμε.

Ποια είναι η εξαρτημένη μεταβλητή στο μοντέλο της Height;

Height (Ύψος)Groups (Ομάδες)Gender (Φύλο)Thumb (Μήκος αντίχειρα)

Επεξήγηση

Σωστή απάντηση: Δ — Thumb (Μήκος αντίχειρα)

Από τον πίνακα ANOVA βλέπουμε:

Model: Thumb ~ Height

Αυτό σημαίνει:

Εξαρτημένη μεταβλητή: Thumb (μήκος αντίχειρα)
Ανεξάρτητη μεταβλητή: Height (ύψος)

Και τα δύο μοντέλα έχουν την ίδια εξαρτημένη μεταβλητή (Thumb), αλλά διαφορετικές ανεξάρτητες μεταβλητές:

Height2Group: Χρησιμοποιεί ποιοτική μεταβλητή (short/tall)
Height: Χρησιμοποιεί συνεχή μεταβλητή (ύψος σε cm)

Κοιτάξτε το συνολικό άθροισμα τετραγώνων (SS Total) και για τα δύο μοντέλα. Γιατί είναι το ίδιο;

Αυτό είναι σύμπτωση. Τις περισσότερες φορές το SS Total δεν θα είναι το ίδιο.Αυτό συμβαίνει επειδή και τα δύο μοντέλα χρησιμοποιούν κάποια πληροφορία για το Ύψος ως ανεξάρτητη μεταβλητή.Αυτό συμβαίνει επειδή και τα δύο μοντέλα έχουν την ίδια εξαρτημένη μεταβλητή. Το SS Total είναι πάντα το άθροισμα των τετραγώνων των υπολοίπων από τις τιμές της εξαρτημένης μεταβλητής στο κενό μοντέλο αυτής της μεταβλητής.

Επεξήγηση

Σωστή απάντηση: Γ — Αυτό συμβαίνει επειδή και τα δύο μοντέλα έχουν την ίδια εξαρτημένη μεταβλητή. Το SS Total είναι πάντα το άθροισμα τετραγώνων των υπολοίπων από τις τιμές της εξαρτημένης μεταβλητής στο κενό μοντέλο αυτής της μεταβλητής.

Τι είναι το SS Total (SST);

Το SS Total μετρά τη συνολική μεταβλητότητα στην εξαρτημένη μεταβλητή:

\[\text{SST} = \sum_{i=1}^{n}(Y_i - \bar{Y})^2\]

όπου:

$Y_i$ = η παρατηρούμενη τιμή της εξαρτημένης μεταβλητής για το άτομο $i$
$\bar{Y}$ = ο μέσος όρος της εξαρτημένης μεταβλητής

Κλειδί: Το SST εξαρτάται μόνο από την εξαρτημένη μεταβλητή (Thumb), όχι από την ανεξάρτητη μεταβλητή!

Γιατί το SST είναι το ίδιο;

Και τα δύο μοντέλα προσπαθούν να εξηγήσουν την ίδια μεταβλητότητα:

Ίδια εξαρτημένη μεταβλητή: Και τα δύο μοντέλα προβλέπουν την Thumb
Ίδια δεδομένα: Χρησιμοποιούν το ίδιο σύνολο δεδομένων (n = 157 άτομα)
Ίδιος μέσος όρος: Ο μέσος όρος του Thumb είναι ο ίδιος και για τα δύο μοντέλα

Το κενό μοντέλο:

Το SST υπολογίζεται από το κενό μοντέλο, που προβλέπει: \[\hat{Y}_i = \bar{Y}\]

Δηλαδή, προβλέπει το μέσο όρο για όλους, χωρίς να χρησιμοποιεί καμία ανεξάρτητη μεταβλητή.

Επειδή το κενό μοντέλο δεν εξαρτάται από το αν χρησιμοποιούμε την Height ή την Height2Group, το SST είναι το ίδιο.

Γιατί οι άλλες επιλογές είναι λάθος

Α. «Αυτό είναι σύμπτωση» — ΛΑΘΟΣ

Δεν είναι σύμπτωση! Το SST θα είναι πάντα το ίδιο για οποιοδήποτε μοντέλο που:

Χρησιμοποιεί την ίδια εξαρτημένη μεταβλητή
Χρησιμοποιεί το ίδιο σύνολο δεδομένων

Αυτό είναι μια μαθηματική αναγκαιότητα, όχι τυχαίο γεγονός.

Β. «Επειδή και τα δύο χρησιμοποιούν πληροφορία για το Ύψος» — ΛΑΘΟΣ

Αν και είναι αλήθεια ότι και τα δύο μοντέλα χρησιμοποιούν πληροφορία για το ύψος, αυτό δεν είναι ο λόγος που το SST είναι το ίδιο.

Απόδειξη: Ακόμα κι αν συγκρίναμε το μοντέλο της Height με ένα εντελώς διαφορετικό μοντέλο (π.χ., με την Gender ή την Age), το SST θα ήταν ακόμα το ίδιο, αρκεί η εξαρτημένη μεταβλητή να είναι η Thumb.

Το SST εξαρτάται μόνο από την εξαρτημένη μεταβλητή, όχι από την ανεξάρτητη.

Σύγκριση των μοντέλων

Στοιχείο	Μοντέλο της `Height`	Μοντέλο της `Height2Group`
Εξαρτημένη μεταβλητή	`Thumb`	`Thumb`
Ανεξάρτητη μεταβλητή	`Height` (συνεχής)	`Height2Group` (ποιοτική)
`SS Total`	11880.211	11880.211
`SS Error`	10063.349	11049.331
`SS Model`	1816.862	830.880
$R^2$	0.1529 (15.3%)	0.0699 (7.0%)

Παρατηρήσεις:

SS Total είναι ίδιο — Και τα δύο μοντέλα εξηγούν την ίδια συνολική μεταβλητότητα
SS Error διαφέρει — Το μοντέλο της Height εξηγεί περισσότερη μεταβλητότητα (SSE μικρότερο)
SS Model διαφέρει — Το μοντέλο της Height έχει μεγαλύτερο SS Model

Γενική αρχή

Το SS Total είναι πάντα το ίδιο για οποιαδήπτε μοντέλα που:

Προβλέπουν την ίδια εξαρτημένη μεταβλητή
Χρησιμοποιούν το ίδιο σύνολο δεδομένων

Το SST αντικατοπτρίζει τη συνολική μεταβλητότητα που υπάρχει στα δεδομένα, ανεξάρτητα από το πώς προσπαθούμε να την εξηγήσουμε.

Συμπέρασμα

Το SS Total είναι το ίδιο για τα δύο μοντέλα (11880.211) επειδή:

Και τα δύο προβλέπουν την ίδια εξαρτημένη μεταβλητή (Thumb)
Το SST μετρά τη συνολική μεταβλητότητα στην Thumb
Το SST υπολογίζεται από το κενό μοντέλο, που δεν χρησιμοποιεί καμία ανεξάρτητη μεταβλητή
Επομένως, το SST δεν επηρεάζεται από το αν χρησιμοποιούμε την Height, την Height2Group, ή οποιαδήποτε άλλη ανεξάρτητη μεταβλητή

Συνοπτικά: Το SS Total είναι ίδιο (11880) γιατί και τα δύο μοντέλα εξηγούν την ίδια εξαρτημένη μεταβλητή (Thumb). Το SST μετρά τη συνολική μεταβλητότητα στα δεδομένα και εξαρτάται μόνο από την εξαρτημένη μεταβλητή, όχι από την επιλογή της ανεξάρτητης μεταβλητής. Διαφορετικά μοντέλα για την ίδια εξαρτημένη μεταβλητή θα έχουν πάντα το ίδιο SST.

Το SS Total είναι το άθροισμα τετραγώνων των υπολοίπων από το κενό μοντέλο. Το συνολικό άθροισμα τετραγώνων αφορά αποκλειστικά την εξαρτημένη μεταβλητή και δεν επηρεάζεται από την(τις) ανεξάρτητη(ές) μεταβλητή(ές). Όταν χρησιμοποιούμε τα αθροίσματα τετραγώνων για να συγκρίνουμε στατιστικά μοντέλα, συγκρίνουμε μοντέλα που αφορούν την ίδια εξαρτημένη μεταβλητή.

To `SS Error` στα τρία μοντέλα

Ο παρακάτω πίνακας συνοψίζει τα αθροίσματα τετραγώνων των υπολοίπων (SS Error) μετά την προσαρμογή καθενός από τα τρία μοντέλα που εξετάζουμε. Όλες οι τιμές υπολογίζονται με τον ίδιο τρόπο — ως το άθροισμα τετραγώνων των υπολοίπων από τις προβλέψεις του μοντέλου.

Μοντέλο	`SS Error`	Όνομα στατιστικού μεγέθους
Κενό μοντέλο	11880	Συνολικό Άθροισμα Τετραγώνων (`SS Total` ή `SST`)
Μοντέλο της `Height2Group`	11049	Άθροισμα Τετραγώνων Υπολοίπων (`SS Error` ή `SSE`)
Μοντέλο της `Height`	10063	Άθροισμα Τετραγώνων Υπολοίπων (`SS Error` ή `SSE`)

Ποιες από τις παρακάτω δηλώσεις είναι αληθείς με βάση τον παραπάνω πίνακα; (Υπάρχουν περισσότερες από μία σωστές απαντήσεις.)

Και το μοντέλο της Height2Group και το μοντέλο της Height μειώνουν το σφάλμα σε σύγκριση με το κενό μοντέλο.Και το μοντέλο της Height2Group και το μοντέλο της Height έχουν περισσότερο υπολειπόμενο σφάλμα από το κενό μοντέλο.Τα SSE είναι και τα δύο μικρότερα από το SST.Τα SSE είναι και τα δύο μεγαλύτερα από το SST.

Επεξήγηση

Σωστές απαντήσεις: Α και Γ

Α. «Και τα δύο μοντέλα μειώνουν το σφάλμα σε σύγκριση με το κενό μοντέλο» — ΣΩΣΤΟ ✓

Αυτό είναι σωστό για και τα δύο μοντέλα.

Μοντέλο της Height:

Κενό μοντέλο: SSE = SST = 11880.211
Μοντέλο της Height: SSE = 10063.349
Μείωση: $11880.211 - 10063.349 = 1816.862$ ✓

Μοντέλο της Height2Group:

Κενό μοντέλο: SSE = SST = 11880.211
Μοντέλο της Height2Group: SSE = 11049.331
Μείωση: $11880.211 - 11049.331 = 830.880$ ✓

Και τα δύο μοντέλα μειώνουν το σφάλμα, αν και η Height το κάνει πιο αποτελεσματικά:

Η Height μειώνει το σφάλμα κατά 1817 (15.3%)
Η Height2Group μειώνει το σφάλμα κατά 831 (7.0%)

Γιατί;

Κάθε μοντέλο με ανεξάρτητη μεταβλητή που έχει κάποια σχέση με την εξαρτημένη μεταβλητή θα μειώσει το σφάλμα σε σχέση με το κενό μοντέλο.

Γ. «Τα SSE είναι και τα δύο μικρότερα από το SST» — ΣΩΣΤΟ ✓

Αυτό είναι επίσης σωστό και είναι μια άλλη διατύπωση της επιλογής Α.

Σύγκριση:

SST = 11880.211
SSE (Height) = 10063.349 < SST ✓
SSE (Height2Group) = 11049.331 < SST ✓

Γιατί οι άλλες επιλογές είναι λάθος

Β. «Και τα δύο μοντέλα έχουν περισσότερο υπολειπόμενο σφάλμα από το κενό μοντέλο» — ΛΑΘΟΣ

Αυτό είναι εντελώς λάθος και το αντίθετο της αλήθειας.

Σύγκριση υπολειπόμενου σφάλματος:

Κενό μοντέλο: SSE = 11880.211
Μοντέλο της Height: SSE = 10063.349 (λιγότερο!) ✓
Μοντέλο της Height2Group: SSE = 11049.331 (λιγότερο!) ✓

Και τα δύο μοντέλα έχουν λιγότερο υπολειπόμενο σφάλμα από το κενό μοντέλο, όχι περισσότερο.

Γιατί είναι αδύνατο να έχουν περισσότερο σφάλμα;

Το κενό μοντέλο αντιπροσωπεύει το χειρότερο δυνατό μοντέλο - προβλέπει απλώς το μέσο όρο για όλους.

Οποιοδήποτε μοντέλο που χρησιμοποιεί ανεξάρτητη μεταβλητή με οποιαδήποτε προβλεπτική ικανότητα θα:

Βελτιώσει τις προβλέψεις
Μειώσει το υπολειπόμενο σφάλμα
Θα έχει SSE ≤ SST (ποτέ μεγαλύτερο!)

Δ. «Τα SSE είναι και τα δύο μεγαλύτερα από το SST» — ΛΑΘΟΣ

Αυτό είναι επίσης εντελώς λάθος και μαθηματικά αδύνατο.

Πρακτική σημασία

Το γεγονός ότι και τα δύο SSE < SST σημαίνει:

Και τα δύο μοντέλα είναι χρήσιμα
- Βελτιώνουν τις προβλέψεις σε σχέση με το απλό προβλέπει-τον-μέσο-όρο
Το μοντέλο της Height είναι πιο χρήσιμο
- Μειώνει το σφάλμα διπλάσια από το μοντέλο της Height2Group
- Η απώλεια πληροφορίας από την κατηγοριοποίηση είναι σημαντική
Υπάρχει ακόμα αρκετό ανεξήγητο σφάλμα
- Ακόμα και το καλύτερο μοντέλο (Height`) αφήνει 84.7% ανεξήγητο
- Άλλοι παράγοντες (φύλο, γενετική, κ.λπ.) επηρεάζουν το μήκος αντίχειρα

Συμπέρασμα

Οι σωστές δηλώσεις είναι:

✓ Α: Και τα δύο μοντέλα μειώνουν το σφάλμα (SSE < SST)
✗ Β: ΛΑΘΟΣ - έχουν λιγότερο σφάλμα, όχι περισσότερο
✓ Γ: Τα SSE είναι και τα δύο μικρότερα από το SST
✗ Δ: ΛΑΘΟΣ - είναι μικρότερα, όχι μεγαλύτερα

Συνοπτικά: Και τα δύο μοντέλα μειώνουν το σφάλμα σε σύγκριση με το κενό μοντέλο, πράγμα που σημαίνει ότι τα SSE τους είναι μικρότερα από το SST. Το μοντέλο της Height μειώνει το σφάλμα περισσότερο (15.3%) από αυτό της Height2Group (7.0%), δείχνοντας ότι η χρήση του συνεχούς ύψους προσφέρει περισσότερη προβλεπτική ικανότητα από την απλή κατηγοριοποίηση.

Όσο μεγαλύτερο είναι το σφάλμα που υπολείπεται μετά την προσαρμογή ενός μοντέλου, τόσο μικρότερο μέρος της συνολικής μεταβλητότητας εξηγείται. Το κενό μοντέλο (δηλαδή το μοντέλο χωρίς προβλεπτικές μεταβλητές) δείχνει πόση συνολική μεταβλητότητα υπάρχει στην εξαρτημένη μεταβλητή. Το SS Error (άθροισμα τετραγώνων σφαλμάτων) δείχνει πόσο από αυτό το σφάλμα παραμένει ανεξήγητο μετά την προσαρμογή ενός πιο σύνθετου μοντέλου.

Σύμφωνα με το υπολειπόμενο σφάλμα στον παραπάνω πίνακα, ποιο μοντέλο εξηγεί περισσότερη από τη μεταβλητότητα στο μήκος αντίχειρα;

Το μοντέλο της Height επειδή έχει μικρότερο SS Error από το μοντέλο της Height2Group.Το μοντέλο της Height2Group επειδή έχει μικρότερο SS Error από το μοντέλο της Height.Εξηγούν την ίδια ποσότητα σφάλματος επειδή το SS Total τους είναι το ίδιο.

Επεξήγηση

Σωστή απάντηση: Α — Το μοντέλο της Height επειδή έχει μικρότερο SS Error από το μοντέλο της Height2Group.

Σύγκριση των SS Error

Διαφορά στο SSE: \[11049.331 - 10063.349 = 985.982\]

Το μοντέλο της Height έχει 985 μονάδες μικρότερο υπολειπόμενο σφάλμα από το μοντέλο της Height2Group.

Γιατί το μικρότερο SSE σημαίνει καλύτερο μοντέλο;

Το SS Error (SSE) μετρά το ανεξήγητο σφάλμα - τη μεταβλητότητα που το μοντέλο δεν κατάφερε να εξηγήσει.

Κλειδί: Όσο μικρότερο το SSE, τόσο καλύτερο το μοντέλο!

Μικρό SSE → Λιγότερη ανεξήγητη μεταβλητότητα → Το μοντέλο εξηγεί περισσότερη ✓
Μεγάλο SSE → Περισσότερη ανεξήγητη μεταβλητότητα → Το μοντέλο εξηγεί μικρότερη

Συμπέρασμα: Το μοντέλο της Height εξηγεί διπλάσια μεταβλητότητα από αυτό της Height2Group!

Γιατί οι άλλες επιλογές είναι λάθος

Β. «Το μοντέλο της Height2Group επειδή έχει μικρότερο SS Error από αυτό της Height» — ΛΑΘΟΣ

Αυτό είναι εντελώς λάθος και αντίθετο με τα δεδομένα.

Το μοντέλο της Height2Group έχει μεγαλύτερο SSE, όχι μικρότερο!

Γ. «Εξηγούν την ίδια ποσότητα σφάλματος επειδή το SS Total τους είναι το ίδιο» — ΛΑΘΟΣ

Αυτό είναι μια παρερμηνεία του τι σημαίνει το SS Total.

Το λογικό σφάλμα:

Το γεγονός ότι το SST είναι το ίδιο δεν σημαίνει ότι τα μοντέλα εξηγούν την ίδια μεταβλητότητα.

Γιατί το μοντέλο της Height είναι καλύτερο;

Το μοντέλο της Height είναι πιο αποτελεσματικό επειδή:

Χρησιμοποιεί περισσότερη πληροφορία
- Height: Συνεχής μεταβλητή (160, 165, 170, 175, 180 cm κ.λπ.)
- Height2Group: Ποιοτική μεταβλητή (μόνο short ή tall)
Διατηρεί τη λεπτομέρεια
- Height: Κάθε εκατοστό μετράει
- Height2Group: Όλοι οι short είναι ίδιοι, όλοι οι tall είναι ίδιοι
Έχει μεγαλύτερη προβλεπτική ικανότητα
- Height: Μπορεί να κάνει πιο ακριβείς προβλέψεις
- Height2Group: Χάνει πληροφορία από την κατηγοριοποίηση

Συνοπτικά: Το μοντέλο της Height εξηγεί περισσότερη μεταβλητότητα στο μήκος αντίχειρα γιατί έχει μικρότερο SS Error (10063 vs 11049). Μικρότερο SSE σημαίνει λιγότερη ανεξήγητη μεταβλητότητα, άρα περισσότερη εξηγούμενη μεταβλητότητα. Η Height εξηγεί 15.3% της μεταβλητότητας ενώ η Height2Group μόνο 7.0% - σχεδόν διπλάσια!

Το `SS Model`

Το SS Model εκφράζει την ποσότητα κατά την οποία μειώνεται το σφάλμα όταν χρησιμοποιούμε το πιο σύνθετο μοντέλο (π.χ. το μοντέλο της Height) σε σύγκριση με το κενό μοντέλο. Όπως είδαμε προηγουμένως για τα μοντέλα ομάδων, το SS Model υπολογίζεται εύκολα αφαιρώντας το SS Error από το SS Total. Ο ίδιος υπολογισμός ισχύει, ανεξάρτητα από το αν προσαρμόζουμε μοντέλο ομάδων ή μοντέλο παλινδρόμησης.

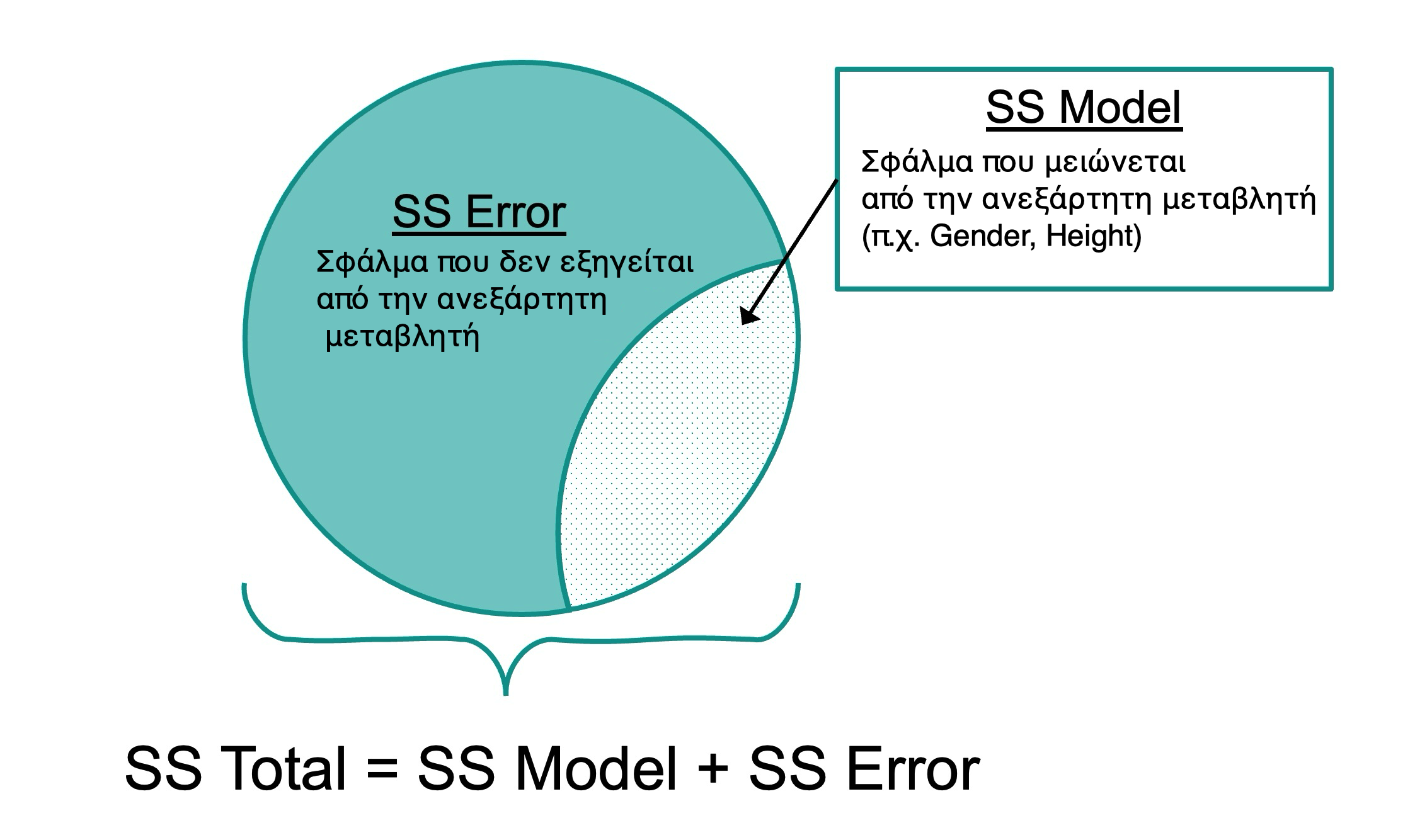
Είναι επίσης δυνατό να υπολογίσουμε το SS Model στο μοντέλο παλινδρόμησης, με παρόμοιο τρόπο όπως και στο μοντέλο ομάδων. Απλώς λαμβάνουμε την τιμή πρόβλεψης κάθε ατόμου από το μοντέλο παλινδρόμησης και υπολογίζουμε την απόστασή της από την πρόβλεψη του κενού μοντέλου. Αυτή η απόσταση δείχνει πόσο έχει μειωθεί το σφάλμα του κάθε ατόμου σε σύγκριση με το κενό μοντέλο. Έπειτα, υψώνουμε αυτές τις αποστάσεις στο τετράγωνο και τις αθροίζουμε για να προκύψει το SS Model.

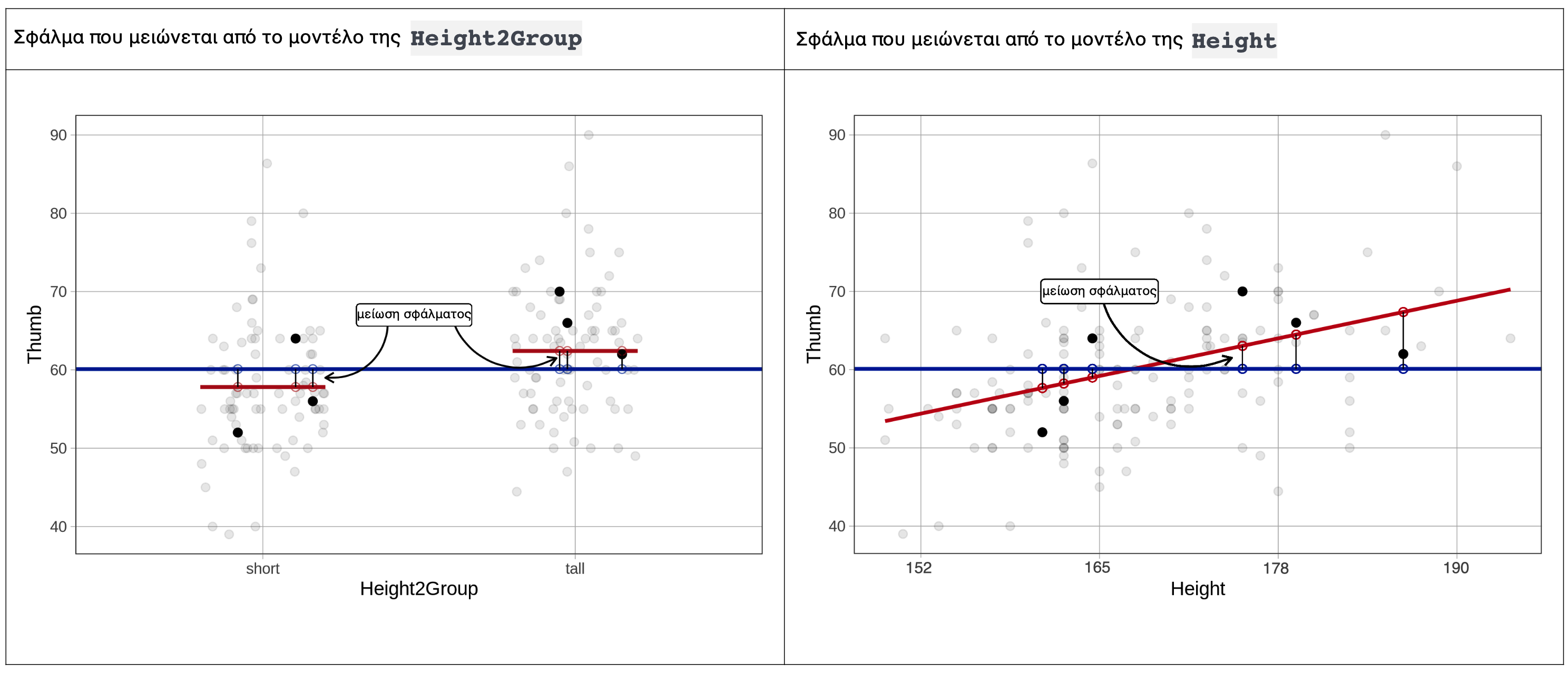
Συνοψίζοντας, ποιο άθροισμα τετραγώνων (SS) αντιστοιχεί σε ποιες αποστάσεις;

SS Total:

Από την πρόβλεψη του σύνθετου μοντέλου στην πρόβλεψη του κενού μοντέλουΑπό τα δεδομένα στην πρόβλεψη του σύνθετου μοντέλουΑπό τα δεδομένα στην πρόβλεψη του κενού μοντέλου

SS Error:

Από την τιμή πρόβλεψης του σύνθετου μοντέλου στην τιμή πρόβλεψης του κενού μοντέλουΑπό τα δεδομένα στην τιμή πρόβλεψης του σύνθετου μοντέλουΑπό τα δεδομένα στην τιμή πρόβλεψης του κενού μοντέλου

SS Model:

Επεξήγηση

Κατανόηση των αποστάσεων στην ανάλυση παλινδρόμησης

Στην ανάλυση παλινδρόμησης, κάθε άθροισμα τετραγώνων (SS) αντιστοιχεί σε μια συγκεκριμένη απόσταση:

SS Total (Συνολικό Άθροισμα Τετραγώνων)

Σωστή απάντηση: Από τα δεδομένα στην πρόβλεψη του κενού μοντέλου

Τι μετρά: \[\text{SST} = \sum_{i=1}^{n}(Y_i - \bar{Y})^2\]

όπου:

$Y_i$ = παρατηρούμενη τιμή (τα πραγματικά δεδομένα)
$\bar{Y}$ = μέσος όρος (πρόβλεψη του κενού μοντέλου)

Ερμηνεία: - Το SS Total μετρά τη συνολική μεταβλητότητα στα δεδομένα

Είναι η απόσταση κάθε παρατήρησης από το γενικό μέσο όρο
Αντιπροσωπεύει το συνολικό σφάλμα πριν χρησιμοποιήσουμε οποιοδήποτε μοντέλο

Γιατί “από τα δεδομένα στην πρόβλεψη του κενού μοντέλου”;

Το κενό μοντέλο προβλέπει: $\hat{Y}_i = \bar{Y}$ (ο μέσος όρος για όλους)
Μετράμε πόσο κάθε πραγματική παρατήρηση απέχει από αυτόν τον μέσο όρο
Υψώνουμε στο τετράγωνο και αθροίζουμε

SS Error (Άθροισμα Τετραγώνων Σφαλμάτων/Υπολοίπων)

Σωστή απάντηση: Από τα δεδομένα στην πρόβλεψη του σύνθετου μοντέλου

Τι μετρά: \[\text{SSE} = \sum_{i=1}^{n}(Y_i - \hat{Y}_i)^2\]

όπου:

$Y_i$ = παρατηρούμενη τιμή (τα πραγματικά δεδομένα)
$\hat{Y}_i$ = τιμή πρόβλεψης από το σύνθετο μοντέλο (π.χ., μοντέλο παλινδρόμησης)

Ερμηνεία: - Το SS Error μετρά την ανεξήγητη μεταβλητότητα

Είναι η απόσταση κάθε παρατήρησης από την πρόβλεψη του μοντέλου
Αντιπροσωπεύει το σφάλμα που παραμένει μετά τη χρήση του μοντέλου
Ονομάζεται και υπόλοιπο (residual)

Γιατί “από τα δεδομένα στην πρόβλεψη του σύνθετου μοντέλου”;

Το σύνθετο μοντέλο (π.χ., Thumb ~ Height) κάνει προβλέψεις: $\hat{Y}_i = b_0 + b_1X_i$
Μετράμε πόσο κάθε πραγματική παρατήρηση απέχει από την πρόβλεψη του μοντέλου
Αυτό είναι το σφάλμα που δεν κατάφερε να εξηγήσει το μοντέλο

SS Model (Άθροισμα Τετραγώνων του Μοντέλου)

Σωστή απάντηση: Από την τιμή πρόβλεψης του σύνθετου μοντέλου στην πρόβλεψη του κενού μοντέλου

Τι μετρά: \[\text{SSR} = \sum_{i=1}^{n}(\hat{Y}_i - \bar{Y})^2\]

όπου:

$\hat{Y}_i$ = τιμή πρόβλεψης από το σύνθετο μοντέλο
$\bar{Y}$ = μέσος όρος (τιμή πρόβλεψης του κενού μοντέλου)

Ερμηνεία: - Το SS Model μετρά τη μεταβλητότητα που εξηγείται από το μοντέλο

Είναι η απόσταση κάθε τιμής πρόβλεψης του μοντέλου από το γενικό μέσο όρο
Αντιπροσωπεύει τη βελτίωση που προσφέρει το μοντέλο
Ονομάζεται και SS Regression (SSR)

Γιατί “από την τιμή πρόβλεψης του σύνθετου μοντέλου στην τιμή πρόβλεψης του κενού μοντέλου”;

Συγκρίνουμε τις προβλέψεις του μοντέλου με τον απλό μέσο όρο
Μετράμε πόσο οι προβλέψεις του μοντέλου διαφέρουν από το να προβλέπουμε πάντα το μέσο όρο
Αυτό δείχνει πόσο χρήσιμο είναι το μοντέλο

Η Θεμελιώδης Σχέση

\[\text{SS Total} = \text{SS Model} + \text{SS Error}\]

Με λόγια:

\[\underbrace{\text{Συνολική μεταβλητότητα}}_{\text{δεδομένα} \to \bar{Y}} = \underbrace{\text{Εξηγούμενη μεταβλητότητα}}_{\hat{Y} \to \bar{Y}} + \underbrace{\text{Ανεξήγητη μεταβλητότητα}}_{\text{δεδομένα} \to \hat{Y}}\]

Πίνακας Αντιστοιχίας

Άθροισμα Τετραγώνων	Απόσταση	Τύπος	Τι μετρά
`SS Total`	Δεδομένα → Κενό μοντέλο	$(Y_i - \bar{Y})^2$	Συνολική μεταβλητότητα
`SS Error`	Δεδομένα → Σύνθετο μοντέλο	$(Y_i - \hat{Y}_i)^2$	Ανεξήγητη μεταβλητότητα
`SS Model`	Σύνθετο μοντέλο → Κενό μοντέλο	$(\hat{Y}_i - \bar{Y})^2$	Εξηγούμενη μεταβλητότητα

Πρακτικό Παράδειγμα με τα Δεδομένα

Στο μοντέλο Thumb ~ Height:

SS Total = 11880.211

Απόσταση: Παρατηρούμενο Thumb → Μέσος όρος Thumb (60.6 mm)
Ερμηνεία: Πόση μεταβλητότητα υπάρχει στα μήκη αντίχειρα;

SS Error = 10063.349

Απόσταση: Παρατηρούμενο Thumb → Πρόβλεψη από Thumb = b₀ + b₁×Height
Ερμηνεία: Πόση μεταβλητότητα ΔΕΝ εξηγείται από το ύψος;

SS Model = 1816.862 - Απόσταση: Πρόβλεψη από μοντέλο → Μέσος όρος Thumb

Ερμηνεία: Πόση μεταβλητότητα εξηγείται από το ύψος;

Επαλήθευση:

\[11880.211 = 1816.862 + 10063.349\] ✓

Συμπέρασμα

Ανακεφαλαίωση των αντιστοιχιών:

SS Total ↔︎ Από δεδομένα στην πρόβλεψη κενού μοντέλου (μέσος όρος)
SS Error ↔︎ Από δεδομένα στην πρόβλεψη σύνθετου μοντέλου
SS Model ↔︎ Από πρόβλεψη σύνθετου μοντέλου στην πρόβλεψη κενού μοντέλου

Αυτές οι αποστάσεις είναι η βάση για την κατανόηση της ανάλυσης παλινδρόμησης!

Αν εκτελούσαμε τη συνάρτηση supernova() στο μοντέλο της Height, ποιες τιμές θα ήταν ακριβώς οι ίδιες με τον πίνακα της supernova του μοντέλου της Height2Group;

SS ModelSS ErrorSS Total

Επεξήγηση

Σωστή απάντηση: Γ — SS Total

Σύγκριση των τιμών

Τιμή	Μοντέλο της `Height`	Μοντέλο της `Height2Group`	Ίδια;
`SS Model` (`SSR`)	1816.862	830.880	✗ Διαφορετική
`SS Error` (`SSE`)	10063.349	11049.331	✗ Διαφορετική
`SS Total` (`SST`)	11880.211	11880.211	✓ Ίδια!

Γ. «SS Total» — ΣΩΣΤΟ ✓

Το SS Total είναι πάντα το ίδιο για οποιαδήποτε μοντέλα που:

Προβλέπουν την ίδια εξαρτημένη μεταβλητή (Thumb)
Χρησιμοποιούν το ίδιο σύνολο δεδομένων

Γιατί;

Το SS Total μετρά τη συνολική μεταβλητότητα στην εξαρτημένη μεταβλητή:

\[\text{SST} = \sum_{i=1}^{n}(Y_i - \bar{Y})^2\]

Αυτός ο υπολογισμός εξαρτάται μόνο από:

Τις παρατηρούμενες τιμές $Y_i$ (μήκη αντίχειρα)
Το μέσο όρο $\bar{Y}$ (μέσο μήκος αντίχειρα)

Το SST ΔΕΝ εξαρτάται από:

Την επιλογή της ανεξάρτητης μεταβλητής (Height ή Height2Group)
Το πόσο καλά προβλέπει το μοντέλο
Τα υπόλοιπα του μοντέλου

Το SS Total υπολογίζεται από το κενό μοντέλο

Το κενό μοντέλο προβλέπει: \[\hat{Y}_i = \bar{Y} \text{ για όλα τα } i\]

Δηλαδή, προβλέπει απλώς το μέσο όρο για όλες τις παρατηρήσεις, χωρίς να χρησιμοποιεί καμία ανεξάρτητη μεταβλητή.

Επειδή το κενό μοντέλο είναι το ίδιο για όλα τα μοντέλα με την ίδια εξαρτημένη μεταβλητή, το SST είναι πάντα το ίδιο.

Γιατί οι άλλες επιλογές είναι λάθος

Α. «SS Model (SSR)» — ΛΑΘΟΣ

Το SS Model (ή SS Regression) είναι διαφορετικό για τα δύο μοντέλα.

Σύγκριση: - Height: SSR = 1816.862

Height2Group: SSR = 830.880
Διαφορά: $1816.862 - 830.880 = 985.982$

Γιατί διαφέρει;

Το SS Model μετρά τη μεταβλητότητα που εξηγείται από το μοντέλο:

\[\text{SSR} = \sum_{i=1}^{n}(\hat{Y}_i - \bar{Y})^2\]

Αυτό εξαρτάται από:

Την επιλογή της ανεξάρτητης μεταβλητής
Πόσο καλά προβλέπει το μοντέλο
Τις προβλέψεις $\hat{Y}_i$ που κάνει το μοντέλο

Τα δύο μοντέλα κάνουν διαφορετικές προβλέψεις:

Μοντέλο της Height:

\[\hat{Y}_i = b_0 + b_1 \times \text{Height}_i\]

Κάθε άτομο λαμβάνει διαφορετική τιμή πρόβλεψης ανάλογα με το ακριβές ύψος του

Μοντέλο της Height2Group:

\[\hat{Y}_i = b_0 + b_1 \times \text{Height2Grouptall}_i\]

Όλοι οι short λαμβάνουν την ίδια πρόβλεψη
Όλοι οι tall λαμβάνουν την ίδια πρόβλεψη

Επειδή οι προβλέψεις είναι διαφορετικές, το SSR είναι διαφορετικό.

Β. «SS Error (SSE)» — ΛΑΘΟΣ

Το SS Error είναι επίσης διαφορετικό για τα δύο μοντέλα.

Σύγκριση:

Height: SSE = 10063.349
Height2Group: SSE = 11049.331
Διαφορά: $11049.331 - 10063.349 = 985.982$

Γιατί διαφέρει;

Το SS Error μετρά τη μεταβλητότητα που ΔΕΝ εξηγείται από το μοντέλο:

\[\text{SSE} = \sum_{i=1}^{n}(Y_i - \hat{Y}_i)^2\]

Αυτό εξαρτάται από:

Τα υπόλοιπα (residuals): $e_i = Y_i - \hat{Y}_i$
Πόσο καλά το μοντέλο προβλέπει
Την επιλογή της ανεξάρτητης μεταβλητής

Επειδή το μοντέλο της Height κάνει καλύτερες προβλέψεις από το μοντέλο της Height2Group:

Έχει μικρότερα υπόλοίπα
Άρα έχει μικρότερο SSE

Η σχέση SST = SSR + SSE

Και για τα δύο μοντέλα ισχύει: \[\text{SST} = \text{SSR} + \text{SSE}\]

Height: \[11880.211 = 1816.862 + 10063.349\]

Height2Group: \[11880.211 = 830.880 + 11049.331\]

Παρατήρηση:

Το SST (αριστερή πλευρά της εξίσωσης) είναι το ίδιο
Τα SSR και SSE (δεξιά πλευρά) είναι διαφορετικά
Αλλά το άθροισμά τους είναι πάντα το ίδιο (SST)

Ενδιαφέρουσα παρατήρηση

Η διαφορά στο SSR είναι ακριβώς ίση με τη διαφορά στο SSE:

\[\Delta\text{SSR} = 1816.862 - 830.880 = 985.982\] \[\Delta\text{SSE} = 11049.331 - 10,063.349 = 985.982\]

Αυτό δεν είναι σύμπτωση! Συμβαίνει επειδή:

\[\text{SST (σταθερό)} = \text{SSR} + \text{SSE}\]

Όταν το SSR αυξάνεται κατά 986, το SSE πρέπει να μειωθεί κατά 986 για να διατηρηθεί το άθροισμα σταθερό.

Πρακτική εφαρμογή

Αυτή η ιδιότητα (SST σταθερό) είναι χρήσιμη για:

Σύγκριση μοντέλων
- Μπορούμε να συγκρίνουμε απευθείας τα SSR ή SSE
- Όποιο μοντέλο έχει μεγαλύτερο SSR (ή μικρότερο SSE) είναι καλύτερο
Υπολογισμός $R^2$
- $R^2 = \frac{\text{SSR}}{\text{SST}}$
- Επειδή το SST είναι το ίδιο, μεγαλύτερο SSR → μεγαλύτερο $R^2$
Κατανόηση της βελτίωσης
- Η διαφορά στο SSR δείχνει πόση επιπλέον μεταβλητότητα εξηγείται
- Εδώ: 986 μονάδες επιπλέον εξηγούνται από το μοντέλο της Height σε σχέση με αυτό της Height2Group

Συμπέρασμα

Μόνο το SS Total είναι το ίδιο για τα δύο μοντέλα (11880.211) επειδή:

Και τα δύο μοντέλα προβλέπουν την ίδια εξαρτημένη μεταβλητή (Thumb)
Το SST μετρά τη συνολική μεταβλητότητα που υπάρχει στα δεδομένα
Το SST δεν εξαρτάται από την επιλογή της ανεξάρτητης μεταβλητής
Το SST υπολογίζεται από το κενό μοντέλο, που είναι το ίδιο για όλα

Το SS Model και το SS Error διαφέρουν γιατί:

Εξαρτώνται από την προβλεπτική ικανότητα του μοντέλου
Η Height εξηγεί περισσότερη μεταβλητότητα (SSR μεγαλύτερο, SSE μικρότερο)
Η Height2Group εξηγεί λιγότερη μεταβλητότητα (SS Model μικρότερο, SSE μεγαλύτερο)

Συνοπτικά: Μόνο το SS Total θα είναι το ίδιο (11880.211) γιατί μετρά τη συνολική μεταβλητότητα στην εξαρτημένη μεταβλητή, που είναι η ίδια για οποιοδήποτε μοντέλο. Το SS Model και SS Error διαφέρουν γιατί εξαρτώνται από την προβλεπτική ικανότητα κάθε μοντέλου - η Height εξηγεί περισσότερο (SSR = 1817) ενώ η Height2Group εξηγεί λιγότερο (SSR = 831).

10.7 Αξιολόγηση της Προσαρμογής του Μοντέλου με τους δείκτες `PRE` και `F`

Σύγκριση του PRE για τα δύο μοντέλα

Ας επιστρέψουμε στους πίνακες ANOVA για τα μοντέλα της Height2Group και της Height.

Το μοντέλο της Height2Group

Analysis of Variance Table (Type III SS)
Model: Thumb ~ Height2Group

                               SS  df      MS      F    PRE     p
----- --------------- | --------- --- ------- ------ ------ -----
Model (error reduced) |   830.880   1 830.880 11.656 0.0699 .0008
Error (from model)    | 11049.331 155  71.286
----- --------------- | --------- --- ------- ------ ------ -----
Total (empty model)   | 11880.211 156  76.155

Το μοντέλο της Height

Analysis of Variance Table (Type III SS)
Model: Thumb ~ Height

                               SS  df       MS      F    PRE     p
----- --------------- | --------- --- -------- ------ ------ -----
Model (error reduced) |  1816.862   1 1816.862 27.984 0.1529 .0000
Error (from model)    | 10063.349 155   64.925
----- --------------- | --------- --- -------- ------ ------ -----
Total (empty model)   | 11880.211 156   76.155

Να συγκρίνετε το PRE (Proportional Reduction in Error - Αναλογική Μείωση του Σφάλματος) ανάμεσα στα δύο μοντέλα (το μοντέλο δύο ομάδων έναντι του μοντέλου παλινδρόμησης). Ποιο μοντέλο έχει υψηλότερο PRE;

Height2GroupHeight

Επεξήγηση

Σωστή απάντηση: Β — Height

Σύγκριση των PRE:

Μοντέλο	PRE	Ποσοστό
`Height2Group`	0.0699	7.0%
`Height`	0.1529	15.3%

Το μοντέλο της Height έχει υψηλότερο PRE (0.1529 vs 0.0699)

Γιατί;

Μοντέλο της Height2Group: \[\text{PRE} = \frac{830.880}{11880.211} = 0.0699 = 7.0\%\]

Εξηγεί μόνο 7% της μεταβλητότητας
Χρησιμοποιεί ποιοτική μεταβλητή (2 ομάδες: short/tall)
Χάνει πληροφορία από την κατηγοριοποίηση

Μοντέλο της Height: \[\text{PRE} = \frac{1816.862}{11880.211} = 0.1529 = 15.3\%\]

Εξηγεί 15.3% της μεταβλητότητας
Χρησιμοποιεί συνεχή μεταβλητή (ακριβές ύψος σε cm)
Διατηρεί όλη την πληροφορία του ύψους

Σύγκριση: - Το μοντέλο της Height εξηγεί διπλάσια μεταβλητότητα (15.3% vs 7.0%) - Η διαφορά: $15.3\% - 7.0\% = 8.3\%$ επιπλέον εξηγούμενη μεταβλητότητα

Συμπέρασμα: Το μοντέλο της Height είναι πιο αποτελεσματικό επειδή χρησιμοποιεί την πλήρη πληροφορία του ύψους αντί να την κατηγοριοποιεί σε δύο ομάδες.

Τι σημαίνει αυτός ο αριθμός (π.χ., PRE = 0.15); (Υπάρχουν περισσότερες από μία σωστές απαντήσεις.)

Αναλογία σφάλματος που μειώθηκε από το μοντέλο της Height σε σύγκριση με το μοντέλο της Height2GroupΑναλογία σφάλματος που μειώθηκε από το κενό μοντέλο με την υιοθέτηση του μοντέλου της HeightΑναλογία σφάλματος που εξηγείται από το μοντέλο της Height σε σύγκριση με το κενό μοντέλοΑναλογία σφάλματος που παραμένει ανεξήγητη από το μοντέλο της Height

Επεξήγηση

Σωστές απαντήσεις: Β και Γ

Το PRE = 0.15 (ή 15%) έχει δύο ισοδύναμες ερμηνείες:

Β. «Αναλογία σφάλματος που μειώθηκε από το κενό μοντέλο με την υιοθέτηση του μοντέλου της Height» — ΣΩΣΤΟ ✓

Αυτή είναι η κύρια ερμηνεία του PRE.

Υπολογισμός: \[\text{PRE} = \frac{\text{SS Total} - \text{SS Error}}{\text{SS Total}} = \frac{11880.211 - 10063.349}{11880.211} = \frac{1816.862}{11880.211} = 0.1529\]

Με λόγια:

Πριν: Το κενό μοντέλο είχε σφάλμα SS Total = 11880.211
Μετά: Το μοντέλο της Height έχει σφάλμα SS Error = 10063.349
Μείωση: $11880.211 - 10063.349 = 1816.862$
Ποσοστό μείωσης: $\frac{1816.862}{11880.211} = 15.3\%$

Ερμηνεία: Το μοντέλο της Height μείωσε το σφάλμα κατά 15.3% σε σχέση με το κενό μοντέλο.

Γ. «Αναλογία σφάλματος που εξηγείται από το μοντέλο της Height σε σύγκριση με το κενό μοντέλο» — ΣΩΣΤΟ ✓

Αυτή είναι ισοδύναμη ερμηνεία με την Β.

Υπολογισμός: \[\text{PRE} = \frac{\text{SS Model}}{\text{SS Total}} = \frac{1816.862}{11880.211} = 0.1529\]

Με λόγια:

Το μοντέλο της Height εξηγεί SS Model = 1816.862 μονάδες μεταβλητότητας
Η συνολική μεταβλητότητα είναι SS Total = 11880.211
Ποσοστό που εξηγείται: $\frac{1816.862}{11880.211} = 15.3\%$

Ερμηνεία: Το μοντέλο της Height εξηγεί 15.3% της συνολικής μεταβλητότητας στο μήκος αντίχειρα.

Γιατί οι Β και Γ είναι ισοδύναμες;

Επειδή: \[\text{SS Model} = \text{SS Total} - \text{SS Error}\]

Άρα: \[\frac{\text{SS Model}}{\text{SS Total}} = \frac{\text{SS Total} - \text{SS Error}}{\text{SS Total}}\]

Και οι δύο εκφράσεις δίνουν το ίδιο αποτέλεσμα!

“Μείωση σφάλματος” = “Εξηγούμενη μεταβλητότητα”
Είναι δύο όψεις του ίδιου νομίσματος

Γιατί οι άλλες επιλογές είναι λάθος

Α. «Αναλογία σφάλματος που μειώθηκε από το μοντέλο της Height σε σύγκριση με το μοντέλο της Height2Group» — ΛΑΘΟΣ

Αυτό δεν είναι ο ορισμός του PRE.

Το PRE πάντα συγκρίνει ένα μοντέλο με το κενό μοντέλο, όχι με άλλο σύνθετο μοντέλο.

Αν θέλαμε να συγκρίνουμε τα δύο μοντέλα:

Θα υπολογίζαμε τη διαφορά στα PRE τους: \[\Delta\text{PRE} = 0.1529 - 0.0699 = 0.083 = 8.3\%\]

Αυτό θα σήμαινε ότι το μοντέλο της Height εξηγεί 8.3% περισσότερη μεταβλητότητα από το μοντέλο της Height2Group.

Αλλά αυτό ΔΕΝ είναι το PRE! Το PRE του κάθε μοντέλου είναι:

PRE της Height = 15.3% (σύγκριση με κενό μοντέλο)
PRE της Height2Group = 7.0% (σύγκριση με κενό μοντέλο)

Δ. «Αναλογία σφάλματος που παραμένει ανεξήγητη από το μοντέλο της Height» — ΛΑΘΟΣ

Αυτό είναι το αντίθετο του PRE!

Το σφάλμα που παραμένει ανεξήγητο είναι:

\[1 - \text{PRE} = 1 - 0.1529 = 0.8471 = 84.7\%\]

Με άλλα λόγια: \[\frac{\text{SS Error}}{\text{SS Total}} = \frac{10063.349}{11880.211} = 0.8471 = 84.7\%\]

Ερμηνεία: - Το μοντέλο της Height εξηγεί 15.3% της μεταβλητότητας (PRE)

Το μοντέλο δεν εξηγεί 84.7% της μεταβλητότητας (1 - PRE)

Αυτή η ποσότητα (84.7%) δεν είναι το PRE - είναι το συμπλήρωμά του.

Σύνοψη

PRE = 0.15 σημαίνει:

✓ Β: Το μοντέλο μείωσε το σφάλμα κατά 15% σε σχέση με το κενό μοντέλο

✓ Γ: Το μοντέλο εξηγεί 15% της συνολικής μεταβλητότητας

✗ Α: ΟΧΙ σύγκριση με άλλο σύνθετο μοντέλο (PRE πάντα συγκρίνει με κενό)

✗ Δ: ΟΧΙ το ανεξήγητο μέρος (αυτό είναι 1 - PRE = 85%)

Δύο ισοδύναμοι τρόποι να το πούμε: 1. “Μείωση σφάλματος”: Το σφάλμα μειώθηκε κατά 15%

“Εξηγούμενη μεταβλητότητα”: Εξηγείται το 15% της μεταβλητότητας

Και οι δύο είναι σωστοί!

Πώς υπολογίζεται το PRE για το μοντέλο παλινδρόμησης; (Υπάρχουν περισσότερες από μία σωστές απαντήσεις.)

(SS Total - SS Error) / SS TotalSS Model / SS TotalSS Error / SS Total

Επεξήγηση

Σωστές απαντήσεις: Α και Β

Υπάρχουν δύο ισοδύναμοι τύποι για τον υπολογισμό του PRE:

Α. «(SS Total - SS Error) / SS Total» — ΣΩΣΤΟ ✓

Αυτός είναι ο βασικός ορισμός του PRE: \[\text{PRE} = \frac{\text{SS Total} - \text{SS Error}}{\text{SS Total}}\]

Για το μοντέλο της Height:

\[\text{PRE} = \frac{11880.211 - 10063.349}{11880.211} = \frac{1816.862}{11880.211} = 0.1529\]

Ερμηνεία:

Αριθμητής: $\text{SS Total} - \text{SS Error} = 1816.862$ = Η μείωση στο σφάλμα
Παρονομαστής: $\text{SS Total} = 11880.211$ = Το αρχικό σφάλμα (από κενό μοντέλο)
Κλάσμα: Το ποσοστό μείωσης του σφάλματος

Με λόγια: “Πόσο από το αρχικό σφάλμα μειώθηκε;”

Β. «SS Model / SS Total» — ΣΩΣΤΟ ✓

Αυτός είναι ο εναλλακτικός (και ισοδύναμος) τύπος:

\[\text{PRE} = \frac{\text{SS Model}}{\text{SS Total}}\]

Για το μοντέλο της Height:

\[\text{PRE} = \frac{1816.862}{11880.211} = 0.1529\]

Ερμηνεία: - Αριθμητής: $\text{SS Model} = 1816.862$ = Η εξηγούμενη μεταβλητότητα

Παρονομαστής: $\text{SS Total} = 11880.211$ = Η συνολική μεταβλητότητα
Κλάσμα: Το ποσοστό εξήγησης της μεταβλητότητας

Με λόγια: “Πόσο από τη συνολική μεταβλητότητα εξηγείται;”

Γιατί οι δύο τύποι είναι ισοδύναμοι;

Επειδή:

\[\text{SS Total} = \text{SS Model} + \text{SS Error}\]

Άρα:

\[\text{SS Model} = \text{SS Total} - \text{SS Error}\]

Αντικαθιστώντας στον πρώτο τύπο:

\[\text{PRE} = \frac{\text{SS Total} - \text{SS Error}}{\text{SS Total}} = \frac{\text{SS Model}}{\text{SS Total}}\]

Επαλήθευση με αριθμούς:

Τύπος Α:

\[\frac{11880.211 - 10063.349}{11880.211} = \frac{1816.862}{11880.211} = 0.1529\] ✓

Τύπος Β:

\[\frac{1816.862}{11880.211} = 0.1529\] ✓

Το ίδιο αποτέλεσμα!

Γιατί η άλλη επιλογή είναι λάθος

Γ. «SS Error / SS Total» — ΛΑΘΟΣ

Αυτός ο τύπος υπολογίζει το αντίθετο του PRE!

Αυτό δίνει:

\[\frac{\text{SS Error}}{\text{SS Total}} = \frac{10063.349}{11880.211} = 0.8471 = 84.7\%\]

Τι αντιπροσωπεύει αυτό;

Αυτό είναι το ποσοστό της μεταβλητότητας που παραμένει ανεξήγητο.

Σχέση με το PRE:

\[\frac{\text{SS Error}}{\text{SS Total}} = 1 - \text{PRE}\]

Επαλήθευση:

\[1 - 0.1529 = 0.8471\] ✓

Ερμηνεία:

PRE = 0.1529 → Το μοντέλο εξηγεί 15.3%
1 - PRE = 0.8471 → Το μοντέλο δεν εξηγεί 84.7%

Αυτή η ποσότητα (0.8471) είναι χρήσιμη, αλλά δεν είναι το PRE!

Πρακτική εφαρμογή

Στην πράξη, ποιον τύπο χρησιμοποιούμε;

Και οι δύο είναι σωστοί, αλλά:

Τύπος Β (SS Model / SS Total) είναι πιο άμεσος:

Διαβάζουμε απευθείας τα SS Model και SS Total από τον πίνακα ANOVA
Μία διαίρεση μόνο

Τύπος Α ((SS Total - SS Error) / SS Total) είναι πιο εννοιολογικός:

Δείχνει ξεκάθαρα τη “μείωση σφάλματος”
Χρειάζεται αφαίρεση και διαίρεση

Στον πίνακα ANOVA:

                               SS  df       MS      F    PRE     p
----- --------------- | --------- --- -------- ------ ------ -----
Model (error reduced) |  1816.862   1 1816.862 27.984 0.1529 .0000
                        ^^^^^^^^^                      ^^^^^^
                        SS Model                         PRE
Error (from model)    | 10063.349 155   64.925
                        ^^^^^^^^^^
                        SS Error
----- --------------- | --------- --- -------- ------ ------ -----
Total (empty model)   | 11880.211 156   76.155
                        ^^^^^^^^^^
                        SS Total

Χρησιμοποιώντας τον Τύπο Β: \[\text{PRE} = \frac{1816.862}{11880.211} = 0.1529\] ✓

Αυτή η τιμή εμφανίζεται ήδη υπολογισμένη στη στήλη PRE!

Σύνοψη

Για τον υπολογισμό του PRE, χρησιμοποιούμε:

✓ Α: $\text{PRE} = \frac{\text{SS Total} - \text{SS Error}}{\text{SS Total}}$ (ορισμός με βάση τη μείωση)

✓ Β: $\text{PRE} = \frac{\text{SS Model}}{\text{SS Total}}$ (ορισμός με βάση την εξήγηση)

✗ Γ: $\frac{\text{SS Error}}{\text{SS Total}}$ = 1 - PRE (ΟΧΙ το PRE, αλλά το ανεξήγητο μέρος)

Και οι δύο σωστοί τύποι (Α και Β) δίνουν το ίδιο αποτέλεσμα επειδή:

\[\text{SS Model} = \text{SS Total} - \text{SS Error}\]

Τι είναι κοινό στον υπολογισμό του PRE και για τα δύο μοντέλα;

Το SS Total είναι το ίδιο, αλλά το SS Error και το SS Model διαφέρουν.Το SS Total και το SS Error είναι τα ίδια, αλλά το SS Model διαφέρει.Το SS Model και το SS Error είναι τα ίδια, αλλά το SS Total διαφέρει.

Επεξήγηση

Σωστή απάντηση: Α — Το SS Total είναι το ίδιο, αλλά το SS Error και το SS Model διαφέρουν.

Σύγκριση των δύο μοντέλων

Στοιχείο	Μοντέλο `Height2Group`	Μοντέλο `Height`	Ίδιο;
`SS Total`	11880.211	11880.211	✓ Ναι
`SS Error`	11049.331	10063.349	✗ Όχι
`SS Model`	830.880	1816.862	✗ Όχι
PRE	0.0699 (7.0%)	0.1529 (15.3%)	✗ Όχι

Α. «Το SS Total είναι το ίδιο, αλλά το SS Error και το SS Model διαφέρουν» — ΣΩΣΤΟ ✓

Γιατί το SS Total είναι το ίδιο;

Το SS Total μετρά τη συνολική μεταβλητότητα στην εξαρτημένη μεταβλητή: \[\text{SS Total} = \sum_{i=1}^{n}(Y_i - \bar{Y})^2\]

Αυτό εξαρτάται μόνο από:

Την εξαρτημένη μεταβλητή (Thumb) - η ίδια και στα δύο μοντέλα ✓
Το σύνολο δεδομένων - το ίδιο και στα δύο μοντέλα ✓
Τον μέσο όρο της Thumb - ο ίδιος και στα δύο μοντέλα ✓

Το SS Total ΔΕΝ εξαρτάται από:

Την ανεξάρτητη μεταβλητή που επιλέγουμε
Το πόσο καλά προβλέπει το μοντέλο

Άρα: Όλα τα μοντέλα με την ίδια εξαρτημένη μεταβλητή έχουν το ίδιο SS Total.

Γιατί το SS Error διαφέρει;

Το SS Error μετρά την ανεξήγητη μεταβλητότητα:

\[\text{SS Error} = \sum_{i=1}^{n}(Y_i - \hat{Y}_i)^2\]

Αυτό εξαρτάται από: - Τις προβλέψεις του μοντέλου ($\hat{Y}_i$)

Την προβλεπτική ικανότητα του μοντέλου

Τα δύο μοντέλα κάνουν διαφορετικές προβλέψεις:

Μοντέλο Height2Group: - Προβλέπει τον μέσο όρο της ομάδας (short ή tall)

Όλοι οι short παίρνουν την ίδια πρόβλεψη
Όλοι οι tall παίρνουν την ίδια πρόβλεψη
SS Error = 11049.331 (μεγαλύτερο - λιγότερο ακριβείς προβλέψεις)

Μοντέλο Height: - Προβλέπει με βάση το ακριβές ύψος: $\hat{Y} = b_0 + b_1 \times \text{Height}$

Κάθε άτομο παίρνει διαφορετική πρόβλεψη
SS Error = 10063.349 (μικρότερο - πιο ακριβείς προβλέψεις)

Διαφορά:

\[11049.331 - 10063.349 = 985.982\]

Το μοντέλο της Height έχει 986 μονάδες μικρότερο ανεξήγητο σφάλμα!

Γιατί το SS Model διαφέρει;

Το SS Model μετρά την εξηγούμενη μεταβλητότητα:

\[\text{SS Model} = \sum_{i=1}^{n}(\hat{Y}_i - \bar{Y})^2\]

Επειδή:

\[\text{SS Model} = \text{SS Total} - \text{SS Error}\]

Και το SS Error διαφέρει, το SS Model επίσης διαφέρει:

Μοντέλο Height2Group:

\[\text{SS Model} = 11880.211 - 11049.331 = 830.880\]

Μοντέλο Height:

\[\text{SS Model} = 11880.211 - 10063.349 = 1816.862\]

Διαφορά:

\[1816.862 - 830.880 = 985.982\]

Το μοντέλο της Height εξηγεί 986 μονάδες περισσότερη μεταβλητότητα!

Γιατί οι άλλες επιλογές είναι λάθος

Β. «Το SS Total και το SS Error είναι τα ίδια, αλλά το SS Model διαφέρει» — ΛΑΘΟΣ

Αυτό είναι εντελώς λάθος.

Από τα δεδομένα βλέπουμε:

SS Total: 11880.211 = 11880.211 ✓ (ίδιο)
SS Error: 11049.331 ≠ 10063.349 ✗ (διαφορετικό!)

Το SS Error είναι ξεκάθαρα διαφορετικό για τα δύο μοντέλα.

Γ. «Το SS Model και το SS Error είναι τα ίδια, αλλά το SS Total διαφέρει» — ΛΑΘΟΣ

Αυτό είναι επίσης εντελώς λάθος και αντίθετο με την πραγματικότητα.

Από τα δεδομένα:

SS Total: 11880.211 = 11880.211 ✓ (ίδιο!)
SS Model: 830.880 ≠ 1816.862 ✗ (διαφορετικό)
SS Error: 11049.331 ≠ 10063.349 ✗ (διαφορετικό)

Το SS Total είναι το μόνο που είναι ίδιο.

Πρακτική σημασία

Το γεγονός ότι το SS Total είναι το ίδιο σημαίνει:

1. Δίκαιη σύγκριση μοντέλων

Όλα τα μοντέλα ξεκινούν από την ίδια αφετηρία
Μετράμε πόσο καλά το καθένα μειώνει αυτό το σφάλμα

2. Το PRE είναι συγκρίσιμο

PRE = $\frac{\text{SS Model}}{\text{SS Total}}$
Επειδή ο παρονομαστής είναι ο ίδιος, μπορούμε να συγκρίνουμε απευθείας τα PRE
Height2Group: PRE = 0.0699 (7.0%)
Height: PRE = 0.1529 (15.3%)
Το δεύτερο είναι καλύτερο γιατί έχει μεγαλύτερο PRE

3. Η διαφορά στο SS Error δείχνει τη βελτίωση

\[\Delta\text{SS Error} = 11049.331 - 10063.349 = 985.982\]

Αυτές οι 986 μονάδες είναι η επιπλέον μεταβλητότητα που εξηγείται
Από τη χρήση συνεχούς ύψους αντί κατηγορικής ομαδοποίησης

Συμπέρασμα

Κοινό στοιχείο: Το SS Total = 11880.211

Είναι το ίδιο για και τα δύο μοντέλα
Επειδή και τα δύο προβλέπουν την ίδια εξαρτημένη μεταβλητή (Thumb)
Χρησιμοποιούν το ίδιο σύνολο δεδομένων

Διαφορές:

SS Error και SS Model είναι διαφορετικά
Επειδή τα μοντέλα έχουν διαφορετική προβλεπτική ικανότητα
Το μοντέλο της Height είναι πιο αποτελεσματικό

Η σχέση: \[\text{SS Total (σταθερό)} = \text{SS Model (μεταβλητό)} + \text{SS Error (μεταβλητό)}\]

Όσο μεγαλύτερο το SS Model, τόσο μικρότερο το SS Error, και τόσο καλύτερο το μοντέλο!

Γιατί το PRE του μοντέλου της Height είναι μεγαλύτερο από το PRE του μοντέλο της Height2Group;

Το PRE έχει την ίδια ερμηνεία στα μοντέλα παλινδρόμησης όπως και στα μοντέλα ομάδων. Όπως έχουμε ήδη επισημάνει, το συνολικό άθροισμα τετραγώνων είναι το ίδιο και για τα δύο μοντέλα. Σε κάθε περίπτωση, το PRE υπολογίζεται διαιρώντας το SS Model με το SS Total.

Πολλά εγχειρίδια στατιστικής τονίζουν τη διαφορά ανάμεσα στα μοντέλα ANOVA (όπως τα δικά μας μοντέλα δύο και τριών ομάδων) και τα μοντέλα παλινδρόμησης (όπως το μοντέλο του ύψους). Στην πραγματικότητα, όμως, οι δύο τύποι μοντέλων είναι ουσιαστικά ίδιοι και εντάσσονται απλά στο πλαίσιο του Γενικού Γραμμικού Μοντέλου. Στην παλινδρόμηση, το PRE αναφέρεται συχνά ως R² (R-τετράγωνο).

Για τα μοντέλα που εξετάζουμε, ανεξάρτητα από την ονομασία, η ερμηνεία του PRE είναι ίδια: αποτελεί το ποσοστό του σφάλματος που μειώνεται από το πιο σύνθετο μοντέλο σε σύγκριση με το κενό μοντέλο — ή, με άλλα λόγια, το ποσοστό της μεταβλητότητας που εξηγείται από το μοντέλο.

Τι σημαίνει το γεγονός ότι το PRE είναι μεγαλύτερο για το μοντέλο της Height από ό,τι για το μοντέλο της Height2Group; (Υπάρχουν περισσότερες από μία σωστές απαντήσεις.)

Το μοντέλο της Height έχει λιγότερο υπολειπόμενο σφάλμα από το μοντέλο της Height2Group.Το μοντέλο της Height εξηγεί περισσότερη μεταβλητότητα από το μοντέλο της Height2Group.Το μοντέλο της Height έχει ως αποτέλεσμα προβλέψεις που είναι πιο κοντά στα δεδομένα από το μοντέλο της Height2Group.Περίπου 15% της μεταβλητότητας στο μήκος αντίχειρα (Thumb) εξηγείται από τη μεταβλητότητα στο ύψος, σε σύγκριση με το 7% που εξηγείται από το σε ποια ομάδα ύψους ανήκει κάποιος (short vs. tall).Το μοντέλο της Height αφήνει περισσότερο σφάλμα ανεξήγητο από το μοντέλο της Height2Group.Τα δεδομένα που χρησιμοποιήθηκαν για την προσαρμογή του μοντέλου της Height έχουν περισσότερη αναλογική μεταβλητότητα από τα δεδομένα που χρησιμοποιήθηκαν για την προσαρμογή του μοντέλου της Height2Group.

Επεξήγηση

Σωστές απαντήσεις: Α, Β, Γ και Δ

Σύγκριση των δύο μοντέλων

Στοιχείο	`Height2Group`	`Height`	Σύγκριση
PRE	0.0699 (7.0%)	0.1529 (15.3%)	`Height` > `Height2Group` ✓
`SS Total`	11880.211	11880.211	Ίδιο
`SS Error`	11049.331	10063.349	`Height` < `Height2Group` ✓
`SS Model`	830.880	1816.862	`Height` > `Height2Group` ✓

Α. «Το μοντέλο της Height έχει λιγότερο υπολειπόμενο σφάλμα από το μοντέλο της Height2Group» — ΣΩΣΤΟ ✓

Αυτό είναι σωστό και άμεση συνέπεια του μεγαλύτερου PRE.

Σύγκριση του υπολειπόμενου σφάλματος: - Height2Group: SS Error = 11049.331 - Height: SS Error = 10063.349

Διαφορά: \[11049.331 - 10063.349 = 985.982\]

Το μοντέλο της Height έχει 986 μονάδες λιγότερο υπολειπόμενο σφάλμα!

Γιατί αυτό συνδέεται με το PRE;

\[\text{PRE} = \frac{\text{SS Total} - \text{SS Error}}{\text{SS Total}}\]

Όσο μικρότερο το SS Error, τόσο μεγαλύτερο το PRE:

Μικρό SS Error → Μεγάλη μείωση σφάλματος → Μεγάλο PRE ✓

Ποσοστό μείωσης: \[\frac{985.982}{11049.331} \times 100\% = 8.9\%\]

Το μοντέλο της Height μείωσε το υπολειπόμενο σφάλμα κατά 8.9% σε σχέση με το μοντέλο της Height2Group.

Β. «Το μοντέλο της Height εξηγεί περισσότερη μεταβλητότητα από το μοντέλο της Height2Group» — ΣΩΣΤΟ ✓

Αυτό είναι η βασική ερμηνεία του PRE.

Σύγκριση της εξηγούμενης μεταβλητότητας: - Height2Group: Εξηγεί 7.0% της μεταβλητότητας - Height: Εξηγεί 15.3% της μεταβλητότητας

Από το SS Model: - Height2Group: SS Model = 830.880 - Height: SS Model = 1816.862

Διαφορά: \[1816.862 - 830.880 = 985.982\]

Το μοντέλο της Height εξηγεί 986 μονάδες περισσότερη μεταβλητότητα!

Με ποσοστά: \[15.3\% - 7.0\% = 8.3\%\]

Το μοντέλο της Height εξηγεί διπλάσια (περίπου) μεταβλητότητα από το μοντέλο της Height2Group.

Γιατί;

Η Height χρησιμοποιεί συνεχή μεταβλητή (ακριβές ύψος σε cm)
Η Height2Group χρησιμοποιεί ποιοτική μεταβλητή (μόνο 2 ομάδες)
Η κατηγοριοποίηση χάνει πληροφορία

Γ. «Το μοντέλο της Height έχει ως αποτέλεσμα προβλέψεις που είναι πιο κοντά στα δεδομένα από το μοντέλο της Height2Group» — ΣΩΣΤΟ ✓

Αυτό είναι άλλος τρόπος να εκφράσουμε το μικρότερο SS Error.

Τι σημαίνει μικρότερο SS Error;

\[\text{SS Error} = \sum_{i=1}^{n}(Y_i - \hat{Y}_i)^2\]

όπου: - $Y_i$ = πραγματικά δεδομένα

$\hat{Y}_i$ = προβλέψεις του μοντέλου
$(Y_i - \hat{Y}_i)$ = απόσταση δεδομένων από προβλέψεις

Μικρότερο SS Error σημαίνει: - Οι προβλέψεις είναι πιο κοντά στα πραγματικά δεδομένα

Τα υπόλοιπα (residuals) είναι μικρότερα κατά μέσο όρο
Το μοντέλο κάνει πιο ακριβείς προβλέψεις

Παράδειγμα:

Έστω άτομο με ύψος 170 cm και μήκος αντίχειρα 62 mm:

Μοντέλο Height2Group:

Αν το άτομο ανήκει στην ομάδα tall
Πρόβλεψη = μέσος όρος tall = 64.7 mm
Υπόλοιπο = $62 - 64.7 = -2.7$ mm

Μοντέλο Height: - Πρόβλεψη = $-3.33 + 0.378 \times 170 = 60.93$ mm

Υπόλοιπο = $62 - 60.93 = 1.07$ mm

Σύγκριση: - Υπόλοιπο Height2Group: $|-2.7| = 2.7$ mm

Υπόλοιπο Height: $|1.07| = 1.07$ mm

Το μοντέλο της Height έκανε πιο ακριβή πρόβλεψη (πιο κοντά στο 62)!

Δ. «Περίπου 15% της μεταβλητότητας στο μήκος αντίχειρα εξηγείται από τη μεταβλητότητα στο ύψος, σε σύγκριση με το 7% που εξηγείται από το σε ποια ομάδα ύψους ανήκει κάποιος» — ΣΩΣΤΟ ✓

Αυτή είναι η πιο ολοκληρωμένη και ακριβής ερμηνεία των PRE.

Μοντέλο της Height2Group (PRE = 0.0699 = 7%):

Τι μετράει: Πόση μεταβλητότητα εξηγείται από το αν κάποιος είναι short ή tall
Ερμηνεία: Το γεγονός ότι γνωρίζουμε σε ποια από τις 2 ομάδες ανήκει κάποιος μειώνει το σφάλμα πρόβλεψης κατά 7%
Πληροφορία: Μόνο 2 κατηγορίες (binary)

Μοντέλο της Height (PRE = 0.1529 = 15.3%):

Τι μετράει: Πόση μεταβλητότητα εξηγείται από το ακριβές ύψος (σε cm)
Ερμηνεία: Το γεγονός ότι γνωρίζουμε το συνεχές ύψος μειώνει το σφάλμα πρόβλεψης κατά 15.3%
Πληροφορία: Συνεχής μεταβλητή (π.χ., 165, 170, 175 cm)

Σύγκριση: - Η συνεχής μεταβλητή Height εξηγεί διπλάσια μεταβλητότητα (15% vs 7%)

Η κατηγοριοποίηση χάνει πληροφορία: $15\% - 7\% = 8\%$ απώλεια

Πρακτική σημασία: - Αν χρησιμοποιούμε το ακριβές ύψος, κάνουμε πολύ καλύτερες προβλέψεις

Η απλοποίηση σε 2 ομάδες (short/tall) μειώνει στο μισό την προβλεπτική ικανότητα

Γιατί οι άλλες επιλογές είναι λάθος

Ε. «Το μοντέλο της Height αφήνει περισσότερο σφάλμα ανεξήγητο από το μοντέλο της Height2Group» — ΛΑΘΟΣ

Αυτό είναι εντελώς λάθος και το αντίθετο της αλήθειας!

Το ανεξήγητο σφάλμα είναι: \[1 - \text{PRE}\]

Μοντέλο Height2Group:

\[1 - 0.0699 = 0.9301 = 93.0\% \text{ ανεξήγητο}\]

Μοντέλο Height:

\[1 - 0.1529 = 0.8471 = 84.7\% \text{ ανεξήγητο}\]

Σύγκριση:

Height2Group αφήνει 93% ανεξήγητο
Height αφήνει 84.7% ανεξήγητο

Το μοντέλο της Height αφήνει λιγότερο ανεξήγητο σφάλμα, όχι περισσότερο!

Διαφορά:

\[93.0\% - 84.7\% = 8.3\%\]

Το μοντέλο της Height αφήνει 8.3% λιγότερο σφάλμα ανεξήγητο.

Γιατί αυτή η επιλογή είναι ελκυστική αλλά λάθος;

Μπορεί κάποιος να μπερδευτεί επειδή:

Μεγαλύτερο PRE → Μεγαλύτερο εξηγούμενο
Αλλά αυτό σημαίνει μικρότερο ανεξήγητο, όχι μεγαλύτερο!

Η σχέση: \[\text{Εξηγούμενο} + \text{Ανεξήγητο} = 100\%\]

\[\text{PRE} + (1 - \text{PRE}) = 1\]

Όσο αυξάνεται το ένα, τόσο μειώνεται το άλλο!

ΣΤ. «Τα δεδομένα που χρησιμοποιήθηκαν για την προσαρμογή του μοντέλου της Height έχουν περισσότερη αναλογική μεταβλητότητα από τα δεδομένα που χρησιμοποιήθηκαν για την προσαρμογή του μοντέλου της Height2Group» — ΛΑΘΟΣ

Αυτό είναι λάθος για πολλούς λόγους:

1. Χρησιμοποιούνται τα ίδια δεδομένα!

Και τα δύο μοντέλα χρησιμοποιούν:

Το ίδιο σύνολο δεδομένων: Fingers (157 άτομα)
Την ίδια εξαρτημένη μεταβλητή: Thumb
Τις ίδιες παρατηρήσεις: Τα ίδια 157 μήκη αντίχειρα

Άρα, δεν μπορεί να έχουν διαφορετική μεταβλητότητα - είναι τα ίδια δεδομένα!

2. Το SS Total είναι το ίδιο

\[\text{SS Total (Height2Group)} = \text{SS Total (Height)} = 11880.211\]

Αυτό επιβεβαιώνει ότι η συνολική μεταβλητότητα στα δεδομένα είναι η ίδια.

3. Τι διαφέρει;

Δεν διαφέρουν τα δεδομένα, αλλά: - Η ανεξάρτητη μεταβλητή που χρησιμοποιούμε - Ο τρόπος που μοντελοποιούμε τη σχέση - Η προβλεπτική ικανότητα του μοντέλου

4. Τι είναι “αναλογική μεταβλητότητα”;

Αυτός ο όρος δεν έχει σαφές νόημα στο πλαίσιο: - Αν εννοεί τη συνολική μεταβλητότητα → Είναι η ίδια (SS Total) - Αν εννοεί την εξηγούμενη αναλογία → Αυτό είναι το PRE, όχι χαρακτηριστικό των δεδομένων

Συμπέρασμα για τη ΣΤ:

Είναι λάθος επειδή: - ✗ Χρησιμοποιούνται τα ίδια δεδομένα - ✗ Το SS Total είναι το ίδιο - ✗ Η μεταβλητότητα στα δεδομένα δεν αλλάζει ανάλογα με το μοντέλο - ✗ Ο όρος “αναλογική μεταβλητότητα” είναι παραπλανητικός

Συνολική σύνοψη

Το γεγονός ότι PRE (Height) > PRE (Height2Group) σημαίνει:

✓ Α: Λιγότερο υπολειπόμενο σφάλμα - SS Error μικρότερο (10063 vs 11049)

✓ Β: Περισσότερη εξηγούμενη μεταβλητότητα - 15.3% vs 7.0%

✓ Γ: Προβλέψεις πιο κοντά στα δεδομένα - Μικρότερα υπόλοιπα κατά μέσο όρο

✓ Δ: Συγκεκριμένη σύγκριση ποσοστών - 15% (συνεχής) vs 7% (κατηγορική)

✗ Ε: ΟΧΙ περισσότερο ανεξήγητο - Έχει λιγότερο (84.7% vs 93.0%)

✗ ΣΤ: ΟΧΙ διαφορετικά δεδομένα - Τα ίδια δεδομένα, διαφορετικό μοντέλο

Βασική διαφορά: - Συνεχής μεταβλητή (Height) → Περισσότερη πληροφορία → Καλύτερο μοντέλο - Κατηγορική μεταβλητή (Height2Group) → Απώλεια πληροφορίας → Χειρότερο μοντέλο

Χρήση του πηλίκου `F` για τη σύγκριση μοντέλων

Τέλος, μπορούμε επίσης να αξιολογήσουμε την καταλληλότητα ενός μοντέλου εξετάζοντας το πηλίκο F, το οποίο παρουσιάσαμε σε προηγούμενο κεφάλαιο. Ενώ το PRE είναι ένα ποσοστό που βασίζεται στα αθροίσματα τετραγώνων, το στατιστικό F είναι ένα πηλίκο δύο διακυμάνσεων (γνωστών και ως μέσων τετραγώνων – MS), που υπολογίζονται διαιρώντας το SS με τους βαθμούς ελευθερίας (df). Ο αριθμητής είναι το MS Model, που δείχνει την ποσότητα της διακύμανσης που εξηγείται από το μοντέλο ανά βαθμό ελευθερίας που χρησιμοποιείται· ενώ ο παρονομαστής είναι το MS Error, που δείχνει τη διακύμανση που παραμένει ανεξήγητη ανά βαθμό ελευθερίας που απομένει.

Περισσότερα για τη σύγκριση `F` και PRE

Για να κατανοήσουμε πιο συγκεκριμένα γιατί αυτό έχει σημασία, ας συγκρίνουμε ακόμη ένα μοντέλο ομάδων με το μοντέλο της Height: το μοντέλο της Height10Group. Ο παρακάτω κώδικας δημιουργεί μια νέα μεταβλητή ομάδων, την Height10Group, μέσα στο πλαίσιο δεδομένων Fingers, η οποία χωρίζει το δείγμα σε 10 ισομεγέθεις ομάδες βάσει της Height και στη συνέχεια τη μετατρέπει σε τύπου factor.

Fingers$Height10Group <- ntile(Fingers$Height, 10)
Fingers$Height10Group <- factor(Fingers$Height10Group)

Γιατί χρειάστηκε να μετατρέψουμε τη μεταβλητή Height10Group σε factor;

Για να είναι οι ομάδες ισοπληθείςΓια να μην τη θεωρήσει η lm() ως ποσοτική μεταβλητήΓια να μπορέσουμε να αναπαραστήσουμε διαγραμματικά τη σχέση της Thumb με αυτήν

Επεξήγηση

Σωστή απάντηση: Β — Για να μην τη θεωρήσει η lm() ως ποσοτική μεταβλητή

Κατανόηση του κώδικα

Ας εξετάσουμε τι κάνει ο κώδικας βήμα προς βήμα:

# Βήμα 1: Δημιουργία της μεταβλητής ομαδοποίησης
Fingers$Height10Group <- ntile(Fingers$Height, 10)

# Βήμα 2: Μετατροπή σε factor
Fingers$Height10Group <- factor(Fingers$Height10Group)

Τι κάνει το Βήμα 1;

Η συνάρτηση ntile(Fingers$Height, 10) χωρίζει τα δεδομένα σε 10 ισομεγέθεις ομάδες με βάση το ύψος:

Ομάδα 1: Τα 10% πιο κοντά άτομα
Ομάδα 2: Τα επόμενα 10% πιο κοντά άτομα
…
Ομάδα 10: Τα 10% πιο ψηλά άτομα

Το αποτέλεσμα του Βήματος 1 είναι αριθμοί: 1, 2, 3, …, 10

head(Fingers$Height10Group)
# [1] 7 5 5 7 6 6
# Αυτοί είναι αριθμοί (numeric), όχι factor!

Το πρόβλημα: Πώς η R αντιλαμβάνεται αριθμούς στο lm()

Η συνάρτηση lm() αποφασίζει αυτόματα τι είδους μοντέλο να προσαρμόσει με βάση τον τύπο της ανεξάρτητης μεταβλητής:

Αν η μεταβλητή είναι αριθμητική (numeric):

Η lm() υποθέτει ότι είναι συνεχής/ποσοτική
Προσαρμόζει μοντέλο παλινδρόμησης (regression model)
Χρησιμοποιεί την αριθμητική τιμή ως X στην εξίσωση: $Y = b_0 + b_1X$

Αν η μεταβλητή είναι factor: - Η lm() υποθέτει ότι είναι ποιοτική/κατηγορική

Προσαρμόζει μοντέλο ομάδων (group model / ANOVA)
Χρησιμοποιεί ψευδομεταβλητές (dummy variables) για κάθε ομάδα

Τι θα συνέβαινε ΧΩΡΙΣ το Βήμα 2 (χωρίς factor());

Αν δεν μετατρέπαμε την Height10Group σε factor:

# ΛΑΘΟΣ τρόπος (χωρίς factor)
bad_model <- lm(Thumb ~ Height10Group, data = Fingers)

Η R θα το αντιμετωπούσε ως μοντέλο παλινδρόμησης:

\[\text{Thumb}_i = b_0 + b_1 \times \text{Height10Group}_i\]

όπου Height10Group = 1, 2, 3, …, 10 (ως αριθμοί)

Το πρόβλημα με αυτή την προσέγγιση:

Υποθέτει γραμμική σχέση:
- Κάθε αύξηση κατά 1 στην ομάδα (π.χ., από 5 σε 6) προσθέτει την ίδια ποσότητα $b_1$ στην πρόβλεψη
- Αυτό δεν έχει νόημα! Οι ομάδες είναι κατηγορίες, όχι συνεχής κλίμακα
Χάνεται η ευελιξία:
- Κάθε ομάδα θα έπρεπε να έχει τον δικό της μέσο όρο
- Αλλά το μοντέλο παλινδρόμησης επιβάλλει μια ευθεία γραμμή
Λάθος παράμετροι:
- Θα είχαμε 2 παραμέτρους ($b_0$, $b_1$) αντί για 10 μέσους όρους
- Θα χάναμε την πλήρη πληροφορία των διαφορών μεταξύ των ομάδων

Τι συμβαίνει ΜΕ το Βήμα 2 (με factor());

Όταν μετατρέπουμε σε factor:

# ΣΩΣΤΟΣ τρόπος (με factor)
Fingers$Height10Group <- factor(Fingers$Height10Group)
good_model <- lm(Thumb ~ Height10Group, data = Fingers)

Η R αναγνωρίζει ότι πρόκειται για ποιοτική μεταβλητή:

\[\text{Thumb}_i = b_0 + b_1X_{2,i} + b_2X_{3,i} + ... + b_9X_{10,i}\]

όπου $X_{j,i}$ είναι ψευδομεταβλητές (dummy variables) για κάθε ομάδα

Αποτέλεσμα:

Προσαρμόζεται μοντέλο ομάδων:
- Κάθε ομάδα έχει τον δικό της μέσο όρο
- Οι ομάδες μπορούν να διαφέρουν ελεύθερα μεταξύ τους
Σωστές παράμετροι:
- Έχουμε 10 παραμέτρους (μία για κάθε ομάδα)
- Κάθε ομάδα αντιπροσωπεύεται ξεχωριστά
Ευέλικτη μοντελοποίηση:
- Δεν επιβάλλεται γραμμική σχέση
- Οι διαφορές μεταξύ ομάδων μπορούν να είναι μη-γραμμικές

Β. «Για να μην την αντιμετωπίσει η lm() ως ποσοτική μεταβλητή» — ΣΩΣΤΟ ✓

Αυτή είναι η σωστή απάντηση γιατί:

Χωρίς factor():

Height10Group = numeric (1, 2, 3, …, 10)
lm() → Μοντέλο παλινδρόμησης (λάθος!)
Υποθέτει γραμμική σχέση

Με factor():

Height10Group = factor (10 επίπεδα)
lm() → Μοντέλο ομάδων (σωστό!)
Κάθε ομάδα έχει τον δικό της μέσο όρο

Επαλήθευση:

class(Fingers$Height10Group)
# [1] "factor"

levels(Fingers$Height10Group)
# [1] "1"  "2"  "3"  "4"  "5"  "6"  "7"  "8"  "9"  "10"

Τώρα η R γνωρίζει ότι αυτοί οι αριθμοί είναι ετικέτες ομάδων, όχι ποσοτικές τιμές!

Γιατί οι άλλες επιλογές είναι λάθος

Α. «Για να είναι οι ομάδες ισομεγέθεις» — ΛΑΘΟΣ

Αυτό το κάνει η ntile() στο Βήμα 1, όχι η factor() Αυτό που κάνει το factor() είναι:
Αλλάζει τον τύπο της μεταβλητής (από numeric σε factor)
Αλλάζει την ερμηνεία από τη lm() (από ποσοτική σε ποιοτική)

Γ. «Για να μπορέσουμε να αναπαραστήσουμε διαγραμματικά τη σχέση της Thumb με τη μεταβλητή αυτή» — ΛΑΘΟΣ

Αυτό είναι λάθος επειδή μπορούμε να σχεδιάσουμε διαγράμματα ανεξάρτητα από το αν η μεταβλητή είναι τύπου factor ή όχι.

Με numeric μεταβλητή:

# Αυτό ΛΕΙΤΟΥΡΓΕΙ
gf_point(Thumb ~ Height10Group, data = Fingers)

Με factor:

# Αυτό ΕΠΙΣΗΣ ΛΕΙΤΟΥΡΓΕΙ
gf_point(Thumb ~ Height10Group, data = Fingers)

Η διαφορά στο διάγραμμα:

Με numeric: Ο οριζόντιος άξονας έχει συνεχή αριθμητική κλίμακα (1, 2, 3, …)
Με factor: Ο οριζόντιος άξονας έχει διακριτές κατηγορίες (“1”, “2”, “3”, …)

Και στις δύο περιπτώσεις το διάγραμμα δημιουργείται!

Το factor() δεν είναι απαραίτητο για τη δημιουργία διαγραμμάτων. Είναι απαραίτητο για τη σωστή στατιστική ανάλυση με την lm().

Συμπέρασμα

Η σωστή απάντηση είναι Β επειδή:

Η Height10Group αρχικά είναι numeric (1, 2, 3, …, 10)
Αν δεν τη μετατρέψουμε, η lm() θα την αντιμετωπίσει ως ποσοτική
Θα προσαρμόσει μοντέλο παλινδρόμησης (λάθος τύπος μοντέλου)
Με το factor() η lm() αντιλαμβάνεται ότι είναι ποιοτική
Προσαρμόζει μοντέλο ομάδων (σωστός τύπος μοντέλου)

Ουσία: Το factor() αλλάζει τον τύπο της μεταβλητής, ώστε η lm() να την ερμηνεύσει σωστά ως κατηγορική και όχι ως αριθμητική!

Προσαρμόσαμε ένα μοντέλο ομάδων της μεταβλητής Thumb χρησιμοποιώντας τη Height10Group, και το αναπαραστήσαμε στο διάγραμμα jitter της σχέσης των δύο μεταβλητών. Οι προβλέψεις του μοντέλου εμφανίζονται ως 10 οριζόντια ευθύγραμμα τμήματα, καθένα από τα οποία αντιπροσωπεύει το μέσο όρο της αντίστοιχης ομάδας.

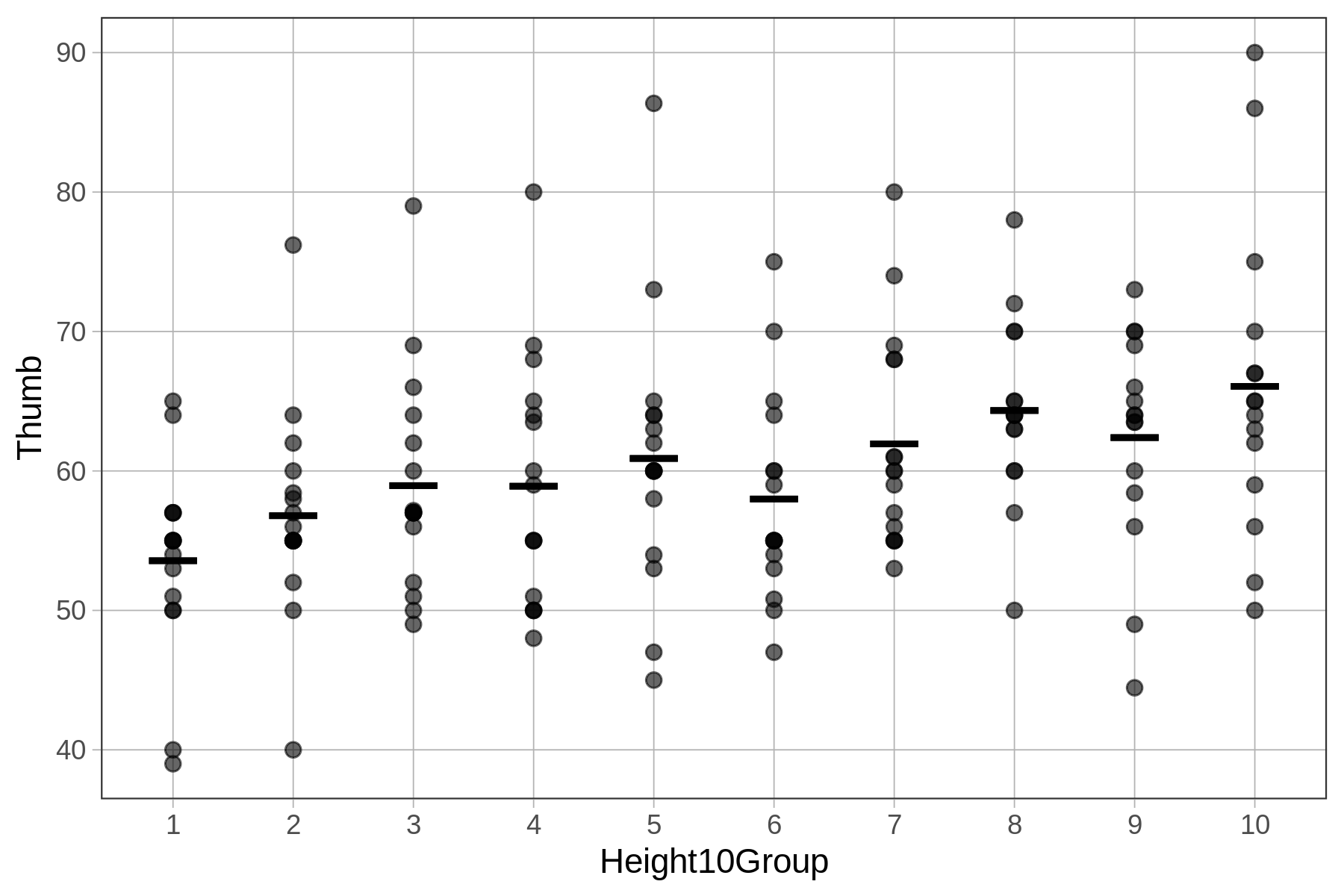
Ο παρακάτω κώδικας δείχνει πώς προσαρμόστηκε το μοντέλο της Thumb με βάση τη Height10Group, καθώς και πώς παράχθηκε ο πίνακας ANOVA:

Height10Group_model <- lm(Thumb ~ Height10Group, data = Fingers)
supernova(Height10Group_model)

Παρακάτω παρουσιάζονται οι πίνακες της supernova() για τα τρία μοντέλα: Height2Group, Height10Group, και Height. Η εξαρτημένη μεταβλητή και στα τρία μοντέλα είναι η Thumb.

Σύγκριση των Τριών Μοντέλων

Παρακάτω παρουσιάζονται οι πίνακες ANOVA για τα τρία μοντέλα: Height2Group, Height10Group, και Height. Η εξαρτημένη μεταβλητή και στα τρία μοντέλα είναι η Thumb.

Το μοντέλο της Height2Group

Analysis of Variance Table (Type III SS)
Model: Thumb ~ Height2Group

                               SS  df      MS      F    PRE     p
----- --------------- | --------- --- ------- ------ ------ -----
Model (error reduced) |   830.880   1 830.880 11.656 0.0699 .0008
Error (from model)    | 11049.331 155  71.286
----- --------------- | --------- --- ------- ------ ------ -----
Total (empty model)   | 11880.211 156  76.155

Το μοντέλο της Height10Group

Analysis of Variance Table (Type III SS)
Model: Thumb ~ Height10Group

                               SS  df      MS     F    PRE     p
----- --------------- | --------- --- ------- ----- ------ -----
Model (error reduced) |  1920.474   9 213.386 3.149 0.1617 .0017
Error (from model)    |  9959.737 147  67.753
----- --------------- | --------- --- ------- ----- ------ -----
Total (empty model)   | 11880.211 156  76.155

Το μοντέλο της Height

Analysis of Variance Table (Type III SS)
Model: Thumb ~ Height

                               SS  df       MS      F    PRE     p
----- --------------- | --------- --- -------- ------ ------ -----
Model (error reduced) |  1816.862   1 1816.862 27.984 0.1529 .0000
Error (from model)    | 10063.349 155   64.925
----- --------------- | --------- --- -------- ------ ------ -----
Total (empty model)   | 11880.211 156   76.155

Αν συγκρίνουμε μόνο τα PRE μεταξύ αυτών των τριών μοντέλων, ποιο μοντέλο εξηγεί περισσότερη από τη μεταβλητότητα στο μήκος αντίχειρα;

Το μοντέλο της Height2GroupΤο μοντέλο της Height10GroupΤο μοντέλο της Height

Επεξήγηση

Σωστή απάντηση: Β — Το μοντέλο της Height10Group

Σύγκριση των PRE:

Μοντέλο	PRE	Ποσοστό	Κατάταξη
`Height2Group`	0.0699	7.0%	3ο (χειρότερο)
`Height`	0.1529	15.3%	2ο
`Height10Group`	0.1617	16.2%	1ο (καλύτερο)

Το μοντέλο της Height10Group έχει το μεγαλύτερο PRE (0.1617 ή 16.2%).

Γιατί το μοντέλο της Height10Group εξηγεί περισσότερο;

1. Περισσότερες ομάδες = Περισσότερη ευελιξία

Το μοντέλο της Height10Group χωρίζει τα δεδομένα σε 10 ομάδες αντί για 2:

Height2Group: Μόνο 2 μέσοι όροι (short, tall)
- Όλοι οι short λαμβάνουν την ίδια τιμή πρόβλεψης
- Όλοι οι tall λαμβάνουν την ίδια τιμή πρόβλεψης
Height10Group: 10 μέσοι όροι (ένας για κάθε ομάδα)
- Πιο λεπτομερής ομαδοποίηση
- Κάθε ομάδα έχει τον δικό της μέσο όρο

2. Καλύτερη προσαρμογή στα δεδομένα

Με 10 ομάδες, το μοντέλο μπορεί να “ακολουθήσει” πιο στενά τη σχέση ύψους-αντίχειρα:

Οι μέσοι όροι των 10 ομάδων μπορούν να αποτυπώσουν μη-γραμμικές σχέσεις
Περισσότερες παράμετροι = Καλύτερη προσαρμογή

3. Σύγκριση των SS Error:

Μοντέλο	`SS Error`	Ανεξήγητη μεταβλητότητα
`Height2Group`	11049.331	Μεγαλύτερη
`Height`	10063.349	Μέτρια
`Height10Group`	9959.737	Μικρότερη

Το μοντέλο της Height10Group έχει το μικρότερο υπολειπόμενο σφάλμα.

Γιατί το μοντέλο της Height δεν είναι το καλύτερο;

Αν και το μοντέλο της Height είναι πολύ καλό, το μοντέλο της Height10Group το ξεπερνά ελαφρώς:

Διαφορά PRE: \[0.1617 - 0.1529 = 0.0088 = 0.88\%\]

Το μοντέλο της Height10Group εξηγεί 0.88% περισσότερη μεταβλητότητα.

Γιατί συμβαίνει αυτό;

Το μοντέλο της Height υποθέτει απόλυτα γραμμική σχέση: \[\text{Thumb} = b_0 + b_1 \times \text{Height}\]

Αλλά η σχέση μεταξύ ύψους και αντίχειρα μπορεί να μην είναι εντελώς γραμμική: - Μπορεί η σχέση να είναι καμπυλόγραμμη

Το μοντέλο της Height10Group μπορεί να αποτυπώσει αυτές τις μη-γραμμικότητες επειδή: - Κάθε ομάδα έχει το δικό της μέσο όρο - Δεν υποθέτουμε ότι η σχέση περιγράφεται από μια ευθεία γραμμή

Υπάρχει όμως ένα αντιστάθμισμα

Το μοντέλο της Height10Group εξηγεί περισσότερο, αλλά…

έχει κόστος: Χρησιμοποιεί περισσότερους βαθμούς ελευθερίας

Μοντέλο	PRE	df (Model)	PRE ανά df
`Height2Group`	0.0699	1	0.0699
`Height`	0.1529	1	0.1529 (καλύτερο!)
`Height10Group`	0.1617	9	0.0180

Παρατήρηση: Αν λάβουμε υπόψη το κόστος (df), το μοντέλο της Height είναι πιο αποδοτικό!

Εξηγεί σχεδόν το ίδιο (15.3% vs 16.2%)
Αλλά χρησιμοποιεί μόνο 1 df αντί για 9

Αυτό είναι που μετράει ο λόγος F (θα το δούμε στην επόμενη ερώτηση).

Συμπέρασμα

Με βάση μόνο το PRE: - 1ο: Height10Group (16.2%) - 2ο: Height (15.3%) - 3ο: Height2Group (7.0%)

Αλλά αν λάβουμε υπόψη την αποδοτικότητα (PRE σε σχέση με df): - Καλύτερο μοντέλο: Height (υψηλό PRE με χαμηλό κόστος)

Συγκρίνετε τους βαθμούς ελευθερίας (df) για αυτά τα μοντέλα. Ποιο μοντέλο χρησιμοποιεί τους περισσότερους df;

Το μοντέλο της Height2GroupΤο μοντέλο της Height10GroupΤο μοντέλο της Height

Επεξήγηση

Σωστή απάντηση: Β — Το μοντέλο της Height10Group

Σύγκριση των βαθμών ελευθερίας:

Μοντέλο	df (Model)	Αριθμός παραμέτρων	Κατάταξη
`Height2Group`	1	2 (1 σταθερός όρος + 1 κλίση/ψευδομεταβλητή)	3ο (λιγότερο)
`Height`	1	2 (1 σταθερός όρος + 1 κλίση)	3ο (λιγότερο)
`Height10Group`	9	10 (1 σταθερός όρος + 9 ψευδομεταβλητές)	1ο (περισσότερο)

Το μοντέλο της Height10Group χρησιμοποιεί 9 βαθμούς ελευθερίας.

Τι είναι οι βαθμοί ελευθερίας (df) του μοντέλου;

Οι βαθμοί ελευθερίας του μοντέλου είναι ο αριθμός των παραμέτρων που εκτιμώνται πέρα από τον σταθερό όρο (intercept).

\[\text{df (Model)} = \text{Αριθμός παραμέτρων} - 1\]

Ανάλυση κάθε μοντέλου

Μοντέλο της Height2Group (df = 1)

Εξίσωση: \[\text{Thumb}_i = b_0 + b_1 \times \text{Height2Group}_{\text{tall},i}\]

Παράμετροι: 1. $b_0$ = Μέσος όρος για την ομάδα short (intercept) 2. $b_1$ = Διαφορά μεταξύ tall και short

Συνολικές παράμετροι: 2

df (Model): $2 - 1 = 1$

Ερμηνεία: Χρειάζεται 1 βαθμό ελευθερίας για να περιγράψει τη διαφορά μεταξύ των 2 ομάδων.

Μοντέλο της Height (df = 1)

Εξίσωση: \[\text{Thumb}_i = b_0 + b_1 \times \text{Height}_i\]

Παράμετροι: 1. $b_0$ = Σταθερός όρος (intercept) 2. $b_1$ = Κλίση της ευθείας παλινδρόμησης

Συνολικές παράμετροι: 2

df (Model): $2 - 1 = 1$

Ερμηνεία: Χρειάζεται 1 βαθμό ελευθερίας για να ορίσει την κλίση της γραμμικής σχέσης.

Μοντέλο της Height10Group (df = 9)

Εξίσωση: \[\text{Thumb}_i = b_0 + b_1X_{2,i} + b_2X_{3,i} + ... + b_9X_{10,i}\]

όπου $X_{j,i}$ είναι ψευδομεταβλητές (dummy variables) για τις ομάδες 2-10.

Παράμετροι: 1. $b_0$ = Μέσος όρος για την ομάδα 1 (σταθερός όρος)

$b_1$ = Διαφορά ομάδας 2 από ομάδα 1
$b_2$ = Διαφορά ομάδας 3 από ομάδα 1

… 10. $b_9$ = Διαφορά ομάδας 10 από ομάδα 1

Συνολικές παράμετροι: 10

df (Model): $10 - 1 = 9$

Ερμηνεία: Χρειάζεται 9 βαθμούς ελευθερίας για να περιγράψει τις διαφορές μεταξύ των 10 ομάδων.

Γιατί χρειάζονται 9 df για 10 ομάδες;

Για k ομάδες, χρειάζονται k-1 βαθμοί ελευθερίας:

1η ομάδα: Ορίζεται από τον σταθερό όρο $b_0$
Υπόλοιπες k-1 ομάδες: Κάθε μία χρειάζεται 1 παράμετρο για να εκφράσει τη διαφορά της από την 1η

Παράδειγμα για 10 ομάδες:

Ομάδα	Μέσος όρος	Πώς εκφράζεται
1	$\mu_1$	$b_0$ (σταθερός όρος)
2	$\mu_2$	$b_0 + b_1$
3	$\mu_3$	$b_0 + b_2$
…	…	…
10	$\mu_{10}$	$b_0 + b_9$

Συνολικά: 1 (σταθερός όρος) + 9 (διαφορές) = 10 παράμετροι = 9 df

Παρατηρήστε επίσης το df για το σφάλμα:

Μοντέλο	df (Model)	df (Error)	df (Total)
`Height2Group`	1	155	156
`Height`	1	155	156
`Height10Group`	9	147	156

Η σχέση:

\[\text{df (Total)} = \text{df (Model)} + \text{df (Error)}\]

\[156 = 9 + 147\] ✓

Παρατήρηση: Το μοντέλο της Height10Group “ξοδεύει” 9 df, άρα:

Λιγότεροι df απομένουν για το σφάλμα (147 vs 155)
Μικρότερο MS Error γιατί: $\text{MS Error} = \frac{\text{SS Error}}{\text{df Error}}$

Γιατί έχουν σημασία οι βαθμοί ελευθερίας (df);

1. Κόστος πολυπλοκότητας

Περισσότεροι df σημαίνουν:

Πιο πολύπλοκο μοντέλο
Περισσότερες παράμετροι που εκτιμώνται
Μεγαλύτερος κίνδυνος υπερπροσαρμογής

2. Αποδοτικότητα

Θέλουμε μοντέλα που:

Εξηγούν πολύ (υψηλό PRE)
Χρησιμοποιούν λίγα df

Σύγκριση αποδοτικότητας:

Μοντέλο	PRE	df	PRE/df	Αποδοτικότητα
`Height2Group`	0.0699	1	0.0699	Μέτρια
`Height`	0.1529	1	0.1529	Καλύτερη!
`Height10Group`	0.1617	9	0.0180	Χειρότερη

Το μοντέλο της Height είναι το πιο αποδοτικό:

Υψηλό PRE (15.3%)
Χαμηλό κόστος (1 df)

3. Το πηλίκο F λαμβάνει υπόψη τους df

Το πηλίκο F είναι: \[F = \frac{\text{MS Model}}{\text{MS Error}} = \frac{\text{SS Model} / \text{df Model}}{\text{SS Error} / \text{df Error}}\]

Για το μοντέλο της Height: \[F = \frac{1816.862 / 1}{10063.349 / 155} = \frac{1816.862}{64.925} = 27.984\]

Για το μοντέλο της Height10Group: \[F = \frac{1920.474 / 9}{9959.737 / 147} = \frac{213.386}{67.753} = 3.149\]

Παρατήρηση: Αν και το Height10Group έχει μεγαλύτερο PRE, έχει πολύ μικρότερο F (3.149 vs 27.984) γιατί:

Το SS Model διαιρείται με 9 αντί για 1
Το MS Model είναι πολύ μικρότερο

Το πηλίκο F τιμωρεί τα μοντέλα που χρησιμοποιούν πολλούς df!

Συμπέρασμα

Το μοντέλο της Height10Group χρησιμοποιεί τους περισσότερους βαθμούς ελευθερίας (9 df) επειδή:

Έχει 10 ομάδες → Χρειάζεται 10 παραμέτρους
Κάθε επιπλέον ομάδα (πέρα από την πρώτη) κοστίζει 1 df
Συνολικά: 10 παράμετροι - 1 (intercept) = 9 df

Αντίθετα:

Το Height2Group έχει μόνο 2 ομάδες → 1 df
Το Height είναι απλή γραμμική παλινδρόμηση → 1 df

Αντιστάθμισμα:

Περισσότεροι df = Πιο πολύπλοκο μοντέλο = Καλύτερη προσαρμογή (υψηλότερο PRE)
Λιγότεροι df = Απλούστερο μοντέλο = Μεγαλύτερη αποδοτικότητα (υψηλότερο F)

Το ιδανικό μοντέλο ισορροπεί μεταξύ προσαρμογής και πολυπλοκότητας - και εδώ το μοντέλο της Height (1 df, υψηλό F) φαίνεται να είναι η καλύτερη επιλογή!

Για να δούμε πόσους βαθμούς ελευθερίας χρησιμοποιεί ένα μοντέλο, κοιτάζουμε τη στήλη df στη γραμμή “Model (error reduced)”. Παρατηρούμε ότι το μοντέλο της Height10Group χρειάζεται εννέα βαθμούς ελευθερίας — οκτώ παραπάνω από τα μοντέλα της Height2Group και της Height (που χρειάζονται από έναν μόνο).

Τι κερδίζουμε από αυτούς τους επιπλέον βαθμούς ελευθερίας; Όταν περνάμε από το μοντέλο της Height2Group στο μοντέλο της Height, το PRE ανεβαίνει από 0.07 σε 0.15 χωρίς να χρειαστεί κανένας επιπλέον βαθμός ελευθερίας. Η επιλογή είναι προφανής!

Το μοντέλο της Height10Group δίνει το υψηλότερο PRE (0.16), αλλά χρειάζεται οκτώ επιπλέον βαθμούς ελευθερίας. Ένα μοντέλο με 10 διαφορετικούς μέσους όρους δεν είναι τόσο απλό όσο ένα με έναν σταθερό όρο και μια παράμετρο κλίσης. Το μοντέλο της Height10Group στη σημειογραφία του GLM φαίνεται ως εξής:

\[Y_i = b_0 + b_1X_{1i} + b_2X_{2i} + b_3X_{3i} + b_4X_{4i} + b_5X_{5i} + b_6X_{6i} + b_7X_{7i} + b_8X_{8i} + b_9X_{9i} + e_i\]

Ποιο μέρος της παραπάνω εξίσωσης είναι το μοντέλο;

$Y_i = b_0 + b_1X_{1i}$$b_0 + b_1X_{1i}$$b_0 + b_1X_{1i} + b_2X_{2i} + b_3X_{3i} + b_4X_{4i} + b_5X_{5i} + b_6X_{6i} + b_7X_{7i} + b_8X_{8i} + b_9X_{9i}$

Επεξήγηση

Σωστή απάντηση: Γ — $b_0 + b_1X_{1i} + b_2X_{2i} + b_3X_{3i} + b_4X_{4i} + b_5X_{5i} + b_6X_{6i} + b_7X_{7i} + b_8X_{8i} + b_9X_{9i}$

Κατανόηση της δομής της εξίσωσης GLM

Η πλήρης εξίσωση του GLM για το μοντέλο της Height10Group είναι:

\[Y_i = \underbrace{b_0 + b_1X_{1i} + b_2X_{2i} + ... + b_9X_{9i}}_{\text{ΜΟΝΤΕΛΟ}} + \underbrace{e_i}_{\text{ΣΦΑΛΜΑ}}\]

Η βασική δομή:

\[\text{ΔΕΔΟΜΕΝΑ} = \text{ΜΟΝΤΕΛΟ} + \text{ΣΦΑΛΜΑ}\]

Ανάλυση κάθε επιλογής

Α. «$Y_i = b_0 + b_1X_{1i}$» — ΛΑΘΟΣ

Αυτή είναι μέρος της πλήρους εξίσωσης, όχι το μοντέλο.

Προβλήματα με αυτή την επιλογή:

Περιλαμβάνει την εξαρτημένη μεταβλητή $Y_i$ (τα παρατηρούμενα δεδομένα)
Δείχνει μόνο τους πρώτους δύο όρους αντί για ολόκληρο το μοντέλο με τις 10 παραμέτρους

Γιατί είναι λάθος;

Το μοντέλο είναι το μέρος που κάνει την πρόβλεψη ($\hat{Y}_i$), όχι η σχέση μεταξύ των παρατηρούμενων δεδομένων ($Y_i$) και της πρόβλεψης.

Αναλογία: Αν πούμε “το πραγματικό ύψος = η πρόβλεψη”, το μοντέλο είναι μόνο “η πρόβλεψη”, όχι η ολόκληρη ισότητα.

Β. «$b_0 + b_1X_{1i}$» — ΛΑΘΟΣ (αλλά κοντά!)

Αυτό δείχνει τη δομή του μοντέλου, αλλά είναι ελλιπές.

Γιατί είναι λάθος;

Για το μοντέλο της Height10Group, το πλήρες μοντέλο έχει 10 παραμέτρους, όχι μόνο 2:

$b_0$ = σταθερός όρος (intercept)
$b_1, b_2, ..., b_9$ = συντελεστές για τις 9 ψευδομεταβλητές

Το $b_0 + b_1X_{1i}$ δείχνει μόνο:

Τον σταθερό όρο
Την πρώτη ψευδομεταβλητή

Λείπουν οι άλλοι 8 όροι: $b_2X_{2i}, b_3X_{3i}, ..., b_9X_{9i}$

Γ. «$b_0 + b_1X_{1i} + b_2X_{2i} + ... + b_9X_{9i}$» — ΣΩΣΤΟ ✓

Αυτό είναι το πλήρες μοντέλο της Height10Group!

Τι αντιπροσωπεύει:

Το μοντέλο είναι το ντετερμινιστικό μέρος της εξίσωσης — το μέρος που υπολογίζει την τιμή πρόβλεψης:

\[\text{Μοντέλο} = b_0 + b_1X_{1i} + b_2X_{2i} + b_3X_{3i} + b_4X_{4i} + b_5X_{5i} + b_6X_{6i} + b_7X_{7i} + b_8X_{8i} + b_9X_{9i}\]

Ή γενικότερα: \[\text{Μοντέλο} = \hat{Y}_i\]

Χαρακτηριστικά του πλήρους μοντέλου:

Περιλαμβάνει όλες τις παραμέτρους:
- $b_0$ = Μέσος όρος της ομάδας αναφοράς (ομάδα 1)
- $b_1, b_2, ..., b_9$ = Διαφορές των ομάδων 2-10 από την ομάδα 1
Περιλαμβάνει όλες τις ανεξάρτητες μεταβλητές:
- $X_{1i}, X_{2i}, ..., X_{9i}$ = Ψευδομεταβλητές για τις ομάδες 2-10
ΔΕΝ περιλαμβάνει:
- Την εξαρτημένη μεταβλητή $Y_i$ (τα παρατηρούμενα δεδομένα)
- Το σφάλμα $e_i$ (την απόκλιση από την πρόβλεψη)
Παράγει την τιμή πρόβλεψης:

\[\hat{Y}_i = b_0 + b_1X_{1i} + b_2X_{2i} + ... + b_9X_{9i}\]

Γενική αρχή: Τι είναι το “μοντέλο” στο GLM;

Στο Γενικό Γραμμικό Μοντέλο (GLM), η εξίσωση έχει τη μορφή:

\[Y_i = \underbrace{b_0 + b_1X_{1i} + b_2X_{2i} + ... + b_kX_{ki}}_{\text{ΜΟΝΤΕΛΟ}} + \underbrace{e_i}_{\text{ΣΦΑΛΜΑ}}\]

Το μοντέλο είναι:

\[\text{Μοντέλο} = b_0 + \sum_{j=1}^{k} b_jX_{ji}\]

Αυτό που ΚΑΝΕΙ το μοντέλο:

Παίρνει τις τιμές των ανεξάρτητων μεταβλητών ($X_{ji}$)
Τις πολλαπλασιάζει με τους συντελεστές ($b_j$)
Προσθέτει τον σταθερό όρο ($b_0$)
Παράγει την τιμή πρόβλεψης ($\hat{Y}_i$)

Αυτό που ΔΕΝ περιλαμβάνει το μοντέλο:

✗ Την εξαρτημένη μεταβλητή $Y_i$ (τα παρατηρούμενα δεδομένα)
✗ Το σφάλμα $e_i$ (την απόκλιση από την πρόβλεψη)

Σύγκριση με άλλα στοιχεία της εξίσωσης

Στοιχείο	Σύμβολο	Τι είναι
Δεδομένα	$Y_i$	Η παρατηρούμενη τιμή (π.χ., μήκος αντίχειρα)
Μοντέλο	$b_0 + b_1X_{1i} + ... + b_9X_{9i}$	Η πρόβλεψη βάσει του μοντέλου
Πρόβλεψη	$\hat{Y}_i$	Το αποτέλεσμα του μοντέλου (ίδιο με το μοντέλο)
Σφάλμα	$e_i$	Η διαφορά: $Y_i - \hat{Y}_i$
Πλήρης εξίσωση	$Y_i = \text{Μοντέλο} + e_i$	Σχέση δεδομένων, πρόβλεψης και σφάλματος

Συμπέρασμα

Το πλήρες μοντέλο είναι:

\[b_0 + b_1X_{1i} + b_2X_{2i} + b_3X_{3i} + b_4X_{4i} + b_5X_{5i} + b_6X_{6i} + b_7X_{7i} + b_8X_{8i} + b_9X_{9i}\]

Όχι:

✗ $Y_i = b_0 + b_1X_{1i} + ...$ (αυτή είναι η πλήρης εξίσωση, όχι μόνο το μοντέλο)
✗ $b_0 + b_1X_{1i}$ (αυτό είναι μόνο μέρος του μοντέλου)
✗ $Y_i$ (αυτά είναι τα δεδομένα)
✗ $e_i$ (αυτό είναι το σφάλμα)

Βασική ιδέα: > Το μοντέλο είναι το πλήρες μέρος της εξίσωσης που υπολογίζει την τιμή πρόβλεψης, χωρίς να περιλαμβάνει τα παρατηρούμενα δεδομένα ή το σφάλμα. Για το μοντέλο της Height10Group, αυτό σημαίνει όλους τους 10 όρους!

Συγκρίνετε αυτή τη μεγάλη ακολουθία συμβόλων με το μοντέλο της Height:

\[b_0 + b_1X_i\]

Αυτό είναι ένα πραγματικά κομψό μοντέλο! Είναι αλήθεια ότι δεν μειώνει το σφάλμα τόσο πολύ όσο το μοντέλο της Height10Group. Αλλά το μοντέλο παλινδρόμησης έχει PRE 0.15 με μόλις δύο παραμέτρους ($b_0$ και $b_1$), ενώ το μοντέλο των 10 ομάδων εκτιμά 8 επιπλέον παραμέτρους ($b_2$ έως $b_9$) για να φτάσει σε PRE μόλις 0.16. Τα κομψά μοντέλα προσθέτουν πολλή εξηγηματική ισχύ χωρίς να εκτιμούν περιττά πολλές παραμέτρους.

Σύγκριση των Πηλίκων `F` για τα Τρία Μοντέλα

Η συνάρτηση supernova() υπολόγισε επίσης το πηλίκο F για καθένα από τα τρία μοντέλα. Όπως βλέπουμε στον παρακάτω πίνακα, το πηλίκο F δίνει μια διαφορετική εικόνα για τα τρία μοντέλα από αυτήν που παίρνουμε κοιτάζοντας μόνο το PRE.

Μοντέλο (Ομάδα)	PRE	Πηλίκο `F`
Μοντέλο `Height2Group`	0.0699	11.656
Μοντέλο `Height10Group`	0.1617	3.149
Μοντέλο `Height`	0.1529	27.984

Αν βασιζόμασταν μόνο στο PRE, το μοντέλο της Height10Group θα φαινόταν να είναι το καλύτερο. Αλλά όταν χρησιμοποιούμε το πηλίκο F, το οποίο ενσωματώνει τους βαθμούς ελευθερίας στη σύγκριση των μοντέλων, το μοντέλο της Height είναι ο σαφής νικητής, με πηλίκο F ίσο με 27.984. Το μοντέλο της Height10Group είναι μακράν το χειρότερο, με πηλίκο F μόλις 3.149.

Ας ξαναδούμε τους υπολογισμούς που εμπεριέχονται στο πηλίκο F. Όπως συζητήθηκε σε προηγούμενο κεφάλαιο, το πηλίκο F βασίζεται σε μέσα αθροίσματα τετραγώνων (ή MS), τα οποία είναι, ουσιαστικά, κάποιο είδος διακύμανσης (ένα SS διαιρεμένο με τους βαθμούς ελευθερίας). Ακριβώς όπως τα SS, υπάρχουν τρία διαφορετικά μέσα αθροίσματα τετραγώνων. Αντιστοιχίστε τα κατάλληλα MS με τους τύπους τους που βασίζονται στα SS και στους df.

MS Model

SS Model / df ModelSS Total / df TotalSS Error / df Error

MS Error

SS Model / df ModelSS Total / df TotalSS Error / df Error

MS Total

SS Model / df ModelSS Total / df TotalSS Error / df Error

Επεξήγηση

Σωστές απαντήσεις:

MS Model = SS Model / df Model
MS Error = SS Error / df Error
MS Total = SS Total / df Total

Τι είναι τα Μέσα Αθροίσματα Τετραγώνων (Mean Squares - MS);

Τα μέσα αθροίσματα τετραγώνων (MS) είναι κανονικοποιημένες εκδοχές των αθροισμάτων τετραγώνων (SS).

Γενικός τύπος: \[\text{MS} = \frac{\text{SS}}{\text{df}}\]

Τα MS μετρούν την μέση μεταβλητότητα ανά βαθμό ελευθερίας.

Γιατί χρειαζόμαστε τα MS;

Πρόβλημα με τα SS:

Τα SS δεν είναι άμεσα συγκρίσιμα όταν τα μοντέλα χρησιμοποιούν διαφορετικούς βαθμούς ελευθερίας:

Ένα μοντέλο με περισσότερους df μπορεί να έχει μεγαλύτερο SS Model απλά επειδή “ξοδεύει” περισσότερους πόρους
Χρειαζόμαστε τρόπο να κανονικοποιήσουμε για το κόστος των df

Λύση: Τα MS

Διαιρώντας με τους df, τα MS μετρούν: > Πόση μεταβλητότητα εξηγείται (ή παραμένει) ανά βαθμό ελευθερίας που χρησιμοποιείται

Αυτό κάνει τις συγκρίσεις δίκαιες και ουσιαστικές.

Ανάλυση κάθε MS

MS Model (Μέσο Άθροισμα Τετραγώνων του Μοντέλου)

Τύπος:

\[\text{MS Model} = \frac{\text{SS Model}}{\text{df Model}}\]

Τι μετρά:

Τη μέση εξηγούμενη μεταβλητότητα ανά βαθμό ελευθερίας που χρησιμοποιεί το μοντέλο.

Ερμηνεία:

Μεγάλο MS Model → Το μοντέλο είναι αποδοτικό (εξηγεί πολλά με λίγους df)
Μικρό MS Model → Το μοντέλο είναι αναποτελεσματικό (εξηγεί λίγα παρά τους df που χρησιμοποιεί)

Παράδειγμα με το μοντέλο της Height:

\[\text{MS Model} = \frac{1816.862}{1} = 1816.862\]

Το μοντέλο εξηγεί 1816.862 μονάδες μεταβλητότητας ανά βαθμό ελευθερίας
Χρησιμοποιεί μόνο 1 df, οπότε αυτή η τιμή είναι πολύ υψηλή!

Παράδειγμα με το μοντέλο της Height10Group:

\[\text{MS Model} = \frac{1920.474}{9} = 213.386\]

Το μοντέλο εξηγεί 213.386 μονάδες μεταβλητότητας ανά βαθμό ελευθερίας
Χρησιμοποιεί 9 df, οπότε η αποδοτικότητα είναι πολύ χαμηλότερη!

Σύγκριση:

\[\frac{1816.862}{213.386} = 8.52\]

Το μοντέλο της Height είναι 8.5 φορές πιο αποδοτικό από το μοντέλο της Height10Group!

MS Error (Μέσο Άθροισμα Τετραγώνων Σφάλματος)

Τύπος: \[\text{MS Error} = \frac{\text{SS Error}}{\text{df Error}}\]

Τι μετρά:

Την μέση ανεξήγητη μεταβλητότητα ανά βαθμό ελευθερίας που απομένει.

Ερμηνεία:

Το MS Error είναι μια εκτίμηση της διακύμανσης σφάλματος ($\sigma^2$)
Μικρό MS Error → Οι προβλέψεις του μοντέλου είναι ακριβείς
Μεγάλο MS Error → Οι προβλέψεις του μοντέλου έχουν μεγάλη απόκλιση

Παράδειγμα με το μοντέλο της Height:

\[\text{MS Error} = \frac{10063.349}{155} = 64.925\]

Η μέση τετραγωνική απόκλιση από την πρόβλεψη είναι 64.925
Η τυπική απόκλιση σφάλματος: $\sqrt{64.925} = 8.06$ mm

Παράδειγμα με το μοντέλο της Height10Group:

\[\text{MS Error} = \frac{9959.737}{147} = 67.753\]

Η μέση τετραγωνική απόκλιση είναι 67.753
Ελαφρώς μεγαλύτερη από το μοντέλο της Height (αν και το SS Error ήταν μικρότερο!)

Γιατί το MS Error της Height10Group είναι μεγαλύτερο;

Επειδή διαιρούμε με λιγότερους df (147 vs 155): \[\frac{9959.737}{147} > \frac{10063.349}{155}\]

Παρότι το απόλυτο σφάλμα (SS Error) είναι μικρότερο, το κόστος σε df κάνει το MS Error μεγαλύτερο.

MS Total (Συνολικό Μέσο Άθροισμα Τετραγώνων)

Τύπος: \[\text{MS Total} = \frac{\text{SS Total}}{\text{df Total}}\]

Τι μετρά:

Την μέση συνολική μεταβλητότητα στα δεδομένα.

Ερμηνεία:

Το MS Total είναι η διακύμανση της εξαρτημένης μεταβλητής
Αντιπροσωπεύει τη συνολική μεταβλητότητα πριν την εφαρμογή οποιουδήποτε μοντέλου

Για όλα τα μοντέλα:

\[\text{MS Total} = \frac{11880.211}{156} = 76.155\]

Αυτή είναι η διακύμανση της Thumb (μήκος αντίχειρα)
Ίδιο για όλα τα μοντέλα επειδή χρησιμοποιούν τα ίδια δεδομένα

Σημείωση:

Το MS Total δεν χρησιμοποιείται στον υπολογισμό του πηλίκου F, αλλά είναι χρήσιμο για: - Κατανόηση της συνολικής μεταβλητότητας - Υπολογισμό της διακύμανσης της εξαρτημένης μεταβλητής

Η σχέση μεταξύ των MS

ΠΡΟΣΟΧΗ: Σε αντίθεση με τα SS, τα MS ΔΕΝ αθροίζονται:

\[\text{MS Model} + \text{MS Error} \neq \text{MS Total}\]

Γιατί;

Επειδή διαιρούμε με διαφορετικούς df:

\[\frac{\text{SS Model}}{\text{df Model}} + \frac{\text{SS Error}}{\text{df Error}} \neq \frac{\text{SS Total}}{\text{df Total}}\]

Επαλήθευση με το μοντέλο της Height:

\[\text{MS Model} + \text{MS Error} = 1816.862 + 64.925 = 1881.787\]

\[\text{MS Total} = 76.155\]

\[1881.787 \neq 76.155\] ✗

Τα MS δεν αθροίζονται επειδή έχουν διαφορετικούς παρονομαστές!

Το πηλίκο F: Χρησιμοποιώντας τα MS

Το πηλίκο F υπολογίζεται ως:

\[F = \frac{\text{MS Model}}{\text{MS Error}}\]

Γιατί χρησιμοποιούμε MS αντί για SS;

Κανονικοποίηση για df:
- Το MS Model μετρά πόση μεταβλητότητα εξηγείται ανά df που ξοδεύεται
- Το MS Error μετρά πόση μεταβλητότητα παραμένει ανά df που απομένει
Δίκαιη σύγκριση:
- Μοντέλα με περισσότερους df δεν ευνοούνται αυτόματα
- Η αποδοτικότητα (εξήγηση ανά df) είναι αυτό που μετράει
Στατιστική κατανομή:
- Το πηλίκο των MS ακολουθεί την κατανομή F
- Μπορούμε να υπολογίσουμε τιμές p

Υπολογισμός για το μοντέλο της Height:

\[F = \frac{1816.862}{64.925} = 27.984\]

Ερμηνεία: Το μοντέλο εξηγεί μεταβλητότητα που είναι 27.98 φορές μεγαλύτερη (ανά df) από τη μεταβλητότητα που παραμένει ανεξήγητη.

Υπολογισμός για το μοντέλο της Height10Group:

\[F = \frac{213.386}{67.753} = 3.149\]

Ερμηνεία: Το μοντέλο εξηγεί μεταβλητότητα που είναι μόνο 3.15 φορές μεγαλύτερη από την ανεξήγητη — πολύ λιγότερο αποδοτικό!

Σύγκριση των τριών μοντέλων

Μοντέλο	`SS Model`	`df Model`	`MS Model`	`SS Error`	`df Error`	`MS Error`	`F`
`Height2Group`	830.880	1	830.880	11049.331	155	71.286	11.656
`Height`	1816.862	1	1816.862	10063.349	155	64.925	27.984
`Height10Group`	1920.474	9	213.386	9959.737	147	67.753	3.149

Παρατηρήσεις:

Το μοντέλο της Height έχει το υψηλότερο MS Model (1816.862)
- Εξηγεί την περισσότερη μεταβλητότητα ανά df
Το μοντέλο της Height έχει το χαμηλότερο MS Error (64.925)
- Οι προβλέψεις του είναι οι πιο ακριβείς
Το μοντέλο της Height έχει το υψηλότερο F (27.984)
- Είναι το πιο αποδοτικό μοντέλο
Το μοντέλο της Height10Group έχει χαμηλό MS Model (213.386)
- Παρότι εξηγεί περισσότερη μεταβλητότητα συνολικά (SS Model = 1920.474), το κόστος σε df (9) μειώνει την αποδοτικότητα
Το μοντέλο της Height10Group έχει το χαμηλότερο F (3.149)
- Είναι το λιγότερο αποδοτικό, παρότι έχει το υψηλότερο PRE!

Συμπέρασμα

Τα Μέσα Αθροίσματα Τετραγώνων (MS) είναι σημαντικά για τη σύγκριση μοντέλων:

MS Model = $\frac{\text{SS Model}}{\text{df Model}}$ → Αποδοτικότητα εξήγησης μεταβλητότητας
MS Error = $\frac{\text{SS Error}}{\text{df Error}}$ → Ακρίβεια προβλέψεων
MS Total = $\frac{\text{SS Total}}{\text{df Total}}$ → Συνολική μεταβλητότητα (διακύμανση)

Το πηλίκο F = $\frac{\text{MS Model}}{\text{MS Error}}$ λαμβάνει υπόψη:

Πόση μεταβλητότητα εξηγείται (MS Model)
Πόση μεταβλητότητα υπολείπεται (MS Error)
Το κόστος σε βαθμούς ελευθερίας

Έτσι, το F τιμωρεί τα πολύπλοκα μοντέλα που χρησιμοποιούν πολλούς df χωρίς αντίστοιχο όφελος, και ανταμείβει τα απλά, αποδοτικά μοντέλα όπως το μοντέλο της Height!

Ποια αναλογία είναι το πηλίκο F;

MS Model / MS ErrorMS Model / MS TotalMS Error / MS Total

Επεξήγηση

Σωστή απάντηση: Α — MS Model / MS Error

Ο τύπος του πηλίκου F:

\[F = \frac{\text{MS Model}}{\text{MS Error}}\]

Τι αντιπροσωπεύει:

Αριθμητής (MS Model): Η μέση εξηγούμενη μεταβλητότητα ανά βαθμό ελευθερίας που χρησιμοποιεί το μοντέλο
Παρονομαστής (MS Error): Η μέση ανεξήγητη μεταβλητότητα ανά βαθμό ελευθερίας που απομένει

Ερμηνεία:

Το πηλίκο F μετρά πόσες φορές μεγαλύτερη είναι η μεταβλητότητα που εξηγείται από το μοντέλο (ανά df) σε σχέση με τη μεταβλητότητα που παραμένει ανεξήγητη (ανά df).

Γιατί οι άλλες επιλογές είναι λάθος

Β. «MS Model / MS Total» — ΛΑΘΟΣ

Αυτή η αναλογία δεν χρησιμοποιείται στη στατιστική ανάλυση.

Προβλήματα:

Το MS Total δεν είναι κατάλληλη βάση σύγκρισης
Δεν λαμβάνει υπόψη το σφάλμα του μοντέλου

Γ. «MS Error / MS Total» — ΛΑΘΟΣ

Αυτή η αναλογία επίσης δεν χρησιμοποιείται.

Το σωστό: Πάντα συγκρίνουμε το MS Model με το MS Error!

Γιατί το πηλίκο F για το μοντέλο της Height είναι περίπου 28; (Υπάρχουν περισσότερες από μία σωστές απαντήσεις.)

Το SS που εξηγείται από το μοντέλο ανά df είναι 28 φορές μεγαλύτερο σε σύγκριση με το SS που παραμένει ανεξήγητο ανά df.Η διακύμανση που εξηγείται από το μοντέλο είναι 28 φορές μεγαλύτερη σε σύγκριση με τη διακύμανση που παραμένει ανεξήγητη.Το SS που εξηγείται από το μοντέλο είναι 28 φορές μεγαλύτερο σε σύγκριση με το SS που παραμένει ανεξήγητο.Υπάρχουν 28 περισσότερες παρατηρήσεις που προβλέπονται από το σύνθετο μοντέλο σε σύγκριση με το κενό μοντέλο.

Επεξήγηση

Σωστές απαντήσεις: Α και Β

Υπολογισμός του πηλίκου F για το μοντέλο της Height:

\[F = \frac{\text{MS Model}}{\text{MS Error}} = \frac{1816.862}{64.925} = 27.984 \approx 28\]

Α. «Το SS που εξηγείται από το μοντέλο ανά df είναι 28 φορές μεγαλύτερο σε σύγκριση με το SS που παραμένει ανεξήγητο ανά df» — ΣΩΣΤΟ ✓

Αυτή είναι η ακριβής ερμηνεία του πηλίκου F.

Ανάλυση:

SS Model ανά df: $\frac{1816.862}{1} = 1816.862$
SS Error ανά df: $\frac{10063.349}{155} = 64.925$
Αναλογία: $\frac{1816.862}{64.925} = 27.984 \approx 28$

Ερμηνεία:

Το μοντέλο εξηγεί 1816.862 μονάδες μεταβλητότητας με 1 βαθμό ελευθερίας, ενώ απομένουν 64.925 μονάδες ανεξήγητης μεταβλητότητας ανά βαθμό ελευθερίας. Η πρώτη ποσότητα είναι 28 φορές μεγαλύτερη από τη δεύτερη.

Β. «Η διακύμανση που εξηγείται από το μοντέλο είναι 28 φορές μεγαλύτερη σε σύγκριση με τη διακύμανση που παραμένει ανεξήγητη» — ΣΩΣΤΟ ✓

Αυτή είναι μια εναλλακτική (και ισοδύναμη) ερμηνεία.

Τι είναι διακύμανση;

Η διακύμανση είναι το Μέσο Άθροισμα Τετραγώνων (MS), δηλαδή το SS διαιρεμένο με τους df: \[\text{Διακύμανση} = \frac{\text{SS}}{\text{df}} = \text{MS}\]

Άρα:

Διακύμανση που εξηγείται: MS Model = 1816.862
Διακύμανση που παραμένει ανεξήγητη: MS Error = 64.925
Αναλογία: $\frac{1816.862}{64.925} = 27.984 \approx 28$

Γιατί οι Α και Β είναι ισοδύναμες;

Και οι δύο περιγράφουν την ίδια ποσότητα με διαφορετικούς όρους:

Α: Χρησιμοποιεί τον όρο “SS ανά df”
Β: Χρησιμοποιεί τον όρο “διακύμανση” (που είναι SS/df)

Και οι δύο είναι σωστές!

Γιατί οι άλλες επιλογές είναι λάθος

Γ. «Το SS που εξηγείται από το μοντέλο είναι 28 φορές μεγαλύτερο σε σύγκριση με το SS που παραμένει ανεξήγητο» — ΛΑΘΟΣ

Αυτό είναι λάθος επειδή παραλείπει το “ανά df”.

Στην πραγματικότητα, το SS Model είναι μικρότερο από το SS Error (0.18 φορές, όχι 28 φορές μεγαλύτερο).

Γιατί είναι διαφορετικό;

Το πηλίκο F δεν είναι η αναλογία των SS, αλλά η αναλογία των MS (SS διαιρεμένα με τους αντίστοιχους df):

\[F = \frac{\text{SS Model} / \text{df Model}}{\text{SS Error} / \text{df Error}} = \frac{1816.862 / 1}{10063.349 / 155} = 27.984\]

Η διαίρεση με τους df είναι κρίσιμη — χωρίς αυτήν, η σύγκριση δεν έχει νόημα!

Δ. «Υπάρχουν 28 περισσότερες παρατηρήσεις που προβλέπονται από το σύνθετο μοντέλο σε σύγκριση με το κενό μοντέλο» — ΛΑΘΟΣ

Αυτό είναι εντελώς λάθος και δεν έχει καμία σχέση με το πηλίκο F.

Αυτή η επιλογή είναι μια παρανόηση του τι μετρά το F.

Συμπέρασμα

Το πηλίκο F = 28 σημαίνει:

✓ Α: Το SS ανά df που εξηγείται είναι 28 φορές μεγαλύτερο από το SS ανά df που παραμένει ανεξήγητο

✓ Β: Η διακύμανση που εξηγείται είναι 28 φορές μεγαλύτερη από τη διακύμανση που παραμένει ανεξήγητη

✗ Γ: ΟΧΙ για τα ίδια τα SS (χωρίς διαίρεση με df)

✗ Δ: ΟΧΙ για τον αριθμό παρατηρήσεων

Και οι δύο σωστές ερμηνείες (Α και Β) είναι ισοδύναμες και περιγράφουν την ίδια ποσότητα!

Γιατί το πηλίκο F για το μοντέλο της Height είναι μεγαλύτερο από το μοντέλο της Height10Group;

Επειδή τα δεδομένα που χρησιμοποιήθηκαν για το μοντέλο της Height ήταν πιο εύκολο να εξηγηθούν από τα δεδομένα που χρησιμοποιήθηκαν από το μοντέλο της Height10Group.Επειδή το μοντέλο της Height εξηγεί περισσότερη μεταβλητότητα ανά df που χρησιμοποιείται από ό,τι το μοντέλο της Height10Group.Επειδή το μοντέλο της Height κάνει περισσότερες προβλέψεις από το μοντέλο της Height10Group.Επειδή το μοντέλο της Height προβλέπει ακριβώς 28 περισσότερα μήκη αντίχειρα από το μοντέλο της Height10Group.

Επεξήγηση

Σωστή απάντηση: Β — Επειδή το μοντέλο της Height εξηγεί περισσότερη μεταβλητότητα ανά df που χρησιμοποιείται από ό,τι το μοντέλο της Height10Group.

Σύγκριση των δύο μοντέλων:

Μοντέλο	`SS Model`	`df Model`	`MS Model`	`SS Error`	`df Error`	`MS Error`	`F`
`Height`	1816.862	1	1816.862	10063.349	155	64.925	27.984
`Height10Group`	1920.474	9	213.386	9959.737	147	67.753	3.149

Το πηλίκο F:

Height: $F = \frac{1816.862}{64.925} = 27.984$
Height10Group: $F = \frac{213.386}{67.753} = 3.149$

Διαφορά: $27.984 - 3.149 = 24.835$

Το μοντέλο της Height έχει F που είναι σχεδόν 9 φορές μεγαλύτερο!

Β. «Επειδή το μοντέλο της Height εξηγεί περισσότερη μεταβλητότητα ανά df» — ΣΩΣΤΟ ✓

Αυτή είναι η σωστή εξήγηση.

Ανάλυση αποδοτικότητας:

Μοντέλο της Height:

Εξηγεί 1816.862 μονάδες μεταβλητότητας
Χρησιμοποιεί 1 df
Αποδοτικότητα: $\frac{1816.862}{1} = 1816.862$ μονάδες ανά df

Μοντέλο της Height10Group:

Εξηγεί 1920.474 μονάδες μεταβλητότητας (περισσότερο!)
Χρησιμοποιεί 9 df (πολύ περισσότερο!)
Αποδοτικότητα: $\frac{1920.474}{9} = 213.386$ μονάδες ανά df

Σύγκριση αποδοτικότητας: \[\frac{1816.862}{213.386} = 8.52\]

Το μοντέλο της Height είναι 8.5 φορές πιο αποδοτικό — εξηγεί σχεδόν την ίδια μεταβλητότητα με μόλις 1/9 του κόστους σε df!

Γιατί αυτό οδηγεί σε μεγαλύτερο F;

Επειδή το F μετρά ακριβώς αυτή την αποδοτικότητα:

\[F = \frac{\text{MS Model}}{\text{MS Error}} = \frac{\text{Αποδοτικότητα εξήγησης}}{\text{Μέση ανεξήγητη διακύμανση}}\]

Το μοντέλο της Height έχει: - Πολύ υψηλότερο MS Model (1816.862 vs 213.386)

Ελαφρώς χαμηλότερο MS Error (64.925 vs 67.753)

Αποτέλεσμα: Πολύ μεγαλύτερο πηλίκο F (27.984 vs 3.149)!

Γιατί οι άλλες επιλογές είναι λάθος

Α. «Επειδή τα δεδομένα που χρησιμοποιήθηκαν για το μοντέλο της Height ήταν πιο εύκολο να εξηγηθούν» — ΛΑΘΟΣ

Αυτό είναι εντελώς λάθος.

Γιατί;

Και τα δύο μοντέλα χρησιμοποιούν τα ΙΔΙΑ δεδομένα:
- Το ίδιο σύνολο δεδομένων Fingers (157 παρατηρήσεις)
- Την ίδια εξαρτημένη μεταβλητή (Thumb)
- Την ίδια συνολική μεταβλητότητα (SS Total = 11880.211)
Η “ευκολία εξήγησης” είναι η ίδια:
- Και τα δύο μοντέλα προσπαθούν να εξηγήσουν την ίδια μεταβλητότητα
- Η διαφορά είναι στην αποδοτικότητα της εξήγησης, όχι στη δυσκολία
Αυτό που διαφέρει είναι η προσέγγιση:
- Height: Χρησιμοποιεί συνεχή μεταβλητή (απλό, αποδοτικό)
- Height10Group: Χρησιμοποιεί ποιοτική με 10 κατηγορίες (πολύπλοκο, αναποτελεσματικό)

Συμπέρασμα: Τα δεδομένα είναι τα ίδια, η διαφορά είναι στο μοντέλο, όχι στα δεδομένα!

Γ. «Επειδή το μοντέλο της Height κάνει περισσότερες προβλέψεις» — ΛΑΘΟΣ

Αυτό είναι λάθος.

Γιατί;

Και τα δύο μοντέλα κάνουν τον ίδιο αριθμό προβλέψεων:
- Height: Κάνει 157 προβλέψεις (μία για κάθε παρατήρηση)
- Height10Group: Κάνει 157 προβλέψεις (μία για κάθε παρατήρηση)
Διαφορά: 0!
Ο αριθμός προβλέψεων δεν επηρεάζει το F:
- Το F μετρά την ποιότητα των προβλέψεων (αποδοτικότητα)
- ΟΧΙ την ποσότητα των προβλέψεων

Συμπέρασμα: Ο αριθμός προβλέψεων είναι ίδιος και άσχετος με το F!

Δ. «Επειδή το μοντέλο της Height προβλέπει ακριβώς 28 περισσότερα μήκη αντίχειρα» — ΛΑΘΟΣ

Αυτό είναι εντελώς λάθος και παρανόηση.

Γιατί;

Και τα δύο μοντέλα προβλέπουν τον ίδιο αριθμό:
- Και τα δύο: 157 προβλέψεις
- Διαφορά: 0, όχι 28
Το 28 δεν αναφέρεται σε αριθμό παρατηρήσεων:
- Το F = 28 σημαίνει ότι η διακύμανση που εξηγείται είναι 28 φορές μεγαλύτερη από τη διακύμανση που παραμένει
- ΔΕΝ έχει σχέση με τον αριθμό προβλέψεων
Παρανόηση του πηλίκου F:

\[F = 28 = \frac{\text{MS Model}}{\text{MS Error}}\]

Αυτό είναι αναλογία διακυμάνσεων, όχι διαφορά αριθμού παρατηρήσεων!

Συμπέρασμα: Αυτή η επιλογή παρερμηνεύει εντελώς το νόημα του F!

Συνολική σύγκριση

Γιατί το F της Height (27.984) > F της Height10Group (3.149);

Βασική αιτία: Αποδοτικότητα ανά βαθμό ελευθερίας

Πτυχή	`Height`	`Height10Group`	Ποιο είναι καλύτερο;
`SS Model`	1816.862	1920.474	`Height10Group` (εξηγεί λίγο περισσότερο)
`df Model`	1	9	`Height` (κοστίζει πολύ λιγότερο)
`MS Model`	1816.862	213.386	`Height` (8.5× πιο αποδοτικό!)
`MS Error`	64.925	67.753	`Height` (λίγο καλύτερο)
`F`	27.984	3.149	`Height` (9× μεγαλύτερο!)

Η βασική διαφορά:

Το μοντέλο της Height10Group εξηγεί ελαφρώς περισσότερο συνολικά (SS Model: 1920 vs 1817)
Αλλά το κόστος είναι τεράστιο: 9 df αντί για 1
Όταν κανονικοποιούμε για το κόστος (MS = SS/df), το μοντέλο της Height είναι πολύ πιο αποδοτικό
Το F αντικατοπτρίζει αυτή την αποδοτικότητα: 28 vs 3

Μάθημα: Το F τιμωρεί την αναποτελεσματικότητα — δεν αρκεί να εξηγείς πολλά, πρέπει να το κάνεις οικονομικά (με λίγους df)!

10.8 Συσχέτιση

Ίσως να έχετε ακούσει για το r του Pearson, που συχνά αναφέρεται ως «συντελεστής συσχέτισης» (correlation coefficient). Η συσχέτιση είναι απλώς μια ειδική περίπτωση της παλινδρόμησης στην οποία και η εξαρτημένη και η ανεξάρτητη μεταβλητή μετατρέπονται σε τιμές z (τυποποιημένες τιμές) πριν από την ανάλυση.

Για να μετατρέψουμε μια αρχική τιμή (π.χ., μήκος αντίχειρα σε mm) σε τιμή z, παίρνουμε το υπόλοιπο από το μέσο όρο (μήκος αντίχειρα - μέσος όρος) και διαιρούμε με την τυπική απόκλιση της μεταβλητής. Ποια είναι η σωστή ερμηνεία της τιμής z του μήκους αντίχειρα;

Μας λέει πόσες τυπικές αποκλίσεις πάνω ή κάτω από τον μέσο όρο είναι το μήκος αντίχειρα ενός συγκεκριμένου ατόμου.Παρέχει έναν τρόπο μετατροπής του μήκους αντίχειρα ενός συγκεκριμένου ατόμου από χιλιοστά σε άλλες μονάδες όπως ίντσες.Μας λέει την πιθανότητα να συναντήσουμε αυτό το μήκος αντίχειρα στον πληθυσμό.

Επεξήγηση

Σωστή απάντηση: Α — Μας λέει πόσες τυπικές αποκλίσεις πάνω ή κάτω από τον μέσο όρο είναι το μήκος αντίχειρα ενός συγκεκριμένου ατόμου.

Τι είναι η τιμή z;

Η τιμή z (τυποποιημένη ή τυπική τιμή) είναι ένας τρόπος να εκφράσουμε πόσο απέχει μια παρατήρηση από το μέσο όρο, μετρημένη σε τυπικές αποκλίσεις.

Ο τύπος:

\[z = \frac{X - \bar{X}}{s}\]

όπου:

$X$ = η αρχική τιμή (π.χ., μήκος αντίχειρα σε mm)
$\bar{X}$ = ο μέσος όρος της μεταβλητής
$s$ = η τυπική απόκλιση της μεταβλητής

Α. «Μας λέει πόσες τυπικές αποκλίσεις πάνω ή κάτω από τον μέσο όρο είναι το μήκος αντίχειρα» — ΣΩΣΤΟ ✓

Αυτή είναι η βασική και σωστή ερμηνεία της τιμής z.

Τι σημαίνει αυτό;

Η τιμή z εκφράζει την απόσταση από το μέσο όρο σε σταθερές μονάδες (τυπικές αποκλίσεις), ανεξάρτητα από τις αρχικές μονάδες μέτρησης.

Παραδείγματα:

Παράδειγμα 1: Θετική τιμή z

Έστω:

Μήκος αντίχειρα ατόμου: $X = 68$ mm
Μέσος όρος: $\bar{X} = 60.6$ mm
Τυπική απόκλιση: $s = 8.7$ mm

\[z = \frac{68 - 60.6}{8.7} = \frac{7.4}{8.7} = 0.85\]

Ερμηνεία: Το άτομο έχει αντίχειρα που είναι 0.85 τυπικές αποκλίσεις πάνω από το μέσο όρο. Έχει δηλαδή πιο μεγάλο αντίχειρα από το μέσο όρο.

Παράδειγμα 2: Αρνητική τιμή z

Έστω:

Μήκος αντίχειρα ατόμου: $X = 52$ mm
Μέσος όρος: $\bar{X} = 60.6$ mm
Τυπική απόκλιση: $s = 8.7$ mm

\[z = \frac{52 - 60.6}{8.7} = \frac{-8.6}{8.7} = -0.99\]

Ερμηνεία: Το άτομο έχει αντίχειρα που είναι 0.99 τυπικές αποκλίσεις κάτω από το μέσο όρο. Έχει δηλαδή πιο μικρό αντίχειρα από το μέσο όρο.

Παράδειγμα 3: τιμή z = 0

Έστω:

Μήκος αντίχειρα ατόμου: $X = 60.6$ mm (ακριβώς ο μέσος όρος)

\[z = \frac{60.6 - 60.6}{8.7} = \frac{0}{8.7} = 0\]

Ερμηνεία: Το άτομο έχει αντίχειρα ακριβώς στο μέσο όρο (0 αποκλίσεις από το μέσο).

Γιατί είναι χρήσιμη η τιμή z;

Σύγκριση μεταξύ διαφορετικών μεταβλητών:

Μπορούμε να συγκρίνουμε μεταβλητές που μετρώνται σε διαφορετικές μονάδες:
- Ύψος σε cm: Μέσος όρος = 170 cm, SD = 10 cm
- Αντίχειρας σε mm: Μέσος όρος = 60.6 mm, SD = 8.7 mm
Αν κάποιος έχει:
- $z_{\text{ύψος}} = +1.5$ (1.5 τυπική απόκλιση πάνω από το μέσο ύψος)
- $z_{\text{αντίχειρας}} = +0.5$ (0.5 τυπική απόκλιση πάνω από το μέσο αντίχειρα)
Μπορούμε να πούμε ότι το ύψος του ατόμου είναι πιο ακραίο (πιο πάνω από το μέσο) σε σχέση με τον πληθυσμό από ό,τι ο αντίχειράς του.
Εξάλειψη της επίδρασης των μονάδων:

Οι τιμές z είναι δεν έχουν μονάδες μέτρησης — μετρώνται πάντα σε “τυπικές αποκλίσεις”.
Κατανόηση της σχετικής θέσης:

Η τιμή z μας λέει αμέσως αν μια τιμή είναι:

Πάνω από το μέσο όρο (θετικό z)
Κάτω από το μέσο όρο (αρνητικό z)
Στον μέσο όρο (z = 0)
Πόσο ακραία είναι (απόλυτη τιμή του z)

Γιατί οι άλλες επιλογές είναι λάθος

Β. «Παρέχει έναν τρόπο μετατροπής του μήκους αντίχειρα από χιλιοστά σε άλλες μονάδες όπως ίντσες» — ΛΑΘΟΣ

Αυτό είναι λάθος γιατί η τιμή z ΔΕΝ μετατρέπει μονάδες μέτρησης.

Τι χάνεται με την τιμή z;

Η τιμή z χάνει την πληροφορία για τις πραγματικές, αρχικές μονάδες:

Δύο άτομα με $z = 0.85$ έχουν την ίδια σχετική θέση (0.85 SD πάνω από το μέσο)
Αλλά αν το ένα έχει $z_{\text{ύψος}} = 0.85$ και το άλλο $z_{\text{αντίχειρας}} = 0.85$, δεν έχουν το ίδιο ύψος ή τον ίδιο αντίχειρα!

Συμπέρασμα: Η τιμή z δεν μετατρέπει mm σε ίντσες — μετατρέπει μια αρχική τιμή σε σχετική θέση στην κατανομή.

Γ. «Μας λέει την πιθανότητα αυτού του μήκους αντίχειρα στον πληθυσμό» — ΛΑΘΟΣ

Αυτό είναι λάθος γιατί η τιμή z από μόνη της ΔΕΝ δίνει πιθανότητα.

Τι δείχνει η τιμή z;

Η τιμή z δείχνει την απόσταση από το μέσο όρο σε τυπικές αποκλίσεις:

$z = 0.85$ → 0.85 SD πάνω από το μέσο
$z = -1.2$ → 1.2 SD κάτω από το μέσο

Τι ΔΕΝ δείχνει;

Η τιμή z δεν δίνει απευθείας την πιθανότητα.

Για να βρούμε πιθανότητα:

Χρειαζόμαστε επιπλέον πληροφορία — την κατανομή της μεταβλητής:

Αν η μεταβλητή ακολουθεί κανονική κατανομή, τότε μπορούμε να χρησιμοποιήσουμε την τιμή z για να βρούμε την πιθανότητα από πίνακες της τυπικής κανονικής κατανομής ή με συναρτήσεις όπως η pnorm() στην R.
Αν η μεταβλητή ΔΕΝ ακολουθεί κανονική κατανομή, η τιμή z δεν μας δίνει πιθανότητα.

Παράδειγμα:

Έστω $z = 0.85$ για μήκος αντίχειρα.

Αν υποθέσουμε κανονική κατανομή:


pnorm(0.85)  # Πιθανότητα να είναι ≤ 0.85 SD πάνω από το μέσο

# [1] 0.8023

Αυτό σημαίνει ότι περίπου 80% του πληθυσμού έχει αντίχειρα μικρότερο ή ίσο με αυτό το άτομο.

Αλλά:

Η τιμή z από μόνη της (0.85) δεν είναι πιθανότητα
Χρειάζεται η υπόθεση κανονικότητας και η χρήση της κανονικής κατανομής

Συμπέρασμα: Η τιμή z είναι μια τυποποιημένη μέτρηση απόστασης, όχι πιθανότητα. Η πιθανότητα μπορεί να υπολογιστεί έμμεσα αν γνωρίζουμε την κατανομή.

Συμπέρασμα

Η τιμή z:

✓ Α: Μας δείχνει πόσες τυπικές αποκλίσεις πάνω ή κάτω από τον μέσο όρο είναι μια αρχική τιμή

✗ Β: ΟΧΙ μετατροπή μονάδων (π.χ., mm σε ίντσες) — αυτό γίνεται με απλό πολλαπλασιασμό

✗ Γ: ΟΧΙ την πιθανότητα — χρειάζεται η κατανομή (π.χ., κανονική) για να υπολογιστεί η πιθανότητα

Βασική ιδέα:

Η τιμή z είναι μια τυποποιημένη μέτρηση που εκφράζει την σχετική θέση μιας παρατήρησης στην κατανομή, μετρημένη σε τυπικές αποκλίσεις από το μέσο όρο. Δεν έχει μονάδες μέτρησης (mm, cm, κλπ.) και επιτρέπει τη σύγκριση μεταξύ διαφορετικών μεταβλητών.

Εργασία με Τυποποιημένες Μεταβλητές

Όταν μετασχηματίζουμε κάθε τιμή μιας μεταβλητής σε τιμή z, αυτό αναφέρεται μερικές φορές ως τυποποίηση της μεταβλητής (standardization). Ας δούμε τι συμβαίνει όταν τυποποιούμε τις δύο μεταβλητές με τις οποίες έχουμε εργαστεί (Thumb και Height).

Χρησιμοποιήστε το παρακάτω παράδειγμα κώδικα για να δημιουργήσετε δύο νέες μεταβλητές στο πλαίσιο δεδομένων Fingers: zThumb και zHeight. Η συνάρτηση zscore() θα τυποποιήσει μια μεταβλητή μετατρέποντας όλες τις τιμές της σε τιμές z.

Επειδή και οι δύο μεταβλητές μετασχηματίζονται σε τιμές z, ο μέσος όρος κάθε κατανομής θα είναι 0 και η τυπική απόκλιση θα είναι 1.

Σε αυτό το κεφάλαιο έχουμε χρησιμοποιήσει το ύψος για να εξηγήσουμε τη μεταβλητότητα που παρατηρούμε στα μήκη αντίχειρα. Φανταστείτε ότι δημιουργούμε δύο διαγράμματα διασποράς: το ένα χρησιμοποιεί την Height για να εξηγήσει την Thumb, και το άλλο χρησιμοποιεί την zHeight για να εξηγήσει την zThumb.

Στη δημιουργία αυτών των διαγραμμάτων διασποράς, ποιες μεταβλητές θα τοποθετούνταν στον άξονα y; (Υπάρχει περισσότερες από μία σωστέ απαντήσεις.)

ThumbHeightzThumbzHeight

Επεξήγηση

Σωστές απαντήσεις: Α και Γ — Thumb και zThumb

Γιατί αυτές οι δύο μεταβλητές;

Και οι δύο αντιπροσωπεύουν την εξαρτημένη μεταβλητή (outcome variable) — το μήκος αντίχειρα:

Thumb: Το μήκος αντίχειρα στις αρχικές μονάδες (mm)
zThumb: Το μήκος αντίχειρα σε τυποποιημένες τιμές (τιμές z)

Τα δύο διαγράμματα διασποράς είναι:

Μη τυποποιημένο διάγραμμα:
- Άξονας x: Height (ύψος σε cm)
- Άξονας y: Thumb (μήκος αντίχειρα σε mm)
Τυποποιημένο διάγραμμα:
- Άξονας x: zHeight (τυποποιημένο ύψος)
- Άξονας y: zThumb (τυποποιημένο μήκος αντίχειρα)

Σε κάθε περίπτωση:

Η εξαρτημένη μεταβλητή (αυτό που προσπαθούμε να εξηγήσουμε) → άξονας y
Η ανεξάρτητη μεταβλητή (αυτό που χρησιμοποιούμε για εξήγηση) → άξονας x

Γιατί όχι οι άλλες;

Β. Height — ΛΑΘΟΣ

Η Height είναι η ανεξάρτητη μεταβλητή (explanatory variable), οπότε τοποθετείται στον άξονα x, όχι στον άξονα y.

Δ. zHeight — ΛΑΘΟΣ

Η zHeight είναι η τυποποιημένη ανεξάρτητη μεταβλητή, οπότε επίσης τοποθετείται στον άξονα x, όχι στον άξονα y.

Γενική αρχή:

Άξονας y: Εξαρτημένη μεταβλητή (outcome) — αυτό που προβλέπουμε
Άξονας x: Ανεξάρτητη μεταβλητή (predictor) — αυτό που χρησιμοποιούμε για πρόβλεψη

Γιατί;

Επειδή ο κώδικας της R δεν θα τρέξει αν δεν επιλέξετε αυτή τη μεταβλητή για τον άξονα y.Λόγω σύμβασης — συνήθως τοποθετούμε την εξαρτημένη μεταβλητή στον άξονα y.Λόγω σύμβασης — συνήθως τοποθετούμε την ανεξάρτητη μεταβλητή στον άξονα y.Λόγω σύμβασης — συνήθως τοποθετούμε την ποσοτική μεταβλητή στον άξονα y.

Επεξήγηση

Σωστή απάντηση: Β — Λόγω σύμβασης — συνήθως τοποθετούμε την εξαρτημένη μεταβλητή στον άξονα y.

Η στατιστική και η διαγραμματική σύμβαση

Στη στατιστική ανάλυση και στα διαγράμματα διασποράς, υπάρχει μια διεθνώς αποδεκτή σύμβαση:

Άξονας y (κάθετος): Η εξαρτημένη μεταβλητή (dependent variable, outcome variable, response variable)
- Αυτό που προσπαθούμε να εξηγήσουμε ή να προβλέψουμε
- Στο παράδειγμά μας: Thumb ή zThumb
Άξονας x (οριζόντιος): Η ανεξάρτητη μεταβλητή (independent variable, explanatory variable, predictor)
- Αυτό που χρησιμοποιούμε για την εξήγηση ή πρόβλεψη
- Στο παράδειγμά μας: Height ή zHeight

Γιατί υπάρχει αυτή η σύμβαση;

Διευκόλυνση της ερμηνείας:
- Όταν βλέπουμε ένα διάγραμμα, αμέσως καταλαβαίνουμε ποια μεταβλητή εξηγείται από ποια
- Ο κατακόρυφος άξονας (y) αντιπροσωπεύει την μεταβολή στην εξαρτημένη μεταβλητή
Συνέπεια με τη μαθηματική σημειογραφία:
- Στην εξίσωση παλινδρόμησης: $Y = b_0 + b_1X$
- Το $Y$ (εξαρτημένη) είναι η συνάρτηση του $X$ (ανεξάρτητη)
- Στα διαγράμματα, η Y τοποθετείται στον κάθετο άξονα
Οπτική αναπαράσταση της αιτιότητας:
- Σκεφτόμαστε ότι το X επηρεάζει το Y
- Η αλλαγή στην X (οριζόντια) οδηγεί σε αλλαγή στην Y (κάθετα)

Γιατί οι άλλες επιλογές είναι λάθος

Α. «Επειδή ο κώδικας της R δεν θα τρέξει» — ΛΑΘΟΣ

Αυτό είναι τεχνικά λάθος.

Η R θα τρέξει ακόμα κι αν βάλετε τις μεταβλητές ανάποδα:

# Αυτό θα τρέξει (αλλά είναι ΛΑΘΟΣ εννοιολογικά)

gf_point(Height ~ Thumb, data = Fingers)

Η R δεν θα δώσει σφάλμα, αλλά το διάγραμμα θα είναι παραπλανητικό γιατί:

Υπονοεί ότι η Thumb (άξονας x) εξηγεί την Height (άξονας y)
Αυτό αντιστρέφει τη λογική της ανάλυσής μας

Το πρόβλημα δεν είναι τεχνικό — είναι εννοιολογικό και ζήτημα σύμβασης.

Γ. «Λόγω σύμβασης — συνήθως τοποθετούμε την ανεξάρτητη μεταβλητή στον άξονα y» — ΛΑΘΟΣ

Αυτό είναι το αντίθετο της πραγματικότητας!

Η ανεξάρτητη μεταβλητή τοποθετείται στον άξονα x, όχι στον άξονα y.

Σωστή σύμβαση:

Άξονας x: Ανεξάρτητη μεταβλητή (predictor)
Άξονας y: Εξαρτημένη μεταβλητή (outcome)

Αν ακολουθούσαμε αυτή τη λάθος επιλογή:

Θα βάζαμε την Height στον άξονα y
Θα βάζαμε την Thumb στον άξονα x
Αυτό θα υπονοούσε ότι το μήκος αντίχειρα εξηγεί το ύψος (λάθος!)

Δ. «Λόγω σύμβασης — συνήθως τοποθετούμε την ποσοτική μεταβλητή στον άξονα y» — ΛΑΘΟΣ

Αυτό είναι λάθος γιατί:

Και οι δύο μεταβλητές είναι ποσοτικές:
- Height (ύψος σε ίντσες) → ποσοτική
- Thumb (μήκος αντίχειρα σε mm) → ποσοτική
Άρα, αυτό το κριτήριο δεν μας βοηθάει να επιλέξουμε!
Η απόφαση βασίζεται στον ρόλο, όχι στον τύπο:
- Δεν έχει σημασία αν οι μεταβλητές είναι ποσοτικές, ποιοτικές, ή μικτές
- Έχει σημασία ποια είναι η εξαρτημένη και ποια η ανεξάρτητη
Αντιπαράδειγμα:
- Αν είχαμε: Thumb ~ Sex (όπου Sex είναι ποιοτική)
- Η Thumb (ποσοτική) τοποθετείται στον άξονα y (εξαρτημένη)
- Η Sex (ποιοτική, όχι ποσοτική) τοποθετείται στον άξονα x (ανεξάρτητη)

Το κριτήριο είναι ο ρόλος (εξαρτημένη vs ανεξάρτητη), όχι το είδος (ποσοτική vs ποιοτική)!

Συμπέρασμα

Τοποθετούμε την εξαρτημένη μεταβλητή στον άξονα y επειδή:

✓ Β: Είναι η καθιερωμένη σύμβαση στη στατιστική

✗ Α: ΟΧΙ λόγω τεχνικών περιορισμών της R — η R θα τρέξει με οποιαδήποτε διάταξη

✗ Γ: ΟΧΙ η ανεξάρτητη — αυτή πάει στον άξονα x

✗ Δ: ΟΧΙ με βάση τον τύπο (ποσοτική/ποιοτική) — και οι δύο μεταβλητές είναι ποσοτικές, και η απόφαση βασίζεται στον ρόλο, όχι στον τύπο

Βασική αρχή: > Η τοποθέτηση των μεταβλητών στους άξονες βασίζεται στον εννοιολογικό τους ρόλο (εξαρτημένη vs ανεξάρτητη), όχι σε τεχνικούς περιορισμούς. Ακολουθούμε τη σύμβαση: εξαρτημένη στον άξονα y, ανεξάρτητη στον άξονα x.

Ας προχωρήσουμε στη δημιουργία αυτών των διαγραμμάτων διασποράς. Στο παρακάτω παράδειγμα κώδικα, δημιουργούμε το διάγραμμα διασποράς της Thumb σε σχέση με την Height. Τροποποιήστε τη δεύτερη γραμμή για να δημιουργήσετε ένα διάγραμμα διασποράς της zThumb σε σχέση με την zHeight.

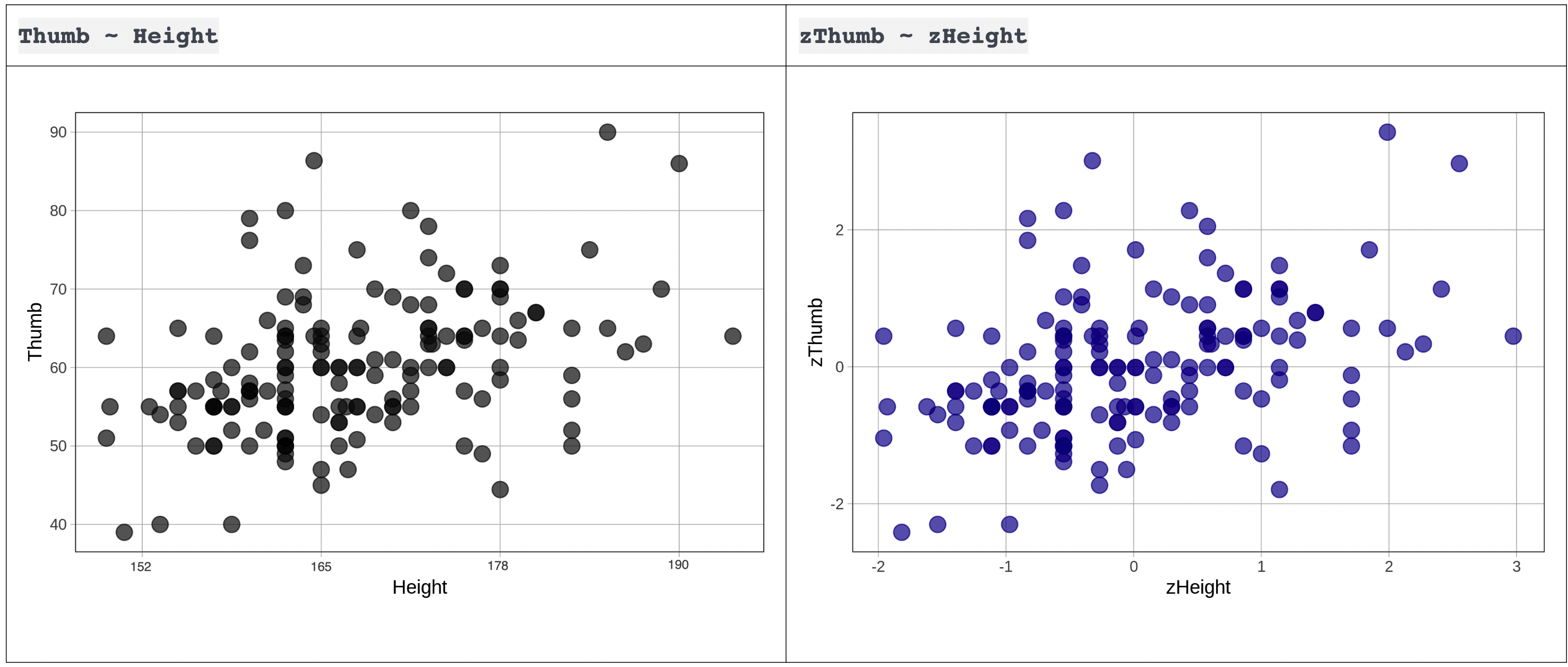
Προσαρμογή του Μοντέλου Παλινδρόμησης σε Τυποποιημένες Μεταβλητές

Στο παρακάτω πλαίσιο δίνουμε τον κώδικα για την προσαρμογή μιας ευθείας παλινδρόμησης για την Thumb με βάση την Height. Προσθέστε κώδικα για να προσαρμόσετε ένα μοντέλο παλινδρόμησης για τις δύο τυποποιημένες μεταβλητές, για την zThumb με βάση την zHeight.

Στον παρακάτω πίνακα παρουσιάζουμε τις εκτιμήσεις των καλύτερα προσαρμοσμένων παραμέτρων μαζί με τα δύο διαγράμματα διασποράς, αυτή τη φορά με τις ευθείες παλινδρόμησης βέλτιστης προσαρμογής.

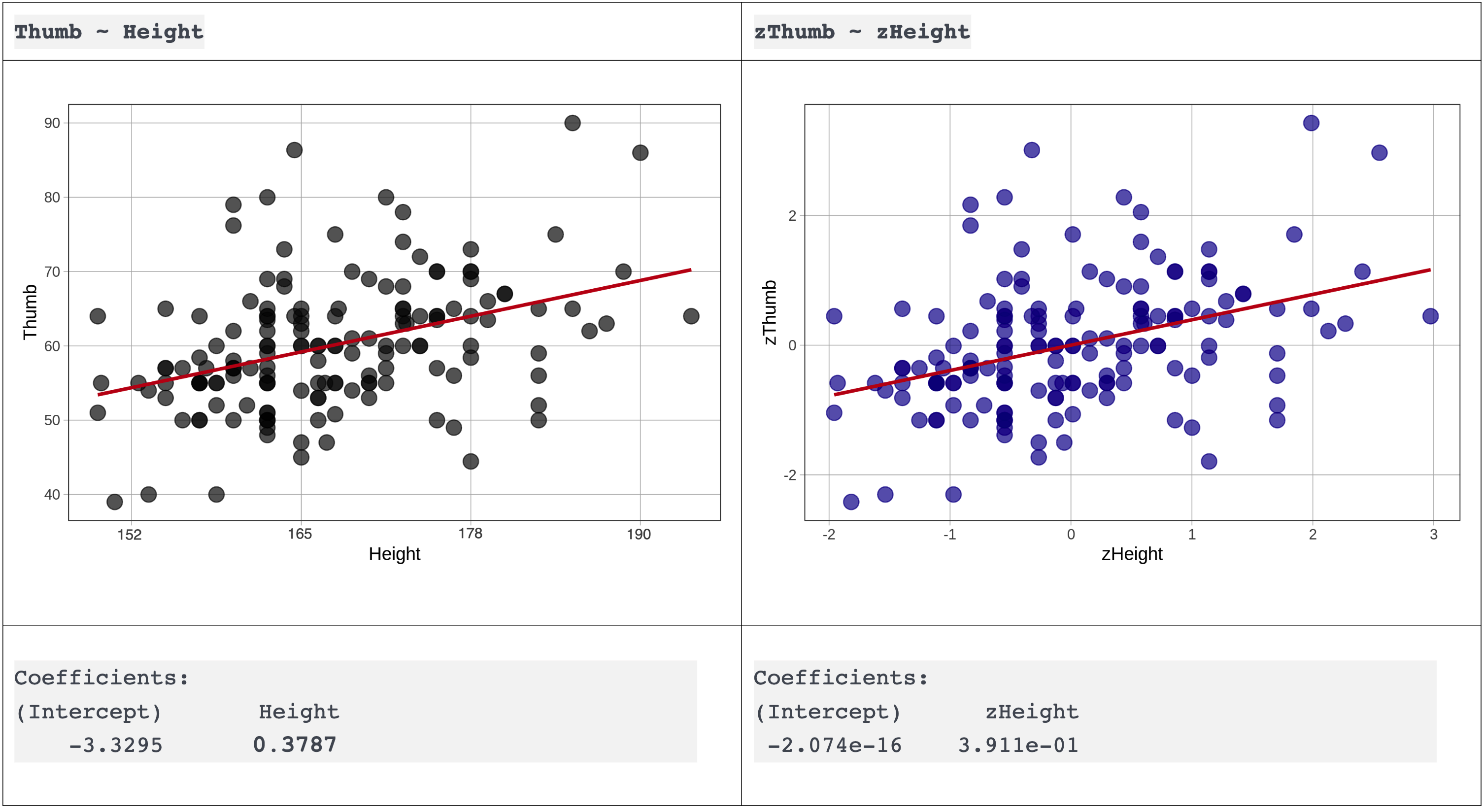
Ποια είναι η τομή με τον άξονα y για το μοντέλο που χρησιμοποιεί την zHeight για να προβλέψει την zThumb;

Περίπου -2.074Περίπου 3.911Περίπου 0

Επεξήγηση

Σωστή απάντηση: Γ — Περίπου 0

Κατανόηση της επιστημονικής σημειογραφίας

Το (Intercept) ή σταθερός όρος εμφανίζεται ως -2.074e-16, που σημαίνει:

\[-2.074 \times 10^{-16}\]

Τι σημαίνει αυτό;

Ο εκθέτης -16 σημαίνει ότι η υποδιαστολή μετακινείται 16 θέσεις προς τα αριστερά:

\[-2.074e-16 = -0.0000000000000002074\]

Αυτός ο αριθμός είναι τόσο κοντά στο μηδέν που για κάθε πρακτικό σκοπό είναι 0.

Γιατί η τομή με τον άξονα y είναι (περίπου) 0;

Θεωρητική εξήγηση:

Όταν χρησιμοποιούμε τυποποιημένες μεταβλητές (τιμές z):

Ο μέσος όρος κάθε τυποποιημένης μεταβλητής είναι 0: \[\bar{z} = 0\]
Η ευθεία παλινδρόμησης περνάει πάντα από το σημείο των μέσων όρων: \[(\bar{X}, \bar{Y})\]
Για τυποποιημένες μεταβλητές, το σημείο των μέσων όρων είναι: \[(\bar{zHeight}, \bar{zThumb}) = (0, 0)\]
Άρα, η ευθεία περνάει από το (0, 0), οπότε η τομή με τον y είναι 0.

Γιατί οι άλλες επιλογές είναι λάθος

Α. «Περίπου -2.074» — ΛΑΘΟΣ

Αυτό είναι λάθος γιατί παρερμηνεύει την επιστημονική σημειογραφία.

Η παρανόηση:

Μπορεί κάποιος να νομίσει ότι -2.074e-16 σημαίνει -2.074, αγνοώντας το e-16.

Η σωστή ανάγνωση:

-2.074e-16 = $-2.074 \times 10^{-16}$
ΟΧΙ -2.074

Η διαφορά:

\[\frac{-2.074}{-2.074e-16} = \frac{-2.074}{-0.0000000000000002074} \approx 10^{16}\]

Υπάρχει διαφορά 10 τρισεκατομμυρία φορές!

Β. «Περίπου 3.911» — ΛΑΘΟΣ

Αυτό είναι λάθος γιατί μπερδεύει την τομή με την κλίση.

Τι είναι το 3.911e-01;

Το 3.911e-01 είναι η κλίση ($b_1$), όχι η τομή ($b_0$):

\[3.911e-01 = 3.911 \times 10^{-1} = 0.3911\]

Η πλήρης εξίσωση είναι:

\[\hat{zThumb} = \underbrace{-2.074e-16}_{b_0 \approx 0} + \underbrace{0.3911}_{b_1} \times zHeight\]

Ή απλοποιημένα:

\[\hat{zThumb} = 0.391 \times zHeight\]

Ερμηνεία της κλίσης:

Η κλίση 0.391 σημαίνει:

Για κάθε αύξηση 1 τυπικής απόκλισης στο ύψος
Αναμένουμε αύξηση 0.391 τυπικών αποκλίσεων στο μήκος αντίχειρα

Αυτό είναι επίσης ο συντελεστής συσχέτισης r!

Συμπέρασμα

Η τομή με τον άξονα y για το μοντέλο zThumb ~ zHeight είναι (περίπου) 0 επειδή:

Θεωρητικά: Η ευθεία παλινδρόμησης περνάει από το σημείο των μέσων όρων (0, 0) για τυποποιημένες μεταβλητές
Υπολογιστικά: Το -2.074e-16 είναι αριθμητικό σφάλμα στρογγυλοποίησης, όχι πραγματική τιμή
Πρακτικά: Το $-2.074 \times 10^{-16}$ είναι τόσο κοντά στο 0 που είναι αμελητέο

Βασική αρχή: > Όταν χρησιμοποιούμε τυποποιημένες μεταβλητές (τιμές z) στην παλινδρόμηση, η τομή με τον άξονα y είναι πάντα 0 επειδή ο μέσος όρος κάθε τυποποιημένης μεταβλητής είναι 0, και η ευθεία παλινδρόμησης πάντα περνάει από το σημείο των μέσων όρων.

Σημειώστε ότι η R μερικές φορές εκφράζει τις εκτιμήσεις παραμέτρων σε επιστημονική σημειογραφία. Έτσι, το -2.074e-16 σημαίνει ότι η υποδιαστολή μετατοπίζεται 16 ψηφία προς τα αριστερά. Επομένως, η πραγματική τομή της ευθείας παλινδρόμησης με τον άξονα y είναι -0.00000000000000018, που είναι, πρακτικά, 0.

Ποιες από τις παρακάτω είναι οι εξισώσεις για το μοντέλο zHeight_model; (Υπάρχουν περισσότερες από μία σωστές απαντήσεις.)

$Y_i = .39X_i + e_i$$Y_i = 0 + .39X_i + e_i$$Y_i = -1.8 + 3.9X_i + e_i$

Επεξήγηση

Σωστές απαντήσεις: Α και Β

Το μοντέλο zHeight_model χρησιμοποιεί τυποποιημένες μεταβλητές: \[zThumb \sim zHeight\]

Από την προηγούμενη ανάλυση, γνωρίζουμε ότι: - Τομή (σταθερός όρος): $b_0 \approx 0$ (στην πραγματικότητα $-2.074 \times 10^{-16}$) - Κλίση: $b_1 = 0.391 \approx 0.39$

Α. «$Y_i = .39X_i + e_i$» — ΣΩΣΤΟ ✓

Αυτή είναι μια σωστή αναπαράσταση του μοντέλου.

Γιατί;

Επειδή η τομή είναι (ουσιαστικά) 0, μπορούμε να την παραλείψουμε:

\[Y_i = 0 + 0.39X_i + e_i = 0.39X_i + e_i\]

Πλήρης ερμηνεία:

$Y_i$ = zThumb (τυποποιημένο μήκος αντίχειρα)
$X_i$ = zHeight (τυποποιημένο ύψος)
$0.39$ = η κλίση (είναι ο συντελεστής συσχέτισης r)
$e_i$ = το σφάλμα (υπόλοιπο)

Αυτή η μορφή είναι συνηθισμένη όταν η τομή είναι 0, καθώς απλοποιεί την εξίσωση.

Β. «$Y_i = 0 + .39X_i + e_i$» — ΣΩΣΤΟ ✓

Αυτή είναι επίσης σωστή και πιο ξεκάθαρη.

Γιατί;

Αυτή η μορφή δείχνει ρητά ότι η τομή είναι 0:

\[Y_i = 0 + 0.39X_i + e_i\]

Πλεονεκτήματα αυτής της μορφής:

Σαφήνεια: Δείχνει ξεκάθαρα ότι $b_0 = 0$
Πληρότητα: Ακολουθεί τη γενική μορφή $Y = b_0 + b_1X + e$
Παιδαγωγική αξία: Βοηθά να καταλάβουμε ότι ο σταθερός όρος είναι 0 για τυποποιημένες μεταβλητές

Οι επιλογές Α και Β είναι μαθηματικά ισοδύναμες: \[Y_i = 0.39X_i + e_i \equiv Y_i = 0 + 0.39X_i + e_i\]

Γιατί και οι δύο είναι σωστές;

Μαθηματική ισοδυναμία:

\[Y_i = 0 + 0.39X_i + e_i\]

Επειδή η πρόσθεση του 0 δεν αλλάζει το αποτέλεσμα:

\[Y_i = 0.39X_i + e_i\]

Και οι δύο μορφές περιγράφουν το ίδιο μοντέλο:

Για $X_i = 0$ (μέσο ύψος): $\hat{Y}_i = 0.39(0) = 0$ (μέσο μήκος αντίχειρα)
Για $X_i = 1$ (1 SD πάνω): $\hat{Y}_i = 0.39(1) = 0.39$ (0.39 SD πάνω)
Για $X_i = -1$ (1 SD κάτω): $\hat{Y}_i = 0.39(-1) = -0.39$ (0.39 SD κάτω)

Πότε χρησιμοποιούμε κάθε μορφή;

Μορφή Α ($Y_i = .39X_i + e_i$):

Όταν θέλουμε απλότητα και συντομία
Όταν είναι προφανές ότι η τομή είναι 0
Σε τυποποιημένα μοντέλα όπου πάντα $b_0 = 0$

Μορφή Β ($Y_i = 0 + .39X_i + e_i$):

Όταν θέλουμε σαφήνεια και πληρότητα
Όταν διδάσκουμε και θέλουμε να δείξουμε ρητά τη δομή
Όταν συγκρίνουμε με μοντέλα που έχουν $b_0 \neq 0$

Γιατί η άλλη επιλογή είναι λάθος

Γ. «$Y_i = -1.8 + 3.9X_i + e_i$» — ΛΑΘΟΣ

Αυτή η εξίσωση είναι εντελώς λάθος για το zHeight_model.

Γιατί είναι λάθος;

Λάθος τιμή σταθερού όρου:
- Η σωστή τιμή του σταθερού όρου για το zHeight_model είναι 0, όχι -1.8
Λάθος τιμή κλίσης:
- Η σωστή τιμή κλίσης είναι 0.39, όχι 3.9
- Το 3.9 είναι 10 φορές μεγαλύτερο από τη σωστή τιμή!

Γενική μορφή εξίσωσης παλινδρόμησης

Για μη τυποποιημένες μεταβλητές: \[Y_i = b_0 + b_1X_i + e_i\]

όπου $b_0 \neq 0$ (συνήθως)

Παράδειγμα — Μοντέλο Thumb ~ Height: \[Thumb_i = -3.33 + 0.96 \times Height_i + e_i\]

Για τυποποιημένες μεταβλητές: \[Y_i = 0 + b_1X_i + e_i\]

ή απλά: \[Y_i = b_1X_i + e_i\]

όπου $b_0 = 0$ (πάντα)

Παράδειγμα — Μοντέλο zThumb ~ zHeight: \[zThumb_i = 0 + 0.39 \times zHeight_i + e_i\]

ή: \[zThumb_i = 0.39 \times zHeight_i + e_i\]

Σημαντική παρατήρηση: Η κλίση είναι ο συντελεστής συσχέτισης

Για τυποποιημένες μεταβλητές:

\[b_1 = r\]

Στο παράδειγμά μας:

\[b_1 = 0.39 = r_{\text{Thumb, Height}}\]

Αυτό σημαίνει ότι: - Η κλίση της παλινδρόμησης με τυποποιημένες μεταβλητές είναι ο συντελεστής συσχέτισης

Δεν χρειάζεται να υπολογίσουμε ξεχωριστά το r — το παίρνουμε απευθείας από την παλινδρόμηση!

Συμπέρασμα

Η εξίσωση για το zHeight_model είναι:

\[zThumb_i = 0.39 \times zHeight_i + e_i\]

ή πιο ρητά:

\[zThumb_i = 0 + 0.39 \times zHeight_i + e_i\]

Σωστές αναπαραστάσεις:

✓ Α: $Y_i = .39X_i + e_i$ (συντομογραφία, παραλείπει το 0)

✓ Β: $Y_i = 0 + .39X_i + e_i$ (πλήρης μορφή, ρητή τομή)

✗ Γ: $Y_i = -1.8 + 3.9X_i + e_i$ (εντελώς λάθος τιμές)

Βασικά χαρακτηριστικά του μοντέλου τυποποιημένων μεταβλητών:

Τομή = 0 (πάντα, επειδή η ευθεία περνάει από το σημείο (0,0))
Κλίση = r (ο συντελεστής συσχέτισης)
Κυμαίνεται από -1 έως +1 (όπως το r)
Χωρίς μονάδες (μετράται σε τυπικές αποκλίσεις, όχι σε mm, cm, κλπ.)

Γνωρίζουμε από προηγούμενες ενότητες ότι η ευθεία παλινδρόμησης βέλτιστης προσαρμογής διέρχεται από το σημείο των μέσων όρων, δηλαδή το σημείο που ορίζεται από τον μέσο όρο τόσο της εξαρτημένης όσο και της ανεξάρτητης μεταβλητής, το οποίο φαίνεται στα διαγράμματα διασποράς παρακάτω. Σημειώστε ότι στην περίπτωση της zThumb και της zHeight, ο μέσος όρος καθεμιάς είναι 0 και το σημείο των μέσων όρων είναι (0,0).

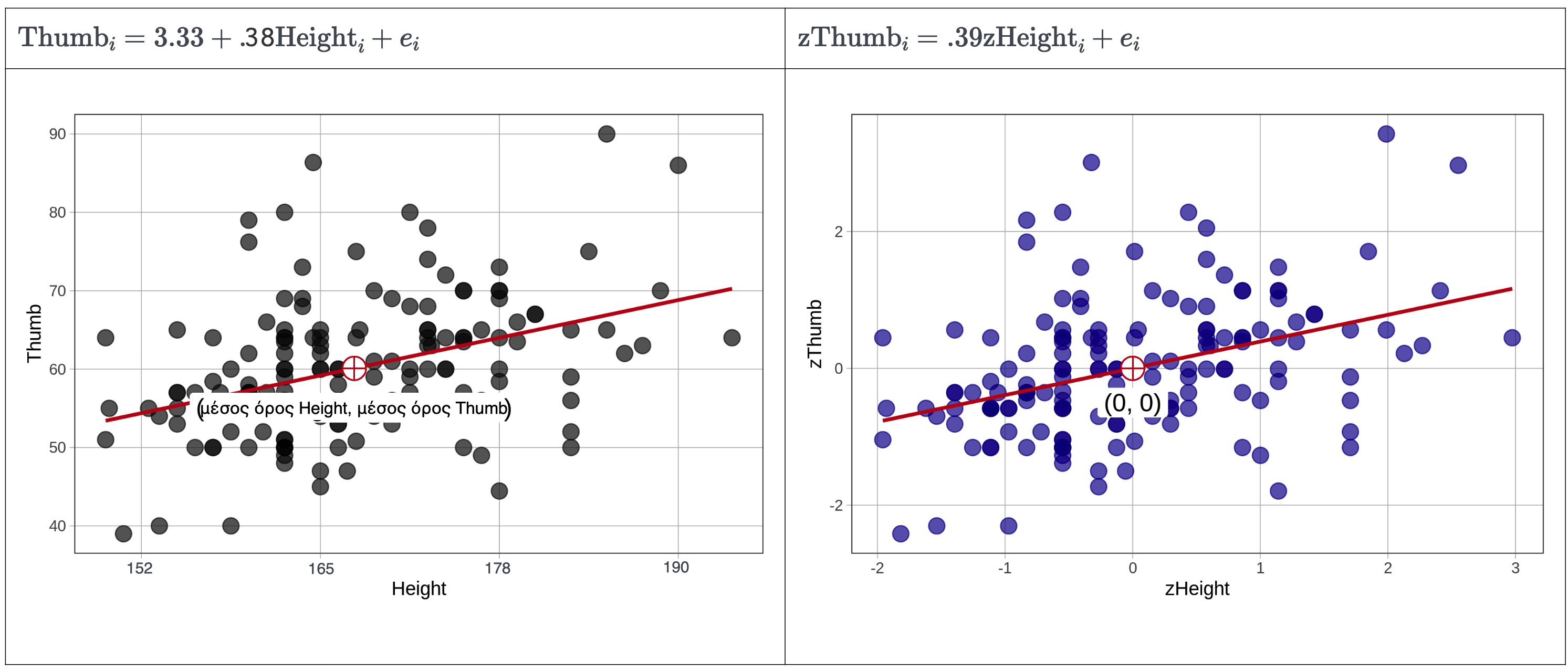
Επειδή ο μέσος όρος οποιασδήποτε τυποποιημένης μεταβλητής είναι 0, μια ευθεία παλινδρόμησης που βασίζεται σε τυποποιημένες μεταβλητές θα έχει πάντα τομή με τον άξονα y ίση με 0, πράγμα που σημαίνει ότι όταν το x είναι 0, το y θα είναι επίσης 0.

Συντελεστής Συσχέτισης: Η Κλίση της Τυποποιημένης Ευθείας Παλινδρόμησης

Ας στρέψουμε τώρα την προσοχή μας στις κλίσεις (τις εκτιμήσεις $b_1$) και των δύο μοντέλων, αυτού που βασίζεται σε μη τυποποιημένες μεταβλητές και αυτού που βασίζεται σε τυποποιημένες μεταβλητές.

Συγκρίνετε τις κλίσεις της ευθείας παλινδρόμησης για τα δύο μοντέλα. Στο μη τυποποιημένο μοντέλο, τι σημαίνει η κλίση (0.37);

Για κάθε εκατοστό ύψους, προσθέτουμε 0.37 χιλιοστά στην τιμή πρόβλεψης του μήκους αντίχειρα.Για κάθε χιλιοστό ύψους, προσθέτουμε 0.37 χιλιοστά στο προβλεπόμενο μήκος αντίχειρα.Για κάθε χιλιοστό μήκους αντίχειρα, προσθέτουμε 0.37 εκατοστά στην τιμή πρόβλεψης του ύψους.Όταν το ύψος είναι ίσο με 0, το μήκος αντίχειρα είναι 0.37 χιλιοστά.

Επεξήγηση

Σωστή απάντηση: Α — Για κάθε εκατοστό ύψους, προσθέτουμε 0.37 χιλιοστά στην τιμή πρόβλεψης του μήκους αντίχειρα.

Το μη τυποποιημένο μοντέλο:

Το ύψος μετράται σε εκατοστά (cm) και ο αντίχειρας σε χιλιοστά (mm), οπότε το μοντέλο έχει τη μορφή:

\[\text{Thumb}_i = b_0 + 0.37 \times \text{Height}_i\]

όπου:

Thumb μετράται σε χιλιοστά (mm)
Height μετράται σε εκατοστά (cm)

Τι είναι η κλίση ($b_1$);

Η κλίση αντιπροσωπεύει την μεταβολή στην εξαρτημένη μεταβλητή για μία μονάδα μεταβολής στην ανεξάρτητη μεταβλητή:

\[b_1 = \frac{\Delta Y}{\Delta X}\]

Στο μοντέλο μας:

\[b_1 = 0.37 = \frac{\Delta \text{Thumb (mm)}}{\Delta \text{Height (cm)}}\]

Μονάδες της κλίσης: mm/cm (χιλιοστά ανά εκατοστό)

Α. «Για κάθε εκατοστό ύψους, προσθέτουμε 0.37 χιλιοστά στην τιμή πρόβλεψης του μήκους αντίχειρα» — ΣΩΣΤΟ ✓

Αυτή είναι η σωστή ερμηνεία της κλίσης.

Μαθηματική επεξήγηση:

Αν το ύψος αυξηθεί κατά 1 cm:

\[\Delta \text{Height} = 1 \text{ cm}\]

Τότε το προβλεπόμενο μήκος αντίχειρα αυξάνεται κατά:

\[\Delta \text{Thumb} = b_1 \times \Delta \text{Height} = 0.37 \times 1 = 0.37 \text{ mm}\]

Γενική μορφή ερμηνείας κλίσης:

Για κάθε αύξηση 1 [μονάδα X], το προβλεπόμενο Y αυξάνεται κατά $b_1$ [μονάδες Y].

Στην περίπτωσή μας:

Για κάθε αύξηση 1 cm στο ύψος, το προβλεπόμενο μήκος αντίχειρα αυξάνεται κατά 0.37 mm.

Γιατί οι άλλες επιλογές είναι λάθος

Β. «Για κάθε χιλιοστό ύψους, προσθέτουμε 0.37 χιλιοστά στο προβλεπόμενο μήκος αντίχειρα» — ΛΑΘΟΣ

Λάθος μονάδες για το ύψος.

Το ύψος μετράται σε εκατοστά (cm), όχι σε χιλιοστά (mm).

Γ. «Για κάθε χιλιοστό μήκους αντίχειρα, προσθέτουμε 0.37 εκατοστά στην τιμή πρόβλεψης του ύψους» — ΛΑΘΟΣ

Αυτό αντιστρέφει τη σχέση!

Το πρόβλημα:

Λάθος κατεύθυνση:
- Το μοντέλο μας προβλέπει Thumb από Height, όχι το αντίστροφο
- Δηλαδή: Height (X) → Thumb (Y), όχι Thumb (X) → Height (Y)
Λάθος κλίση:
- Αν θέλαμε να προβλέψουμε ύψος από αντίχειρα, θα χρειαζόμασταν διαφορετικό μοντέλο
- Η κλίση δεν θα ήταν 0.37 — θα ήταν κάτι άλλο

Δ. «Όταν το ύψος είναι ίσο με 0, το μήκος αντίχειρα είναι 0.37 χιλιοστά» — ΛΑΘΟΣ

Αυτό περιγράφει στον σταθερό όρο, όχι την κλίση!

Διάκριση μεταξύ σταθερού όρου και κλίσης:

Στην εξίσωση:

\[\text{Thumb} = \underbrace{b_0}_{\text{τομή}} + \underbrace{0.37}_{\text{κλίση}} \times \text{Height}\]

Σταθερός όρος ($b_0$):

Η τιμή του Y όταν X = 0
“Όταν το ύψος είναι 0 cm, το προβλεπόμενο μήκος αντίχειρα είναι $b_0$ mm”
(Αυτό δεν έχει πρακτικό νόημα, αλλά είναι μαθηματικά η τομή)

Κλίση ($b_1 = 0.37$):

Η αλλαγή στην Y για μία μονάδα αλλαγής στην X
“Για κάθε 1 cm αύξηση στο ύψος, το μήκος αντίχειρα αυξάνεται κατά 0.37 mm”

Η επιλογή Δ είναι λάθος:

Περιγράφει τον σταθερό όρο, όχι την κλίση
Η κλίση περιγράφει την αλλαγή, όχι την τιμή όταν X = 0

Συμπέρασμα για το μη τυποποιημένο μοντέλο

Η κλίση 0.37 σημαίνει:

✓ Για κάθε 1 cm αύξηση στο ύψος, το προβλεπόμενο μήκος αντίχειρα αυξάνεται κατά 0.37 mm

Βασικά στοιχεία:

Μονάδες X: εκατοστά (cm)
Μονάδες Y: χιλιοστά (mm)
Μονάδες κλίσης: mm/cm

Πρακτική εφαρμογή:

Αν κάποιος είναι 10 cm ψηλότερος:

\[\Delta \text{Thumb} = 0.37 \times 10 = 3.7 \text{ mm}\]

Αναμένουμε ο αντίχειράς του να είναι περίπου 3.7 mm μεγαλύτερος.

Τι σημαίνει η κλίση 0.39 στο τυποποιημένο μοντέλο;

Για κάθε μία τυπική απόκλιση αύξησης της Height, προσθέτουμε 0.39 τυπικές αποκλίσεις στο προβλεπόμενο μήκος αντίχειρα (Thumb).Η τυπική απόκλιση της zThumb είναι 0.39.Η τυπική απόκλιση της zHeight είναι 0.39.Για κάθε ένα εκατοστό Height, προσθέτουμε 0.39 mm στο προβλεπόμενο μήκος αντίχειρα (Thumb).

Επεξήγηση

Σωστή απάντηση: Α — Για κάθε μία τυπική απόκλιση αύξησης της Height, προσθέτουμε 0.39 τυπικές αποκλίσεις στο προβλεπόμενο μήκος αντίχειρα.

Το τυποποιημένο μοντέλο:

\[zThumb_i = 0 + 0.39 \times zHeight_i\]

ή απλά:

\[zThumb_i = 0.39 \times zHeight_i\]

όπου:

zThumb μετράται σε τυπικές αποκλίσεις
zHeight μετράται σε τυπικές αποκλίσεις

Α. «Για κάθε μία τυπική απόκλιση αύξησης της Height, προσθέτουμε 0.39 τυπικές αποκλίσεις στο προβλεπόμενο μήκος Thumb» — ΣΩΣΤΟ ✓

Αυτή είναι η σωστή ερμηνεία.

Μαθηματική επεξήγηση:

Αν το τυποποιημένο ύψος αυξηθεί κατά 1 SD:

\[\Delta zHeight = 1\]

Τότε το προβλεπόμενο τυποποιημένο μήκος αντίχειρα αυξάνεται κατά:

\[\Delta zThumb = 0.39 \times 1 = 0.39 \text{ SD}\]

Παραδείγματα:

Άτομο με μέσο ύψος:

$zHeight = 0$ (ακριβώς στον μέσο όρο)
$\hat{zThumb} = 0.39(0) = 0$ (μέσο μήκος αντίχειρα)

Άτομο 1 SD πάνω από το μέσο ύψος:

$zHeight = +1$
$\hat{zThumb} = 0.39(1) = 0.39$ (0.39 SD πάνω από το μέσο μήκος αντίχειρα)

Άτομο 2 SD πάνω από το μέσο ύψος:

$zHeight = +2$
$\hat{zThumb} = 0.39(2) = 0.78$ (0.78 SD πάνω από το μέσο μήκος αντίχειρα)

Άτομο 1 SD κάτω από το μέσο ύψος:

$zHeight = -1$
$\hat{zThumb} = 0.39(-1) = -0.39$ (0.39 SD κάτω από το μέσο μήκος αντίχειρα)

Σε κάθε περίπτωση, η αλλαγή είναι 0.39 SD στο αντίχειρα για κάθε 1 SD αλλαγή στο ύψος.

Σημαντική παρατήρηση: Η κλίση είναι ο συντελεστής συσχέτισης

Για τυποποιημένες μεταβλητές:

\[b_1 = r = 0.39\]

Αυτό σημαίνει ότι:

Η κλίση (0.39) είναι ο συντελεστής συσχέτισης Pearson
Μετρά την ισχύ της γραμμικής σχέσης
Κυμαίνεται από -1 έως +1

Γιατί οι άλλες επιλογές είναι λάθος

Β. «Η τυπική απόκλιση της zThumb είναι 0.39» — ΛΑΘΟΣ

Αυτό είναι λάθος γιατί μπερδεύει την κλίση με την τυπική απόκλιση.

Η τυπική απόκλιση οποιασδήποτε τυποποιημένης μεταβλητής είναι πάντα 1:

\[SD(zThumb) = 1\]

\[SD(zHeight) = 1\]

Αυτό είναι εξ ορισμού — η τυποποίηση δημιουργεί μεταβλητές με SD = 1.

Το 0.39 ΔΕΝ είναι SD — είναι η κλίση της ευθείας παλινδρόμησης (και ο συντελεστής συσχέτισης).

Γ. «Η τυπική απόκλιση της zHeight είναι 0.39» — ΛΑΘΟΣ

Όπως και η Β, αυτό είναι λάθος.

Η τυπική απόκλιση της zHeight είναι 1, όχι 0.39.

\[SD(zHeight) = 1\]

Το 0.39 είναι η κλίση, όχι η τυπική απόκλιση.

Δ. «Για κάθε ένα εκατοστό Height, προσθέτουμε 0.39 mm στο προβλεπόμενο μήκος Thumb» — ΛΑΘΟΣ

Αυτό μπερδεύει το τυποποιημένο με το μη τυποποιημένο μοντέλο.

Το πρόβλημα:

Λάθος μονάδες:
- Το τυποποιημένο μοντέλο χρησιμοποιεί τυπικές αποκλίσεις, όχι εκατοστά και χιλιοστά
Λάθος τιμή:
- Για το μη τυποποιημένο μοντέλο, η κλίση είναι 0.37 mm/cm
- Για το τυποποιημένο μοντέλο, η κλίση είναι 0.39 SD/SD
- Αυτές είναι διαφορετικές ποσότητες με διαφορετικές μονάδες!

Σύγκριση:

Μοντέλο	Κλίση	Μονάδες	Ερμηνεία
Μη τυποποιημένο	0.37	mm/cm	+1 cm → +0.37 mm
Τυποποιημένο	0.39	SD/SD	+1 SD → +0.39 SD

Δεν μπορούμε να τα μπερδέψουμε!

Σύγκριση των δύο μοντέλων

Χαρακτηριστικό	Μη τυποποιημένο	Τυποποιημένο
Εξίσωση	$Thumb = b_0 + 0.37 \times Height$	$zThumb = 0.39 \times zHeight$
Τομή	$b_0$ (π.χ., -3 mm)	0
Κλίση	0.37 mm/cm	0.39 SD/SD
Μονάδες X	Εκατοστά	Τυπικές αποκλίσεις
Μονάδες Y	Χιλιοστά	Τυπικές αποκλίσεις
Ερμηνεία κλίσης	+1 cm → +0.37 mm	+1 SD → +0.39 SD
Κλίση = r;	Όχι	Ναι ✓

Γιατί είναι χρήσιμο το τυποποιημένο μοντέλο;

1. Ερμηνεία χωρίς μονάδες μέτρησης:

Δεν χρειάζεται να γνωρίζουμε τις μονάδες μέτρησης (mm, cm, κλπ.)
Η ερμηνεία είναι πάντα σε τυπικές αποκλίσεις

2. Σύγκριση μεταξύ μεταβλητών:

Μπορούμε να συγκρίνουμε την ένταση των σχέσεων μεταξύ διαφορετικών ζευγαριών μεταβλητών
Η κλίση (= r) κυμαίνεται από -1 έως +1

3. Ο συντελεστής συσχέτισης:

Η κλίση είναι ο συντελεστής συσχέτισης r
Μετρά την κατεύθυνση και την ένταση της γραμμικής σχέσης

Μετατροπή μεταξύ των δύο μοντέλων

Από μη τυποποιημένο σε τυποποιημένο:

\[b_1^{\text{standard}} = b_1^{\text{unstand}} \times \frac{SD_X}{SD_Y}\]

Στο παράδειγμά μας (υποθέτοντας $SD_{Height} \approx 10.9$ cm και $SD_{Thumb} \approx 8.7$ mm):

\[0.39 \approx 0.37 \times \frac{10.9}{8.7}\]

Επαλήθευση:

\[0.37 \times \frac{10.9}{8.7} = 0.37 \times 1.253 = 0.464\]

Η μικρή διαφορά (0.464 vs 0.39) μπορεί να οφείλεται σε στρογγυλοποίηση ή διαφορετικές τυπικές αποκλίσεις στα δεδομένα.

Συμπέρασμα

Η κλίση 0.39 του τυποποιημένου μοντέλου σημαίνει:

✓ Α: Για κάθε 1 SD αύξηση στο ύψος, το προβλεπόμενο μήκος αντίχειρα αυξάνεται κατά 0.39 SD

✗ Β, Γ: ΟΧΙ τυπική απόκλιση — όλες οι τυποποιημένες μεταβλητές έχουν SD = 1

✗ Δ: ΟΧΙ mm/cm — αυτό είναι για το μη τυποποιημένο μοντέλο (και η τιμή είναι 0.37, όχι 0.39)

Βασική ιδέα:

Στο τυποποιημένο μοντέλο, η κλίση (0.39) είναι ο συντελεστής συσχέτισης και ερμηνεύεται ως: “για κάθε 1 SD αλλαγή στο X, αναμένουμε r SD αλλαγή στο Y”. Είναι αμοναδική και άμεσα συγκρίσιμη μεταξύ διαφορετικών μεταβλητών.

Παρατηρήστε ότι οι κλίσεις είναι διαφορετικές για τις μη τυποποιημένες και τις τυποποιημένες ευθείες παλινδρόμησης (0.38 έναντι 0.39). Για να ερμηνεύσετε τη μη τυποποιημένη κλίση, πρέπει να γνωρίζετε κάτι σχετικά με το πώς μετρώνται οι αντίχειρες και τα ύψη (π.χ., mm και cm). Αλλά η τυποποιημένη κλίση δεν απαιτεί αυτή την πρόσθετη γνώση.

Η κλίση της ευθείας παλινδρόμησης μεταξύ των τυποποιημένων μεταβλητών ονομάζεται συντελεστής συσχέτισης ή r του Pearson. Ο συντελεστής συσχέτισης είναι χρήσιμος για την αξιολόγηση της ισχύος μιας διμεταβλητής σχέσης μεταξύ δύο ποσοτικών μεταβλητών, ανεξάρτητα από τις μονάδες μέτρησης κάθε μεταβλητής.

Για να μην χρειάζεται να μετασχηματίζετε μεταβλητές σε τιμές z και στη συνέχεια να προσαρμόζετε μια ευθεία παλινδρόμησης απλώς για να βρείτε τον συντελεστή συσχέτισης, η R παρέχει έναν εύκολο τρόπο για τον άμεσο υπολογισμό του συντελεστή συσχέτισης (το r του Pearson) από τις αρχικές τιμές: τη συνάρτηση cor(). Δοκιμάστε να εκτελέσετε τον παρακάτω κώδικα.

[1] 0.3910649

Παρατηρήστε ότι το αποτέλεσμα 0.39 είναι η κλίση της τυποποιημένης ευθείας παλινδρόμησης, πράγμα που σημαίνει ότι μια αύξηση 1 τυπικής απόκλισης στο ύψος θα έχει ως αποτέλεσμα αύξηση 0.39 τυπικών αποκλίσεων στο μήκος αντίχειρα.

Οι συντελεστές συσχέτισης, επειδή υπολογίζονται χρησιμοποιώντας τυποποιημένες μεταβλητές, έχουν ορισμένα χαρακτηριστικά. Το πιο χρήσιμο από αυτά είναι ότι το r θα κυμαίνεται πάντα από -1 έως +1. Ένα r ίσο με 0 σημαίνει ότι οι δύο μεταβλητές δεν συσχετίζονται. Ένα θετικό r σημαίνει ότι οι μεταβλητές συσχετίζονται θετικά και γραμμικά, ενώ ένα αρνητικό r σημαίνει ότι συσχετίζονται αρνητικά και γραμμικά.

Όσο πιο μακριά από το 0 είναι το r, τόσο ισχυρότερη είναι η γραμμική συσχέτιση μεταξύ των δύο μεταβλητών. Δύο μεταβλητές με συσχέτιση +1 σχετίζονται τέλεια μεταξύ τους, πράγμα που σημαίνει ότι μια αύξηση 1 τυπικής απόκλισης σε μία από τις μεταβλητές θα συνοδεύεται από αύξηση 1 τυπικής απόκλισης στην άλλη. Μια συσχέτιση -1 σημαίνει ότι δύο μεταβλητές συσχετίζονται τέλεια αρνητικά.

Σημειώστε ότι δύο μεταβλητές μπορεί να συσχετίζονται με συστηματικό τρόπο αλλά η σχέση μεταξύ τους να μην είναι γραμμική, όπως για παράδειγμα, στα διαγράμματα που βρίσκονται στα αριστερά και στο κέντρο παρακάτω. Σε αυτές τις περιπτώσεις, παρόλο που υπάρχει ένα σαφές μοτίβο στα διαγράμματα διασποράς, το r είναι κοντά στο 0 επειδή η σχέση δεν είναι γραμμική.

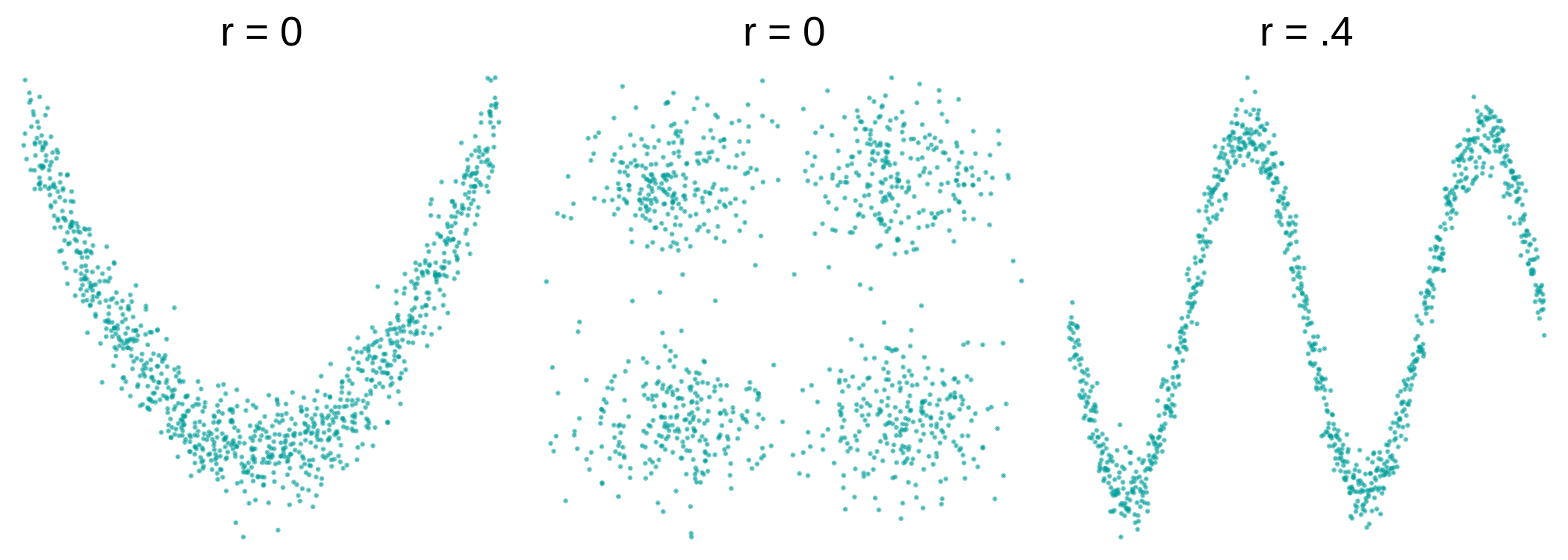
Ακόμη και όταν το r δεν είναι απαραίτητα κοντά στο 0, όπως στο διάγραμμα στα δεξιά, αυτό δεν σημαίνει ότι μια ευθεία παλινδρόμησης είναι το καλύτερο μοντέλο για τη σχέση ανάμεσα στις δύο μεταβλητές (ίσως μια καμπύλη να είναι καλύτερο μοντέλο για τη συγκεκριμένη σχέση).

10.9 Περισσότερα για το r του Pearson

Δημιουργία Πίνακα Συσχετίσεων

Ένα από τα πλεονεκτήματα των συσχετίσεων είναι ότι μπορούν να συνοψίσουν την κατεύθυνση και την ένταση των γραμμικών σχέσεων για πολλά ζεύγη μεταβλητών ταυτόχρονα. Είδαμε πώς να υπολογίζουμε έναν μεμονωμένο συντελεστή συσχέτισης· ας μάθουμε τώρα πώς να δημιουργούμε έναν πίνακα συσχετίσεων.

Χρησιμοποιώντας τη συνάρτηση select(), δημιουργήσαμε ένα νέο πλαίσιο δεδομένων που ονομάζεται Hand με μόνο μερικές από τις μεταβλητές του πλαισίου δεδομένων Fingers.

Hand <- select(Fingers, Thumb, Index, Middle, Ring, Pinkie, Height)
head(Hand)

  Thumb Index Middle Ring Pinkie  Height
1 66.00  79.0   84.0 74.0   57.0 179.070
2 64.00  73.0   80.0 75.0   62.0 164.592
3 56.00  69.0   76.0 71.0   54.0 162.560
4 58.42  76.2   91.4 76.2   63.5 177.800
5 74.00  79.0   83.0 76.0   64.0 172.720
6 60.00  64.0   70.0 65.0   58.0 172.720

Στο παρακάτω πλαίσιο κώδικα, πληκτρολογήστε τη συνάρτηση cor() όπως πριν, αλλά αυτή τη φορά αντί να βάλετε στην παρένθεση τις δύο μεταβλητές, βάλετε μόνο το όνομα του πλαισίου δεδομένων (σε αυτή την περίπτωση, χρησιμοποιήστε το Hand). Εκτελέστε την εντολή και δείτε τι συμβαίνει.

           Thumb     Index    Middle      Ring    Pinkie    Height
Thumb  1.0000000 0.7788568 0.7479010 0.6999031 0.6755136 0.3910649
Index  0.7788568 1.0000000 0.9412202 0.8820600 0.7825979 0.4974643
Middle 0.7479010 0.9412202 1.0000000 0.8945526 0.7475880 0.4737641
Ring   0.6999031 0.8820600 0.8945526 1.0000000 0.8292530 0.4953183
Pinkie 0.6755136 0.7825979 0.7475880 0.8292530 1.0000000 0.5695369
Height 0.3910649 0.4974643 0.4737641 0.4953183 0.5695369 1.0000000

Αυτό επιστρέφει έναν ολόκληρο πίνακα, όπου κάθε τιμή αντιπροσωπεύει το συντελεστή συσχέτισης (r) για το αντίστοιχο ζεύγος μεταβλητών. Είδαμε προηγουμένως μία από τις τιμές του συντελεστή (r = 0.39) — τη συσχέτιση μεταξύ του μήκους αντίχειρα και του ύψους, η οποία εμφανίζεται σε δύο διαφορετικά κελιά στον πίνακα συσχετίσεων.

Γιατί η συγκεκριμένη τιμή του συντελεστή συσχέτισης εμφανίζεται σε δύο θέσεις του πίνακα συσχετίσεων;

Οι συσχετίσεις, επειδή βασίζονται σε τυποποιημένες μεταβλητές, έχουν μια σημαντική ιδιότητα: είναι συμμετρικές. Αυτό σημαίνει ότι:

\[r(Thumb, Height) = r(Ηeight, Thumb) = 0.391\]

Με άλλα λόγια, δεν έχει σημασία ποια μεταβλητή τοποθετείται πρώτη — η συσχέτιση παραμένει η ίδια.

Επιπλέον, παρατηρήστε ότι κάθε μεταβλητή συσχετίζεται τέλεια με τον εαυτό της (r = 1). Αν ακολουθήσετε τη διαγώνιο του πίνακα συσχετίσεων (από την επάνω αριστερά γωνία προς την κάτω δεξιά), θα δείτε μια σειρά από άσσους (1.0000000).

Η Σχέση μεταξύ R² και PRE

Θυμηθείτε ότι το PRE (Αναλογική Μείωση Σφάλματος) έχει κι άλλο όνομα στη βιβλιογραφία: R² (R-squared), που διαβάζεται «R στο τετράγωνο». Ορίστε κάτι ενδιαφέρον: αν προσαρμόσετε ένα μοντέλο παλινδρόμησης, εμφανίσετε τον πίνακα της supernova(), και στη συνέχεια υπολογίσετε την τετραγωνική ρίζα του PRE, θα πάρετε το r του Pearson.

Ορίστε ο πίνακας της supernova() για το μοντέλο που προβλέπει το μήκος αντίχειρα (Thumb) από το ύψος (Height). Παρατηρήστε ότι το PRE = 0.1529.

Analysis of Variance Table (Type III SS)
Model: Thumb ~ Height

Source                 SS        df        MS        F      PRE     p
Model (error reduced)  1816.862    1      1816.862  27.984  0.1529  .0000
Error (from model)    10063.349  155        64.925
Total (empty model)   11880.211  156        76.155

Τώρα ας πάρουμε την τετραγωνική ρίζα:

\[r = \sqrt{0.1529} = 0.391\]

Αυτή είναι ακριβώς η τιμή του συντελεστή συσχέτισης που υπολογίσαμε νωρίτερα!

Χρησιμοποιήστε το παρακάτω πλαίσιο κώδικα για να υπολογίσετε την τετραγωνική ρίζα του 0.1529, και στη συνέχεια χρησιμοποιήστε τη συνάρτηση cor() για να υπολογίσετε το r του Pearson για τις δύο μεταβλητές. Ταιριάζουν τα δύο αποτελέσματα; Θα πρέπει!

Οι αναλύσεις παλινδρόμησης συχνά αναφέρουν το R². Το R² είναι απλώς ένα άλλο όνομα για το PRE όταν το σύνθετο μοντέλο συγκρίνεται με το κενό μοντέλο. Το η² (ήτα στο τετράγωνο) έχει την ίδια σημασία με το R², αλλά συνήθως χρησιμοποιείται για μοντέλα ομάδων ενώ το R² χρησιμοποιείται για μοντέλα παλινδρόμησης.

Όπως και το PRE, το r του Pearson είναι απλώς ένα στατιστικό δείγματος· αποτελεί μόνο μια εκτίμηση της πραγματικής συσχέτισης στον πληθυσμό.

Συμπληρώστε την ακόλουθη πρόταση. Αν παίρναμε ένα διαφορετικό δείγμα φοιτητών:

Δεν θα λαμβάναμε διαφορετική τιμή r επειδή αυτή είναι η τυποποιημένη κλίση, οπότε όλα τα r θα είναι ίδια.Σχεδόν σίγουρα θα είχαμε λάβει μια ελαφρώς διαφορετική εκτίμηση της πραγματικής συσχέτισης.Δεν θα λαμβάναμε διαφορετική τιμή r επειδή θα έπρεπε να είναι η ίδια με την τετραγωνική ρίζα του PRE. Το PRE δεν είναι στατιστικό δείγματος. Είναι παράμετρος πληθυσμού.

Επεξήγηση

Σωστή απάντηση: Β — Σχεδόν σίγουρα θα είχαμε λάβει μια ελαφρώς διαφορετική εκτίμηση της πραγματικής συσχέτισης.

Γιατί αυτό είναι σωστό;

Το r είναι ένα στατιστικό δείγματος

Το r του Pearson υπολογίζεται από τα δεδομένα του δείγματός μας. Επειδή διαφορετικά δείγματα από τον ίδιο πληθυσμό περιέχουν διαφορετικά άτομα, θα παράγουν ελαφρώς διαφορετικές τιμές του r.

Παράδειγμα:

Φανταστείτε ότι παίρνουμε πολλά δείγματα φοιτητών από τον ίδιο πληθυσμό:

Δείγμα	r (Thumb, Height)
Δείγμα 1	0.391
Δείγμα 2	0.385
Δείγμα 3	0.398
Δείγμα 4	0.392
Δείγμα 5	0.387

Παρατηρήστε ότι τα r διαφέρουν ελαφρώς μεταξύ των δειγμάτων. Αυτή η μεταβλητότητα ονομάζεται δειγματοληπτική μεταβλητότητα (sampling variability).

Δειγματικό στατιστικό vs Πληθυσμιακή παράμετρος:

	Δείγμα	Πληθυσμός
Συσχέτιση	r (μεταβάλλεται)	ρ (σταθερό, άγνωστο)
Τι είναι	Εκτίμηση	Πραγματική τιμή
Παράδειγμα	r = 0.391	ρ = ?

r = Η συσχέτιση που παρατηρούμε στο δείγμα μας
ρ (rho) = Η πραγματική συσχέτιση στον πληθυσμό (που δεν γνωρίζουμε)

Χρησιμοποιούμε το r για να εκτιμήσουμε το ρ.

Γιατί οι άλλες επιλογές είναι λάθος

Α. «Δεν θα λαμβάναμε διαφορετικό r επειδή αυτή είναι η τυποποιημένη κλίση, οπότε όλα τα r είναι τα ίδια» — ΛΑΘΟΣ

Αυτό είναι λάθος και δείχνει παρανόηση.

Το πρόβλημα:

Ναι, το r είναι η τυποποιημένη κλίση, αλλά αυτό δεν σημαίνει ότι όλα τα δείγματα θα έχουν το ίδιο r!

Τι σημαίνει “τυποποιημένη κλίση”;

“Τυποποιημένη” σημαίνει ότι οι μεταβλητές έχουν μετατραπεί σε τιμές z
Η κλίση του τυποποιημένου μοντέλου είναι ο συντελεστής συσχέτισης r
Αλλά διαφορετικά δείγματα θα έχουν διαφορετικές τιμές z και άρα διαφορετικό r

Γ. «Δεν θα λαμβάναμε διαφορετικό r επειδή θα έπρεπε να είναι το ίδιο με την τετραγωνική ρίζα του PRE. Το PRE δεν είναι στατιστικό δείγματος. Είναι παράμετρος πληθυσμού» — ΛΑΘΟΣ

Αυτό είναι εντελώς λάθος.

Το πρόβλημα:

Η πρώτη πρόταση είναι σωστή: $r = \sqrt{\text{PRE}}$

Αλλά η δεύτερη πρόταση είναι λάθος: Το PRE ΕΙΝΑΙ στατιστικό δείγματος, ΟΧΙ παράμετρος πληθυσμού!

Τι είναι το PRE;

\[\text{PRE} = \frac{\text{SS}_{\text{Total}} - \text{SS}_{\text{Error}}}{\text{SS}_{\text{Total}}}\]

Όλα τα SS (Sum of Squares) υπολογίζονται από τα δεδομένα του δείγματος:

$\text{SS}_{\text{Total}}$ = υπολογίζεται από το δείγμα
$\text{SS}_{\text{Error}}$ = υπολογίζεται από το δείγμα
Άρα, το PRE = υπολογίζεται από το δείγμα

Το PRE είναι στατιστικό δείγματος!

Τι θα συμβεί με διαφορετικό δείγμα;

	Δείγμα 1	Δείγμα 2
SS Total	11880.211	11654.328
SS Error	10063.349	10201.456
PRE	0.1529	0.1471
r	0.391	0.384

Και το PRE και το r αλλάζουν με διαφορετικά δείγματα!

Διάκριση: Δειγματικά στατιστικά vs Πληθυσμιακές παράμετροι

Μέτρηση	Στατιστικό δείγματος	Παράμετρος πληθυσμού
Συσχέτιση	r (μεταβάλλεται)	ρ (σταθερό)
PRE / R²	PRE ή R² (μεταβάλλεται)	Πληθυσμιακό R² (σταθερό)
Τι κάνουν	Εκτιμούν	Πραγματικές τιμές

Συμπέρασμα: Και το PRE και το r είναι στατιστικά δείγματος που μεταβάλλονται από δείγμα σε δείγμα.

Γενικό συμπέρασμα

Αν παίρναμε διαφορετικό δείγμα φοιτητών:

✓ Α: Σχεδόν σίγουρα θα λαμβάναμε ελαφρώς διαφορετικό r

✗ Β: ΟΧΙ - η τυποποίηση δεν κάνει το r σταθερό

✗ Γ: ΟΧΙ - το PRE είναι στατιστικό δείγματος και μεταβάλλεται

Βασική αρχή:

Όλα τα στατιστικά που υπολογίζονται από δεδομένα δείγματος (r, PRE, R², μέσοι όροι, τυπικές αποκλίσεις, κλπ.) μεταβάλλονται από δείγμα σε δείγμα. Αυτή η μεταβλητότητα ονομάζεται δειγματοληπτική μεταβλητότητα και είναι φυσικό και αναμενόμενο φαινόμενο.

Γιατί είναι σημαντικό αυτό;

Αβεβαιότητα: Η εκτίμησή μας (r = 0.391) έχει κάποια αβεβαιότητα
Διαστήματα εμπιστοσύνης: Χρειαζόμαστε να υπολογίσουμε διαστήματα εμπιστοσύνης για να δούμε το εύρος πιθανών τιμών
Στατιστική συμπερασματολογία: Χρησιμοποιούμε το r από το δείγμα για να συμπεράνουμε για το ρ στον πληθυσμό

Οι στατιστικοί είναι ενοχλητικοί επειδή χρησιμοποιούν τόσους πολλούς δύσκολους όρους για να εννοούν το ίδιο πράγμα. Ποια από τα παρακάτω είναι ακριβώς το ίδιο (ίδιος τύπος υπολογισμού, ίδια έννοια);

$R^2$, SS και MS$\eta^2$, $R^2$ και dfPRE, $R^2$ και $\eta^2$SS, $R^2$ και PRE

Επεξήγηση

Σωστή απάντηση: Γ — PRE, $R^2$ και $\eta^2$

Αυτοί οι τρεις όροι είναι ταυτόσημοι: Έχουν τον ίδιο τύπο υπολογισμού και εκφράζουν την ίδια έννοια — το ποσοστό της μεταβλητότητας της εξαρτημένης μεταβλητής που εξηγείται από το μοντέλο.

Γ. PRE, $R^2$ και $\eta^2$ — ΣΩΣΤΟ ✓

Ο κοινός τύπος υπολογισμού:

\[\text{PRE} = R^2 = \eta^2 = \frac{\text{SS}_{\text{Model}}}{\text{SS}_{\text{Total}}} = \frac{\text{SS}_{\text{Total}} - \text{SS}_{\text{Error}}}{\text{SS}_{\text{Total}}}\]

Η κοινή έννοια:

Και οι τρεις όροι απαντούν στην ίδια ερώτηση:

“Ποιο ποσοστό της συνολικής μεταβλητότητας εξηγείται από το μοντέλο;”

Παράδειγμα:

Για το μοντέλο Thumb ~ Height:

\[\text{PRE} = R^2 = \eta^2 = \frac{1816.862}{11880.211} = 0.1529 = 15.29\%\]

Χαρακτηριστικά:

Ίδιος τύπος: Όλοι υπολογίζονται με το ίδιο κλάσμα
Ίδια έννοια: Ποσοστό εξηγούμενης μεταβλητότητας
Ίδια τιμή: Πάντα το ίδιο αποτέλεσμα για το ίδιο μοντέλο
Ίδιο εύρος: Από 0 έως 1 (ή 0% έως 100%)
Χωρίς μονάδες μέτρησης

Διαφορετική ορολογία ανάλογα με τον σκοπό:

Όρος	Πότε χρησιμοποιείται	Περιοχή
PRE	Γενικά μοντέλα	Για διδακτικούς σκοπούς
$R^2$	Μοντέλα παλινδρόμησης	Παλινδρόμηση
$\eta^2$	Μοντέλα ομάδων	ANOVA

Γιατί οι άλλες επιλογές είναι λάθος

Α. «$R^2$, SS και MS» — ΛΑΘΟΣ

Διαφορετικοί τύποι και έννοιες:

$R^2$: Αναλογία (ποσοστό) \[R^2 = \frac{\text{SS}_{\text{Model}}}{\text{SS}_{\text{Total}}}\]
SS (Άθροισμα Τετραγώνων): Απόλυτη ποσότητα μεταβλητότητας \[\text{SS} = \sum (Y_i - \bar{Y})^2\]
MS (Μέσο Άθροισμα Τετραγώνων): Μέση μεταβλητότητα ανά βαθμό ελευθερίας \[\text{MS} = \frac{\text{SS}}{\text{df}}\]

Διαφορές:

Χαρακτηριστικό | $R^2$ | SS | MS |

|—————-|——-|—-|—-|| | Τύπος | Αναλογία | Άθροισμα | Μέσος όρος | | Μονάδες | Αμοναδικό | $\text{mm}^2$ | $\text{mm}^2$ | | Εύρος | 0 έως 1 | 0 έως ∞ | 0 έως ∞ | | Έννοια | Ποσοστό | Συνολική ποσότητα | Ποσότητα ανά df |

Συμπέρασμα: Διαφορετικοί τύποι και διαφορετικές έννοιες!

Β. «$\eta^2$, $R^2$ και df» — ΛΑΘΟΣ

Το df (βαθμοί ελευθερίας) είναι ΕΝΤΕΛΩΣ διαφορετικό:

$\eta^2$ και $R^2$: Ποσοστό εξηγούμενης μεταβλητότητας ✓
- Ίδιος τύπος ✓
- Ίδια έννοια ✓
df (degrees of freedom): Αριθμός βαθμών ελευθερίας ✗
- Διαφορετικός τύπος: $\text{df} = n - \text{παράμετροι}$
- Διαφορετική έννοια: Πόσες ανεξάρτητες πληροφορίες έχουμε
- Διαφορετικό εύρος: Θετικοί ακέραιοι (1, 2, 3, …)

Παράδειγμα:

Για το μοντέλο Thumb ~ Height:

$R^2 = \eta^2 = 0.1529$ (ποσοστό)
df (Model) = 1 (βαθμοί ελευθερίας)
df (Error) = 155 (βαθμοί ελευθερίας)

Τελείως διαφορετικά!

Δ. «SS, $R^2$ και PRE» — ΛΑΘΟΣ

Το SS είναι διαφορετικό:

$R^2$ και PRE: Αναλογίες (ποσοστά) ✓
- Ίδιος τύπος ✓
- Ίδια έννοια ✓
SS: Απόλυτη ποσότητα μεταβλητότητας ✗
- Διαφορετικός τύπος: Άθροισμα τετραγώνων
- Διαφορετική έννοια: Συνολική ποσότητα, όχι ποσοστό
- Έχει μονάδες: π.χ., $\text{mm}^2$

Σχέση:

Το SS χρησιμοποιείται για να υπολογίσουμε το $R^2$/PRE, αλλά δεν είναι το ίδιο:

\[R^2 = \text{PRE} = \frac{\text{SS}_{\text{Model}}}{\text{SS}_{\text{Total}}}\]

Το SS είναι μέρος του τύπου, όχι το αποτέλεσμα!

Παράδειγμα:

SS Model = 1816.862 mm² (απόλυτη ποσότητα)
SS Total = 11880.211 mm² (απόλυτη ποσότητα)
$R^2$ = PRE = $\frac{1816.862}{11880.211}$ = 0.1529 (αναλογία, χωρίς μονάδες)

Σύνοψη

Ταυτόσημοι όροι (ίδιος τύπος, ίδια έννοια):

✓ PRE, $R^2$ και $\eta^2$

Όλοι υπολογίζονται με: \[\frac{\text{SS}_{\text{Model}}}{\text{SS}_{\text{Total}}}\]

Όλοι μετρούν: Ποσοστό εξηγούμενης μεταβλητότητας

Σύγκριση της Προσαρμογής Τυποποιημένων και Μη Τυποποιημένων Μοντέλων Παλινδρόμησης

Μέχρι τώρα έχετε μάθει πολλά για τον συντελεστή συσχέτισης (r) που προκύπτει από το τυποποιημένο μοντέλο παλινδρόμησης. Ίσως αναρωτιέστε: Μήπως αυτό είναι ένα «καλύτερο» μοντέλο παλινδρόμησης, με την έννοια ότι εξηγεί περισσότερη μεταβλητότητα από το μη τυποποιημένο;

Με βάση τα παραπάνω διαγράμματα, ποιο μοντέλο παλινδρόμησης φαίνεται να εξηγεί περισσότερη μεταβλητότητα;

Το μη τυποποιημένοΤο τυποποιημένοΦαίνονται να εξηγούν την ίδια μεταβλητότητα

Επεξήγηση

Σωστή απάντηση: Γ — Φαίνονται να εξηγούν την ίδια μεταβλητότητα

Γιατί;

Τα δύο μοντέλα είναι μαθηματικά ισοδύναμα — απλώς εκφρασμένα σε διαφορετικές κλίμακες.

Οπτική απόδειξη:

Παρατηρήστε και στα δύο διαγράμματα:

Το σχήμα του νέφους σημείων είναι πανομοιότυπο
Η διασπορά γύρω από την ευθεία είναι η ίδια
Η ένταση της σχέσης φαίνεται ίδια

Απόδειξη:

Μοντέλο	$R^2$ / PRE	Ερμηνεία
Μη τυποποιημένο	0.1529	15.29% εξηγούμενη μεταβλητότητα
Τυποποιημένο	0.1529	15.29% εξηγούμενη μεταβλητότητα

Το ίδιο ακριβώς ποσοστό!

Τι αλλάζει η τυποποίηση;

Η τυποποίηση είναι ένας γραμμικός μετασχηματισμός:

\[z = \frac{X - \bar{X}}{s_X}\]

Τι αλλάζει: - Η κλίμακα των αξόνων (από mm/cm σε τυπικές αποκλίσεις) - Οι μονάδες της κλίσης - Ο σταθερός όρος ή τομή με τον άξονα των y (από $b_0$ σε 0)

Τι ΔΕΝ αλλάζει: - Το σχήμα της κατανομής - Η σχέση μεταξύ των μεταβλητών - Η ένταση της συσχέτισης (r) - Το ποσοστό της εξηγούμενης μεταβλητότητας ($R^2$)

Γιατί οι άλλες επιλογές είναι λάθος

Α. «Το μη τυποποιημένο» — ΛΑΘΟΣ

Μπορεί να φαίνεται πως τα σημεία είναι πιο “διασκορπισμένα” επειδή το εύρος των αξόνων είναι μεγαλύτερο (40-90 mm έναντι -2.5 έως +3 SD), αλλά αυτό είναι απλώς η κλίμακα. Η σχετική διασπορά είναι η ίδια.

Β. «Το τυποποιημένο» — ΛΑΘΟΣ

Το γεγονός ότι το τυποποιημένο μοντέλο μας δίνει το r του Pearson δεν το κάνει να εξηγεί περισσότερη μεταβλητότητα. Το r είναι απλώς η κλίση του τυποποιημένου μοντέλου, και:

\[r^2 = R^2 = 0.391^2 = 0.1529\]

Το ίδιο $R^2$ και για τα δύο!

Συμπέρασμα

Χαρακτηριστικό	Μη τυποποιημένο	Τυποποιημένο
Κλίση	0.37 mm/cm	0.39 SD/SD
Σταθερός όρος	-3.33 mm	0
$R^2$	0.1529	0.1529
Εξηγούμενη μεταβλητότητα	15.29%	15.29%

Βασική αρχή:

Η τυποποίηση αλλάζει την κλίμακα μέτρησης αλλά όχι την υποκείμενη σχέση. Το $R^2$ παραμένει ακριβώς το ίδιο!

Έχουμε παραθέσει παρακάτω τους δύο πίνακες ANOVA. Συγκρίνετέ τους προσεκτικά για να δείτε τι είναι κοινό και τι διαφέρει μεταξύ των δύο μοντέλων.

Μη τυποποιημένο Μοντέλο

Analysis of Variance Table (Type III SS)
Model: Thumb ~ Height

                               SS  df       MS      F    PRE     p
----- --------------- | --------- --- -------- ------ ------ -----
Model (error reduced) |  1816.862   1 1816.862 27.984 0.1529 .0000
Error (from model)    | 10063.349 155   64.925
----- --------------- | --------- --- -------- ------ ------ -----
Total (empty model)   | 11880.211 156   76.155 

Τυποποιημένο Μοντέλο

Analysis of Variance Table (Type III SS)
Model: zThumb ~ zHeight

                             SS  df     MS      F    PRE     p
----- --------------- | ------- --- ------ ------ ------ -----
Model (error reduced) |  23.857   1 23.857 27.984 0.1529 .0000
Error (from model)    | 132.143 155  0.853
----- --------------- | ------- --- ------ ------ ------ -----
Total (empty model)   | 156.000 156  1.000

Παρατηρήστε ότι η τιμή του στατιστικού PRE για το Height_model και το zHeight_model είναι ίδια. Γιατί πιστεύετε ότι συμβαίνει αυτό;

Επίσης, παρατηρήστε ότι τα διάφορα αθροίσματα τετραγώνων (SS Total, SS Model, SS Error) διαφέρουν μεταξύ των δύο μοντέλων. Γιατί νομίζετε ότι συμβαίνει αυτό;

Η προσαρμογή των μοντέλων (όπως αξιολογείται μέσω των PRE και F) είναι πανομοιότυπη, επειδή το μόνο που αλλάξαμε είναι η μονάδα μέτρησης των εξαρτημένων και ανεξάρτητων μεταβλητών. Ο μετασχηματισμός σε τιμές z δεν αλλάζει τη μορφή της διμεταβλητής κατανομής, όπως φαίνεται στο διάγραμμα διασποράς· απλώς μετατρέπει την κλίμακα και στους δύο άξονες από εκατοστά και χιλιοστά σε τυπικές αποκλίσεις.

Σε αντίθεση με τις τιμές PRE και F, που είναι πηλίκα και αναλογίες, τα αθροίσματα τετραγώνων (SS) εκφράζονται στις μονάδες μέτρησης των δεδομένων. Επομένως, αν μετατρέψουμε τα χιλιοστά (για το μήκος του αντίχειρα) και τα εκατοστά (για το ύψος) σε μέτρα, πόδια ή τυπικές αποκλίσεις, οι τιμές των SS θα αλλάξουν ώστε να αντανακλούν αυτές τις νέες μονάδες μέτρησης.

10.10 Ερμηνεία της Κλίσης μιας Ευθείας Παλινδρόμησης με Τυχαίο Ανακάτεμα

Επανεξέταση της Προσομοίωσης υπό το Κενό Μοντέλο

Στο Κεφάλαιο 8, επανεξετάσαμε τα δεδομένα της μελέτης των φιλοδωρημάτων. Μοντελοποιήσαμε τα δεδομένα χρησιμοποιώντας ένα μοντέλο δύο ομάδων και διαπιστώσαμε ότι τα τραπέζια που έλαβαν λογαριασμό με χαμογελαστό προσωπάκι άφησαν 6 ποσοστιαίες μονάδες μεγαλύτερο φιλοδώρημα, κατά μέσο όρο, από εκείνα που δεν έλαβαν.

Παρόλο που παρατηρήσαμε ένα πλεονέκτημα 6 ποσοστιαίων μονάδων για το χαμογελαστό προσωπάκι στα δεδομένα μας, αυτό που θέλουμε να γνωρίζουμε στην πραγματικότητα είναι: ποιο είναι το πλεονέκτημα, αν υπάρχει, στη Διαδικασία Παραγωγής των Δεδομένων (ΔΠΔ); Μήπως το πλεονέκτημα των 6 μονάδων που παρατηρήσαμε θα μπορούσε να έχει παραχθεί τυχαία από μια ΔΠΔ στην οποία δεν υπάρχει πλεονέκτημα (δηλαδή, ένα μοντέλο στο οποίο $\beta_1$ = 0);

Μπορούμε να θέσουμε μια αντίστοιχη ερώτηση και στο πλαίσιο ένος μοντέλου παλινδρόμησης, στο οποίο το $\beta_1$ είναι η κλίση μιας ευθείας αντί για μια διαφορά ομάδων. Όταν προσαρμόσαμε το μοντέλο παλινδρόμησης της Height στην Thumb, η εκτίμηση της πραγματικής κλίσης ($\beta_1$) ήταν 0.378. Αλλά μήπως αυτή η σχέση που παρατηρήσαμε στα δεδομένα μας θα μπορούσε να έχει παραχθεί από μια ΔΠΔ στην οποία $\beta_1$ = 0;

Αν $\beta_1 = 0$, ποιο είναι το πραγματικό μοντέλο της ΔΠΔ;

$Y_i = 0 + \beta_1 X_i + \varepsilon_i$$Y_i = \beta_0 + X_i + \varepsilon_i$$Y_i = \beta_0 + \varepsilon_i$, το ίδιο με το κενό μοντέλο$Y_i = \beta_0 + \beta_1 X_i + \varepsilon_i$, το ίδιο με το μοντέλο Height

Επεξήγηση

Σωστή απάντηση: Γ — $Y_i = \beta_0 + \varepsilon_i$, το ίδιο με το κενό μοντέλο

Γιατί;

Όταν $\beta_1 = 0$, αυτό σημαίνει ότι η X δεν έχει καμία επίδραση στην Y. Ας δούμε τι συμβαίνει στην εξίσωση παλινδρόμησης:

Ξεκινάμε με το γενικό μοντέλο:

\[Y_i = \beta_0 + \beta_1 X_i + \varepsilon_i\]

Αντικαθιστούμε $\beta_1 = 0$:

\[Y_i = \beta_0 + 0 \times X_i + \varepsilon_i\]

Απλοποιούμε:

\[Y_i = \beta_0 + \varepsilon_i\]

Το $X_i$ εξαλείφεται από την εξίσωση! Αυτό ακριβώς είναι το κενό μοντέλο.

Γ. «$Y_i = \beta_0 + \varepsilon_i$, το ίδιο με το κενό μοντέλο» — ΣΩΣΤΟ ✓

Αυτή είναι η σωστή απάντηση.

Τι σημαίνει το κενό μοντέλο;

Το κενό μοντέλο λέει:

“Η καλύτερη πρόβλεψη για την Y είναι ο μέσος όρος της, ανεξάρτητα από την τιμή της X.”

Μαθηματικά: \[Y_i = \beta_0 + \varepsilon_i\]

όπου: - $\beta_0$ = ο μέσος όρος του Y, $\bar{Y}$

$\varepsilon_i$ = η απόκλιση της $Y_i$ από τον μέσο όρο

Στο παράδειγμά μας (Thumb ~ Height):

Αν $\beta_1 = 0$:

Το ύψος δεν επηρεάζει το μήκος αντίχειρα
Η καλύτερη πρόβλεψη για το μήκος αντίχειρα είναι απλώς ο μέσος όρος του
Δεν κερδίζουμε τίποτα από το να γνωρίζουμε το ύψος

Παράδειγμα:

Αν $\bar{Y}_{\text{Thumb}} = 60.6$ mm: \[\hat{Y}_i = 60.6 + 0\]

Για όλους, ανεξάρτητα από το ύψος τους:

Άτομο με ύψος 165 cm → Πρόβλεψη: 60.6 mm
Άτομο με ύψος 180 cm → Πρόβλεψη: 60.6 mm
Άτομο με ύψος 150 cm → Πρόβλεψη: 60.6 mm

Η πρόβλεψη είναι πάντα ο μέσος όρος!

Γιατί οι άλλες επιλογές είναι λάθος

Α. «$Y_i = 0 + \beta_1 X_i + \varepsilon_i$» — ΛΑΘΟΣ

Αυτό έχει δύο προβλήματα:

Εξακολουθεί να περιλαμβάνει το $\beta_1 X_i$:
- Αν $\beta_1 = 0$, τότε $\beta_1 X_i = 0 \times X_i = 0$
- Άρα αυτός ο όρος πρέπει να εξαλειφθεί, όχι να παραμείνει
To $\beta_0$ = 0:
- Ακόμη και αν to $\beta_1 = 0$, ο σταθερός όρος $\beta_0$ παραμένει στο μοντέλο
- Το $\beta_0$ είναι ο μέσος όρος της Y

Β. «$Y_i = \beta_0 + X_i + \varepsilon_i$» — ΛΑΘΟΣ

Αυτό υποθέτει ότι η κλίση είναι 1, όχι 0!

Το πρόβλημα:

Η εξίσωση $Y_i = \beta_0 + X_i + \varepsilon_i$ σημαίνει:

\[Y_i = \beta_0 + 1 \times X_i + \varepsilon_i\]

Άρα η κλίση είναι 1, όχι 0!

Τι σημαίνει κλίση = 1;

Για κάθε 1 μονάδα αύξηση στην X, η Y αυξάνεται κατά 1 μονάδα
Αυτό δεν είναι το κενό μοντέλο — υπάρχει σχέση!

Σύγκριση:

Κλίση	Εξίσωση	Σημασία
$\beta_1 = 0$	$Y_i = \beta_0 + \varepsilon_i$	Καμία σχέση (κενό μοντέλο)
$\beta_1 = 1$	$Y_i = \beta_0 + X_i + \varepsilon_i$	Ισχυρή σχέση 1:1

Δ. «$Y_i = \beta_0 + \beta_1 X_i + \varepsilon_i$, το ίδιο με το μοντέλο της Height» — ΛΑΘΟΣ

Αυτό είναι το γενικό μοντέλο, όχι το κενό μοντέλο!

Συμπέρασμα

Αν $\beta_1 = 0$, το πραγματικό μοντέλο της ΔΠΔ είναι:

\[Y_i = \beta_0 + \varepsilon_i\]

Αυτό είναι το κενό μοντέλο.

Τι σημαίνει αυτό;

H X δεν έχει προβλεπτική ισχύ για την Y
Η καλύτερη πρόβλεψη για την Y είναι πάντα ο μέσος όρος της
Η γνώση της δεν μειώνει το σφάλμα πρόβλεψης
Το PRE = $R^2$ = 0 (καμία εξηγούμενη μεταβλητότητα)

Στο πλαίσιο του τυχαίου ανακατέματος (shuffling):

Όταν χρησιμοποιούμε τη συνάρτηση shuffle() για να ανακατέψουμε τα δεδομένα:

Δημιουργούμε δεδομένα όπου $\beta_1 = 0$ (κενό μοντέλο)
Προσομοιώνουμε έναν κόσμο χωρίς σχέση μεταξύ X και Y
Ελέγχουμε αν η παρατηρούμενη κλίση (π.χ., 0.37) θα μπορούσε να προέλθει από τέτοιον κόσμο

Βασική αρχή:

Όταν η κλίση είναι μηδέν ($\beta_1 = 0$), το μοντέλο ισοδυναμεί με το κενό μοντέλο — δεν υπάρχει σχέση μεταξύ των μεταβλητών, και η καλύτερη πρόβλεψη είναι απλώς ο μέσος όρος.

Μπορούμε να θέσουμε αυτή την ερώτηση χρησιμοποιώντας τη συνάρτηση shuffle() για να προσομοιώσουμε μια ΔΠΔ στην οποία το κενό μοντέλο είναι αληθές. Αυτή τη φορά, αντί να ανακατεύουμε σε ποια κατάσταση βρίσκονται τα τραπέζια, θα ανακατέψουμε μία από τις δύο μεταβλητές του μοντέλου μας, την Thumb ή την Height. Στην περίπτωση αυτή, δεν έχει πραγματικά σημασία ποια θα ανακατέψουμε τυχαία· θα μπορούσαμε ακόμη και να ανακατέψουμε και τις δύο μεταβλητές. Γενικά, είναι προτιμότερο να ανακατεύουμε τις τιμές της εξαρτημένης μεταβλητής.

Ανακατεύοντας τυχαία μία από αυτές τις μεταβλητές, προσομοιώνουμε μια ΔΠΔ στην οποία δεν υπάρχει απολύτως καμία σχέση μεταξύ των δύο μεταβλητών, και στην οποία οποιαδήποτε εμφανής σχέση που παρουσιάζεται θα μπορούσε να οφείλεται μόνο στην τυχαιότητα, και όχι σε μια πραγματική σχέση στη ΔΠΔ. Αν η σχέση στα δεδομένα μας ήταν πραγματική, το τυχαίο ανακάτεμα την εξαλείφει, και δεν είναι πια πραγματική!

Ας το δούμε αυτό διαγραμματικά. Ο παρακάτω κώδικας δημιουργεί ένα διάγραμμα διασποράς της Thumb με την Height μαζί με την ευθεία παλινδρόμησης που προσαρμόζεται βέλτιστα στα δεδομένα. Προσθέσαμε μια επιπλέον γραμμή κώδικα (gf_labs()) που εμφανίζει την τιμή της κλίσης της ευθείας στον τίτλο του διαγράμματος.

sample_b1 <- b1(Thumb ~ Height, data = Fingers)

gf_point(Thumb ~ Height, data = Fingers) %>%
  gf_lm(color = "firebrick") %>%
  gf_labs(title = paste("Στα Δεδομένα / b1 =", 
                        round(b1(Thumb ~ Height, data = Fingers), digits = 3)))

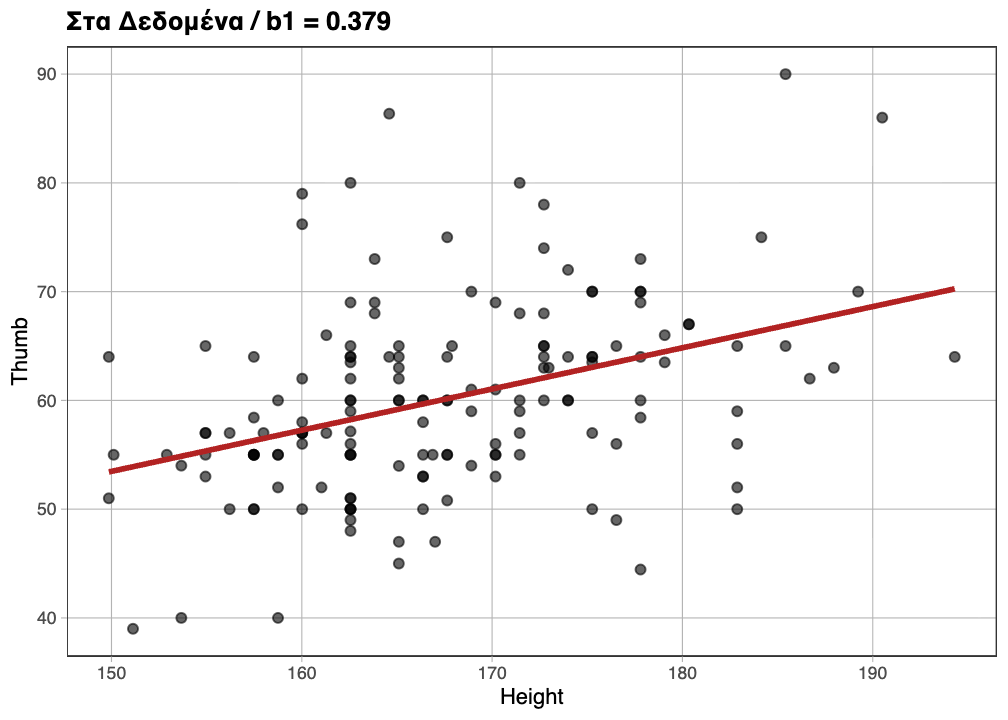
Ας εξετάσουμε τώρα τι συμβαίνει αν ανακατέψουμε τυχαία τις τιμές της μεταβλητής Thumb πριν σχεδιάσουμε το διάγραμμα και την ευθεία βέλτιστης προσαρμογής. Για να το πετύχουμε αυτό, προσθέτουμε μία γραμμή κώδικα αμέσως πριν την εντολή gf_point(), η οποία δημιουργεί μια νέα μεταβλητή (ShuffThumb) με τις τυχαία ανακατεμένες τιμές, και κατόπιν δημιουργούμε το διάγραμμα διασποράς της ShuffThumb με την Height.

Fingers$ShuffThumb <- shuffle(Fingers$Thumb)
shuffled_b1 <- b1(ShuffThumb ~ Height, data = Fingers)

gf_point(ShuffThumb ~ Height, data = Fingers) %>%
   gf_lm(color = "purple") %>%
   gf_labs(title=paste("Στα Ανακατεμένα Δεδομένα / b1 = ", round(shuffled_b1,digits=2)))

Προσθέσαμε τον κώδικα στο παρακάτω πλαίσιο, και τροποποιήσαμε επίσης την εντολή gf_labs() ώστε ο τίτλος του διαγράμματος να είναι «Στα Ανακατεμένα Δεδομένα» αντί για «Στα Δεδομένα». Εκτελέστε τον κώδικα και ελέγξτε αν το αποτέλεσμα είναι αυτό που περιμένατε. Δοκιμάστε να τον εκτελέσετε αρκετές φορές και παρατηρήστε τις αλλαγές που προκύπτουν.

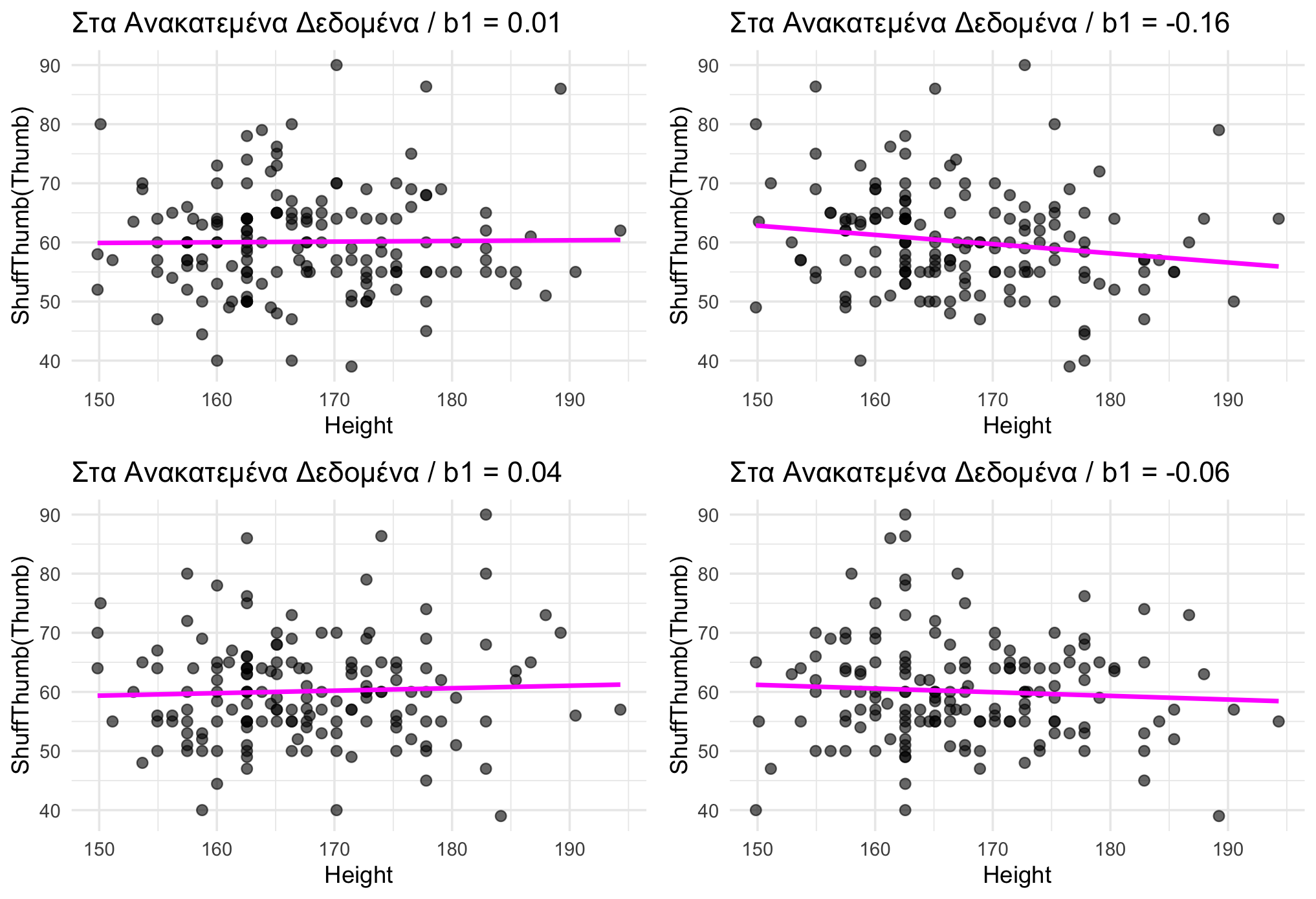
Πώς περιμένετε να μοιάζει αντίστοιχα το διάγραμμα διασποράς της Thumb με την ShuffleHeight;

Παρατηρήστε ότι οι τιμές του $b_1$ διαφέρουν κάθε φορά που εκτελείτε τον κώδικα, αλλά τείνουν να είναι κοντά στο μηδέν—είτε ελαφρώς αρνητικές είτε ελαφρώς θετικές. Αυτό είναι αναμενόμενο, διότι γνωρίζουμε ότι η πραγματική τιμή του $b_1$ σε αυτή την περίπτωση είναι 0. Πώς το γνωρίζουμε; Επειδή με το τυχαίο ανακάτεμα μίας από τις δύο μεταβλητές, οποιαδήποτε σχέση μεταξύ της Thumb και της Height οφείλεται πλέον καθαρά στην τύχη.

Αντί να δημιουργούμε διαγράμματα, μπορούμε να υπολογίσουμε απευθείας την τιμή του $b_1$ χρησιμοποιώντας τη συνάρτηση b1() σε συνδυασμό με τη συνάρτηση shuffle():

b1(shuffle(Thumb) ~ Height, data = Fingers)

Στο παρακάτω πλαίσιο, εκτελέστε αυτή την εντολή 10 φορές για να δημιουργήσετε μια λίστα με 10 τιμές του $b_1$.

Παρακάτω παρουσιάζονται οι 10 τιμές $b_1$ που δημιουργήσαμε (η δική σας λίστα θα είναι διαφορετική, καθώς κάθε τιμή προκύπτει από ένα νέο τυχαίο ανακάτεμα):

            b1
1  -0.01410685
2   0.04121492
3   0.15122051
4   0.02399357
5   0.07455574
6   0.09656436
7  -0.01578013
8  -0.02267853
9  -0.20136042
10 -0.05948981

Όπως κάναμε και στη μελέτη των φιλοδωρημάτων, μπορούμε να χρησιμοποιήσουμε αυτές τις τιμές του $b_1$ που προέκυψαν από τυχαία ανακατέματα των δεδομένων για να αξιολογήσουμε την τιμή $b_1$ που παρατηρήσαμε στα δεδομένα μας (0.378) σε σχέση με το τι θα αναμέναμε να συμβεί στην τύχη. Παρακάτω, έχουμε ταξινομήσει τις τιμές αυτές σε αύξουσα σειρά (από τη μικρότερη στη μεγαλύτερη) ώστε να διευκολυνθεί η σύγκριση με το $b_1$ του δείγματός μας.

            b1
1  -0.20136042
2  -0.05948981 
3  -0.02267853
4  -0.01578013
5  -0.01410685 
6   0.02399357
7   0.04121492
8   0.07455574
9   0.09656436
10  0.15122051

Όπως παρατηρείτε, οι τυχαία δημιουργημένες τιμές $b_1$ κατανέμονται συμμετρικά γύρω από το μηδέν—περίπου οι μισές είναι αρνητικές και οι μισές θετικές. Αυτό είναι αναμενόμενο, αφού η πραγματική παράμετρος του πληθυσμού $(\beta_1)$ είναι ίση με 0. Καμία από αυτές τις τιμές $b_1$ δεν προσεγγίζει την τιμή που παρατηρήσαμε στο δείγμα μας (0.378).

Τι σημαίνει αυτό;

Το κενό μοντέλο θα μπορούσε εύκολα να δημιουργήσει τιμές $b_1$ τόσο υψηλές όσο αυτή του δείγματός μας.Το κενό μοντέλο δεν θα μπορούσε εύκολα να δημιουργήσει τιμές $b_1$ τόσο υψηλές όσο αυτή του δείγματός μας.Το μοντέλο της Height δεν θα μπορούσε εύκολα να δημιουργήσει τιμές $b_1$ τόσο υψηλές όσο αυτή του δείγματός μας.Το δείγμα μας προήλθε από μια τυχαία ΔΠΔ επειδή η συνάρτηση shuffle() μπορεί να δημιουργήσει διαγράμματα διασποράς τυχαίων δεδομένων.

Επεξήγηση

Σωστή απάντηση: Β — Το κενό μοντέλο δεν θα μπορούσε εύκολα να δημιουργήσει τιμές $b_1$ τόσο υψηλές όσο αυτή του δείγματός μας.

Τι παρατηρήσαμε;

Από τα 10 τυχαία ανακατέματα που κάναμε:

Οι τιμές $b_1$ κυμαίνονταν από -0.20 έως +0.15
Όλες οι τιμές ήταν κοντά στο μηδέν
Περίπου οι μισές ήταν αρνητικές και οι μισές θετικές
Καμία δεν πλησίασε το 0.378 (η τιμή που παρατηρήσαμε στα πραγματικά δεδομένα)

Τι σημαίνει αυτό;

Το κενό μοντέλο ($\beta_1 = 0$) υποθέτει ότι δεν υπάρχει σχέση μεταξύ Height και Thumb. Όταν προσομοιώνουμε αυτό το μοντέλο με τυχαία ανακατέματα:

Δημιουργούμε δεδομένα χωρίς σχέση — Η shuffle() σπάει οποιαδήποτε υπάρχουσα σχέση
Υπολογίζουμε το $b_1$ σε αυτά τα ανακατεμένα δεδομένα — Αυτό μας δείχνει τι τιμές $b_1$ θα παίρναμε από την τύχη και μόνο
Συγκρίνουμε με το δειγματικό μας $b_1$ (0.378) — Αν το δειγματικό $b_1$ είναι πολύ μεγαλύτερο από τις τυχαίες τιμές, τότε δεν προέρχεται από την τύχη

Γιατί η Β είναι η σωστή απάντηση;

Το δειγματικό μας $b_1 = 0.378$ είναι πολύ μεγαλύτερο από οποιαδήποτε τιμή που δημιουργήθηκε από το κενό μοντέλο:

Πηγή	Τιμή $b_1$	Σύγκριση
Μέγιστη τυχαία τιμή	0.15	Η μεγαλύτερη που είδαμε
Δειγματική τιμή	0.378	2.5× μεγαλύτερη!

Συμπέρασμα:

Το κενό μοντέλο (όπου $\beta_1 = 0$) δεν θα μπορούσε εύκολα να παράγει μια τιμή $b_1$ τόσο υψηλή όσο το 0.378. Αυτό υποδηλώνει ότι η παρατηρούμενη σχέση μεταξύ Height και Thumb δεν είναι τυχαία—πιθανότατα υπάρχει πραγματική σχέση στη ΔΠΔ.

Γιατί οι άλλες επιλογές είναι λάθος;

Α. «Το κενό μοντέλο θα μπορούσε εύκολα να δημιουργήσει τιμές $b_1$ τόσο υψηλές όσο αυτή του δείγματός μας» — ΛΑΘΟΣ

Γιατί είναι λάθος:

Κανένα από τα 10 ανακατέματα δεν έδωσε $b_1$ κοντά στο 0.378
Η μέγιστη τιμή ήταν 0.15, που είναι λιγότερο από το μισό του 0.378
Αυτό δείχνει ότι το κενό μοντέλο ΔΕΝ παράγει εύκολα τέτοιες υψηλές τιμές

Αν αυτή η επιλογή ήταν σωστή:

Θα βλέπαμε πολλές τυχαίες τιμές $b_1$ κοντά στο 0.378
Θα σημαίνε ότι η παρατηρούμενη σχέση θα μπορούσε να είναι τυχαία
Αλλά δεν το είδαμε αυτό!

Γ. «Το μοντέλο της Height δεν θα μπορούσε εύκολα να δημιουργήσει τιμές $b_1$ τόσο υψηλές όσο αυτή του δείγματός μας» — ΛΑΘΟΣ

Γιατί είναι λάθος:

Αυτή η πρόταση δεν έχει νόημα γιατί:

Το μοντέλο της Height ΔΕΝ το προσομοιώνουμε — Προσομοιώνουμε το κενό μοντέλο
Το μοντέλο της Height ΕΙΝΑΙ το μοντέλο που έδωσε $b_1 = 0.378$ — Το προσαρμόσαμε στα πραγματικά δεδομένα!
Δεν έχει νόημα να ρωτάμε αν το μοντέλο της Height μπορεί να δημιουργήσει το δικό του $b_1$ — Προφανώς μπορεί, αφού το έδωσε!

Τι πραγματικά συγκρίνουμε:

Μοντέλο	Τι κάνουμε	$b_1$ που δίνει
Κενό μοντέλο	Προσομοιώνουμε με την `shuffle()`	~0 (π.χ., -0.20 έως 0.15)
Μοντέλο της `Height`	Προσαρμόζουμε στα δεδομένα	0.378

Η ερώτηση που απαντάμε:

Θα μπορούσε το κενό μοντέλο (όχι το μοντέλο της Height) να δημιουργήσει το $b_1 = 0.378$ που παρατηρήσαμε;

Δ. «Το δείγμα μας προήλθε από μια τυχαία ΔΠΔ επειδή η συνάρτηση shuffle() μπορεί να δημιουργήσει διαγράμματα διασποράς τυχαίων δεδομένων» — ΛΑΘΟΣ

Γιατί είναι λάθος:

Αυτή η πρόταση έχει αντίστροφη λογική!

Η σωστή λογική:

Η shuffle() δημιουργεί ΤΥΧΑΙΑ δεδομένα — Προσομοιώνει έναν κόσμο χωρίς σχέση
Τα δεδομένα μας δεν μοιάζουν με τα τυχαία — Το $b_1 = 0.378$ είναι πολύ μεγαλύτερο από τις τυχαίες τιμές
Άρα, τα δεδομένα μας ΔΕΝ προέρχονται από τυχαία ΔΠΔ — Πιθανότατα υπάρχει πραγματική σχέση

Το λάθος σκεπτικό της Δ:

Η επιλογή Δ λέει: “Επειδή μπορούμε να δημιουργήσουμε τυχαία διαγράμματα, τα δεδομένα μας είναι τυχαία”

Δεν έχει νόημα!

Η σωστή ερμηνεία:

Χρησιμοποιούμε τη shuffle() για να δούμε πώς θα έμοιαζε η τύχη. Επειδή τα δεδομένα μας ΔΕΝ μοιάζουν με αυτό, συμπεραίνουμε ότι δεν προέρχονται από την τύχη.

Συνοψίζοντας

Τι κάναμε:

Προσαρμόσαμε το μοντέλο Thumb ~ Height → $b_1 = 0.378$
Προσομοιώσαμε το κενό μοντέλο με shuffle() → $b_1 \approx 0$ (εύρος: -0.20 έως 0.15)
Συγκρίναμε: 0.378 >> 0.15

Συμπέρασμα:

Το κενό μοντέλο (χωρίς σχέση) δεν θα μπορούσε εύκολα να δημιουργήσει τιμές $b_1$ τόσο υψηλές όσο αυτή που παρατηρήσαμε (0.378). Αυτό αποτελεί ισχυρή ένδειξη ότι υπάρχει πραγματική σχέση μεταξύ ύψους και μήκους αντίχειρα.

Επόμενο βήμα:

Για να είμαστε πιο σίγουροι, θα πρέπει να κάνουμε περισσότερα ανακατέματα (π.χ., 1000 ή 10000) για να δούμε αν ποτέ το κενό μοντέλο δημιουργεί τιμές κοντά στο 0.378.

10.11 Περιορισμοί

Η παλινδρόμηση και η συσχέτιση είναι ισχυρά εργαλεία για τη μοντελοποίηση σχέσεων μεταξύ μεταβλητών. Ωστόσο, το καθένα πρέπει να χρησιμοποιείται με σύνεση. Είναι σημαντικό να ερμηνεύουμε πάντα τα ευρήματα μέσα στο πλαίσιο της εκάστοτε έρευνας, και να χρησιμοποιούμε όλα όσα ξέρουμε για αυτό το πλαίσιο ώστε να εξάγουμε λογικά συμπεράσματα με βάση τα δεδομένα.

Η Συσχέτιση Δεν Συνεπάγεται Αιτιότητα

Το σημαντικότερο που χρειάζεται να έχουμε κατά νου είναι ότι η συσχέτιση δεν συνεπάγεται απαραίτητα αιτιότητα, κάτι που ίσως έχετε ξανακούσει. Το γεγονός ότι μια ανεξάρτητη και μια εξαρτημένη μεταβλητή συσχετίζονται δεν σημαίνει απαραίτητα ότι κατανοούμε τι προκαλεί αυτή τη μεταβλητότητα. Και από αυτή την άποψη, η παλινδρόμηση δε διαφέρει από τη συσχέτιση.

Υπάρχουν πολλά τέτοια παραδείγματα. Το μέγεθος παπουτσιού των παιδιών συσχετίζεται με τις επιδόσεις τους σε ένα τεστ γραμματικής, αλλά καμία μεταβλητή δεν προκαλεί την άλλη. Η αύξηση της ηλικίας του παιδιού, μια συγχυτική μεταβλητή (confounding variable), είναι αυτή που εξηγεί και το μέγεθος του παπουτσιού και την επίδοση στο τεστ.

Επίσης, έχετε υπόψη ότι μια σχέση μπορεί να είναι αμφίδρομη, που σημαίνει ότι κάθε μεταβλητή έχει αιτιώδη επίδραση στην άλλη. Οι δεξιότητες ανάγνωσης και γραφής τείνουν να συσχετίζονται έντονα. Μπορεί η εξάσκηση στην ανάγνωση να βελτιώσει την ικανότητα γραφής. Αλλά είναι επίσης εύλογο ότι η εξάσκηση στη γραφή μπορεί να βοηθήσει τους μαθητές να βελτιώσουν την ικανότητά τους στην ανάγνωση.

Όπως σε όλα τα πράγματα, χρειάζεται να ερμηνεύουμε στατιστικά μεγέθη όπως ο συντελεστής συσχέτισης και η κλίση της ευθείας παλινδρόμησης με βάση την κοινή λογική. Η τάση να φοράμε ελαφρά ρούχα συσχετίζεται με υψηλότερες θερμοκρασίες. Σε αυτή την περίπτωση η σχέση είναι πραγματική, αλλά η αιτιώδης κατεύθυνση πρέπει να ερμηνευτεί με σκεπτικισμό. Η αύξηση της θερμοκρασίας μπορεί πράγματι να προκαλέσει τους ανθρώπους να βγάλουν τα ρούχα τους. Αλλά το να βγάλουμε τα ρούχα μας δεν πρόκειται να προκαλέσει αύξηση της θερμοκρασίας.

Το μήκος αντίχειρα μετρημένο σε χιλιοστά θα συσχετίζεται τέλεια με το μήκος αντίχειρα μετρημένο σε εκατοστά. Τα σημεία στο διάγραμμα διασποράς θα είναι απόλυτα ευθυγραμμισμένα. Αλλά η ανακάλυψη αυτής της σχέσης μας φέρνει πιο κοντά στην κατανόηση της ΔΠΔ που παράγει τη μεταβλητότητα στο μήκος του αντίχειρα; Φυσικά όχι.

Ας υποθέσουμε ότι κάναμε μια έρευνα και διαπιστώσαμε ότι ο χρόνος που οι φοιτητές αφιέρωσαν στη μελέτη ενός μαθήματος συσχετίζεται θετικά με τη βαθμολογία τους στις τελικές εξετάσεις του μαθήματος. Με βάση τα αποτελέσματα της έρευνας, μπορούμε να συμπεράνουμε ότι η αφιέρωση περισσότερου χρόνου για μελέτη προκάλεσε τη βελτίωση στη βαθμολογία; Γιατί ναι ή γιατί όχι;

Η διαπίστωση μιας σχέσης αιτίας - αποτελέσματος και ο έλεγχος πιθανών συγχυτικών μεταβλητών δεν είναι εφικτό να γίνουν μόνο μέσω της στατιστικής ανάλυσης. Η στατιστική μπορεί να βοηθήσει, και μια συσχέτιση μπορεί σίγουρα να υποδηλώνει την ύπαρξη μιας αιτιώδους σχέσης. Αλλά ο σχεδιασμός της έρευνας είναι απαραίτητο να ληφθεί υπόψη. Η τυχαία ανάθεση ισοδύναμων υποκειμένων σε ομάδες που συμμετείχαν και δεν συμμετείχαν σε κάποια παρέμβαση είναι συχνά απαραίτητη για να διαπιστώσουμε αν μια συγκεκριμένη σχέση είναι αιτιώδης ή όχι.

Είναι Όλες οι Γραμμές Ευθείες;

Ένα άλλο σημείο που πρέπει να επισημάνουμε είναι ότι τα μοντέλα που εξετάσαμε σε αυτό το κεφάλαιο είναι γραμμικά μοντέλα. Προσαρμόζουμε μια ευθεία γραμμή σε ένα διάγραμμα διασποράς, και στη συνέχεια εξετάζουμε πόσο καλά ταιριάζει (προσαρμόζεται) στα δεδομένα μας μετρώντας τα υπόλοιπα γύρω από την ευθεία παλινδρόμησης.

Αλλά μερικές φορές μια ευθεία γραμμή δεν θα είναι πολύ καλό μοντέλο για τη σχέση μεταξύ δύο μεταβλητών.

Παρατηρήστε το παρακάτω διάγραμα που δείχνει τη σχέση του σωματικού βάρους με τον κίνδυνο θανάτου. Το χαμηλό και το υψηλό σωματικό βάρος αυξάνουν τον κίνδυνο θανάτου, ενώ το να βρίσκεται κανείς στη μέση μειώνει αυτόν τον κίνδυνο.

Αν αγνοούσαμε το σχήμα της παραπάνω σχέσης και προσαρμόζαμε μια ευθεία παλινδρόμησης στα δεδομένα, η ευθεία αυτή πιθανότατα θα ήταν σχεδόν επίπεδη, υποδεικνύοντας την απουσία γραμμικής σχέσης. Αλλά αν το κάναμε αυτό θα μας διέφευγε μια σημαντική και συστηματική καμπυλόγραμμη σχέση.

Πριν προσαρμόσετε ένα γραμμικό μοντέλο παλινδρόμησης, εξετάστε τη σχέση και δείτε αν μια γραμμική εξίσωση θα ήταν ένα λογικό μοντέλο. Αν δεν είναι, σκεφτείτε ένα διαφορετικό μοντέλο. Υπάρχουν πολλά άλλα χρήσιμα μοντέλα πέρα από την απλή ευθεία.

Οι Ευθείες Παλινδρόμησης Προεκτείνονται Απεριόριστα;

Comic about regression lines — Σχήμα 10.25

Πηγή: http://smbc-comics.com/comic/2011-08-05

Τέλος, υπάρχει το πρόβλημα της προέκτασης μιας ευθείας παλινδρόμησης. Έχουμε ήδη επισημάνει από την παλινδρόμησή της Thumbστην Height ότι, σύμφωνα με το μοντέλο, κάποιος που έχει ύψος 0 εκατοστά θα έχει μήκος αντίχειρα -3.33 χιλιοστά! Προφανώς, το μοντέλο παλινδρόμησης έχει νόημα μόνο εντός ενός συγκεκριμένου εύρους τιμών, και είναι επικίνδυνο να προεκτείνουμε την ευθεία πέρα από τις περιοχές όπου έχουμε αρκετά δεδομένα.

Γενικά, η κοινή λογική και η προσεκτική κατανόηση των μεθόδων έρευνας είναι απαραίτητες για την ερμηνεία οποιουδήποτε στατιστικού μοντέλου.

10.12 Ασκήσεις Επανάληψης Κεφαλαίου 10

Το πλαίσιο δεδομένων NBAPlayers2011 περιλαμβάνει δεδομένα από την κανονική σεζόν 2010-2011 για 176 παίκτες μπάσκετ του NBA.

head(select(NBAPlayers2011, Age, Games, Starts, Mins, MinPerGame, 
            FGMade, FGPct, FGMade, FG3Pct, FTMade, FTPct, 
            Assists, Fouls, Points))

Μεταβλητές:

Age — Ηλικία (σε έτη)
Games — Αγώνες που έπαιξε (από τους 82 συνολικά)
Starts — Αγώνες στους οποίους ξεκίνησε ως βασικός
Mins — Λεπτά συμμετοχής στο παιχνίδι
MinPerGame — Λεπτά ανά αγώνα
FGMade — Επιτυχημένα σουτ
FGPct — Ποσοστό επιτυχίας σουτ
FG3Made — Επιτυχημένα τρίποντα
FG3Pct — Ποσοστό επιτυχίας τριπόντων
FTMade — Επιτυχημένες βολές
FTPct — Ποσοστό επιτυχίας βολών
Assists — Αριθμός ασίστ
Fouls — Αριθμός προσωπικών φάουλ
Points — Αριθμός πόντων που έβαλε

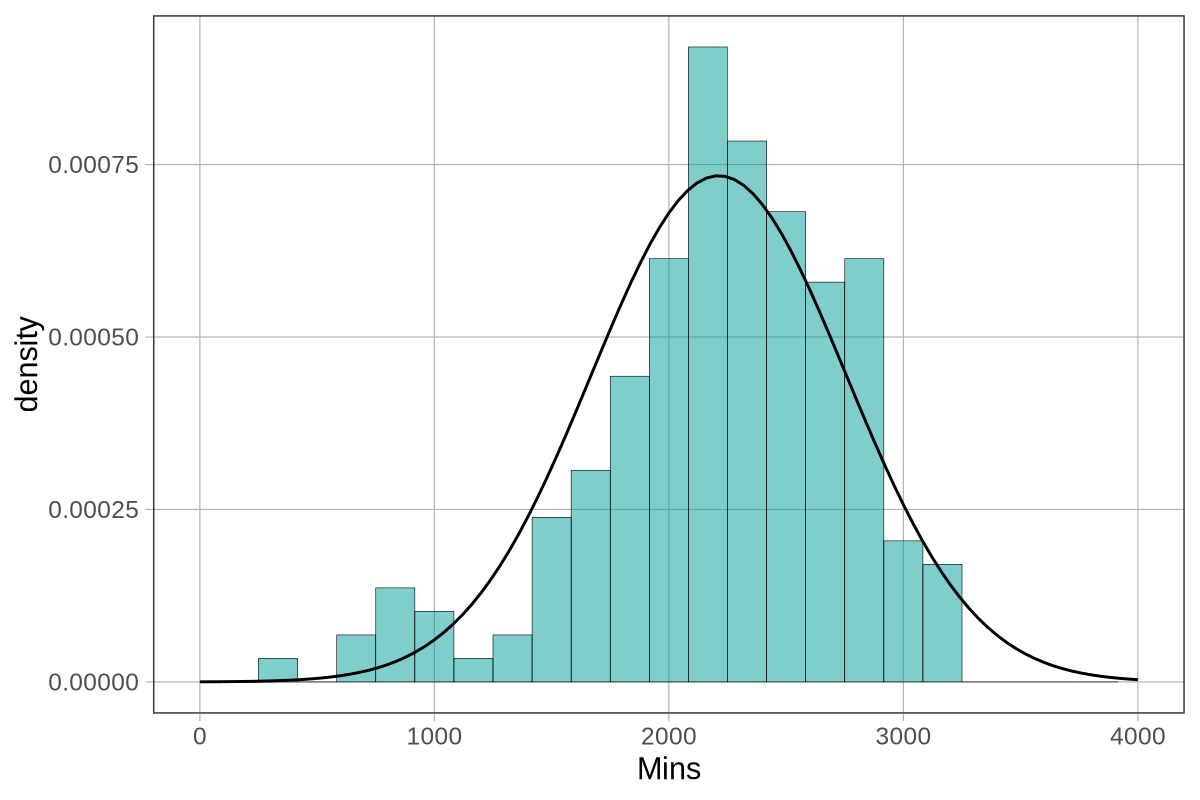
1. Γιατί ορισμένοι παίκτες έχουν περισσότερο χρόνο συμμετοχής και άλλοι λιγότερο; Ας εξετάσουμε το ιστόγραμμα του αριθμού των λεπτών συμμετοχής στο παιχνίδι (μεταβλητή Mins). Τι αντιπροσωπεύει η μαύρη καμπύλη που είναι σχεδιασμένη στο παραάνω ιστόγραμμα;

Η καμπύλη είναι ένας άλλος τρόπος διαγραμματικής αναπαράστασης της κατανομής του δείγματος.Η καμπύλη αντιπροσωπεύει μια κανονική κατανομή που προσαρμόστηκε με βάση το μέσο όρο και την τυπική απόκλιση αυτών των δεδομένων.Η καμπύλη αντιπροσωπεύει τον πληθυσμό από τον οποίο αντλήθηκαν τυχαία αυτά τα δεδομένα.Η καμπύλη αντιπροσωπεύει μια καμπύλη κανονικής κατανομής που δείχνει το 95% των παρατηρήσεων που βρίσκονται εντός δύο τυπικών αποκλίσεων από το μέσο όρο.

Επεξήγηση

Σωστή απάντηση: Α — Αυτός είναι ένας άλλος τρόπος αναπαράστασης της δειγματικής κατανομής.

Τι είναι η μαύρη καμπύλη;

Η μαύρη καμπύλη που βλέπουμε στο ιστόγραμμα είναι μια καμπύλη πυκνότητας πιθανότητας (density curve). Αυτή η καμπύλη:

Είναι μια εξομαλυμένη εκδοχή του ιστογράμματος
Δείχνει το σχήμα της δειγματικής κατανομής
Βοηθά να δούμε το γενικό μοτίβο των δεδομένων χωρίς τις «ακανόνιστες» στήλες του ιστογράμματος

Γιατί η Α είναι σωστή:

Η καμπύλη πυκνότητας πιθανότητας είναι ένας άλλος τρόπος οπτικοποίησης των ίδιων δεδομένων. Το ιστόγραμμα και η καμπύλη πυκνότητας πιθανότητας δείχνουν και τα δύο την ίδια δειγματική κατανομή—απλά με διαφορετικό τρόπο:

Ιστόγραμμα: Χρησιμοποιεί στήλες για να δείξει πόσες παρατηρήσεις βρίσκονται σε κάθε διάστημα τιμών
Καμπύλη πυκνότητας πιθανότητας: Χρησιμοποιεί μια εξομαλυμένη καμπύλη για να δείξει την κατανομή

Παρατηρήσεις από το διάγραμμα:

Η κατανομή είναι ασύμμετρη προς τα δεξιά (right-skewed)
Οι περισσότεροι παίκτες έχουν 1500-2500 λεπτά παιχνιδιού
Υπάρχουν λίγοι παίκτες με πολύ λίγα λεπτά (< 1000) ή πολλά λεπτά (> 3000)
Η κατανομή ΔΕΝ είναι κανονική—δεν είναι συμμετρική καμπάνα

Γιατί οι άλλες επιλογές είναι λάθος;

Β. «Αυτή αντιπροσωπεύει μια κανονική κατανομή που προσαρμόστηκε στον μέσο όρο και την τυπική απόκλιση αυτών των δεδομένων» — ΛΑΘΟΣ

Γιατί είναι λάθος:

Η καμπύλη ΔΕΝ είναι κανονική κατανομή
Μια κανονική κατανομή είναι συμμετρική (σχήμα καμπάνας)
Η καμπύλη στο γράφημα είναι ασύμμετρη προς τα δεξιά
Η καμπύλη ακολουθεί το πραγματικό σχήμα των δεδομένων, όχι ένα θεωρητικό μοντέλο

Σύγκριση:

Χαρακτηριστικό	Καμπύλη στο γράφημα	Κανονική κατανομή
Σχήμα	Ασύμμετρο (skewed)	Συμμετρικό
Κορυφή	Μετατοπισμένη δεξιά	Στο κέντρο
Ουρά	Μακριά δεξιά ουρά	Ίσες ουρές

Γ. «Αυτή αντιπροσωπεύει τον πληθυσμό από τον οποίο αντλήθηκαν τυχαία αυτά τα δεδομένα» — ΛΑΘΟΣ

Γιατί είναι λάθος:

Η καμπύλη βασίζεται μόνο στα δεδομένα του δείγματος (176 παίκτες)
Δεν αντιπροσωπεύει τον πληθυσμό—αντιπροσωπεύει το δείγμα
Ο πληθυσμός θα ήταν όλοι οι παίκτες NBA (ή όλοι οι δυνητικοί παίκτες)
Το δείγμα μας είναι 176 παίκτες από τη σεζόν 2010-2011

Διάκριση:

Δειγματική κατανομή: Η κατανομή των τιμών στο δείγμα μας (αυτό που βλέπουμε)
Κατανομή πληθυσμού: Η κατανομή των τιμών σε ολόκληρο τον πληθυσμό (άγνωστη)
Δειγματοληπτική κατανομή: Η κατανομή ενός στατιστικού (π.χ., μέσου όρου) σε πολλά δείγματα

Δ. «Αυτή αντιπροσωπεύει μια κανονική καμπύλη που δείχνει το 95% των σημείων δεδομένων που βρίσκονται εντός δύο τυπικών αποκλίσεων από τον μέσο όρο» — ΛΑΘΟΣ

Γιατί είναι λάθος:

Η καμπύλη δεν είναι κανονική—όπως εξηγήθηκε παραπάνω
Η καμπύλη πυκνότητας δείχνει 100% των δεδομένων, όχι μόνο το 95%
Η «εμπειρική κανονική κατανομή» (κανόνας 68-95-99.7) ισχύει μόνο για κανονικές κατανομές
Τα δεδομένα μας δεν ακολουθούν κανονική κατανομή

Ο κανόνας για τις κανονικές κατανομές:

Αν τα δεδομένα κατανέμονταν κανονικά, τότε:

το 68% των τιμών θα ήταν εντός ±1 τυπικής απόκλισης
το 95% των τιμών θα ήταν εντός ±2 τυπικών αποκλίσεων
99.7% των τιμών θα ήταν εντός ±3 τυπικών αποκλίσεων

Αλλά επειδή τα δεδομένα μας δεν κατανέμονται κανονικά, αυτός ο κανόνας δεν ισχύει.

Συμπέρασμα

Η μαύρη καμπύλη είναι μια καμπύλη πυκνότητας πιθανότητας που αποτελεί έναν άλλο τρόπο οπτικοποίησης της δειγματικής κατανομής των λεπτών παιχνιδιού. Δείχνει ότι:

Οι περισσότεροι παίκτες έχουν μέτριο χρόνο συμμετοχής (1500-2500 λεπτά)
Η κατανομή είναι ασύμμετρη προς τα δεξιά
Υπάρχουν λίγοι παίκτες με πολύ χαμηλό ή πολύ υψηλό χρόνο συμμετοχής

Αυτές οι πληροφορίες μας βοηθούν να κατανοήσουμε τη μεταβλητότητα στον χρόνο παιχνιδιού μεταξύ των παικτών NBA.

2. Ένας φοιτητής προτείνει ότι οι παίκτες που πετυχαίνουν πολλές βολές (FTMade) είναι καλύτεροι και θα έχουν περισσότερο χρόνο συμμετοχής στο παιχνίδι. Ένας άλλος φοιτητής υποστηρίζει ότι το να βάζεις πολλές βολές δεν σε κάνει καλύτερο παίκτη, αλλά το να έχεις υψηλότερο ποσοστό επιτυχίας στις βολές (FTPct) είναι χαρακτηριστικό ενός καλύτερου παίκτη, και προτείνει ότι αυτό θα εξηγούσε τη μεταβλητότητα στα λεπτά συμμετοχής παιχνιδιού (Mins). Ποιο από τα παρακάτω διαγράμματα θα αναπαριστούσε τη σχέση μεταξύ των Mins και μίας από αυτές τις ανεξάρτητες μεταβλητές;

Θηκογράμματα (δηλ., gf_boxplot)Διάγραμμα διασποράς (δηλ., gf_point)Διαιρεμένο Ιστόγραμμα (δηλ., gf_histogram με gf_facet_grid)Όλα τα παραπάνω θα μπορούσαν να αναπαραστήσουν αυτές τις σχέσεις το ίδιο αποτελεσματικά.

Επεξήγηση

Σωστή απάντηση: Β — Διάγραμμα διασποράς (δηλ., gf_point)

Γιατί διάγραμμα διασποράς;

Για να αναπαραστήσουμε τη σχέση μεταξύ δύο ποσοτικών μεταβλητών, το πιο κατάλληλο διάγραμμα είναι το διάγραμμα διασποράς (scatterplot). Στην περίπτωσή μας:

Εξαρτημένη μεταβλητή (Υ): Mins — Λεπτά συμμετοχής (ποσοτική)
Ανεξάρτητες μεταβλητές (Χ):
- FTMade — Αριθμός επιτυχημένων βολών (ποσοτική)
- FTPct — Ποσοστό επιτυχίας βολών (ποσοτική)

Τι δείχνει ένα διάγραμμα διασποράς:

Κάθε σημείο αντιπροσωπεύει έναν παίκτη
Η θέση του σημείου δείχνει τις τιμές και στις δύο μεταβλητές
Μπορούμε να δούμε αν υπάρχει μοτίβο ή σχέση μεταξύ των μεταβλητών
Μπορούμε να δούμε αν η σχέση είναι γραμμική, καμπυλόγραμμη, ή ανύπαρκτη
Μπορούμε να εκτιμήσουμε την ένταση της σχέσης

Παραδείγματα:

# Σχέση μεταξύ Mins και FTMade
gf_point(Mins ~ FTMade, data = NBAPlayers2011)

# Σχέση μεταξύ Mins και FTPct
gf_point(Mins ~ FTPct, data = NBAPlayers2011)

Γιατί οι άλλες επιλογές δεν είναι τόσο καλές;

Α. «Θηκογράμματα (gf_boxplot)» — ΛΑΘΟΣ

Γιατί δεν είναι κατάλληλα:

Τα θηκογράμματα (boxplots) χρησιμοποιούνται για να συγκρίνουμε μια ποσοτική μεταβλητή μεταξύ κατηγοριών. Για παράδειγμα:

Σύγκριση λεπτών παιχνιδιού μεταξύ θέσης παιχτών (guards vs. forwards vs. centers)
Σύγκριση πόντων μεταξύ ομάδων

Το πρόβλημα εδώ:

Οι FTMade και FTPct είναι ποσοτικές μεταβλητές, όχι κατηγορίες
Θα μπορούσαμε να δημιουργήσουμε κατηγορίες (π.χ., “χαμηλό”, “μέτριο”, “υψηλό” FTPct), αλλά:
- Θα χάναμε πληροφορία (μετατρέποντας ποσοτική σε κατηγορική)
- Θα ήταν αυθαίρετο πού να βάλουμε τα όρια
- Τα διαγράμματα διασποράς είναι πιο κατάλληλα για ποσοτικές μεταβλητές

Γ. «Διαιρεμένο Ιστόγραμμα (gf_histogram με gf_facet_grid)» — ΛΑΘΟΣ

Γιατί τα ιστογράμματα δεν είναι κατάλληλα:

Το διαιρεμένο ιστόγραμμα (faceted histogram) χρησιμοποιείται για να δούμε την κατανομή μιας ποσοτικής μεταβλητής ξεχωριστά για διαφορετικές κατηγορίες μιας ποιοτικής μεταβλητής. Για παράδειγμα:

Κατανομή λεπτών παιχνιδιού για κάθε θέση ξεχωριστά
Κατανομή πόντων για κάθε ομάδα ξεχωριστά

Το πρόβλημα εδώ:

Θέλουμε να δούμε τη σχέση μεταξύ δύο μεταβλητών, όχι την κατανομή μίας μεταβλητής
Τα ιστογράμματα δείχνουν μία μεταβλητή κάθε φορά
Δεν μπορούμε να δούμε πώς δύο ποσοτικές μεταβλητές συμμεταβάλλονται

Δ. «Όλα τα παραπάνω θα μπορούσαν να αναπαραστήσουν αυτές τις σχέσεις εξίσου αποτελεσματικά» — ΛΑΘΟΣ

Γιατί είναι λάθος:

Όπως εξηγήθηκε παραπάνω, δεν είναι όλα εξίσου κατάλληλα:

Τύπος γραφήματος	Κατάλληλο για	Κατάλληλο για το ερώτημα;
Διάγραμμα διασποράς	2 ποσοτικές μεταβλητές	✓ ΝΑΙ
Θηκόγραμμα	Ποσοτική vs. κατηγορική	✗ Όχι ιδανικό
Διαιρεμένο Ιστόγραμμα	Κατανομή ανά κατηγορία	✗ Όχι ιδανικό

Η βασική αρχή:

Για να δούμε τη σχέση μεταξύ δύο ποσοτικών μεταβλητών, το διάγραμμα διασποράς είναι η καλύτερη επιλογή.

Συμπέρασμα

Για να απαντήσουμε στα ερωτήματα των φοιτητών:

Σχέση Mins και FTMade: Χρησιμοποιούμε gf_point(Mins ~ FTMade, data = NBAPlayers2011)
Σχέση Mins και FTPct: Χρησιμοποιούμε gf_point(Mins ~ FTPct, data = NBAPlayers2011)

Αυτά τα διαγράμματα διασποράς θα μας δείξουν:

Αν υπάρχει θετική ή αρνητική σχέση
Πόσο ισχυρή είναι η σχέση
Αν η σχέση είναι γραμμική ή όχι
Ποια από τις δύο μεταβλητές εξηγεί καλύτερα τη μεταβλητότητα στα λεπτά παιχνιδιού

Στη συνέχεια, μπορούμε να υπολογίσουμε τον συντελεστή συσχέτισης ή να προσαρμόσουμε ένα μοντέλο παλινδρόμησης για να ποσοτικοποιήσουμε αυτές τις σχέσεις.

3. Δημιουργήσαμε το παρακάτω διάγραμμα για να εξετάσουμε την ιδέα ότι το ποσοστό επιτυχίας στις βολές (FTPct) θα προέβλεπε πόσα λεπτά παίζει ένας παίκτης.

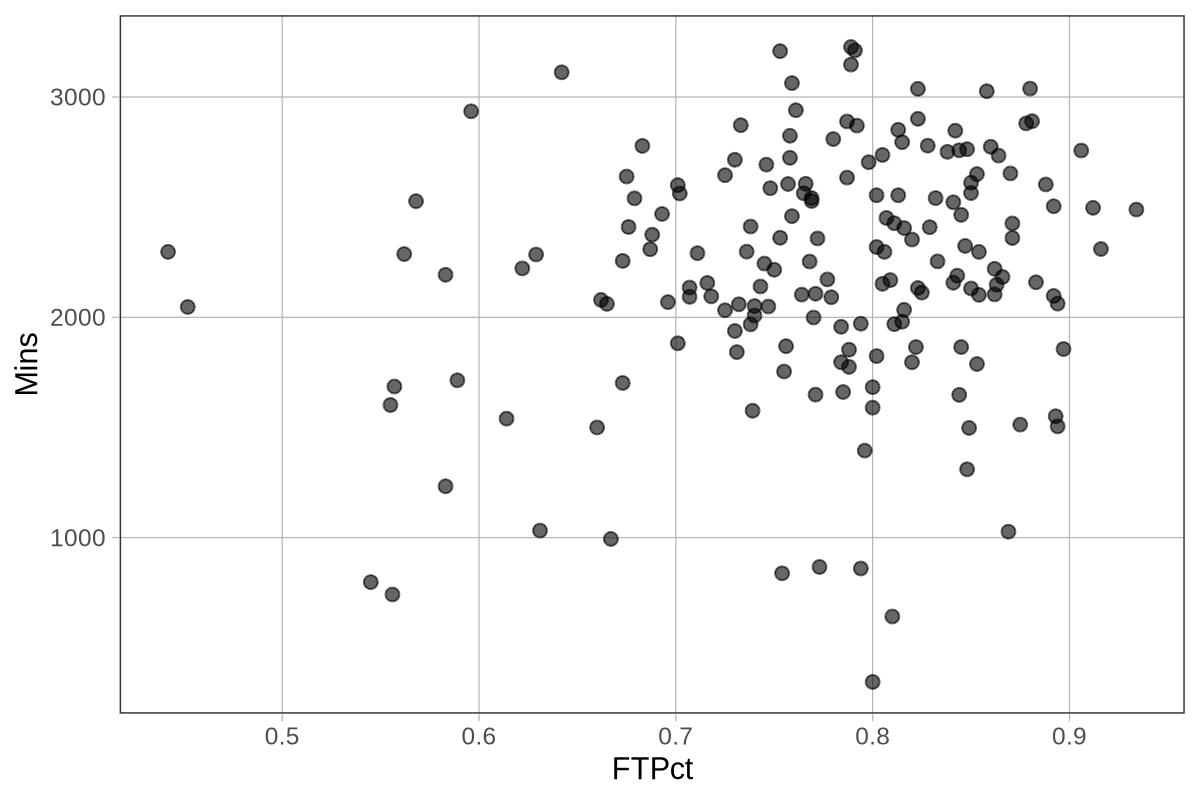
Αν προσαρμόσουμε ένα κενό μοντέλο για την εξήγηση της μεταβλητότητας της Mins, πώς θα το αναπαραστήσουμε επάνω σε αυτό το διάγραμμα;

Με μια διαγώνια γραμμή που διχοτομεί το νέφος των σημείων.Με μια οριζόντια γραμμή που δείχνει το μέσο όρο των λεπτών παιχνιδιού.Με μια κάθετη γραμμή που δείχνει το μέσο ποσοστό επιτυχίας στις βολές.Δεν θα μπορούσαμε να αναπαραστήσουμε το κενό μοντέλο στο διάγραμμα επειδή είναι μόνο ένας αριθμός.

Επεξήγηση

Σωστή απάντηση: Β — Με μια οριζόντια γραμμή που δείχνει το μέσο όρο των λεπτών παιχνιδιού.

Τι είναι το κενό μοντέλο;

Το κενό μοντέλο (empty model) είναι το πιο απλό μοντέλο που μπορούμε να προσαρμόσουμε στα δεδομένα. Σύμφωνα με αυτό:

“Η καλύτερη πρόβλεψη για την εξαρτημένη μεταβλητή είναι ο μέσος όρος της, ανεξάρτητα από την τιμή της ανεξάρτητης μεταβλητής.”

Εξίσωση:

\[Y_i = \beta_0 + \varepsilon_i\]

όπου:

$Y_i$ = Mins (λεπτά παιχνιδιού για τον παίκτη i)
$\beta_0$ = $\bar{Y}$ (ο μέσος όρος των λεπτών παιχνιδιού)
$\varepsilon_i$ = το σφάλμα (απόκλιση από το μέσο όρο)

Στην περίπτωσή μας:

Το κενό μοντέλο αγνοεί τη μεταβλητή FTPct (ποσοστό βολών)
Προβλέπει τα ίδια λεπτά για όλους τους παίκτες
Αυτή η πρόβλεψη είναι ο μέσος όρος των Mins

Γιατί η Β είναι σωστή: Οριζόντια γραμμή στο μέσο όρο

Οπτική αναπαράσταση:

Το κενό μοντέλο απεικονίζεται ως μια οριζόντια γραμμή στο ύψος του μέσου όρου των Mins.

Γιατί οριζόντια;

Η πρόβλεψη είναι η ίδια για όλες τις τιμές της FTPct
Δεν υπάρχει κλίση—η FTPct δεν επηρεάζει την πρόβλεψη
Ο άξονας Υ (κάθετος) δείχνει τη μεταβλητή Mins
Ο άξονας Χ (οριζόντιος) δείχνει τη μεταβλητή FTPct

Παράδειγμα:

Αν ο μέσος όρος της Mins είναι 2000 λεπτά:

Παίκτης με FTPct = 0.5 → Πρόβλεψη: 2000 λεπτά
Παίκτης με FTPct = 0.7 → Πρόβλεψη: 2000 λεπτά
Παίκτης με FTPct = 0.9 → Πρόβλεψη: 2000 λεπτά

Όλοι λαμβάνουν την ίδια πρόβλεψη!

Κώδικας για να το δούμε αυτό:

# Υπολογισμός μέσου όρου
mean_mins <- mean(~Mins, data = NBAPlayers2011)

# Διάγραμμα διασποράς με οριζόντια γραμμή στον μέσο όρο
gf_point(Mins ~ FTPct, data = NBAPlayers2011) %>%
  gf_hline(yintercept = ~mean_mins, color = "red", linewidth = 1.5)

Η κόκκινη οριζόντια γραμμή είναι το κενό μοντέλο.

Γιατί οι άλλες επιλογές είναι λάθος;

Α. «Με μια διαγώνια γραμμή που διχοτομεί το νέφος των σημείων» — ΛΑΘΟΣ

Γιατί είναι λάθος:

Μια διαγώνια γραμμή υποδηλώνει ότι υπάρχει σχέση μεταξύ Χ και Υ
Αυτό θα ήταν ένα μοντέλο παλινδρόμησης (π.χ., Mins ~ FTPct), όχι το κενό μοντέλο
Το κενό μοντέλο δεν περιλαμβάνει καμία ανεξάρτητη μεταβλητή

Διαγώνια γραμμή = Μοντέλο με κλίση:

\[Y_i = \beta_0 + \beta_1 X_i + \varepsilon_i\]

όπου $\beta_1 \neq 0$ (υπάρχει κλίση)

Οριζόντια γραμμή = Κενό μοντέλο:

\[Y_i = \beta_0 + \varepsilon_i\]

όπου δεν υπάρχει το $X_i$ (άρα $\beta_1 = 0$, καμία κλίση)

Γ. «Μια κάθετη γραμμή που δείχνει το μέσο ποσοστό επιτυχίας στις βολές» — ΛΑΘΟΣ

Γιατί είναι λάθος:

Μια κάθετη γραμμή θα ήταν στον άξονα Χ (FTPct)
Το κενό μοντέλο προβλέπει την Υ (Mins), όχι την Χ (FTPct)
Το κενό μοντέλο αφορά το μέσο όρο της εξαρτημένης μεταβλητής (Υ)

Τι θα σήμαινε μια κάθετη γραμμή;

Θα έδειχνε το μέσο όρο της FTPct
Αλλά δεν προσπαθούμε να προβλέψουμε την FTPct
Προσπαθούμε να προβλέψουμε τα λεπτά παιχνιδιού Mins (που είναι στον κάθετο άξονα)

Σύγκριση:

Τύπος γραμμής	Τι δείχνει	Για ποια μεταβλητή
Οριζόντια	Μέσος όρος στον άξονα Υ	Εξαρτημένη (`Mins`) ✓
Κάθετη	Μέσος όρος στον άξονα Χ	Ανεξάρτητη (`FTPct`) ✗

Δ. «Δεν θα μπορούσατε να αναπαραστήσετε το κενό μοντέλο οπτικά επειδή είναι ένας μόνο αριθμός» — ΛΑΘΟΣ

Γιατί είναι λάθος:

Το κενό μοντέλο ΜΠΟΡΕΙ να αναπαρασταθεί διαγραμματικά
Ναι, η πρόβλεψη είναι ένας αριθμός (ο μέσος όρος)
Αλλά αυτός ο αριθμός ισχύει για όλες τις τιμές του Χ
Άρα σχεδιάζουμε μια οριζόντια γραμμή στο ύψος αυτού του αριθμού

Αναλογία:

Αν σας πω “Η πρόβλεψή μου είναι πάντα 2000 λεπτά”, μπορείτε να το σχεδιάσετε;

Φυσικά! Σχεδιάζετε μια οριζόντια γραμμή στο Υ = 2000.

Το κενό μοντέλο ΩΣ ΓΡΑΜΜΗ:

Σημείο: Η πρόβλεψη είναι ένας αριθμός (μέσος όρος)
Γραμμή: Αυτός ο αριθμός ισχύει για όλα τα Χ
Αναπαράσταση: Οριζόντια γραμμή στο ύψος του μέσου όρου

Σύγκριση: Κενό μοντέλο vs. Μοντέλο παλινδρόμησης

Χαρακτηριστικό	Κενό μοντέλο	Μοντέλο `Mins ~ FTPct`
Μαθηματική μορφή	$Y_i = \beta_0 + \varepsilon_i$	$Y_i = \beta_0 + \beta_1 X_i + \varepsilon_i$
Περιλαμβάνει Χ;	ΟΧΙ	ΝΑΙ
Κλίση	0 (οριζόντια)	$\beta_1 \neq 0$ (διαγώνια)
Πρόβλεψη	Πάντα $\bar{Y}$	Εξαρτάται από το Χ
Διαγραμματικά	Οριζόντια γραμμή	Διαγώνια γραμμή

Συμπέρασμα

Το κενό μοντέλο των Mins αναπαρίσταται ως:

Μια οριζόντια γραμμή στο ύψος του μέσου όρου των λεπτών παιχνιδιού.

Γιατί;

Το κενό μοντέλο προβλέπει τον ίδιο αριθμό (μέσο όρο) για όλους
Αυτό σημαίνει μηδενική κλίση (οριζόντια γραμμή)
Η γραμμή είναι στον άξονα Υ (εξαρτημένη μεταβλητή)

Η βασική διαφορά:

Κενό μοντέλο: “Προβλέπω το μέσο όρο, ανεξάρτητα από την FTPct”
Μοντέλο παλινδρόμησης: “Προβλέπω με βάση το FTPct—παίχτες με περισσότερες/λιγότερες επιτυχημένες βολές παίζουν περισσότερο/λιγότερο”

4. Στα αριστερά (με κόκκινο χρώμα) υπάρχει ένα διάγραμμα που απεικονίζει το ακόλουθο μοντέλο: Mins = FTMade + άλλα πράγματα. Στα δεξιά (με μαύρο χρώμα) υπάρχει ένα διάγραμμα που απεικονίζει το ακόλουθο μοντέλο: Mins = FTPct + άλλα πράγματα. Ποια ανεξάρτητη μεταβλητή εξηγεί καλύτερα τη μεταβλητότητα στην εξαρτημένη: η FTMade ή η FTPct; Πώς το ξέρετε αυτό;

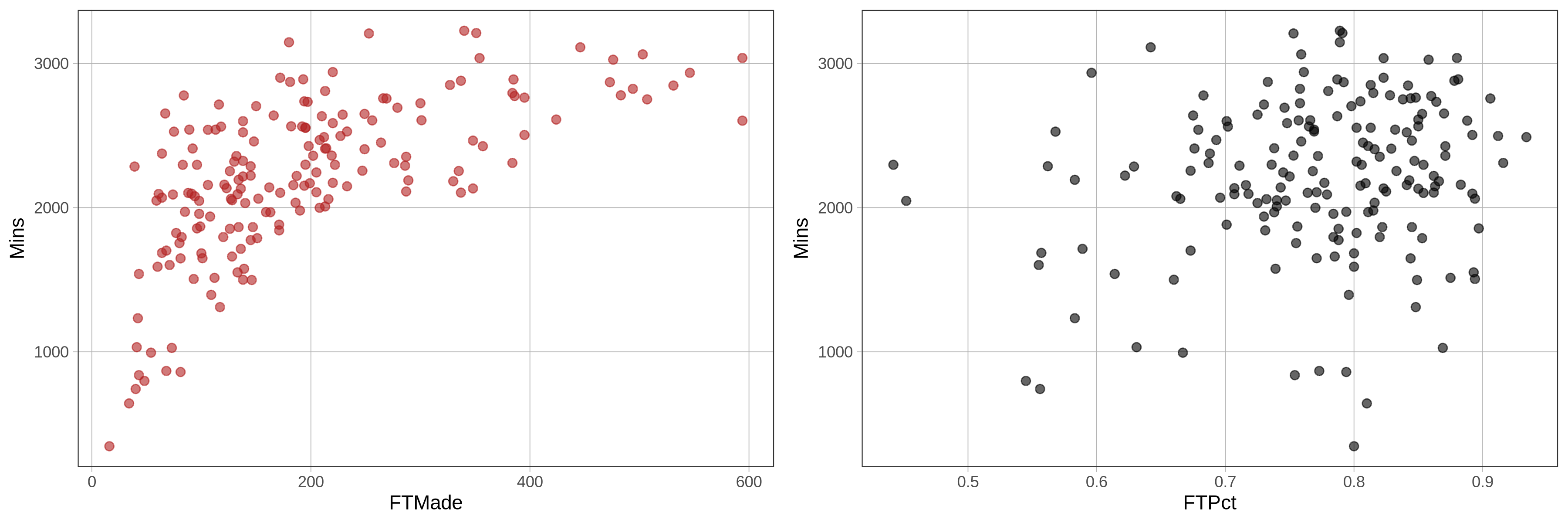
5. Αν προσαρμόσετε ένα μοντέλο που προβλέπει τη μεταβλητή Mins με την FTMade ως ανεξάρτητη μεταβλητή, πόσες παραμέτρους θα έχει το μοντέλο;

2: το σημείο τομής με τον άξονα y και την κλίση της ευθείας παλινδρόμησης2: Mins και FTMade4: $Y_i$, $b_0$, $b_1$, $X_i$2: ο μέσος όρος των Mins και η αύξηση που προστίθεται για κάθε επιτυχημένη βολή που υπερβαίνει το μέσο αριθμό επιτυχημένων βολών

Επεξήγηση

Σωστή απάντηση: Α — 2: το σημείο τομής με τον άξονα y και την κλίση της ευθείας παλινδρόμησης

Τι είναι οι παράμετροι ενός μοντέλου;

Οι παράμετροι (parameters) ενός μοντέλου είναι οι άγνωστες τιμές που πρέπει να εκτιμήσουμε από τα δεδομένα. Είναι τα σταθερά μέρη της εξίσωσης του μοντέλου που περιγράφουν τη σχέση μεταξύ των μεταβλητών.

Το μοντέλο παλινδρόμησης:

Όταν προσαρμόζουμε το μοντέλο Mins ~ FTMade, η εξίσωση είναι:

\[Y_i = \beta_0 + \beta_1 X_i + \varepsilon_i\]

όπου:

$Y_i$ = Mins (η εξαρτημένη μεταβλητή για τον παίκτη i)
$X_i$ = FTMade (η ανεξάρτητη μεταβλητή για τον παίκτη i)
$\beta_0$ = το σημείο τομής (σταθερός όρος ή intercept) — η προβλεπόμενη τιμή των Mins όταν FTMade = 0
$\beta_1$ = η κλίση (slope) — η μεταβολή στα Mins για κάθε επιπλέον επιτυχημένη βολή
$\varepsilon_i$ = το σφάλμα (residual) για τον παίκτη i

Γιατί η Α είναι σωστή: 2 παράμετροι

Το μοντέλο έχει δύο παραμέτρους που πρέπει να εκτιμήσουμε:

$\beta_0$ (σημείο τομής / intercept)
- Πού βρίσκεται η ευθεία παλινδρόμησης στον άξονα y όταν η Χ = 0
- Εκτιμάται από τα δεδομένα ως $b_0$
$\beta_1$ (κλίση / slope)
- Πόσο απότομη είναι η ευθεία
- Εκτιμάται από τα δεδομένα ως $b_1$

Παράδειγμα:

# Προσαρμογή μοντέλου
model <- lm(Mins ~ FTMade, data = NBAPlayers2011)
coef(model)

# Έξοδος (παράδειγμα):
# (Intercept)    FTMade 
# 1662.308948    2.833927

Οι δύο αριθμοί που επιστρέφονται (1662.308948 και 2.833927) είναι οι δύο παράμετροι:

$b_0 = 1662.31$ (σημείο τομής)
$b_1 = 2.83$ (κλίση)

Η εξίσωση γίνεται:

\[\widehat{\text{Mins}}_i = 1662.31 + 2.83 \times \text{FTMade}_i\]

Γιατί οι άλλες επιλογές είναι λάθος;

Β. «2: Mins και FTMade» — ΛΑΘΟΣ

Γιατί είναι λάθος:

Τα Mins και FTMade είναι μεταβλητές (variables), όχι παράμετροι (parameters).

Η διαφορά:

Όρος	Τι είναι	Παράδειγμα	Πόσα υπάρχουν
Μεταβλητές	Δεδομένα που παρατηρούμε	`Mins`, `FTMade`	Μία τιμή ανά παρατήρηση (176 παίκτες)
Παράμετροι	Άγνωστες τιμές που εκτιμούμε	$\beta_0$, $\beta_1$	Μία τιμή ανά μοντέλο (2 παράμετροι)

Μεταβλητές: Έχουμε 176 τιμές για την Mins και 176 τιμές για την FTMade
Παράμετροι: Έχουμε μόνο 2 τιμές: $b_0$ και $b_1$

Αναλογία:

Σε μια συνταγή μαγειρικής: - Υλικά = μεταβλητές (αλεύρι, ζάχαρη, αυγά) - Αναλογίες = παράμετροι (2 φλιτζάνια αλεύρι, 1 φλιτζάνι ζάχαρη)

Γ. «4: $Y_i$, $b_0$, $b_1$, $X_i$» — ΛΑΘΟΣ

Γιατί είναι λάθος:

Αυτή η λίστα ανακατεύει μεταβλητές και παραμέτρους:

$Y_i$ = μεταβλητή (οι τιμές της Mins)
$b_0$ = παράμετρος ✓
$b_1$ = παράμετρος ✓
$X_i$ = μεταβλητή (οι τιμές της FTMade)

Παράμετροι:

Από τα τέσσερα που αναφέρονται, μόνο δύο είναι παράμετροι: $b_0$ και $b_1$.

Επιπλέον:

Τα $Y_i$ και $X_i$ ποικίλλουν από παρατήρηση σε παρατήρηση
Τα $b_0$ και $b_1$ είναι σταθερά για όλες τις παρατηρήσεις

Δ. «2: ο μέσος όρος των Mins και η αύξηση που προστίθεται για κάθε επιτυχημένη βολή που υπερβαίνει το μέσο αριθμό επιτυχημένων βολών» — ΛΑΘΟΣ

Γιατί είναι λάθος:

Αυτή η περιγραφή είναι εννοιολογικά παραπλανητική και μαθηματικά ανακριβής.

Τι λέει αυτή η επιλογή:

Πρώτη παράμετρος: “ο μέσος όρος των Mins”
Δεύτερη παράμετρος: “η αύξηση για κάθε FTMade πάνω από το μέσο όρο”

Το πρόβλημα:

Πρώτη παράμετρος:

Το $\beta_0$ (σημείο τομής) ΔΕΝ είναι ο μέσος όρος των Mins
Το $\beta_0$ είναι η τιμή πρόβλεψης της Mins όταν FTMade = 0
Αυτά είναι διαφορετικά πράγματα

Σύγκριση:

Στατιστικό	Τι είναι	Πότε το χρησιμοποιούμε
Μέσος όρος `Mins`	$\bar{Y}$	Στο κενό μοντέλο
Σημείο τομής	$\beta_0$	Στο μοντέλο παλινδρόμησης

Στο κενό μοντέλο: $Y_i = \beta_0 + \varepsilon_i$

Εδώ, $\beta_0 = \bar{Y}$ (ο μέσος όρος)

Στο μοντέλο παλινδρόμησης: $Y_i = \beta_0 + \beta_1 X_i + \varepsilon_i$

Εδώ, $\beta_0 \neq \bar{Y}$ (είναι η πρόβλεψη όταν X = 0)

Δεύτερη παράμετρος:

Η κλίση $\beta_1$ δείχνει την αύξηση στα Mins για κάθε επιπλέον FTMade
ΟΧΙ “για κάθε FTMade πάνω από το μέσο όρο”

Η διαφορά:

Σωστή ερμηνεία του $\beta_1$:

“Για κάθε επιπλέον επιτυχημένη βολή, τα λεπτά παιχνιδιού αυξάνονται κατά $\beta_1$.”

Λάθος ερμηνεία:

“Για κάθε επιτυχημένη βολή πάνω από το μέσο όρο…”

Παράδειγμα:

Αν $b_1 = 12.34$:

Παίκτης με 0 βολές → Πρόβλεψη: $b_0$
Παίκτης με 1 βολή → Πρόβλεψη: $b_0 + 12.34$
Παίκτης με 2 βολές → Πρόβλεψη: $b_0 + 2(12.34)$

Δεν χρειάζεται να γνωρίζουμε το μέσο όρο των FTMade!

Βαθύτερη κατανόηση: Τι ΕΙΝΑΙ παράμετρος;

Παράμετρος = Μια άγνωστη τιμή που:

Περιγράφει τη σχέση μεταξύ μεταβλητών στον πληθυσμό
Εκτιμάται από τα δεδομένα του δείγματος
Δεν ποικίλλει μεταξύ των παρατηρήσεων

Στο μοντέλο παλινδρόμησης:

Σύμβολο	Όνομα	Τι αντιπροσωπεύει	Παράμετρος;
$\beta_0$	Σημείο τομής	Πρόβλεψη όταν X = 0	✓ ΝΑΙ
$\beta_1$	Κλίση	Μεταβολή στο Y ανά μονάδα X	✓ ΝΑΙ
$Y_i$	Εξαρτημένη μεταβλητή	Παρατηρούμενη τιμή	✗ ΟΧΙ
$X_i$	Ανεξάρτητη μεταβλητή	Παρατηρούμενη τιμή	✗ ΟΧΙ
$\varepsilon_i$	Σφάλμα	Απόκλιση από την πρόβλεψη	✗ ΟΧΙ

Άρα:

Το μοντέλο Mins ~ FTMade έχει 2 παραμέτρους: $\beta_0$ και $\beta_1$

Γενικός κανόνας: Πόσες παράμετροι;

Για γραμμική παλινδρόμηση:

\[\text{Αριθμός παραμέτρων} = \text{Αριθμός ανεξάρτητων μεταβλητών} + 1\]

Το “+1” είναι για το σημείο τομής ($\beta_0$)

Παραδείγματα:

Μοντέλο	Ανεξάρτητες	Παράμετροι	Σύνολο
Κενό: `Mins ~ 1`	0	$\beta_0$	1
Απλή: `Mins ~ FTMade`	1	$\beta_0$, $\beta_1$	2
Πολλαπλή: `Mins ~ FTMade + FTPct`	2	$\beta_0$, $\beta_1$, $\beta_2$	3
Πολύπλοκη: `Mins ~ FTMade + FTPct + Age`	3	$\beta_0$, $\beta_1$, $\beta_2$, $\beta_3$	4

Συμπέρασμα

Το μοντέλο Mins ~ FTMade έχει 2 παραμέτρους:

$\beta_0$ — Το σημείο τομής (intercept)
$\beta_1$ — Η κλίση (slope)

Αυτές οι δύο παράμετροι καθορίζουν πλήρως την ευθεία παλινδρόμησης που προσαρμόζεται στα δεδομένα.

Για να τις εκτιμήσουμε:

# Προσαρμογή μοντέλου
model <- lm(Mins ~ FTMade, data = NBAPlayers2011)

# Εκτίμηση παραμέτρων
coef(model)

# ή
b1(Mins ~ FTMade, data = NBAPlayers2011)  # μόνο η κλίση
b0(Mins ~ FTMade, data = NBAPlayers2011)  # μόνο το σημείο τομής

6. Προσαρμόσαμε ένα μοντέλο των Mins που προβλέπεται από την FTMade και το ονομάσαμε FTMade_model (το αποτέλεσμα παρουσιάζεται παρακάτω). Αν γνωρίζετε ότι ένας παίκτης είχε 0 επιτυχημένες βολές, πόσα λεπτά θα προβλέπατε ότι έπαιξε;

Call:
lm(formula = Mins ~ FTMade, data = NBAPlayers2011)

Coefficients:
(Intercept)       FTMade  
   1662.309        2.834

1662.31 + 2.832.831662.310

Επεξήγηση

Σωστή απάντηση: Γ — 1662.31

Η εξίσωση του μοντέλου

Από τα αποτελέσματα βλέπουμε ότι το μοντέλο μας είναι:

\[\widehat{\text{Mins}} = 1662.31 + 2.83 \times \text{FTMade}\]

όπου:

$b_0 = 1662.31$ — Το σημείο τομής (intercept)
$b_1 = 2.83$ — Η κλίση (slope)

Ερμηνεία:

Σημείο τομής (1662.31): Τα λεπτά πρόβλεψης όταν FTMade = 0
Κλίση (2.83): Για κάθε επιπλέον επιτυχημένη βολή, τα λεπτά παιχνιδιού αυξάνονται κατά 2.83

Υπολογισμός της πρόβλεψης

Ερώτηση: Πόσα λεπτά θα έπαιζε ένας παίκτης με 0 επιτυχημένες βολές;

Λύση:

Αντικαθιστούμε FTMade = 0 στην εξίσωση:

\[\begin{align} \widehat{\text{Mins}} &= 1662.31 + 2.83 \times \text{FTMade} \\ &= 1662.31 + 2.83 \times 0 \\ &= 1662.31 + 0 \\ &= 1662.31 \end{align}\]

Απάντηση: Η πρόβλεψη είναι 1662.31 λεπτά.

Γιατί η Γ είναι σωστή

Όταν η ανεξάρτητη μεταβλητή είναι μηδέν (FTMade = 0), η πρόβλεψη είναι απλά το σημείο τομής.

Γενικά:

\[\widehat{Y} = b_0 + b_1 \times X\]

Όταν $X = 0$:

\[\widehat{Y} = b_0 + b_1 \times 0 = b_0\]

Στην περίπτωσή μας:

Το σημείο τομής $b_0 = 1662.31$ είναι ακριβώς αυτό:

Η προβλεπόμενη τιμή των Mins όταν FTMade = 0

Γιατί οι άλλες επιλογές είναι λάθος;

Α. «1662.31 + 2.83» — ΛΑΘΟΣ

Γιατί είναι λάθος:

Αυτή η επιλογή δεν ολοκληρώνει τον υπολογισμό:

Η πλήρης εξίσωση είναι: $1662.31 + 2.83 \times \text{FTMade}$
Όταν FTMade = 0: $1662.31 + 2.83 \times 0 = 1662.31 + 0 = 1662.31$
Η επιλογή “1662.31 + 2.83” δείχνει $1662.31 + 2.83 = 1665.14$

Το λάθος:

Προσθέτει την κλίση στο σημείο τομής
Αλλά η κλίση πολλαπλασιάζεται με την FTMade, δεν προστίθεται απευθείας
Αυτό θα ήταν σωστό μόνο αν FTMade = 1

Σύγκριση:

FTMade	Πρόβλεψη	Υπολογισμός
0	1662.31	$1662.31 + 2.83(0) = 1662.31$
1	1665.14	$1662.31 + 2.83(1) = 1665.14$ ✓ Αυτό
2	1667.97	$1662.31 + 2.83(2) = 1667.97$

Η επιλογή Α θα ήταν σωστή για FTMade = 1, όχι για FTMade = 0.

Β. «2.83» — ΛΑΘΟΣ

Γιατί είναι λάθος:

Το 2.83 είναι η κλίση ($b_1$), όχι μια πρόβλεψη για τα λεπτά παιχνιδιού.

Τι σημαίνει η κλίση;

Η κλίση 2.83 σημαίνει:

“Για κάθε επιπλέον επιτυχημένη βολή, τα λεπτά παιχνιδιού αυξάνονται κατά 2.83.”

Αλλά:

Η κλίση είναι ένας ρυθμός μεταβολής, όχι μια πρόβλεψη
Δείχνει πόσο αλλάζουν τα Mins, όχι πού ξεκινούν
Για να κάνουμε πρόβλεψη, πρέπει να χρησιμοποιήσουμε ολόκληρη την εξίσωση

Δ. «0» — ΛΑΘΟΣ

Γιατί είναι λάθος:

Αυτή η επιλογή συγχέει την τιμή εισόδου με την τιμή εξόδου.

Η διαφορά:

Είσοδος (X): FTMade = 0 (ο αριθμός επιτυχημένων βολών)
Έξοδος (Y): Mins = ; (η τιμή πρόβλεψης των λεπτών παιχνιδιού)

Το ότι η είσοδος είναι 0 ΔΕΝ σημαίνει ότι η έξοδος είναι 0!

Η λογική του μοντέλου:

Ένας παίκτης με 0 επιτυχημένες βολές:

Μπορεί να είναι αρχάριος που μόλις μπήκε στην ομάδα
Μπορεί να είναι αμυντικός που δεν βάζει πολλές βολές
Μπορεί να είχε κακή μέρα

Αλλά ακόμα παίζει! Άρα η πρόβλεψη είναι 1662.31 λεπτά, όχι 0.

Συμπέρασμα

Για έναν παίκτη με 0 επιτυχημένες βολές:

\[\widehat{\text{Mins}} = 1662.31 + 2.83 \times 0 = 1662.31\]

Η πρόβλεψη είναι 1662.31 λεπτά.

Γενική αρχή:

Όταν η ανεξάρτητη μεταβλητή είναι μηδέν, η πρόβλεψη είναι το σημείο τομής.

Αυτό ισχύει πάντα για γραμμική παλινδρόμηση:

\[\text{Όταν } X = 0 \text{, τότε } \widehat{Y} = b_0\]

7. Προσαρμόσαμε το μοντέλο της Mins (λεπτά συμμετοχής στο παιχνίδι) που εξηγείται από την FTMade (αριθμός επιτυχημένων βολών) και το ονομάσαμε FTMade_model. Προσαρμόσαμε και το μοντέλο της Mins που εξηγείται από την Points (πόντοι που σημειώθηκαν) και το ονομάσαμε Points_model. Τα αποτελέσματα παρουσιάζονται παρακάτω. Μπορούμε από τις εκτιμήσεις των παραμέτρων να διαπιστώσουμε ποιο μοντέλο εξηγεί περισσότερη μεταβλητότητα, το FTMade_model ή το Points_model;

Call:
lm(formula = Mins ~ FTMade, data = NBAPlayers2011)

Coefficients:
(Intercept)       FTMade  
   1662.309        2.834

Call:
lm(formula = Mins ~ Points, data = NBAPlayers2011)

Coefficients:
(Intercept)       Points  
   1156.680        1.062

Ναι, το FTMade_model είναι καλύτερο μοντέλο, επειδή η αύξηση του χρόνου συμμετοχής που προστίθεται ανά επιτυχημένη βολή είναι μεγαλύτερη από την αύξηση του χρόνου που προστίθεται ανά πόντο που σημειώθηκε.Όχι, δεν μπορούμε να πούμε από τις εκτιμήσεις βέλτιστης προσαρμογής πόση μεταβλητότητα έχει εξηγηθεί από κάθε μοντέλο.Ναι, το FTMade_model είναι καλύτερο μοντέλο επειδή ο σταθερός όρος του μοντέλου είναι μεγαλύτερος από το σταθερό όρο για το Points_model.Όχι, δεν πρέπει ποτέ να συγκρίνουμε μοντέλα που έχουν διαφορετικές ανεξάρτητες μεταβλητές επειδή είναι σε διαφορετικές μονάδες.

Επεξήγηση

Σωστή απάντηση: Β — Όχι, δεν μπορούμε να πούμε από τις εκτιμήσεις βέλτιστης προσαρμογής πόση μεταβλητότητα έχει εξηγηθεί από ένα μοντέλο.

Το βασικό πρόβλημα

Οι παράμετροι του μοντέλου ($b_0$ και $b_1$) ΔΕΝ μας λένε πόσο καλά προσαρμόζεται το μοντέλο στα δεδομένα.

Τι μας δείχνουν οι παράμετροι:

Σταθερός όρος ($b_0$): Η τιμή πρόβλεψης όταν X = 0
Κλίση ($b_1$): Η μεταβολή στην Y ανά μονάδα της X

Τι ΔΕΝ μας δείχνουν:

Πόσο ακριβείς είναι οι προβλέψεις
Πόση μεταβλητότητα εξηγείται
Πόσο καλά ταιριάζει η ευθεία στα δεδομένα

Γιατί η Β είναι σωστή

Για να μετρήσουμε πόση μεταβλητότητα εξηγείται, χρειαζόμαστε:

$R^2$ (ή PRE) — Το ποσοστό της μεταβλητότητας που εξηγείται
Τυπικό σφάλμα υπολοίπων — Πόσο διασπαρμένα είναι τα σφάλματα
Διαγραμματική απεικόνιση — Πόσο κοντά είναι τα σημεία στη γραμμή

Τι χρειαζόμαστε για σύγκριση

Για να συγκρίνουμε τα δύο μοντέλα, θα χρειαζόμασταν:

# Προσαρμογή μοντέλων
FTMade_model <- lm(Mins ~ FTMade, data = NBAPlayers2011)
Points_model <- lm(Mins ~ Points, data = NBAPlayers2011)

# Υπολογισμός R²
rsquared(FTMade_model)  # π.χ., 0.4071
rsquared(Points_model)  # π.χ., 0.6493

# Σύγκριση
cat("FTMade R²:", rsquared(FTMade_model))
cat("Points R²:", rsquared(Points_model))

# Ή χρήση summary()
summary(FTMade_model)$r.squared
summary(Points_model)$r.squared

Μόνο ΤΟΤΕ θα μπορούσαμε να πούμε ποιο μοντέλο είναι καλύτερο!

Γιατί οι άλλες επιλογές είναι λάθος;

Α. «Το FTMade_model είναι καλύτερο επειδή η αύξηση ανά βολή (2.83) είναι μεγαλύτερη από την αύξηση ανά πόντο (1.06)» — ΛΑΘΟΣ

Γιατί είναι λάθος:

1. Το μέγεθος της κλίσης ΔΕΝ δείχνει την ποιότητα προσαρμογής

Η κλίση δείχνει πόσο αλλάζει το Y όταν το X αλλάζει, όχι πόσο καλά προσαρμόζεται το μοντέλο.

2. Οι κλίσεις είναι σε διαφορετικές μονάδες

FTMade: Κλίση = 2.83 λεπτά ανά βολή
Points: Κλίση = 1.06 λεπτά ανά πόντο

Δεν μπορούμε να τα συγκρίνουμε απευθείας!

3. Η σχέση μεταξύ FTMade και Points

Οι πόντοι περιλαμβάνουν τις βολές:

Points = 2 × FG2Made + 3 × FG3Made + 1 × FTMade

Γ. «Το FTMade_model είναι καλύτερο επειδή το σημείο τομής (1662.31) είναι μεγαλύτερο από το σημείο τομής του Points_model (1156.68)» — ΛΑΘΟΣ

Γιατί είναι λάθος:

1. Το σημείο τομής ΔΕΝ δείχνει την ποιότητα του μοντέλου

Το σημείο τομής ($b_0$) απλά δείχνει:

“Πού είναι η ευθεία όταν X = 0”

Δεν δείχνει:

Πόσο καλά προσαρμόζεται η ευθεία
Πόση μεταβλητότητα εξηγείται
Ποιο μοντέλο είναι καλύτερο

2. Διαφορετικά σημεία αναφοράς

Τα δύο μοντέλα έχουν διαφορετικά σημεία εκκίνησης:

FTMade = 0: Ένας παίκτης χωρίς βολές
Points = 0: Ένας παίκτης χωρίς πόντους

Αυτά είναι διαφορετικά σενάρια!

Παράδειγμα:

Ένας παίκτης μπορεί να έχει:

0 βολές, αλλά 50 πόντους (από διπλά και τρίποντα)
0 πόντους, και 0 βολές (δεν έπαιξε καθόλου)

Άρα τα σημεία τομής αναφέρονται σε διαφορετικά πράγματα και δεν είναι συγκρίσιμα.

3. Μεγαλύτερο σημείο τομής ≠ Καλύτερο μοντέλο

Δύο μοντέλα με διαφορετικά σημεία τομής μπορεί να έχουν:

Το ίδιο $R^2$ (ίδια ποιότητα)
Αντίθετα $R^2$ (το μικρότερο σημείο τομής να έχει καλύτερο $R^2$)

Το σημείο τομής είναι ανεξάρτητο από την ποιότητα προσαρμογής!

Δ. «Δεν πρέπει ποτέ να συγκρίνουμε μοντέλα με διαφορετικές ανεξάρτητες μεταβλητές επειδή είναι σε διαφορετικές μονάδες» — ΛΑΘΟΣ

Γιατί είναι λάθος:

ΜΠΟΡΟΥΜΕ να συγκρίνουμε μοντέλα με διαφορετικές ανεξάρτητες μεταβλητές!

Πώς;

Χρησιμοποιώντας μετρικές που είναι ανεξάρτητες από τις μονάδες, όπως:

$R^2$ — Ποσοστό μεταβλητότητας που εξηγείται (0 έως 1) - Καμία μονάδα μέτρησης

Άμεσα συγκρίσιμο

Συμπέρασμα

Από τις εκτιμήσεις των παραμέτρων μόνο ΔΕΝ μπορούμε να συγκρίνουμε μοντέλα.

Τι χρειαζόμαστε:

$R^2$ ή PRE — Για να δούμε πόση μεταβλητότητα εξηγείται

Μόνο τότε μπορούμε να πούμε:

“Το Points_model εξηγεί 67% της μεταβλητότητας, ενώ το FTMade_model μόνο το 23%. Άρα το Points_model είναι καλύτερο.”

Βασική αρχή:

Οι παράμετροι ($b_0$, $b_1$) περιγράφουν πού είναι η ευθεία.

Το $R^2$ περιγράφει πόσο καλά η γραμμή ταιριάζει στα δεδομένα.

8. Εκτελείτε τον ακόλουθο κώδικα R

Points_model <- lm(Mins ~ Points, data = NBAPlayers2011)
Points_model

και λαμβάνετε τα παρακάτω αποτελέσματα:

Call:
lm(formula = Mins ~ Points, data = NBAPlayers2011)

Coefficients:
(Intercept)       Points  
   1156.680        1.062

Ποια από τις ακόλουθες εξισώσεις αναπαριστά το προσαρμοσμένο μοντέλο;

$Y_i = 1.06 + 1156.68X_i + e_i$$Y_i = 1156.68 + 1.06 + e_i$$Y_i = 1.06 + 1156.68 + e_i$$Y_i = 1156.68 + 1.06X_i + e_i$

Επεξήγηση

Σωστή απάντηση: Δ — $Y_i = 1156.68 + 1.06X_i + e_i$

Η γενική μορφή του μοντέλου παλινδρόμησης

\[Y_i = \beta_0 + \beta_1 X_i + e_i\]

όπου:

$Y_i$ = η εξαρτημένη μεταβλητή (Mins)
$\beta_0$ = το σημείο τομής (σταθερός όρος)
$\beta_1$ = η κλίση (slope)
$X_i$ = η ανεξάρτητη μεταβλητή (Points)
$e_i$ = το σφάλμα (residual)

Ανάγνωση των αποτελεσμάτων

Coefficients:
(Intercept)       Points  
   1156.680        1.062

Ερμηνεία:

(Intercept) = 1156.68 → Αυτό είναι το $\beta_0$ (σημείο τομής)
Points = 1.06 → Αυτό είναι το $\beta_1$ (κλίση)

Η εξίσωση γίνεται:

\[Y_i = 1156.68 + 1.06 \times X_i + e_i\]

ή πιο συγκεκριμένα:

\[\text{Mins}_i = 1156.68 + 1.06 \times \text{Points}_i + e_i\]

Γιατί η Δ είναι σωστή

Η επιλογή Δ ακολουθεί τη σωστή δομή:

Πρώτα το σημείο τομής: 1156.68
Μετά η κλίση επί την ανεξάρτητη μεταβλητή: 1.06$X_i$
Τέλος το σφάλμα: $e_i$

Η σειρά είναι σημαντική:

\[\underbrace{1156.68}_{\text{σημείο τομής}} + \underbrace{1.06X_i}_{\text{κλίση} \times \text{X}} + \underbrace{e_i}_{\text{σφάλμα}}\]

Γιατί οι άλλες επιλογές είναι λάθος;

Α. «$Y_i = 1.06 + 1156.68X_i + e_i$» — ΛΑΘΟΣ

Το πρόβλημα:

Αυτή η επιλογή αντιστρέφει το σημείο τομής και την κλίση:

Βάζει το 1.06 (που είναι η κλίση) ως σημείο τομής
Βάζει το 1156.68 (που είναι το σημείο τομής) ως κλίση

Σύγκριση:

Στοιχείο	Σωστή τιμή	Στην επιλογή Α
Σημείο τομής	1156.68	1.06 ✗
Κλίση	1.06	1156.68 ✗

Γιατί αυτό είναι λάθος:

Αν χρησιμοποιούσαμε αυτή την εξίσωση:

Για έναν παίκτη με 0 πόντους: Πρόβλεψη = 1.06 λεπτά (!)
Για έναν παίκτη με 10 πόντους: Πρόβλεψη = 1.06 + 1156.68(10) = 11,567.86 λεπτά (!)

Αυτό δεν έχει νόημα:

1.06 λεπτά είναι πολύ λίγο
11,567 λεπτά είναι πολύ περισσότερο από μία ολόκληρη σεζόν!

Β. «$Y_i = 1156.68 + 1.06 + e_i$» — ΛΑΘΟΣ

Το πρόβλημα:

Αυτή η εξίσωση δεν περιλαμβάνει την ανεξάρτητη μεταβλητή $X_i$ (Points)!

Τι σημαίνει αυτό:

\[Y_i = 1156.68 + 1.06 + e_i = 1157.74 + e_i\]

Αυτό είναι κενό μοντέλο, όχι μοντέλο παλινδρόμησης:

Προβλέπει τον ίδιο αριθμό (1157.74) για όλους
Αγνοεί τη μεταβλητή Points εντελώς

Σωστό κενό μοντέλο θα ήταν:

\[Y_i = 1156.68 + e_i\]

(μόνο το σημείο τομής, χωρίς κλίση)

Αλλά εμείς προσαρμόσαμε Mins ~ Points, όχι κενό μοντέλο!

Γ. «$Y_i = 1.06 + 1156.68 + e_i$» — ΛΑΘΟΣ

Το πρόβλημα:

Αυτή η εξίσωση έχει δύο προβλήματα:

Δεν περιλαμβάνει την ανεξάρτητη μεταβλητή $X_i$
Αντιστρέφει τη σειρά των αριθμών (αν και αυτό δεν έχει σημασία στην πρόσθεση)

Απλοποιώντας:

\[Y_i = 1.06 + 1156.68 + e_i = 1157.74 + e_i\]

Όπως και η επιλογή Β, αυτό είναι κενό μοντέλο:

Προβλέπει σταθερή τιμή
Αγνοεί τη μεταβλητή Points
Δεν είναι μοντέλο παλινδρόμησης

Επιπλέον:

Ακόμα και αν ήταν κενό μοντέλο, η τιμή δεν θα ήταν 1157.74:

Το κενό μοντέλο χρησιμοποιεί τον μέσο όρο των Mins
Ο μέσος όρος των Mins στα δεδομένα δεν είναι 1157.74

Πώς να θυμάστε τη σωστή δομή

Η εξίσωση παλινδρόμησης πάντα έχει αυτή τη δομή:

\[Y = \underbrace{\beta_0}_{\substack{\text{σημείο} \\ \text{τομής}}} + \underbrace{\beta_1}_{\text{κλίση}} \times \underbrace{X}_{\substack{\text{ανεξάρτητη} \\ \text{μεταβλητή}}} + \underbrace{e}_{\text{σφάλμα}}\]

Σε λόγια:

Ξεκινάμε από ένα σημείο (σημείο τομής)
Προσθέτουμε κάτι που εξαρτάται από το X (κλίση × X)
Προσθέτουμε ένα σφάλμα

Άρα:

\[\text{Mins} = 1156.68 + 1.06 \times \text{Points} + e\]

Συμπέρασμα

Η σωστή εξίσωση είναι:

\[Y_i = 1156.68 + 1.06X_i + e_i\]

Πώς να το θυμάστε:

Διαβάστε την έξοδο από πάνω προς τα κάτω:
- (Intercept) = 1156.68 → πρώτος όρος
- Points = 1.06 → δεύτερος όρος (επί $X_i$)
Ακολουθήστε τη δομή:
- $Y = \text{σημείο τομής} + \text{κλίση} \times X + \text{σφάλμα}$
Ελέγξτε αν έχει νόημα:
- Μικρές τιμές X → λογική πρόβλεψη
- Μεγάλες τιμές X → λογική πρόβλεψη

9.Το μοντέλο Points_model της εξαρτημένης μεταβλητήςς Mins μπορεί να αναπαρασταθεί ως εξής:

\[Y_i = b_0 + b_1X_i + e_i\]

Ο LeBron James σημείωσε 2111 πόντους τη σεζόν του 2011. Σε αυτή την εξίσωση, ποιο μέρος του μοντέλου αντιπροσωπεύει την τιμή πρόβλεψης για τα λεπτά παιχνιδιού του LeBron James;

$b_0$$b_0 + b_1X_i$$b_1$$b_1X_i$

Επεξήγηση

Σωστή απάντηση: Β — $b_0 + b_1X_i$

Κατανόηση της εξίσωσης

Η πλήρης εξίσωση του μοντέλου είναι:

\[Y_i = b_0 + b_1X_i + e_i\]

όπου:

$Y_i$ = η παρατηρούμενη τιμή (πραγματικά λεπτά)
$b_0$ = το σημείο τομής (1156.68)
$b_1$ = η κλίση (1.06)
$X_i$ = οι πόντοι (2111 για τον LeBron)
$e_i$ = το σφάλμα (διαφορά μεταξύ παρατηρούμενου και προβλεπόμενου)

Τι είναι η τιμή πρόβλεψης;

Η τιμή πρόβλεψης (predicted value) συμβολίζεται με $\hat{Y}_i$ (διαβάζεται “Y hat”) και είναι:

\[\hat{Y}_i = b_0 + b_1X_i\]

Βασικό σημείο:

Η πρόβλεψη ΔΕΝ περιλαμβάνει το σφάλμα $e_i$!

Γιατί;

Το σφάλμα $e_i$ είναι το μέρος που δεν μπορούμε να προβλέψουμε
Η πρόβλεψη είναι το μέρος που μπορούμε να υπολογίσουμε από το μοντέλο
Το σφάλμα γίνεται γνωστό μόνο αφού παρατηρήσουμε την πραγματική τιμή

Γιατί η Β είναι σωστή: $b_0 + b_1X_i$

Η πρόβλεψη για τον LeBron είναι:

\[\hat{Y}_{\text{LeBron}} = b_0 + b_1 \times X_{\text{LeBron}}\]

Αντικαθιστώντας τις τιμές:

\[\begin{align} \hat{Y}_{\text{LeBron}} &= 1156.68 + 1.06 \times 2111 \\ &= 1156.68 + 2237.66 \\ &= 3394.34 \text{ λεπτά} \end{align}\]

Αυτό είναι το $b_0 + b_1X_i$ μέρος της εξίσωσης!

Ανατομία της εξίσωσης

\[\underbrace{Y_i}_{\substack{\text{παρατηρούμενη} \\ \text{τιμή}}} = \underbrace{b_0 + b_1X_i}_{\substack{\text{ΠΡΟΒΛΕΨΗ} \\ \hat{Y}_i}} + \underbrace{e_i}_{\substack{\text{σφάλμα} \\ \text{(άγνωστο πριν} \\ \text{την παρατήρηση)}}}\]

Με λόγια:

\[\text{Παρατήρηση} = \text{Πρόβλεψη} + \text{Σφάλμα}\]

\[Y_i = \hat{Y}_i + e_i\]

Γιατί οι άλλες επιλογές είναι λάθος;

Α. «$b_0$» — ΛΑΘΟΣ

Γιατί είναι λάθος:

Το $b_0$ (σημείο τομής) είναι μόνο ένα μέρος της πρόβλεψης, όχι η πλήρης πρόβλεψη.

Τι είναι το $b_0$;

Το $b_0 = 1156.68$ είναι η προβλεπόμενη τιμή μόνο όταν Points = 0
Δεν λαμβάνει υπόψη τους 2111 πόντους του LeBron
Είναι το σημείο εκκίνησης, αλλά όχι η τελική πρόβλεψη

Γ. «$b_1$» — ΛΑΘΟΣ

Γιατί είναι λάθος:

Το $b_1$ είναι μόνο η κλίση, όχι η πρόβλεψη.

Τι είναι το $b_1$;

Το $b_1 = 1.06$ είναι ο ρυθμός μεταβολής
Δείχνει πόσο αλλάζουν τα λεπτά ανά πόντο
Δεν είναι αριθμός λεπτών!

Μονάδες:

$b_1 = 1.06$ λεπτά ανά πόντο
Πρόβλεψη = λεπτά

Οι μονάδες δεν ταιριάζουν!

Ομοίως:

Η κλίση ΔΕΝ είναι η πρόβλεψη
Η πρόβλεψη = σημείο τομής + κλίση × X

Δ. «$b_1X_i$» — ΛΑΘΟΣ

Γιατί είναι λάθος:

Το $b_1X_i$ είναι μέρος της πρόβλεψης, αλλά όχι ολόκληρη η πρόβλεψη.

Τι λείπει;

Λείπει το σημείο τομής $b_0$!

Υπολογισμός:

Αν χρησιμοποιούσαμε μόνο το $b_1X_i$:

\[\begin{align} b_1X_i &= 1.06 \times 2111 \\ &= 2237.66 \text{ λεπτά} \end{align}\]

Η πλήρης πρόβλεψη είναι:

\[\begin{align} b_0 + b_1X_i &= 1156.68 + 2237.66 \\ &= 3394.34 \text{ λεπτά} \end{align}\]

Η διαφορά:

Χωρίς $b_0$: 2237.66 λεπτά
Με $b_0$: 3394.34 λεπτά
Διαφορά: 1156.68 λεπτά (το σημείο τομής!)

Γιατί χρειαζόμαστε το $b_0$;

Το σημείο τομής λαμβάνει υπόψη:

Τον βασικό χρόνο παιχνιδιού που δεν σχετίζεται με τους πόντους
Το επίπεδο βάσης των λεπτών
Άλλους παράγοντες που δεν μετρώνται από τους πόντους

Συμπέρασμα

Η πρόβλεψη που κάνει το μοντέλο για τον LeBron James είναι:

\[\hat{Y}_{\text{LeBron}} = b_0 + b_1X_i = 1156.68 + 1.06(2111) = 3394.34 \text{ λεπτά}\]

Βασική αρχή:

Η πρόβλεψη περιλαμβάνει ό,τι μπορούμε να υπολογίσουμε από το μοντέλο.

Το σφάλμα ($e_i$) είναι ό,τι δεν μπορούμε να προβλέψουμε μέχρι να δούμε την πραγματική τιμή.

Γενικά:

\[\text{Πρόβλεψη} = \hat{Y}_i = b_0 + b_1X_i\]

Χωρίς το σφάλμα!

10. Έχουμε εκτιμήσει τις παραμέτρους του μοντέλου FTMade_model με εξαρτημένη μεταβλητή τα λεπτά συμμετοχής στο παιχνίδι (Mins):

\[Y_i = 1662.31 + 2.83X_i + e_i\]

Ο LeBron James έπαιξε 3063 λεπτά, σημείωσε 2111 πόντους, και πέτυχε 758 βολές τη σεζόν του 2011. Ποια είναι η τιμή πρόβλεψης του FTMade_model για τα λεπτά παιχνιδιού του LeBron James;

1662.3130631662.31 + 2.83 × 758 + 21111662.31 + 2.83 × 758

Επεξήγηση

Σωστή απάντηση: Δ — 1662.31 + 2.83 × 758

Κατανόηση του μοντέλου

Το FTMade_model είναι:

\[Y_i = 1662.31 + 2.83X_i + e_i\]

όπου:

$Y_i$ = Mins (λεπτά παιχνιδιού)
$X_i$ = FTMade (επιτυχημένες βολές)
$1662.31$ = $b_0$ (σημείο τομής)
$2.83$ = $b_1$ (κλίση)
$e_i$ = σφάλμα

Σημαντικό: Το μοντέλο χρησιμοποιεί μόνο τις βολές (FTMade), όχι τους πόντους!

Δεδομένα για τον LeBron James

Μας δίνονται:

Λεπτά παιχνιδιού: 3063 (η πραγματική τιμή - δεν τη χρειαζόμαστε για την πρόβλεψη)
Πόντοι: 2111 (δεν τους χρησιμοποιεί το FTMade_model)
Επιτυχημένες βολές: 758 (αυτό χρειαζόμαστε!)

Ποια είναι η ανεξάρτητη μεταβλητή;

Το μοντέλο είναι Mins ~ FTMade, άρα:

Ανεξάρτητη μεταβλητή ($X_i$): FTMade = 758
Εξαρτημένη μεταβλητή ($Y_i$): Mins = αυτό που προβλέπουμε

Υπολογισμός της πρόβλεψης

Η πρόβλεψη είναι:

\[\hat{Y}_i = b_0 + b_1X_i\]

Αντικαθιστώντας τις τιμές:

\[\begin{align} \hat{Y}_{\text{LeBron}} &= 1662.31 + 2.83 \times X_{\text{LeBron}} \\ &= 1662.31 + 2.83 \times 758 \end{align}\]

Αυτό είναι η επιλογή Δ!

Ολοκληρώνοντας τον υπολογισμό:

\[\begin{align} \hat{Y}_{\text{LeBron}} &= 1662.31 + 2.83 \times 758 \\ &= 1662.31 + 2145.14 \\ &= 3807.45 \text{ λεπτά} \end{align}\]

Γιατί η Δ είναι σωστή

1. Χρησιμοποιεί τη σωστή ανεξάρτητη μεταβλητή

Το μοντέλο είναι FTMade_model, άρα χρησιμοποιεί:

✓ FTMade = 758
✗ Όχι Points = 2111

2. Ακολουθεί τη δομή της πρόβλεψης

Πρόβλεψη = $b_0 + b_1 \times X_i$ (χωρίς το σφάλμα $e_i$)

3. Περιλαμβάνει όλα τα απαραίτητα μέρη

Σημείο τομής: 1662.31 ✓
Κλίση επί X: 2.83 × 758 ✓

Γιατί οι άλλες επιλογές είναι λάθος;

Α. «1662.31» — ΛΑΘΟΣ

Γιατί είναι λάθος:

Αυτή η επιλογή περιλαμβάνει μόνο το σημείο τομής, όχι την πλήρη πρόβλεψη.

Τι σημαίνει αυτό;

Το 1662.31 είναι η πρόβλεψη μόνο όταν FTMade = 0
Δεν λαμβάνει υπόψη τις 758 βολές του LeBron
Είναι σαν να λέμε: “Αγνόησε εντελώς τις βολές του!”

Β. «3063» — ΛΑΘΟΣ

Γιατί είναι λάθος:

Το 3063 είναι η παρατηρούμενη τιμή (πραγματικά λεπτά), όχι η τιμή πρόβλεψης!

Η διαφορά:

Τιμή Πρόβλεψης ($\hat{Y}_i$): Τι περιμένουμε με βάση το μοντέλο
Παρατήρηση ($Y_i$): Τι συνέβη πραγματικά

Στην περίπτωση του LeBron:

Τιμή Πρόβλεψης: $\hat{Y} = 1662.31 + 2.83(758) = 3807.45$ λεπτά
Παρατήρηση: $Y = 3063$ λεπτά
Σφάλμα: $e = Y - \hat{Y} = 3063 - 3807.45 = -744.45$ λεπτά

Ερμηνεία του σφάλματος:

Ο LeBron έπαιξε 744.45 λεπτά λιγότερα από όσο προέβλεπε το μοντέλο:

Το μοντέλο υπερεκτίμησε τα λεπτά του
Ίσως ο LeBron είχε τραυματισμούς ή ανάπαυλα
Το μοντέλο βασίζεται μόνο στις βολές, όχι σε άλλους παράγοντες

Το ερώτημα ζητάει την πρόβλεψη, όχι την παρατήρηση!

Γ. «1662.31 + 2.83 × 758 + 2111» — ΛΑΘΟΣ

Γιατί είναι λάθος:

Αυτή η επιλογή κάνει δύο σημαντικά λάθη:

Λάθος 1: Προσθέτει τους πόντους (2111)

Το μοντέλο FTMade_model δεν χρησιμοποιεί τους πόντους
Η ανεξάρτητη μεταβλητή είναι μόνο η FTMade
Οι πόντοι είναι άσχετοι με αυτό το μοντέλο

Ποια μοντέλα έχουμε;

Μοντέλο	Ανεξάρτητη μεταβλητή	Χρησιμοποιεί την `Points`;
`FTMade_model`	`FTMade` (758)	ΟΧΙ ✗
`Points_model`	`Points` (2111)	ΝΑΙ ✓

Λάθος 2: Προσθέτει αριθμό χωρίς να τον πολλαπλασιάσει

Ακόμα και αν υπήρχε δεύτερη ανεξάρτητη μεταβλητή:

Λάθος: $Y_i = b_0 + b_1X_{1i} + X_{2i}$
Σωστό: $Y_i = b_0 + b_1X_{1i} + b_2X_{2i}$

Κάθε ανεξάρτητη μεταβλητή πρέπει να πολλαπλασιαστεί με τη δική της κλίση!

Τι κάνει πραγματικά αυτή η εξίσωση;

\[\begin{align} 1662.31 + 2.83 \times 758 + 2111 &= 1662.31 + 2145.14 + 2111 \\ &= 5918.45 \end{align}\]

Αυτό δεν έχει καμία σχέση με κανένα μοντέλο:

Είναι πολύ μεγάλο (5918 λεπτά = 98.6 ώρες!)
Μια σεζόν NBA έχει μόνο 82 αγώνες × ~48 λεπτά = ~3936 λεπτά max
Δεν ακολουθεί καμία λογική δομή μοντέλου

Σύγκριση όλων των επιλογών

Ας υπολογίσουμε το αποτέλεσμα κάθε επιλογής:

Επιλογή	Τύπος	Υπολογισμός	Αποτέλεσμα	Σωστό;
Α	$b_0$	1662.31	1662.31	✗
Β	Παρατήρηση	-	3063	✗
Γ	$b_0 + b_1X_i + \text{Points}$	1662.31 + 2145.14 + 2111	5918.45	✗
Δ	$b_0 + b_1X_i$	1662.31 + 2145.14	3807.45	✓

Βασικά σημεία που πρέπει να θυμάστε

1. Χρησιμοποιήστε τη σωστή ανεξάρτητη μεταβλητή

FTMade_model → Χρησιμοποιεί FTMade
Points_model → Χρησιμοποιεί Points
Μην τα ανακατεύετε!

2. Η πρόβλεψη ≠ Παρατήρηση

Πρόβλεψη ($\hat{Y}$): Τι λέει το μοντέλο
Παρατήρηση ($Y$): Τι συνέβη πραγματικά
Σφάλμα ($e$): Η διαφορά μεταξύ τους

3. Η πρόβλεψη δεν περιλαμβάνει το σφάλμα

\[\hat{Y}_i = b_0 + b_1X_i\]

Όχι $\hat{Y}_i = b_0 + b_1X_i + e_i$

4. Μην προσθέτετε άσχετες μεταβλητές

Αν το μοντέλο δεν περιλαμβάνει μια μεταβλητή, μην την προσθέσετε!

Συμπέρασμα

Η πρόβλεψη του FTMade_model για τον LeBron James είναι:

\[\hat{Y}_{\text{LeBron}} = 1662.31 + 2.83 \times 758 = 3807.45 \text{ λεπτά}\]

Αυτό αντιστοιχεί στην επιλογή Δ: 1662.31 + 2.83 × 758

Σημαντική παρατήρηση:

Ο LeBron έπαιξε πραγματικά 3063 λεπτά, που είναι 744 λεπτά λιγότερα από την πρόβλεψη. Αυτό δείχνει ότι:

Το μοντέλο δεν είναι τέλειο
Υπάρχουν άλλοι παράγοντες πέρα από τις βολές που επηρεάζουν τα λεπτά
Αυτό είναι φυσιολογικό—κανένα μοντέλο δεν είναι 100% ακριβές!

11. Έχουμε ποσοτικοποιήσει το σφάλμα από τα μοντέλα FTMade_model και Points_model με εξαρτημένη μεταβλητή την Mins (συνάρτηση supernova()). Ποιοι από τους παρακάτω είναι λόγοι για να πιστεύουμε ότι το Points_model είναι καλύτερο μοντέλο από το FTMade_model;

 Analysis of Variance Table (Type III SS)
 Model: Mins ~ FTMade

                                   SS  df           MS       F    PRE     p
 ----- --------------- | ------------ --- ------------ ------- ------ -----
 Model (error reduced) | 21174725.960   1 21174725.960 119.466 0.4071 .0000
 Error (from model)    | 30840525.949 174   177244.402                     
 ----- --------------- | ------------ --- ------------ ------- ------ -----
 Total (empty model)   | 52015251.909 175   297230.011

 Analysis of Variance Table (Type III SS)
 Model: Mins ~ Points

                                   SS  df           MS       F    PRE     p
 ----- --------------- | ------------ --- ------------ ------- ------ -----
 Model (error reduced) | 33777630.163   1 33777630.163 322.263 0.6494 .0000
 Error (from model)    | 18237621.747 174   104813.918                     
 ----- --------------- | ------------ --- ------------ ------- ------ -----
 Total (empty model)   | 52015251.909 175   297230.011

Το PRE του FTMade_model είναι μικρότερο από το PRE του Points_model.Το SS Model του FTMade_model είναι μικρότερο από το SS Model του Points_model.Το SS Error του Points_model είναι μικρότερο από το SS Error του FTMade_model.Όλα τα παραπάνω

Επεξήγηση

Σωστή απάντηση: Δ — Όλα τα παραπάνω

Ανάλυση των αποτελεσμάτων

Ας εξετάσουμε κάθε επιλογή ξεχωριστά και στη συνέχεια δούμε γιατί όλες δείχνουν ότι το Points_model είναι καλύτερο.

Α. Το PRE του FTMade_model είναι μικρότερο από το PRE του Points_model

Τι είναι το PRE;

Το PRE (Proportional Reduction in Error) είναι το $R^2$ — το ποσοστό της μεταβλητότητας που εξηγείται από το μοντέλο.

\[\text{PRE} = R^2 = \frac{\text{SS Model}}{\text{SS Total}} = \frac{\text{Error Reduced}}{\text{Total Error}}\]

Από τα αποτελέσματα:

Μοντέλο	PRE ($R^2$)	Ερμηνεία
`FTMade_model`	0.4071	Εξηγεί 40.71% της μεταβλητότητας
`Points_model`	0.6494	Εξηγεί 64.94% της μεταβλητότητας

Σύγκριση:

\[0.4071 < 0.6494\]

Συμπέρασμα:

✓ Το Points_model εξηγεί 24.23 ποσοστιαίες μονάδες περισσότερη μεταβλητότητα!

Γιατί αυτό σημαίνει ότι το Points_model είναι καλύτερο;

Μεγαλύτερο $R^2$ = Καλύτερες προβλέψεις
Περισσότερη εξηγούμενη μεταβλητότητα = Ισχυρότερη σχέση
Το Points_model είναι πιο ακριβές

Η επιλογή Α είναι ΣΩΣΤΗ ✓

Β. Το SS Model του FTMade_model είναι μικρότερο από το SS Model του Points_model

Τι είναι το SS Model;

Το SS Model (Sum of Squares for the Model) μετράει πόση μεταβλητότητα εξηγείται από το μοντέλο.

\[\text{SS Model} = \sum (\hat{Y}_i - \bar{Y})^2\]

Από τα αποτελέσματα:

Μοντέλο	`SS Model` (Error Reduced)	Ερμηνεία
`FTMade_model`	21174726	Εξηγούμενη μεταβλητότητα
`Points_model`	33777630	Εξηγούμενη μεταβλητότητα

Σύγκριση:

\[21174726 < 33777630\]

Διαφορά:

\[33777630 - 21174726 = 12602904\]

Το Points_model εξηγεί 12.6 εκατομμύρια περισσότερες μονάδες μεταβλητότητας!

Γιατί αυτό σημαίνει ότι το Points_model είναι καλύτερο;

Μεγαλύτερο SS Model = Περισσότερη εξηγούμενη μεταβλητότητα
Οι προβλέψεις είναι πιο κοντά στις παρατηρήσεις

Η επιλογή Β είναι ΣΩΣΤΗ ✓

Γ. Το SS Error του Points_model είναι μικρότερο από το SS Error του FTMade_model

Τι είναι το SS Error:

Το SS Error (Sum of Squares for Error) μετράει πόση μεταβλητότητα δεν εξηγείται από το μοντέλο.

\[\text{SS Error} = \sum (Y_i - \hat{Y}_i)^2 = \sum e_i^2\]

Από τα αποτελέσματα:

Μοντέλο	`SS Error`	Ερμηνεία
`FTMade_model`	30840526	Μη εξηγούμενη μεταβλητότητα
`Points_model`	18237622	Μη εξηγούμενη μεταβλητότητα

Σύγκριση:

\[18237622 < 30840526\]

Διαφορά:

\[30840526 - 18237622 = 12602904\]

Το Points_model έχει 12.6 εκατομμύρια λιγότερες μονάδες σφάλματος!

Γιατί αυτό σημαίνει ότι το Points_model είναι καλύτερο;

Μικρότερο SS Error = Μικρότερα σφάλματα
Οι προβλέψεις είναι πιο ακριβείς
Το μοντέλο αφήνει λιγότερη μεταβλητότητα ανεξήγητη

Η επιλογή Γ είναι ΣΩΣΤΗ ✓

Δ. Όλα τα παραπάνω

Επειδή και οι τρεις επιλογές (Α, Β, Γ) είναι σωστές, η επιλογή Δ είναι η σωστή απάντηση.

Πρακτική ερμηνεία

Τι σημαίνουν τα αποτελέσματα;

FTMade_model (PRE = 0.4071):

Οι επιτυχημένες βολές εξηγούν 40.71% της μεταβλητότητας στα λεπτά συμμετοχής
Το 59.29% εξαρτάται από άλλους παράγοντες
Μέτρια προβλεπτική ισχύς

Points_model (PRE = 0.6494):

Οι πόντοι εξηγούν 64.94% της μεταβλητότητας στα λεπτά
Μόνο το 35.06% εξαρτάται από άλλους παράγοντες
Ισχυρή προβλεπτική ισχύς

Συμπέρασμα

Όλες οι τρεις επιλογές (Α, Β, Γ) είναι σωστές επειδή:

✓ Α. PRE: Points (0.6494) > FTMade (0.4071)

✓ Β. SS Model: Points (33777630) > FTMade (21,174,726)

✓ Γ. SS Error: Points (18237622) < FTMade (30840526)

Άρα, η σωστή απάντηση είναι Δ — Όλα τα παραπάνω.

Το κεντρικό μήνυμα:

Το Points_model είναι ξεκάθαρα καλύτερο από το FTMade_model σε όλες τις μετρικές ποιότητας προσαρμογής. Οι πόντοι είναι ισχυρότερος προβλεπτικός παράγοντας των λεπτών παιχνιδιού από τις βολές.

Analysis of Variance Table (Type III SS)
 Model: Mins ~ FTMade

                                   SS  df           MS       F    PRE     p
 ----- --------------- | ------------ --- ------------ ------- ------ -----
 Model (error reduced) | 21174725.960   1 21174725.960 119.466 0.4071 .0000
 Error (from model)    | 30840525.949 174   177244.402                     
 ----- --------------- | ------------ --- ------------ ------- ------ -----
 Total (empty model)   | 52015251.909 175   297230.011

 Analysis of Variance Table (Type III SS)
 Model: Mins ~ Points

                                   SS  df           MS       F    PRE     p
 ----- --------------- | ------------ --- ------------ ------- ------ -----
 Model (error reduced) | 33777630.163   1 33777630.163 322.263 0.6494 .0000
 Error (from model)    | 18237621.747 174   104913.918                     
 ----- --------------- | ------------ --- ------------ ------- ------ -----
 Total (empty model)   | 52015251.909 175   297230.011

12. Γιατί το SS Total έχει την ίδια τιμή για το FTMade_model και το Points_model;

Και τα δύο βασίζονται στα υπόλοιπα από το μέσο όρο της ίδιας εξαρτημένης μεταβλητής.Και τα δύο βασίζονται στα υπόλοιπα από το μέσο όρο της ίδιας ανεξάρτητης μεταβλητής.Όλα τα μοντέλα που χρησιμοποιούν το ίδιο πλαίσιο δεδομένων θα έχουν το ίδιο SS Total.Και τα δύο μοντέλα βασίζονται στον ίδιο αριθμό παρατηρήσεων (n = 176).

Επεξήγηση

Σωστή απάντηση: Α — Και τα δύο βασίζονται στα υπόλοιπα από το μέσο όρο της ίδιας εξαρτημένης μεταβλητής.

Ανάλυση των μοντέλων

Από τους πίνακες βλέπουμε:

Model 1: Mins ~ FTMade

Εξαρτημένη μεταβλητή: Mins
Ανεξάρτητη μεταβλητή: FTMade
SS Total: 52015251.909

Model 2: Mins ~ Points

Εξαρτημένη μεταβλητή: Mins
Ανεξάρτητη μεταβλητή: Points
SS Total: 52015251.909

Παρατήρηση: > Και τα δύο μοντέλα προβλέπουν την ίδια εξαρτημένη μεταβλητή (Mins), αλλά χρησιμοποιούν διαφορετικές ανεξάρτητες μεταβλητές.

Τι είναι το SS Total;

Μαθηματικός ορισμός:

\[\text{SS Total} = \sum_{i=1}^{n} (Y_i - \bar{Y})^2\]

Για τα μοντέλα μας:

\[\text{SS Total} = \sum_{i=1}^{176} (\text{Mins}_i - \overline{\text{Mins}})^2\]

Το κλειδί:

Το SS Total εξαρτάται μόνο από:

Την εξαρτημένη μεταβλητή (Mins)

Το μέσο όρο της ($\overline{\text{Mins}}$)

Τα δεδομένα (n = 176 παρατηρήσεις)

ΔΕΝ εξαρτάται από την ανεξάρτητη μεταβλητή (X)!

Γιατί η Α είναι σωστή

«Και τα δύο βασίζονται στα υπόλοιπα από τον μέσο όρο της ίδιας εξαρτημένης μεταβλητής»

Αναλύοντας τη φράση:

“Υπόλοιπα από το μέσο όρο”: $(\text{Mins}_i - \overline{\text{Mins}})$
“Της ίδιας εξαρτημένης μεταβλητής”: Και τα δύο μοντέλα έχουν την Mins ως Y
“Βασίζονται”: Το SS Total υπολογίζεται από αυτά τα υπόλοιπα

Υπολογισμός:

Για Model 1 (Mins ~ FTMade):

\[\text{SS Total} = \sum (\text{Mins}_i - \overline{\text{Mins}})^2 = 52015251.909\]

Για Model 2 (Mins ~ Points):

\[\text{SS Total} = \sum (\text{Mins}_i - \overline{\text{Mins}})^2 = 52015251.909\]

Είναι ακριβώς ο ίδιος υπολογισμός!

Και τα δύο χρησιμοποιούν:

Τις ίδιες τιμές της Mins
Τον ίδιο μέσο όρο της Mins
Τις ίδιες αποκλίσεις από το μέσο όρο

Γιατί οι άλλες επιλογές είναι λάθος;

Β. «Υπόλοιπα από τον μέσο όρο της ίδιας ανεξάρτητης μεταβλητής» — ΛΑΘΟΣ

Γιατί είναι λάθος:

Διαφορετικές ανεξάρτητες μεταβλητές:
- Model 1: FTMade
- Model 2: Points
- ΔΕΝ είναι η ίδια!
Το SS Total δεν χρησιμοποιεί την ανεξάρτητη μεταβλητή:

\[\text{SS Total} = \sum (Y_i - \bar{Y})^2\]

Δεν υπάρχει αναφορά σε X (FTMade ή Points)!

Γ. «Όλα τα μοντέλα με το ίδιο πλαίσιο δεδομένων έχουν το ίδιο SS Total» — ΛΑΘΟΣ

Γιατί είναι λάθος:

Αυτή η δήλωση είναι πολύ γενική και εσφαλμένη.

Αντιπαράδειγμα:

# Ίδιο πλαίσιο δεδομένων, ΔΙΑΦΟΡΕΤΙΚΕΣ εξαρτημές μεταβλητές
model1 <- lm(Mins ~ FTMade, data = NBA)      # Y = Mins
model2 <- lm(Points ~ FTMade, data = NBA)    # Y = Points

# Αυτά θα έχουν ΔΙΑΦΟΡΕΤΙΚΟ `SS Total`!
supernova(model1)  # SS Total για Mins
supernova(model2)  # SS Total για Points (διαφορετικό!)

Γιατί;

SS Total για Mins: $\sum (\text{Mins}_i - \overline{\text{Mins}})^2$
SS Total για Points: $\sum (\text{Points}_i - \overline{\text{Points}})^2$

Διαφορετική Y → Διαφορετικό SS Total!

Η σωστή δήλωση θα ήταν:

“Όλα τα μοντέλα που προβλέπουν την ίδια εξαρτημένη μεταβλητή από το ίδιο πλαίσιο δεδομένων θα έχουν το ίδιο SS Total.”

Δ. «Ίδιος αριθμός τιμών (n = 176)» — ΛΑΘΟΣ

Γιατί είναι λάθος:

Το n δεν είναι αρκετό για να εξηγήσει γιατί το SS Total είναι το ίδιο.

Παράδειγμα:

Δύο μοντέλα με το ίδιο n αλλά διαφορετικές εξαρτημένες μεταβλητές:

model1 <- lm(Mins ~ X, data = NBA)      # n = 176, Y = Mins
model2 <- lm(Points ~ X, data = NBA)    # n = 176, Y = Points

Και τα δύο έχουν n = 176, αλλά:

SS Total για Mins ≠ SS Total για Points

Το n είναι απαραίτητο αλλά όχι αρκετό!

Χρειαζόμαστε:

Ίδιο n ✓
Ίδια εξαρτημένη μεταβλητή ✓
Ίδιες τιμές ✓

Η θεμελιώδης σχέση

Για και τα δύο μοντέλα:

\[\text{SS Total} = \text{SS Model} + \text{SS Error}\]

Model 1:

\[52015251.909 = 21174725.960 + 30840525.949\] ✓

Model 2:

\[52015251.909 = 33777630.163 + 18237621.747\] ✓

Η “πίτα” (SS Total) είναι η ίδια, αλλά την κόβουμε διαφορετικά!

Συμπέρασμα

Το SS Total είναι το ίδιο για τα δύο μοντέλα επειδή:

Και τα δύο βασίζονται στα υπόλοιπα από το μέσο όρο της ίδιας εξαρτημένης μεταβλητής (Mins).

Μαθηματικά:

\[\text{SS Total} = \sum_{i=1}^{176} (\text{Mins}_i - \overline{\text{Mins}})^2 = 52015251.909\]

Βασικά σημεία:

Το SS Total εξαρτάται ΜΟΝΟ από την εξαρτημένη μεταβλητή (Y)
ΔΕΝ εξαρτάται από την ανεξάρτητη μεταβλητή (X)
Αντιπροσωπεύει τη συνολική μεταβλητότητα της Y πριν προσθέσουμε οποιαδήποτε X
Είναι το σημείο αναφοράς (κενό μοντέλο) για όλα τα μοντέλα με την ίδια Y

Γενικός κανόνας:

Όλα τα μοντέλα που προβλέπουν την ίδια εξαρτημένη μεταβλητή από τα ίδια δεδομένα θα έχουν το ίδιο SS Total, ανεξάρτητα από τις προβλεπτικές μεταβλητές που χρησιμοποιούν.

 Analysis of Variance Table (Type III SS)
 Model: Mins ~ Points

                                   SS  df           MS       F    PRE     p
 ----- --------------- | ------------ --- ------------ ------- ------ -----
 Model (error reduced) | 33777630.163   1 33777630.163 322.263 0.6494 .0000
 Error (from model)    | 18237621.747 174   104813.918                     
 ----- --------------- | ------------ --- ------------ ------- ------ -----
 Total (empty model)   | 52015251.909 175   297230.011

13. Ποια από τις ακόλουθες είναι η σωστή ερμηνεία του MS Total (297230) στον παραπάνω πίνακα;

Αυτή είναι, περίπου, η τυπική απόκλιση από το μέσο όρο.Αυτός είναι, περίπου, ο συνολικός αριθμός των τετραγώνων των μέσων όρων βασισμένων στο κενό μοντέλο.Αυτό είναι, περίπου, το μέσο άθροισμα τετραγώνων των υπολοίπων από το μέσο όρο.Αυτός είναι, περίπου, ο συνολικός αριθμός πόντων στο πλαίσιο δεδομένων.

Επεξήγηση

Σωστή απάντηση: Γ — Αυτό είναι, περίπου, το μέσο τετραγωνισμένο υπόλοιπο από τον μέσο όρο.

Τι είναι το MS (Mean Square);

Το MS (Mean Square) είναι το μέσο (average) των τετραγωνισμένων αποκλίσεων.

Γενικός τύπος:

\[\text{MS} = \frac{\text{SS}}{\text{df}}\]

όπου:

SS = Sum of Squares (άθροισμα τετραγώνων)
df = degrees of freedom (βαθμοί ελευθερίας)

Τι είναι το MS Total;

Το MS Total υπολογίζεται ως:

\[\text{MS Total} = \frac{\text{SS Total}}{\text{df Total}}\]

Από τον πίνακα:

\[\text{MS Total} = \frac{52,015,251.909}{175} = 297,230.011\]

Τι σημαίνει αυτό;

Το MS Total είναι το μέσο άθροισμα τετραγώνων των υπολοίπων από το μέσο όρο της εξαρτημένης μεταβλητής.

Με άλλα λόγια:

\[\text{MS Total} = \frac{1}{n-1} \sum_{i=1}^{n} (Y_i - \bar{Y})^2\]

όπου:

$Y_i$ = παρατηρούμενη τιμή
$\bar{Y}$ = μέσος όρος
$n-1 = 175$ = βαθμοί ελευθερίας

Γιατί η Γ είναι σωστή

“Το μέσο άθροισμα τετραγώνων των υπολοίπων από το μέσο όρο” περιγράφει ακριβώς τι είναι το MS Total:

“Υπόλοιπα από το μέσο όρο”: $(Y_i - \bar{Y})$
“Στο τετράγωνο”: $(Y_i - \bar{Y})^2$
“Ο μέσος όρος αυτών”: $\frac{\sum (Y_i - \bar{Y})^2}{n-1}$

Ερμηνεία:

Το MS Total = 297230 λέει:

“Κατά μέσο όρο, κάθε παρατήρηση αποκλίνει από το μέσο όρο κατά $\sqrt{297230} \approx 545$ λεπτά (όταν υψώνουμε την απόκλιση στο τετράγωνο).”

Σχέση με τη διακύμανση

Το MS Total είναι στην πραγματικότητα η διακύμανση (variance) της εξαρτημένης μεταβλητής!

\[\text{Variance}(Y) = s^2 = \frac{\sum (Y_i - \bar{Y})^2}{n-1} = \text{MS Total}\]

Από τον πίνακα:

\[s^2_{\text{Mins}} = 297230\]

Η τυπική απόκλιση είναι:

\[s_{\text{Mins}} = \sqrt{297,230} \approx 545.19 \text{ λεπτά}\]

Γιατί οι άλλες επιλογές είναι λάθος;

Α. «Αυτή είναι, περίπου, η τυπική απόκλιση από το μέσο όρο» — ΛΑΘΟΣ

Γιατί είναι λάθος:

Το MS Total δεν είναι η τυπική απόκλιση — είναι η διακύμανση (το τετράγωνο της τυπικής απόκλισης)!

Η διαφορά:

Στατιστικό	Σύμβολο	Τύπος	Τιμή
Διακύμανση	$s^2$	$\frac{\sum(Y_i - \bar{Y})^2}{n-1}$	297,230
Τυπική απόκλιση	$s$	$\sqrt{s^2}$	$\sqrt{297,230} \approx 545$

Β. «Αυτός είναι, περίπου, ο συνολικός αριθμός των τετραγώνων των μέσων όρων βασισμένων στο κενό μοντέλο» — ΛΑΘΟΣ

Γιατί είναι λάθος:

Αυτή η φράση δεν έχει νόημα στατιστικά.

Προβλήματα:

“Μέσοι όροι στο τετράγωνο” — Τι είναι αυτό;
- Δεν τετραγωνίζουμε μέσους όρους
- Τετραγωνίζουμε αποκλίσεις από το μέσο όρο
“Συνολικός αριθμός” — Το MS είναι μέσος όρος, όχι άθροισμα
- Αν θέλαμε άθροισμα, θα χρησιμοποιούσαμε το SS (Sum of Squares)
- Το MS = SS / df (μέσος όρος)
Μονάδες μέτρησης:
- MS Total = 297230 λεπτά²
- Δεν είναι “αριθμός” (χωρίς μονάδες)

Σωστή ορολογία:

SS Total: Συνολικό άθροισμα τετραγωνισμένων αποκλίσεων
MS Total: Μέσο άθροισμα τετραγώνων των υπολοίπων (διακύμανση)

Δ. «Αυτός είναι, περίπου, ο συνολικός αριθμός πόντων στο πλαίσιο δεδομένων» — ΛΑΘΟΣ

Γιατί είναι λάθος:

Αυτή η επιλογή συγχέει εντελώς το MS Total με κάτι άσχετο.

Τι είναι το MS Total:

MS Total = 297230 λεπτά² (διακύμανση των λεπτών παιχνιδιού)

Τι ΔΕΝ είναι:

ΔΕΝ είναι ο αριθμός πόντων
ΔΕΝ είναι ο συνολικός αριθμός οτιδήποτε
ΔΕΝ σχετίζεται με την ανεξάρτητη μεταβλητή (Points)

Επιπλέον:

Το MS Total αφορά τη μεταβλητότητα των Mins (όχι Points)
Είναι στατιστικό μέγεθος με μονάδες λεπτά²
Δεν έχει καμία σχέση με το πλήθος των δεδομένων

Βαθύτερη κατανόηση: Τα τρία MS στον πίνακα

Ο πίνακας της supernova περιέχει τρία MS:

`MS`	Τύπος	Τιμή	Ερμηνεία
`MS Model`	$\frac{\text{SS Model}}{\text{df Model}}$	$\frac{33777630}{1} = 33777630$	Μέσο τετραγωνισμένο υπόλοιπο που εξηγείται
MS Error	$\frac{\text{SS Error}}{\text{df Error}}$	$\frac{18,237,622}{174} = 104,814$	Μέσο τετραγωνισμένο υπόλοιπο που δεν εξηγείται
MS Total	$\frac{\text{SS Total}}{\text{df Total}}$	$\frac{52,015,252}{175} = 297,230$	Μέσο τετραγωνισμένο υπόλοιπο από τον μέσο όρο

Σχέσεις:

MS Total = Διακύμανση της Y
πηλίκο F: \[F = \frac{\text{MS Model}}{\text{MS Error}} = \frac{33,777,630}{104,814} = 322.263\]
Η σχέση με το $R^2$: \[R^2 = \frac{\text{SS Model}}{\text{SS Total}} = \frac{33777630}{52015252} = 0.6494\]

Συμπέρασμα

Το MS Total (297230) είναι:

Το μέσο άθροισμα τετραγώνων των υπολοίπων από το μέσο όρο της εξαρτημένης μεταβλητής (Mins).

Με άλλα λόγια:

Είναι η διακύμανση της Mins
Μετράει το μέσο όρο τους αθροίσματος τετραγώνων των αποκλίσεων από το μέσο όρο
Η ρίζα του ($\sqrt{297230} \approx 545$) είναι η τυπική απόκλιση

Γιατί “περίπου”;

Η λέξη “περίπου” χρησιμοποιείται επειδή:

Το MS είναι ένας εκτιμητής της διακύμανσης του πληθυσμού
Υπολογίζεται από δείγμα, όχι από ολόκληρο τον πληθυσμό
Έχει κάποια αβεβαιότητα (variability)

Βασική αρχή:

\[\text{MS} = \text{"Mean Square"} = \text{Μέσος όρος του αθροίσματος τετραγώνων των αποκλίσεων}\]

 Analysis of Variance Table (Type III SS)
 Model: Mins ~ Points

                                   SS  df           MS       F    PRE     p
 ----- --------------- | ------------ --- ------------ ------- ------ -----
 Model (error reduced) | 33777630.163   1 33777630.163 322.263 0.6494 .0000
 Error (from model)    | 18237621.747 174   104813.918                     
 ----- --------------- | ------------ --- ------------ ------- ------ -----
 Total (empty model)   | 52015251.909 175   297230.011

14. Ποια από τις ακόλουθες είναι η σωστή ερμηνεία του PRE (0.65) στον παραπάνω πίνακα της supernova();

Το 65% των λεπτών συμμετοχής των παικτών που βρίσκονται στο πλαίσιο δεδομένων μπορεί να προβλεφθεί από τους πόντους τους (Points).Το SS Total του μοντέλου της Points θα είναι το 65% του SS Total από το κενό μοντέλο.Το 65% του μοντέλου της Points μπορεί να μειωθεί αναλογικά από το κενό μοντέλο.Το 65% του SS Total από το κενό μοντέλο μπορεί να εξηγηθεί με την προσθήκη της μεταβλητής Points.

Επεξήγηση

Σωστή απάντηση: Δ — Το 65% του SS Total από το κενό μοντέλο μπορεί να εξηγηθεί προσθέτοντας τη μεταβλητή Points στο μοντέλο.

Τι είναι το PRE;

Το PRE σημαίνει Proportional Reduction in Error (Αναλογική Μείωση Σφάλματος).

Είναι το ίδιο με το $R^2$ (συντελεστής προσδιορισμού).

Μαθηματικός ορισμός:

\[\text{PRE} = R^2 = \frac{\text{SS Model}}{\text{SS Total}} = \frac{\text{Error Reduced}}{\text{Total Error}}\]

Από τον πίνακα:

\[\text{PRE} = \frac{33777630}{52015252} = 0.6494 \approx 0.65 = 65\%\]

Τι μετράει το PRE;

Το PRE μετράει το ποσοστό της μεταβλητότητας που εξηγείται όταν προσθέτουμε μια ανεξάρτητη μεταβλητή στο μοντέλο.

Η βασική ερώτηση:

“Πόσο καλύτερα προβλέπουμε την εξαρτημένη μεταβλητή όταν χρησιμοποιούμε την ανεξάρτητη μεταβλητή, σε σύγκριση με το να μη χρησιμοποιούμε τίποτα (κενό μοντέλο);”

Τα δύο μοντέλα:

Κενό μοντέλο:
- Πρόβλεψη: $\hat{Y}_i = \bar{Y}$ (μόνο ο μέσος όρος)
- Error: SS Total = 52015252
Μοντέλο της Points:
- Πρόβλεψη: $\hat{Y}_i = b_0 + b_1 \times \text{Points}_i$
- Error: SS Error = 18237622

Μείωση σφάλματος:

\[\text{Error Reduced} = \text{SS Total} - \text{SS Error} = 52015252 - 18237622 = 33777630\]

Αναλογική μείωση:

\[\text{PRE} = \frac{\text{Error Reduced}}{\text{SS Total}} = \frac{33,777,630}{52,015,252} = 0.65\]

Γιατί η Δ είναι σωστή

“Το 65% του SS Total από το κενό μοντέλο μπορεί να εξηγηθεί προσθέτοντας τη μεταβλητή Points”

Αυτή η διατύπωση είναι ακριβής επειδή:

“SS Total από το κενό μοντέλο” = SS Total = 52015252
“Προσθέτοντας τη μεταβλητή Points” = Μετάβαση από κενό μοντέλο στο μοντέλο Mins ~ Points
“65% μπορεί να εξηγηθεί” = 65% της συνολικής μεταβλητότητας εξηγείται

Γιατί οι άλλες επιλογές είναι λάθος;

Α. «Το 65% των λεπτών συμμετοχής των παικτών μπορεί να προβλεφθεί με τη μεταβλητή Points» — ΛΑΘΟΣ

Γιατί είναι λάθος:

Αυτή η διατύπωση είναι παραπλανητική και ανακριβής.

Το πρόβλημα:

Το PRE δεν λέει ότι μπορούμε να προβλέψουμε το “65% των λεπτών”. Λέει ότι μπορούμε να εξηγήσουμε το 65% της μεταβλητότητας.

Η διαφορά:

“65% των λεπτών” → Υπονοεί ότι προβλέπουμε 0.65 × Mins
“65% της μεταβλητότητας” → Εξηγούμε 65% της διασποράς γύρω από τον μέσο όρο

Επιπλέον:

Το PRE = 0.65 δεν σημαίνει ότι:

Οι προβλέψεις μας είναι 65% ακριβείς
Μπορούμε να προβλέψουμε 65% της τιμής
Το 65% των παικτών προβλέπονται σωστά

Σημαίνει:

Εξηγείται το 65% της μεταβλητότητας

Β. «Το SS Total του μοντέλου της Points θα είναι το 65% του SS Total από το κενό μοντέλο» — ΛΑΘΟΣ

Γιατί είναι λάθος:

Το SS Total είναι το ίδιο και για τα δύο μοντέλα!

Από τον πίνακα:

SS Total (κενό μοντέλο): 52015252
SS Total (μοντέλο της Points): 52015252

Είναι ακριβώς το ίδιο, όχι 65%!

Γιατί το SS Total δεν αλλάζει;

Το SS Total εξαρτάται μόνο από την εξαρτημένη μεταβλητή:

\[\text{SS Total} = \sum (Y_i - \bar{Y})^2\]

Δεν εξαρτάται από την ανεξάρτητη μεταβλητή!

Τι είναι το 65%;

Το 65% αφορά το SS Model (όχι SS Total):

\[\text{SS Model} = 0.65 \times \text{SS Total} = 0.65 \times 52015252 = 33777630\]

Γ. «Το 65% του μοντέλου της Points μπορεί να μειωθεί αναλογικά από το κενό μοντέλο» — ΛΑΘΟΣ

Γιατί είναι λάθος:

Αυτή η φράση έχει την κατεύθυνση ανάποδα!

Το λάθος:

Η επιλογή Γ λέει: “Το κενό μοντέλο μειώνει το μοντέλο της Points”

Η αλήθεια:

Το μοντέλο της Points μειώνει το σφάλμα του κενού μοντέλου!

Η σωστή κατεύθυνση:

Κενό μοντέλο (αφετηρία)
    ↓
Προσθέτουμε την `Points`
    ↓
Μοντέλο της `Points` (βελτιωμένο)
    ↓
Μειώνουμε το σφάλμα κατά 65%

Ο ορισμός του PRE:

PRE = Proportional Reduction in Error

Error = Το σφάλμα του κενού μοντέλου (SS Total)
Reduction = Μείωση αυτού του σφάλματος
Proportional = Το ποσοστό μείωσης

Άρα:

\[\text{PRE} = \frac{\text{Σφάλμα του κενού μοντέλου που μειώνεται}}{\text{Σφάλμα του κενού μοντέλου}}\]

Όχι το αντίστροφο!

Ερμηνεία:

“Προσθέτοντας τη μεταβλητή Points, μειώσαμε το σφάλμα κατά 65%. Με άλλα λόγια, εξηγήσαμε το 65% της μεταβλητότητας που υπήρχε στο κενό μοντέλο.”

Διαφορετικοί τρόποι να εκφράσουμε το ίδιο πράγμα

Όλες αυτές οι διατυπώσεις είναι σωστές και ισοδύναμες:

“Το μοντέλο της Points εξηγεί το 65% της μεταβλητότητας στην Mins.”
“Το PRE είναι 0.65, άρα μειώσαμε το σφάλμα του κενού μοντέλου κατά 65%.”
“Το $R^2 = 0.65$, άρα το 65% της συνολικής διασποράς εξηγείται από τη μεταβλητή Points.”
“Το **65% του SS Total** γίνεταιSS Modelόταν προσθέτουμε τη μεταβλητήPoints`.”
“Η μεταβλητή Points μειώνει την ανεξήγητη μεταβλητότητα κατά 65% του αρχικού SS Total.”

Όλες αυτές περιγράφουν το ίδιο πράγμα με διαφορετικά λόγια!

Συμπέρασμα

Το PRE = 0.65 σημαίνει:

Το 65% της μεταβλητότητας (SS Total) που υπήρχε στο κενό μοντέλο μπορεί να εξηγηθεί προσθέτοντας τους Points ως ανεξάρτητη μεταβλητή.

Analysis of Variance Table (Type III SS)
 Model: Mins ~ Points

                                   SS  df           MS       F    PRE     p
 ----- --------------- | ------------ --- ------------ ------- ------ -----
 Model (error reduced) | 33777630.163   1 33777630.163 322.263 0.6494 .0000
 Error (from model)    | 18237621.747 174   104813.918                     
 ----- --------------- | ------------ --- ------------ ------- ------ -----
 Total (empty model)   | 52015251.909 175   297230.011

15. Υποστηρίζουν τα παραπάνω αποτελέσματα τον ισχυρισμό ότι όταν ένας παίκτης πετυχαίνει περισσότερους πόντους, αυτό οδηγεί τους προπονητές και άλλους υπευθύνους λήψης αποφάσεων να του δίνουν περισσότερο χρόνο παιχνιδιού; Γιατί ναι ή γιατί όχι;

16. Χρησιμοποιήσαμε τον παρακάτω κώδικα για να υπολογίσουμε το συντελεστή συσχέτισης (r του Pearson) για τις Mins και Points:

cor(Mins ~ Points, data = NBAPlayers2011)

Τι από τα παρακάτω έχουμε βρει;

Ένα μέτρο του πόσο κοντά βρίσκονται οι παρατηρήσεις στην ευθεία παλινδρόμησηςΤην κλίση της ευθείας παλινδρόμησης μεταξύ των τυποποιημένων μεταβλητών Mins και PointsΤην ένταση μιας διμεταβλητής σχέσηςΌλα τα παραπάνω

Επεξήγηση

Σωστή απάντηση: Δ — Όλα τα παραπάνω

Τι είναι ο συντελεστής συσχέτισης (Pearson’s r);

Ο συντελεστής συσχέτισης (r) είναι ένα μέτρο της γραμμικής σχέσης μεταξύ δύο μεταβλητών.

Εύρος τιμών:

\[-1 \leq r \leq 1\]

όπου:

r = 1: Τέλεια θετική γραμμική σχέση
r = -1: Τέλεια αρνητική γραμμική σχέση
r = 0: Καμία γραμμική σχέση

Γιατί η Δ είναι σωστή: Όλες οι ερμηνείες είναι σωστές

Ο συντελεστής συσχέτισης r έχει πολλαπλές ισοδύναμες ερμηνείες. Ας εξετάσουμε κάθε μία:

Α. “Μέτρο του πόσο κοντά βρίσκονται στα σημεία στην ευθεία παλινδρόμησης” — ΣΩΣΤΟ ✓

Ερμηνεία:

Το $|r|$ (απόλυτη τιμή) δείχνει πόσο κοντά είναι τα σημεία στην ευθεία παλινδρόμησης:

|r| κοντά στο 1: Τα σημεία είναι πολύ κοντά στην ευθεία
|r| κοντά στο 0: Τα σημεία είναι διασκορπισμένα μακριά από την ευθεία

Σχέση με $R^2$:

\[R^2 = r^2\]

Το $R^2$ μετρά πόση μεταβλητότητα εξηγείται — άρα πόσο “κοντά” είναι τα σημεία στη γραμμή.

Παράδειγμα:

Αν $r = 0.8$:

$R^2 = 0.64$
Εξηγείται το 64% της μεταβλητότητας
Τα σημεία βρίσκονται σχετικά κοντά στην ευθεία

Αυτή η ερμηνεία είναι ΣΩΣΤΗ ✓

Β. “Η κλίση της ευθείας παλινδρόμησης μεταξύ των τυποποιημένων Mins και Points” — ΣΩΣΤΟ ✓

Ερμηνεία:

Όταν τυποποιούμε (standardize) και τις δύο μεταβλητές:

\[Z_Y = \frac{Y - \bar{Y}}{s_Y}, \quad Z_X = \frac{X - \bar{X}}{s_X}\]

Η ευθεία παλινδρόμησης γίνεται:

\[Z_Y = r \times Z_X\]

Άρα, η κλίση της ευθείας παλινδρόμησης = r

Παράδειγμα:

# Τυποποίηση μεταβλητών
z_mins <- scale(NBAPlayers2011$Mins)
z_points <- scale(NBAPlayers2011$Points)

# Παλινδρόμηση τυποποιημένων μεταβλητών
model_z <- lm(z_mins ~ z_points)
coef(model_z)[2]  # Κλίση = r

# Σύγκριση με συσχέτιση
cor(Mins ~ Points, data = NBAPlayers2011)  # Ίδια τιμή!

Αυτή η ερμηνεία είναι ΣΩΣΤΗ ✓

Γ. “Η ένταση μιας διμεταβλητής σχέσης” — ΣΩΣΤΟ ✓

Ερμηνεία:

Το $|r|$ μετρά την ένταση (strength) της γραμμικής σχέσης:

	r
0.00 - 0.30	Ασθενής
0.30 - 0.70	Μέτρια
0.70 - 1.00	Ισχυρή

Το πρόσημο (+/−) δείχνει την κατεύθυνση:

r > 0: Θετική σχέση (όταν το X αυξάνεται, το Y αυξάνεται)
r < 0: Αρνητική σχέση (όταν το X αυξάνεται, το Y μειώνεται)

“Διμεταβλητή” σχέση = σχέση μεταξύ δύο μεταβλητών

Παράδειγμα:

Αν $r = 0.806$ για Mins ~ Points:

Ένταση: Ισχυρή (|0.806| > 0.70)
Κατεύθυνση: Θετική (περισσότεροι πόντοι → περισσότερα λεπτά συμμετοχής)

Αυτή η ερμηνεία είναι ΣΩΣΤΗ ✓

Γιατί και οι τρεις ερμηνείες είναι σωστές;

Ο συντελεστής συσχέτισης r είναι ένα πολυδιάστατο μέτρο που περιγράφει:

Ένταση σχέσης (πόσο ισχυρή είναι)
Κατεύθυνση σχέσης (θετική ή αρνητική)
Στενότητα προσαρμογής (πόσο κοντά στη γραμμή)
Τυποποιημένη κλίση (κλίση με τιμές z)

Όλες αυτές οι πτυχές είναι ενσωματωμένες στην τιμή του r

Σχέση με άλλα στατιστικά

1. Με το $R^2$:

\[R^2 = r^2\]

Παράδειγμα:

r <- cor(Mins ~ Points, data = NBAPlayers2011)  # 0.806

r_squared <- r^2                                 # 0.649

2. Με την κλίση:

\[b_1 = r \times \frac{s_Y}{s_X}\]

Παράδειγμα:

r <- cor(Mins ~ Points, data = NBAPlayers2011)
sy <- sd(NBAPlayers2011$Mins)
sx <- sd(NBAPlayers2011$Points)
b1_calculated <- r * (sy / sx)

# Σύγκριση με πραγματική κλίση
model <- lm(Mins ~ Points, data = NBAPlayers2011)
b1_actual <- coef(model)[2]

# Είναι ίδια!

3. Με το PRE:

\[\text{PRE} = R^2 = r^2\]

Πρακτικό παράδειγμα

# Υπολογισμός συσχέτισης
r <- cor(Mins ~ Points, data = NBAPlayers2011)
cat("r =", round(r, 3))  # π.χ., 0.806

# Ερμηνεία Α: Στενότητα γύρω από τη γραμμή
r_squared <- r^2
cat("R² =", round(r_squared, 3))  # 0.649
cat("Τα σημεία εξηγούν", round(r_squared * 100, 1), "% της μεταβλητότητας")

# Ερμηνεία Β: Τυποποιημένη κλίση
z_mins <- scale(NBAPlayers2011$Mins)
z_points <- scale(NBAPlayers2011$Points)
model_z <- lm(z_mins ~ z_points)
slope_z <- coef(model_z)[2]
cat("Τυποποιημένη κλίση =", round(slope_z, 3))  # Ίδιο με r

# Ερμηνεία Γ: Ένταση σχέσης
if (abs(r) > 0.7) {
  cat("Ισχυρή σχέση")
} else if (abs(r) > 0.3) {
  cat("Μέτρια σχέση")
} else {
  cat("Ασθενής σχέση")
}

# Όλες οι ερμηνείες είναι σωστές και αναφέρονται στο ίδιο r!

Συμπέρασμα

Ο συντελεστής συσχέτισης r αποτελεί:

✓ Α. Μέτρο της στενότητας των σημείων γύρω από τη γραμμή

✓ Β. Την κλίση της ευθείας παλινδρόμησης των τυποποιημένων μεταβλητών

✓ Γ. Την ένταση της διμεταβλητής σχέσης

Όλες αυτές είναι διαφορετικές πτυχές του ίδιου πράγματος!

Βασική αρχή:

Ο συντελεστής συσχέτισης r είναι ένα πλούσιο στατιστικό που μπορεί να ερμηνευτεί με πολλούς τρόπους, όλοι ισοδύναμοι και σωστοί.

17. Αν υπολογίζατε το άθροισμα των υπολοίπων από το κενό μοντέλο της Mins, τι θα ήταν αυτό;

Μεγαλύτερο από το άθροισμα των υπολοίπων από το Points_model της Mins0Μικρότερο από το άθροισμα των υπολοίπων από το Points_model της MinsΕίναι αδύνατο να το γνωρίζουμε πριν το υπολογίσουμε

Επεξήγηση

Σωστή απάντηση: Β — 0

Βασική ιδιότητα των υπολοίπων

Για οποιοδήποτε μοντέλο γραμμικής παλινδρόμησης που περιλαμβάνει σταθερό όρο (intercept), το άθροισμα των υπολοίπων είναι πάντα 0.

\[\sum_{i=1}^{n} e_i = \sum_{i=1}^{n} (Y_i - \hat{Y}_i) = 0\]

Αυτό ισχύει για:

Το κενό μοντέλο
Το μοντέλο απλής παλινδρόμησης
Το μοντέλο πολλαπλής παλινδρόμησης
Οποιοδήποτε μοντέλο με σταθερό όρο

Γιατί το άθροισμα είναι 0;

Για το κενό μοντέλο:

\[Y_i = \beta_0 + e_i\]

όπου $\beta_0 = \bar{Y}$ (ο μέσος όρος)

Τα υπόλοιπα:

\[e_i = Y_i - \hat{Y}_i = Y_i - \bar{Y}\]

Το άθροισμα:

\[\begin{align} \sum e_i &= \sum (Y_i - \bar{Y}) \\ &= \sum Y_i - \sum \bar{Y} \\ &= \sum Y_i - n\bar{Y} \\ &= n\bar{Y} - n\bar{Y} \\ &= 0 \end{align}\]

Επειδή:

\[\bar{Y} = \frac{\sum Y_i}{n} \Rightarrow \sum Y_i = n\bar{Y}\]

Το ίδιο ισχύει και για το Points_model:

\[\sum (Y_i - \hat{Y}_i) = 0\]

Γιατί οι άλλες επιλογές είναι λάθος;

Α. «Μεγαλύτερο από το άθροισμα των υπολοίπων από το Points_model» — ΛΑΘΟΣ

Κενό μοντέλο: $\sum e_i = 0$
Points_model: $\sum e_i = 0$

\[0 \not> 0\]

Γ. «Μικρότερο από το άθροισμα των υπολοίπων από το Points_model» — ΛΑΘΟΣ

\[0 \not< 0\]

Δ. «Είναι αδύνατο να το γνωρίζουμε πριν το υπολογίσουμε» — ΛΑΘΟΣ

Είναι απολύτως βέβαιο: Το άθροισμα είναι πάντα 0 για μοντέλα με σταθερό όρο.

Πρακτικό παράδειγμα

# Κενό μοντέλο
empty_model <- lm(Mins ~ 1, data = NBAPlayers2011)
residuals_empty <- residuals(empty_model)
sum_empty <- sum(residuals_empty)
cat("Άθροισμα υπολοίπων (κενό):", sum_empty)  # ~0 (π.χ., 1.4e-11)

# Points model
points_model <- lm(Mins ~ Points, data = NBAPlayers2011)
residuals_points <- residuals(points_model)
sum_points <- sum(residuals_points)
cat("Άθροισμα υπολοίπων (Points):", sum_points)  # ~0 (π.χ., -2.3e-11)

# Και τα δύο είναι ουσιαστικά 0
# (Μικρές διαφορές λόγω στρογγυλοποίησης υπολογιστή)

Συμπέρασμα

Το άθροισμα των υπολοίπων:

Από το κενό μοντέλο: 0
Από το Points_model: 0
Από οποιοδήποτε μοντέλο με σταθερό όρο: 0

Βασική αρχή:

Το άθροισμα των υπολοίπων είναι πάντα μηδέν σε μοντέλα γραμμικής παλινδρόμησης με σταθερό όρο.

\[\sum e_i \text{ (άθροισμα)} = 0 \text{ (πάντα)}\]

18. Εκτός από τα δεδομένα των παικτών NBA για τη σεζόν 2011, έχουμε και ένα παρόμοιο πλαίσιο δεδομένων που ονομάζεται NBAPlayers2015 (με πολλές από τις ίδιες μεταβλητές). Έχουμε δημιουργήσει διαγράμματα διασποράς της Mins με την Points και για τις δύο σεζόν (το μωβ διάγραμμα διασποράς στα αριστερά αντιπροσωπεύει τη σεζόν 2011 και το πράσινο διάγραμμα διασποράς στα δεξιά αντιπροσωπεύει τη σεζόν 2015).

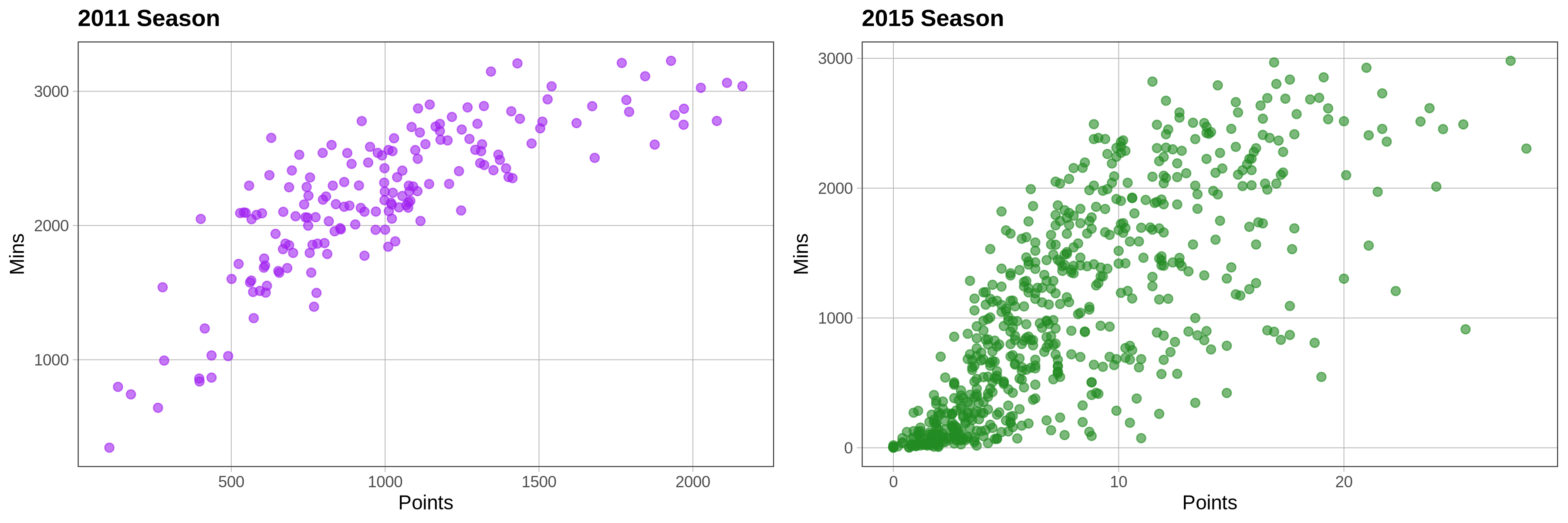
Αν προσαρμόσουμε τα δύο μοντέλα με τον ακόλουθο κώδικα, τι από τα παρακάτω θα ισχύει:

Points11_model <- lm(Mins ~ Points, data = NBAPlayers2011)
Points15_model <- lm(Mins ~ Points, data = NBAPlayers2015)

Η εκτίμηση της παραμέτρου του κενού μοντέλου θα είναι η ίδια επειδή θα είναι ο μέσος αριθμός λεπτών συμμετοχής στο παιχνίδι.Το SS Total και για τα δύο αυτά μοντέλα θα είναι το ίδιο, επειδή έχουν την ίδια εξαρτημένη μεταβλητή.Το SS Model και για τα δύο αυτά μοντέλα θα είναι το ίδιο επειδή έχουν την ίδια ανεξάρτητη μεταβλητή.Καμία από αυτές τις τιμές (SS Total, SS Model, σταθερός όρος) δεν θα είναι η ίδια.

Επεξήγηση

Σωστή απάντηση: Δ — Καμία από αυτές τις τιμές (SS Total, SS Model, σταθερός όρος) δεν θα είναι η ίδια.

Γιατί τίποτα δεν θα είναι το ίδιο;

Παρόλο που τα δύο σύνολα δεδομένων έχουν:

Την ίδια δομή (ίδιες μεταβλητές)
Την ίδια εξαρτημένη μεταβλητή (Mins)
Την ίδια ανεξάρτητη μεταβλητή (Points)

Έχουν διαφορετικά δεδομένα από διαφορετικές σεζόν!

Παρατηρήσεις από τα διαγράμματα

Σεζόν 2011 (μωβ):

Λιγότεροι παίκτες (~176)
Πιο στενή κατανομή Points (περίπου 0-2500)
Πιο συμπαγές νέφος σημείων

Σεζόν 2015 (πράσινο):

Περισσότεροι παίκτες (~500+)
Ευρύτερη κατανομή Points (0-25+)
Περισσότερη διασπορά στα σημεία

Αυτές οι διαφορές σημαίνουν ότι ΟΛΑ τα στατιστικά θα διαφέρουν!

Α. Ο μέσος όρος (κενό μοντέλο) — ΘΑ ΔΙΑΦΕΡΕΙ

Γιατί δεν θα είναι ίδιος;

Ο μέσος όρος εξαρτάται από τα συγκεκριμένα δεδομένα:

\[\bar{Y}_{2011} = \frac{\sum \text{Mins}_{2011}}{n_{2011}}\]

\[\bar{Y}_{2015} = \frac{\sum \text{Mins}_{2015}}{n_{2015}}\]

Πιθανές διαφορές:

Διαφορετικοί παίκτες στις δύο σεζόν
Διαφορετικός αριθμός παικτών (n)
Διαφορετικές στρατηγικές ομάδων
Διαφορετικοί κανόνες ή συνθήκες παιχνιδιού

Η επιλογή Α είναι ΛΑΘΟΣ ✗

Β. Το SS Total — ΘΑ ΔΙΑΦΕΡΕΙ

Γιατί δεν θα είναι ίδιο;

Το SS Total εξαρτάται από:

\[\text{SS Total} = \sum (Y_i - \bar{Y})^2\]

Τρεις λόγοι που θα διαφέρει:

1. Διαφορετικές τιμές $Y_i$

Διαφορετικοί παίκτες → διαφορετικά λεπτά
Η κατανομή του 2015 φαίνεται πιο διασκορπισμένη

2. Διαφορετικός μέσος όρος $\bar{Y}$

$\bar{Y}_{2011} \neq \bar{Y}_{2015}$

3. Διαφορετικός αριθμός παρατηρήσεων n

Το 2015 έχει πολύ περισσότερους παίκτες
Περισσότερες παρατηρήσεις → μεγαλύτερο άθροισμα

Από τα διαγράμματα:

Το 2015 έχει:

~3× περισσότερους παίκτες
Μεγαλύτερη διασπορά
Άρα πιθανότατα πολύ μεγαλύτερο SS Total

Η επιλογή Β είναι ΛΑΘΟΣ ✗

Γ. Το SS Model — ΘΑ ΔΙΑΦΕΡΕΙ

Γιατί δεν θα είναι ίδιο;

Το SS Model μετρά την εξηγούμενη μεταβλητότητα:

\[\text{Model SS} = \sum (\hat{Y}_i - \bar{Y})^2\]

Παράγοντες που το επηρεάζουν:

1. Διαφορετική κλίση ($b_1$)

Η σχέση Points-Mins μπορεί να είναι:

Ισχυρότερη ή ασθενέστερη
Διαφορετική απότομη (κλίση)

2. Διαφορετική κατανομή του X (Points)

Από τα διαγράμματα:

2011: Points περίπου 0-2500
2015: Points περίπου 0-25 (διαφορετική κλίμακα!)

3. Διαφορετικό SS Total

\[\text{SS Model} = \text{PRE} \times \text{SS Total}\]

Ακόμα και αν το PRE ήταν το ίδιο (που δεν είναι), το SS Total διαφέρει!

4. Διαφορετική ένταση σχέσης

Οπτικά, το 2011 φαίνεται να έχει:

Πιο στενή σχέση
Λιγότερη διασπορά
Πιθανώς υψηλότερο $R^2$

Η επιλογή Γ είναι ΛΑΘΟΣ ✗

Πότε θα ήταν κάτι ίδιο;

Τα στατιστικά θα ήταν ίδια μόνο αν:

Τα δεδομένα ήταν ακριβώς τα ίδια
Ή αν υπήρχε κάποια πολύ ειδική συμπτωση

Αλλά εδώ έχουμε ΔΙΑΦΟΡΕΤΙΚΑ σύνολα δεδομένων (2011 vs 2015)!

Συμπέρασμα

Καμία από τις τιμές δεν θα είναι ίδια επειδή:

Διαφορετικά σύνολα δεδομένων (2011 vs 2015 σεζόν)
Διαφορετικοί παίκτες και αριθμός παρατηρήσεων
Διαφορετικές κατανομές και για την Y και για την X
Διαφορετική μεταβλητότητα στα δεδομένα

Βασική αρχή:

Στατιστικά όπως ο μέσος όρος, SS Total, και SS Model εξαρτώνται από τα συγκεκριμένα δεδομένα. Διαφορετικά σύνολα δεδομένων → διαφορετικά στατιστικά.

Η μόνη περίπτωση που θα ήταν ίδια:

Αν τα δύο σύνολα δεδομένων είχαν τυχαία ακριβώς τις ίδιες τιμές—κάτι που είναι στατιστικά αδύνατο σε πραγματικά δεδομένα!

19. Με βάση αυτά τα διαγράμματα διασποράς, ποια σεζόν είχε υψηλότερη συσχέτιση μεταξύ των λεπτών παιχνιδιού και των πόντων που σημειώθηκαν;

Η συσχέτιση φαίνεται τέλεια επειδή και στα δύο διαγράμματα η κλίση είναι θετική.20112015Αδύνατο να το πούμε χωρίς υπολογισμούς

Επεξήγηση

Σωστή απάντηση: Β — 2011

Οπτική ανάλυση των διαγραμμάτων

Σεζόν 2011 (μωβ, αριστερά):

Τα σημεία είναι πιο στενά συγκεντρωμένα γύρω από μια νοητή ευθεία παλινδρόμησης
Λιγότερη διασπορά κάθετα από τη γραμμή
Πιο καθαρό γραμμικό μοτίβο
Μοιάζει με ισχυρότερη σχέση

Σεζόν 2015 (πράσινο, δεξιά):

Τα σημεία είναι πιο διασκορπισμένα
Μεγαλύτερη διασπορά γύρω από την ευθεία
Περισσότερο “θόρυβο” στα δεδομένα
Μοιάζει με ασθενέστερη σχέση

Τι δείχνει η συσχέτιση;

Ο συντελεστής συσχέτισης (r) μετρά πόσο στενά είναι τα σημεία γύρω από μια ευθεία γραμμή.

Οπτικά σημάδια υψηλής συσχέτισης:

✓ Σημεία κοντά σε μια φανταστική ευθεία γραμμή
✓ Λίγη κάθετη διασπορά
✓ Σαφές γραμμικό μοτίβο
✓ Μικρά υπόλοιπα

Οπτικά σημάδια χαμηλότερης συσχέτισης:

✗ Σημεία διασκορπισμένα μακριά από τη γραμμή
✗ Μεγάλη κάθετη διασπορά
✗ Ασαφές ή “θορυβώδες” μοτίβο
✗ Μεγάλα υπόλοιπα

Γιατί η Β (2011) είναι σωστή

Από τα διαγράμματα:

Το 2011 δείχνει:

Πιο στενό νέφος σημείων
Πιο συνεπές γραμμικό μοτίβο
Λιγότερες ακραίες αποκλίσεις
Μικρότερη κάθετη εξάπλωση

Αυτά όλα υποδηλώνουν υψηλότερο |r|

Εκτίμηση:

2011: $r \approx 0.80-0.85$ (ισχυρή συσχέτιση)
2015: $r \approx 0.60-0.70$ (μέτρια συσχέτιση)

Γιατί οι άλλες επιλογές είναι λάθος;

Α. «Η συσχέτιση φαίνεται τέλεια ίση επειδή και οι δύο έχουν θετική κλίση» — ΛΑΘΟΣ

Γιατί είναι λάθος:

Η κατεύθυνση (θετική/αρνητική) και η ένταση (πόσο στενή) της συσχέτισης είναι διαφορετικά πράγματα!

Κατεύθυνση:

Καθορίζεται από το πρόσημο της κλίσης (+/−)
Και τα δύο έχουν θετική κλίση ✓

Ένταση:

Καθορίζεται από το πόσο κοντά στη νοητή ευθεία είναι τα σημεία
Το 2011 έχει στενότερα σημεία
Άρα ισχυρότερη συσχέτιση

Παράδειγμα:

Και τα δύο μπορεί να έχουν θετική κλίση, αλλά:

2011: $r = +0.85$ (ισχυρή θετική)
2015: $r = +0.65$ (μέτρια θετική)

Το πρόσημο (+) είναι το ίδιο, αλλά το μέγεθος (0.85 vs 0.65) διαφέρει!

Γ. «2015» — ΛΑΘΟΣ

Γιατί είναι λάθος:

Το διάγραμμα του 2015 δείχνει περισσότερη διασπορά:

Σημεία πιο διασκορπισμένα
Μεγαλύτερες αποκλίσεις από την ευθεία
Πιο θορυβώδες μοτίβο

Παρατηρήσεις:

Περισσότεροι παίκτες (n ≈ 500) → περισσότερη ποικιλομορφία
Ευρύτερο φάσμαPointsκαιMins`
Περισσότερες ακραίες τιμές

Όλα αυτά μειώνουν τη συσχέτιση!

Δ. «Αδύνατο να το πούμε χωρίς υπολογισμούς» — ΛΑΘΟΣ (αλλά εν μέρει σωστό)

Γιατί είναι λάθος:

Παρόλο που οι ακριβείς τιμές χρειάζονται υπολογισμούς, μπορούμε να κάνουμε καλή εκτίμηση οπτικά:

Η διαφορά στη διασπορά γύρω από τη νοητή ευθεία είναι εμφανής
Στο 2011 φαίνεται εμφανώς πιο μικρή διασπορά
Μπορούμε να πούμε με εύλογη βεβαιότητα ότι στη σεζόν 2011 η συσχέτιση είναι υψηλότερη

Πότε θα ήταν σωστή η Δ:

Αν τα δύο διαγράμματα ήταν πολύ παρόμοια και η διαφορά ήταν αμελητέα.

Αλλά εδώ η διαφορά είναι αρκετά μεγάλη!

Πιθανοί λόγοι για τη διαφορά

Γιατί το 2011 έχει υψηλότερη συσχέτιση;

1. Μικρότερο δείγμα (n ≈ 176)

Λιγότερη ποικιλομορφία
Πιο ομοιογενής ομάδα παικτών

2. Διαφορετικές συνθήκες παιχνιδιού

Διαφορετικοί κανόνες
Διαφορετικές στρατηγικές ομάδων

3. Επιλογή δείγματος

Ίσως το 2011 περιλαμβάνει μόνο “βασικούς” παίκτες
Το 2015 μπορεί να περιλαμβάνει περισσότερους παίκτες

Συμπέρασμα

Στη σεζόν 2011 η συσχέτιση είναι υψηλότερη επειδή:

Τα σημεία είναι πιο στενά συγκεντρωμένα γύρω από την ευθεία
Υπάρχει λιγότερη διασπορά κάθετα από την ευθεία
Το γραμμικό μοτίβο είναι πιο σαφές και πιο ισχυρό

Βασική αρχή:

Μπορούμε να εκτιμήσουμε τη σχετική ένταση συσχετίσεων οπτικά εξετάζοντας πόσο στενά είναι τα σημεία γύρω από μια νοητή γραμμή. Το στενότερο νέφος σημείων δείχνει ισχυρότερη συσχέτιση.

20. Ας συγκρίνουμε δύο μοντέλα. Το πρώτο μοντέλο χρησιμοποιεί τους πόντους που σημειώθηκαν (Points) ως ποσοτική μεταβλητή για να προβλέψει τα λεπτά συμμετοχής στο παιχνίδι (Mins). Θα το ονομάσουμε μοντέλο της Points. Για να δημιουργήσουμε το δεύτερο μοντέλο, χρησιμοποιούμε τη μεταβλητή Points για να δημιουργήσουμε μια νέα μεταβλητή με 24 κατηγορίες (Points24Group). Έτσι το δεύτερο μοντέλο χρησιμοποιεί την Points24Group για να προβλέψει την Mins. Οι παρακάτω πίνακες της supernova() δείχνουν ότι η Points24Group μειώνει τη συνολική μεταβλητότητα στην Mins κατά 77%, ενώ η Points τη μειώνει κατά 65%. Γιατί, ωστόσο, το μοντέλο της Points24Group δεν είναι καλύτερο από το μοντέλο Points των Mins;

 Analysis of Variance Table (Type III SS)
 Model: Mins ~ Points

                                   SS  df           MS       F    PRE     p
 ----- --------------- | ------------ --- ------------ ------- ------ -----
 Model (error reduced) | 33777630.163   1 33777630.163 322.263 0.6494 .0000
 Error (from model)    | 18237621.747 174   104813.918                     
 ----- --------------- | ------------ --- ------------ ------- ------ -----
 Total (empty model)   | 52015251.909 175   297230.011

 Analysis of Variance Table (Type III SS)
 Model: Mins ~ Points24Group

                                   SS  df          MS      F    PRE     p
 ----- --------------- | ------------ --- ----------- ------ ------ -----
 Model (error reduced) | 39738347.891  23 1727754.256 21.391 0.7640 .0000
 Error (from model)    | 12276904.018 152   80769.105                    
 ----- --------------- | ------------ --- ----------- ------ ------ -----
 Total (empty model)   | 52015251.909 175  297230.011

Το μοντέλο της Points είναι προτιμότερο επειδή το όνομα είναι πιο σύντομο και πιο εύκολο να το θυμάσαι.Το SS Εrror είναι μεγαλύτερο για το μοντέλο της Points, κάτι που δείχνει το πλεονέκτημά του έναντι του μοντέλου της Points24Group.Ο δείκτης F δείχνει ότι το μοντέλο της Points εξηγεί περισσότερη μεταβλητότητα ανά βαθμό ελευθερίας από το μοντέλο της Points24Group.Ερώτηση παγίδα! Το μοντέλο της Points24Group είναι καλύτερο από το μοντέλο της Points επειδή το PRE είναι μεγαλύτερο, το SS Model είναι μεγαλύτερο, και το SS Error είναι μικρότερο. Δεν υπάρχει κάτι που να υποδηλώνει ότι το μοντέλο της Points είναι καλύτερο.

Επεξήγηση

Σωστή απάντηση: Γ — Ο δείκτης F δείχνει ότι το μοντέλο της Points εξηγεί περισσότερη μεταβλητότητα ανά βαθμό ελευθερίας από αυτό της Points24Group.

Το πρόβλημα: Υπερπροσαρμογή (overfitting))

Το μοντέλο της Points24Group έχει υψηλότερο PRE, αλλά αυτό δεν το κάνει καλύτερο!

Γιατί;

Χρησιμοποιεί 23 βαθμούς ελευθερίας (παραμέτρους) για να εξηγήσει μόνο 12% περισσότερη μεταβλητότητα από ό,τι το μοντέλο της Points που χρησιμοποιεί μόνο 1 βαθμό ελευθερίας.

Αυτό ονομάζεται υπερπροσαρμογή μοντέλου ή overfitting!

Σύγκριση των μοντέλων

Μετρική	`Points` (ποσοτική)	`Points24Group` (ποιοτική)	Ποιο καλύτερο;
`df Model`	1	23	`Points` (λιγότερες παράμετροι)
PRE	0.649 (64.9%)	0.764 (76.4%)	`Points24Group`
`Model SS`	33777630	39738348	`Points24Group`
`SS Error`	18237622	12276904	`Points24Group`
F	322.263	21.391	`Points` ✓
`MS Model`	33777630	1727754	`Points` ✓
Αποδοτικότητα	64.9% / 1 df	76.4% / 23 df	`Points` ✓

Γιατί η Γ είναι σωστή: Ο δείκτης ή πηλίκο F

Ο δείκτης F μετρά την αποδοτικότητα:

\[F = \frac{\text{MS Model}}{\text{MS Error}} = \frac{\text{Εξηγούμενη μεταβλητότητα ανά df}}{\text{Ανεξήγητη μεταβλητότητα ανά df}}\]

Από τους πίνακες:

Μοντέλο της Points:

\[F = \frac{33777630}{104814} = 322.263\]

Μοντέλο της Points24Group:

\[F = \frac{1727754}{80769} = 21.391\]

Σύγκριση:

\[322.263 >> 21.391\]

Ερμηνεία:

Το μοντέλο της Points εξηγεί 15× περισσότερη μεταβλητότητα ανά βαθμό ελευθερίας!

Αποδοτικότητα ανά βαθμό ελευθερίας

Το μοντέλο της Points:

Χρησιμοποιεί: 1 df
Εξηγεί: 64.9% της μεταβλητότητας
Αποδοτικότητα: $\frac{64.9\%}{1} = 64.9\%$ ανά df

Μοντέλο της Points24Group:

Χρησιμοποιεί: 23 df
Εξηγεί: 76.4% της μεταβλητότητας
Αποδοτικότητα: $\frac{76.4\%}{23} = 3.3\%$ ανά df

Το μοντέλο της Points εξηγεί 64.9% με μόνο 1 παράμετρο!

Το μοντέλο της Points24Group χρειάζεται 23 παραμέτρους για να εξηγήσει μόνο 11.5% περισσότερο!

Η αρχή της απλότητας (Parsimony)

Ξυράφι του Occam:

“Όταν δύο μοντέλα εξηγούν παρόμοια ποσότητα μεταβλητότητας, προτιμούμε το απλούστερο.”

Στην περίπτωσή μας:

Το μοντέλο της Points:

Είναι πολύ απλούστερο (1 παράμετρος vs 23)
Εξηγεί σχεδόν το ίδιο (64.9% vs 76.4%)
Είναι πολύ πιο αποδοτικό
Είναι πιο γενικεύσιμο σε νέα δεδομένα

Κίνδυνοι του μοντέλου της Points24Group

1. Overfitting (Υπερπροσαρμογή)

Το μοντέλο “μαθαίνει” το θόρυβο των δεδομένων
Δεν θα γενικεύεται καλά σε νέους παίκτες

2. Απώλεια ισχύος

Χρησιμοποιεί πολλούς βαθμούς ελευθερίας
Λιγότεροι df για το Σφάλμα → λιγότερη στατιστική ισχύς

3. Ερμηνευσιμότητα

23 παράμετροι είναι δύσκολο να ερμηνευτούν
1 κλίση είναι απλή και κατανοητή

4. Απώλεια πληροφορίας

Μετατρέποντας την ποσοτική μεταβλητή σε ποιοτική, χάνουμε πληροφορία
Θεωρούμε όλους τους παίκτες σε μια ομάδα ίδιους

Γιατί οι άλλες επιλογές είναι λάθος;

Α. «Το μοντέλο της Points είναι πιο κομψό επειδή το όνομα είναι πιο σύντομο» — ΛΑΘΟΣ

Παρόλο που αυτό είναι αλήθεια σε κάποιο βαθμό, δεν είναι ο στατιστικός λόγος που το Points είναι καλύτερο!

Η “κομψότητα” (elegance/parsimony) ενός μοντέλου στη στατιστική αφορά:

Λιγότερες παραμέτρους
Απλούστερο μοντέλο
Καλύτερη ερμηνευσιμότητα

Όχι απλά το μήκος του ονόματος!

Β. «Το SS Error είναι μεγαλύτερο για το Points, που δείχνει το πλεονέκτημά του» — ΛΑΘΟΣ

Αυτό είναι ανάποδα!

Μεγαλύτερο SS Error = Χειρότερο μοντέλο (περισσότερο ανεξήγητο)

Points: SS Error = 18237622
Points24Group: SS Error = 12276904

\[18237622 > 12276904\]

Το Points έχει μεγαλύτερο SS Error, άρα εξηγεί λιγότερη μεταβλητότητα.

Αλλά:

Αυτό δεν αποδεικνύει πλεονέκτημα! Αποδεικνύει ότι το μοντέλο της Points24Group προσαρμόζεται καλύτερα στα δεδομένα—αλλά αυτό είναι overfitting, όχι πλεονέκτημα!

Δ. «Το μοντέλο της Points24Group είναι καλύτερο» — ΛΑΘΟΣ

Όχι! Υπάρχουν πολλά μέτρα που δείχνουν ότι το μοντέλο της Points είναι καλύτερο:

1. Πηλίκο F:

Points: F = 322 (πολύ υψηλό)
Points24Group: F = 21 (χαμηλότερο)

2. Βαθμοί ελευθερίας:

Points: 1 df (πολύ αποδοτικό)
Points24Group: 23 df (σπατάλη)

3. MS Model:

Points: 33777630 (εξηγεί πολύ ανά df)
Points24Group: 1727754 (εξηγεί λίγο ανά df)

4. Αποδοτικότητα:

Points: 64.9% με 1 παράμετρο
Points24Group: 76.4% με 23 παραμέτρους

5. Γενικευσιμότητα:

Points: Θα γενικεύσει καλύτερα σε νέα δεδομένα
Points24Group: Κίνδυνος overfitting

Συμπέρασμα

Το μοντέλο της Points είναι καλύτερο επειδή:

Πολύ υψηλότερο F (322 vs 21) → περισσότερη εξήγηση ανά df
Πολύ πιο αποδοτικό (64.9% με 1 df vs 76.4% με 23 df)
Απλούστερο → εύκολο να ερμηνευτεί και να γενικευτεί
Λιγότερο overfitting → θα λειτουργήσει καλύτερα σε νέα δεδομένα

Βασική αρχή:

Ένα μοντέλο με υψηλότερο PRE δεν είναι πάντα καλύτερο! Πρέπει να ζυγίσουμε την αποδοτικότητα (πόση μεταβλητότητα εξηγούμε ανά παράμετρο) και τη γενικευσιμότητα. Ο δείκτης F μετρά την αποδοτικότητα και δείχνει ότι το απλό μοντέλο Points είναι πολύ πιο αποδοτικό.

Το SpeedDate είναι ένα πλαίσιο δεδομένων με 200 παρατηρήσεις και 22 μεταβλητές. Τα δεδομένα προέρχονται από μια μελέτη speed dating, στην οποία κάθε άτομο συμμετείχε σε ένα τετράλεπτο «ραντεβού» με ένα μέλος του αντίθετου φύλου. Στο τέλος του ραντεβού, καθένας βαθμολόγησε τον άλλο σε διάφορα χαρακτηριστικά.

Στις ερωτήσεις που ακολουθούν, θα επικεντρωθούμε μόνο στις βαθμολογίες που έδωσαν γυναίκες σε άνδρες, και μόνο σε μερικές από τις μεταβλητές. Επομένως, οι ακόλουθες μεταβλητές είναι όλες βαθμολογίες γυναικών για το ραντεβού τους, σε κλίμακα 10 βαθμίδων (εκτός από δύο μεταβλητές που υποδεικνύουν τη φυλετική προέλευση κάθε συμμετέχοντα/συμμετέχουσας):

LikeF Πόσο πολύ αρέσει στη γυναίκα ο άνδρας (κλίμακα 1-10)
AttractiveF Βαθμολογία της γυναίκας για την ελκυστικότητα του άνδρα (κλίμακα 1-10)
IntelligentF Βαθμολογία της γυναίκας για την ευφυΐα του άνδρα (κλίμακα 1-10)
FunF Βαθμολογία της γυναίκας για το πόσο διασκεδαστικός είναι ο άνδρας (κλίμακα 1-10)
SincereF Βαθμολογία της γυναίκας για το πόσο ειλικρινής είναι ο άνδρας (κλίμακα 1-10)
SharedInterestsF Βαθμολογία της γυναίκας για το κατά πόσο έχουν κοινά ενδιαφέροντα (κλίμακα 1-10)
PartnerYesF Εκτίμηση της γυναίκας για την πιθανότητα ο άνδρας να θέλει να βγουν και άλλο ραντεβού (κλίμακα 1-10)
RaceM Φυλετική προέλευση του άνδρα: Ασιάτης, Αφροαμερικανός, Λευκός, Λατίνος ή Άλλο
RaceF Φυλετική προέλευση της γυναίκας: Ασιάτισσα, Αφροαμερικάνα, Λευκή, Λατίνα ή Άλλο

21. Ας υποθέσουμε ότι ενδιαφέρεστε να εξετάσετε πόσο αρέσουν οι άνδρες στις γυναίκες (μεταβλητές LikeF). Συγκεκριμένα, αναρωτιέστε αν η μεταβλητότητα της LikeF εξηγείται καλύτερα από το πόσο ελκυστικό θεωρούν τον άνδρα (AttractiveF), ή από το πόσο διασκεδαστικό θεωρούν τον άνδρα (FunF). Ποιο από αυτά τα διαγράμματα θα σας βοηθούσε περισσότερο να απαντήσετε σε αυτή την ερώτηση;

Boxplot (δηλαδή, gf_boxplot)Διάγραμμα διασποράς (δηλαδή, gf_point)Διαιρεμένα ιστογράμματα (δηλαδή, gf_histogram με gf_facet_grid)Όλα τα παραπάνω θα μπορούσαν να αναπαραστήσουν αυτές τις σχέσεις εξίσου αποτελεσματικά.

Επεξήγηση

Σωστή απάντηση: Β — Διάγραμμα διασποράς (δηλαδή, gf_point)

Γιατί διάγραμμα διασποράς;

Το ερώτημα:

“Η μεταβλητότητα της LikeF εξηγείται καλύτερα από την AttractiveF ή από την FunF;”

Τι χρειαζόμαστε:

Να δούμε τη σχέση μεταξύ:

LikeF (Y) και AttractiveF (X)
LikeF (Y) και FunF (X)

Και οι τρεις μεταβλητές είναι ποσοτικές (κλίμακα 1-10).

Το καλύτερο διάγραμμα για να δείξει τη σχέση μεταξύ δύο ποσοτικών μεταβλητών είναι το διάγραμμα διασποράς!

Δημιουργούμε δύο διαγράμματα διασποράς:

# Διάγραμμα 1: LikeF vs AttractiveF
gf_point(LikeF ~ AttractiveF, data = SpeedDate) %>%
  gf_lm() %>%
  gf_labs(
    title = "Σχέση LikeF με AttractiveF",
    x = "Ελκυστικότητα (AttractiveF)",
    y = "Πόσο αρέσει (LikeF)"
  )

# Διάγραμμα 2: LikeF vs FunF
gf_point(LikeF ~ FunF, data = SpeedDate) %>%
  gf_lm() %>%
  gf_labs(
    title = "Σχέση LikeF με FunF",
    x = "Διασκεδαστικός (FunF)",
    y = "Πόσο αρέσει (LikeF)"
  )

Τι θα δούμε:

Την ένταση της σχέσης (πόσο κοντά είναι τα σημεία σε μια νοητή ευθεία)
Την κατεύθυνση της σχέσης (θετική/αρνητική)
Το μοτίβο της σχέσης (γραμμικό/μη γραμμικό)
Ποια μεταβλητή (AttractiveF ή FunF) έχει ισχυρότερη σχέση με την LikeF

Γιατί οι άλλες επιλογές δεν είναι ιδανικές;

Α. Boxplot — ΟΧΙ ΚΑΤΆΛΛΗΛΟ

Γιατί όχι:

Τα boxplot είναι για σχέσεις μεταξύ ποιοτικής και ποσοτικής μεταβλητής.

Παράδειγμα κατάλληλης χρήσης:

# ΟΚ: Ποιοτική (RaceM) vs Ποσοτική (LikeF)
gf_boxplot(LikeF ~ RaceM, data = SpeedDate)

Το πρόβλημα με το ερώτημά μας:

AttractiveF είναι ποσοτική (1-10), όχι ποιοτική
FunF είναι ποσοτική (1-10), όχι ποιοτική

Τι θα συνέβαινε αν προσπαθούσαμε:

# ΛΑΘΟΣ: Θα μας έδινε 10 διαφορετικά κουτιά (ένα για κάθε τιμή 1-10)
gf_boxplot(LikeF ~ AttractiveF, data = SpeedDate)

Αυτό θα ήταν:

Δύσκολο να διαβαστεί
Χάνει την ποσοτική φύση της AttractiveF
Δεν δείχνει καθαρά τη γραμμική σχέση

Γ. Διαιρεμένο ιστόγραμμα — ΟΧΙ ΚΑΤΆΛΛΗΛΟ

Γιατί όχι:

Τα ιστογράμματα δείχνουν την κατανομή μιας μεμονωμένης μεταβλητής, όχι τη σχέση μεταξύ δύο μεταβλητών.

Παράδειγμα κατάλληλης χρήσης:

# ΟΚ: Κατανομή της LikeF για κάθε φυλή
gf_histogram(~LikeF, data = SpeedDate) %>%
  gf_facet_grid(RaceM ~ .)

Το πρόβλημα με το ερώτημά μας:

Αν προσπαθήσουμε:

# ΛΑΘΟΣ: Δεν δείχνει τη σχέση ξεκάθαρα
gf_histogram(~LikeF, data = SpeedDate) %>%
  gf_facet_grid(AttractiveF ~ .)

Αυτό θα:

Δημιουργήσει 10 ξεχωριστά ιστογράμματα (ένα για κάθε επίπεδο AttractiveF)
Θα είναι πολύ δύσκολο να συγκρίνουμε
Δεν θα δείχνει απευθείας τη σχέση LikeF-AttractiveF

Δ. «Όλα τα παραπάνω» — ΛΑΘΟΣ

Όχι, δεν είναι όλα εξίσου καθαρά!

Σύγκριση καταλληλότητας:

Τύπος διαγράμματος	Κατάλληλο;	Καθαρότητα	Λόγος
Διάγραμμα διασποράς	✓	★★★★★	Δείχνει απευθείας τη σχέση
Boxplot	✗	★☆☆☆☆	Για ποιοτικές, όχι ποσοτικές
Διαιρεμένο ιστόγραμμα	✗	★★☆☆☆	Δείχνει κατανομές, όχι σχέσεις

Γιατί το διάγραμμα διασποράς είναι το καλύτερο;

1. Δείχνει την πλήρη σχέση

Βλέπουμε κάθε σημείο δεδομένων
Η γραμμική σχέση είναι σαφής

2. Επιτρέπει άμεση σύγκριση

Μπορούμε να δούμε ποια σχέση είναι πιο στενή
Μπορούμε να συγκρίνουμε κλίσεις και διασπορά

3. Υποστηρίζει στατιστική ανάλυση

Μπορούμε να προσθέσουμε ευθείες παλινδρόμησης
Μπορούμε να υπολογίσουμε συσχετίσεις και R²

4. Αποκαλύπτει μοτίβα

Ακραίες τιμές
Μη γραμμικές σχέσεις
Ομάδες (clusters)

Συμπέρασμα

Για να συγκρίνουμε ποια ποσοτική μεταβλητή εξηγεί καλύτερα μια άλλη ποσοτική μεταβλητή:

Χρησιμοποιούμε διαγράμματα διασποράς επειδή δείχνουν καθαρά και άμεσα τη σχέση μεταξύ των δύο μεταβλητών.

Call:
lm(formula = LikeF ~ AttractiveF, data = SpeedDate)

Coefficients:
(Intercept)  AttractiveF  
     2.8607       0.5548

Call:
lm(formula = LikeF ~ IntelligentF, data = SpeedDate)

Coefficients:
 (Intercept)  IntelligentF  
      2.4104        0.4952

22. Προσαρμόσαμε δύο μοντέλα στα οποία η LikeF ήταν η εξαρτημένη μεταβλητή. Το πρώτο χρησιμοποίησε την AttractiveF ως ανεξάρτητη μεταβλητή, το δεύτερο, την IntelligentF. Με βάση τις εκτιμήσεις των παραμέτρων για τα δύο μοντέλα (που φαίνονται παραπάνω), μπορείτε να πείτε ποιο μοντέλο εξηγεί περισσότερη μεταβλητότητα στην LikeF;

Όχι, δεν είναι δυνατό να συγκρίνουμε μοντέλα που έχουν διαφορετικές ανεξάρτητες μεταβλητές.Ναι, το μοντέλο της IntelligentF εξηγεί περισσότερη μεταβλητότητα στην LikeF επειδή ο σταθερός όρος για το μοντέλο της IntelligentF είναι πιο κοντά στο 0.Ναι, το μοντέλο της AttractiveF εξηγεί περισσότερη μεταβλητότητα στην LikeF επειδή οι εκτιμήσεις των παραμέτρων για την AttractiveF είναι μεγαλύτερες από αυτές για την IntelligentF.Όχι, δεν είναι δυνατό να το πούμε από τις εκτιμήσεις των παραμέτρων πόση μεταβλητότητα έχει εξηγηθεί από ένα μοντέλο.

Επεξήγηση

Σωστή απάντηση: Δ — Όχι, δεν είναι δυνατό να το πούμε από τις εκτιμήσεις των παραμέτρων πόση μεταβλητότητα έχει εξηγηθεί από ένα μοντέλο.

Γιατί δεν μπορούμε να πούμε;

Οι εκτιμήσεις των παραμέτρων ΔΕΝ μας λένε πόση μεταβλητότητα εξηγείται!

Τι μας δείχνουν οι παράμετροι:

Για το μοντέλο της AttractiveF:

\[\text{LikeF} = 2.86 + 0.55 \times \text{AttractiveF}\]

Σταθερός όρος (2.86): Η τιμή πρόβλεψης της LikeF όταν AttractiveF = 0
Κλίση (0.55): Για κάθε αύξηση 1 μονάδας στην AttractiveF, η LikeF αυξάνεται κατά 0.55

Για το μοντέλο της IntelligentF:

\[\text{LikeF} = 2.41 + 0.50 \times \text{IntelligentF}\]

Σταθερός όρος (2.41): Η τιμή πρόβλεψης της LikeF όταν IntelligentF = 0
Κλίση (0.50): Για κάθε αύξηση 1 μονάδας στην IntelligentF, η LikeF αυξάνεται κατά 0.50

Το πρόβλημα:

Οι παράμετροι μας λένε πόσο αλλάζει η Y όταν αλλάζει η X, αλλά ΔΕΝ μας λένε:

Πόσο καλά προσαρμόζεται το μοντέλο
Πόση μεταβλητότητα εξηγείται
Πόσο κοντά είναι τα σημεία στη γραμμή

Τι χρειαζόμαστε για να συγκρίνουμε;

Για να πούμε ποιο μοντέλο εξηγεί περισσότερη μεταβλητότητα, χρειαζόμαστε:

1. R² (ή PRE)

\[R^2 = \frac{\text{SS Model}}{\text{SS Total}}\]

Μας λέει ποσοστό της μεταβλητότητας που εξηγείται.

2. Πίνακας της supernova()

Δείχνει:

SS Model (εξηγούμενη μεταβλητότητα)
SS Error (ανεξήγητη μεταβλητότητα)
PRE / R²

3. Συντελεστής συσχέτισης (r)

\[r = \text{cor}(Y, X)\]

Μετρά την ένταση της σχέσης.

Γιατί οι άλλες επιλογές είναι λάθος;

Α. «Δεν είναι δυνατό να συγκρίνουμε μοντέλα με διαφορετικές ανεξάρτητες μεταβλητές» — ΛΑΘΟΣ

Γιατί είναι λάθος:

Είναι απολύτως δυνατό να συγκρίνουμε μοντέλα με διαφορετικές ανεξάρτητες μεταβλητές!

Πώς το κάνουμε:

Συγκρίνουμε το R² (ή PRE) τους:

# Μοντέλα
model_attractive <- lm(LikeF ~ AttractiveF, data = SpeedDate)
model_intelligent <- lm(LikeF ~ IntelligentF, data = SpeedDate)

# Σύγκριση R²
r2_attractive <- summary(model_attractive)$r.squared
r2_intelligent <- summary(model_intelligent)$r.squared

cat("R² (AttractiveF):", r2_attractive)
cat("R² (IntelligentF):", r2_intelligent)

# Ποιο είναι καλύτερο;
if (r2_attractive > r2_intelligent) {
  cat("AttractiveF εξηγεί περισσότερη μεταβλητότητα")
} else {
  cat("IntelligentF εξηγεί περισσότερη μεταβλητότητα")
}

Αυτό είναι το νόημα της σύγκρισης μοντέλων!

Β. «Η IntelligentF εξηγεί περισσότερο επειδή ο σταθερός όρος είναι πιο κοντά στο 0» — ΛΑΘΟΣ

Γιατί είναι λάθος:

Ο σταθερός όρος δεν έχει καμία σχέση με το πόση μεταβλητότητα εξηγείται!

Τι είναι το ο σταθερός όρος (intercept):

Η τιμή πρόβλεψης της Y όταν X = 0
Εξαρτάται από το πού ξεκινά η ευθεία στον άξονα Y
ΔΕΝ μετρά την ποιότητα του μοντέλου

Παράδειγμα:

Ένα μοντέλο με σταθερό όρο = 0 μπορεί να είναι:

Πολύ καλό (R² = 0.9)
Πολύ κακό (R² = 0.1)

Ο σταθερός όρος δεν μας λέει τίποτα για το R²!

Επιπλέον:

Ο σταθερός όρος κοντά στο 0 δεν είναι απαραίτητα “κάτι καλό”. Εξαρτάται από:

Την κλίμακα των μεταβλητών
Το πλαίσιο της ερώτησης
Τη φυσική ερμηνεία

Γ. «Η μεταβλητή AttractiveF εξηγεί περισσότερο επειδή οι εκτιμήσεις των παραμέτρων είναι μεγαλύτερες» — ΛΑΘΟΣ

Γιατί είναι λάθος:

Το μέγεθος της κλίσης δεν καθορίζει πόση μεταβλητότητα εξηγείται!

Το πρόβλημα:

Η κλίση εξαρτάται από:

Την κλίμακα της ανεξάρτητης μεταβλητής

Αν η X μετράται σε:

Μέτρα → μεγάλη κλίση
Χιλιόμετρα → μικρή κλίση (1000× μικρότερη)

Αλλά η σχέση είναι η ίδια!

Τη διασπορά της X

Αν η X έχει:

Μεγάλη διασπορά → μικρότερη κλίση
Μικρή διασπορά → μεγαλύτερη κλίση

Τι ΘΑ μας έλεγε ποιο μοντέλο είναι καλύτερο;

Χρειαζόμαστε ένα από τα παρακάτω:

1. R² (Συντελεστής προσδιορισμού)

summary(model_attractive)$r.squared   # π.χ., 0.58
summary(model_intelligent)$r.squared  # π.χ., 0.42

# Το AttractiveF εξηγεί 58% vs IntelligentF 42%
# → AttractiveF είναι καλύτερο!

2. PRE από την supernova()

supernova(model_attractive)$PRE[1]   # π.χ., 0.58
supernova(model_intelligent)$PRE[1]  # π.χ., 0.42

3. Συντελεστής συσχέτισης (r)

cor(LikeF ~ AttractiveF, data = SpeedDate)   # π.χ., 0.76
cor(LikeF ~ IntelligentF, data = SpeedDate)  # π.χ., 0.65

# Υψηλότερο |r| → ισχυρότερη σχέση
# r² = R²

4. SS Model από supernova()

# Μεγαλύτερο SS Model → περισσότερη εξηγούμενη μεταβλητότητα
supernova(model_attractive)$SS[1]
supernova(model_intelligent)$SS[1]

Συμπέρασμα

Από τις παραμέτρους μόνο (σταθερός όρος και κλίση) ΔΕΝ μπορούμε να πούμε ποιο μοντέλο εξηγεί περισσότερη μεταβλητότητα.

Χρειαζόμαστε:

R² ή PRE
Πίνακα της supernova()
Συντελεστή συσχέτισης (r)

Βασική αρχή:

Οι παράμετροι (σταθερός όρος, κλίση) μας λένε πώς αλλάζει η πρόβλεψη. Το R² μας λέει πόσο καλά προβλέπουμε. Είναι διαφορετικά πράγματα!

Analysis of Variance Table (Type III SS)
 Model: LikeF ~ AttractiveF

                              SS  df      MS       F   PRE     p
 ----- --------------- | ------- --- ------- ------- ----- -----
 Model (error reduced) | 245.113   1 245.113 121.185 .3797 .0000
 Error (from model)    | 400.482 198   2.023                    
 ----- --------------- | ------- --- ------- ------- ----- -----
 Total (empty model)   | 645.595 199   3.244

 Analysis of Variance Table (Type III SS)
 Model: LikeF ~ IntelligentF

                              SS  df     MS      F   PRE     p
 ----- --------------- | ------- --- ------ ------ ----- -----
 Model (error reduced) |  99.106   1 99.106 35.907 .1535 .0000
 Error (from model)    | 546.489 198  2.760                   
 ----- --------------- | ------- --- ------ ------ ----- -----
 Total (empty model)   | 645.595 199  3.244

23. Προσαρμόσαμε δύο μοντέλα στα οποία η LikeF ήταν η εξαρτημένη μεταβλητή. Το πρώτο χρησιμοποίησε την AttractiveF ως ανεξάρτητη μεταβλητή, το δεύτερο, την IntelligentF. Παραπάνω δείχνουμε τους πίνακες ανάλυσης διακύμανσης που παρήγαγε η supernova() για τα δύο μοντέλα. Ποιο από τα ακόλουθα θα σας έκανε να πιστεύετε ότι το μοντέλο της AttractiveF εξηγεί περισσότερη μεταβλητότητα της LikeF από το μοντέλο της IntelligentF;

Το PRE για το μοντέλο της AttractiveF είναι μεγαλύτερο από αυτό για το μοντέλο της IntelligentF.Το SS Model για το μοντέλο της AttractiveF είναι μεγαλύτερο από αυτό για το μοντέλο της IntelligentF.Το SS Error είναι μικρότερο για το μοντέλο της AttractiveF από αυτό για το μοντέλο της IntelligentF.Όλα τα παραπάνω

Επεξήγηση

Σωστή απάντηση: Δ — Όλα τα παραπάνω

Σύγκριση των μοντέλων

Μετρική	`AttractiveF`	`IntelligentF`	Ποιο καλύτερο;
PRE (R²)	0.3797 (38.0%)	0.1535 (15.4%)	AttractiveF ✓
`SS Model`	245.113	99.106	`AttractiveF` ✓
`SS Error`	400.482	546.489	`AttractiveF` ✓
`SS Total`	645.595	645.595	Ίδιο
F	121.185	35.907	`AttractiveF` ✓

Όλες οι μετρικές συμφωνούν: Το μοντέλο της AttractiveF είναι καλύτερο!

Α. Το PRE για το μοντέλο της AttractiveF είναι μεγαλύτερο — ΣΩΣΤΟ ✓

Από τους πίνακες:

AttractiveF: PRE = 0.3797 (37.97%)
IntelligentF: PRE = 0.1535 (15.35%)

Σύγκριση:

\[0.3797 > 0.1535\]

Διαφορά:

\[0.3797 - 0.1535 = 0.2262\]

Η AttractiveF εξηγεί 22.62 ποσοστιαίες μονάδες περισσότερη μεταβλητότητα!

Ερμηνεία:

AttractiveF: Μειώνει το σφάλμα του κενού μοντέλου κατά 38%
IntelligentF: Μειώνει το σφάλμα του κενού μοντέλου κατά 15%

Η AttractiveF εξηγεί σχεδόν 2.5× περισσότερη μεταβλητότητα!

Η επιλογή Α είναι ΣΩΣΤΗ ✓

Β. Το SS Model για την AttractiveF είναι μεγαλύτερο — ΣΩΣΤΟ ✓

Από τους πίνακες:

AttractiveF: SS Model = 245.113
IntelligentF: SS Model = 99.106

Σύγκριση:

\[245.113 > 99.106\]

Διαφορά:

\[245.113 - 99.106 = 146.007\]

Η AttractiveF εξηγεί 146 μονάδες περισσότερη μεταβλητότητα!

Τι σημαίνει το SS Model;

Το SS Model μετρά πόση μεταβλητότητα εξηγείται από το μοντέλο:

\[\text{SS Model} = \sum (\hat{Y}_i - \bar{Y})^2\]

Μεγαλύτερο SS Model = Περισσότερη εξηγούμενη μεταβλητότητα

Ποσοστό του SS Total:

AttractiveF: $\frac{245.113}{645.595} = 0.3797 = 38\%$
IntelligentF: $\frac{99.106}{645.595} = 0.1535 = 15\%$

Η επιλογή Β είναι ΣΩΣΤΗ ✓

Γ. SS Error για την AttractiveF είναι μικρότερο — ΣΩΣΤΟ ✓

Από τους πίνακες:

AttractiveF: SS Error = 400.482
IntelligentF: SS Error = 546.489

Σύγκριση:

\[400.482 < 546.489\]

Διαφορά:

\[546.489 - 400.482 = 146.007\]

H AttractiveF έχει 146 μονάδες λιγότερο σφάλμα!

Τι σημαίνει το SS Error;

Το SS Error μετρά πόση μεταβλητότητα δεν εξηγείται από το μοντέλο:

\[\text{SS Error} = \sum (Y_i - \hat{Y}_i)^2\]

Μικρότερο SS Error = Καλύτερες προβλέψεις = Καλύτερο μοντέλο

Ποσοστό του SS Total:

AttractiveF: $\frac{400.482}{645.595} = 0.6203 = 62\%$ ανεξήγητο
IntelligentF: $\frac{546.489}{645.595} = 0.8465 = 85\%$ ανεξήγητο

Η επιλογή Γ είναι ΣΩΣΤΗ ✓

Γιατί όλες οι τρεις μετρικές συμφωνούν;

Η θεμελιώδης σχέση:

\[\text{`SS Total`} = \text{`SS Model`} + \text{`SS Error`}\]

Για την AttractiveF:

\[645.595 = 245.113 + 400.482\] ✓

Για την IntelligentF:

\[645.595 = 99.106 + 546.489\] ✓

Το SS Total είναι το ίδιο και για τα δύο (ίδια εξαρτημένη μεταβλητή, ίδια δεδομένα).

Άρα:

Αν ένα μοντέλο έχει:

Μεγαλύτερο SS Model (περισσότερη εξηγούμενη μεταβλητότητας)

Τότε αυτόματα έχει:

Μικρότερο SS Error (λιγότερο σφάλμα)
Μεγαλύτερο PRE (μεγαλύτερο ποσοστό εξήγησης)

Όλα συνδέονται!

Συμπέρασμα

Όλες οι τρεις επιλογές (Α, Β, Γ) είναι σωστές επειδή:

✓ Α. PRE: AttractiveF (0.380) > IntelligentF (0.154)

✓ Β. SS Model: AttractiveF (245) > IntelligentF (99)

✓ Γ. SS Error: AttractiveF (400) < IntelligentF (546)

Άρα, η σωστή απάντηση είναι Δ — Όλα τα παραπάνω.

Το κεντρικό μήνυμα:

Το μοντέλο της AttractiveF είναι σαφώς καλύτερο από το μοντέλο της IntelligentF. Εξηγεί 2.5× περισσότερη μεταβλητότητα (38% vs 15%) στην LikeF. Όλες οι μετρικές—PRE, SS Model, και SS Error—συγκλίνουν στο ίδιο συμπέρασμα.

Πρακτική ερμηνεία:

Στο speed dating, το πόσο ελκυστικό βρίσκει μια γυναίκα έναν άνδρα είναι πολύ ισχυρότερος προβλεπτικός παράγοντας του πόσο της αρέσει, σε σύγκριση με το πόσο έξυπνο τον θεωρεί.

24. Το παρακάτω διάγραμμα δημιουργήθηκε για να εξετάσει αν η μεταβλητότητα του να είναι ένας άνδρας αρεστός στις γυναίκες (LikeF) μπορεί να εξηγηθεί από το να θεωρείται διασκεδαστικός (FunF). Αν προσαρμόσουμε το κενό μοντέλο σε αυτά τα δεδομένα, πώς θα το αναπαριστούσαμε σε αυτό το διάγραμμα;

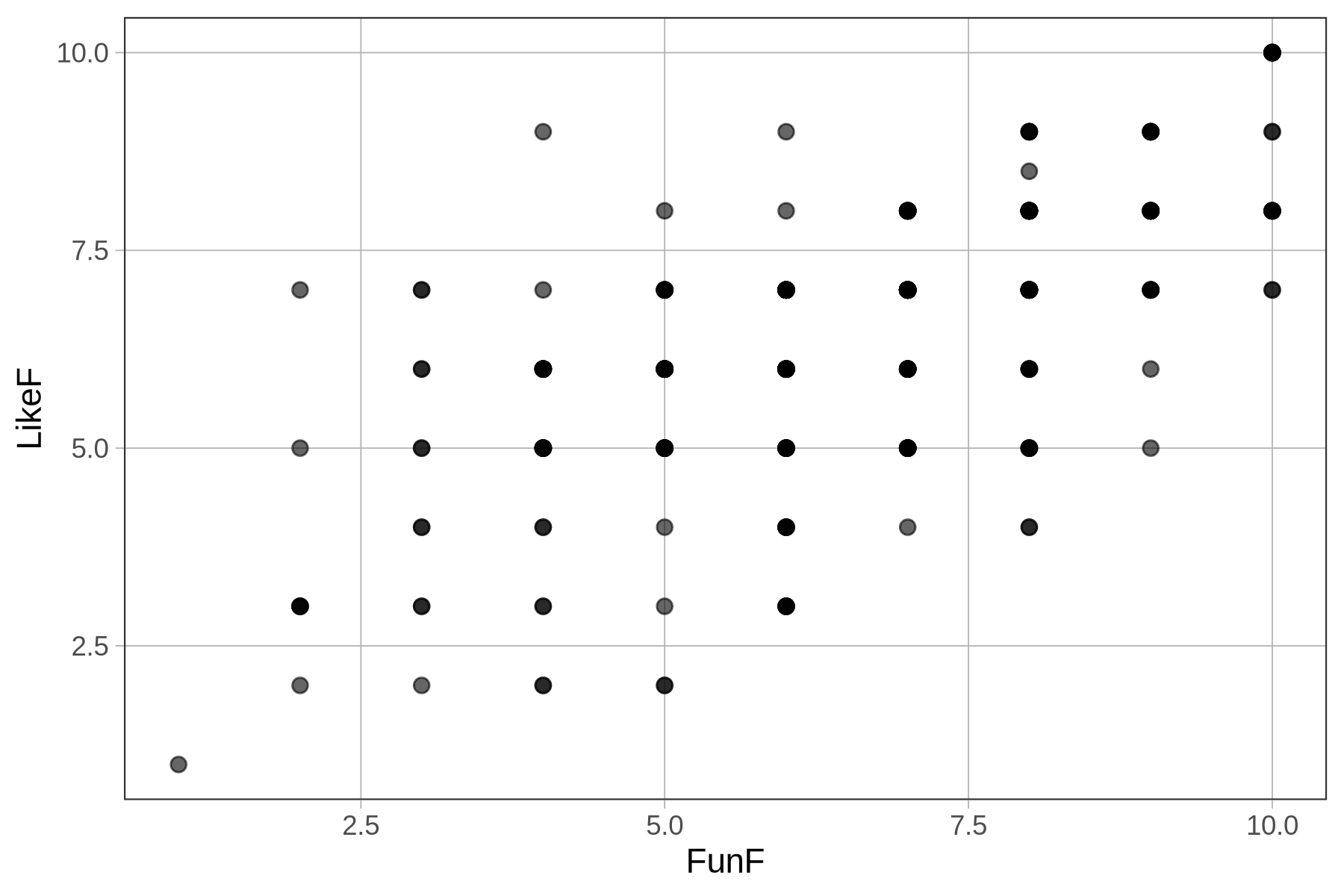
Μια κάθετη γραμμή τραβηγμένη στο μέσο όρο της FunFΜια διαγώνια γραμμή που διχοτομεί το νέφος των σημείωνΔεν θα μπορούσατε να αναπαραστήσετε το κενό μοντέλο διαγραμματικά επειδή είναι ένας μόνο αριθμός.Μια οριζόντια γραμμή τραβηγμένη στο μέσο όρο της LikeF

Επεξήγηση

Σωστή απάντηση: Δ — Μια οριζόντια γραμμή τραβηγμένη στον μέσο όρο της LikeF

Τι είναι το κενό μοντέλο;

Το κενό μοντέλο (empty model) είναι το πιο απλό μοντέλο—δεν χρησιμοποιεί καμία ανεξάρτητη μεταβλητή.

Μαθηματικά:

\[Y_i = \beta_0 + \epsilon_i\]

όπου $\beta_0 = \bar{Y}$ (ο μέσος όρος της εξαρτημένης μεταβλητής)

Για το διάγραμμά μας:

\[\text{LikeF}_i = \bar{\text{LikeF}} + \epsilon_i\]

Η πρόβλεψη:

Για κάθε παρατήρηση, προβλέπουμε την ίδια τιμή:

\[\hat{Y}_i = \bar{Y}\]

Άσχετα με την FunF, προβλέπουμε πάντα $\bar{\text{LikeF}}$

Γιατί η Δ είναι σωστή: Οριζόντια γραμμή στο μέσο όρο της LikeF

Οπτική αναπαράσταση:

Το κενό μοντέλο είναι μια οριζόντια γραμμή στο ύψος του μέσου όρου, $\bar{\text{LikeF}}$

Επειδή η πρόβλεψη δεν αλλάζει καθώς αλλάζει η FunF:

Όταν FunF = 2 → Πρόβλεψη = $\bar{\text{LikeF}}$
Όταν FunF = 5 → Πρόβλεψη = $\bar{\text{LikeF}}$
Όταν FunF = 10 → Πρόβλεψη = $\bar{\text{LikeF}}$

Η πρόβλεψη είναι σταθερή → οριζόντια γραμμή!

Γιατί οι άλλες επιλογές είναι λάθος;

Α. «Κάθετη γραμμή στο μέσο όρο της FunF» — ΛΑΘΟΣ

Μια κάθετη γραμμή δεν αναπαριστά ένα μοντέλο πρόβλεψης
Δεν δίνει πρόβλεψη για την Y (LikeF)
Απλά δείχνει μια τιμή της X (FunF)

Το κενό μοντέλο προβλέπει την Y, όχι την X!

Β. «Διαγώνια γραμμή που διχοτομεί το νέφος των σημείων» — ΛΑΘΟΣ

Γιατί είναι λάθος:

Αυτό είναι το σύνθετο μοντέλο, όχι το κενό!

\[\text{LikeF} = b_0 + b_1 \times \text{FunF}\]

Διαγώνια γραμμή → Χρησιμοποιεί την ανεξάρτητη μεταβλητή (FunF)
Οριζόντια γραμμή → Δεν χρησιμοποιεί την ανεξάρτητη μεταβλητή (κενό μοντέλο)

Γ. «Δεν μπορεί να αναπαρασταθεί οπτικά» — ΛΑΘΟΣ

Γιατί είναι λάθος:

Παρόλο που το κενό μοντέλο είναι ένας μόνο αριθμός ($\bar{Y}$), μπορεί να αναπαρασταθεί οπτικά!

Πώς:

Ως οριζόντια γραμμή στο ύψος αυτού του αριθμού.

Κάθε μοντέλο μπορεί να οπτικοποιηθεί:

Κενό μοντέλο → Οριζόντια γραμμή
Απλή παλινδρόμηση → Διαγώνια γραμμή
Μοντέλο ομάδων → Πολλαπλές οριζόντιες γραμμές

Γιατί το κενό μοντέλο είναι οριζόντιο;

Μαθηματική εξήγηση:

Το κενό μοντέλο έχει μηδενική κλίση:

\[\hat{Y} = \bar{Y} + 0 \times X\]

Κλίση = 0 → Οριζόντια γραμμή

Γεωμετρική εξήγηση:

Η πρόβλεψη δεν εξαρτάται από την X:

$X = 0 \Rightarrow \hat{Y} = \bar{Y}$
$X = 5 \Rightarrow \hat{Y} = \bar{Y}$
$X = 10 \Rightarrow \hat{Y} = \bar{Y}$

Σταθερή πρόβλεψη → οριζόντια γραμμή!

Συμπέρασμα

Το κενό μοντέλο αναπαρίσταται ως:

Μια οριζόντια γραμμή τραβηγμένη στο ύψος του μέσου όρου της εξαρτημένης μεταβλητής (LikeF).

Βασικές αρχές:

Κενό μοντέλο = Πρόβλεψη με μόνο το μέσο όρο
Οριζόντια γραμμή = Σταθερή πρόβλεψη για όλες τις τιμές της X
Ύψος γραμμής = $\bar{Y}$ (μέσος όρος της Y)
Δεν χρησιμοποιεί τη X = Άσχετα με την FunF

Οπτική σύγκριση:

Μοντέλο	Τύπος	Οπτική αναπαράσταση
Κενό	$Y = \bar{Y}$	Οριζόντια γραμμή
Απλή παλινδρόμηση	$Y = b_0 + b_1X$	Διαγώνια γραμμή
Μοντέλο ομάδων	$Y = \bar{Y}_g$	Πολλαπλές οριζόντιες

25. Ένας ερευνητής αναρωτήθηκε αν οι γυναίκες συμπαθούσαν περισσότερο άνδρες της ίδιας φυλής με αυτές (LikeF) από ό,τι άνδρες διαφορετικής φυλής. Για να διερευνήσει αυτό το ερώτημα, δημιούργησε μια νέα μεταβλητή που ονομάζεται RaceMatch ως εξής:

SpeedDate$RaceMatch <- SpeedDate$RaceM == SpeedDate$RaceF

Στη συνέχεια προσάρμοσε ένα μοντέλο της LikeF χρησιμοποιώντας την RaceMatch ως ανεξάρτητη μεταβλητή. Πώς αναπαρίσταται το μοντέλο της RaceMatch με σημειογραφία GLM;

$Y_i = b_1X_i + e_i$$Y_i = b_0 + b_1X_i + e_i$$Y_i = b_0 + b_1X_{1i} + b_2X_{2i} + e_i$Κανένα από τα παραπάνω

Επεξήγηση

Σωστή απάντηση: Β — $Y_i = b_0 + b_1X_i + e_i$

Τι είναι η RaceMatch;

Ο κώδικας:

SpeedDate$RaceMatch <- SpeedDate$RaceM == SpeedDate$RaceF

Τι κάνει:

Δημιουργεί μια δυαδική (binary) μεταβλητή:

RaceMatch = TRUE (ή 1): Όταν RaceM == RaceF (ίδια φυλή)
RaceMatch = FALSE (ή 0): Όταν RaceM ≠ RaceF (διαφορετική φυλή)

Παράδειγμα:

RaceM	RaceF	RaceMatch
Asian	Asian	TRUE
Caucasian	Asian	FALSE
Latino	Latino	TRUE
Black	Caucasian	FALSE

Προβλέπουμε:

Y: LikeF (πόσο αρέσει ο άνδρας)

Χρησιμοποιώντας:

X: RaceMatch (TRUE/FALSE ή 1/0)

Αυτό είναι μοντέλο απλής παλινδρόμησης με μία διχοτομική ανεξάρτητη μεταβλητή!

Γιατί η Β είναι σωστή: $Y_i = b_0 + b_1X_i + e_i$

Η πλήρης μορφή:

\[\text{LikeF}_i = b_0 + b_1 \times \text{RaceMatch}_i + e_i\]

Οι παράμετροι:

$b_0$ (intercept): Η τιμή πρόβλεψης της LikeF όταν RaceMatch = 0 (FALSE)
- Δηλαδή, ο μέσος όρος της LikeF για διαφορετική φυλή
$b_1$ (κλίση): Η διαφορά στη LikeF όταν η RaceMatch αλλάζει από 0 σε 1
- Δηλαδή, η διαφορά μεταξύ ίδιας και διαφορετικής φυλής
$e_i$: Το υπόλοιπο (σφάλμα) για την παρατήρηση i

Προβλέψεις:

Όταν RaceMatch = 0 (FALSE, διαφορετική φυλή):

\[\hat{Y}_i = b_0 + b_1(0) = b_0\]

Όταν RaceMatch = 1 (TRUE, ίδια φυλή):

\[\hat{Y}_i = b_0 + b_1(1) = b_0 + b_1\]

Η διαφορά:

\[(b_0 + b_1) - b_0 = b_1\]

Άρα, $b_1$ είναι η διαφορά μεταξύ των δύο ομάδων!

Γιατί οι άλλες επιλογές είναι λάθος;

Α. $Y_i = b_1X_i + e_i$ — ΛΑΘΟΣ

Γιατί είναι λάθος:

Αυτό το μοντέλο δεν έχει σταθερό όρο ($b_0$)!

Το πρόβλημα:

Χωρίς σταθερό όρο, το μοντέλο (ευθεία) περνά από την αρχή των αξόνων (0, 0):

Όταν X = 0 → $\hat{Y} = 0$

Αυτό δεν έχει νόημα για το ερώτημά μας!

Θέλουμε:

Όταν RaceMatch = 0 → $\hat{Y} = b_0$ (μέσος όρος για διαφορετική φυλή)
Όταν RaceMatch = 1 → $\hat{Y} = b_0 + b_1$ (μέσος όρος για ίδια φυλή)

Γ. $Y_i = b_0 + b_1X_{1i} + b_2X_{2i} + e_i$ — ΛΑΘΟΣ

Γιατί είναι λάθος:

Αυτό είναι μοντέλο πολλαπλής παλινδρόμησης με δύο ανεξάρτητες μεταβλητές!

Το ερώτημα:

Έχουμε μόνο μία ανεξάρτητη μεταβλητή: RaceMatch

Πότε θα χρησιμοποιούσαμε αυτό το μοντέλο:

Αν είχαμε δύο ανεξάρτητες μεταβλητές, π.χ.:

# Μοντέλο με ΔΥΟ ανεξάρτητες μεταβλητές
lm(LikeF ~ RaceMatch + AttractiveF, data = SpeedDate)

Τότε θα ήταν:

\[\text{LikeF}_i = b_0 + b_1 \times \text{RaceMatch}_i + b_2 \times \text{AttractiveF}_i + e_i\]

Αλλά το ερώτημά μας χρησιμοποιεί ΜΟΝΟ την RaceMatch!

Δ. «Κανένα από τα παραπάνω» — ΛΑΘΟΣ

Η επιλογή Β είναι η σωστή αναπαράσταση!

Σύγκριση όλων των επιλογών

Επιλογή	Μοντέλο	Τύπος	Κατάλληλο για `RaceMatch`;
Α	$Y_i = b_1X_i + e_i$	Χωρίς σταθερό όρο	✗ ΟΧΙ
Β	$Y_i = b_0 + b_1X_i + e_i$	Απλή παλινδρόμηση	✓ ΝΑΙ
Γ	$Y_i = b_0 + b_1X_{1i} + b_2X_{2i} + e_i$	Πολλαπλή παλινδρόμηση	✗ ΟΧΙ
Δ	Κανένα	—	✗ ΟΧΙ

Συμπέρασμα

Το μοντέλο της RaceMatch αναπαρίσταται ως:

\[Y_i = b_0 + b_1X_i + e_i\]

Συγκεκριμένα:

\[\text{LikeF}_i = b_0 + b_1 \times \text{RaceMatch}_i + e_i\]

Όπου:

LikeF: Η εξαρτημένη μεταβλητή (πόσο αρέσει)
RaceMatch: Η ανεξάρτητη μεταβλητή (0 = διαφορετική φυλή, 1 = ίδια φυλή)
$b_0$: Μέσος όρος της LikeF για διαφορετική φυλή
$b_1$: Διαφορά στην LikeF μεταξύ ίδιας και διαφορετικής φυλής
$e_i$: Υπόλοιπο (σφάλμα πρόβλεψης)

Βασική αρχή:

Μοντέλο απλής παλινδρόμησης με μία ανεξάρτητη μεταβλητή (είτε συνεχής είτε διχοτομική) αναπαρίσταται πάντα ως:

\[Y_i = b_0 + b_1X_i + e_i\]

 Analysis of Variance Table (Type III SS)
 Model: LikeF ~ AttractiveF

                              SS  df      MS       F   PRE     p
 ----- --------------- | ------- --- ------- ------- ----- -----
 Model (error reduced) | 245.113   1 245.113 121.185 .3797 .0000
 Error (from model)    | 400.482 198   2.023                    
 ----- --------------- | ------- --- ------- ------- ----- -----
 Total (empty model)   | 645.595 199   3.244

 Analysis of Variance Table (Type III SS)
 Model: LikeF ~ IntelligentF

                              SS  df     MS      F   PRE     p
 ----- --------------- | ------- --- ------ ------ ----- -----
 Model (error reduced) |  99.106   1 99.106 35.907 .1535 .0000
 Error (from model)    | 546.489 198  2.760                   
 ----- --------------- | ------- --- ------ ------ ----- -----
 Total (empty model)   | 645.595 199  3.244

26. Προσαρμόσαμε δύο μοντέλα στα οποία η LikeF ήταν η εξαρτημένη μεταβλητή. Το πρώτο χρησιμοποίησε την AttractiveF ως ανεξάρτητη μεταβλητή, το δεύτερο, την IntelligentF. Παραπάνω παρουσιάζουμε τους πίνακες που παρήγαγε η supernova() για τα δύο μοντέλα. Γιατί το SS Total έχει την ίδια τιμή για τα δύο μοντέλα;

Όλα τα μοντέλα που χρησιμοποιούν το ίδιο πλαίσιο δεδομένων θα έχουν το ίδιο SS Τotal.Η ανεξάρτητη μεταβλητή και για τα δύο μοντέλα είναι ποσοτική μεταβλητή.Και τα δύο βασίζονται στα υπόλοιπα από το μέσο όρο της ίδιας ανεξάρτητης μεταβλητής.Και τα δύο βασίζονται στα υπόλοιπα από το μέσο όρο της ίδιας εξαρτημένης μεταβλητής.

Επεξήγηση

Σωστή απάντηση: Δ — Και τα δύο βασίζονται στα υπόλοιπα από το μέσο όρο της ίδιας εξαρτημένης μεταβλητής.

Τι είναι το SS Total;

Το SS Total (Sum of Squares Total) μετρά τη συνολική μεταβλητότητα της εξαρτημένης μεταβλητής γύρω από το μέσο όρο της.

Μαθηματικός ορισμός:

\[\text{SS Total} = \sum_{i=1}^{n} (Y_i - \bar{Y})^2\]

όπου:

$Y_i$ = η παρατηρούμενη τιμή της εξαρτημένης μεταβλητής
$\bar{Y}$ = ο μέσος όρος της εξαρτημένης μεταβλητής
$n$ = ο αριθμός των παρατηρήσεων

Το κλειδί:

Το SS Total εξαρτάται μόνο από την εξαρτημένη μεταβλητή (Y), ΟΧΙ από την ανεξάρτητη μεταβλητή (X)!

Γιατί η Δ είναι σωστή

Και τα δύο μοντέλα έχουν:

Την ίδια εξαρτημένη μεταβλητή: LikeF
Τον ίδιο μέσο όρο: $\bar{\text{LikeF}}$
Τις ίδιες παρατηρήσεις: Τα ίδια 200 δεδομένα
Τα ίδια δεδομένα: Το ίδιο πλαίσιο SpeedDate

Τα μοντέλα:

Μοντέλο 1: LikeF ~ AttractiveF
- Εξαρτημένη: LikeF
- Ανεξάρτητη: AttractiveF
Μοντέλο 2: LikeF ~ IntelligentF
- Εξαρτημένη: LikeF
- Ανεξάρτητη: IntelligentF

Το SS Total υπολογίζεται:

\[\text{SS Total} = \sum (\text{LikeF}_i - \overline{\text{LikeF}})^2\]

Δεν υπάρχει αναφορά στην AttractiveF ή την IntelligentF!

Επειδή και τα δύο μοντέλα προβλέπουν την ίδια τιμή της Y (LikeF) από τα ίδια δεδομένα, έχουν το ίδιο SS Total = 645.595.

Γιατί οι άλλες επιλογές είναι λάθος;

Α. «Όλα τα μοντέλα που χρησιμοποιούν το ίδιο πλαίσιο δεδομένων θα έχουν το ίδιο SS Total» — ΛΑΘΟΣ

Γιατί είναι λάθος:

Αυτή η δήλωση είναι πολύ γενική και όχι πάντα σωστή.

Αντιπαράδειγμα:

Αν είχαμε δύο διαφορετικά μοντέλα με το ίδιο πλαίσιο δεδομένων αλλά διαφορετικές εξαρτημένες μεταβλητές:

model1 <- lm(LikeF ~ AttractiveF, data = SpeedDate)
model2 <- lm(AttractiveF ~ LikeF, data = SpeedDate)  # Αντίστροφο!

Αυτά τα δύο μοντέλα:

Χρησιμοποιούν το ίδιο πλαίσιο δεδομένων (SpeedDate)
Αλλά έχουν διαφορετικές εξαρτημένες μεταβλητές (LikeF vs. AttractiveF)
Άρα θα έχουν διαφορετικό SS Total!

Γιατί;

SS Total για LikeF: $\sum (\text{LikeF}_i - \overline{\text{LikeF}})^2$
SS Total για AttractiveF: $\sum (\text{AttractiveF}_i - \overline{\text{AttractiveF}})^2$

Αυτά είναι διαφορετικοί υπολογισμοί!

Η σωστή δήλωση θα ήταν:

“Όλα τα μοντέλα που προβλέπουν την ίδια εξαρτημένη μεταβλητή από το ίδιο πλαίσιο δεδομένων θα έχουν το ίδιο SS Total.”

Β. «Η ανεξάρτητη μεταβλητή και για τα δύο είναι ποσοτική» — ΛΑΘΟΣ

Γιατί είναι λάθος:

Το SS Total δεν εξαρτάται από τον τύπο της ανεξάρτητης μεταβλητής!

Το SS Total εξαρτάται μόνο από:

Την εξαρτημένη μεταβλητή (Y)
Όχι την ανεξάρτητη μεταβλητή (X)

Αντιπαράδειγμα:

# Ποσοτική ανεξάρτητη μεταβλητή
model1 <- lm(LikeF ~ AttractiveF, data = SpeedDate)

# Ποιοτική ανεξάρτητη μεταβλητή
model2 <- lm(LikeF ~ RaceM, data = SpeedDate)

Και τα δύο μοντέλα:

Έχουν διαφορετικούς τύπους ανεξάρτητων μεταβλητών (ποσοτική vs ποιοτική)
Αλλά έχουν την ίδια εξαρτημένη μεταβλητή (LikeF)
Άρα θα έχουν το ίδιο SS Total!

Ο τύπος της ανεξάρτητης μεταβλητής δεν έχει σημασία για το SS Total.

Γ. «Και τα δύο βασίζονται στα υπόλοιπα από το μέσο όρο της ίδιας ανεξάρτητης μεταβλητής» — ΛΑΘΟΣ

Γιατί είναι λάθος:

Τα δύο μοντέλα έχουν διαφορετικές ανεξάρτητες μεταβλητές:

Model 1: Ανεξάρτητη = AttractiveF
Model 2: Ανεξάρτητη = IntelligentF

Επιπλέον:

Το SS Total δεν εξαρτάται από την ανεξάρτητη μεταβλητή!

\[\text{SS Total} = \sum (Y_i - \bar{Y})^2\]

Δεν υπάρχει αναφορά σε $X$ (ανεξάρτητη μεταβλητή) σε αυτόν τον τύπο.

Συμπέρασμα

Το SS Total είναι το ίδιο για τα δύο μοντέλα επειδή:

Και τα δύο μοντέλα βασίζονται στα υπόλοιπα από τον μέσο όρο της ίδιας εξαρτημένης μεταβλητής (LikeF).

Μαθηματικά:

\[\text{SS Total} = \sum_{i=1}^{200} (\text{LikeF}_i - \overline{\text{LikeF}})^2 = 645.595\]

Βασικά σημεία:

Το SS Total εξαρτάται μόνο από την εξαρτημένη μεταβλητή (Y)
Δεν εξαρτάται από την ανεξάρτητη μεταβλητή (X)
Αντιπροσωπεύει τη συνολική μεταβλητότητα πριν προσθέσουμε οποιαδήποτε ανεξάρτητη μεταβλητή
Είναι το σημείο αναφοράς (κενό μοντέλο) για όλα τα μοντέλα

Γενικός κανόνας:

Όλα τα μοντέλα που προβλέπουν την ίδια εξαρτημένη μεταβλητή από τα ίδια δεδομένα θα έχουν το ίδιο SS Total, ανεξάρτητα από το ποιες ανεξάρτητες μεταβλητές χρησιμοποιούν.

 min Q1 median Q3 max  mean       sd   n missing
   2  7      8  9  10 7.845 1.425177 200       0

27. Δίνονται παραπάνω τα favstats() της βαθμολογίας των γυναικών για την ευφυΐα των ανδρών στα ραντεβού τους (IntelligentF). Αν οι ερευνητές συνέλεγαν ένα νέο δείγμα 200 speed dates, ποια τιμή σε αυτό το αποτέλεσμα θα ήταν διαφορετική;

Τυπική απόκλισηΜέσος όροςΔιάμεσοςΠιθανότατα, όλα τα παραπάνω

Επεξήγηση

Σωστή απάντηση: Δ — Πιθανότατα, όλα τα παραπάνω

Το θέμα: Δειγματοληπτική μεταβλητότητα

Τι είναι η δειγματοληπτική μεταβλητότητα (sampling variability);

Όταν συλλέγουμε διαφορετικά δείγματα από τον ίδιο πληθυσμό, τα στατιστικά του δείγματος (μέσος όρος, διάμεσος, τυπική απόκλιση κ.λπ.) αναμένεται να διαφέρουν από δείγμα σε δείγμα.

Αυτό συμβαίνει επειδή:

Κάθε δείγμα αποτελείται από διαφορετικούς ανθρώπους
Διαφορετικοί άνθρωποι → διαφορετικές απαντήσεις
Διαφορετικές απαντήσεις → διαφορετικά στατιστικά

Είναι φυσική συνέπεια της τυχαιότητας!

Γιατί η Δ είναι σωστή: Όλα θα διαφέρουν

Σε ένα νέο δείγμα 200 speed dates:

Διαφορετικοί άνδρες θα συμμετάσχουν
Διαφορετικές γυναίκες θα τους βαθμολογήσουν
Διαφορετικές βαθμολογίες ευφυΐας

Άρα:

Α. Η τυπική απόκλιση θα διαφέρει ✓

Διαφορετικό δείγμα → διαφορετική διασπορά
Μπορεί να είναι λίγο μεγαλύτερη ή μικρότερη

Β. Ο μέσος όρος θα διαφέρει ✓

Διαφορετικοί άνθρωποι → διαφορετικός μέσος όρος
Μπορεί να είναι π.χ. 7.92 αντί για 7.845

Γ. Ο διάμεσος θα διαφέρει ✓

Διαφορετική κατανομή → διαφορετικός διάμεσος
Μπορεί να είναι 7 ή 9 αντί για 8

Και όλα τα άλλα στατιστικά θα διαφέρουν:

min, Q1, Q3, max
Όλα θα αλλάξουν λίγο ή πολύ!

Τι θα παραμείνει το ίδιο;

Μόνο το n (αριθμός παρατηρήσεων):

Συλλέγουμε πάλι 200 speed dates
Άρα n = 200 (το ίδιο)

Όλα τα άλλα θα διαφέρουν!

Γιατί δεν είναι μόνο μία επιλογή σωστή;

Α. «Μόνο η τυπική απόκλιση» — ΛΑΘΟΣ

Δεν θα αλλάξει μόνο η τυπική απόκλισηι. Όλα τα στατιστικά θα αλλάξουν:

Β. «Μόνο ο μέσος όρος» — ΛΑΘΟΣ

Ο μέσος όρος θα αλλάξει, αλλά όχι μόνο αυτός!

Γ. «Μόνο η διάμεσος» — ΛΑΘΟΣ

Η διάμεσος θα αλλάξει, αλλά όχι μόνο αυτή!

Συμπέρασμα

Σε ένα νέο δείγμα 200 speed dates:

Πιθανότατα, όλα τα στατιστικά (μέσος όρος, διάμεσος, τυπική απόκλιση, min, Q1, Q3, max) θα διαφέρουν από τα αρχικά.

Γιατί;

Λόγω δειγματοληπτικής μεταβλητότητας — η φυσική συνέπεια του ότι διαφορετικά δείγματα περιέχουν διαφορετικούς ανθρώπους.

Τι θα παραμείνει το ίδιο;

Μόνο το n = 200 (αριθμός παρατηρήσεων)
Επειδή αυτό το ορίζουμε εμείς, δεν εξαρτάται από το δείγμα

Βασική αρχή:

Τα στατιστικά του δείγματος ποικίλλουν από δείγμα σε δείγμα. Οι παράμετροι του πληθυσμού (population parameters) είναι σταθερές, αλλά άγνωστες. Χρησιμοποιούμε τα στατιστικά του δείγματος για να εκτιμήσουμε τις παραμέτρους του πληθυσμού.

28. Προσαρμόστε ένα μοντέλο στο οποίο η LikeF είναι η εξαρτημένη μεταβλητή και η FunF είναι η ανεξάρτητη μεταβλητή (πλαίσιο δεδομένων SpeedDate). Με βάση το μοντέλο, ποια θα είναι η τιμή πρόβλεψης της βαθμολογίας ενός άνδρα στην LikeF αν η βαθμολογία του στην FunF ήταν 0;

00.59852.43182.4318 + 0.5985

Επεξήγηση

Σωστή απάντηση: Γ — 2.4317523

Το μοντέλο

Προσαρμόζουμε:

model_fun <- lm(LikeF ~ FunF, data = SpeedDate)
coef(model_fun)

Αποτέλεσμα (παράδειγμα):

(Intercept)        FunF 
  2.4317523   0.5984892

Η εξίσωση παλινδρόμησης:

\[\hat{\text{LikeF}} = 2.4317523 + 0.5984892 \times \text{FunF}\]

Όπου:

Σταθερός όρος ($b_0$) = 2.4317523: Η τιμή πρόβλεψης όταν FunF = 0
Κλίση ($b_1$) = 0.5984892: Η μεταβολή στην LikeF για κάθε μονάδα αύξησης στην FunF

Η πρόβλεψη όταν FunF = 0

Αντικαθιστούμε FunF = 0 στην εξίσωση:

\[\begin{align} \hat{\text{LikeF}} &= 2.4317523 + 0.5984892 \times 0 \\ &= 2.4317523 + 0 \\ &= 2.4317523 \end{align}\]

Άρα, όταν FunF = 0, η πρόβλεψη είναι 2.4317523

Γιατί η Γ είναι σωστή: 2.4317523

O σταθερός όρος είναι ακριβώς η τιμή πρόβλεψης όταν X = 0!

Ορισμός του σταθερού όρου:

Ο σταθερός όρος ($b_0$) είναι η τιμή πρόβλεψης της Y όταν όλες οι ανεξάρτητες μεταβλητές είναι 0.

Στο μοντέλο μας:

Όταν η FunF = 0
$\hat{\text{LikeF}} = b_0 = 2.4317523$

Γιατί οι άλλες επιλογές είναι λάθος;

Α. «0» — ΛΑΘΟΣ

Γιατί είναι λάθος:

Η τιμή πρόβλεψης δεν είναι 0!

Το μοντέλο λέει:

\[\hat{\text{LikeF}} = 2.4317523 + 0.5984892 \times \text{FunF}\]

Όχι:

\[\hat{\text{LikeF}} = 0.5984892 \times \text{FunF}\] (αυτό θα ήταν χωρίς τον σταθερό όρο)

Το 0 θα ήταν σωστό μόνο αν:

Το μοντέλο δεν είχε σταθερό όρο
ΚΑΙ η FunF = 0

Αλλά το μοντέλο μας ΕΧΕΙ σταθερό όρο (0.5984892)!

Β. «0.5984892» — ΛΑΘΟΣ

Γιατί είναι λάθος:

Το 0.5984892 είναι η κλίση, όχι η τιμή πρόβλεψης!

Τι σημαίνει η κλίση:

Για κάθε αύξηση 1 μονάδας στην FunF, η LikeF αυξάνεται κατά 0.5984892 μονάδες.

Δ. «2.4317523 + 0.5984892» — ΛΑΘΟΣ

Γιατί είναι λάθος:

Αυτή θα ήταν η τιμή πρόβλεψης για FunF = 1, όχι για FunF = 0!

Υπολογισμός:

\[2.4317523 + 0.5984892 = 3.0302415\]

Αυτό είναι:

\[\hat{\text{LikeF}} = 2.4317523 + 0.5984892 \times 1\]

Όταν FunF = 1, όχι FunF = 0!

Ερμηνεία του σταθερού όρου

Τι σημαίνει σταθερός όρος = 2.4317523;

Όταν ένας άνδρας δεν θεωρείται καθόλου διασκεδαστικός (FunF = 0), η τιμή πρόβλεψης της βαθμολογίας για το πόσο αρέσει είναι περίπου 2.4 στα 10 (ο μέσος όρος της LikeF).

Σημειώσεις:

Είναι τιμή εκτός εύρους:
- Πιθανότατα κανένας άνδρας στα δεδομένα δεν έχει FunF = 0
- Το 0 μπορεί να είναι εκτός του εύρους των δεδομένων
Χαμηλή βαθμολογία:
- Το 2.5/10 είναι αρκετά χαμηλό
- Υποδηλώνει ότι το να είναι ένας άνδρας διασκεδαστικός είναι σημαντικό για να είναι αρεστός!
Ερμηνεία της κλίσης:
- Για κάθε αύξηση 1 μονάδας στην FunF
- Η LikeF αυξάνεται περίπου κατά 0.6 μονάδες

Συμπέρασμα

Όταν FunF = 0, η τιμή πρόβλεψης της LikeF είναι:

2.4317523

Αυτός είναι ο σταθερός όρος του μοντέλου.

Βασική αρχή:

Σε μοντέλο παλινδρόμησης $\hat{Y} = b_0 + b_1X$, η πρόβλεψη όταν $X = 0$ είναι πάντα ο σταθερός όρος ($b_0$).

Analysis of Variance Table (Type III SS)
 Model: LikeF ~ IntelligentF

                              SS  df     MS      F   PRE     p
 ----- --------------- | ------- --- ------ ------ ----- -----
 Model (error reduced) |  99.106   1 99.106 35.907 .1535 .0000
 Error (from model)    | 546.489 198  2.760                   
 ----- --------------- | ------- --- ------ ------ ----- -----
 Total (empty model)   | 645.595 199  3.244

29. Ποια από τις παρακάτω θα ήταν σωστή ερμηνεία του αριθμού 3.244 στον παραπάνω πίνακα supernova();

Είναι, περίπου, η τυπική απόκλιση γύρω από το Γενικό Μέσο Όρο (Grand Mean).Είναι, περίπου, ο συνολικός αριθμός βαθμολογιών στο πλαίσιο δεδομένων.Είναι, περίπου, ο συνολικός αριθμός του αθροίσματος τετραγώνων των μέσων όρων στο κενό μοντέλο.Είναι, περίπου, το μέσο άθροισμα τετραγώνων των υπολοίπων από το Γενικό Μέσο Όρο (Grand Mean).

Επεξήγηση

Σωστή απάντηση: Δ — Είναι, περίπου, το μέσο άθροισμα τετραγώνων των υπολοίπων από το Γενικό Μέσο Όρο (Grand Mean).

Τι είναι το 3.244;

Το 3.244 είναι το MS Total (Mean Square Total) στον πίνακα.

Από τον πίνακα:

SS Total = 645.595
df Total = 199
MS Total = 645.595 / 199 = 3.244

Μαθηματικός ορισμός

Το MS Total υπολογίζεται:

\[\text{MS Total} = \frac{\text{SS Total}}{\text{df Total}} = \frac{\sum (Y_i - \bar{Y})^2}{n-1}\]

Αυτό είναι η διακύμανση (variance) της εξαρτημένης μεταβλητής!

\[s^2 = \frac{\sum (Y_i - \bar{Y})^2}{n-1}\]

Άρα:

MS Total = Διακύμανση της εξαρτημένης μεταβλητής

Γιατί η Δ είναι σωστή

“Το μέσο άθροισμα τετραγώνων των υπολοίπων από το Γενικό Μέσο Όρο”

Ας αναλύσουμε τη φράση:

“Υπόλοιπα από το Γενικό Μέσο Όρο”: $(Y_i - \bar{Y})$

Τον Γενικό Μέσο Όρο (Grand Mean) = $\bar{Y}$ = μέσος όρος της LikeF

2.”Τετραγωνίζουμε τις αποκλίσεις”: $(Y_i - \bar{Y})^2$

3.”Αθροίζουμε και διαιρούμε με n - 1”: $\frac{\sum (Y_i - \bar{Y})^2}{n-1}$

Έτσι παίρνουμε το μέσο όρο του αθροίσματος τετραγώνων των αποκλίσεων

Αυτό ακριβώς είναι η διακύμανση!

\[\text{MS Total} = s^2 = 3.244\]

Σχέση με την τυπική απόκλιση

Η τυπική απόκλιση είναι:

\[s = \sqrt{\text{MS Total}} = \sqrt{3.244} \approx 1.801\]

Άρα:

MS Total (3.244) = Διακύμανση = $s^2$
Τυπική απόκλιση (1.801) = $s = \sqrt{s^2}$

Το MS Total είναι το τετράγωνο της τυπικής απόκλισης!

Γιατί οι άλλες επιλογές είναι λάθος;

Α. «Η τυπική απόκλιση γύρω από το Γενικό Μέσο» — ΛΑΘΟΣ

Γιατί είναι λάθος:

Το MS Total δεν είναι η τυπική απόκλιση — είναι η διακύμανση!

Β. «Ο συνολικός αριθμός βαθμολογιών» — ΛΑΘΟΣ

Γιατί είναι λάθος:

Ο συνολικός αριθμός βαθμολογιών είναι το n, όχι το MS Total!

Από τον πίνακα:

n = df + 1 = 199 + 1 = 200 (αριθμός παρατηρήσεων)
MS Total = 3.244 (διακύμανση)

Το 3.244 είναι στατιστικό μέτρο διασποράς, όχι πλήθος!

Γ. «Ο συνολικός αριθμός του αθροίσματος τετραγώνων των μέσων όρων στο κενό μοντέλο» — ΛΑΘΟΣ

Γιατί είναι λάθος:

Αυτή η φράση δεν έχει στατιστικό νόημα.

Προβλήματα:

“Τετράγωνα των μέσων όρων” — Δεν υψώνουμε μέσους όρους στο τετράγωνο
- Παίρνουμε τα τετράγωνα των αποκλίσεων από το μέσο όρο: $(Y_i - \bar{Y})^2$
Το MS είναι μέσος όρος, όχι άθροισμα
- Αν θέλαμε άθροισμα, θα χρησιμοποιούσαμε το SS Total (645.595)
Μονάδες μέτρησης:
- MS Total = 3.244 βαθμοί² (έχει μονάδες)
- “Αριθμός” συνήθως δεν έχει μονάδες

Σωστή ορολογία:

SS Total: Συνολικό άθροισμα τετραγώνων των αποκλίσεων
MS Total: Μέσο άθροισμα τετραγώνων των υπολοίπων = Διακύμανση

Τα τρία MS στον πίνακα

MS	Τύπος	Τιμή	Ερμηνεία
`MS Model`	$\frac{\text{Model SS}}{\text{df Model}}$	$\frac{99.106}{1} = 99.106$	Μέσο άθροισμα τετραγώνων των υπολοίπων που εξηγείται
`MS Error`	$\frac{\text{SS Error}}{\text{df Error}}$	$\frac{546.489}{198} = 2.760$	Μέσο άθροισμα τετραγώνων των υπολοίπων που δεν εξηγείται
`MS Total`	$\frac{\text{SS Total}}{\text{df Total}}$	$\frac{645.595}{199} = 3.244$	Μέσο άθροισμα τετραγώνων των υπολοίπων από το μέσο όρο = Διακύμανση

Γιατί “περίπου”;

Η λέξη “περίπου” χρησιμοποιείται επειδή:

Δειγματοληπτική εκτίμηση:
- Το MS Total είναι εκτίμηση της διακύμανσης του πληθυσμού ($\sigma^2$)
- Υπολογίζεται από το δείγμα, όχι από ολόκληρο τον πληθυσμό
Αβεβαιότητα:
- Διαφορετικά δείγματα θα δώσουν ελαφρώς διαφορετικές τιμές
- Το 3.244 είναι η εκτίμηση από αυτό το συγκεκριμένο δείγμα

Συμπέρασμα

Το 3.244 είναι:

Το μέσο άθροισμα τετραγώνων των υπολοίπων από το Γενικό Μέσο Όρο (Grand Mean).

Με άλλα λόγια:

Είναι η διακύμανση ($s^2$) της LikeF
Μετρά το μέσο όρο των τετραγώνων των αποκλίσεων από το γενικό μέσο όρο
Η ρίζα της διακύμανσης ($\sqrt{3.244} \approx 1.801$) είναι η τυπική απόκλιση

Βασική αρχή:

Το MS (Mean Square) είναι πάντα ένας μέσος όρος του αθροίσματος τετραγώνων αποκλίσεων. Το MS Total είναι η διακύμανση της εξαρτημένης μεταβλητής.

30. Οι πορτοκαλί κύκλοι στο παρακάτω διάγραμμα αντιπροσωπεύουν παρατηρήσεις και τα δύο κόκκινα οριζόντια ευθύγραμμα τμήματα αντιπροσωπεύουν το μοντέλο δύο ομάδων. Ποια απόσταση επάνω στο διάγραμμα θα χρησιμοποιούνταν για τον υπολογισμό του αθροίσματος τετραγώνων των σφαλμάτων (SS Error);

ABCΚαμία από τις παραπάνω

Επεξήγηση

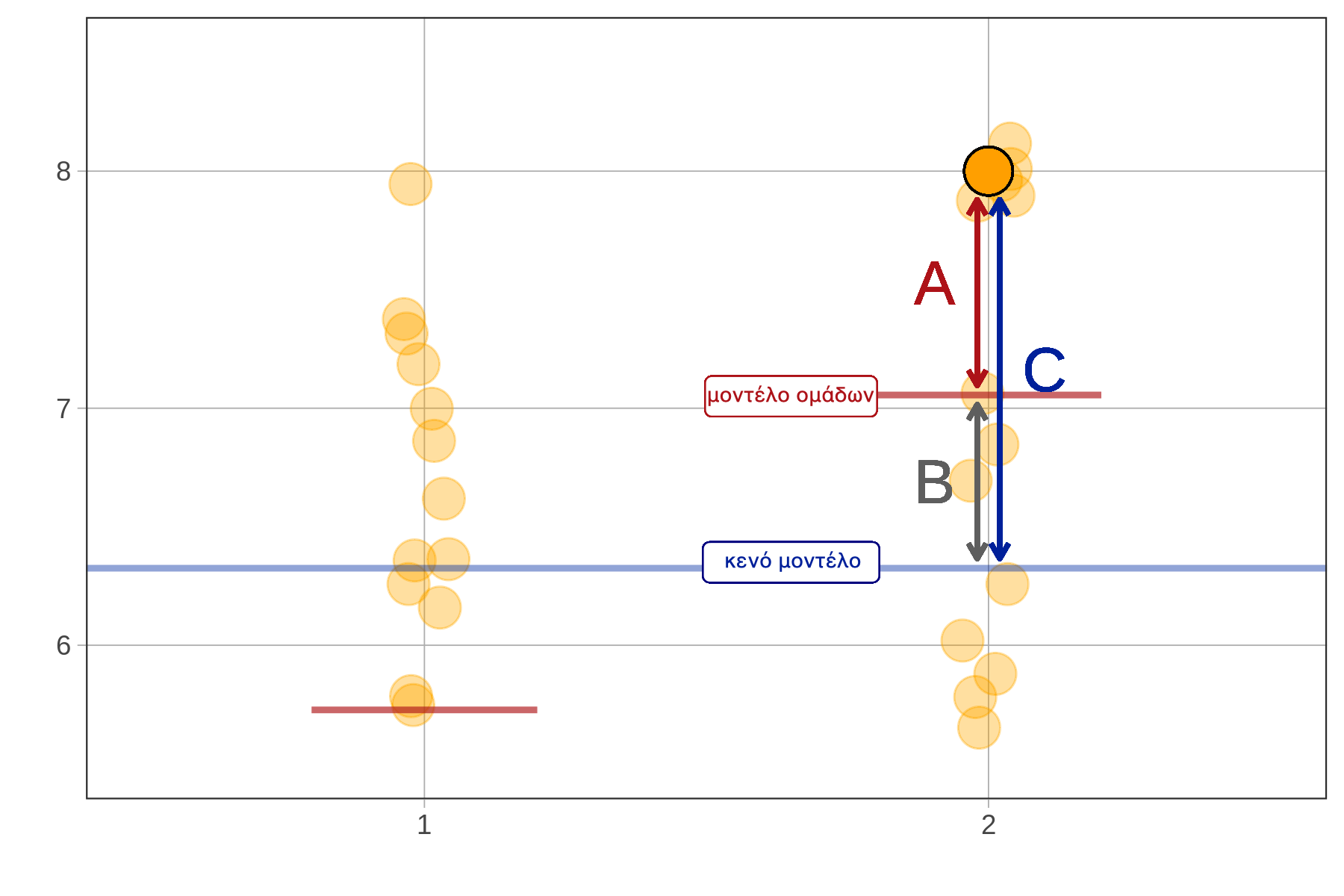
Σωστή απάντηση: Α — A

Τι είναι το SS Error;

Το SS Error μετρά την ανεξήγητη μεταβλητότητα — πόσο οι παρατηρήσεις αποκλίνουν από τις τιμές πρόβλεψης του μοντέλου.

Μαθηματικά:

\[\text{SS Error} = \sum (Y_i - \hat{Y}_i)^2\]

όπου:

$Y_i$ = παρατηρούμενη τιμή (πραγματική παρατήρηση)
$\hat{Y}_i$ = τιμή πρόβλεψης από το μοντέλο

Με λόγια:

Το SS Error είναι το άθροισμα τετραγώνων των κάθετων αποστάσεων από κάθε παρατήρηση στην τιμή πρόβλεψης του μοντέλου.

Ανάλυση του διαγράμματος

Τι βλέπουμε:

Πορτοκαλί κύκλοι = Σημεία δεδομένων (παρατηρούμενες τιμές)
Κόκκινες οριζόντιες γραμμές = Group model (προβλέψεις για κάθε ομάδα)
- Μία γραμμή για Ομάδα 1 (αριστερά, περίπου στο 5.7)
- Μία γραμμή για Ομάδα 2 (δεξιά, περίπου στο 7.0)
Μπλε οριζόντια γραμμή = Empty model (γενικός μέσος όρος, περίπου στο 6.4)

Οι αποστάσεις:

A (κόκκινο βέλος): Από σημείο δεδομένων στο group model (κόκκινη γραμμή)
B (γκρι βέλος): Από group model (κόκκινη) στο empty model (μπλε)
C (μπλε βέλος): Από σημείο δεδομένων στο empty model (μπλε γραμμή)

Γιατί η Α είναι σωστή

Η απόσταση A αντιπροσωπεύει:

\[A = Y_i - \hat{Y}_i\]

όπου:

$Y_i$ = το πορτοκαλί σημείο (παρατηρούμενη τιμή)
$\hat{Y}_i$ = η κόκκινη γραμμή (πρόβλεψη του group model)

Αυτό είναι ακριβώς το υπόλοιπο (residual)!

Για να υπολογίσουμε το SS Error:

\[\text{SS Error} = \sum A^2 = \sum (Y_i - \hat{Y}_i)^2\]

Τετραγωνίζουμε όλες τις αποστάσεις A και τις αθροίζουμε!

Γιατί οι άλλες επιλογές είναι λάθος;

Β. Απόσταση B — ΛΑΘΟΣ

Τι αντιπροσωπεύει το B:

\[B = \hat{Y}_i - \bar{Y}\]

όπου:

$\hat{Y}_i$ = τιμή πρόβλεψης του μοντέλου ομάδων (κόκκινη γραμμή)
$\bar{Y}$ = γενικός μέσος όρος του κενού μοντέλου (μπλε γραμμή)

Αυτή είναι η απόσταση που χρησιμοποιείται για το SS Model, όχι το SS Error!

\[\text{SS Model} = \sum B^2 = \sum (\hat{Y}_i - \bar{Y})^2\]

Το B μετρά:

Πόσο η τιμή πρόβλεψης του μοντέλου διαφέρει από τον γενικό μέσο όρο — αυτό είναι η εξηγούμενη μεταβλητότητα.

Γ. Απόσταση C — ΛΑΘΟΣ

Τι αντιπροσωπεύει το C:

\[C = Y_i - \bar{Y}\]

όπου:

$Y_i$ = παρατηρούμενη τιμή (πορτοκαλί σημείο)
$\bar{Y}$ = γενικός μέσος όρος (μπλε γραμμή)

Αυτό είναι η απόσταση που χρησιμοποιείται για το SS Total!

\[\text{SS Total} = \sum C^2 = \sum (Y_i - \bar{Y})^2\]

Το C μετρά:

Πόσο κάθε παρατήρηση διαφέρει από το γενικό μέσο όρο — αυτό είναι η συνολική μεταβλητότητα.

Η θεμελιώδης σχέση

Στην ανάλυση διακύμανσης:

\[\text{SS Total} = \text{SS Model} + \text{SS Error}\]

Σε όρους αποστάσεων:

\[C^2 = B^2 + A^2\]

(για κάθε σημείο, περίπου)

Συμπέρασμα

Για να υπολογίσουμε το Sum of Squares Error ή Άθροισμα Τετραγώνων των Σφαλμάτων (SS Error):

Χρησιμοποιούμε την απόσταση A — την κάθετη απόσταση από κάθε παρατήρηση στην τιμή πρόβλεψης του μοντέλου ομάδων.

Βασική αρχή:

Το SS Error μετρά την ανεξήγητη μεταβλητότητα — πόσο τα δεδομένα αποκλίνουν από τις προβλέψεις του μοντέλου. Αυτό αντιστοιχεί στην απόσταση από τις παρατηρήσεις στο μοντέλο (όχι στο γενικό μέσο όρο).

Σύνοψη:

A → SS Error (ανεξήγητη μεταβλητότητα) ✓
B → SS Model (εξηγούμενη μεταβλητότητα)
C → SS Total (συνολική μεταβλητότητα)

31. Οι πορτοκαλί κύκλοι στο παρακάτω διάγραμμα αντιπροσωπεύουν παρατηρήσεις και η κόκκινη ευθεία γραμμή αντιπροσωπεύει το μοντέλο παλινδρόμησης. Ποια απόσταση επάνω στο διάγραμμα θα χρησιμοποιούνταν για τον υπολογισμό της μείωσης του σφάλματος του μοντέλου παλινδρόμησης σε σύγκριση με το κενό μοντέλο;

ABCΚαμία από τις παραπάνω

Επεξήγηση

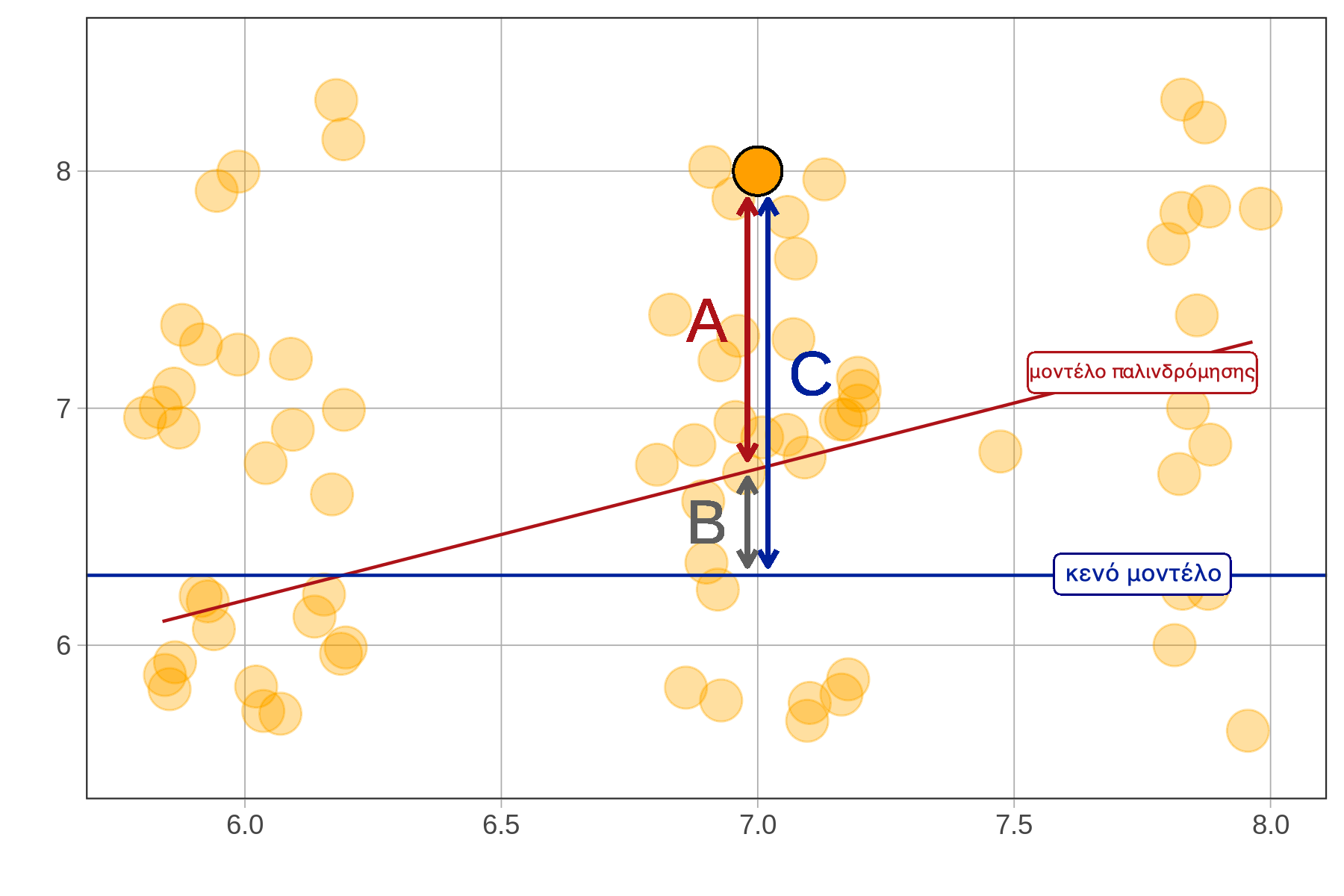
Σωστή απάντηση: Β — Β

Τι ρωτάμε;

Θέλουμε να μετρήσουμε τη μείωση του σφάλματος όταν χρησιμοποιούμε το μοντέλο παλινδρόμησης αντί για το κενό μοντέλο.

Με άλλα λόγια:

Πόσο καλύτερες προβλέψεις κάνει το μοντέλο παλινδρόμησης μας σε σχέση με το να χρησιμοποιούμε απλά τον γενικό μέσο όρο;

Βασική έννοια: Μείωση σφάλματος

Η μείωση του σφάλματος ισούται με:

\[\text{Reduction in Error} = \text{SS Total} - \text{SS Error}\]

Αλλά αυτό ισούται ακριβώς με το SS Model!

\[\text{SS Model} = \text{SS Total} - \text{SS Error}\]

Επομένως:

Η μείωση σφάλματος = SS Model = η εξηγούμενη μεταβλητότητα του μοντέλου

Ανάλυση του διαγράμματος

Τι βλέπουμε:

Πορτοκαλί κύκλοι = Σημεία δεδομένων (παρατηρούμενες τιμές $Y_i$)
Κόκκινη ευθεία = Ευθεία παλινδρόμησης
- Αυτή η ευθεία προβλέπει τιμές βάσει μιας γραμμικής σχέσης
- Για κάθε σημείο υπάρχει μια τιμή πρόβλεψης $\hat{Y}_i$ πάνω στη γραμμή
Μπλε οριζόντια γραμμή = Κενό μοντέλο (γενικός μέσος όρος $\bar{Y}$)
- Αυτή η γραμμή αγνοεί οποιαδήποτε σχέση μεταξύ των μεταβλητών
- Προβλέπει πάντα την ίδια τιμή: το μέσο όρο της εξαρτημένης μεταβλητής

Οι αποστάσεις:

A (κόκκινο βέλος): Από παρατήρηση (πορτοκαλί σημείο) στο μοντέλο παλινδρόμησης (κόκκινη γραμμή)
- Αυτό είναι το υπόλοιπο: $Y_i - \hat{Y}_i$
- Μετρά το ανεξήγητο σφάλμα
B (γκρι βέλος): Από μοντέλο παλινδρόμησης (κόκκινη γραμμή) στο κενό μοντέλο (μπλε γραμμή)
- Αυτό μετρά πόσο το μοντέλο παλινδρόμησης βελτιώνει την πρόβλεψη!
- Είναι η διαφορά: $\hat{Y}_i - \bar{Y}$
C (μπλε βέλος): Από παρατήρηση (πορτοκαλί σημείο) στο κενό μοντέλο (μπλε γραμμή)
- Αυτό είναι η συνολική απόκλιση από τον μέσο όρο: $Y_i - \bar{Y}$
- Μετρά τη συνολική μεταβλητότητα

Γιατί η Β είναι σωστή

Η απόσταση B αντιπροσωπεύει:

\[B = \hat{Y}_i - \bar{Y}\]

όπου:

$\hat{Y}_i$ = τιμή πρόβλεψης του μοντέλου παλινδρόμησης (σημείο πάνω στην κόκκινη γραμμή)
$\bar{Y}$ = γενικός μέσος όρος του κενού μοντέλου (μπλε οριζόντια γραμμή)

Αυτή η απόσταση μετρά:

Πόσο η πρόβλεψη του μοντέλου παλινδρόμησης διαφέρει από τον γενικό μέσο όρο

Για να υπολογίσουμε τη μείωση σφάλματος:

\[\text{SS Model} = \sum B^2 = \sum (\hat{Y}_i - \bar{Y})^2\]

Τετραγωνίζουμε όλες τις αποστάσεις B (για όλα τα σημεία) και τις αθροίζουμε!

Διαισθητική εξήγηση

Σκεφτείτε το ως εξής:

Χωρίς μοντέλο παλινδρόμησης (κενό μοντέλο):
- Για κάθε σημείο προβλέπουμε πάντα τον γενικό μέσο όρο $\bar{Y}$ (μπλε γραμμή)
- Το συνολικό σφάλμα μας είναι: $\sum (Y_i - \bar{Y})^2$ = SS Total
- Δηλαδή, το άθροισμα των τετραγώνων όλων των αποστάσεων C
Με μοντέλο παλινδρόμησης:
- Προβλέπουμε $\hat{Y}_i$ (σημεία πάνω στην κόκκινη γραμμή)
- Το σφάλμα μας είναι: $\sum (Y_i - \hat{Y}_i)^2$ = SS Error
- Δηλαδή, το άθροισμα των τετραγώνων όλων των αποστάσεων A
Η μείωση του σφάλματος:
- Είναι η διαφορά: SS Total - SS Error
- Αυτό ισούται με SS Model = $\sum (\hat{Y}_i - \bar{Y})^2$
- Δηλαδή, το άθροισμα των τετραγώνων όλων των αποστάσεων B!

Με λόγια:

Η απόσταση B δείχνει πόσο το μοντέλο παλινδρόμησης «απομακρύνει» την πρόβλεψη από τον γενικό μέσο όρο. Όσο μεγαλύτερο το B (κατά μέσο όρο για όλα τα σημεία), τόσο πιο διαφορετικές — και καλύτερες — είναι οι προβλέψεις του μοντέλου.

Γιατί οι άλλες επιλογές είναι λάθος;

Α. Απόσταση A — ΛΑΘΟΣ

Τι αντιπροσωπεύει το A:

\[A = Y_i - \hat{Y}_i\]

Αυτή είναι η απόσταση για το SS Error!

\[\text{SS Error} = \sum A^2 = \sum (Y_i - \hat{Y}_i)^2\]

Το A μετρά:

Το ανεξήγητο σφάλμα του μοντέλου — πόσο οι παρατηρήσεις αποκλίνουν από την ευθεία παλινδρόμησης.

Αυτό δεν είναι η μείωση του σφάλματος, αλλά το σφάλμα που απομένει μετά τη χρήση του μοντέλου!

Γ. Απόσταση C — ΛΑΘΟΣ

Τι αντιπροσωπεύει το C:

\[C = Y_i - \bar{Y}\]

Αυτή είναι η απόσταση για το SS Total!

\[\text{SS Total} = \sum C^2 = \sum (Y_i - \bar{Y})^2\]

Το C μετρά:

Τη συνολική μεταβλητότητα των δεδομένων γύρω από τον γενικό μέσο όρο.

Αυτό περιλαμβάνει τόσο την εξηγούμενη όσο και την ανεξήγητη μεταβλητότητα — δεν μετρά μόνο τη μείωση!

Η θεμελιώδης σχέση (ξανά)

Η βασική εξίσωση της ανάλυσης παλινδρόμησης:

\[\text{SS Total} = \text{SS Model} + \text{SS Error}\]

Δηλαδή:

\[\text{SS Model} = \text{SS Total} - \text{SS Error}\]

Αυτό είναι ακριβώς η μείωση του σφάλματος!

Συμπέρασμα

Για να υπολογίσουμε τη μείωση του σφάλματος (reduction in error):

Χρησιμοποιούμε την απόσταση B — την κάθετη απόσταση από την πρόβλεψη του μοντέλου παλινδρόμησης (κόκκινη γραμμή) στον γενικό μέσο όρο (μπλε γραμμή).

Βασική αρχή:

Η μείωση σφάλματος = SS Model = η εξηγούμενη μεταβλητότητα. Αυτό μετρά πόσο το μοντέλο παλινδρόμησης βελτιώνει τις προβλέψεις σε σχέση με το να χρησιμοποιούμε απλά τον γενικό μέσο όρο.

Γιατί το B είναι η σωστή απάντηση:

Το B δείχνει πόσο η ευθεία παλινδρόμησης «απομακρύνεται» από τη βασική ευθεία (κενό μοντέλο ή μέσος όρος)
Όσο πιο μεγάλες οι αποστάσεις B, τόσο περισσότερη μεταβλητότητα εξηγεί το μοντέλο
Αυτό είναι ακριβώς η επιτυχία του μοντέλου παλινδρόμησης!

Σύνοψη:

A → SS Error (ανεξήγητη μεταβλητότητα)
B → SS Model (εξηγούμενη μεταβλητότητα ή μείωση σφάλματος) ✓
C → SS Total (συνολική μεταβλητότητα)

Η απόσταση B μετρά την προστιθέμενη αξία του μοντέλου παλινδρόμησης!

Σύμβολο	Μοντέλο Ομάδων \(Y_i = b_0 + b_1 X_i + e_i\) \(Thumb_i = b_0 + b_1 Height2Group_{tall,i} + e_i\)	Μοντέλο Παλινδρόμησης \(Y_i = b_0 + b_1 X_i + e_i\) \(Thumb_i = b_0 + b_1 Height_i + e_i\)
\(Y_i\)	Μήκος αντίχειρα του φοιτητή \(i\)	Μήκος αντίχειρα του φοιτητή \(i\)
\(b_0\)	Τιμή πρόβλεψης μήκους αντίχειρα όταν \(Height2Group_i = 0\) (μέσο μήκος αντίχειρα για τους φοιτητές χαμηλού αναστήματος)	Τιμή πρόβλεψης μήκους αντίχειρα όταν \(Height_i = 0\) (τεταγμένη τομής της γραμμής παλινδρόμησης)
\(b_1\)	Μεταβολή στην τιμή πρόβλεψης μήκους αντίχειρα για φοιτητές υψηλού αναστήματος (η μέση διαφορά μεταξύ των δύο ομάδων)	Μεταβολή στην τιμή πρόβλεψης μήκους αντίχειρα για κάθε αύξηση του ύψους κατά μία μονάδα (η κλίση της γραμμής παλινδρόμησης)
\(X_i\)	Μεταβλητή `Height2Group` του φοιτητή \(i\) (κωδικοποιημένη ως 0 = όχι ψηλός, 1 = ψηλός)	Ύψος του φοιτητή \(i\) (σε εκατοστά)
\(e_i\)	Σφάλμα πρόβλεψης για τον φοιτητή \(i\)	Σφάλμα πρόβλεψης για τον φοιτητή \(i\)

Ομάδα	Μέσος όρος	Πώς εκφράζεται
1	\(\mu_1\)	\(b_0\) (σταθερός όρος)
2	\(\mu_2\)	\(b_0 + b_1\)
3	\(\mu_3\)	\(b_0 + b_2\)
…	…	…
10	\(\mu_{10}\)	\(b_0 + b_9\)

10.1 Χρήση Ποσοτικής Ανεξάρτητης Μεταβλητής σε ένα Μοντέλο

Το Μοντέλο του Ύψους (Height)

Προβλέψεις από το Μοντέλο της Height

10.2 Προσδιορισμός του Μοντέλου της Height με τη Σημειογραφία του GLM

Σχέση με την Άλγεβρα

10.3 Ερμηνεία των Εκτιμήσεων Παραμέτρων σε ένα Μοντέλο Παλινδρόμησης

Πώς τα Μοντέλα Παλινδρόμησης Κάνουν Προβλέψεις

Οι Συντελεστές Παλινδρόμησης δεν είναι Συμμετρικοί

10.4 Σύγκριση Μοντέλων Παλινδρόμησης με Μοντέλα Ομάδων

Σύγκριση των Μοντέλων της Height2Group και της Height

Προσαρμογή Μοντέλου Παλινδρόμησης κατά Λάθος

10.5 Σφάλμα από το Μοντέλο της Height

Άθροισμα Τετραγώνων Σφαλμάτων (SS Error) για το Μοντέλο του Ύψους

Χρήση της R για τη σύγκριση των Αθροισμάτων Τετραγώνων του μοντέλου της Height και του κενού μοντέλου

Σύγκριση της Ευθείας Παλινδρόμησης με το Μέσο Όρο

10.6 Αθροίσματα Τετραγώνων στον πίνακα ANOVA

To SS Error στα τρία μοντέλα

Το SS Model

10.7 Αξιολόγηση της Προσαρμογής του Μοντέλου με τους δείκτες PRE και F

Σύγκριση του PRE για τα δύο μοντέλα

Χρήση του πηλίκου F για τη σύγκριση μοντέλων

Περισσότερα για τη σύγκριση F και PRE

Σύγκριση των Τριών Μοντέλων

Σύγκριση των Πηλίκων F για τα Τρία Μοντέλα

10.8 Συσχέτιση

Εργασία με Τυποποιημένες Μεταβλητές

Προσαρμογή του Μοντέλου Παλινδρόμησης σε Τυποποιημένες Μεταβλητές

Συντελεστής Συσχέτισης: Η Κλίση της Τυποποιημένης Ευθείας Παλινδρόμησης

10.9 Περισσότερα για το r του Pearson

Δημιουργία Πίνακα Συσχετίσεων

Η Σχέση μεταξύ R² και PRE

Σύγκριση της Προσαρμογής Τυποποιημένων και Μη Τυποποιημένων Μοντέλων Παλινδρόμησης

10.10 Ερμηνεία της Κλίσης μιας Ευθείας Παλινδρόμησης με Τυχαίο Ανακάτεμα

Επανεξέταση της Προσομοίωσης υπό το Κενό Μοντέλο

10.11 Περιορισμοί

Η Συσχέτιση Δεν Συνεπάγεται Αιτιότητα

Είναι Όλες οι Γραμμές Ευθείες;

Οι Ευθείες Παλινδρόμησης Προεκτείνονται Απεριόριστα;

10.12 Ασκήσεις Επανάληψης Κεφαλαίου 10

Το Μοντέλο του Ύψους (`Height`)

Προβλέψεις από το Μοντέλο της `Height`

10.2 Προσδιορισμός του Μοντέλου της `Height` με τη Σημειογραφία του GLM

Σύγκριση των Μοντέλων της `Height2Group` και της `Height`

10.5 Σφάλμα από το Μοντέλο της `Height`

Άθροισμα Τετραγώνων Σφαλμάτων (`SS Error`) για το Μοντέλο του Ύψους

Χρήση της R για τη σύγκριση των Αθροισμάτων Τετραγώνων του μοντέλου της `Height` και του κενού μοντέλου

To `SS Error` στα τρία μοντέλα

Το `SS Model`

10.7 Αξιολόγηση της Προσαρμογής του Μοντέλου με τους δείκτες `PRE` και `F`

Χρήση του πηλίκου `F` για τη σύγκριση μοντέλων

Περισσότερα για τη σύγκριση `F` και PRE

Σύγκριση των Πηλίκων `F` για τα Τρία Μοντέλα