empty_model <- lm(Thumb ~ NULL, data = Fingers)
gf_dhistogram(~ Thumb, data = Fingers) %>%
gf_facet_grid(Gender ~ .) %>%
gf_model(empty_model)8 Κεφάλαιο: Προσθήκη Ανεξάρτητης Μεταβλητής στο Μοντέλο
Όλες οι επιστημονικές εργασίες είναι, από τη φύση τους, ατελείς και ενδέχεται να ανατραπούν ή να τροποποιηθούν με την πρόοδο της γνώσης. Ωστόσο, αυτό δεν μας δίνει το δικαίωμα να αγνοούμε τη γνώση που ήδη διαθέτουμε ούτε να αναβάλλουμε τη δράση που φαίνεται αναγκαία στη δεδομένη στιγμή.
— Bradford Hill
8.1 Εξήγηση της Μεταβλητότητας
Έχουμε αφιερώσει μεγάλο μέρος του χρόνου μας στο κενό μοντέλο (empty model) και ίσως αναρωτιέστε: «Ποιος είναι ο σκοπός αυτού του μοντέλου;» Η στατιστική υποτίθεται ότι μας βοηθά να εξηγήσουμε τη μεταβλητότητα και να κάνουμε καλύτερες προβλέψεις για την εξαρτημένη μεταβλητή με βάση άλλες μεταβλητές. Ωστόσο, το κενό μοντέλο δε φαίνεται να κάνει πολύ καλές προβλέψεις. Ναι, ο μέσος όρος είναι το σημείο σε μια κατανομή που μειώνει το άθροισμα τετραγώνων των αποκλίσεων από αυτό όσο το δυνατό περισσότερο. Αλλά σίγουρα αυτό δε θεωρείται εξήγηση της μεταβλητότητας!
Πράγματι, δεν είναι. Ξεκινήσαμε με το κενό μοντέλο, αλλά αυτό δεν είναι εκεί που θέλουμε να φτάσουμε. Θα χρησιμοποιήσουμε το κενό μοντέλο ως σημείο αναφοράς για να μας βοηθήσει να δούμε αν πιο σύνθετα μοντέλα που περιλαμβάνουν ανεξάρτητες μεταβλητές είναι καλύτερα. Σημειώστε ότι, παρόλο που θα αναφερόμαστε στα μοντέλα αυτού του κεφαλαίου ως «σύνθετα», αυτά θεωρούνται ακόμα σχετικά απλά. Εννοούμε απλώς ότι αυτά τα μοντέλα είναι πιο σύνθετα από το κενό μοντέλο.
Εξήγηση της Μεταβλητότητας στο Μήκος Αντίχειρα
Ας ξεκινήσουμε επανεξετάζοντας τι εννοούμε με τον όρο εξήγηση της μεταβλητότητας. Νωρίτερα στο μάθημα, αναπτύξαμε μια διαισθητική ιδέα για το τι σημαίνει να εξηγούμε τη μεταβλητότητα, συγκρίνοντας την κατανομή μιας εξαρτημένης μεταβλητής για δύο διαφορετικές ομάδες παρατηρήσεων.
Για παράδειγμα, εξετάσαμε την κατανομή του μήκους αντίχειρα ανά φύλο, την οποία μπορούμε να δούμε στα δύο ιστογράμματα πυκνότητας πιθανότητας που ακολουθούν. Επιπλέον, έχουμε προβάλει στα ιστογράμματα την πρόβλεψη του κενού μοντέλου (δηλαδή το συνολικό μέσο όρο του μήκους αντίχειρα) ως σημείο αναφοράς. Η τιμή πρόβλεψης του κενού μοντέλου θα ήταν αυτή που θα χρησιμοποιούσαμε αν δε γνωρίζαμε το φύλο ενός ατόμου.
 Μπορούμε να εξετάσουμε την ίδια σχέση (με το κενό μοντέλο) σε ένα διάγραμμα διασποράς με τυχαία μετατόπιση (διάγραμμα jitter).
Μπορούμε να εξετάσουμε την ίδια σχέση (με το κενό μοντέλο) σε ένα διάγραμμα διασποράς με τυχαία μετατόπιση (διάγραμμα jitter).
empty_model <- lm(Thumb ~ NULL, data = Fingers)
gf_jitter(Thumb ~ Gender, data = Fingers, width = .1) %>%
gf_model(empty_model)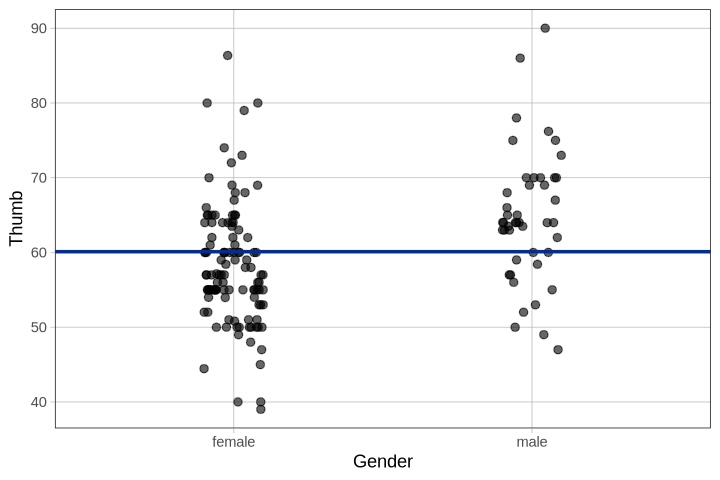
Η διαγραμματική αναπαράσταση των δεδομένων ανά φύλο μας βοηθά να εξετάσουμε τι σχέση που υπάρχει μεταξύ του φύλου και του μήκους του αντίχειρα. Εφαρμόζοντας τον άτυπο ορισμό μας για την εξήγηση της μεταβλητότητας, φαίνεται από το διάγραμμα ότι αν γνωρίζουμε το φύλο ενός ατόμου, μπορούμε να κάνουμε μια λίγο καλύτερη εκτίμηση για το μήκος του αντίχειρά του/της.
Σύμφωνα με το κενό μοντέλο, θα προβλέπαμε ότι το μήκος του αντίχειρα ενός μελλοντικού φοιτητή είναι 60.1 χιλιοστά (δηλαδή, ο συνολικός μέσος όρος του μήκους του αντίχειρα). Πώς θα μπορούσε η γνώση του φύλου ενός φοιτητή να αλλάξει την πρόβλεψή μας για το μήκος του αντίχειρά του/της;
Όπως είδαμε, μπορούμε να εκφράσουμε άτυπα αυτή τη σχέση μεταξύ του φύλου και του μήκους αντίχειρα με μια λεκτική εξίσωση:
Μήκος αντίχειρα = Φύλο + Σφάλμα
Θα αναφερόμαστε σε αυτό το μοντέλο ως μοντέλο του Φύλου για το μήκος αντίχειρα, με την έννοια ότι η μοναδική ανεξάρτητη μεταβλητή στο μοντέλο μας είναι το φύλο. Το Φύλο, ωστόσο, δεν εξηγεί ολόκληρη τη μεταβλητότητα στο μήκος του αντίχειρα (υπάρχει ακόμα σφάλμα), αλλά φαίνεται να εξηγεί κάποιο μέρος της.
Ποσοτικοποίηση του Μοντέλου του Φύλου
Στο προηγούμενο κεφάλαιο αναπτύξαμε το πρώτο μας πραγματικό στατιστικό μοντέλο, το κενό μοντέλο. Όπως αποδείχθηκε, η καλύτερη πρόβλεψη για το μήκος του αντίχειρα ενός μελλοντικού φοιτητή, αν δεν γνωρίζουμε τίποτα για αυτόν, είναι απλώς ο μέσος όρος της εξαρτημένης μεταβλητής, Thumb. Ονομάσαμε αυτό το κενό μοντέλο, μοντέλο μίας παραμέτρου, επειδή η πρόβλεψή μας βασιζόταν σε μία μόνο εκτίμηση: το μέσο όρο.
Ας δούμε αν μπορούμε να ακολουθήσουμε μια παρόμοια προσέγγιση για να περάσουμε από το άτυπο μοντέλο του Φύλου (μεταβλητή Gender), που εκφράσαμε με μια εξίσωση λέξεων, σε ένα πραγματικό στατιστικό μοντέλο που μπορούμε να χρησιμοποιήσουμε για να κάνουμε συγκεκριμένες ποσοτικές προβλέψεις για το μήκος του αντίχειρα άλλων φοιτητών, που δεν περιλαμβάνονται στο δείγμα μας.
Αν θέλαμε να κάνουμε διαφορετικές προβλέψεις για τα μήκη αντίχειρα των γυναικών και των ανδρών, ποια από τις παρακάτω στρατηγικές σας φαίνεται πιο λογική;
Σωστή απάντηση: Β
Γιατί η Β είναι σωστή:
Χρησιμοποιούμε τον μέσο όρο ανά ομάδα για να κάνουμε προβλέψεις:
# Μέσος αντίχειρας για γυναίκες
mean_female <- mean(Thumb[Sex == "female"])
# Μέσος αντίχειρας για άνδρες
mean_male <- mean(Thumb[Sex == "male"])
# Προβλέψεις:
# Γυναίκα → mean_female
# Άνδρας → mean_maleΑυτό είναι είναι γνωστό ως μοντέλο ομάδων (group model): Thumb ~ Gender
Γιατί οι άλλες είναι λάθος:
Α - “Μέσος μεγαλύτερων vs μικρότερων” - ΛΑΘΟΣ:
Αυτή η προσέγγιση:
Χωρίζει βάσει μήκους, όχι φύλου
Δεν χρησιμοποιεί την πληροφορία του φύλου
Είναι κυκλική λογική: χρησιμοποιεί το αποτέλεσμα (μήκος) για να προβλέψει το ίδιο το αποτέλεσμα
Γ - “Μέγιστο για άνδρες, ελάχιστο για γυναίκες” - ΛΑΘΟΣ:
Χρησιμοποιώντας τιμές στα άκρα της κατανομής:
Το max και min δεν είναι αντιπροσωπευτικές τιμές
Δεν είναι καλές προβλέψεις για την “τυπική” παρατήρηση
Ο μέσος όρος ελαχιστοποιεί το σφάλμα, όχι το max/min
Συμπέρασμα:
Η σωστή στρατηγική είναι να χρησιμοποιήσουμε το μέσο μήκος αντίχειρα ανά φύλο. Αυτό:
Χρησιμοποιεί την ανεξάρτητη μεταβλητή (φύλο) για να προβλέψει την εξαρτημένη (μήκος)
Δίνει διαφορετικές προβλέψεις για κάθε ομάδα
Χρησιμοποιεί το μέσο όρο, που ελαχιστοποιεί το σφάλμα
Μπορούμε να μετατρέψουμε το μοντέλο του Φύλου σε στατιστικό μοντέλο με παρόμοιο τρόπο όπως κάναμε για το κενό μοντέλο. Αυτή τη φορά, αντί να προβλέψουμε το μήκος αντίχειρα ενός μελλοντικού φοιτητή με το συνολικό μέσο όρο, θα το προβλέψουμε ως το μέσο όρο του μήκους αντίχειρα για το φύλο του. Έτσι, αν είναι γυναίκα, θα προβλέψουμε το μήκος του αντίχειρά της ως την τιμή του μέσου μήκους αντίχειρα των γυναικών, και αν είναι άνδρας, την τιμή του μέσου των ανδρών.
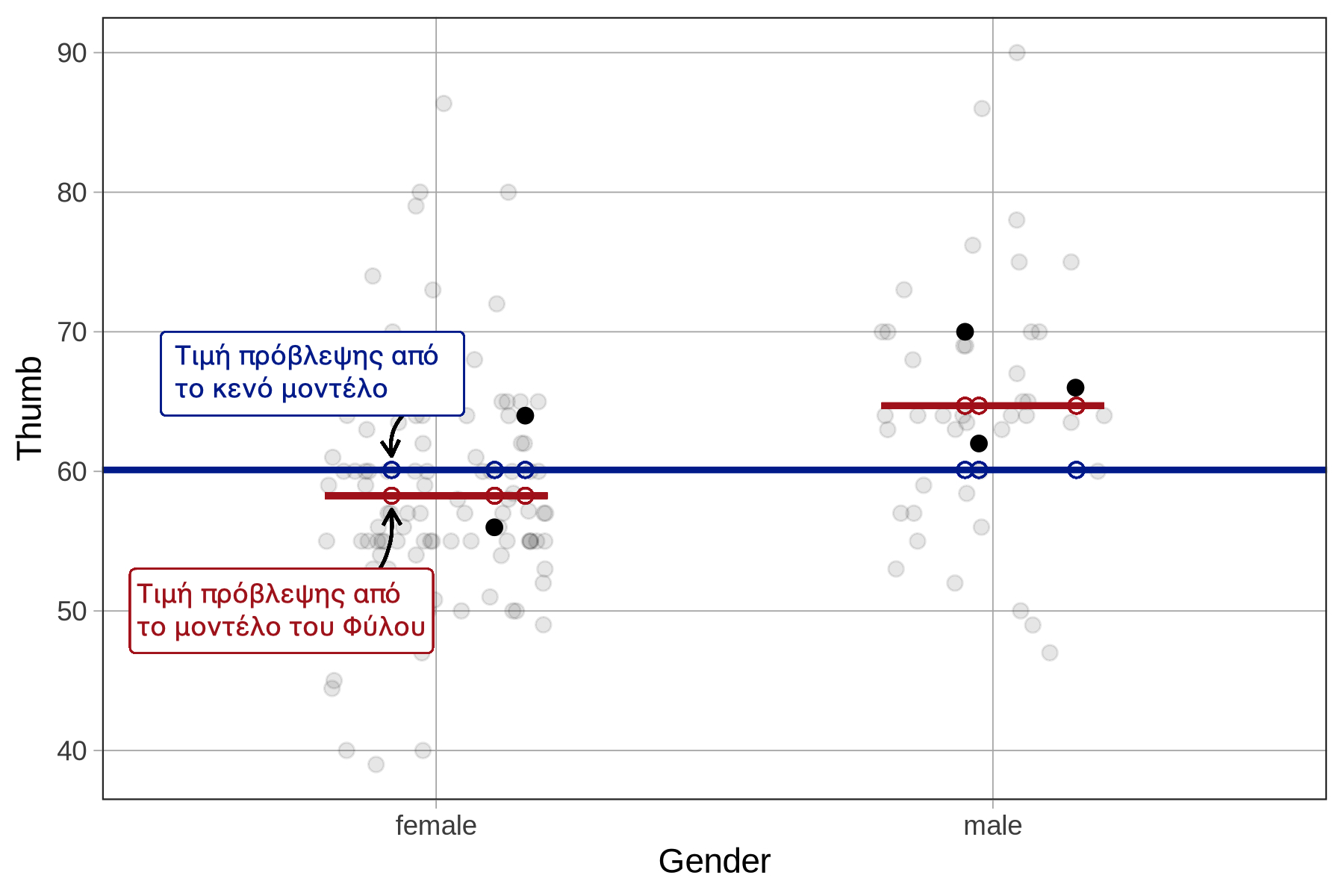
Αυτό είναι ένα μοντέλο δύο παραμέτρων, επειδή θα χρειαστεί να κάνουμε δύο εκτιμήσεις, μία για κάθε φύλο. Έχουμε προσθέσει μια διαγραμματική αναπαράσταση του μοντέλου του Φύλου στο παρακάτω διάγραμμα (οι κόκκινες οριζόντιες γραμμές), πλέον της αναπαράστασης του κενού μοντέλου (η μπλε οριζόντια γραμμή).
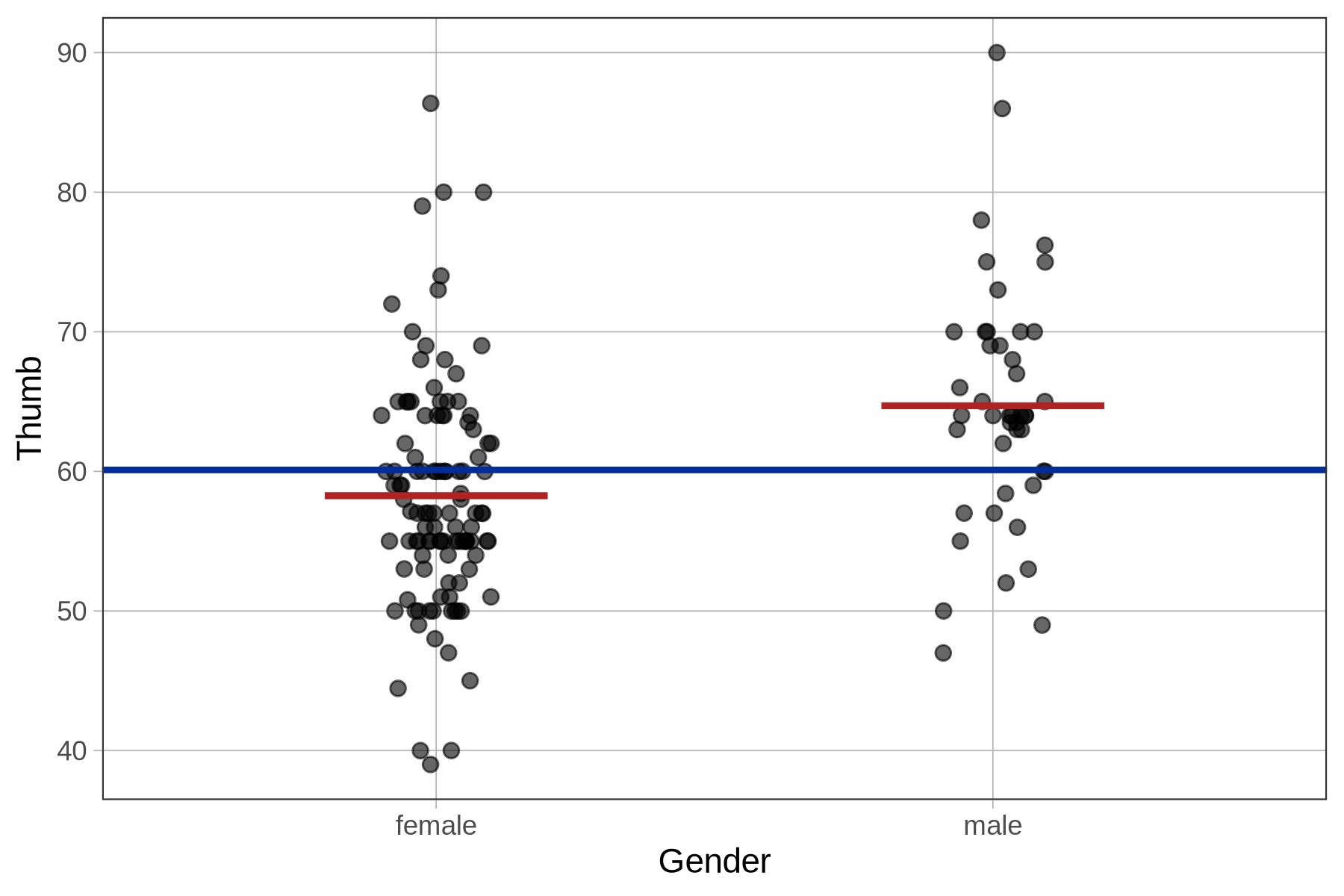
Με βάση το διάγραμμα, τι θα προέβλεπε το μοντέλο του Φύλου (Gender) για το μήκος αντίχειρα μιας φοιτήτριας;
Με βάση το διάγραμμα, τι θα προέβλεπε το μοντέλο του Φύλου (Gender) για το μήκος αντίχειρα ενός άνδρα φοιτητή; (Υπάρχουν περισσότερες από μία σωστές απαντήσεις.)
Ανάλυση του διαγράμματος:
Το διάγραμμα δείχνει:
Μπλε οριζόντια γραμμή: Γενικός μέσος όρος (~60mm) - κενό μοντέλο
Κόκκινη γραμμή αριστερά: Μέσος όρος για γυναίκες (~58mm)
Κόκκινη γραμμή δεξιά: Μέσος όρος για άνδρες (~65mm)
Ερώτηση - Πρόβλεψη για γυναίκες:
Σωστή απάντηση: Α (Περίπου 58)
Η κόκκινη γραμμή για τις γυναίκες (αριστερά) βρίσκεται στα ~58mm.
Ερώτηση - Πρόβλεψη για άνδρες:
Σωστές απαντήσεις: Γ και Δ
Γ. Περίπου 65 - ΣΩΣΤΟ ✓
Η κόκκινη γραμμή για τους άνδρες (δεξιά) βρίσκεται στα ~65mm.
Δ. Περίπου 7mm περισσότερο - ΣΩΣΤΟ ✓
Η διαφορά μεταξύ των προβλέψεων:
Οι άνδρες έχουν κατά μέσο όρο 7mm μεγαλύτερο αντίχειρα.
Γιατί οι άλλες είναι λάθος:
Α. Περίπου 58 - ΛΑΘΟΣ:
- Αυτή είναι η πρόβλεψη για γυναίκες, όχι για άνδρες
Β. Περίπου 60 - ΛΑΘΟΣ:
Αυτός είναι ο γενικός μέσος όρος (μπλε γραμμή - κενό μοντέλο)
Όχι η πρόβλεψη του μοντέλου του Φύλου για τους άνδρες
Ε. 7mm λιγότερο - ΛΑΘΟΣ:
Οι άνδρες έχουν μεγαλύτερο, όχι μικρότερο μήκος αντίχειρα
65 > 58, άρα +7mm, όχι -7mm
Το μοντέλο του Φύλου δίνει διαφορετικές προβλέψεις για κάθε φύλο, χρησιμοποιώντας το μέσο όρο της κάθε ομάδας.
Στη συνέχεια αυτού του κεφαλαίου θα δούμε πώς να χρησιμοποιήσουμε την R για να προσαρμόσουμε το μοντέλο του Φύλου στα δεδομένα Fingers, πώς να ερμηνεύσουμε τις εκτιμήσεις των παραμέτρων, πώς να γράψουμε το μοντέλο στη σημειολογία του Γενικού Γραμμικού Μοντέλου (GLM), πώς να ποσοτικοποιήσουμε το σφάλμα γύρω από το μοντέλο και πώς να συγκρίνουμε το μοντέλο με το κενό μοντέλο.
8.2 Χρήση της R για την Προσαρμογή του Μοντέλου Ομάδων
Τώρα που γνωρίζουμε τι κάνει το μοντέλο του Φύλου – δηλαδή, ότι παράγει δύο διαφορετικές τιμές πρόβλεψης, μία για κάθε φύλο – ας χρησιμοποιήσουμε την R για να προσαρμόσουμε το μοντέλο στα δεδομένα και να δούμε πώς το μοντέλο κάνει αυτές τις προβλέψεις.
Ας δούμε αν μπορείτε να προσαρμόσετε το μοντέλο του Φύλου (Gender) για το μήκος αντίχειρα (Thumb). Για να βρούμε το καλύτερο κενό μοντέλο (το μέσο όρο), γράψαμε:
Ποια από τις παρακάτω γραμμές κώδικα νομίζετε ότι θα χρησιμοποιούσαμε για να προσαρμόσουμε το μοντέλο του Φύλου;
Σωστή απάντηση: Γ
Σύνταξη της lm():
Για το μοντέλο του Φύλου:
Εξαρτημένη μεταβλητή (Y):
Thumb(αυτό που προβλέπουμε)Ανεξάρτητη μεταβλητή (X):
Gender(αυτό που χρησιμοποιούμε για πρόβλεψη)Δεδομένα:
Fingers(το πλαίσιο δεδομένων)
Άρα:
Γιατί οι άλλες είναι λάθος:
Α. lm(Gender ~ NULL, data = Fingers) - ΛΑΘΟΣ:
Αυτό θα προσπαθούσε να προβλέψει την Gender (ως εξαρτημένη)
Θέλουμε να προβλέψουμε την Thumb, όχι την Gender
Β. lm(Thumb ~ Thumb, data = Fingers) - ΛΑΘΟΣ:
Αυτό προσπαθεί να προβλέψει την Thumb με τον εαυτό της
Κυκλική λογική: χρησιμοποιεί το αποτέλεσμα για να προβλέψει το αποτέλεσμα
Δε χρησιμοποιεί την Gender καθόλου
Δ. lm(Fingers ~ Thumb, data = Gender) - ΛΑΘΟΣ:
Λάθος όνομα πλαισίου δεδομένων: το
Genderδεν είναι πλαίσιο δεδομένωνΛάθος εξαρτημένη μεταβλητή:
Fingersείναι το πλαίσιο δεδομένων, όχι μεταβλητή
Συμπέρασμα:
Για να προσαρμόσουμε το μοντέλο του Φύλου, χρησιμοποιούμε:
Αυτό λέει στην R: “Πρόβλεψε την Thumb με βάση την Gender, με δεδομένα από το Fingers.”
Στο παρακάτω πλαίσιο, έχουμε γράψει κώδικα για να προσαρμόσουμε το μοντέλο του Φύλου και να το αποθηκεύσουμε στο αντικείμενο Gender_model. Χρησιμοποιήστε τον τελεστή διοχέτευσης (%>%) για να προβάλετε τις προβλέψεις του μοντέλου του Φύλου σε ένα διάγραμμα jitter με την εντολή gf_model(Gender_model).
Αν θέλετε να αλλάξετε το χρώμα των τιμών πρόβλεψης του μοντέλου (όπως κάναμε στο παραπάνω διάγραμμα), μπορείτε να προσθέσετε στη συνάρτηση gf_model() την παράμετρο color = "red".
Δημιουργία Προβλέψεων από το Μοντέλο του Φύλου
Το μοντέλο του Φύλου αναπαρίσταται στο διάγραμμα με δύο γραμμές επειδή παράγει δύο διαφορετικές τιμές πρόβλεψης ανάλογα με το Φύλο του φοιτητή. Ας χρησιμοποιήσουμε τη συνάρτηση predict() για να δούμε πώς γίνεται αυτό.
Παρατηρήστε ότι τώρα, αντί να λάβουμε μόνο μία μοναδική τιμή πρόβλεψης (όπως την 60.1 του κενού μοντέλου), λάβαμε δύο διαφορετικές τιμές (64.7 και 58.3). Με τον παρακάτω κώδικα, αποθηκεύσαμε αυτές τις τιμές πρόβλεψης στο πλαίσιο δεδομένων Fingers ως μια νέα μεταβλητή που ονομάζεται Gender_predict και εμφανίσαμε τις τιμές των Gender, Thumb και Gender_predict για 6 από τους φοιτητές.
Fingers$Gender_predict <- predict(Gender_model)
head(select(Fingers, Gender, Thumb, Gender_predict))
Gender Thumb Gender_predict
1 male 66.00 64.70267
2 female 64.00 58.25585
3 female 56.00 58.25585
4 male 58.42 64.70267
5 female 74.00 58.25585
6 female 60.00 58.25585Το μοντέλο του Φύλου λαμβάνει υπόψη το φύλο κάθε φοιτητή για να κάνει την πρόβλεψή του. Αν ο φοιτητής είναι άνδρας, το μοντέλο προβλέπει το μήκος του αντίχειρα ως 64.7 χιλιοστά, και αν είναι γυναίκα, προβλέπει 58.3 χιλιοστά.
Τι είναι η μεταβλητή Gender_predict;
Σωστή απάντηση: Β
Τι είναι η Gender_predict:
Η μεταβλητή Gender_predict περιέχει τις τιμές πρόβλεψης για το μήκος αντίχειρα (Thumb) που δημιουργεί το μοντέλο του Φύλου για κάθε φοιτητή, με βάση το φύλο του.
Γιατί οι άλλες είναι λάθος:
Α - “Πρόβλεψη φύλου” - ΛΑΘΟΣ:
Το μοντέλο χρησιμοποιεί το φύλο ως ανεξάρτητη μεταβλητή
Προβλέπει το μήκος αντίχειρα
Δεν προβλέπει το φύλο - το φύλο είναι γνωστό
Γ - “Διαφορά μεταξύ μοντέλων” - ΛΑΘΟΣ:
Αυτό θα ήταν κάτι σαν:
Gender_predict - Empty_predictΤο
Gender_predictείναι οι προβλέψεις από το μοντέλο του Φύλου, όχι η διαφορά
Σύγκριση με το κενό μοντέλο:
# Empty model
Empty_predict: 60.10 για ΟΛΟΥΣ
# Gender model
Gender_predict: 64.70 για άνδρες
58.26 για γυναίκεςΣυμπέρασμα:
Η Gender_predict είναι η πρόβλεψη του μήκους αντίχειρα για κάθε φοιτητή, βασισμένη στο φύλο του. Το μοντέλο χρησιμοποιεί το φύλο ως μεταβλητή εισόδου για να προβλέψει το μήκος αντίχειρα - όχι το αντίστροφο. Κάθε άνδρας παίρνει την ίδια τιμή πρόβλεψης (μέσος όρος ανδρών) και κάθε γυναίκα παίρνει την ίδια τιμή πρόβλεψης (μέσος όρος γυναικών).
Μπορούμε να εκτελέσουμε τη συνάρτηση favstats() για να επιβεβαιώσουμε ότι αυτές οι δύο προβλέψεις του μοντέλου είναι, στην πραγματικότητα, οι μέσοι όροι των μήκους του αντίχειρα για τους φοιτητές κάθε φύλου.
favstats(Thumb ~ Gender, data=Fingers)
Gender min Q1 median Q3 max mean sd n missing
1 female 39 54 57 63.125 86.36 58.25585 8.034694 112 0
2 male 47 60 64 70.000 90.00 64.70267 8.764933 45 0Ναι, είναι: οι μέσοι όροι των δύο ομάδων του φύλου είναι ίδιοι με τις τιμές πρόβλεψης που δίνονται από το Gender_model.
Ερμηνεία των Αποτελεσμάτων της lm() για το Μοντέλο του Φύλου
Προσαρμόσαμε το μοντέλο του Φύλου με τη συνάρτηση lm() και στη συνέχεια χρησιμοποιήσαμε αυτό το μοντέλο για να λάβουμε προβλέψεις. Ωστόσο, δεν έχουμε ακόμα εξετάσει τις καλύτερες εκτιμήσεις των παραμέτρων του μοντέλου.
Υπενθυμίζουμε ότι για το κενό μοντέλο εκτιμήσαμε μία παράμετρο (\(\beta_0\)), το μέσο όρο. Για το μοντέλο τoυ Φύλου, θα εκτιμήσουμε δύο παραμέτρους (\(\beta_0\) και \(\beta_1\)). Με βάση τις τιμές πρόβλεψης του μοντέλου που συζητήσαμε προηγουμένως, θα περιμένε κανείς αυτές οι δύο εκτιμήσεις των παραμέτρων να είναι οι μέσοι όροι των δύο φύλων. Ας το εξετάσουμε αυτό.
Στο παρακάτω τμήμα κώδικα, έχουμε προσαρμόσει και αποθηκεύσει το μοντέλο του Φύλου στο αντικείμενο της R Gender_model. Προσθέστε κώδικα για να εμφανίσετε το περιεχόμενό του ώστε να μπορέσουμε να δούμε τις εκτιμήσεις των παραμέτρων.
Call:
lm(formula = Thumb ~ Gender, data = Fingers)
Coefficients:
(Intercept) Gendermale
58.256 6.447Όπως αναμενόταν, βλέπουμε δύο εκτιμήσεις παραμέτρων. Αλλά αυτές δεν είναι οι δύο τιμές που ίσως περιμέναμε. Θα περίμενε κανείς να πάρουμε τους μέσους όρους των δύο ομάδων του φύλου: περίπου 58 και 65.
Η εκτίμηση με την ετικέτα Intercept στα αποτελέσματα (58.256) φαίνεται να είναι ο μέσος όρος του μήκους αντίχειρα των γυναικών. Αλλά πώς πρέπει να ερμηνεύσουμε τη δεύτερη τιμή (6.447), αυτή με την ετικέτα Gendermale;
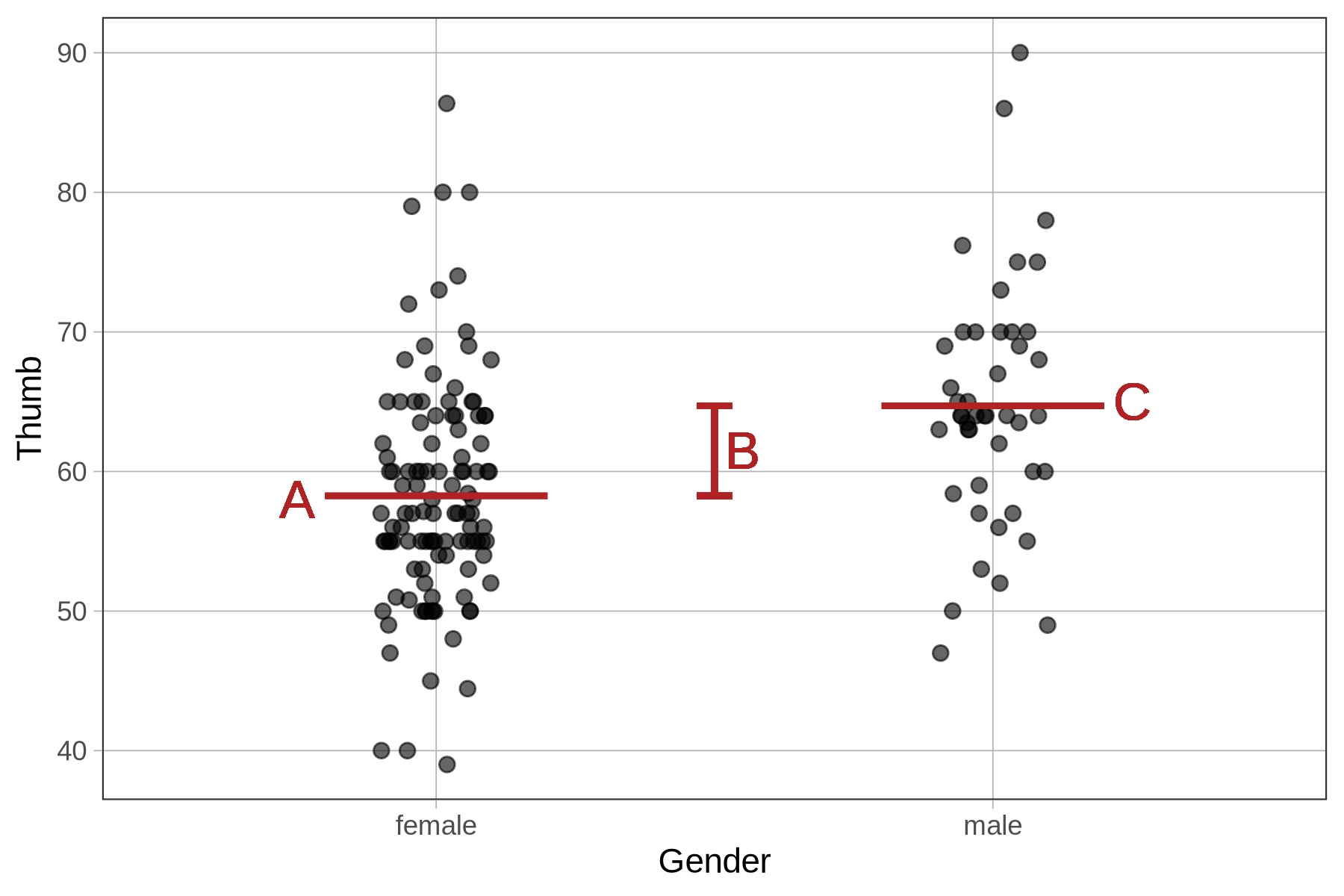
Σε ποιο σημείο βλέπετε στο διάγραμμα την εκτίμηση με την ετικέτα Intercept (58.256);
Σε ποιο σημείο βλέπετε στο διάγραμμα την εκτίμηση με την ετικέτα Gendermale (6.447);
Ερώτηση - Intercept:
Σωστή απάντηση: Α
Ο σταθερός όρος ή Intercept (58.256) είναι η γραμμή Α - ο μέσος όρος για τις γυναίκες (ομάδα αναφοράς).
Ερώτηση - Gendermale:
Σωστή απάντηση: Β
Η Gendermale (6.447) είναι το Β - η διαφορά μεταξύ ανδρών και γυναικών.
Ανάλυση του μοντέλου:
Εξίσωση μοντέλου:
\[\text{Thumb} = 58.256 + 6.447 \times (\text{Gender}_{\text{male}})\]
Όπου:
Gender_male = 0 αν γυναίκα
Gender_male = 1 αν άνδρας
Υπολογισμοί:
# Για γυναίκες (Gender_male = 0)
Thumb = 58.256 + 6.447×0 = 58.256
# Αυτό είναι το A
# Για άνδρες (Gender_male = 1)
Thumb = 58.256 + 6.447×1 = 64.703
# Αυτό είναι το C
# Διαφορά (άνδρες - γυναίκες)
64.703 - 58.256 = 6.447
# Αυτό είναι το B (η απόσταση)Τι αντιπροσωπεύει το καθένα:
Α (γραμμή στις γυναίκες):
Intercept = 58.256
Μέσος όρος για την ομάδα αναφοράς (γυναίκες)
Η “βασική” πρόβλεψη
Β (κάθετη γραμμή):
Gendermale = 6.447
Η διαφορά που προσθέτουμε για τους άνδρες
Πόσο μεγαλύτερο μέσο μήκος αντίχειρα έχουν οι άνδρες
C (γραμμή στους άνδρες):
Πρόβλεψη για τους άνδρες = 64.703
Intercept + Gendermale
58.256 + 6.447
Συμπέρασμα:
Intercept (58.256) → Γραμμή Α (μέσος όρος γυναικών)
Gendermale (6.447) → Απόσταση Β (διαφορά μεταξύ ομάδων)
Η Intercept δείχνει από πού ξεκινάμε (ομάδα αναφοράς), και η Gendermale δείχνει πόσο προσθέτουμε για την άλλη ομάδα.
Call:
lm(formula = Thumb ~ Gender, data = Fingers)
Coefficients:
(Intercept) Gendermale
58.256 6.447Αν εξετάσουμε προσεκτικά τα αποτελέσματα του μοντέλου που δημιουργήθηκε με την lm(), η ετικέτα Gendermale για τη δεύτερη εκτίμηση είναι στην πραγματικότητα χρήσιμη. Αν και θα ήταν βοηθητικό αν η R είχε βάλει κάποιο σημείο στίξης μεταξύ του Gender και του male, η ετικέτα αυτή δείχνει ότι η τιμή της δεύτερης παραμέτρου είναι η ποσότητα που χρειάζεται για να περάσουμε από το μέσο όρο της πρώτης ομάδας (female), που αναφέρεται ως Intercept, στο μέσο όρο της δεύτερης ομάδας, male.
Πράγματι, αυτό ισχύει: 58.3 + 6.4 = 64.7. Αυτή είναι η τιμή πρόβλεψης του μοντέλου του Φύλου για το μήκος αντίχειρα ενός φοιτητή.
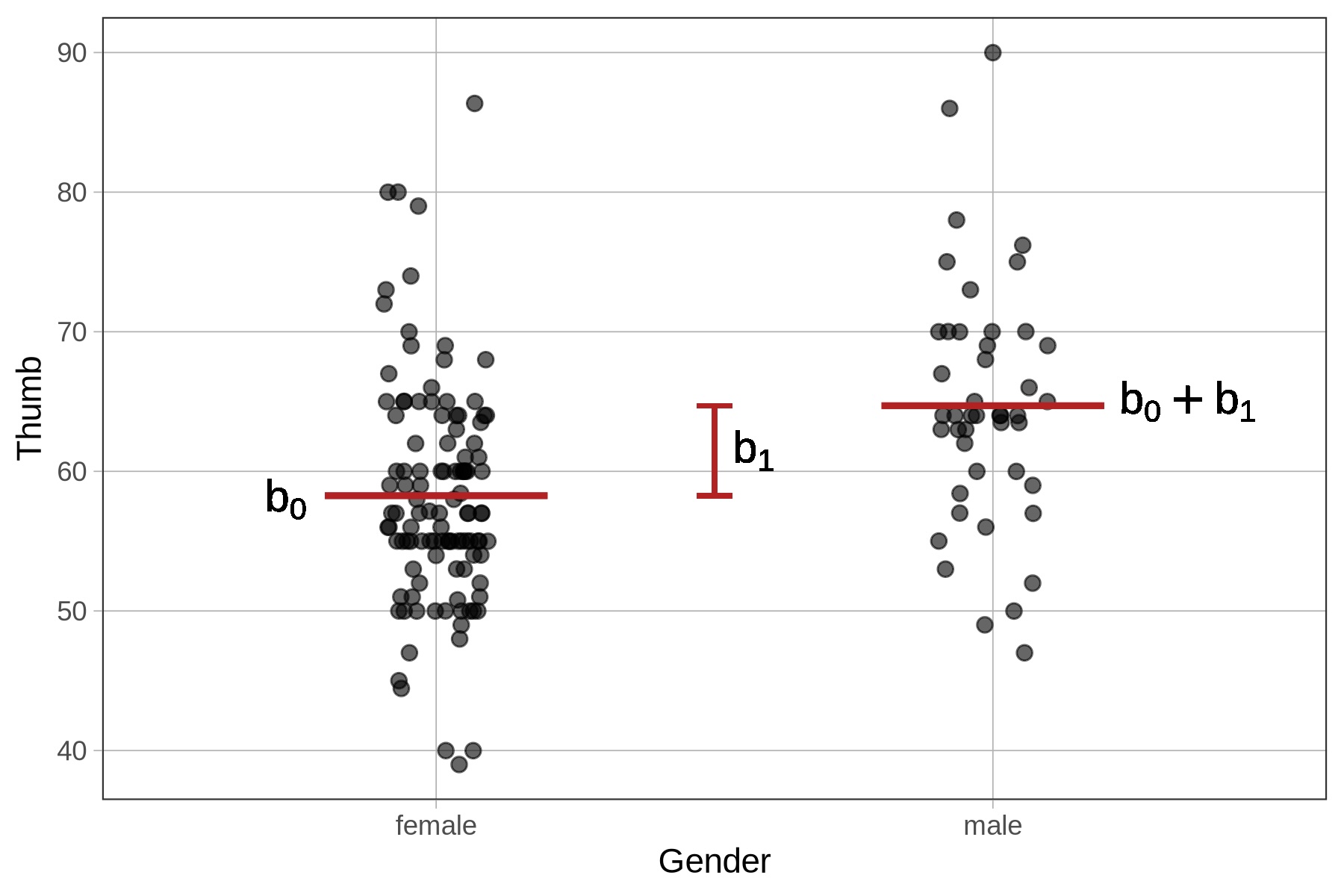
Οι Εκτιμήσεις \(b_0\) και \(b_1\)
Ενώ το κενό μοντέλο ήταν ένα μοντέλο μίας παραμέτρου (δίνοντας μόνο μία εκτίμηση, \(b_0\), για το συνολικό μέσο όρο), το μοντέλο του Φύλου είναι ένα μοντέλο δύο παραμέτρων (δύο εκτιμήσεις, \(b_0\) και \(b_1\)). Η μία από τις εκτιμήσεις αντιστοιχεί στο δειγματικό μέσο όρο για τις γυναίκες φοιτήτριες, ενώ η άλλη είναι η ποσότητα που πρέπει να προστεθεί στην πρώτη για να πάρουμε το δειγματικό μέσο όρο για τους άντρες (όπως φαίνεται στο παρακάτω διάγραμμα).
 Τα αποτελέσματα της
Τα αποτελέσματα της lm() μας δίνουν τις τιμές \(b_0\) και \(b_1\) που προσαρμόζονται καλύτερα στα δεδομένα.
Call:
lm(formula = Thumb ~ Gender, data = Fingers)
Coefficients:
(Intercept) Gendermale
58.256 6.447Αντιστοιχίστε τα αποτελέσματα της lm() με τα κατάλληλα σύμβολα στη σημειογραφία του GLM (\(b_0\) και \(b_1\)).
Ερώτηση 1: Gendermale → ;
Ερώτηση 2: (Intercept) → ;
Αντιστοιχίστε τις τιμές του προσαρμοσμένου μοντέλου με τα κατάλληλα σύμβολα στη σημειογραφία του GLM.
Ερώτηση 1: 58.3 → ;
Ερώτηση 2: 6.4 → ;
Αντιστοιχίστε τα σύμβολα του GLM με τη σημασία αυτών των τιμών.
Ερώτηση 1: \(b_1\) → ;
Ερώτηση 2: \(b_0\) → ;
Εξίσωση μοντέλου:
\[\text{Thumb} = b_0 + b_1 \times (\text{Gender}_{\text{male}})\]
\[\text{Thumb} = 58.3 + 6.4 \times (\text{Gender}_{\text{male}})\]
Ερμηνεία:
\(b_0\) = 58.3 (Intercept):
Το μέσο μήκος αντίχειρα των γυναικών
Η πρόβλεψη για την ομάδα αναφοράς (reference group)
Όταν Gender = female → Thumb = 58.3
\(b_1\) = 6.4 (Gendermale):
Η ποσότητα που προστίθεται για τους άνδρες
Η διαφορά: άνδρες - γυναίκες
Όταν Gender = male → Thumb = 58.3 + 6.4 = 64.7
Υπολογισμοί:
Η παράμετρος \(b_0\) αντιπροσωπεύει το μέσο όρο της πρώτης ομάδας (female). Η \(b_1\) αντιπροσωπεύει την ποσότητα που πρέπει να προστεθεί στην \(b_0\) για να πάρουμε την πρόβλεψη του μοντέλου για τη δεύτερη ομάδα, που σε αυτή την περίπτωση είναι οι άνδρες (male).
8.3 Σημειολογία GLM για το Μοντέλο Ομάδων
Ίσως σκεφτήκατε ότι θα ήταν αρκετό να περιγράψουμε το μοντέλο του Φύλου απλώς ως δύο μέσους όρους. Όμως, όπως και με το κενό μοντέλο, είναι χρήσιμο να μάθουμε πώς ένα μοντέλο δύο ομάδων αναπαρίσταται στη σημειολογία του Γενικού Γραμμικού Μοντέλου (GLM). Αυτό θα μας φανεί χρήσιμο καθώς αναπτύσσουμε πιο σύνθετα μοντέλα.
Το Μοντέλο του Φύλου στη Σημειολογία του GLM
Η πλήρης εξίσωση για το μοντέλο του Φύλου περιλαμβάνει τόσο το \(b_0\) όσο και το \(b_1\). Υπάρχουν διάφοροι τρόποι να διατυπώσουμε αυτό το μοντέλο, αλλά εμείς θα το γράψουμε ως εξής:
\(Y_i = b_0 + b_1 X_i + e_i\)
Μπορούμε επίσης να το γράψουμε με πιο συγκεκριμένο τρόπο ως εξής:
\(\text{Thumb}_i = b_0 + b_1 \text{Gender}_i + e_i\)
Με βάση τα αποτελέσματα της lm(), μπορούμε να αντικαταστήσουμε τις εκτιμήσεις στο μοντέλο.
Call:
lm(formula = Thumb ~ Gender, data = Fingers)
Coefficients:
(Intercept) Gendermale
58.256 6.447Ποιές από τις παρακάτω εξισώσεις αντιστοιχούν στο προσαρμοσμένο μοντέλο του Φύλου; (Υπάρχουν περισσότερες από μία σωστές απαντήσεις.)
Σωστές απαντήσεις: Γ και Ε
Σωστή μορφή μοντέλου:
\[\text{Thumb}_i = 58.3 + 6.4 \times \text{Gendermale}_i + e_i\]
Όπου:
58.3 = Intercept (\(b_0\)) - μέσος όρος γυναικών
6.4 = Gendermale (\(b_1\)) - διαφορά
Gendermale = 0 για γυναίκες, 1 για άνδρες
Γιατί η Γ είναι σωστή:
\[\text{Thumb}_i = 58.3 + 6.4\text{Gendermale}_i + e_i\]
Αυτή είναι η ακριβής μορφή με:
Σωστή εξαρτημένη μεταβλητή (Thumb)
Σωστό intercept (58.3)
Σωστός συντελεστής (6.4)
Σωστή σειρά όρων
Γιατί η Ε είναι σωστή:
\[Y_i = 58.3 + 6.4X_i + e_i\]
Αυτή είναι η γενική μορφή όπου:
\(Y\) = Thumb (εξαρτημένη)
\(X\) = Gendermale (ανεξάρτητη)
Ίδιοι αριθμοί: 58.3 και 6.4
Γιατί οι άλλες είναι λάθος:
Α - ΛΑΘΟΣ:
\[\text{Thumb}_i = 6.4 + 58.3\text{Gendermale}_i + e_i\]
Αντεστραμμένοι συντελεστές
Το 6.4 δεν είναι το intercept
Το 58.3 δεν είναι ο συντελεστής του Gender
Β - ΛΑΘΟΣ:
\[\text{Thumb}_i = 6.4 + 6.4\text{Gendermale}_i + e_i\]
Λάθος intercept (6.4 αντί για 58.3)
Θα έδινε: γυναίκες = 6.4 mm (πολύ χαμηλό!)
Δ - ΛΑΘΟΣ:
\[\text{Gender}_i = 58.3 + 6.4\text{Thumb}_i + e_i\]
Αντεστραμμένες εξαρτημένη και ανεξάρτητη
Προβλέπει Gender από Thumb (λάθος κατεύθυνση)
Δεν έχει νόημα: το Gender είναι ποιοτική μεταβλητή
Είναι σημαντικό να παρατηρήσουμε, πρώτον, ότι τόσο το κενό μοντέλο όσο και το μοντέλο του Φύλου με δύο ομάδες ξεκινούν με το \(Y_i\) στα αριστερά της ισότητας και τελειώνουν με το \(e_i\). Και στα δύο μοντέλα, το \(Y_i\) αντιπροσωπεύει το μήκος του αντίχειρα για το φοιτητή \(i\), και το \(e_i\) αντιπροσωπεύει το σφάλμα ή το υπόλοιπο μεταξύ της πρόβλεψης για το μήκος του αντίχειρα και του πραγματικού μήκους του αντίχειρα για το φοιτητή \(i\).
Για το μοντέλο δύο ομάδων, το τμήμα ΜΟΝΤΕΛΟ της εξίσωσης ΔΕΔΟΜΕΝΑ = ΜΟΝΤΕΛΟ + ΣΦΑΛΜΑ είναι τώρα πιο σύνθετο: \(b_0 + b_1X_i\) αντί απλώς \(b_0\) (για το κενό μοντέλο). Και στις δύο περιπτώσεις, ωστόσο, το μοντέλο μπορεί να θεωρηθεί ως μία συνάρτηση που παράγει μία τιμή πρόβλεψης για κάθε παρατήρηση στην εξαρτημένη μεταβλητή (σε αυτή την περίπτωση, μήκος αντίχειρα φοιτητή).
Σημειώστε ότι η εκτίμηση παραμέτρου \(b_0\) έχει διαφορετική σημασία από ό,τι στο κενό μοντέλο. Είναι η πρώτη εκτίμηση παράμετρου και στα δύο μοντέλα. Αλλά στο κενό μοντέλο, που έχει μόνο μία παράμετρο, αντιπροσωπεύει το μέσο όρο της Thumb για ολόκληρο το δείγμα, ενώ στο μοντέλο δύο ομάδων (με δύο παραμέτρους), αντιπροσωπεύει το μέσο όρο της πρώτης ομάδας (σε αυτή την περίπτωση, των γυναικών).
Ίσως σας μπερδεύει το να χρησιμοποιούμε το ίδιο σύμβολο για να αναπαριστήσουμε δύο διαφορετικές ιδέες. Όμως, αυτή η ευελιξία είναι που καθιστά το Γενικό Γραμμικό Μοντέλο τόσο ισχυρό και τόσο… γενικό.
Σε αντίθεση με το κενό μοντέλο, αυτό το πιο σύνθετο μοντέλο (\(b_0 + b_1X_i\)) μπορεί να δώσει δύο διαφορετικές προβλέψεις ανάλογα με το αν ο φοιτητής είναι γυναίκα ή άνδρας.
Με βάση αυτό που γνωρίζετε για τα \(b_0\) και \(b_1\) μέχρι στιγμής, τι χρησιμοποιεί το μοντέλο για να προβλέψει το μήκος αντίχειρα μιας γυναίκας φοιτήτριας;
Με βάση αυτό που γνωρίζετε για τα \(b_0\) και \(b_1\) μέχρι στιγμής, τι χρησιμοποιεί το μοντέλο για να προβλέψει το μήκος αντίχειρα ενός άνδρα φοιτητή;
Το μοντέλο:
\[\text{Thumb}_i = b_0 + b_1 \times \text{Gendermale}_i\]
Όπου:
\(b_0 = 58.3\) (intercept - μέσος όρος γυναικών)
\(b_1 = 6.4\) (διαφορά)
Gendermale = 0 για γυναίκες, 1 για άντρες
Ερώτηση - Πρόβλεψη για γυναίκες:
Σωστή απάντηση: Α (\(b_0\))
Για γυναίκες: Gendermale = 0
\[\text{Thumb} = b_0 + b_1 \times 0 = b_0\]
\[\text{Thumb} = 58.3 + 6.4 \times 0 = 58.3 \text{ mm}\]
Γιατί οι άλλες είναι λάθος:
\(b_1\): Αυτή είναι η διαφορά, όχι η πρόβλεψη
\(b_0 + b_1\): Αυτή είναι η πρόβλεψη για άνδρες
\(b_0 \times b_1\): Πολλαπλασιασμός δεν χρησιμοποιείται
Ερώτηση - Πρόβλεψη για άνδρες:
Σωστή απάντηση: Γ (\(b_0 + b_1\))
Για άνδρες: Gendermale = 1
\[\text{Thumb} = b_0 + b_1 \times 1 = b_0 + b_1\]
\[\text{Thumb} = 58.3 + 6.4 \times 1 = 64.7 \text{ mm}\]
Γιατί οι άλλες είναι λάθος:
\(b_0\): Αυτή είναι η πρόβλεψη για τις γυναίκες
\(b_1\): Μόνο η διαφορά, όχι η πλήρης πρόβλεψη
\(b_0 \times b_1\): Λάθος πράξη
Σύνοψη:
Γυναίκες: Thumb = b₀ = 58.3 mm
Άνδρες: Thumb = b₀ + b₁ = 64.7 mm
Διαφορά: b₁ = 6.4 mmΤο μοντέλο προσθέτει το \(b_1\) για τους άνδρες, δεν το πολλαπλασιάζει.
Ερμηνεία του συμβόλου \(X_i\)
Έχουμε αναπτύξει την ιδέα ότι το \(b_0\) είναι ο μέσος όρος της πρώτης ομάδας, και το \(b_0 + b_1\) είναι ο μέσος όρος της δεύτερης ομάδας. Αλλά η συνάρτηση που οδηγεί σε μια τιμή πρόβλεψης για κάθε παρατήρηση στο μοντέλο δύο ομάδων είναι η εξής: \(Y_i = b_0 + b_1X_i\). Σε αυτό το μοντέλο, τι ρόλο παίζει το \(X_i\);
Όπως φαίνεται χρειαζόμαστε το \(X_i\) για να μπορεί το μοντέλο να υπολογίσει δύο τιμές. Δείτε πώς λειτουργεί. Το \(X_i\) αντιπροσωπεύει τη μεταβλητή ομαδοποίησης – την ανεξάρτητη μεταβλητή μας, Gender – αλλά με έναν ιδιαίτερο τρόπο. Ονομάζεται ψευδομεταβλητή (dummy variable), που σημαίνει ότι η R τη δημιουργεί ειδικά για να λειτουργήσει το μοντέλο.
Η R παίρνει τη μεταβλητή Gender και την επανακωδικοποιεί σε μια νέα μεταβλητή (\(X_i\)) που μπορεί να πάρει μόνο μία από δύο τιμές: 0 ή 1. Στο μοντέλο δύο ομάδων, η \(X_i\) κωδικοποιείται ως 1 αν ο φοιτητής ανήκει στη δεύτερη ομάδα (male), και ως 0 αν ο φοιτητής δεν ανήκει στη δεύτερη ομάδα (δηλαδή, ανήκει σε μια διαφορετική ομάδα από την ομάδα male).
Αν ένας φοιτητής δεν ανήκει στην ομάδα male σε αυτό το σύνολο δεδομένων, τότε σε ποια ομάδα ανήκει;
Σωστή απάντηση: Α
Στο πλαίσιο δεδομένων Fingers:
Η μεταβλητή Gender έχει δύο κατηγορίες:
femalemale
Δυαδική ποιοτική μεταβλητή:
Αν ένας φοιτητής δεν είναι male, τότε είναι female.
Δεν υπάρχουν άλλες επιλογές στα δεδομένα.
Γιατί οι άλλες είναι λάθος:
Β - “Δεν έχει αντίχειρα” - ΛΑΘΟΣ:
Όλοι οι φοιτητές στο σύνολο δεδομένων έχουν μέτρηση αντίχειρα
Το Gender δεν σχετίζεται με το αν έχουν αντίχειρα
Γ - “Δεν είναι δυνατόν να γνωρίζουμε” - ΛΑΘΟΣ:
Στο συγκεκριμένο σύνολο δεδομένων, το Gender είναι δυαδικό
Αν όχι male → τότε female
Σημείωση:
Στον πραγματικό κόσμο, το φύλο/gender μπορεί να είναι πιο περίπλοκο. Αλλά στο συγκεκριμένο σύνολο δεδομένων που χρησιμοποιούμε, υπάρχουν μόνο αυτές οι δύο κατηγορίες.
Αν και σε αυτά τα δεδομένα, το να πούμε ότι ένας φοιτητής δεν είναι άνδρας ισοδυναμεί με το να πούμε ότι είναι γυναίκα, είναι σημαντικό να σκεφτόμαστε το \(X_i = 0\) ως το ότι ο φοιτητής δεν ανήκει στην ομαδα των ανδρών. Η διατήρηση αυτής της λεπτής διάκρισης στο μυαλό μας θα μας βοηθήσει να κατανοήσουμε πώς λειτουργούν οι ψευδομεταβλητές όταν έχουμε μοντέλα με περισσότερες από δύο ομάδες.
Ο λόγος που η εκτίμηση παραμέτρου \(b_0\) ονομάζεται σημείο τομής (Intercept) στα αποτελέσματα της lm() είναι επειδή αντιστοιχεί στην τιμή πρόβλεψης του μήκους αντίχειρα όταν η \(X_i\) είναι ίση με 0 – με άλλα λόγια, όταν το φύλο δεν είναι άνδρας. Μπορούμε να σκεφτούμε την εκτίμηση παραμέτρου που η R ονόμασε Gendermale (\(b_1\)), ως την κλίση μιας ευθείας. Είναι η ποσότητα μεταβολής στην τιμή πρόβλεψης του μήκους αντίχειρα όταν η τιμή της \(X_i\) αυξάνεται κατά μία μονάδα (δηλαδή όταν το φύλο είναι άνδρας).
Στο μοντέλο του Φύλου, \(b_0 + b_1X_i\), ποιο από τα παρακάτω περιγράφει το \(b_0\) (ή Intercept στα αποτελέσματα της lm());
Ποιος είναι ο ορισμός του \(b_1\) (ή Gendermale στα αποτελέσματα της lm()) για το μοντέλο του Φύλου;
Το μοντέλο:
\[Y_i = b_0 + b_1X_i\]
Όπου:
\(Y\) = Thumb (εξαρτημένη)
\(X\) = Gendermale (0 για γυναίκες, 1 για άνδρες)
Ερώτηση - Ορισμός \(b_0\):
Σωστή απάντηση: Α
Το \(b_0\) (Intercept) είναι η πρόβλεψη όταν \(X_i = 0\).
Το \(b_0\) είναι η βασική τιμή - η πρόβλεψη για την ομάδα αναφοράς (όταν όλες οι ανεξάρτητες μεταβλητές = 0).
Ερώτηση - Ορισμός \(b_1\):
Σωστή απάντηση: Δ
Το \(b_1\) (Gendermale) είναι η ποσότητα που πρέπει να προστεθεί όταν το \(X_i\) αυξάνεται κατά 1 μονάδα.
# Όταν το X αλλάζει από 0 → 1 (γυναίκα → άνδρας)
Γυναίκα: Y = b₀ = 58.3
Άνδρας: Y = b₀ + b₁ = 58.3 + 6.4 = 64.7
# Διαφορά (slope):
b₁ = 6.4 mmΤο \(b_1\) είναι η κλίση - πόσο αλλάζει η πρόβλεψη όταν το \(X\) αυξάνεται κατά 1.
Γιατί οι άλλες είναι λάθος:
Για \(b_0\):
Β (όταν X=1): Αυτό είναι \(b_0 + b_1\), όχι μόνο \(b_0\)
Γ (ανεξάρτητα από X): Αυτό θα ήταν για το κενό μοντέλο, όχι για μοντέλο με ανεξάρτητη μεταβλητή
Δ (προσαρμογή): Αυτό είναι ο ορισμός του \(b_1\)
Για \(b_1\):
Α (όταν X=0): Αυτό είναι ο ορισμός του \(b_0\)
Β (όταν X=1): Αυτό είναι \(b_0 + b_1\), όχι μόνο \(b_1\)
Γ (ανεξάρτητα): Το \(b_1\) εξαρτάται από το X
Συμπέρασμα:
\(b_0\): Από πού ξεκινάμε (πρόβλεψη όταν X=0)
\(b_1\): Πόσο προσθέτουμε (αλλαγή για κάθε μονάδα αύξησης της X)
8.4 Πώς το Μοντέλο Κάνει Προβλέψεις
Ορίστε το μοντέλο με την καλύτερη προσαρμογή στα δεδομένα του μήκους αντίχειρα και το φύλο ως ανεξάρτητη μεταβλητή:
\(\text{Thumb}_i = b_0 + b_1 \cdot \text{Gender}_i + e_i\)
\(\text{Thumb}_i = 58.256 + 6.447 \cdot \text{Gender}_i + e_i\)
Έχοντας κατανοήσει τι είναι το \(X_i\) (δηλαδή, το \(\text{Gender}_i\)), μπορείτε τώρα να χρησιμοποιήσετε το μοντέλο για να κάνετε προβλέψεις. Αν \(X_i = 1\), τότε ο φοιτητής είναι άνδρας. Σε αυτή την περίπτωση, η πρόβλεψη για το μήκος αντίχειρα θα είναι \(b_0 + b_1 * 1\). (Υπενθύμιση: Ο αστερίσκος στην R χρησιμοποιείται για την πράξη του πολλαπλασιασμού, οπότε τον χρησιμοποιούμε και ως σύμβολο της ίδιας πράξης στο πλαίσιο του GLM.)
Αν ένας φοιτητής είναι άνδρας, τότε το \(X_i\) θα λάβει την τιμή 1. Ποιο από τα παρακάτω θα προβλέψει το μήκος αντίχειρα ενός άνδρα φοιτητή;
Αν ένας φοιτητής δεν είναι άνδρας, τότε το \(X_i\) θα λάβει την τιμή 0. Ποιο από τα παρακάτω θα προβλέψει το μήκος αντίχειρα μιας γυναίκας φοιτήτριας; (Υπάρχουν περισσότερες από μία σωστές απαντήσεις.)
Το μοντέλο:
\[\text{Thumb} = 58.3 + 6.4 \times X_i\]
Όπου \(X_i\) = Gendermale (0 για γυναίκες, 1 για άνδρες)
Ερώτηση - Άνδρας φοιτητής:
Σωστή απάντηση: Α
Για άνδρες: \(X_i = 1\)
\[\text{Thumb} = 58.3 + (6.4 \times 1)\]
\[\text{Thumb} = 58.3 + 6.4 = 64.7 \text{ mm}\]
Ερώτηση - Γυναίκα φοιτήτρια:
Σωστές απαντήσεις: Β, Δ, Ε
Για γυναίκες: \(X_i = 0\)
Β: \(58.3 + (6.4 \times 0)\) ✓
- Η πλήρης εξίσωση με X=0
Δ: \(58.3 + 0\) ✓
- Απλοποιημένο: \(6.4 \times 0 = 0\)
Ε: \(58.3\) ✓
- Πλήρως απλοποιημένο
Και τα τρία είναι μαθηματικά ισοδύναμα:
\[58.3 + (6.4 \times 0) = 58.3 + 0 = 58.3\]
Γιατί οι άλλες είναι λάθος:
Α (για γυναίκες): \(58.3 + (6.4 \times 1)\) - ΛΑΘΟΣ
- Αυτό είναι για άνδρες, όχι γυναίκες
Γ: \(58.3 \times (6.4 \times 58.3)\) - ΛΑΘΟΣ
- Λάθος πράξεις - χρησιμοποιούμε πρόσθεση, όχι πολλαπλασιασμό
Σύνοψη:
Αν \(X_i = 0\), που σημαίνει ότι ο φοιτητής δεν είναι στην ομάδα male, η εκτίμηση της δεύτερης παραμέτρου δεν θα προστεθεί, επειδή \(b_1\) επί 0 ισούται με 0. Και εφόσον η δεύτερη παράμετρος θα εξαλειφθεί, η τιμή πρόβλεψης θα είναι απλώς το \(b_0\), που είναι ο μέσος όρος του μήκους αντίχειρα των γυναικών.
Το \(X_i\) είναι μια μεταβλητή, που σημαίνει ότι μπορεί να πάρει διαφορετική τιμή για διαφορετικούς φοιτητές στο πλαίσιο δεδομένων. Δείχνουμε ότι αυτό είναι μια μεταβλητή βάζοντας ένα δείκτη \(i\) μετά το \(X\). Η τιμή της \(X_i\) θα είναι είτε 0 είτε 1, επειδή κάθε φοιτητής σε αυτό το σύνολο δεδομένων είναι ή δεν είναι άνδρας.
Το \(b_0\) δεν έχει δείκτη \(i\). Μπορεί να διαφέρει μεταξύ των φοιτητών;
Σωστή απάντηση: Α
Το \(b_0\) είναι μια σταθερά, όχι μεταβλητή.
Διάκριση συμβόλων:
Με δείκτη i: Χωρίς δείκτη i:
─────────────── ────────────────
Yᵢ b₀
Xᵢ b₁
eᵢ
Ποικίλλει ανά Σταθερό για
άτομο όλουςΓιατί το \(b_0\) δεν διαφέρει:
Το \(b_0 = 58.3\) mm είναι:
Ο μέσος όρος για όλες τις γυναίκες
Μία τιμή για ολόκληρο το μοντέλο
Σταθερή - δεν αλλάζει από άτομο σε άτομο
Τι ποικίλλει:
# Σταθερές (ίδιες για όλους)
b₀ = 58.3 # για κάθε γυναίκα
b₁ = 6.4 # για κάθε άνδρα
# Μεταβλητές (αλλάζουν ανά άτομο)
Yᵢ: Thumb₁ = 66.0, Thumb₂ = 64.0, Thumb₃ = 56.0, ...
Xᵢ: Gender₁ = 1, Gender₂ = 0, Gender₃ = 0, ...
eᵢ: e₁ = 1.3, e₂ = 5.7, e₃ = -2.3, ...Παράδειγμα:
# Φοιτήτρια 1 (γυναίκα)
Y₁ = b₀ + b₁×0 = 58.3 + 0 = 58.3
# ↑ ↑
# σταθερά
# Φοιτήτρια 2 (γυναίκα)
Y₂ = b₀ + b₁×0 = 58.3 + 0 = 58.3
# ↑ ↑
# ίδια σταθερά!
# Το b₀ παραμένει 58.3 για όλες τις γυναίκεςΣυμπέρασμα:
Το \(b_0\) είναι η εκτίμηση μιας παράμετρου του μοντέλου - μία σταθερή τιμή που αντιπροσωπεύει το μέσο μήκος αντίχειρα των γυναικών. Δεν έχει δείκτη \(i\) επειδή δεν αλλάζει από φοιτητή σε φοιτητή - είναι η ίδια για όλους. Αυτό που ποικίλλει είναι το \(Y_i\) (το πραγματικό μήκος αντίχειρα κάθε ατόμου), το \(X_i\) (το φύλο κάθε ατόμου), και το \(e_i\) (το σφάλμα κάθε πρόβλεψης).
Πώς Γνωρίζει η R Ποιο Φύλο να Αναπαραστήσει με \(X_i = 1\);
Η απάντηση σε αυτή την ερώτηση είναι: Η R δε γνωρίζει· απλώς παίρνει όποια ομάδα έρχεται πρώτη αλφαβητικά (σε αυτή την περίπτωση, το female) και την καθιστά ομάδα αναφοράς (reference group). Ο μέσος όρος της ομάδας αναφοράς είναι η πρώτη εκτίμηση παραμέτρου (\(b_0\) ή Intercept στα αποτελέσματα της lm()).
Στη συνέχεια, η R παίρνει τη δεύτερη ομάδα (σε αυτή την περίπτωση, το male) και την αναπαριστά με την ψευδομεταβλητή \(X_i\). Αν το \(X_i\) κωδικοποιηθεί ως 1, τότε ο φοιτητής είναι άνδρας. Αν κωδικοποιηθεί ως 0, τότε ο φοιτητής δεν είναι άνδρας.
Ας υποθέσουμε ότι αλλάξατε την ετικέτα για το male σε man και την ετικέτα για το female σε woman. Επειδή η λέξη man προηγείται αλφαβητικά της λέξης woman, το man γίνεται η ομάδα αναφοράς, και ο μέσος όρος του γίνεται τώρα η εκτίμηση για το Intercept (\(b_0\)).
Σε αυτήν τη νέα υποθετική περίπτωση όπου το man είναι τώρα η ομάδα αναφοράς, η τιμή του \(b_1\) θα ήταν αρνητική ή θετική;
Σωστή απάντηση: Α
Τρέχουσα κατάσταση (female = ομάδα αναφοράς):
Thumb = 58.3 + 6.4×(Gendermale)
Γυναίκες: 58.3 mm (ομάδα αναφοράς)
Άνδρες: 64.7 mm (ομάδα αναφοράς + 6.4)
b₁ = +6.4 (θετικό - άνδρες έχουν μεγαλύτερο μήκος αντίχειρα)Υποθετική κατάσταση (male = ομάδα αναφοράς):
Thumb = 64.7 + b₁×(Genderwoman)
Άνδρες: 64.7 mm (νέα ομάδα αναφοράς)
Γυναίκες: 58.3 mm (νέα ομάδα αναφοράςe + b₁)
# Για να πάμε από 64.7 → 58.3:
64.7 + b₁ = 58.3
b₁ = 58.3 - 64.7 = -6.4
b₁ = -6.4 (αρνητικό - γυναίκες έχουν μικρότερο μήκος αντίχειρα)Γιατί αρνητικό:
Οι γυναίκες έχουν μικρότερο μήκος αντίχειρα από τους άνδρες:
Διαφορά: 58.3 - 64.7 = -6.4 mm
Για να πάμε από άνδρες (64.7) σε γυναίκες (58.3), αφαιρούμε την ποσότητα 6.4
Γιατί οι άλλες είναι λάθος:
Β - “Αλλάζει μεταξύ φοιτητών” - ΛΑΘΟΣ:
Το \(b_1\) είναι σταθερά, όχι μεταβλητή
Δεν έχει δείκτη \(i\)
Δεν αλλάζει από άτομο σε άτομο
Γ - “Δεν θα άλλαζε” - ΛΑΘΟΣ:
Το \(b_1\) θα άλλαζε πρόσημο
Από +6.4 → -6.4
Η απόλυτη τιμή παραμένει ίδια, αλλά το πρόσημο αλλάζει
Συμπέρασμα:
Το πρόσημο του \(b_1\) εξαρτάται από ποια ομάδα είναι η ομάδα αναφοράς. Αν οι άνδρες γίνουν η ομάδα αναφοράς, τότε το \(b_1\) θα είναι αρνητικό (-6.4) επειδή οι γυναίκες έχουν μικρότερο μέσο όρο και χρειάζεται να αφαιρέσουμε αυτήν την ποσότητα για να φτάσουμε από την ομάδα αναφοράς (άνδρες) στην άλλη ομάδα (γυναίκες).
Όταν μια μεταβλητή έχει οριστεί ως ποιοτική στην R (π.χ., τύπου factor), είναι πραγματικά αδιάφορο πώς θα την κωδικοποιήσετε. Μπορείτε να κωδικοποιήσετε τις κατηγορίες της μεταβλητής Gender με οποιουσδήποτε χαρακτήρες επιλέξετε (π.χ., female ή woman), ή με οποιουσδήποτε αριθμούς επιλέξετε (π.χ., 1 και 2, 0 και 1, ή 1 και 500). Όπως και αν κωδικοποιήσετε τις τιμές της μεταβλητής, η R θα θεωρήσει την κατηγορία που έρχεται πρώτη ως το Intercept (\(b_0\)) και στη συνέχεια την επόμενη ως μια ανεξάρτητη ψευδομεταβλητή, της οποίας τις τιμές θα κωδικοποιήσει με 0 ή 1.
8.5 Υπολειπόμενο Σφάλμα από το Μοντέλο Ομάδων
Προηγουμένως, υπολογίσαμε τα υπόλοιπα (residuals) από το κενό μοντέλο της Thumb ξεκινώντας με το πραγματικό μήκος του αντίχειρα για κάθε φοιτητή και στη συνέχεια αφαιρώντας από αυτό την τιμή πρόβλεψης που πήραμε από το μοντέλο. Στο κενό μοντέλο, όλοι οι φοιτητές είχαν την ίδια τιμή πρόβλεψης.
ΔΕΔΟΜΕΝΑ = ΠΡΟΒΛΕΨΗ ΜΟΝΤΕΛΟΥ + ΥΠΟΛΟΙΠΟ
ΥΠΟΛΟΙΠΟ = ΔΕΔΟΜΕΝΑ - ΠΡΟΒΛΕΨΗ ΜΟΝΤΕΛΟΥ
Για το μοντέλο του Φύλου, θα χρησιμοποιήσουμε την ίδια μέθοδο, με τη μόνη διαφορά ότι αυτή τη φορά θα υπάρχουν δύο διαφορετικές προβλέψεις του μοντέλου, ανάλογα με το φύλο του φοιτητή. Και σε αυτήν την περίπτωση, η τιμή πρόβλεψης για κάθε άτομο, που τώρα εξαρτάται από το φύλο του, αφαιρείται από το πραγματικό μήκος του αντίχειρά του για να υπολογίσουμε το υπόλοιπο.
Ποιες από τις παρακάτω εξισώσεις είναι ορθές, ανεξάρτητα από το αν μιλάμε για το κενό μοντέλο ή το μοντέλο του Φύλου; (Υπάρχουν περισσότερες από μία σωστές απαντήσεις.)
Σωστές απαντήσεις: Β και Γ
Θεμελιώδης εξίσωση:
\[\text{ΔΕΔΟΜΕΝΑ} = \text{ΜΟΝΤΕΛΟ} + \text{ΣΦΑΛΜΑ}\]
Επαναδιατυπώνοντας:
\[\text{ΣΦΑΛΜΑ} = \text{ΔΕΔΟΜΕΝΑ} - \text{ΜΟΝΤΕΛΟ}\]
Αυτή η εξίσωση ισχύει για κάθε μοντέλο.
Β. υπόλοιπο = μήκος αντίχειρα - πρόβλεψη (ΣΩΣΤΟ) ✓
Ίδια μορφή και για τα δύο μοντέλα!
Γ. ΣΦΑΛΜΑ = ΔΕΔΟΜΕΝΑ - ΜΟΝΤΕΛΟ (ΣΩΣΤΟ) ✓
Αυτή είναι η γενική εξίσωση που ισχύει πάντα.
Γιατί οι άλλες είναι λάθος:
Α. υπόλοιπο = κενό μοντέλο + μοντέλο του Φύλου (ΛΑΘΟΣ):
Δεν έχει νόημα να προσθέσεις δύο μοντέλα
Τα υπολοιπα υπολογίζονται από ένα μοντέλο τη φορά
Δ. ΜΟΝΤΕΛΟ = ΣΦΑΛΜΑ (ΛΑΘΟΣ):
Αυτό είναι το αντίστροφο της σωστής σχέσης
Σωστό: ΔΕΔΟΜΕΝΑ = ΜΟΝΤΕΛΟ + ΣΦΑΛΜΑ
Άρα: ΜΟΝΤΕΛΟ = ΔΕΔΟΜΕΝΑ - ΣΦΑΛΜΑ
Ε. ΣΦΑΛΜΑ = ΔΕΔΟΜΕΝΑ + ΜΟΝΤΕΛΟ (ΛΑΘΟΣ):
Λάθος πρόσημο
Σωστό: ΣΦΑΛΜΑ = ΔΕΔΟΜΕΝΑ - ΜΟΝΤΕΛΟ
Συμπέρασμα:
Οι εξισώσεις που ισχύουν πάντα, ανεξάρτητα από το μοντέλο:
υπόλοιπο = μήκος αντίχειρα - πρόβλεψη
ΣΦΑΛΜΑ = ΔΕΔΟΜΕΝΑ - ΜΟΝΤΕΛΟ
Αυτές είναι δύο εκφράσεις της ίδιας θεμελιώδους αρχής - η μία με συγκεκριμένα ονόματα μεταβλητών, η άλλη με γενικά σύμβολα.
Οι τιμές των υπολοίπων για 6 από τους φοιτητές αναπαρίστανται στα παρακάτω διαγράμματα τόσο για το κενό μοντέλο (αριστερά) όσο και για το μοντέλο του Φύλου (δεξιά). Παρατηρήστε ότι η θέση των 6 παρατηρήσεων είναι η ίδια και στα δύο μοντέλα· τα πραγματικά μήκη των αντίχειρων αυτών των φοιτητών δεν αλλάζουν.
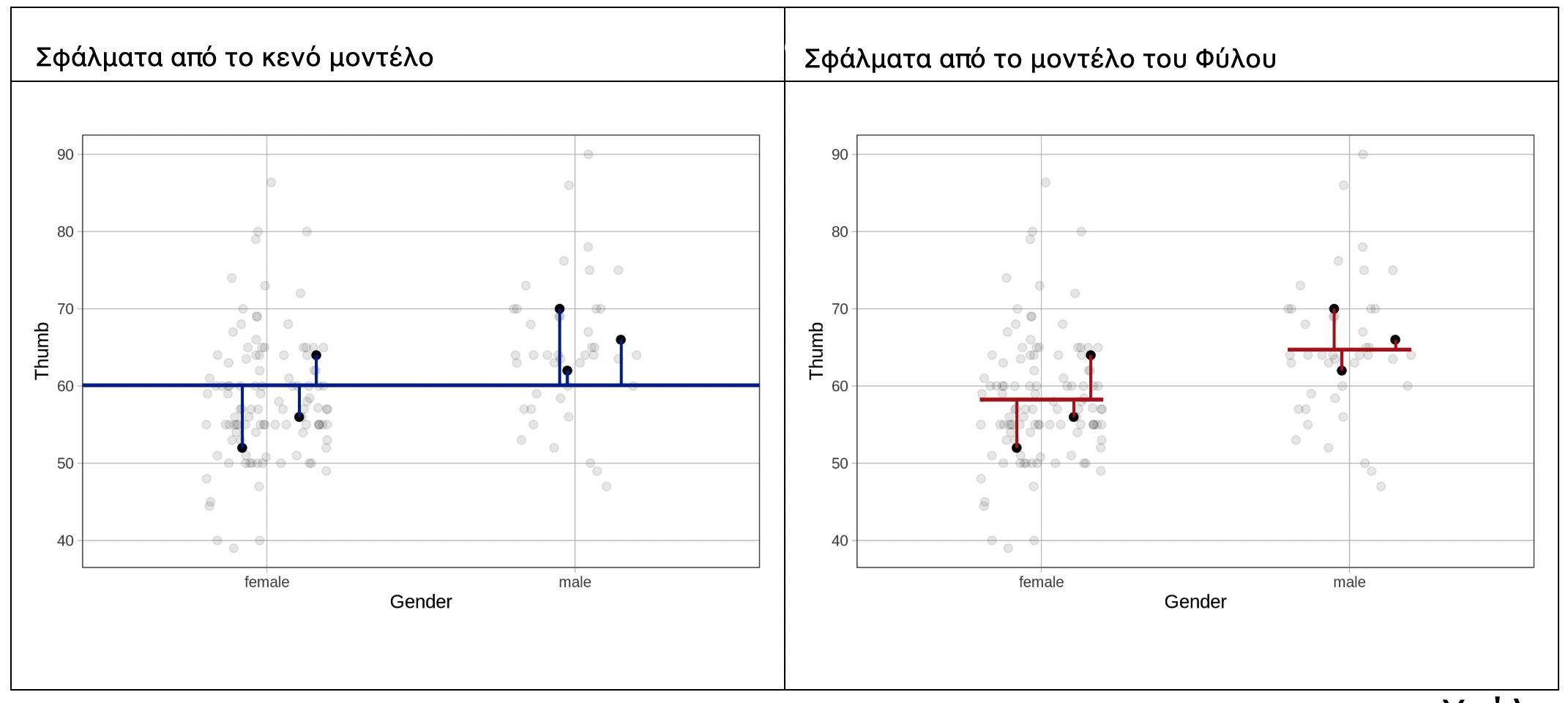
Οι τιμές πρόβλεψης και τα υπόλοιπα των δύο μοντέλων, ωστόσο, είναι διαφορετικες. Για το κενό μοντέλο, το υπόλοιπο κάθε φοιτητή υπολογίζεται σε σχέση με το μέσο όρο του μήκους αντίχειρα όλων των φοιτητών στο σύνολο δεδομένων. Για το μοντέλο του Φύλου, το υπόλοιπο κάθε φοιτητή υπολογίζεται σε σχέση με την τιμή πρόβλεψης του μήκους αντίχειρα για το φύλο του.
Κάτι που πρέπει να έχετε κατά νου είναι ότι η εξέταση των υπολοίπων μπορεί να σας βοηθήσει να ερμηνεύσετε τα δεδομένα σας. Πάρτε, για παράδειγμα, τον άνδρα φοιτητή του οποίου το μήκος του αντίχειρα είναι κυκλωμένο στα παρακάτω διαγράμματα. Η εξέταση των υπολοίπων μπορεί να σας βοηθήσει να δείτε κάτι ενδιαφέρον γι’ αυτόν τον φοιτητή.
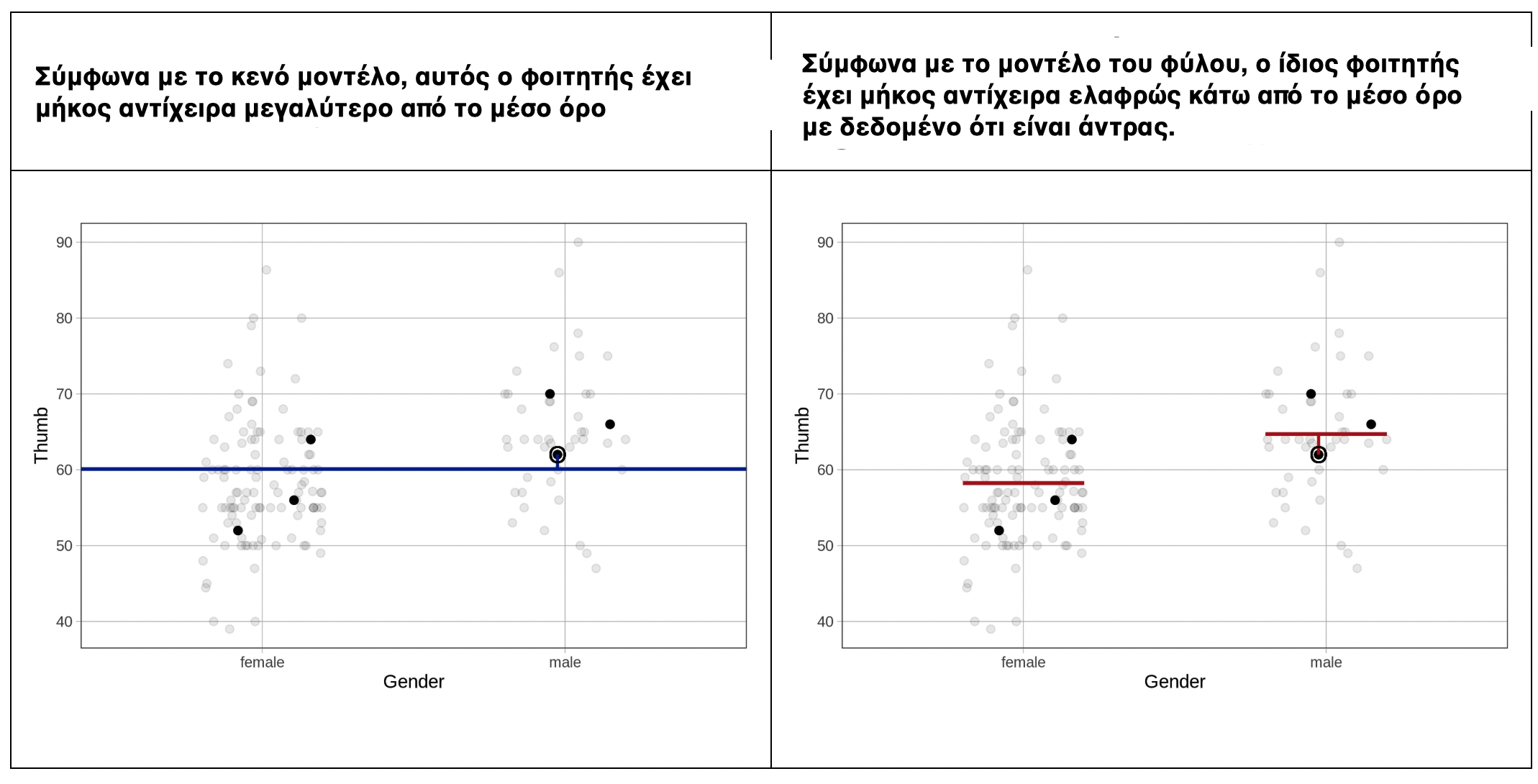
Γιατί το μήκος αντίχειρα του φοιτητή (σε κύκλο στα παραπάνω διαγράμματα) είναι υψηλότερο με βάση την πρόβλεψη του κενού μοντέλου αλλά χαμηλότερο με βάση την πρόβλεψη του μοντέλου του φύλου;
Σωστή απάντηση: Β
Ανάλυση του φοιτητή (άνδρας με μήκος αντίχειρα ≈ 62 mm):
Διάγραμμα στα αριστερά - Κενό μοντέλο:
Μπλε γραμμή: Πρόβλεψη κενού μοντέλου = 60.1 mm (μέσος όλων)
Πραγματικό: μήκος αντίχειρα = 62 mm
Σχέση: 62 > 60.1 → πάνω από την τιμή πρόβλεψης
Διάγραμμα στα δεξιά - Μοντέλο του φύλου:
Κόκκινη γραμμή (άνδρες): Πρόβλεψη μοντέλου του Φύλου = 64.7 mm
Πραγματικό: Thumb = 62 mm
Σχέση: 62 < 64.7 → κάτω από την τιμή πρόβλεψης
Σύνοψη:
Κενό μοντέλο: 60.1mm < 62mm (πάνω από την τιμή πρόβλεψης)
Πραγματικό: 62mm
Μοντέλο του φύλου: 62mm < 64.7mm (κάτω από την τιμή πρόβλεψης)Γιατί συμβαίνει αυτό:
Αυτός ο άνδρας έχει:
Μεγαλύτερο αντίχειρα από το γενικό μέσο όρο (60.1)
Μικρότερο αντίχειρα από το μέσο όρο των ανδρών (64.7)
Υπόλοιπα:
# Υπόλοιπο κενού μοντέλου
e_empty = 62 - 60.1 = +1.9mm (θετικό)
# Υπόλοιπο μοντέλου του Φύλου
e_gender = 62 - 64.7 = -2.7mm (αρνητικό)Γιατί η Α είναι λάθος:
Ο αντίχειρας δεν μίκρυνε
Το μήκος είναι σταθερό (62 mm)
Αυτό που αλλάζει είναι η πρόβλεψη του μοντέλου, όχι τα δεδομένα
Το μοντέλο του φύλου είναι συνολικά καλύτερο:
Κενό μοντέλο: |e| = 1.9mm
Μοντέλο του φύλου: |e| = 2.7mm
Για το συγκεκριμένο φοιτητή, το κενό μοντέλο είναι πιο κοντά!
Αλλά συνολικά, όπως θα δούμε παρακάτω, το μοντέλο του Φύλου έχει μικρότερο
άθροισμα τετραγώνων σφαλμάτων.Συμπέρασμα:
Το μήκος αντίχειρα αυτού του άνδρα (62mm) βρίσκεται μεταξύ των δύο προβλέψεων επειδή είναι πάνω από το γενικό μέσο (60.1) αλλά κάτω από το μέσο των ανδρών (64.7). Τα δεδομένα δεν άλλαξαν - αλλάζουν οι προβλέψεις όταν χρησιμοποιούμε διαφορετικά μοντέλα.
Χρήση της R για τον Υπολογισμό των Υπολοίπων από το Μοντέλο του Φύλου
Όπως χρησιμοποιήσαμε προηγουμένως τη συνάρτηση predict() για να δημιουργήσουμε μια τιμή πρόβλεψης μήκους αντίχειρα για κάθε φοιτητή στο πλαίσιο δεδομένων, μπορούμε να χρησιμοποιήσουμε τη συνάρτηση resid() για να υπολογίσουμε το υπόλοιπο του μοντέλου για κάθε φοιτητή. Το έχουμε κάνει με τον παρακάτω κώδικα και εμφανίσαμε τον πίνακα δεδομένων μόνο για τους 6 πρώτους φοιτητές.
Fingers$Gender_predict <- predict(Gender_model)
Fingers$Gender_resid <- resid(Gender_model)
head(select(Fingers, Gender, Thumb, Gender_predict, Gender_resid))
Gender Thumb Gender_predict Gender_resid
1 male 66.00 64.70267 1.297333
2 female 64.00 58.25585 5.744152
3 female 56.00 58.25585 -2.255848
4 male 58.42 64.70267 -6.282667
5 female 74.00 58.25585 15.744152
6 female 60.00 58.25585 1.744152Ρίξτε μια ματιά στα παραπάνω αποτελέσματα. Ισχύει ακόμα ότι ΔΕΔΟΜΕΝΑ = ΜΟΝΤΕΛΟ + ΣΦΑΛΜΑ; Εξηγήστε πώς μπορείτε να το καταλάβετε αυτό από τα αποτελέσματα;
Η εξίσωση του GLM για το μοντέλο του Φύλου είναι:
\[Y_i = b_0 + b_1X_i + e_i\]
Σε τι από τα παρακάτω αντιστοιχεί η στήλη Gender_predict;
Σωστή απάντηση: Δ (\(b_0 + b_1X_i\))
Ανάλυση του μοντέλου:
\[Y_i = b_0 + b_1X_i + e_i\]
Το Gender_predict είναι η πρόβλεψη, που είναι το μοντέλο χωρίς το σφάλμα.
Γιατί οι άλλες είναι λάθος:
Α - \(Y_i\) - ΛΑΘΟΣ:
Αυτό είναι το πραγματικό μήκος αντίχειρα (τα δεδομένα)
Όχι η πρόβλεψη
Β - \(b_0\) - ΛΑΘΟΣ:
Αυτό είναι μόνο η πρόβλεψη για τις γυναίκες (58.26)
Όχι για όλους
Γ - \(b_0 + b_1\) - ΛΑΘΟΣ:
Αυτό είναι μόνο η πρόβλεψη για τους άνδρες (64.7)
Λείπει το \(X_i\) που καθορίζει την ομάδα
Ε - \(e_i\) - ΛΑΘΟΣ:
Αυτό είναι το υπόλοιπο
Όχι η πρόβλεψη
Σωστή σχέση:
Gender_predict = b₀ + b₁Xᵢ
Αν Xᵢ = 0 (γυναίκα): 58.3 + 6.4×0 = 58.3
Αν Xᵢ = 1 (άνδρας): 58.3 + 6.4×1 = 64.7Το Gender_predict είναι η πρόβλεψη του μοντέλου: b_0 + b_1X_i$
Σε τι από τα παρακάτω αντιστοιχεί η στήλη Gender_resid;
Σωστή απάντηση: Ε (\(e_i\))
Ορισμός υπολοίπου:
\[e_i = Y_i - (b_0 + b_1X_i)\]
Το Gender_resid είναι το υπόλοιπο - η διαφορά μεταξύ πραγματικής τιμής και τιμής πρόβλεψης.
Γιατί οι άλλες είναι λάθος:
Α (\(Y_i\)): Πραγματικά δεδομένα (Thumb)
Β (\(b_0\)): Intercept (σταθερός όρος)
Γ, Δ: Τιμές προβλέψης του μοντέλου
Το Gender_resid = \(e_i\) (το σφάλμα/υπόλοιπο)
8.6 Διαγραμματική Αναπαράσταση των Υπολοίπων του Μοντέλου
Ίσως αναρωτιέστε, γιατί ασχολούμαστε με τη δημιουργία και την αποθήκευση των υπολοίπων. Υπάρχουν πολλοί λόγοι, αλλά μια σύντομη απάντηση είναι: μας βοηθά να κατανοήσουμε το σφάλμα γύρω από το μοντέλο μας και μπορεί να οδηγήσει σε τρόπους βελτίωσης του μοντέλου.
Όπως το πρώτο πράγμα που κάνουμε όταν εξετάζουμε ένα σύνολο δεδομένων είναι να ελέγξουμε τις κατανομές των μεταβλητών, έτσι είναι καλό να αποκτήσουμε τη συνήθεια να εξετάζουμε τις κατανομές των υπολοίπων μετά την προσαρμογή ενός νέου μοντέλου.
Στο παρακάτω πλαίσιο, δίνουμε τον κώδικα για να δημιουργήσουμε διαιρεμένα ιστογράμματα του μήκους αντίχειρα ανά Φύλο. Δοκιμάστε να τον τροποποιήσετε για να δημιουργήσετε ιστογράμματα των υπολοίπων (Gender_resid) ανά Φύλο. Συγκρίνετε τα ιστογράμματα των υπολοίπων από το μοντέλο του Φύλου με τα ιστογράμματα του μήκους του αντίχειρα.
Παρουσιάζουμε τα ιστογράμματα του μήκους αντίχειρα (Thumb) ανά Φύλο (σε τιρκουάζ) δίπλα στα ιστογράμματα του Gender_resid ανά Φύλο (σε πιο σκούρο γκρι).
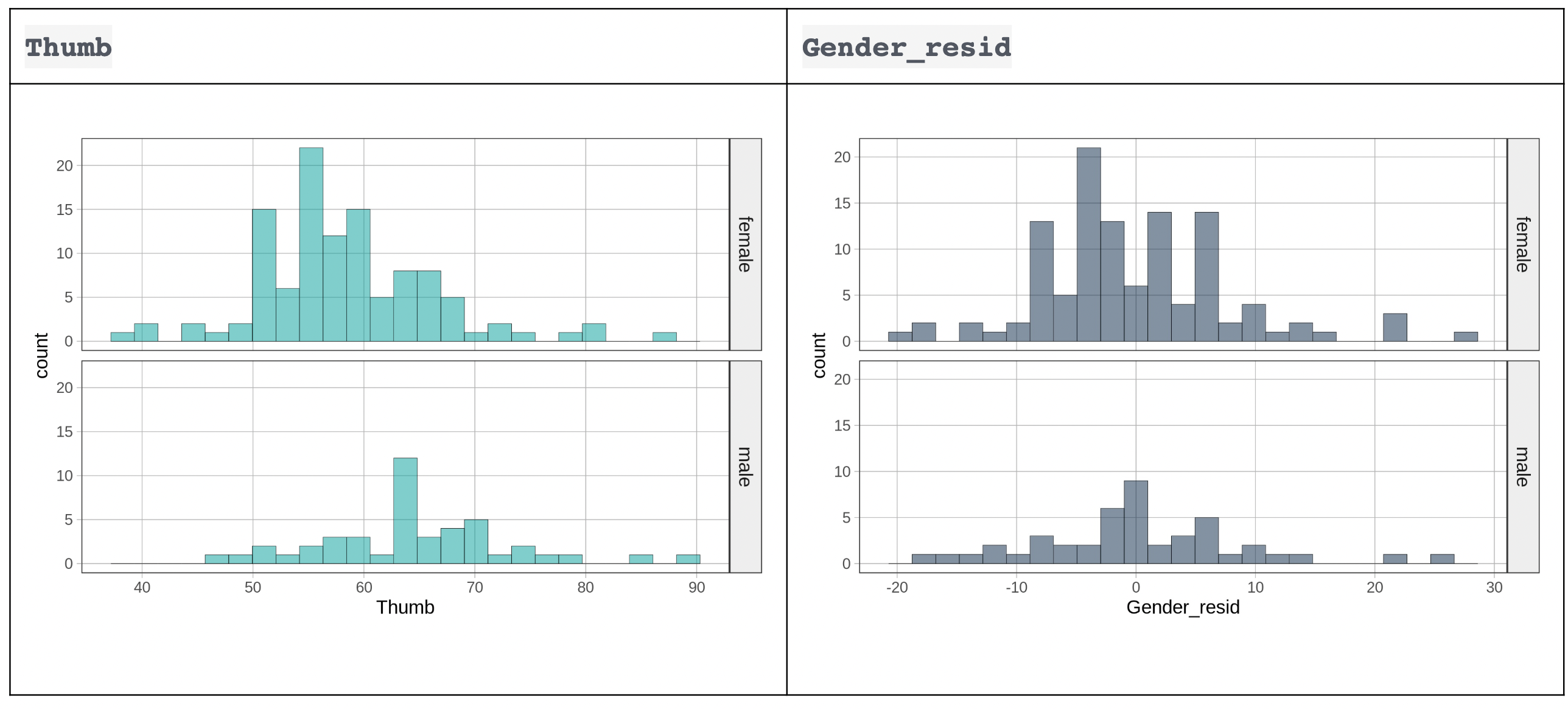
Τι παρατηρείτε σχετικά με αυτά τα ζευγάρια ιστογραμμάτων;
Σωστή απάντηση: Α
Ανάλυση ιστογραμμάτων:
Thumb (γαλάζιο - αριστερά):
Γυναίκες: Κεντραρισμένες γύρω από 55-60 mm
Άνδρες: Κεντραρισμένοι γύρω από 65 mm
Σαφής μετατόπιση: Οι άνδρες έχουν υψηλότερες τιμές
Gender_resid (γκρι - δεξιά):
Γυναίκες: Κεντραρισμένες γύρω στο 0
Άνδρες: Κεντραρισμένοι γύρω στο 0
Καμία μετατόπιση: Και οι δύο ομάδες έχουν παρόμοια κατανομή
Γιατί συμβαίνει αυτό:
Το μοντέλο του Φύλου αφαιρεί την επίδραση του φύλου:
Τι σημαίνει αυτό:
Τα υπόλοιπα αντιπροσωπεύουν αυτό που απομένει αφού αφαιρέσουμε την επίδραση του φύλου:
Gender_resid = Thumb - Gender_predict
# Για γυναίκες
resid = Thumb - 58.3
# Για άνδρες
resid = Thumb - 64.7
# Και οι δύο κατανομές κεντράρονται στο 0!Συμπέρασμα:
Το μοντέλο του Φύλου εξουδετερώνει τις συστηματικές διαφορές μεταξύ ανδρών και γυναικών. Τα υπόλοιπα δείχνουν το μέρος της μεταβλητότητας που δεν εξηγείται - πόσο κάθε άτομο αποκλίνει από το μέσο όρο της ομάδας του. Αυτός είναι ο στόχος ενός καλού μοντέλου: να αφαιρέσει τα συστηματικά μοτίβα, αφήνοντας υπόλοιπα που κεντράρονται στο 0 για όλες τις ομάδες.
Τα υπόλοιπα του μοντέλου του Φύλου αντιπροσωπεύουν τη μεταβλητότητα που απομένει μετά την αφαίρεση του μέρους της μεταβλητότητας που μπορεί να εξηγηθεί από το Φύλο. Τα παρακάτω διαγράμματα παρουσιάζουν το μέσο όρο της Thumb (αριστερά) και το μέσο όρο των Gender_resid για τις δύο ομάδες Φύλου (δεξιά).
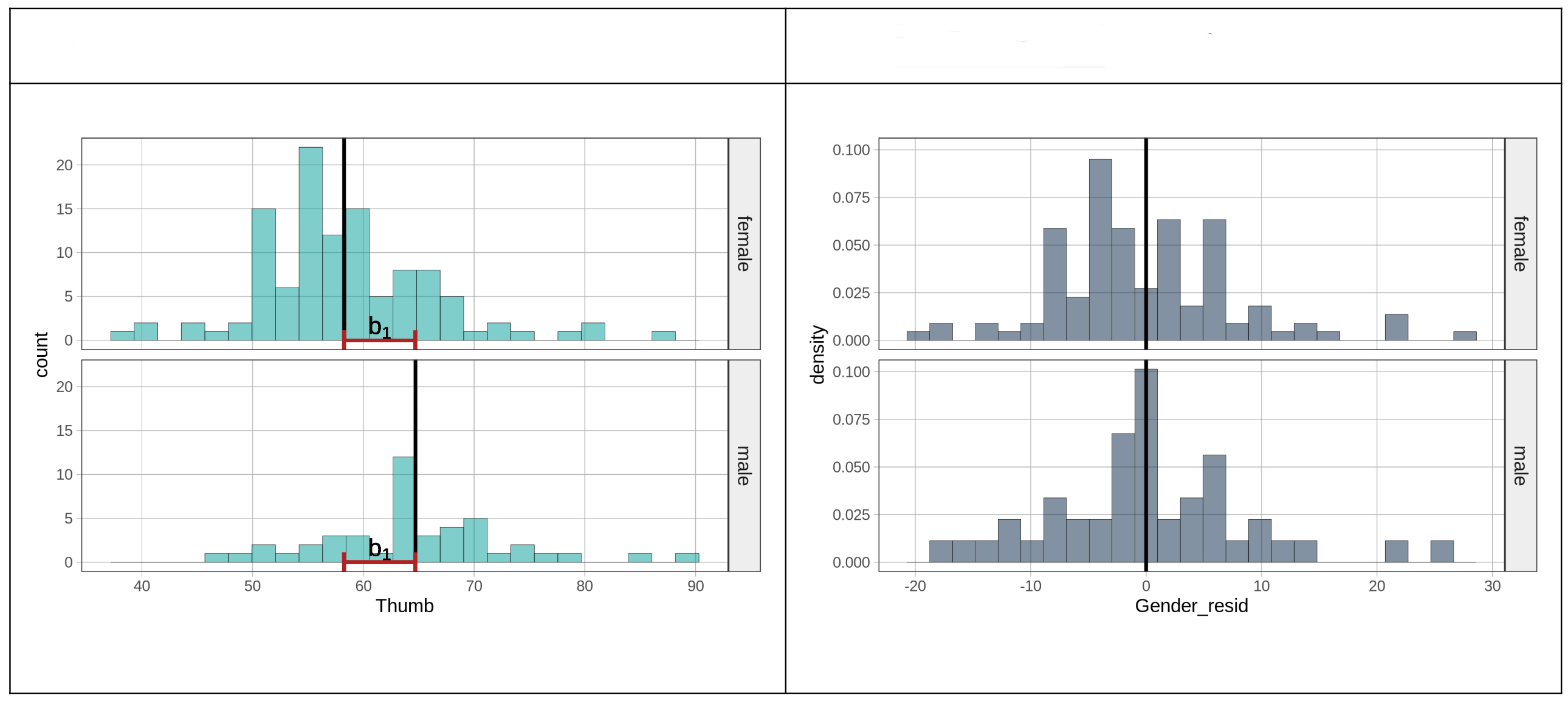
Παραπάνω, στο ιστόγραμμα των υπολοίπων (με σκούρο γκρι), γιατί οι μέσοι όροι των υπολοίπων του μοντέλου του φύλου (Gender_resid) για τις δύο ομάδες δεν διαφέρουν πλέον;
Παραπάνω, στο ιστόγραμμα των υπολοίπων (με σκούρο γκρι), γιατί οι μέσοι όροι των υπολοίπων του μοντέλου του φύλου (Gender_resid) για τις δύο ομάδες είναι ίσοι με 0;
Πρώτη ερώτηση: Όλα αληθή
Όλες οι δηλώσεις περιγράφουν το ίδιο πράγμα με διαφορετικούς τρόπους:
Α, Β, Γ, Δ είναι όλες ισοδύναμες:
# Α: Αφαιρούμε τους μέσους όρους των ομάδων
resid_female = Thumb - 58.3
resid_male = Thumb - 64.7
# Β: Εφαρμόζουμε το μοντέλο του Φύλου
resid = Thumb - Gender_predict
# Γ: Αφαιρούμε τις επιδράσεις του Φύλου
resid = DATA - MODEL(Gender)
# Δ: Λαμβάνουμε υπόψη τη μεταβλητότητα του Φύλου
resid = Thumb - (b₀ + b₁×Gender)
# Όλα υπολογίζουν το ίδιο πράγμα!Δεύτερη ερώτηση: Σωστή απάντηση Α
Θεμελιώδης ιδιότητα υπολοίπων:
\[\sum_{i=1}^{n} e_i = 0\]
Άρα:
\[\bar{e} = \frac{\sum e_i}{n} = \frac{0}{n} = 0\]
Γιατί τα υπόλοιπα αθροίζουν σε 0:
Για κάθε ομάδα:
# Γυναίκες
eᵢ = Thumbᵢ - 58.3
Σeᵢ = ΣThumbᵢ - n×58.3
= n×58.3 - n×58.3 # επειδή mean(Thumb_female)=58.3
= 0 ✓
# Άνδρες - ίδια λογική
Σeᵢ = 0 ✓Γιατί οι άλλες είναι λάθος:
Β - “Μέσο μήκος = 0” - ΛΑΘΟΣ:
Το μέσο μήκος αντίχειρα δεν είναι 0
Το μέσο των υπολοόπων είναι 0
Γ - “Σύμπτωση” - ΛΑΘΟΣ:
Δεν είναι σύμπτωση!
Τα υπόλοιπα πάντα έχουν μέσο όρο 0
Αυτό είναι μαθηματικό θεώρημα
Συμπέρασμα:
Τα υπόλοιπα έχουν μέσο όρο 0 για κάθε ομάδα επειδή αφαιρούμε το μέσο όρο της ομάδας από κάθε παρατήρηση. Αυτή είναι θεμελιώδης ιδιότητα των υπολοίπων - είναι ισορροπημένα γύρω από τις προβλέψεις του μοντέλου.
8.7 Σφάλμα που Μειώνεται από το Μοντέλο Ομάδων
Θυμηθείτε ότι ο στόχος μας με την προσθήκη μιας ανεξάρτητης μεταβλητής στο μοντέλο ήταν να εξηγήσουμε τη μεταβλητότητα της εξαρτημένης μεταβλητής, ή, με άλλα λόγια, να μειώσουμε το σφάλμα σε σύγκριση με το κενό μοντέλο.
Για να γνωρίζουμε ότι το σφάλμα έχει μειωθεί, και κατά πόσο έχει μειωθεί, θα συγκρίνουμε το άθροισμα τετραγώνων των σφαλμάτων από το κενό μοντέλο με το άθροισμα τετραγώνων των σφαλμάτων από το μοντέλο του Φύλου. Αν το άθροισμα τετραγώνων των σφαλμάτων από το μοντέλο του Φύλου είναι μικρότερο, τότε έχει μειώσει το σφάλμα σε σύγκριση με το κενό μοντέλο.
Γιατί χρησιμοποιούμε το άθροισμα τετραγώνων των υπολοίπων αντί για απλά το άθροισμα των υπολοίπων για να μετρήσουμε το συνολικό σφάλμα από ένα μοντέλο;
Σωστή απάντηση: Α
Το πρόβλημα με το \(\sum e_i\):
\[\sum_{i=1}^{n} e_i = 0 \text{ πάντα!}\]
Αυτό ισχύει για:
Το κενό μοντέλο (ένας μέσος όρος)
Το μοντέλο του Φύλου (δύο μέσοι όροι)
Οποιοδήποτε μοντέλο που χρησιμοποιεί μέσους όρους
Γιατί οι άλλες είναι λάθος:
Β - “Γίνεται αρνητικό” - ΛΑΘΟΣ:
Το \(\sum e_i\) παραμένει 0, δεν γίνεται αρνητικό
Αυτό ισχύει ανεξάρτητα από τον αριθμό ομάδων
Γ - “Ακρίβεια” - ΑΝΑΚΡΙΒΕΣ:
Δεν είναι θέμα ακρίβειας
Το πρόβλημα είναι ότι \(\sum e_i = 0\) πάντα
Δεν μπορεί να μετρήσει σφάλμα
Συμπέρασμα:
Χρησιμοποιούμε το Άθροισμα Τετραγώνων των Υπολοίπων (\(\sum e_i^2\)) επειδή το απλό άθροισμα (\(\sum e_i\)) είναι πάντα 0 για μοντέλα που χρησιμοποιούν μέσους όρους. Το τετράγωνο μετατρέπει όλα τα υπόλοιπα σε θετικούς αριθμούς, επιτρέποντάς μας να μετρήσουμε και να συγκρίνουμε το συνολικό σφάλμα μεταξύ διαφορετικών μοντέλων.
Για το κενό μοντέλο, παίρνουμε κάθε υπόλοιπο από την πρόβλεψη του μοντέλου (το μέσο όρο για όλους τους φοιτητές) και το υψώνουμε στο τετράγωνο. Στη συνέχεια, προσθέτουμε αυτά τα τετραγωνικά υπόλοιπα για να πάρουμε το άθροισμα τετραγώνων των υπολοίπων από το κενό μοντέλο. Η ειδική ονομασία που χρησιμοποιούμε για να αναφερθούμε στο άθροισμα τετραγώνων των υπολοίπων από το κενό μοντέλο είναι Συνολικό Άθροισμα Τετραγώνων (Sum of Squares Total - SS Total).
Έχουμε αναπαραστήσει αυτή την ιδέα για τις έξι επιλεγμένες παρατηρήσεις μας στο διάγραμμα στα αριστερά που βρίσκεται παρακάτω. Τα υπόλοιπα αναπαρίστανται με κάθετες γραμμές από κάθε τιμή προς την πρόβλεψη του κενού μοντέλου. Το τετράγωνο καθενός από αυτά τα υπόλοιπα αναπαρίσταται, κυριολεκτικά, από ένα τετράγωνο.
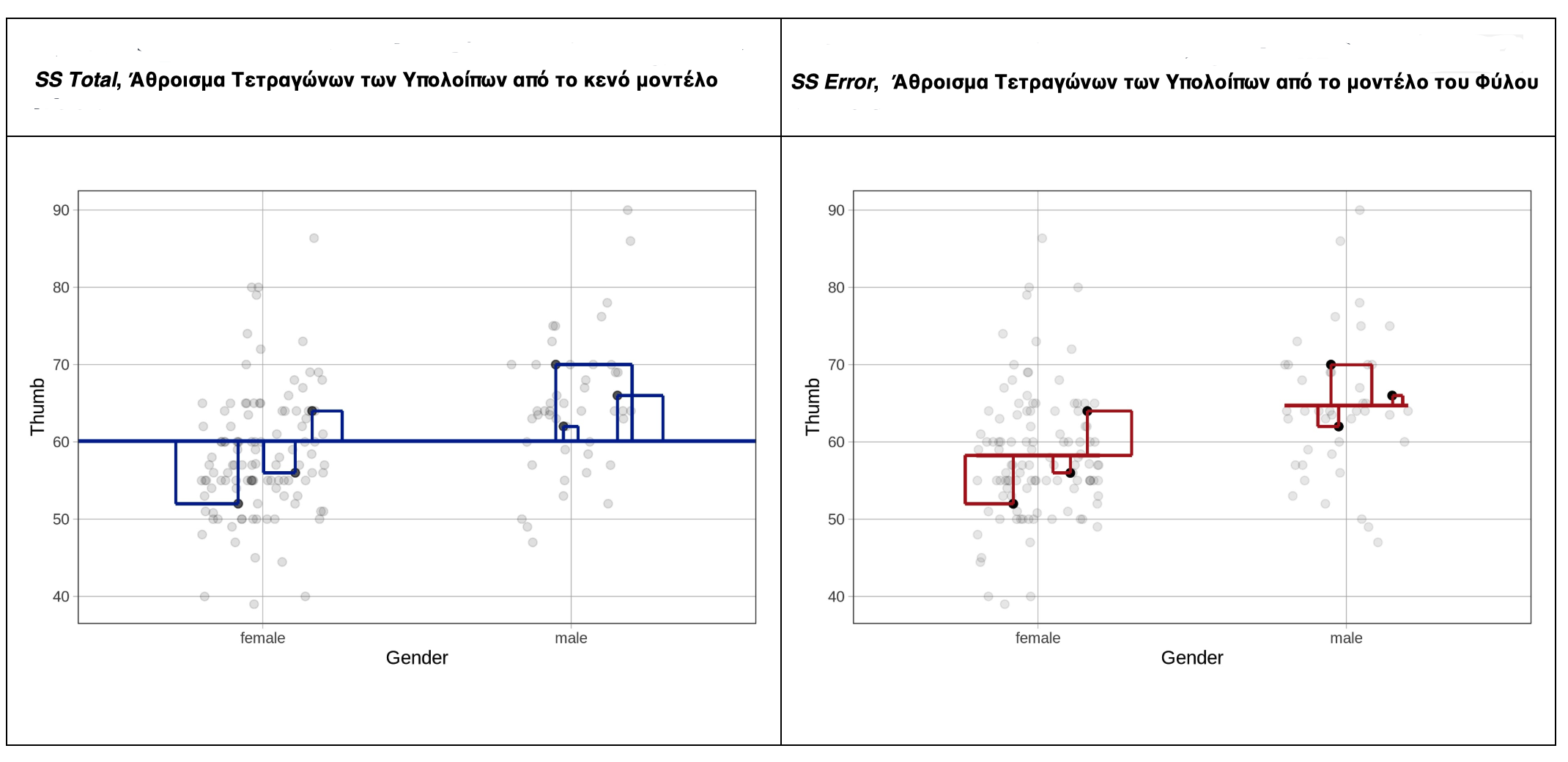
Για το μοντέλο του Φύλου (που βρίσκεται στο διάγραμμα στα δεξιά), ακολουθούμε την ίδια προσέγγιση, μόνο που αυτή τη φορά τα υπόλοιπα βασίζονται στις προβλέψεις του μοντέλου του Φύλου. Πάλι, μπορούμε να προσθέσουμε αυτά τα τετράγωνα των υπολοίπων σε ολόκληρο το σύνολο δεδομένων για να πάρουμε το άθροισμα τετραγώνων των σφαλμάτων από το μοντέλο.
Αν και η διαδικασία για τον υπολογισμό των αθροισμάτων τετραγώνων είναι πανομοιότυπη για το κενό μοντέλο και τo μοντέλο του Φύλου, για το μοντέλο του Φύλου (και τελικά, για όλα τα μοντέλα εκτός από το κενό μοντέλο) ονομάζουμε αυτό το άθροισμα Άθροισμα Τετραγώνων των Σφαλμάτων (Sum of Squared Errors - SS Error).
Στο παραπάνω διάγραμμα, κοιτάξτε προσεκτικά τα τετραγωνικά σφάλματα για το δείγμα των 6 παρατηρήσεων τόσο από το κενό μοντέλο όσο και από το μοντέλο του Φύλου. Προσπαθήστε νοερά να προσθέσετε τα 6 τετράγωνα για κάθε μοντέλο. Μόνο με βάση αυτά τα 6 τετραγωνικά σφάλματα, ποιο μοντέλο νομίζετε ότι θα είχε μικρότερο άθροισμα τετραγώνων;
Πώς ονομάζουμε τα αθροίσματα τετραγώνων που απομένουν από αυτά τα δύο μοντέλα;
Πρώτη Ερώτηση - Σωστή απάντηση: Β (Μοντέλο του Φύλου)
Οπτική σύγκριση:
Από το διάγραμμα φαίνεται ότι:
Κενό μοντέλο (μπλε): Μεγαλύτερα τετράγωνα, ειδικά για σημεία μακριά από τη μπλε γραμμή
Μοντέλο του Φύλου (κόκκινο): Μικρότερα τετράγωνα, γιατί κάθε ομάδα έχει δικό της μέσο
Το μοντέλο του Φύλου προσαρμόζεται καλύτερα στα δεδομένα.
Δεύτερη Ερώτηση - Σωστή απάντηση: Β
Ονοματολογία SS:
Κενό μοντέλο → SS Total:
Τα υπόλοιπα από το κενό μοντέλο αντιπροσωπεύουν τη συνολική μεταβλητότητα
Αυτό είναι το SS Total - η συνολική μεταβλητότητα
Το μοντέλο του Φύλου → SS Error:
Τα υπόλοιπα από το μοντέλο του Φύλου αντιπροσωπεύουν το σφάλμα που απομένει
Αυτό είναι το SS Error - η μη εξηγημένη μεταβλητότητα
Σχέση:
\[\text{SS Total} = \text{SS Model} + \text{SS Error}\]
Όπου:
SS Total: Από το κενό μοντέλο
SS Error: Από το μοντέλο του Φύλου
SS Model: Η μεταβλητότητα που εξηγείται από το Φύλο
\[\text{SS Model} = \text{SS Total} - \text{SS Error}\]
Συμπέρασμα:
Το μοντέλο του Φύλου έχει μικρότερο Άθροισμα Τετραγώνων (SS) επειδή χρησιμοποιεί περισσότερη πληροφορία (φύλο). Ονομάζουμε το SS από το κενό μοντέλο SS Total και το SS από το μοντέλο του Φύλου SS Error.
Όταν η R προσαρμόζει ένα μοντέλο – συμπεριλαμβανομένου του κενού μοντέλου – οι συγκεκριμένες τιμές των εκτιμήσεων παραμέτρων (τα \(b\)) ελαχιστοποιούν το άθροισμα τετραγώνων των υπολοίπων.
Για να προσαρμόσει το κενό μοντέλο, η συνάρτηση lm() υπολογίζει την τιμή του \(b_0\) που δίνει το μικρότερο δυνατό άθροισμα τετραγώνων των σφαλμάτων (γνωστό και ως SS Total), το οποίο γνωρίζουμε ότι είναι ο μέσος όρος του μήκους αντίχειρα (Thumb). Κατά τον ίδιο τρόπο, για να προσαρμόσει το μοντέλο του Φύλου, η συνάρτηση υπολογίζει τις τιμές των \(b_0\) και \(b_1\) που δίνουν το μικρότερο δυνατό άθροισμα τετραγώνων των σφαλμάτων (SS Error) για το συγκεκριμένο σύνολο δεδομένων.
Τι θα προσπαθούσε να ελαχιστοποιήσει ένα μοντέλο με κάποια άλλη ανεξάρτητη μεταβλητή (π.χ., RaceEthnic ή Height);
Ποιο θα είναι συνήθως μικρότερο; το SS Total ή το SS Error;
Πρώτη ερώτηση - Σωστή απάντηση: Β (SS Error)
Ένα μοντέλο με μία ανεξάρτητη μεταβλητή πάντα προσπαθεί να ελαχιστοποιήσει το SS Error - το άθροισμα τετραγώνων των σφαλμάτων από το μοντέλο.
Γιατί όχι το SS Total:
- Το SS Total είναι η συνολική μεταβλητότητα (από το κενό μοντέλο)
Δεύτερη ερώτηση - Σωστή απάντηση: Β (SS Error)
Σχέση:
\[\text{SS Total} = \text{SS Model} + \text{SS Error}\]
Επαναδιατυπώνοντας:
\[\text{SS Error} = \text{SS Total} - \text{SS Model}\]
Επειδή SS Model ≥ 0:
\[\text{SS Error} \leq \text{SS Total}\]
Το SS Error είναι πάντα μικρότερο ή ίσο από το SS Total.
Πότε είναι ίσα:
Όταν το SS Model = 0
Όταν η ανεξάρτητη μεταβλητή δεν εξηγεί τίποτα
…και το μοντέλο δεν είναι καλύτερο από το κενό μοντέλο
Συμπέρασμα:
Το SS Error είναι πάντα μικρότερο ή ίσο από το SS Total, επειδή προσθέτοντας ανεξάρτητες μεταβλητές μπορεί μόνο να μειώσει (ή να διατηρήσει) το σφάλμα, ποτέ να το αυξήσει.
8.8 Χρήση του Αθροίσματος Τετραγώνων των Σφαλμάτων για τη Σύγκριση του Μοντέλου Ομάδων με το Κενό Μοντέλο
Για να υπολογίσουμε το άθροισμα τετραγώνων των σφαλμάτων για κάθε μοντέλο, δεν χρειάζεται να προσθέσουμε μια νέα στήλη στο πλαίσιο δεδομένων. Αντίθετα, μπορούμε απλώς να υπολογίσουμε τα υπόλοιπα από κάθε μοντέλο, να τα τετραγωνίσουμε και να τα αθροίσουμε.
Στο παρακάτω πλαίσιο κώδικα, υπολογίζουμε το Συνολικό Άθροισμα Τετραγώνων (SS) για το κενό μοντέλο. Προσθέστε κώδικα για τον υπολογισμό του Αθροίσματος Τετραγώνων των Σφαλμάτων (SS Error) για το μοντέλο του Φύλου. (Έχουμε ήδη δημιουργήσει και αποθηκεύσει τα δύο μοντέλα: το κενό μοντέλο και το μοντέλο του Φύλου.)
11880.21
10546.01Από τα αποτελέσματα διαπιστώνουμε ότι με την προσθήκη του Φύλου ως ανεξάρτητη μεταβλητή στο μοντέλο έχουμε μειώσει το σφάλμα. Ενώ το άθροισμα τετραγώνων των σφαλμάτων γύρω από το κενό μοντέλο (SS Total) ήταν 11880, για το μοντέλο του Φύλου (SS Error) ήταν 10546. Τώρα έχουμε μια ποσοτική βάση για να ισχυριστούμε ότι το μοντέλο του Φύλου είναι καλύτερο μοντέλο για τα δεδομένα μας απ’ ό,τι το κενό μοντέλο.
Αυτή η ιδέα παρουσιάζεται στο παρακάτω διάγραμμα Venn.

Τι αντιπροσωπεύει ολόκληρος ο τιρκουάζ κύκλος (αριστερά);
Τι αντιπροσωπεύει το τιρκουάζ τμήμα του κύκλου (δεξιά);
Ερώτηση - Σωστή απάντηση: Β
Ολόκληρος ο τιρκουάζ κύκλος (αριστερά) = SS Total
Αντιπροσωπεύει τη συνολική μεταβλητότητα στο μήκος αντίχειρα - ολόκληρο το σφάλμα όταν χρησιμοποιούμε μόνο το μέσο όρο για πρόβλεψη.
Ερώτηση - Σωστή απάντηση: Γ
Το τιρκουάζ τμήμα του κύκλου (δεξιά) = SS Error (από το μοντέλο του Φύλου)
Αντιπροσωπεύει το υπολοιπόμενο σφάλμα αφού χρησιμοποιήσουμε το Φύλο για να βελτιώσουμε τις προβλέψεις.
Η γραμμοσκιασμένη περιοχή (Σφάλμα που μειώνεται από το μοντέλο) αντιπροσωπεύει:
\[\text{SS Model} = \text{SS Total} - \text{SS Error}\]
Τη μεταβλητότητα που εξηγείται από τη μεταβλητή Gender.
Χρήση της supernova() για τον Υπολογισμό του Αθροίσματος Τετραγώνων των Σφαλμάτων
Στο σημείο αυτό θα παρουσιάσουμε έναν ευκολότερο τρόπο να συνοψίσουμε τα διαφορετικά αθροίσματα τετραγώνων με πίνακες ANOVA (ANalysis Of VAriance).
Έχουμε παρουσιάσει τη συνάρτηση supernova() ως έναν τρόπο να λάβουμε το Συνολικό Άθροισμα Τετραγώνων (SS Total) για το κενό μοντέλο. Μπορούμε να χρησιμοποιήσουμε την ίδια συνάρτηση για να λάβουμε το Άθροισμα Τετραγώνων των Σφαλμάτων (SS Error) από το μοντέλο του Φύλου και άλλα παρόμοια μοντέλα.
Στο παρακάτω πλαίσιο κώδικα έχουμε δημιουργήσει και αποθηκεύσει δύο μοντέλα: το empty_model και το Gender_model. Εκτελέστε τον κώδικα όπως είναι και θα εμφανίσετε τον πίνακα ANOVA για το κενό μοντέλο. Να τροποποιήσετε τον κώδικα για να εμφανίσετε τον πίνακα ANOVA για το μοντέλο του Φύλου.
Analysis of Variance Table (Type III SS)
Model: Thumb ~ Gender
SS df MS F PRE p
----- --------------- | --------- --- -------- ------ ------ -----
Model (error reduced) | 1334.203 1 1334.203 19.609 0.1123 .0000
Error (from model) | 10546.008 155 68.039
----- --------------- | --------- --- -------- ------ ------ -----
Total (empty model) | 11880.211 156 76.155Παρατηρήστε ότι o πίνακας ANOVA για το Gender_model περιλαμβάνει τόσο το SS Error (αναφέρεται ως Error (from model)) όσο και το SS Total, δηλαδή το σφάλμα από το κενό μοντέλο (αναφέρεται ως Total (empty model)). Ας εστιάσουμε σε αυτά τα δύο αθροίσματα τετραγώνων.
Ποια είναι η μονάδα μέτρησης αυτών των αθροισμάτων τετραγώνων;
Σωστή απάντηση: Δ (\(mm^2\))
Λογική:
Το μήκος αντίχειραThumb μετριέται σε χιλιοστά (mm).
\[\text{SS} = \sum(Y_i - \bar{Y})^2\]
Επειδή τετραγωνίζουμε τις αποκλίσεις:
Απόκλιση: \(mm\)
Τετράγωνο απόκλισης: \((mm)^2 = mm^2\)
Άθροισμα τετραγώνων: \(mm^2\)
Γιατί οι άλλες είναι λάθος:
A (cm), B (mm), E (ίντσες): Γραμμικές μονάδες, όχι τετραγωνικές
C (cm²): Λάθος μονάδα - τα δεδομένα είναι σε mm, όχι cm
Συμπέρασμα:
Τα Αθροίσματα Τετραγώνων μετρώνται σε τετραγωνικά χιλιοστά (\(mm^2\)) επειδή υψώνουμε στο τετράγωνο μετρήσεις που έγιναν σε χιλιοστά.
Γιατί νομίζετε ότι το άθροισμα τετραγώνων για το κενό μοντέλο είναι μεγαλύτερο από αυτό για το μοντέλο του Φύλου; (Υπάρχουν περισσότερες από μία σωστές απαντήσεις.)
Σωστές απαντήσεις: Γ και Δ
Και οι δύο απαντήσεις εκφράζουν την ίδια θεμελιώδη αρχή:
\[\text{SS Total} = \text{SS Model} + \text{SS Error}\]
Γ. Το μοντέλο του Φύλου εξηγεί περισσότερη μεταβλητότητα:
Όταν προσθέτουμε το Φύλο, το μοντέλο εξηγεί μέρος της μεταβλητότητας (SS Model > 0)
Αυτό μειώνει το υπόλοιπο σφάλμα: SS Error < SS Total
Το κενό μοντέλο έχει SS Model = 0, οπότε όλη η μεταβλητότητα είναι σφάλμα
Δ. Διαφορά στην επεξηγηματική ικανότητα:
Κενό μοντέλο: SS Model = 0 (δεν εξηγεί τίποτα)
Μοντέλο Φύλου: SS Model > 0 (εξηγεί μέρος)
Επομένως: SS Error (Φύλο) < SS Total (Κενό)
Γιατί οι άλλες είναι λάθος:
Α. “Κενό μοντέλο καλύτερο” - ΛΑΘΟΣ:
Το αντίθετο είναι αληθές
Μικρότερο SS σημαίνει καλύτερο μοντέλο (λιγότερο σφάλμα)
Το μοντέλο του Φύλου έχει μικρότερο SS, άρα είναι καλύτερο
Β. “Περισσότεροι βαθμοί ελευθερίας” - ΛΑΘΟΣ:
Το κενό μοντέλο έχει περισσότερους df (n-1 = 313)
Το μοντέλο Φύλου έχει λιγότερους df (n-2 = 312)
Αλλά το SS δεν αυξάνεται απαραίτητα με περισσότερους df
Το SS Total είναι μεγαλύτερο επειδή το μοντέλο δεν εξηγεί μεταβλητότητα, όχι λόγω df
Ε. “Δυαδικές τιμές μικρότερα τετράγωνα” - ΛΑΘΟΣ:
Το SS υπολογίζεται από τα υπόλοιπα της εξαρτημένης μεταβλητής (Thumb)
Όχι από την ανεξάρτητη μεταβλητή (Gender)
Συμπέρασμα:
Το SS του μοντέλου του Φύλου είναι μικρότερο επειδή το μοντέλο χρησιμοποιεί πληροφορία (το φύλο) για να εξηγήσει μέρος της μεταβλητότητας στο μήκος αντίχειρα. Το κενό μοντέλο δεν χρησιμοποιεί καμία πληροφορία, οπότε όλη η μεταβλητότητα παραμένει ανεξήγητη.
Το SS Total είναι το μικρότερο άθροισμα τετραγώνων που θα μπορούσαμε να λάβουμε χωρίς να προσθέσουμε καμία ανεξάρτητη μεταβλητή στο μοντέλο. Αντιπροσωπεύει τη συνολική μεταβλητότητα της εξαρτημένης μεταβλητής που θα θέλαμε να εξηγήσουμε. Με αυτό ως αφετηρία, μπορούμε να μειώσουμε το σφάλμα προσθέτοντας μία ανεξάρτητη μεταβλητή στο μοντέλο (σε αυτή την περίπτωση, την Gender).
Η προσθήκη μιας ανεξάρτητης μεταβλητής στο μοντέλο μπορεί να μειώσει το άθροισμα τετραγώνων του σφάλματος, αλλά δεν μπορεί να το αυξήσει. Στη χειρότερη περίπτωση, αν το νέο μοντέλο δεν οδηγεί σε καλύτερες προβλέψεις από το κενό μοντέλο τότε το άθροισμα τετραγώνων του σφάλματος θα παραμείνει το ίδιο. Αλλά είναι σπάνιο μια ανεξάρτητη μεταβλητή να μην έχει καθόλου προβλεπτική αξία.
8.9 Διαμέριση του Αθροίσματος Τετραγώνων σε Μοντέλου και Σφάλματος
ΔΕΔΟΜΕΝΑ = ΜΟΝΤΕΛΟ + ΣΦΑΛΜΑ
Η στατιστική μοντελοποίηση αφορά εξ ολοκλήρου στην εξήγηση της μεταβλητότητας. Το SS Total δείχνει πόση συνολική μεταβλητότητα υπάρχει για να εξηγηθεί. Όταν προσαρμόζουμε ένα μοντέλο (όπως έχουμε κάνει με το μοντέλο του Φύλου), αυτό το μοντέλο εξηγεί κάποιο μέρος της συνολικής μεταβλητότητας και αφήνει κάποιο μέρος της ακόμα ανεξήγητο. Το μέρος που εξηγούμε ονομάζεται SS Model· το μέρος που μένει ανεξήγητο, SS Error.
Αυτές οι σχέσεις παρουσιάζονται στο παρακάτω διάγραμμα: Το SS Total μπορεί να θεωρηθεί ως το άθροισμα του SS Model (η ποσότητα της μεταβλητότητας που εξηγείται από ένα πιο σύνθετο μοντέλο) και του SS Error, η ποσότητα που μένει ανεξήγητη μετά την προσαρμογή του μοντέλου. Όπως ισχύει η εξίσωση ΔΕΔΟΜΕΝΑ = ΜΟΝΤΕΛΟ + ΣΦΑΛΜΑ, έτσι ισχύει και η εξίσωση SS Total = SS Model + SS Error.

Διαμερισμός των Αθροισμάτων Τετραγώνων
Ας δούμε πώς γίνεται αυτός ο διαμερισμός του συνολικού αθροίσματος τετραγώνων στον παρακάτω πίνακα ANOVA για το μοντέλο φύλου. Κοιτάξτε μόνο τη στήλη με την ετικέτα SS. Οι δύο γραμμές που σχετίζονται με το μοντέλο του Φύλου (Model και Error) αθροίζουν στη γραμμή Total (SS Total για το κενό μοντέλο): 1334 + 10546 = 11880.
Analysis of Variance Table (Type III SS)
Model: Thumb ~ Gender
SS df MS F PRE p
----- --------------- | --------- --- -------- ------ ------ -----
Model (error reduced) | 1334.203 1 1334.203 19.609 0.1123 .0000
Error (from model) | 10546.008 155 68.039
----- --------------- | --------- --- -------- ------ ------ -----
Total (empty model) | 11880.211 156 76.155Ας βάλουμε αυτούς τους αριθμούς πίσω στο διάγραμμα Venn του μοντέλου του Φύλου (βλ. παρακάτω διάγραμμα). Το SS Total, που αναπαριστάται από τον ολόκληρο κύκλο, μπορεί να επιμεριστεί σε δύο μέρη: SS Model και SS Error.

Το γραμμοσκιασμένο μέρος (SS Model, που είναι 1334 για το μοντέλο του Φύλου) αντιπροσωπεύει το μέρος του SS Total που εξηγείται από το μοντέλο. Ένας άλλος τρόπος να το σκεφτούμε αυτό είναι ως τη μείωση του σφάλματος (μετρημένη σε άθροισμα τετραγώνων) που επιτυγχάνεται από το μοντέλο του Φύλου σε σχέση με το κενό μοντέλο.
Υπολογισμός του SS Model
Υπάρχουν δύο τρόποι να υπολογίσουμε το SS Model. Ο ένας είναι να αφαιρέσουμε απλώς το SS Error (σφάλμα από τις προβλέψεις του μοντέλου του Φύλου) από το SS Total (σφάλμα γύρω από το μέσο όρο, ή το κενό μοντέλο):
\[\text{SS Model} = \text{SS Total} - \text{SS Error}\]
Ένας άλλος τρόπος είναι να υπολογίσουμε τη μείωση του σφάλματος που επιτυγχάνεται όταν περνάμε από το κενό μοντέλο στο μοντέλο του Φύλου, ξεχωριστά για κάθε παρατήρηση, στη συνέχεια να υψώσουμε στο τετράγωνο και να αθροίσουμε τις τιμές για να πάρουμε το SS Model.
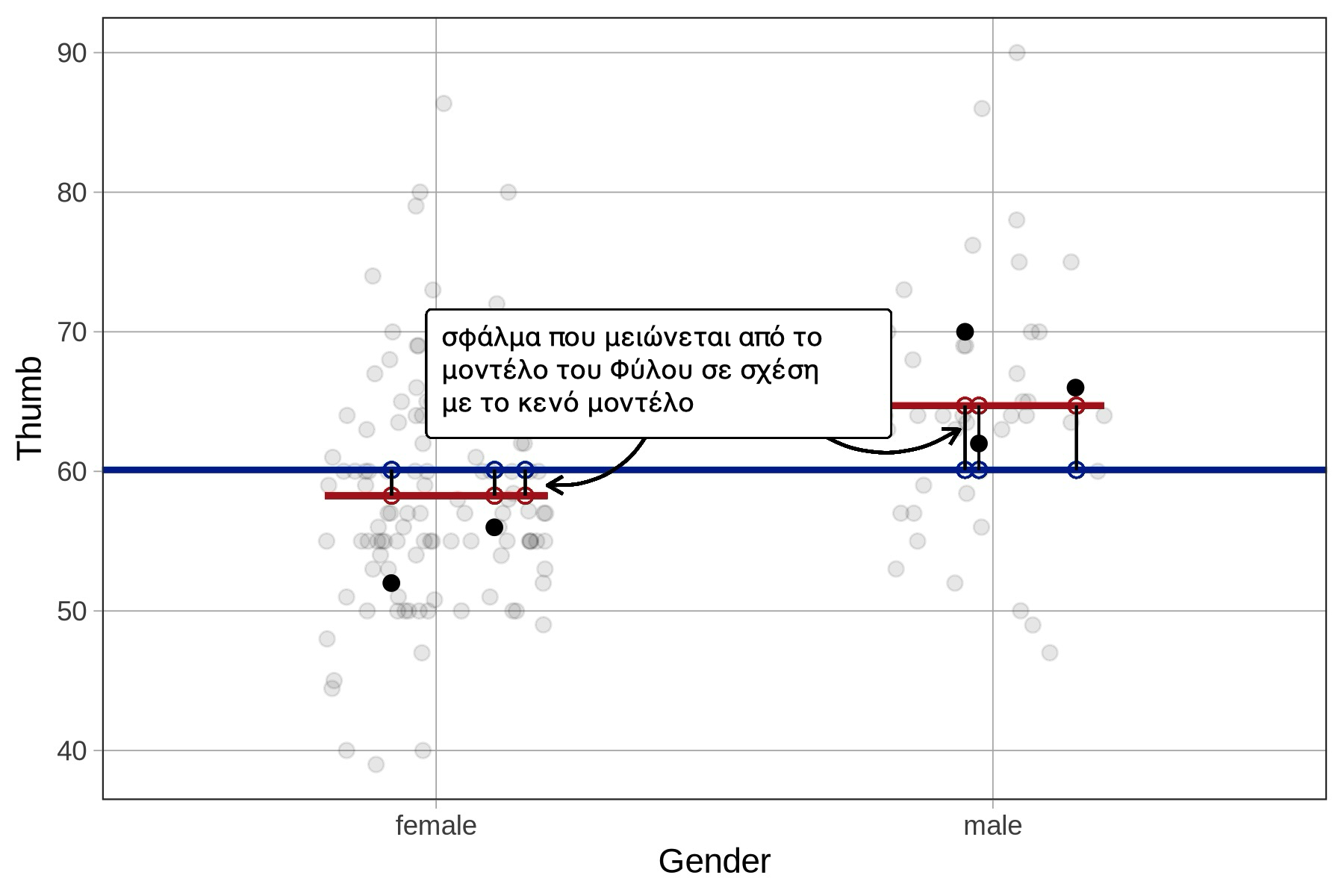
Ας το δούμε αυτό διαγραμματικά. Στο παρακάτω διάγραμμα, για μια συγκεκριμένη παρατήρηση στην ομάδα female παίρνουμε την απόσταση ανάμεσα στην τιμή πρόβλεψής της με βάση το μοντέλο του Φύλου και την τιμή πρόβλεψής της με βάση το κενό μοντέλο, και υψώνουμε την απόσταση αυτή στο τετράγωνο. Αν το κάνουμε αυτό για κάθε παρατήρηση και στη συνέχεια αθροίσουμε τα τετράγωνα, θα πάρουμε το SS Model.
Ποιες από τις παρακάτω δηλώσεις είναι αληθείς σχετικά με την απόσταση από την τιμή πρόβλεψης κάθε ατόμου με βάση το μοντέλο φύλου έως την τιμή πρόβλεψής του με βάση το κενό μοντέλο; (Υπάρχουν περισσότερες από μία σωστές απαντήσεις)
Ποια από τις παρακάτω γραμμές κώδικα θα επέστρεφε τις αποστάσεις που χρησιμοποιούνται για τον υπολογισμό του SS Model;
Πρώτη ερώτηση - Όλες είναι σωστές (Α, Β, Γ, Δ)
Α. Ίδιες για κάθε ομάδα φύλου - ΣΩΣΤΟ ✓
# Για όλες τις γυναίκες:
απόσταση = 58.3 - 60.1 = -1.8 mm
# Για όλους τους άνδρες:
απόσταση = 64.7 - 60.1 = +4.6 mm
# Ίδια εντός κάθε ομάδας!Β. Το κενό διάστημα μεταξύ των γραμμών - ΣΩΣΤΟ ✓
Διαγραμματικά, αυτές οι αποστάσεις είναι το κενό διάστημα μεταξύ:
Της μπλε γραμμής (κενό μοντέλο)
Των κόκκινων γραμμών (μοντέλο του Φύλου)
Γ. Δεν είναι υπόλοιπα - ΣΩΣΤΟ ✓
# Υπόλοιπα από το κενό μοντέλο:
e_empty = Thumb - 60.1
# Υπόλοιπα από το μοντέλο του Φύλου:
e_gender = Thumb - Gender_predict
# Αποστάσεις μεταξύ των μοντέλων:
distance = Gender_predict - 60.1
# Είναι διαφορετικά!Δ. Δεν χρειαζόμαστε πραγματικά δεδομένα - ΣΩΣΤΟ ✓
Μπορούμε να τα υπολογίσουμε:
# Χωρίς να γνωρίζουμε το αρχικό μήκος αντίχειρα:
distance_female = 58.3 - 60.1 = -1.8
distance_male = 64.7 - 60.1 = +4.6
# Χρειαζόμαστε μόνο τις προβλέψεις!Δεύτερη ερώτηση - Σωστή απάντηση: Α
predict(Gender_model) - predict(empty_model)
# Αυτό υπολογίζει:
distances = Gender_predict - Empty_predict
# Για κάθε άτομο:
# Γυναίκες: 58.3 - 60.1 = -1.8
# Άνδρες: 64.7 - 60.1 = +4.6
# Για το SS Model:
SS_Model = sum(distances^2)Γιατί οι άλλες είναι λάθος:
Β. resid(Gender_model) - resid(empty_model) - ΛΑΘΟΣ:
- Αυτό είναι διαφορά υπολοίπων, όχι διαφορά προβλέψεων
Γ. supernova(Gender_model) - supernova(empty_model) - ΛΑΘΟΣ:
Η
supernova()επιστρέφει πίνακα, όχι διάνυσμα αποστάσεωνΔεν μπορούμε να αφαιρέσουμε έτσι τους πίνακες
Δ. predict(Gender_model) - Fingers$Thumb - ΛΑΘΟΣ:
Αυτά είναι τα υπόλοιπα από το μοντέλο του φύλου
Όχι οι αποστάσεις μεταξύ μοντέλων
Συμπέρασμα:
Οι επιμέρους αποστάσεις που αποτελούν το SS Model είναι οι διαφορές μεταξύ των προβλέψεων των δύο μοντέλων. Αυτές είναι σταθερές εντός κάθε ομάδας και δεν εξαρτώνται από τα πραγματικά δεδομένα - μόνο από τις τιμές πρόβλεψης των δύο μοντέλων.
Από τα αποτελέσματα της supernova() διαπιστώνουμε ότι το SS Model για το μοντέλο του Φύλου είναι περίπου ίσο με 1334. Αλλά ας χρησιμοποιήσουμε την R για να το υπολογίσουμε πιο αναλυτικά, να δούμε αν παίρνουμε το ίδιο αποτέλεσμα, και να εμβαθύνουμε στην κατανόηση των αποτελεσμάτων της supernova().
Στο παρακάτω πλαίσιο κώδικα, έχουν ήδη δημιουργηθεί τα αντικείμενα empty_model και Gender_model. Η επόμενη γραμμή κώδικα υπολογίζει όλες τις διαφορές μεταξύ των προβλέψεων των δύο μοντέλων και τις αποθηκεύει ως μια νέα μεταβλητή που ονομάζεται error_reduced. Εκτελέστε την για να δείτε πώς είναι αυτή η μεταβλητή. Στη συνέχεια, τροποποιήστε τον κώδικα για να τετραγωνίσετε και να αθροίσετε τις τιμές της ώστε να υπολογίσετε το SS Model (ποσότητα σφάλματος που μειώνεται από το μοντέλο).
1334.2038.10 Χρήση της Αναλογικής Μείωσης του Σφάλματος (PRE) για τη Σύγκριση Δύο Μοντέλων
Έχουμε ποσοτικοποιήσει τη μεταβλητότητα που έχει εξηγηθεί από το μοντέλο μας: 1334 τετραγωνικά χιλιοστά. Αλλά είναι αυτή πολλή ή λίγη; Θα ήταν ευκολότερο να το διαπιστώσουμε αυτό αν γνωρίζαμε την αναλογία ή το ποσοστό της συνολικής μείωσης του σφάλματος αντί για την ποσότητα του μειωμένου σφάλματος μετρημένη σε \(mm^2\).
Αν ρίξετε μια ματιά ξανά στον πίνακα της supernova() για το μοντέλου του Φύλου, θα δείτε μια στήλη με τίτλο PRE. Το PRE σημαίνει Proportional Reduction in Error (Αναλογική Μείωση του Σφάλματος).
Analysis of Variance Table (Type III SS)
Model: Thumb ~ Gender
SS df MS F PRE p
----- --------------- | --------- --- -------- ------ ------ -----
Model (error reduced) | 1334.203 1 1334.203 19.609 0.1123 .0000
Error (from model) | 10546.008 155 68.039
----- --------------- | --------- --- -------- ------ ------ -----
Total (empty model) | 11880.211 156 76.155Το PRE υπολογίζεται ως το πηλίκο δύο αθροίσματων τετραγώνων. Είναι απλώς το SS Model (δηλαδή, το άθροισμα τετραγώνων που μειώνεται από το μοντέλο) διαιρεμένο με το SS Total (ή, το συνολικό άθροισμα τετραγώνων στην εξαρτημένη μεταβλητή με βάση το κενό μοντέλο). Μπορούμε να το αναπαραστήσουμε με μια εξίσωση:
\[\text{PRE} = \frac{\text{SS Model}}{\text{SS Total}}\]
 Όταν υπολογίζουμε το PRE με αυτόν τον τρόπο, στην ουσία συγκρίνουμε ένα σύνθετο μοντέλο (π.χ., το μοντέλο του Φύλου) με το κενό μοντέλο. Βάσει αυτής της εξίσωσης, το PRE μπορεί να ερμηνευθεί ως η αναλογία ή το ποσοστό της συνολικής μεταβλητότητας της εξαρτημένης μεταβλητής που εξηγείται από την ανεξάρτητη μεταβλητή. Αυτό μας δείχνει κάτι για την αξία του στατιστικού μας μοντέλου. Για παράδειγμα, στο σύνολο δεδομένων
Όταν υπολογίζουμε το PRE με αυτόν τον τρόπο, στην ουσία συγκρίνουμε ένα σύνθετο μοντέλο (π.χ., το μοντέλο του Φύλου) με το κενό μοντέλο. Βάσει αυτής της εξίσωσης, το PRE μπορεί να ερμηνευθεί ως η αναλογία ή το ποσοστό της συνολικής μεταβλητότητας της εξαρτημένης μεταβλητής που εξηγείται από την ανεξάρτητη μεταβλητή. Αυτό μας δείχνει κάτι για την αξία του στατιστικού μας μοντέλου. Για παράδειγμα, στο σύνολο δεδομένων Fingers, η επίδραση του Φύλου στο μήκος αντίχειρα εξηγεί το .11 (ή 11%) της μεταβλητότητας στο μήκος του αντίχειρα. Όχι και τόσο άσχημα, καθώς πρόκειται για μία μόνο ανεξάρτητη μεταβλητή.
Είναι σημαντικό να θυμόμαστε ότι το SS Model στον αριθμητή της παραπάνω εξίσωσης αντιπροσωπεύει τη μείωση του σφάλματος όταν περνάμε από το κενό μοντέλο στο πιο σύνθετο μοντέλο, το οποίο περιλαμβάνει μία ανεξάρτητη μεταβλητή. Για να το κάνουμε πιο σαφές, μπορούμε να ξαναγράψουμε την παραπάνω εξίσωση ως εξής:
\[\text{PRE} = \frac{(\text{SS Total} - \text{SS Error})}{\text{SS Total}}\]
Ο αριθμητής αυτής της εξίσωσης ξεκινά με το σφάλμα από το απλό (κενό) μοντέλο (SS Total), και στη συνέχεια αφαιρεί το σφάλμα από το σύνθετο μοντέλο (SS Error) για να πάρει το σφάλμα που μειώνεται από το σύνθετο μοντέλο ((SS Model). Το πηλίκο αυτής της ποσότητας μείωσης του σφάλματος με το SS Total πολλαπλασιασμένο με το 100 δίνει το ποσοστό του συνολικού σφάλματος στο κενό μοντέλο που έχει μειωθεί από το σύνθετο μοντέλο.
Αν έχετε δύο μοντέλα για την ίδια εξαρτημένη μεταβλητή και το ένα είναι πιο σύνθετο από το άλλο, ποιο συνήθως θα έχει το μεγαλύτερο Άθροισμα Τετραγώνων των Σφαλμάτων (Sum of Squares Error ή SS Error);
Σωστή απάντηση: Β (Το απλό μοντέλο)
Θεμελιώδης αρχή:
Προσθέτοντας ανεξάρτητες μεταβλητές σε ένα μοντέλο μπορεί μόνο να μειώσει (ή να διατηρήσει) το SS Error, ποτέ να το αυξήσει.
\[\text{SS Error (απλό)} \geq \text{SS Error (σύνθετο)}\]
Παράδειγμα:
# Απλό μοντέλο (empty)
lm(Thumb ~ 1)
SS_Error = 10000 mm²
# Πιο σύνθετο (+ Gender)
lm(Thumb ~ Gender)
SS_Error = 8000 mm² # Μικρότερο!
# Ακόμα πιο σύνθετο (+ Gender + Height)
lm(Thumb ~ Gender + Height)
SS_Error = 6000 mm² # Ακόμα μικρότερο!Γιατί συμβαίνει αυτό:
\[\text{SS Total} = \text{SS Model} + \text{SS Error}\]
Το SS Total είναι σταθερό (από το κενό μοντέλο)
Όσο αυξάνεται το SS Model (εξηγούμε περισσότερη μεταβλητότητα)
Τόσο μειώνεται το SS Error (λιγότερη ανεξήγητη μεταβλητότητα)
Εξαίρεση - όταν είναι ίσα:
Αν η νέα μεταβλητή δεν εξηγεί τίποτα:
SS Model δεν αυξάνεται (= 0)
SS Error παραμένει το ίδιο
# Αν προσθέσουμε τυχαίο θόρυβο ως μεταβλητή:
lm(Thumb ~ random_noise)
SS_Error ≈ SS_Total (αναμένουμε να είναι περίπου ίσα)Γιατί οι άλλες είναι λάθος:
Α. “Σύνθετο μοντέλο” - ΛΑΘΟΣ:
- Το αντίθετο - το σύνθετο μοντέλο έχει μικρότερο SS Error
Γ. “Ίδια” - ΛΑΘΟΣ (συνήθως):
Μόνο αν η νέα μεταβλητή δεν εξηγεί τίποτα
Συνήθως το σύνθετο μοντέλο εξηγεί κάτι
Δ. “Αδύνατο να προσδιοριστεί” - ΛΑΘΟΣ:
- Μπορούμε να είμαστε σίγουροι: απλό ≥ σύνθετο
Συμπέρασμα:
Το κενό μοντέλο θα έχει συνήθως μεγαλύτερο SS Error επειδή εξηγεί λιγότερη μεταβλητότητα από το σύνθετο μοντέλο. Κάθε επιπλέον ανεξάρτητη μεταβλητή αναμένεται να μειώσει το σφάλμα. Ωστόσο, όπως θα δούμε σε επόμενα κεφάλαια, αν και ένα πιο σύνθετο μοντέλο είναι πιο ακριβές, δεν είναι απαραίτητα καλύτερο από ένα πιο απλό μοντέλο.
Η τιμή του PRE στον παραπάνω πίνακα ANOVA (.11) προκύπτει από τη σύγκριση του μοντέλου του Φύλου με το κενό μοντέλο, αλλά το PRE γενικά μπορεί να χρησιμοποιηθεί για τη σύγκριση οποιουδήποτε σύνθετου μοντέλου με ένα απλούστερο. Για το σκοπό αυτό, θα παραθέσουμε μια εκδοχή της ίδιας εξίσωσης που είναι πιο γενική:
\[\text{PRE} = \frac{\text{SS Error}_{\text{απλό}} - \text{SS Error}_{\text{σύνθετο}}}{\text{SS Error}_{\text{απλό}}}\]
Ο δείκτης PRE είναι γνωστός στη βιβλιογραφία και με άλλα ονόματα. Στο πλαίσιο της ANOVA (Analysis of Variance) είναι γνωστός ως \(\eta^2\). Σε επόμενο κεφάλαιο, θα παρουσιάσουμε τον ίδιο δείκτη στο πλαίσιο της γραμμικής παλινδρόμησης, όπου είναι γνωστός ως \(R^2\). Προς το παρόν, το μόνο που χρειάζεται να γνωρίζετε είναι ότι αυτοί είναι διαφορετικοί όροι που αναφέρονται στο ίδιο πράγμα.
Ποια από τα παρακάτω είναι αληθή για το PRE; (Υπάρχουν περισσότερες από μία σωστές απαντήσεις.)
Σωστές απαντήσεις: Β και Γ
Β. Κυμαίνεται από 0 έως 1 - ΣΩΣΤΟ ✓
Το PRE είναι αναλογία:
Ελάχιστο: 0 (το σύνθετο μοντέλο δεν εξηγεί τίποτα)
Μέγιστο: 1 (το σύνθετο μοντέλο εξηγεί τα πάντα)
\[0 \leq \text{PRE} \leq 1\]
Γ. Αναλογία εξηγούμενης μεταβλητότητας - ΣΩΣΤΟ ✓
\[\text{PRE} = \frac{\text{SS}_{\text{Model}}}{\text{SS}_{\text{Total}}} = \frac{\text{Μείωση σφάλματος}}{\text{Συνολικό σφάλμα}}\]
Ερμηνεία: “Ποιο ποσοστό της μεταβλητότητας εξηγείται από το μοντέλο;”
Γιατί οι άλλες είναι λάθος:
Α. “Σε μονάδες mm” - ΛΑΘΟΣ:
Το PRE δεν έχει μονάδες
Είναι αναλογία: \(\frac{mm^2}{mm^2}\) → οι μονάδες ακυρώνονται
Δ. “Αναλογία ανεξήγητης” - ΛΑΘΟΣ:
Αυτό θα ήταν: \(\frac{SS_{Error}}{SS_{Total}}\) = 1 - PRE
Το PRE μετράει το εξηγούμενο μέρος, όχι το ανεξήγητο
Ε. “\(SS_{Total} - SS_{Error}\)” - ΛΑΘΟΣ:
Αυτό είναι το \(SS_{Model}\) (σε \(mm^2\)), όχι το PRE
Το PRE είναι η αναλογία: \(\frac{SS_{Model}}{SS_{Total}}\)
Παράδειγμα:
SS_Total = 10000 mm²
SS_Error = 8000 mm²
SS_Model = 2000 mm²
# PRE (χωρίς μονάδες)
PRE = 2000 / 10000 = 0.20 = 20%
# Ερμηνεία:
# "Το Φύλο εξηγεί 20% της μεταβλητότητας στο μήκος αντίχειρα"Συμπέρασμα:
Το PRE είναι μια αναλογία χωρίς μονάδες που κυμαίνεται από 0 έως 1 και αντιπροσωπεύει το ποσοστό της μεταβλητότητας που εξηγείται από το σύνθετο μοντέλο. Είναι το ίδιο με το \(\eta^2\) στην ANOVA και το \(R^2\) στην παλινδρόμηση.
Τι δείχνει το PRE;
Σωστή απάντηση: Β
PRE = Αναλογική Μείωση του Σφάλματος
\[\text{PRE} = \frac{\text{SS}_{\text{Model}}}{\text{SS}_{\text{Total}}} = \frac{\text{Μείωση σφάλματος}}{\text{Συνολικό σφάλμα}}\]
Σημαίνει: Η αναλογία (proportion) της μεταβλητότητας που εξηγείται από το μοντέλο.
Γιατί οι άλλες είναι λάθος:
Α. “Αριθμός τετραγωνικών mm” - ΛΑΘΟΣ:
Αυτό θα ήταν το \(SS_{Model}\) (σε \(mm^2\))
Το PRE είναι αναλογία (0 έως 1), όχι απόλυτη ποσότητα
Γ. “Ανεξήγητη μεταβλητότητα” - ΛΑΘΟΣ:
Αυτό θα ήταν: \(\frac{SS_{Error}}{SS_{Total}}\) = 1 - PRE
Το PRE μετράει το μέρος της μεταβλητότητας που εξηγείται, όχι αυτό που παραμένει ανεξήγητο
Δ. “Άθροισμα τετραγώνων του σφάλματος που εξηγείται” - ΛΑΘΟΣ:
Παράδοξο: το “σφάλμα” δεν “εξηγείται”
Το μοντέλο εξηγεί μεταβλητότητα, όχι το σφάλμα
Παράδειγμα:
Συμπέρασμα:
Το PRE είναι η αναλογία της μεταβλητότητας που εξηγείται από το μοντέλο - ένας δείκτης από 0 έως 1 που δείχνει πόσο καλά το μοντέλο εξηγεί τη μεταβλητότητα στα δεδομένα.
8.11 Ασκήσεις Επανάληψης Κεφαλαίου 8
Η επόμενη ομάδα ερωτήσεων αναφέρονται σε ένα πλαίσιο δεδομένων που ονομάζεται FatMice18, το οποίο περιέχει δεδομένα για 18 ποντίκια. Τα ποντίκια υποβλήθηκαν τυχαία σε μία από δύο θεραπείες με φως: LD (κύκλος φως/σκοτάδι) ή LL (φως κατά τη διάρκεια της ημέρας και φως τη νύχτα επίσης). Οι ερευνητές παρακολούθησαν το βάρος που κέρδισε κάθε ποντίκι (σε γραμμάρια) κατά τη διάρκεια των τεσσάρων εβδομάδων αυτής της παρέμβασης.
Οι μεταβλητές στο πλαίσιο δεδομένων είναι:
Light: Ομάδα Θεραπείας με φως: LD ή LLWgtGain4: Αύξηση βάρους σε γραμμάρια κατά τη διάρκεια των τεσσάρων εβδομάδωνCageLoc: Η τοποθεσία του κλουβιού στο ερευνητικό εργαστήριο, στην επάνω σειρά (top row) ή την κάτω σειρά (bottom row)
Αποτέλεσμα της head(FatMice18):
Light WgtGain4 CageLoc
1 LL 10 top row
2 LL 10 top row
3 LL 11 bottom row
4 LL 9 bottom row
5 LL 12 top row
6 LL 9 bottom row1. Αν προσαρμόσουμε με την lm() ένα μοντέλο με εξαρτημένη μεταβλητή την WgtGain4 και ανεξάρτητη μεταβλητή την Light, πώς υπολογίζεται το σφάλμα του μοντέλου για κάθε ποντίκι;
Σωστή απάντηση: Δ
Υπολογισμός υπολοίπου:
Για το μοντέλο με ανεξάρτητη την Light:
\[e_i = \text{WgtGain4}_i - \text{mean(WgtGain4 για την ομάδα Light του ποντικιού)}\]
Παράδειγμα:
# Ποντίκι 1: LL, WgtGain4 = 10
mean_LL = 10.2 # μέσος ομάδας LL
error = 10 - 10.2 = -0.2 γραμμάρια
# Ποντίκι με LD, WgtGain4 = 7
mean_LD = 6.5 # μέσος ομάδας LD
error = 7 - 6.5 = 0.5 γραμμάριαΓιατί οι άλλες είναι λάθος:
Α. “Μέσος ομάδας από το Γενικό Μέσο Όρο” - ΛΑΘΟΣ:
Αυτό υπολογίζει το SS Model, όχι το SS Error
Δείχνει τη διαφορά μεταξύ μοντέλων, όχι σφάλμα
Β. “Μεταξύ των δύο μέσων” - ΛΑΘΟΣ:
- Αυτό είναι μία τιμή (διαφορά ομάδων), όχι σφάλμα για κάθε ποντίκι
Γ. “Από το Γενικό Μέσο Όρο” - ΛΑΘΟΣ:
Αυτό είναι το σφάλμα από το κενό μοντέλο
Όχι από το μοντέλο της Light
Συμπέρασμα:
Το σφάλμα για κάθε ποντίκι είναι η απόσταση από το μέσο της ομάδας του - όχι από το γενικό μέσο.
Analysis of Variance Table (Type III SS)
Model: WgtGain4 ~ Light
SS df MS F PRE p
----- --------------- | ------- -- ------- ------ ------ -----
Model (error reduced) | 112.500 1 112.500 24.398 0.6039 .0001
Error (from model) | 73.778 16 4.611
----- --------------- | ------- -- ------- ------ ------ -----
Total (empty model) | 186.278 17 10.952. Παραπάνω παρουσιάζεται ο πίνακας της ANOVA (το αποτέλεσμα της supernova()) για το Light_model, που χρησιμοποιεί τη μεταβλητή Light για να εξηγήσει τη μεταβλητότητα της WgtGain4. Τι σημαίνει η τιμή του δείκτη PRE;
Σωστή απάντηση: Δ
Ερμηνεία PRE = 0.60:
\[\text{PRE} = \frac{\text{SS Model}}{\text{SS Total}} = \frac{112.5}{186.278} = 0.6039\]
Σημαίνει: Το 60% της συνολικής μεταβλητότητας (από το κενό μοντέλο) εξηγείται από την Light.
Γιατί οι άλλες είναι λάθος:
Α. “Πιθανότητα 0.60” - ΛΑΘΟΣ:
Το PRE δεν είναι πιθανότητα
Είναι αναλογία εξηγούμενης μεταβλητότητας
Β. “0.60 του Light_model” - ΛΑΘΟΣ:
Το PRE αναφέρεται στο SS Total (από το κενό μοντέλο)
Όχι στο SS από το Light_model
Γ. “0.60 του δείγματος” - ΛΑΘΟΣ:
Το PRE δεν αναφέρεται σε αναλογία ποντικιών
Αναφέρεται σε αναλογία μεταβλητότητας
Επαλήθευση:
SS_Total = 186.278
SS_Model = 112.500
SS_Error = 73.778
PRE = SS_Model / SS_Total
= 112.5 / 186.278
= 0.6039
# Επίσης:
PRE = (SS_Total - SS_Error) / SS_Total
= (186.278 - 73.778) / 186.278
= 0.6039 ✓Ερμηνεία:
“Το 60% της μεταβλητότητας στην αύξηση βάρους εξηγείται από το είδος θεραπείας με φως. Το υπόλοιπο 40% οφείλεται σε άλλους παράγοντες.”
Analysis of Variance Table (Type III SS)
Model: WgtGain4 ~ Light
SS df MS F PRE p
----- --------------- | ------- -- ------- ------ ------ -----
Model (error reduced) | 112.500 1 112.500 24.398 0.6039 .0001
Error (from model) | 73.778 16 4.611
----- --------------- | ------- -- ------- ------ ------ -----
Total (empty model) | 186.278 17 10.95
Coefficients:
(Intercept) LightLL
5.889 5.0003. Δείχνουν τα παραπάνω αποτελέσματα ότι η θεραπεία LL (φως κατά τη διάρκεια της ημέρας και της νύχτας) προκαλεί στα ποντίκια να τρώνε περισσότερο;
Σωστή απάντηση: Α
Κρίσιμη διάκριση:
Το πείραμα μπορεί να δείξει αιτιότητα για: - Θεραπεία → Αύξηση βάρους ✓
Το πείραμα δεν μπορεί να δείξει αιτιότητα για: - Θεραπεία → Περισσότερη κατανάλωση τροφής ✗
Γιατί:
Η ερώτηση είναι αν η θεραπεία με φως προκαλεί στα ποντίκια να τρώνε περισσότερο. Αλλά:
Δε μετρήθηκε η πρόσληψη τροφής - μόνο η αύξηση βάρους
-
Η αύξηση βάρους μπορεί να οφείλεται σε άλλους μηχανισμούς:
Μειωμένος μεταβολισμός
Μειωμένη σωματική δραστηριότητα
Αλλαγές στην αποθήκευση λίπους
Ορμονικές αλλαγές
Γιατί οι άλλες είναι λάθος:
Β. “Ναι, λόγω τυχαίας ανάθεσης” - ΛΑΘΟΣ:
Η τυχαία ανάθεση επιτρέπει αιτιώδη συμπεράσματα
Αλλά μόνο για το μετρούμενο αποτέλεσμα (αύξηση βάρους)
Όχι για μη μετρούμενες μεταβλητές (κατανάλωση τροφής)
Γ. “Ναι, λόγω μεγάλου F και PRE” - ΛΑΘΟΣ:
Το μέγεθος του F και PRE δείχνουν την ένταση της σχέσης
Όχι το μηχανισμό πίσω από τη σχέση
Δ. “Όχι, λόγω προϋπαρχουσών διαφορών” - ΛΑΘΟΣ:
Η τυχαία ανάθεση ελέγχει για προϋπάρχουσες διαφορές
Αυτό δεν είναι το πρόβλημα εδώ
Συμπέρασμα:
Μπορούμε να ισχυρούμε ότι: - ✓ “Η θεραπεία LL προκαλεί αύξηση βάρους”
Δεν μπορούμε να ισχυριστούμε ότι: - ✗ “Η θεραπεία LL προκαλεί αυξημένη κατανάλωση τροφής”
Για να απαντήσουμε στη δεύτερη ερώτηση, θα χρειαζόμασταν δεδομένα για την πρόσληψη τροφής.
4. Ας υποθέσουμε ότι υπολογίζουμε τα υπόλοιπα τόσο από το κενό μοντέλο όσο και από το σύνθετο μοντέλο. Τι είναι παρόμοιο σχετικά με αυτά τα δύο σύνολα υπολοίπων;
Σωστή απάντηση: Γ
Θεμελιώδης ομοιότητα:
Και τα δύο σύνολα υπολοίπων υπολογίζονται με τον ίδιο τρόπο:
\[\text{υπόλοιπο} = \text{ΔΕΔΟΜΕΝΑ} - \text{ΜΟΝΤΕΛΟ}\]
Για το κενό μοντέλο:
Για το μοντέλο της Light:
Κοινή ιδιότητα:
Και τα δύο μετρούν την απόσταση από την πρόβλεψη - η διαφορά είναι ότι χρησιμοποιούν διαφορετικές προβλέψεις.
Γιατί οι άλλες είναι λάθος:
Α. “Μειώνονται με προσοχή” - ΛΑΘΟΣ:
Τα υπόλοιπα αντιπροσωπεύουν πραγματική μεταβλητότητα, όχι σφάλματα μέτρησης
Ακόμα και με τέλεια μέτρηση, θα υπάρχουν υπόλοιπα
Τα ποντίκια έχουν πραγματικές διαφορές που δεν εξηγούνται από το μοντέλο
Β. “Διαφορά από Γενικό Μέσο Όρο” - ΛΑΘΟΣ:
Αυτό ισχύει μόνο για το κενό μοντέλο
Το μοντέλο της Light χρησιμοποιεί μέσους ομάδων, όχι το Γενικό Μέσο Όρο
Δ. “Ίδιες τιμές” - ΛΑΘΟΣ:
Οι τιμές των υπολοίπων είναι διαφορετικές
Το μοντέλο της Light έχει μικρότερα υπόλοιπα (καλύτερες προβλέψεις)
# Ποντίκι 1: LL, WgtGain4 = 10
e_empty = 10 - 8.389 = 1.611
e_light = 10 - 10.889 = -0.889
# Διαφορετικές τιμές!Συμπέρασμα:
Η κοινή αρχή είναι ότι και τα δύο σύνολα υπολοίπων υπολογίζονται ως ΔΕΔΟΜΕΝΑ - ΜΟΝΤΕΛΟ. Η διαφορά είναι στο τι χρησιμοποιεί κάθε μοντέλο ως τιμή πρόβλεψης:
Κενό μοντέλο: Ένας μέσος όρος για όλους
Μοντέλο της Light: Διαφορετικοί μέσοι όροι για κάθε ομάδα
Analysis of Variance Table (Type III SS)
Model: WgtGain4 ~ Light
SS df MS F PRE p
----- --------------- | ------- -- ------- ------ ------ -----
Model (error reduced) | 112.500 1 112.500 24.398 0.6039 .0001
Error (from model) | 73.778 16 4.611
----- --------------- | ------- -- ------- ------ ------ -----
Total (empty model) | 186.278 17 10.955. Δίνεται παραπάνω ο πίνακας ANOVA για το Light_model, που χρησιμοποιεί την Light για να εξηγήσει τη μεταβλητότητα της WgtGain4. Γιατί το άθροισμα τετραγώνων των σφαλμάτων του μοντέλου (SS Error = 73.78) είνα μικρότερο από το συνολικό άθροισμα τετραγώνων (SS Total = 186.28);
Σωστή απάντηση: Α
Η λογική:
\[\text{SS Total} = \text{SS Model} + \text{SS Error}\]
\[186.278 = 112.500 + 73.778\]
SS Total (από το κενό μοντέλο):
Το άθροισμα τετραγώνων των υπολοίπων από το Γενικό Μέσο Όρο (8.389g)
Όλη η μεταβλητότητα είναι “σφάλμα” (καμία εξήγηση μεταβλητότητας)
SS Error (από το μοντέλο της Light):
Το άθροισμα τετραγώνων των υπολοίπων από τους μέσους όρους των ομάδων (LL: 10.889, LD: 5.889)
Η ανεξήγητη μεταβλητότητα (μετά την εξήγηση μέρους της από την Light)
Γιατί SS Error < SS Total:
Επειδή το μοντέλο της Light εξηγεί μέρος της μεταβλητότητας:
112.5 \(mm^2\) εξηγείται (SS Model)
73.8 \(mm^2\) παραμένει ανεξήγητο (SS Error)
Γιατί οι άλλες είναι λάθος:
Β. “SS total από σύνθετο” - ΛΑΘΟΣ:
Το αντίθετο είναι αληθές
SS Total είναι από το απλό κενό μοντέλο
SS Error είναι από το σύνθετο από το μοντέλο της Light
Γ. “Σφάλμα στον κώδικα” - ΛΑΘΟΣ:
Είναι σωστό το SS Error < SS Total
Αυτό συμβαίνει πάντα όταν το μοντέλο εξηγεί κάτι
Δ. “Εξαρτάται από την ανεξάρτητη” - ΛΑΘΟΣ:
- Και τα δύο SS υπολογίζονται από τα υπόλοιπα της εξαρτημένης μεταβλητής (WgtGain4)
Συμπέρασμα:
Το SS Error είναι μικρότερο επειδή το μοντέλο της Light χρησιμοποιεί καλύτερες τιμές πρόβλεψης (μέσους όρους των ομάδων αντί του Γενικού Μέσου Όρου), μειώνοντας τα υπόλοιπα και άρα το συνολικό άθροισμα τετραγώνων.
Analysis of Variance Table (Type III SS)
Model: WgtGain4 ~ Light
SS df MS F PRE p
----- --------------- | ------- -- ------- ------ ------ -----
Model (error reduced) | 112.500 1 112.500 24.398 0.6039 .0001
Error (from model) | 73.778 16 4.611
----- --------------- | ------- -- ------- ------ ------ -----
Total (empty model) | 186.278 17 10.95
Analysis of Variance Table (Type III SS)
Model: WgtGain4 ~ CageLoc
SS df MS F PRE p
----- ----------------- ------- -- ------ ----- ------ -----
Model (error reduced) | 14.803 1 14.803 1.381 0.0795 .2571
Error (from model) | 171.475 16 10.717
----- ----------------- ------- -- ------ ----- ------ -----
Total (empty model) | 186.278 17 10.9586. Αν βασιστούμε στους δύο παραπάνω πίνακες ANOVA, θα υποστηρίζαμε ότι η Light (επάνω πίνακας) εξηγεί περισσότερη μεταβλητότητα στη WgtGain4 από ό,τι η CageLoc (η τοποθεσία του κλουβιού, κάτω πίνακας). Ποια στοιχεία του πίνακα θα υποστήριζαν αυτό το επιχείρημα;
Σωστή απάντηση: Γ (Και τα δύο)
Και τα δύο μέτρα δείχνουν ότι η Light εξηγεί περισσότερη μεταβλητότητα:
Α. PRE (Αναλογική Μείωση του Σφάλματος):
Light: PRE = 0.6039 (60.4%)
CageLoc: PRE = 0.0795 (7.95%)
Light εξηγεί ~60% της μεταβλητότητας
CageLoc εξηγεί ~8% τηςμεταβλητότηταςΒ. SS Model (Άθροισμα Τετραγώνων Σφαλμάτων του Μοντέλου):
Light: SS_Model = 112.500mm²
CageLoc: SS_Model = 14.803mm²
Η Light εξηγεί 112.5mm²
Η CageLoc εξηγεί 14.8mm²Και τα δύο οδηγούν στο ίδιο συμπέρασμα:
Η Light είναι πολύ ισχυρότερος προβλεπτικός παράγοντας:
PRE: 60% vs 8% (7.6× περισσότερο)
SS Model: 112.5 vs 14.8 (7.6× περισσότερο)
Οπτική σύγκριση:
SS Total = 186.278 mm²
Light Model:
├─ SS Model: 112.5 ████████████████████████ (60%)
└─ SS Error: 73.8 ███████████████ (40%)
CageLoc Model:
├─ SS Model: 14.8 ███ (8%)
└─ SS Error: 171.5 ████████████████████████████████████ (92%)Συμπέρασμα:
Και το PRE και το SS Model υποστηρίζουν τον ισχυρισμό ότι η Light εξηγεί σημαντικά περισσότερη μεταβλητότητα από την CageLoc. Στην πραγματικότητα, αυτά τα δύο μέτρα είναι συνδέονται αλγεβρικά μεταξύ τους (\(\text{PRE} = \frac{\text{SS Model}}{\text{SS Total}}\)).
7. Για το πλαίσιο δεδομένων FatMice18, να εκτελέσετε την lm() για να προσαρμόσετε το μοντέλο με εξαρτημένη μεταβλητή τη WgtGain4, και την Light ως ανεξάρτητη μεταβλητή. Αν η εξίσωση \(Y_i = b_0 + b_1X_1 + e_i\) αναπαριστά το προσαρμοσμένο μοντέλο, ποια είναι η τιμή του \(b_1\);
Σωστή απάντηση: Α (5.000)
Από τα δεδομένα που δόθηκαν νωρίτερα:
Coefficients:
(Intercept) LightLL
5.889 5.000Το μοντέλο:
\[\text{WgtGain4} = b_0 + b_1 \times \text{LightLL}\]
\[\text{WgtGain4} = 5.889 + 5.000 \times \text{LightLL}\]
Όπου:
\(b_0 = 5.889\) (intercept, μέσος όρος της ομάδας LD)
\(b_1 = 5.000\) (η ποσότητα κερδισμένου βάρους που προστίθεται στην ομάδα LL)
Ερμηνεία του \(b_1 = 5.000\):
Τα ποντίκια στην ομάδα LL κερδίζουν κατά μέσο όρο 5 γραμμάρια περισσότερο βάρος από τα ποντίκια στην ομάδα LD.
# LD group (LightLL = 0):
WgtGain4 = 5.889 + 5.000×0 = 5.889g
# LL group (LightLL = 1):
WgtGain4 = 5.889 + 5.000×1 = 10.889g
# Διαφορά:
10.889 - 5.889 = 5.000gΓιατί οι άλλες είναι λάθος:
Β. 5.889 - ΛΑΘΟΣ:
Αυτό είναι το \(b_0\) (intercept)
Ο μέσος όρος της ομάδας αναφοράς (LD)
Γ. “Αριθμός ποντικιών” - ΛΑΘΟΣ:
Το \(b_1\) είναι συντελεστής, όχι μέγεθος δείγματος
Μετράει τη διαφορά σε γραμμάρια
Δ. “Αν είναι στην LL” - ΛΑΘΟΣ:
Αυτό περιγράφει την ανεξάρτητη μεταβλητή \(X_i\) (0 ή 1)
Όχι τον συντελεστή \(b_1\) (5.000)
Συμπέρασμα:
Το \(b_1 = 5.000\) γραμμάρια είναι η εκτίμηση της διαφοράς στην αύξηση βάρους μεταξύ των ομάδων LL και LD.
SS df MS F PRE p
----- ----------------- ------- -- -------- ----- ------ -----
Model (error reduced) | 2638.1 1 2638.361 ?
Error (from model) | 7845.3 80 98.079
----- ----------------- ------- -- -------- ----- ------ -----
Total (empty model) | 10484.7 81 129.4418. Με βάση τις πληροφορίες που παρουσιάζονται στον παραπάνω πίνακα ANOVA, πώς θα υπολογίζατε την τιμή του δείκτη PRE (κατά προσέγγιση);
Σωστή απάντηση: Α
Τύπος PRE:
\[\text{PRE} = \frac{\text{SS Model}}{\text{SS Total}}\]
Υπολογισμός:
Γιατί οι άλλες είναι λάθος:
Β. “2638 / 98” - ΛΑΘΟΣ:
Το 98 είναι το MS Error (Mean Square), όχι το SS Total
Αυτός ο λόγος δεν έχει νόημα ως αναλογία ή ποσοστό
Γ. “7846 / 10485” - ΛΑΘΟΣ:
Αυτό θα υπολόγιζε το: \(\frac{\text{SS Error}}{\text{SS Total}}\)
Αυτό είναι το ποσοστό της ανεξήγητης μεταβλητότητας = 1 - PRE
Όχι το PRE (ποσοστό εξηγούμενης μεταβλητότητας)
Επαλήθευση:
# Μέθοδος 1: Χρησιμοποιώντας SS Model
PRE = 2638.1 / 10484.7 = 0.2516
# Μέθοδος 2: Χρησιμοποιώντας μείωση σφάλματος
PRE = (SS_Total - SS_Error) / SS_Total
= (10484.7 - 7845.3) / 10484.7
= 2639.4 / 10484.7
= 0.2517 ✓
# Μικρή διαφορά λόγω στρογγυλοποίησηςΣυμπέρασμα:
Για να υπολογίσετε το PRE, διαιρέστε το SS Model (2638) με το SS Total (10485), που εξηγεί περίπου το 0.25 ή 25% της μεταβλητότητας.
Το StudentSurvey είναι ένα πλαίσιο δεδομένων με 362 παρατηρήσεις στις ακόλουθες 17 μεταβλητές:
Year: Έτος σπουδώνGender: Φύλο φοιτητή: F ή MSmoke: Καπνιστής; No ή YesAward: Προτίμηση για βραβείο: Academy, Nobel, ή OlympicHigherSAT: Ποια επίδοση στη δοκιμασία SAT είναι υψηλότερη; Math ή VerbalExercise: Ώρες άσκησης ανά εβδομάδαTV: Ώρες παρακολούθησης τηλεόρασης ανά εβδομάδαHeight: Ύψος (σε ίντσες)Weight: Βάρος (σε λίβρες)Siblings: Αριθμός αδελφώνBirthOrder: Σειρά γέννησης, 1 = μεγαλύτεροVerbalSAT: Βαθμολογία στη δοκιμασία Verbal SATMathSAT: Βαθμολογία στη δοκιμασία Math SATSAT: Σύνθετη βαθμολογία Verbal + Math SATGPA: Βαθμός πτυχίουPulse: Σφυγμός (χτύποι ανά λεπτό)Piercings: Αριθμός piercing στο σώμα
9. Να χρησιμοποιήσετε την lm() για να εξετάσετε το μοντέλο που περιλαμβάνει το φύλο (Gender) για να εξηγήσει το ύψος (Height) στο πλαίσιο δεδομένων StudentSurvey. Πόσες ίντσες πρέπει να προσθέσετε στο μέσο ύψος για τις γυναίκες για να πάρετε το μέσο ύψος για τους άνδρες;
Σωστή απάντηση: Γ (5.151)
Το μοντέλο:
model <- lm(Height ~ Gender, data = StudentSurvey)
coef(model)
# (Intercept) GenderM
# 65.694611 5.151134 Ερμηνεία:
\[\text{Height} = 65.694611 + 5.151134 \times \text{GenderM}\]
Όπου:
\(b_0 = 65.694611\) ίντσες = μέσο ύψος γυναικών
\(b_1 = 5.151134\) ίντσες = διαφορά ύψους (άνδρες - γυναίκες)
Υπολογισμοί:
# Γυναίκες (GenderM = 0):
Height_F = 65.694611 + 5.151134×0 = 65.694611 ίντσες
# Άνδρες (GenderM = 1):
Height_M = 65.694611 + 5.151134×1 = 70.84574 ίντσες
# Διαφορά:
Height_M - Height_F = 70.84574 - 65.694611 = 5.151129 ίντσεςΤο \(b_1\) είναι η απάντηση:
Ο συντελεστής GenderM = 5.151 αντιπροσωπεύει πόσες ίντσες πρέπει να προσθέσετε στο μέσο ύψος των γυναικών για να πάρετε το μέσο ύψος των ανδρών.
Συμπέρασμα:
Οι άνδρες είναι κατά μέσο όρο 5.151 ίντσες ψηλότεροι από τις γυναίκες σε αυτό το δείγμα φοιτητών.
10. Να χρησιμοποιήσετε ξανά την lm() για να εξετάσετε το μοντέλο που περιλαμβάνει το φύλο (Gender) για να εξηγήσει το ύψος (Height) στο πλαίσιο δεδομένων StudentSurvey. Ποιο είναι το μέσο ύψος για τις γυναίκες;
Σωστή απάντηση: Δ (65.695)
Το μοντέλο:
Το intercept (\(b_0\)) είναι το μέσο ύψος των γυναικών:
\[\text{Height} = b_0 + b_1 \times \text{GenderM}\]
Για γυναίκες (GenderM = 0):
\[\text{Height}_F = 65.695 + 5.151 \times 0 = 65.695 \text{ ίντσες}\]
Γιατί οι άλλες είναι λάθος:
Α. 63.896 - ΛΑΘΟΣ:
- Μπορεί να είναι άλλο στατιστικό από το αποτέλεσμα
Β. 70.846 - ΛΑΘΟΣ:
Αυτό είναι το μέσο ύψος των ανδρών
\(65.695 + 5.151 = 70.846\) ίντσες
Γ. 51.51 - ΛΑΘΟΣ:
Πολύ χαμηλό για μέσο ύψος
Η τιμή του \(b_1\) με την υποδιαστολή μια θέση στα δεξιά (5.151)
Απάντηση:
Το \(b_0\) σε ένα μοντέλο με μια ποιοτική ανεξάρτητη μεταβλητή αντιπροσωπεύει το μέσο όρο της ομάδας αναφοράς (γυναίκες). Άρα το μέσο ύψος των γυναικών είναι 65.695 ίντσες.
11. Προσαρμόστε ένα μοντέλο χρησιμοποιώντας τo φύλο (Gender) για να εξηγήσετε τη μεταβλητότητα στον αριθμό των piercing στο σώμα (Piercings) και παρατηρήστε τις εκτιμήσεις των παραμέτρων. Ποιο από τα παρακάτω είναι σωστό για τους άνδρες φοιτητές;
Σωστή απάντηση: Β
Το μοντέλο:
model <- lm(Piercings ~ Gender, data = StudentSurvey)
coef(model)
# Αποτέλεσμα:
# (Intercept) GenderM
# 3.378698 -3.206823
# Πρόβλεψη για τους άνδρες:
# Piercings = 3.378698 + (-3.206823)×1 = 0.1719Η πρόβλεψη του μοντέλου:
\[\text{Piercings}_M = b_0 + b_1 = 3.378698 + (-3.206823) = 0.171875\]
Αυτό είναι ο μέσος αριθμός των piercing για τους άντρες στο δείγμα.
Γιατί οι άλλες είναι λάθος:
Α. “Περιμένετε 1.71 piercing” - ΛΑΘΟΣ:
- Η πρόβλεψη είναι 0.171 κατά μέσο όρο, όχι 1.71
Γ. “2.98 χαμηλότερος” - ΛΑΘΟΣ:
Αυτό περιγράφει το \(b_1\) (τη διαφορά των μέσων όρων)
Η διαφορά δεν είναι 2.98 αλλά 3.206823
Δ. “Σφάλμα 0.17” - ΛΑΘΟΣ:
- Το 0.171 είναι η τιμή πρόβλεψης, όχι το σφάλμα
Συμπέρασμα:
Η πρόβλεψη του μοντέλου για έναν άνδρα φοιτητή είναι ο μέσος αριθμός piercing των ανδρών: 0.171.
12. Να εκτελέστε την favstats() για τον αριθμό των αδελφών (Siblings) στο πλαίσιο δεδομένων StudentSurvey. Σε ποια τιμή της μεταβλητής θα ήταν μικρότερο το άθροισμα τετραγώνων των σφαλμάτων;
Σωστή απάντηση: Δ (1.7)
Θεμελιώδης αρχή:
Το άθροισμα των τετραγώνων των σφαλμάτων ελαχιστοποιείται στο μέσο όρο (mean).
\[\text{SS} = \sum_{i=1}^{n}(Y_i - \bar{Y})^2\]
Αυτό το SS είναι ελάχιστο όταν χρησιμοποιούμε το μέσο όρο \(\bar{Y}\) ως πρόβλεψη.
Από την favstats():
favstats(~Siblings, data = StudentSurvey)
# min Q1 median Q3 max mean sd n missing
# 0 1 1 2 8 1.726519 1.179142 362 0
# Ο μέσος όρος είναι 1.7 αδέλφιαΓιατί ο μέσος όρος ελαχιστοποιεί το SS:
Αν χρησιμοποιήσουμε οποιαδήποτε άλλη τιμή εκτός από το μέσο όρο, το SS θα είναι μεγαλύτερο:
# Αν χρησιμοποιήσουμε mean = 1.7:
SS_mean = Σ(Siblings - 1.7)² → Ελάχιστο
# Αν χρησιμοποιήσουμε 0:
SS_0 = Σ(Siblings - 0)² → Μεγαλύτερο
# Αν χρησιμοποιήσουμε 1:
SS_1 = Σ(Siblings - 1)² → Μεγαλύτερο
# Αν χρησιμοποιήσουμε 2:
SS_2 = Σ(Siblings - 2)² → ΜεγαλύτεροΓιατί οι άλλες είναι λάθος:
Α, Β, Γ (0, 1, 2) - ΛΑΘΟΣ:
Αυτές μπορεί να είναι η διάμεσος (median = 1) ή άλλα στατιστικά
Αλλά μόνο ο μέσος όρος ελαχιστοποιεί το άθροισμα τετραγώνων
Η διάμεσος ελαχιστοποιεί το άθροισμα των απόλυτων αποκλίσεων, όχι το άθροισμα τετραγώνων
Μαθηματική απόδειξη:
Το SS γύρω από μια τιμή \(c\):
\[\text{SS}(c) = \sum_{i=1}^{n}(Y_i - c)^2\]
Παραγωγίζοντας ως προς \(c\) και θέτοντας ίσο με 0:
\[\frac{d}{dc}\text{SS}(c) = -2\sum_{i=1}^{n}(Y_i - c) = 0\]
\[\sum_{i=1}^{n}Y_i = nc\]
\[c = \frac{\sum Y_i}{n} = \bar{Y}\]
Συμπέρασμα:
Το άθροισμα τετραγώνων των σφαλμάτων ελαχιστοποιείται στο μέσο όρο του αριθμού των αδελφών, που είναι 1.7. Αυτός είναι ο λόγος που το κενό μοντέλο χρησιμοποιεί πάντα το μέσο όρο ως τιμή πρόβλεψης.