6  Κεφάλαιο: Ένα Απλό Μοντέλο

Στην ουσία όλα τα μοντέλα αποτελούν προσεγγίσεις και όλες οι προσεγγίσεις είναι λανθασμένες. Ωστόσο, κάποιες προσεγγίσεις είναι χρήσιμες.

— George Box

Δεν είναι δουλειά των μοντέλων να είναι «αληθή». Τα μοντέλα είναι εργαλεία σκέψης.

— Christian Hennig

---

Σε αυτό το μέρος του μαθήματος αναπτύσσουμε την έννοια του στατιστικού μοντέλου. Δημιουργούμε στατιστικά μοντέλα προκειμένου να:

• Εξηγήσουμε τη μεταβλητότητα σε μια εξαρτημένη μεταβλητή χρησιμοποιώντας μία ή περισσότερες ανεξάρτητες μεταβλητές, και να κατανοήσουμε καλύτερα τη Διαδικασία Παραγωγής Δεδομένων·
• Προβλέψουμε τις τιμές μελλοντικών παρατηρήσεων ή δειγμάτων·
• Καταλήξουμε σε τεκμηριωμένες προτάσεις για να βελτιώσουμε τα αποτελέσματα του συστήματος που μελετάμε.

Θα ξεκινήσουμε με την έννοια του μοντέλου, και στη συνέχεια θα αναπτύξουμε την έννοια του στατιστικού μοντέλου. Θα παρουσιάσουμε ένα απλό μοντέλο, το κενό μοντέλο, και από εκεί θα αρχίσουμε να αναπτύσσουμε τη σημαντική έννοια του σφάλματος. Επίσης θα εισάγουμε μαθηματικά σύμβολα για την περιγραφή των στατιστικών μοντέλων.

6.1 Τι Είναι ένα Μοντέλο και σε τι μας Χρειάζεται;

Μπορεί να έχετε ακούσει να μιλούν για στατιστικά μοντέλα. Κάποιος μπορεί να πει, «Δημιουργήσαμε ένα μοντέλο με βάση τα δεδομένα», ή «Το μοντέλο μας προβλέπει ότι…». Οι περισσότεροι άνθρωποι που ακούν τέτοιες εκφράσεις απλά κουνούν το κεφάλι τους συγκαταβατικά. Αλλά μέσα τους αναρωτιούνται: τι μπορεί να σημαίνει αυτό;

Παρουσιάζουμε την ιδέα του μοντέλου με μια αναλογία. Ας υποθέσουμε ότι θέλετε να εκτιμήσετε το εμβαδόν σε τετραγωνικά χιλιόμετρα του Νομού Καβάλας. (Υποθέστε, προς το παρόν, ότι δεν μπορείτε απλά να το ψάξετε στο Διαδίκτυο!) Κάτι τέτοιο δεν είναι εύκολο, επειδή ο Νομός Καβάλας έχει ακανόνιστο σχήμα και ένα νησί, όπως φαίνεται παρακάτω.

Σχήμα 6.1

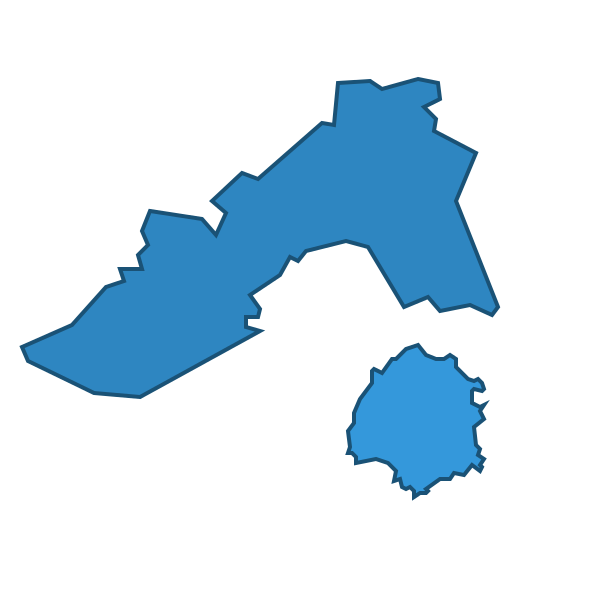
Ένας τρόπος να προσεγγίσουμε αυτό το πρόβλημα θα ήταν να μοντελοποιήσουμε το εμβαδόν του Νομού χρησιμοποιώντας γεωμετρικά σχήματα—συγκεκριμένα, ορθογώνια, τρίγωνα και κύκλους. Αν σχεδιάσουμε ένα ορθογώνιο, δύο τρίγωνα και έναν κύκλο, και τα συνδυάσουμε με τον σωστό τρόπο, μπορούμε να πάρουμε κάτι που να μοιάζει κάπως με τον Νομό Καβάλας.

Σχήμα 6.2

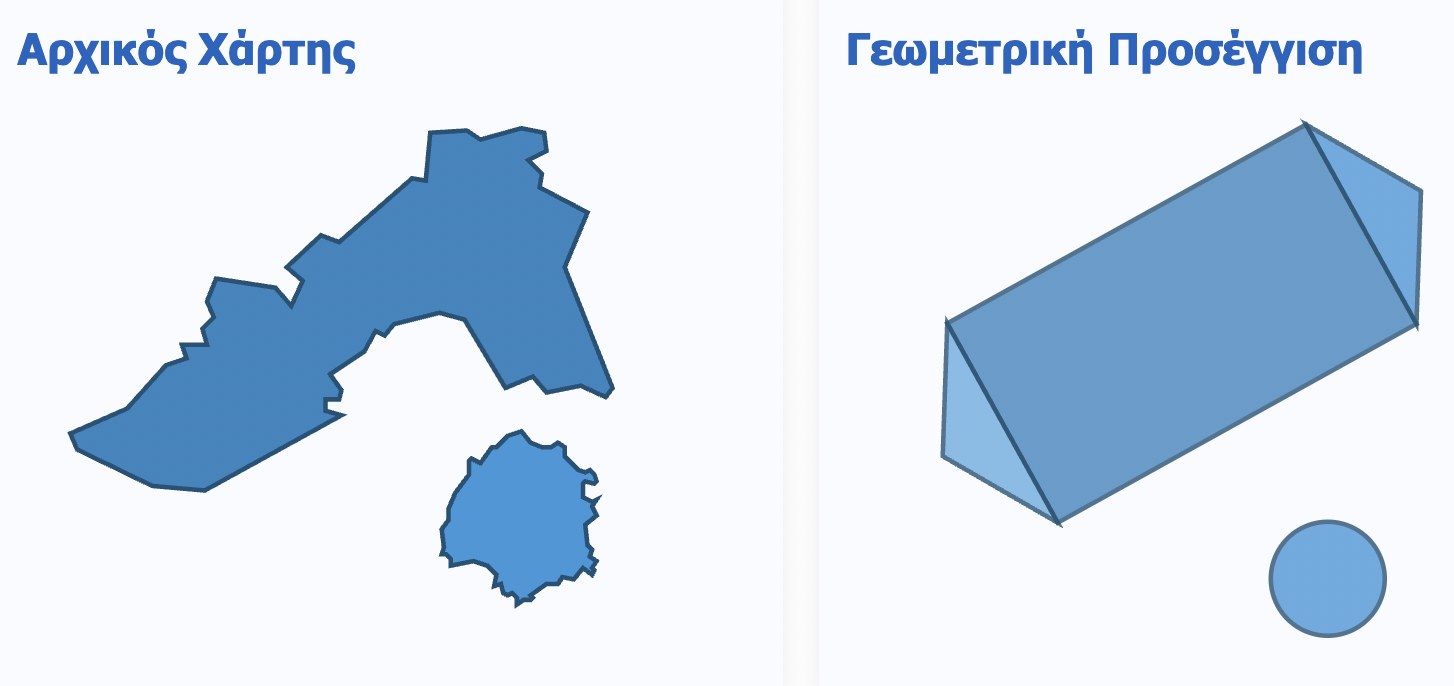
Όπως μπορείτε, ωστόσο, να διαπιστώσετε από το παραπάνω Σχήμα το μοντέλο μας δεν είναι πολύ καλό. Τα περισσότερα μοντέλα, στην πραγματικότητα, είναι αρκετά κακά. Αν και το εμβαδόν του σχήματος πλησιάζει κάπως αυτό του Νομού Καβάλας, υπάρχουν πολλές λεπτομέρειες που δεν αποτυπώνονται στο μοντέλο. Αλλά, είναι καλύτερο από το τίποτα! Και, επειδή γνωρίζουμε πώς να υπολογίσουμε το εμβαδόν ενός ορθογωνίου, το εμβαδόν ενός τριγώνου και ενός κύκλου, αν είμαστε διατεθειμένοι να υποθέσουμε ότι το μοντέλο μας είναι τουλάχιστον αποδεκτό, μπορούμε εύκολα να υπολογίσουμε μια εκτίμηση για το εμβαδόν του Ν. Καβάλας.

Ας πάμε την αναλογία λίγο παραπέρα. Αφότου έχουμε αποφασίσει να μοντελοποιήσουμε το εμβαδόν του Ν. Καβάλας με ένα ορθογώνιο, δύο τρίγωνα και έναν κύκλο, προσπαθούμε να κάνουμε το μοντέλο να προσαρμοστεί όσο καλύτερα γίνεται στον αρχικό χάρτη. Για να το κάνουμε αυτό προσαρμόζουμε το μέγεθος και τον προσανατολισμό των γεωμετρικών σχημάτων. Ακολουθούν δύο άλλα παραδείγματα.

Σχήμα 6.3

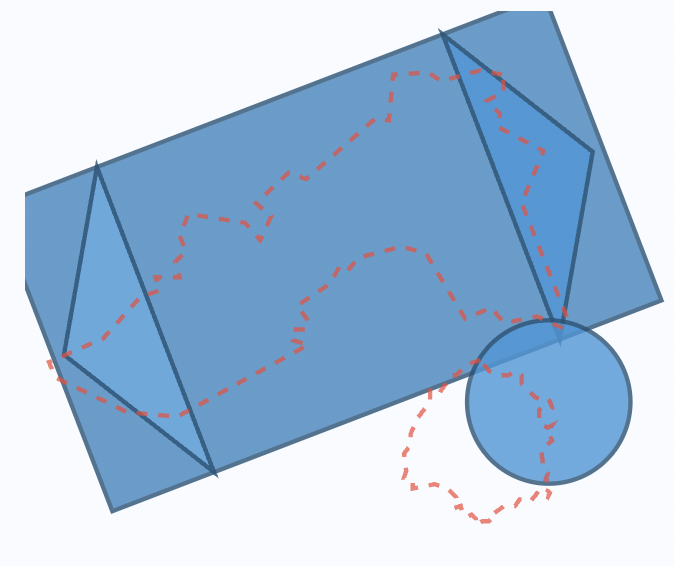
Παρατηρήστε ότι στο παραπάνω σχήμα το μοντέλο μας φαίνεται ότι έχει υπερεκτιμήσει το εμβαδόν του Ν. Καβάλας, επειδή έχουμε κάνει τα σχήματα πολύ μεγάλα.

Σχήμα 6.4

Αντίθετα, στο παραπάνω σχήμα το μοντέλο φαίνεται ότι έχει υποεκτιμήσει το εμβαδόν του Νομού, ενώ το αρχικό μας μοντέλο στο Σχήμα 6.2 είναι καλύτερο. Θα μπορούσαμε να πούμε ότι το αρχικό μας μοντέλο είναι το «μοντέλο με την καλύτερη προσαρμογή» από τα τρία.

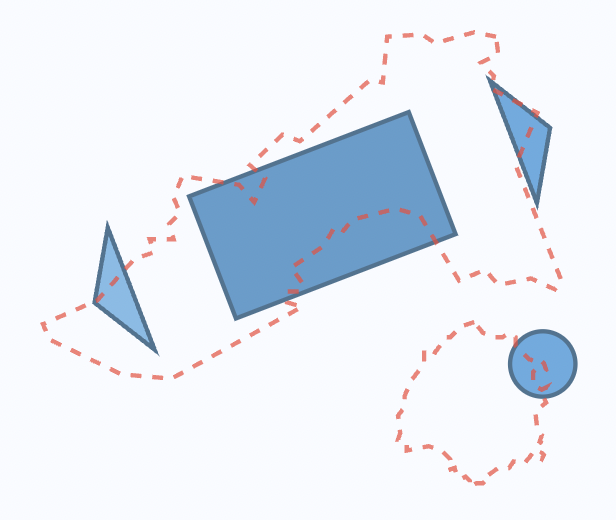
Σημειώστε ότι η κρίση μας για την προσαρμογή ή μη του μοντέλου βασίζεται τόσο την περιοχή του Νομού που δεν καλύπτεται από το μοντέλο μας (δείτε τα τμήματα που προεξέχουν στο Σχήμα 6.4), όσο και την περιοχή που βρίσκεται εκτός των ορίων του Νομού αλλά καλύπτεται από το μοντέλο (δείτε τα τμήματα που δεν επικαλύπτονται με τον Νομό στο Σχήμα 6.3). Είναι χρήσιμο να σκεφτόμαστε αυτές τις δύο περιοχές ως αποκλίσεις από το μοντέλο, ή ως το σφάλμα του μοντέλου μας.

Αν γράψουμε μια λεκτική εξίσωση για να αναπαραστήσουμε αυτό το μοντέλο, θα μπορούσε να μοιάζει κάπως έτσι:

Εμβαδόν Ν. Καβάλας = Εμβαδόν Γεωμετρικών Σχημάτων + Άλλα Πράγματα

Τα «άλλα πράγματα» θα ήταν οι αποκλίσεις από το μοντέλο, τόσο οι θετικές όσο και οι αρνητικές. Είναι χρήσιμο να σκεφτόμαστε το μοντέλο με την καλύτερη προσαρμογή ως εκείνο που ελαχιστοποιεί τις αποκλίσεις (ή το σφάλμα), κάνοντας τα «άλλα πράγματα» όσο το δυνατόν μικρότερα.

Από τη στιγμή που έχουμε δημιουργήσει μοντέλα, μπορούμε να είμαστε πιο συγκεκριμένοι για το τι εννοούμε με τη φράση «άλλα πράγματα». Τα «άλλα πράγματα» είναι το σφάλμα που προκύπτει από το μοντέλο και μπορούμε να ξαναγράψουμε την εξίσωσή μας ως εξής:

Εμβαδόν Ν. Καβάλας = Εμβαδόν Γεωμετρικών Σχημάτων + Σφάλμα

Τέλος, είναι σημαντικό να τονίσουμε ότι το γεωμετρικό μας μοντέλο είναι μια μεγάλη υπεραπλούστευση όλων των διαφορετικών χαρακτηριστικών του Νομού Καβάλας για τα οποία κάποιος θα μπορούσε να ενδιαφέρεται. Αυτό ισχύει για όλα τα μοντέλα: υπεραπλουστεύουν κάποιες πτυχές της πραγματικότητας, και εστιάζουν μόνο στη διάσταση που μας ενδιαφέρει περισσότερο.

6.2 Μοντελοποίηση μιας Κατανομής με Έναν Μόνο Αριθμό

Βασιζόμενοι σε αυτή την έννοια του μοντέλου, ας αναπτύξουμε τώρα τι εννοούμε όταν λέμε στατιστικό μοντέλο. Ενώ στην προηγούμενη ενότητα δημιουργήσαμε ένα μοντέλο για να μας βοηθήσει να εκτιμήσουμε το εμβαδόν του Ν. Καβάλας, τώρα θέλουμε να δημιουργήσουμε ένα μοντέλο που μπορούμε να χρησιμοποιήσουμε για να χαρακτηρίσουμε μια κατανομή.

Όπως θα δείτε στα επόμενα κεφάλαια, τα στατιστικά μοντέλα είναι πολύ χρήσιμα. Τα χρησιμοποιούμε για να συνοψίσουμε κατανομές. Τα χρησιμοποιούμε για να κάνουμε προβλέψεις σχετικά με το ποια θα μπορούσε να είναι η επόμενη παρατήρηση που θα προστεθεί σε μια κατανομή ενός δείγματος. Τα χρησιμοποιούμε, επίσης, για να εξηγήσουμε τη μεταβλητότητα σε μία μεταβλητή με μια άλλη. Αλλά θα ξεκινήσουμε με το απλούστερο μοντέλο, το οποίο χρησιμοποιεί έναν μόνο αριθμό για να χαρακτηρίσει μια κατανομή.

Στο πιο βασικό επίπεδο, ένα στατιστικό μοντέλο μπορεί να θεωρηθεί ως μια συνάρτηση που παράγει μια τιμή πρόβλεψης για κάθε παρατήρηση σε μια κατανομή. Με τη λέξη «συνάρτηση» δεν εννοούμε μια συνάρτηση της R· εννοούμε μια μαθηματική διαδικασία για τον υπολογισμό μιας τιμής με βάση τα δεδομένα. Τα απλούστερα μοντέλα που θα εξετάσουμε παράγουν την ίδια τιμή πρόβλεψης για κάθε παρατήρηση σε μια κατανομή—μία μόνο τιμή για να χαρακτηρίσουμε μια ολόκληρη κατανομή.

Αν έπρεπε να διαλέξετε μία μόνο τιμή για να αντιπροσωπεύσετε μια ολόκληρη κατανομή, πώς θα τη διαλέγατε; Και ποια θα ήταν αυτή; Σκεπτόμενοι με διαφορετικό τρόπο: αν θέλατε να προβλέψετε ποια θα ήταν η τιμή της επόμενης τυχαία επιλεγμένης παρατήρησης, ποια τιμή θα ήταν η καλύτερη πρόβλεψή σας; Ας δούμε μερικά παραδείγματα.

Σχήμα 6.5

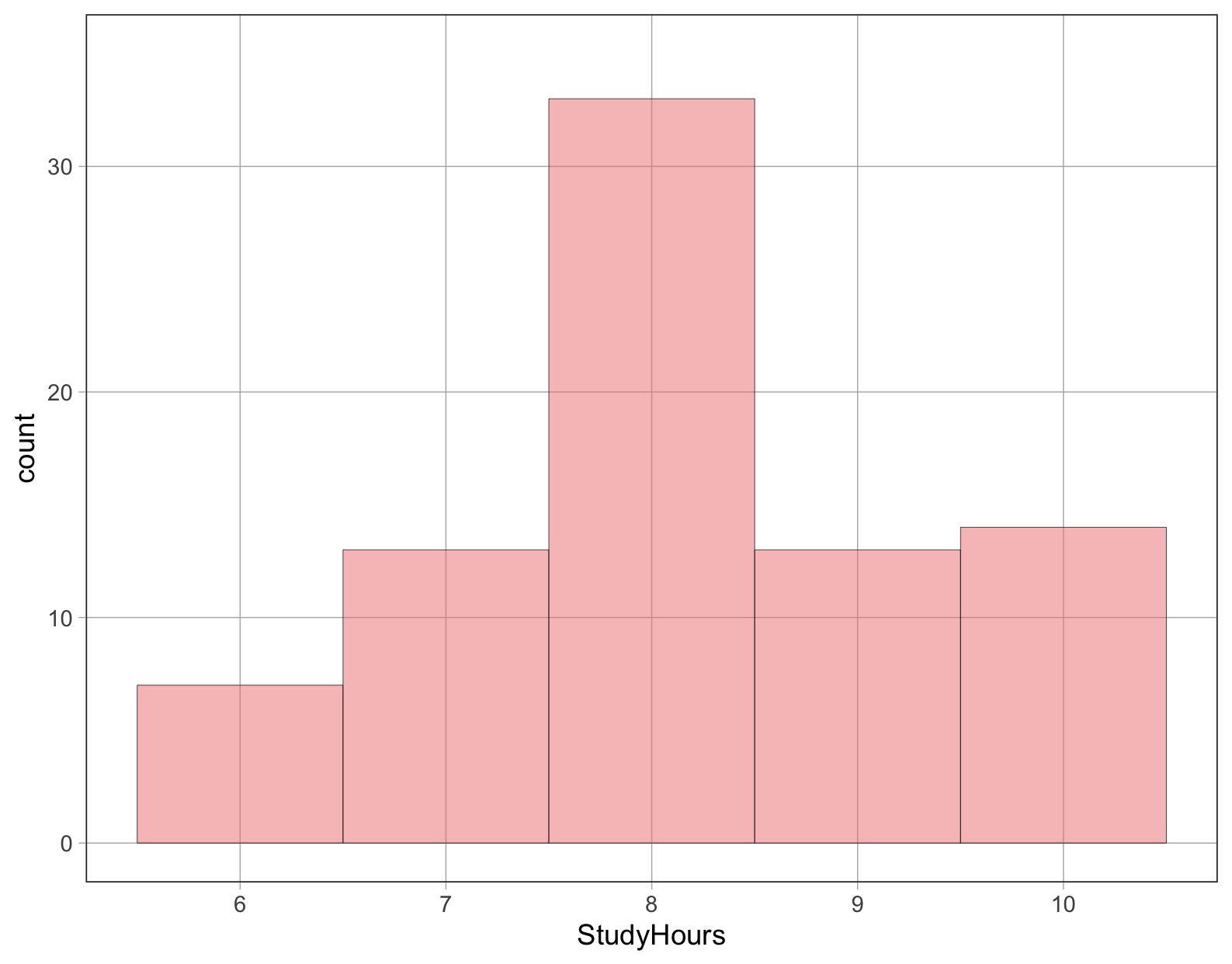
Ποια τιμή θα επιλέγατε για να αναπαραστήσετε ή να μοντελοποιήσετε την παραπάνω κατανομή των ωρών μελέτης (StudyHours) φοιτητών και γιατί; Αν θέλατε να προβλέψετε την τιμή των ωρών μελέτης του επόμενου τυχαία επιλεγμένου φοιτητή, ποια τιμή θα επιλέγατε ως την πρόβλεψή σας;

Σχήμα 6.6

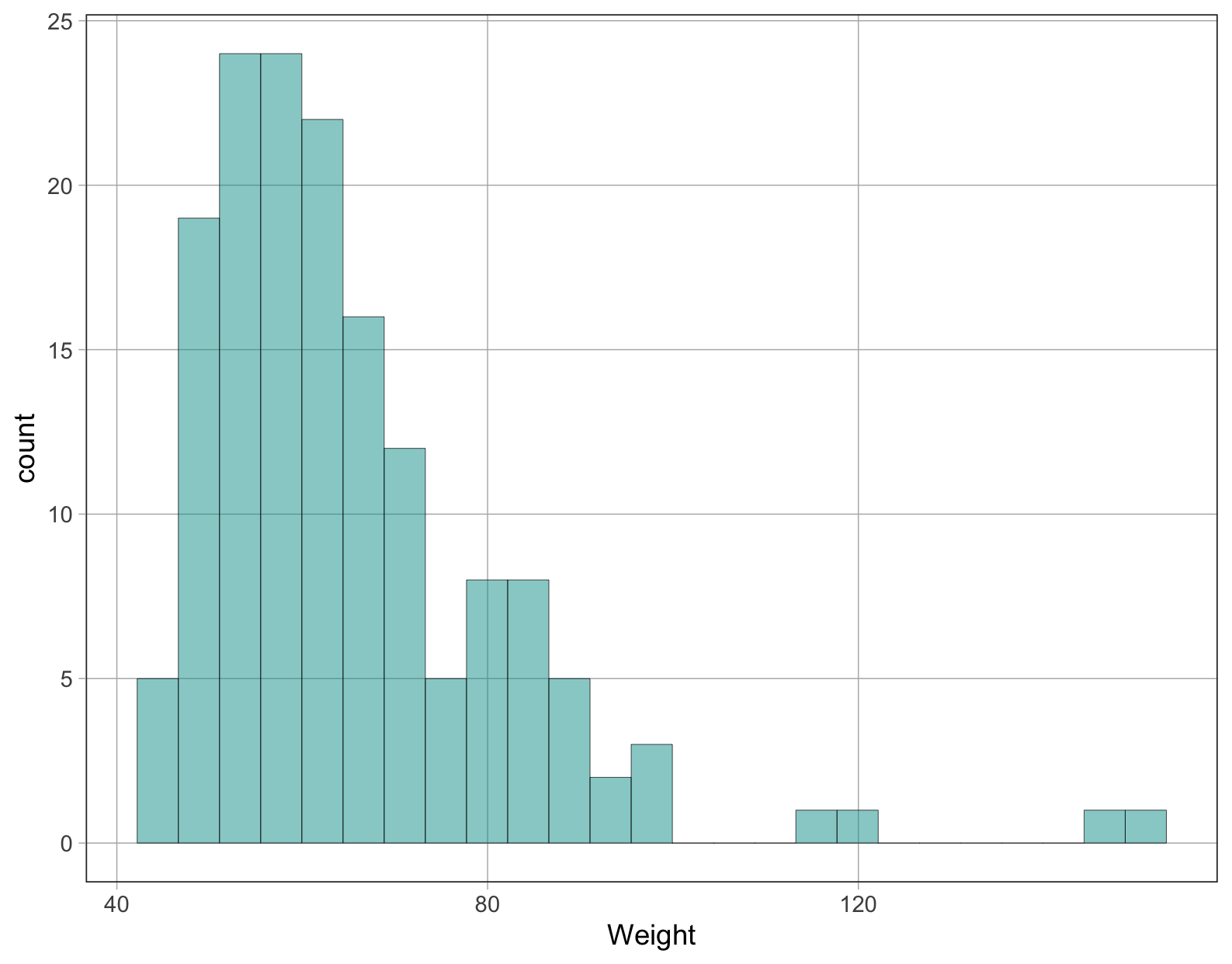
Ποια τιμή θα επιλέγατε για να αναπαραστήσετε ή να μοντελοποιήσετε την παραπάνω κατανομή του βάρους (Weight) φοιτητών και γιατί; Αν θέλατε να προβλέψετε την τιμή του βάρους του επόμενου τυχαία επιλεγμένου φοιτητή, ποια τιμή θα ήταν η πρόβλεψή σας;

Σχήμα 6.7

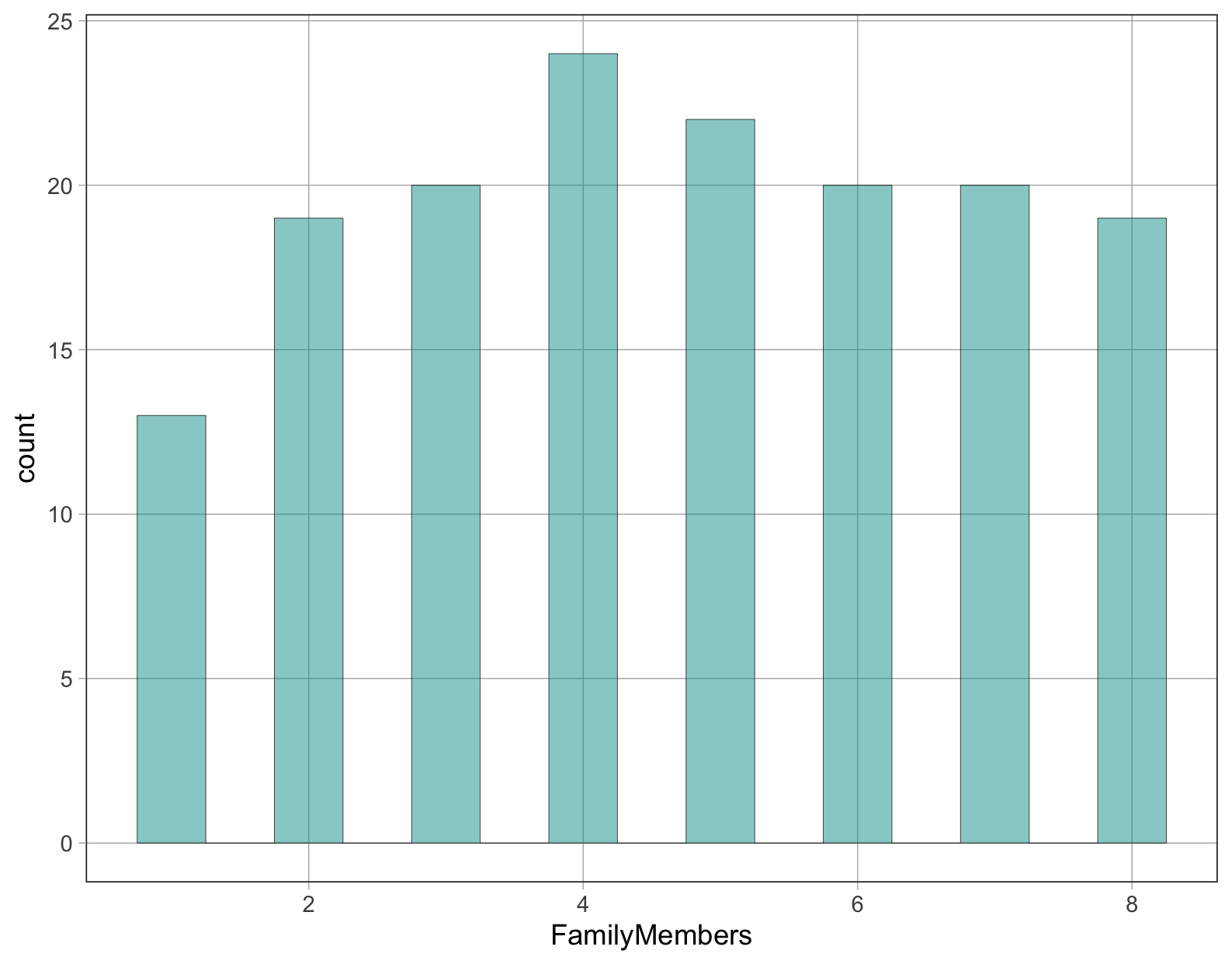
Ποια τιμή θα επιλέγατε για να αναπαραστήσετε ή να μοντελοποιήσετε την παραπάνω κατανομή του αριθμού μελών οικογενείας (FamilyMembers) φοιτητή και γιατί; Αν θέλατε να προβλέψετε την τιμή του αριθμού μελών της οικογένειας του επόμενου τυχαία επιλεγμένου φοιτητή, ποια τιμή θα ήταν η πρόβλεψή σας;

Σχήμα 6.8

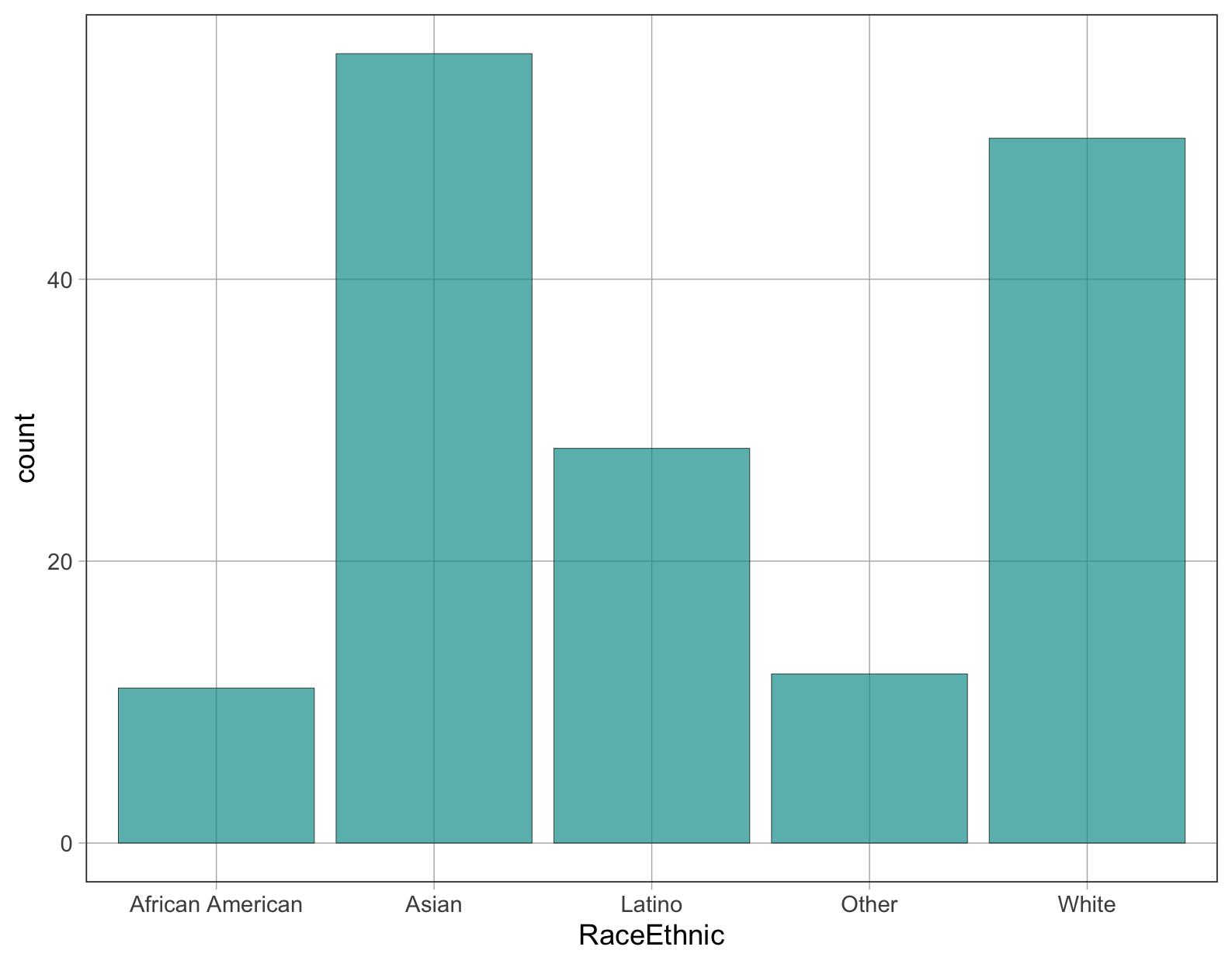
Ποια τιμή θα επιλέγατε για να αναπαραστήσετε ή να μοντελοποιήσετε την παραπάνω κατανομή της φυλετικής προέλευσης (RaceEthnic) φοιτητή και γιατί; Αν θέλατε να προβλέψετε τη φυλετική προέλευση του επόμενου τυχαία επιλεγμένου φοιτητή, ποια τιμή θα ήταν η πρόβλεψή σας;

Σχήμα 6.9

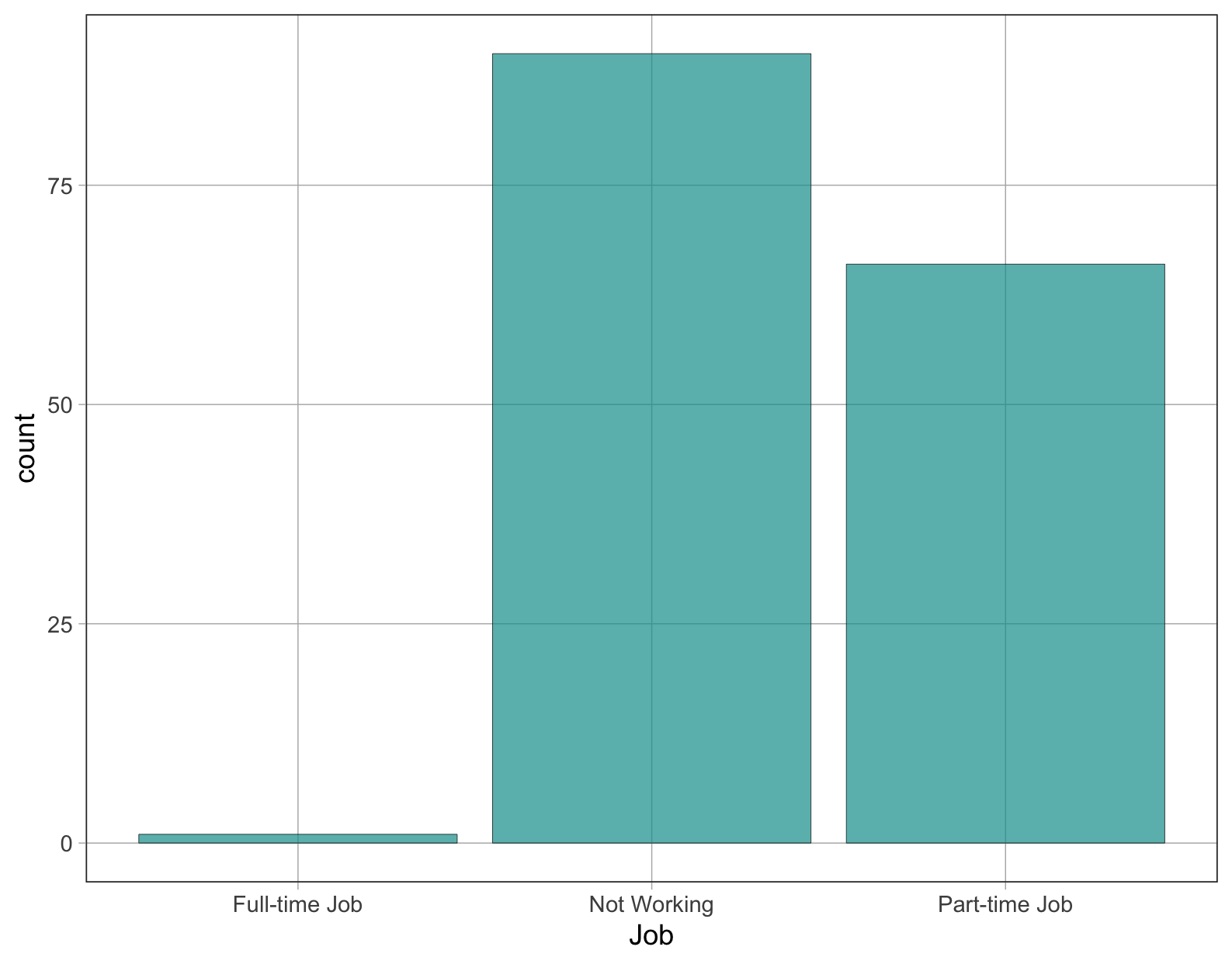
Ποια τιμή θα επιλέγατε να αναπαραστήσετε ή να μοντελοποιήσετε την παραπάνω κατανομή του είδους απασχόλησης (Job) φοιτητή και γιατί; Αν θέλατε να προβλέψετε το είδος απασχόλησης του επόμενου τυχαία επιλεγμένου φοιτητή, ποια τιμή θα ήταν η πρόβλεψή σας;

Ανάλογα με το είδος μιας μεταβλητής (π.χ., ποσοτική ή ποιοτική), και με το σχήμα της κατανομής, θα χρησιμοποιούμε διαφορετικές διαδικασίες (ή διαφορετικές συναρτήσεις) για την επιλογή μιας μόνο τιμής ως μοντέλου.

Για μια ποσοτική μεταβλητή της οποίας η κατανομή είναι περίπου συμμετρική και με σχήμα καμπάνας, μία τιμή που βρίσκεται ακριβώς στο κέντρο της κατανομής θα μπορούσε να είναι το μοντέλο με την καλύτερη προσαρμογή. (Θυμηθείτε: δεν λέμε ότι ένα τόσο απλό μοντέλο είναι ένα καλό μοντέλο—απλώς ότι είναι καλύτερο από το τίποτα!) Αν μια κατανομή είναι ασύμμετρη στα αριστερά ή στα δεξιά, το καλύτερο μοντέλο θα μπορούσε να είναι μια τιμή προς το σημείο όπου θα ήταν το κέντρο, αν αγνοούσατε τη μακριά ουρά προς τη μία ή την άλλη πλευρά. Για μια ποιοτική μεταβλητή, το καλύτερο μοντέλο είναι γενικά η κατηγορία που είναι πιο συχνή.

Μοντέλο και Σφάλμα

Ας εστιάσουμε μόνο σε κατανομές ποσοτικών μεταβλητών. Ρίξτε μια ματιά στις δύο παρακάτω κατανομές για τις μεταβλητές 1 και 2.

Σχήμα 6.10

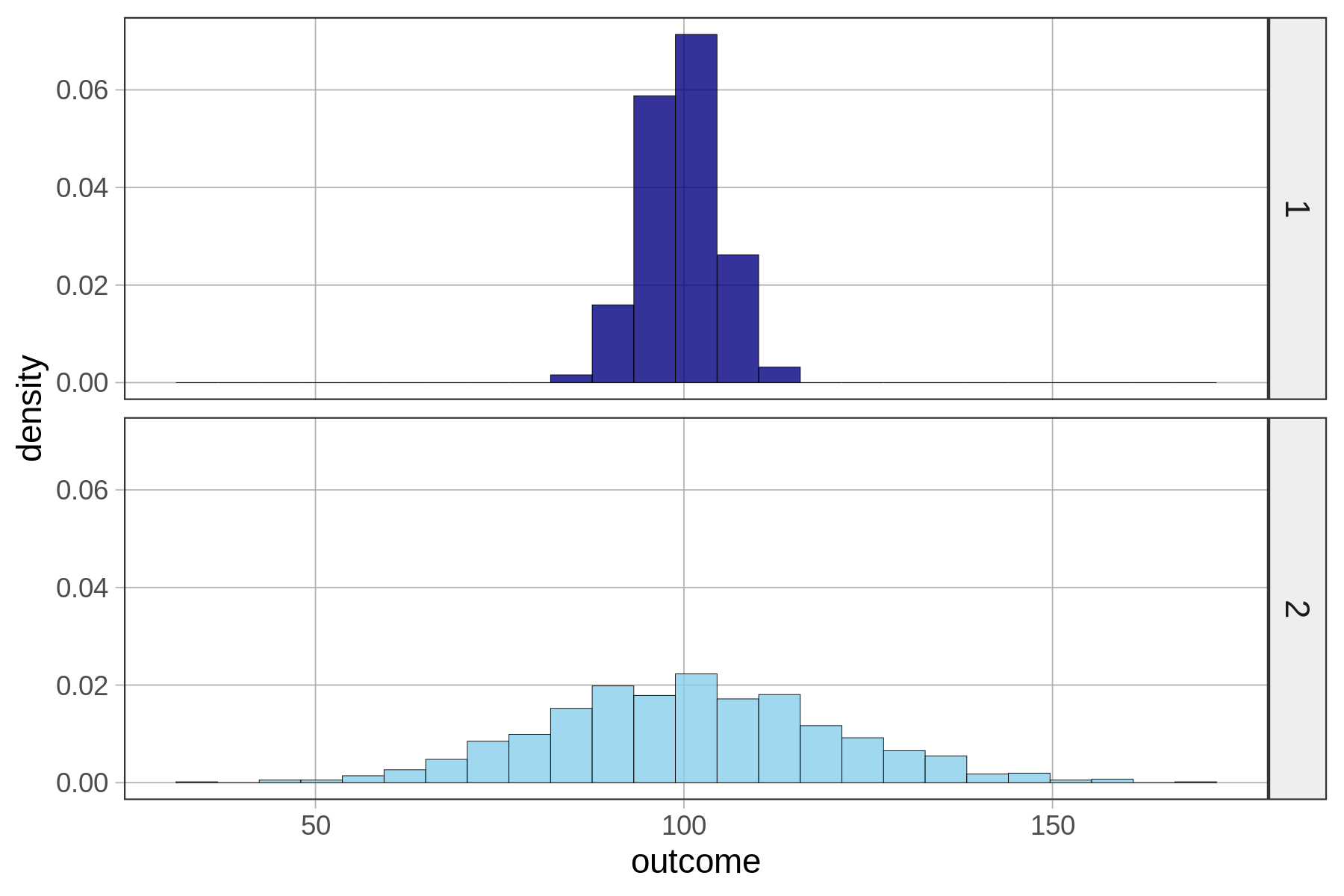
Ποια τιμή θα επιλέγατε ως το καλύτερο μοντέλο για την κατανομή 1 (με το σκούρο μπλε) και γιατί;

Ποια τιμή θα επιλέγατε ως το καλύτερο μοντέλο για την κατανομή 2 (με το γαλάζιο) και γιατί;

Σε ποια κατανομή (1 ή 2) προσαρμόζεται το μοντέλο καλύτερα στα δεδομένα; Γιατι;

Ένας μόνο αριθμός—ακόμα και ένας καλά επιλεγμένος αριθμός—δεν είναι ένα πολύ καλό μοντέλο. Μπορεί να είναι ένα καλύτερο μοντέλο για τη μεταβλητή 1 από ό,τι για τη μεταβλητή 2 παραπάνω, αλλά εξακολουθεί να μην είναι πολύ καλό. Οι περισσότερες τιμές δεν είναι ίδιες με την τιμή που επιλέγουμε ως μοντέλο.

Κάτι που μας φέρνει σε μια άλλη σημαντική έννοια: αφού επιλέξουμε έναν αριθμό για να μοντελοποιήσουμε μια κατανομή (και θα μιλήσουμε σύντομα για το πώς το κάνουμε αυτό), μπορούμε να σκεφτούμε τη μεταβλητότητα γύρω από αυτόν τον αριθμό ως σφάλμα, ακριβώς όπως θεωρήσαμε τα μέρη του Ν. Καβάλας που δεν καλύπτονταν από τα γεωμετρικά σχήματα ως σφάλμα.

Αν χρησιμοποιήσουμε μία μόνο τιμή για να μοντελοποιήσουμε την κατανομή μιας ποσοτικής μεταβλητής, το σφάλμα από το μοντέλο μπορεί να θεωρηθεί ως η απόκλιση των παρατηρούμενων τιμών από αυτήν την τιμή πρόβλεψης. Όπως μόλις είδαμε, ένα μοντέλο μιας τιμής για μια κατανομή με μικρότερη διασπορά φαίνεται να έχει λιγότερο σφάλμα, και επομένως καλύτερη προσαρμογή, από ένα μοντέλο μιας τιμής για μια κατανομή με μεγαλύτερη διασπορά. Ο λόγος για αυτό είναι ότι το σφάλμα γύρω από το μοντέλο είναι μεγαλύτερο για την κατανομή με μεγαλύτερη διασπορά.

Η ιδέα της μοντελοποίησης μιας κατανομής με έναν μόνο αριθμό μας δίνει έναν πιο συγκεκριμένο και λεπτομερή τρόπο σκέψης για τα μοντέλα μας. Ενώ σκεφτόμασταν το παράδειγμα του Ν. Καβάλας ως εξής:

Εμβαδόν του Ν. Καβάλας = Εμβαδόν Γεωμετρικών Σχημάτων + Σφάλμα

Μπορούμε να σκεφτούμε ένα στατιστικό μοντέλο ως εξής:

ΔΕΔΟΜΕΝΑ = ΜΟΝΤΕΛΟ + ΣΦΑΛΜΑ

Κάθε παρατήρηση σε μια κατανομή μπορεί να αναλυθεί σε δύο μέρη: το μοντέλο (δηλαδή, τον αριθμό που χρησιμοποιούμε για να αντιπροσωπεύσουμε ολόκληρη την κατανομή), και την απόκλιση της παρατήρησης από το μοντέλο (το σφάλμα).

6.3 Η Διάμεσος έναντι του Μέσου Όρου ως Μοντέλο

Αφού αναπτύξαμε την ιδέα ότι ένας μόνο αριθμός μπορεί να χρησιμεύσει ως στατιστικό μοντέλο για μια κατανομή, τώρα ρωτάμε: ποιον μοναδικό αριθμό πρέπει να επιλέξουμε; Συζητούσαμε προηγουμένως για την επιλογή ενός αριθμού στο κέντρο μιας συμμετρικής, κανονικής κατανομής. Αλλά τώρα θέλουμε να γίνουμε πιο συγκεκριμένοι.

Θυμηθείτε ότι στην προηγούμενη ενότητα ορίσαμε ένα στατιστικό μοντέλο ως μια συνάρτηση που παράγει μια τιμή πρόβλεψης για κάθε παρατήρηση. Με βάση αυτόν τον ορισμό, μπορούμε τώρα να ρωτήσουμε: ποια συνάρτηση θα μπορούσαμε να χρησιμοποιήσουμε που θα παράγει την ίδια τιμή πρόβλεψης για όλες τις παρατηρήσεις σε μια κατανομή;

Διάμεσος και Μέσος Όρος: Δύο Πιθανές Συναρτήσεις για τη Δημιουργία Προβλέψεων Μοντέλου

Αν προσπαθούσαμε να επιλέξουμε έναν αριθμό για να μοντελοποιήσουμε την κατανομή μιας ποιοτικής μεταβλητής, θα έπρεπε να επιλέξουμε την επικρατούσα τιμή· πραγματικά, δεν υπάρχουν αρκετές επιλογές στην περίπτωση αυτή. Αν πρόκειται να προβλέψετε την τιμή μιας νέας παρατήρησης σε μια ποιοτική μεταβλητή, η πρόβλεψη θα πρέπει να είναι μία από τις κατηγορίες και αναμένεται να κάνετε λάθος λιγότερες φορές αν επιλέξετε την κατηγορία που παρατηρείται πιο συχνά.

Για μια ποσοτική μεταβλητή, οι στατιστικολόγοι συνήθως επιλέγουν ή τη διάμεσο ή τον αριθμητικό μέσο όρο. Η διάμεσος είναι απλώς η μεσαία τιμή μιας κατανομής. Ας πάρουμε για παράδειγμα την ακόλουθη κατανομή πέντε αριθμών:

\(5, 5, 5, 10, 20\)

Η διάμεσος είναι 5, που σημαίνει ότι αν βάλετε όλους τους αριθμούς σε αύξουσα σειρά, ο αριθμός στη μέση είναι το 5. Μπορείτε να δείτε ότι η διάμεσος δεν επηρεάζεται από ακραίες τιμές. Έτσι, αν αλλάζατε το 20 σε αυτή την κατανομή σε 20.000, η διάμεσος θα εξακολουθούσε να είναι το 5. (Αν υπάρχει άρτιος αριθμός τιμών, η διάμεσος υπολογίζεται ως ο μέσος όρος των δύο μεσαίων τιμών.)

Για να υπολογίσουμε τον αριθμητικό μέσο όρο αυτής της κατανομής, απλώς προσθέτουμε όλους τους αριθμούς στο δείγμα, και στη συνέχεια διαιρούμε με το μέγεθος του δείγματος, που είναι 5. Έτσι, ο μέσος όρος αυτής της κατανομής είναι 9. Τόσο ο μέσος όρος όσο και η διάμεσος είναι δείκτες του πού βρίσκεται το κέντρο της κατανομής, αλλά ορίζουν το «κέντρο» με διαφορετικούς τρόπους: το 5 και το 9 αντιπροσωπεύουν πολύ διαφορετικά σημεία σε αυτή την κατανομή.

Στην R, αυτά και άλλα στατιστικά είναι πολύ εύκολο να υπολογιστούν με τη συνάρτηση favstats(). Δημιουργήστε μια μεταβλητή που ονομάζεται outcome και αναθέστε τις τιμές: \(5, 5, 5, 10, 20\). Στη συνέχεια, εκτελέστε τη συνάρτηση favstats() στη μεταβλητή outcome.

Αν ο στόχος μας είναι απλώς να αντιπροσωπεύσουμε μια κατανομή με μία μόνο τιμή, μερικές φορές η διάμεσος είναι καλύτερη, και μερικές φορές ο μέσος όρος είναι καλύτερος.

Για την απλή κατανομή που συζητήσαμε παραπάνω (\(5, 5, 5, 10, 20\)), θα μπορούσαμε να βρούμε λόγους για να προτιμήσουμε τόσο τη διάμεσο όσο και το μέσο όρο. Με ποια έννοια θα μπορούσε η διάμεσος να είναι καλύτερο μοντέλο για αυτήν την κατανομή; Με ποια έννοια θα μπορούσε ο μέσος όρος να είναι καλύτερο μοντέλο;

Αν προσπαθείτε να επιλέξετε μία τιμή που θα προέβλεπε καλύτερα ποια θα μπορούσε να είναι η επόμενη τυχαία επιλεγμένη τιμή, η διάμεσος θα μπορούσε κάλλιστα να είναι καλύτερη από τον μέσο όρο για αυτή την κατανομή. Με μόνο πέντε τιμές, το γεγονός ότι τρεις από αυτές είναι το 5 μας οδηγεί να πιστεύουμε ότι η επόμενη τιμή θα μπορούσε να είναι επίσης το 5.

Από την άλλη πλευρά, δεν γνωρίζουμε τίποτα για τη Διαδικασία Παραγωγής Δεδομένων για αυτές τις τιμές. Το γεγονός ότι υπάρχουν μόνο πέντε τιμές υποδεικνύει ότι αυτή η κατανομή πιθανώς δεν είναι μια καλή αναπαράσταση της υποκείμενης κατανομής του πληθυσμού. Ο πληθυσμός θα μπορούσε να είναι κανονικός, ή ομοιόμορφος, οπότε ο μέσος όρος θα ήταν ένα καλύτερο μοντέλο από τη διάμεσο. Το θέμα είναι ότι απλώς δεν μπορούμε να ξέρουμε.

Αναγνωρίζοντας αυτόν τον περιορισμό, εξετάζουμε παρακάτω τις κατανομές αρκετών ποσοτικών μεταβλητών. Για κάθε μεταβλητή, δημιουργήστε ένα ιστόγραμμα και υπολογίστε τα favstats(). Στη συνέχεια αποφασίστε ποια τιμή πιστεύετε ότι θα ήταν ένα καλύτερο μοντέλο για την κατανομή – η διάμεσος ή ο μέσος όρος.

Μεταβλητή 1: Βαθμολογία Φοιτητών στο πλαίσιο δεδομένων Fingers

Σημειώστε ότι υπάρχουν δύο τρόποι να ζητήσετε από την favstats() ή την gf_histogram() να ανακτήσουν μια μεταβλητή που βρίσκεται μέσα σε ένα πλαίσιο δεδομένων: με τη χρήση του $ ως εξής: favstats(Fingers$GradePredict)· ή με τη χρήση ενός συνδυασμού των ~ και data = ως εξής: favstats(~ GradePredict, data = Fingers). Προτιμούμε να χρησιμοποιούμε τη δεύτερη εκδοχή με το σύμβολο tilde (~) επειδή ταιριάζει καλύτερα με άλλες συναρτήσεις που θα μάθουμε.

Σχήμα 6.11

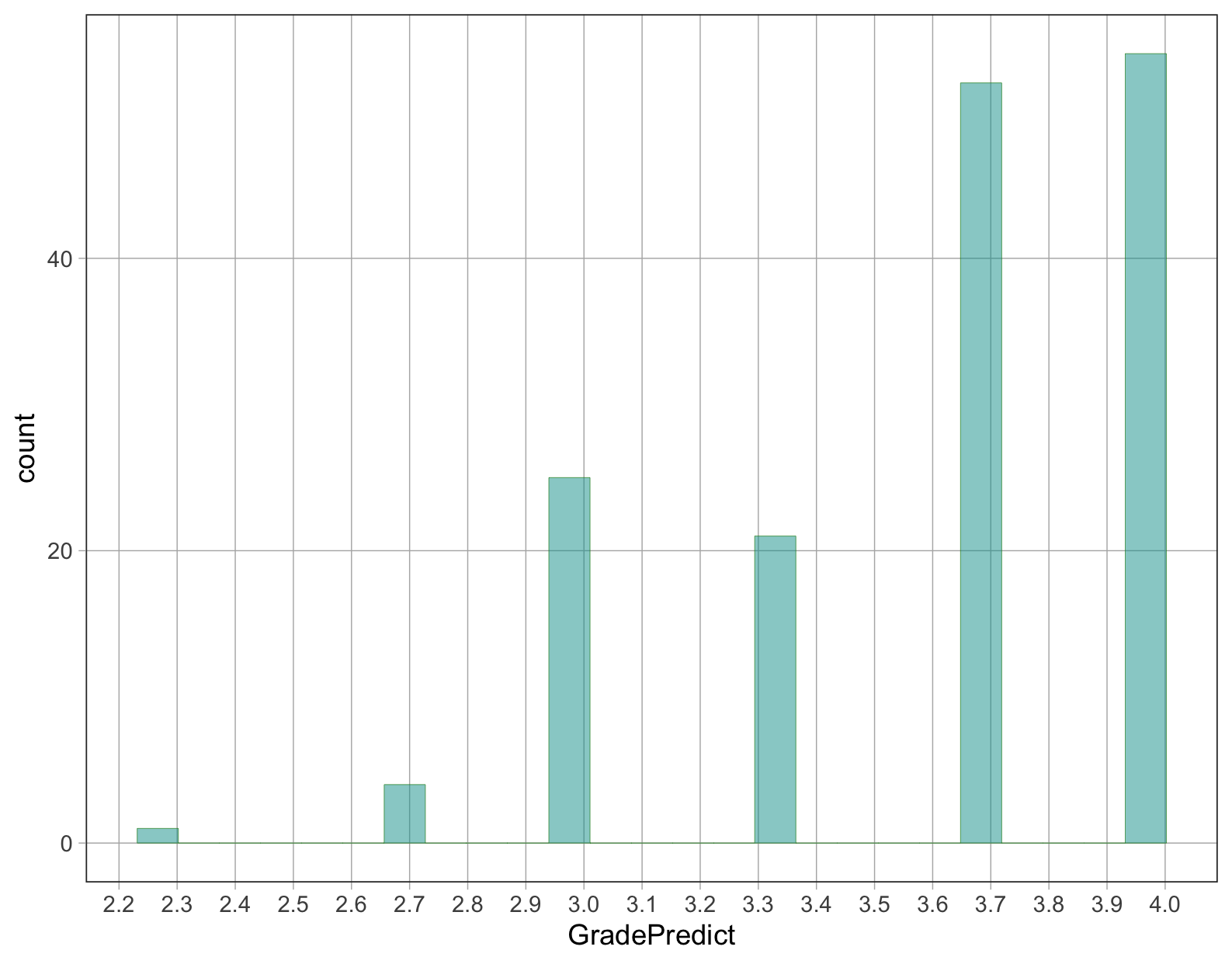
Ποια τιμή θεωρείτε ότι είναι καλύτερο μοντέλο, η διάμεσος ή ο μέσος όρος;

Μεταβλητή 2: Μήκη Αντίχειρα στο πλαίσιο δεδομένων Fingers

Σχήμα 6.12

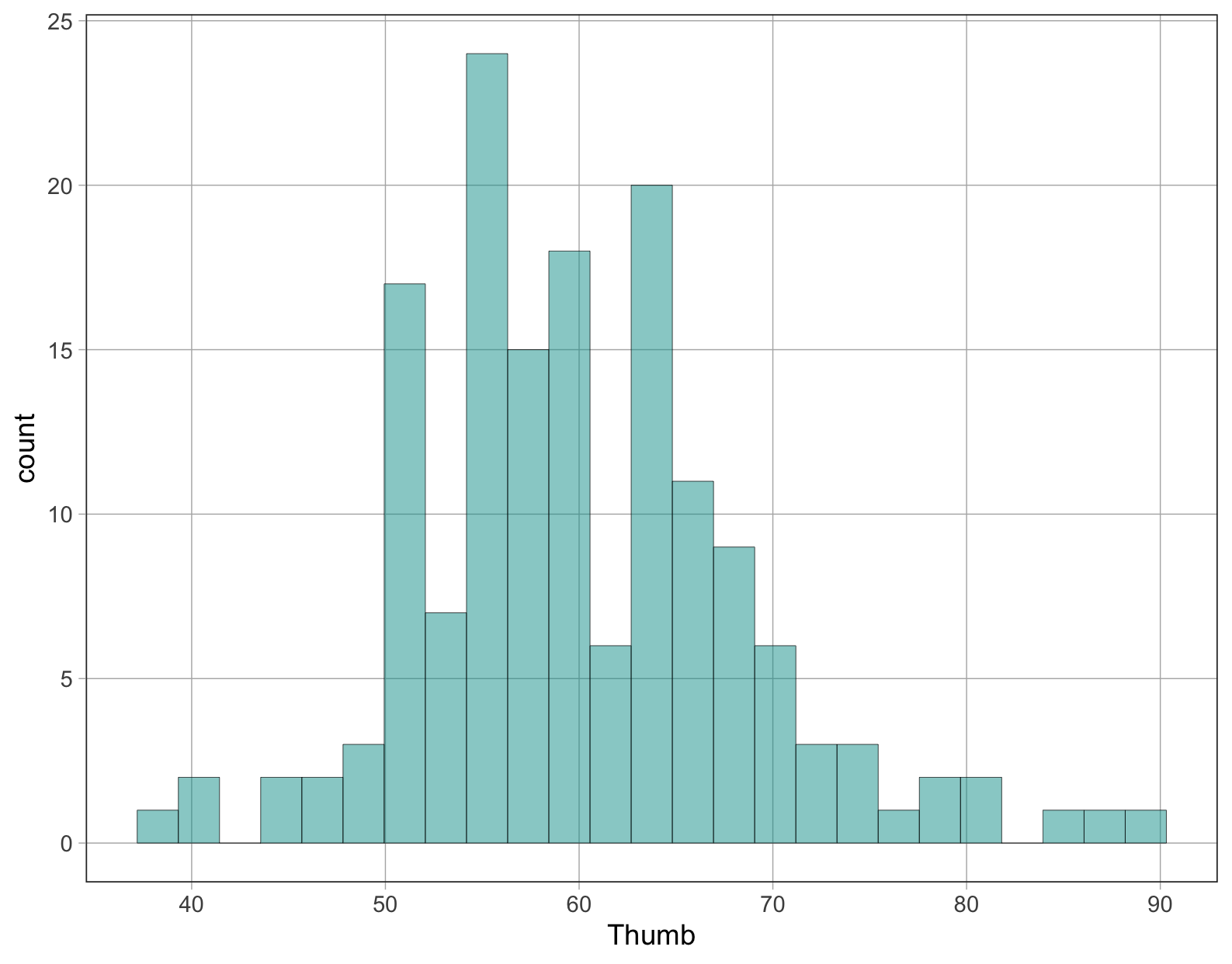
Ποια τιμή θεωρείτε ότι είναι καλύτερο μοντέλο, η διάμεσος ή ο μέσος όρος;

Μεταβλητή 3: Ηλικία φοιτητών στο πλαίσιο δεδομένων TeachingMethods

Σχήμα 6.13

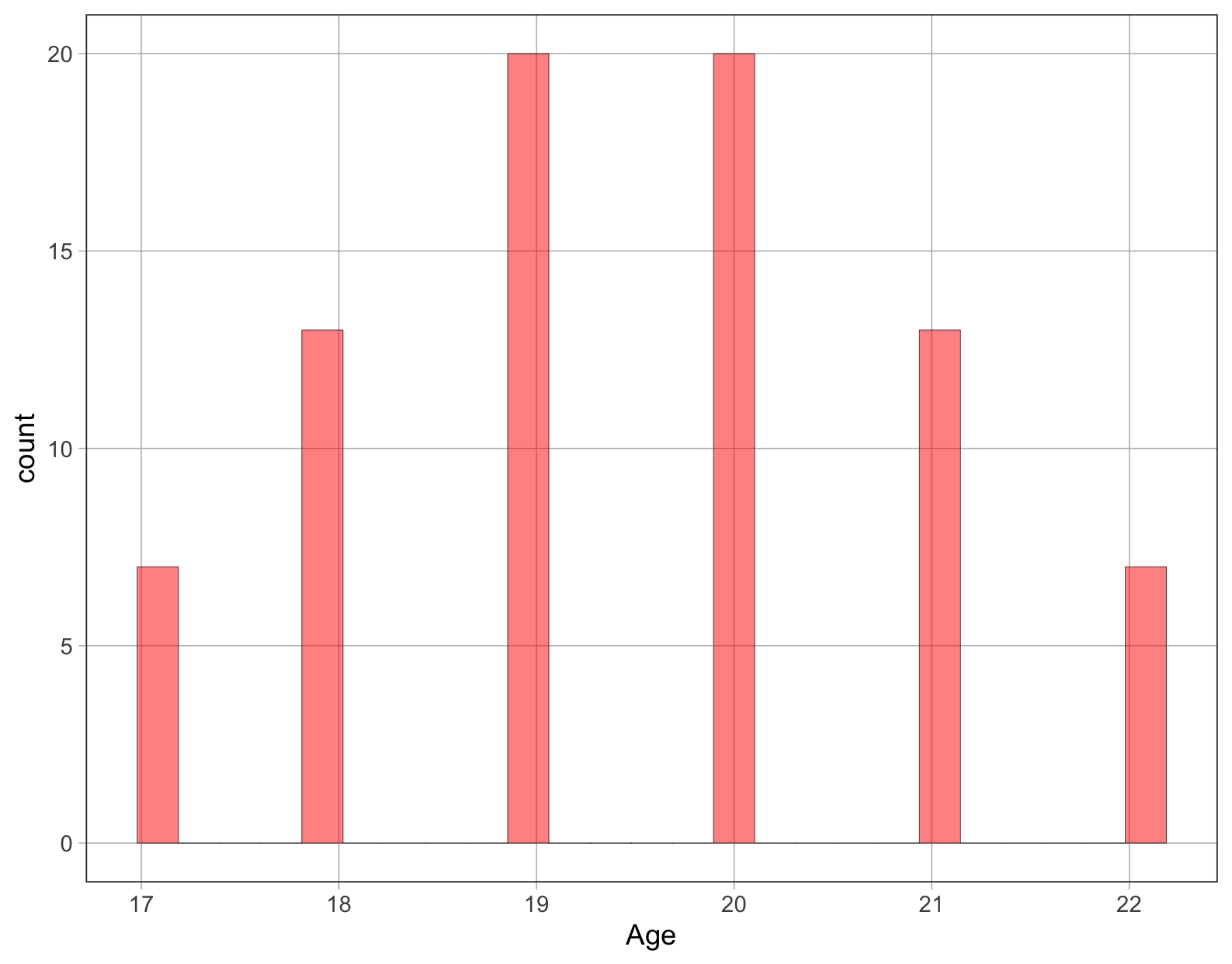
Ποια τιμή θεωρείτε ότι είναι καλύτερο μοντέλο, η διάμεσος ή ο μέσος όρος;

Γενικά, όταν η κατανομή είναι ασύμμετρη προς τη μία ή την άλλη κατεύθυνση η διάμεσος συνήθως είναι μια πιο ουσιαστική σύνοψη μιας κατανομής σε σχέση με τον μέσο όρο. Κατ’ αυτόν τον τρόπο, μειώνεται η σημασία της ουράς της κατανομής, εστιάζοντας περισσότερο στο μέρος της κατανομής όπου βρίσκονται οι περισσότερες τιμές. Ο μέσος όρος είναι μια καλή σύνοψη όταν η κατανομή είναι πιο συμμετρική.

Αλλά, αν ο στόχος μας είναι να δημιουργήσουμε ένα στατιστικό μοντέλο της κατανομής του πληθυσμού, σχεδόν πάντα—ειδικά σε αυτό το μάθημα—θα χρησιμοποιούμε τον μέσο όρο. Θα εμβαθύνουμε λίγο για να δούμε το γιατί. Αλλά πρώτα, μια σύντομη παράκαμψη για να δούμε πώς μπορούμε να προβάλλουμε τη διάμεσο και τον μέσο όρο σε ένα ιστόγραμμα.

Προβολή Διαμέσου και Μέσου Όρου σε Ιστογράμματα

Γνωρίζετε ήδη τον τρόπο να δημιουργήσετε ένα ιστόγραμμα. Ας προσθέσουμε μια κάθετη γραμμή για να δείξουμε πού βρίσκεται ο μέσος όρος. Γνωρίζουμε από τα favstats() ότι ο μέσος όρος είναι 9, οπότε μπορούμε απλώς να προσθέσουμε μια κάθετη γραμμή που διασταυρώνει τον άξονα x στο 9. Ας τη χρωματίσουμε μπλε.

Δοκιμάστε να τροποποιήσετε αυτόν τον κώδικα για να σχεδιάσετε μια μωβ γραμμή για τη διάμεσο αυτού του μικρού συνόλου αριθμών. (Η διάμεσος είναι 5.)

Μπορείτε να συνδέσετε αυτές τις εντολές (με τη χρήση του τελεστή %>%) για να προβάλλετε και τις δύο γραμμές μέσου όρου και διαμέσου στο ίδιο ιστόγραμμα. (Αυτή τη φορά, χρησιμοποιήσαμε τις συναρτήσεις mean() και median() αντί να πληκτρολογούμε τις πραγματικές τιμές.)

gf_histogram(~ outcome) %>%
  gf_vline(xintercept = mean(outcome), color = "blue") %>%
  gf_vline(xintercept = median(outcome), color = "purple")

Σημειώστε ότι υπάρχει μια σχετική συνάρτηση που ονομάζεται gf_hline(), η οποία σχεδιάζει μια οριζόντια γραμμή σε ένα διάγραμμα (δέχεται ως παράμετρο την yintercept).

6.4 Εξερευνώντας τον Μέσο Όρο

Είναι αρκετά εύκολο να κατανοήσουμε τι σημαίνει ότι η διάμεσος είναι η μεσαία τιμή μιας κατανομής, αλλά με ποια έννοια είναι ο μέσος όρος μια κεντρική τιμή; Ένας τρόπος να σκεφτούμε τον μέσο όρο είναι ως το σημείο ισορροπίας της κατανομής, το σημείο στο οποίο τα πράγματα πάνω από αυτό ισούνται με τα πράγματα κάτω από αυτό. Αλλά τι εξισορροπεί; Ποια είναι «τα πράγματα» που είναι ίσα και στις δύο πλευρές του μέσου όρου;

Μπορεί να σκεφτεί κανείς ότι «όσα είναι κάτω από τον μέσο όρο εξισορροπούνται με όσα είναι πάνω από αυτόν». Αλλά αυτό δεν ισχύει: αν έχουμε τις τιμές 5, 5, 5 κάτω από τον μέσο όρο και 10, 20 πάνω από αυτόν, τότε 5 + 5 + 5 = 15 δεν ισούται με 10 + 20 = 30. Δηλαδή, το άθροισμα των τιμών κάτω από τον μέσο όρο δεν ταιριάζει με το άθροισμα των τιμών πάνω από τον μέσο όρο.

Εδώ βοηθάει να σκεφτούμε την απόκλιση κάθε τιμής από τον μέσο όρο, η οποία θα είναι αρνητική για τιμές κάτω από τον μέσο όρο και θετική για τιμές πάνω από αυτόν. Στο παράδειγμά μας (5, 5, 5, 10, 20), καθεμιά από τις τιμές 5 βρίσκεται 4 μονάδες κάτω από τον μέσο όρο (9), δηλαδή απόκλιση -4. Αν το σκεφτείτε με αυτόν τον τρόπο, το άθροισμα των αποκλίσεων κάτω από τον μέσο όρο (-12) εξισορροπεί το άθροισμα των αποκλίσεων πάνω από τον μέσο όρο (+1 και +11, δηλαδή +12).

Θα αποκαλούμε επίσης αυτές τις διαφορές υπόλοιπα ή κατάλοιπα (residuals). Η λέξη απόκλιση (deviation) αναφέρεται συγκεκριμένα σε διαφορές πάνω και κάτω από τον μέσο όρο, αλλά υπόλοιπα πιο γενικά σημαίνει διαφορές πάνω και κάτω από οποιοδήποτε μοντέλο της κατανομής, το οποίο θα μπορούσε να είναι ο μέσος όρος, η διάμεσος, η επικρατούσα τιμή κ.λπ.

Σχήμα 6.14

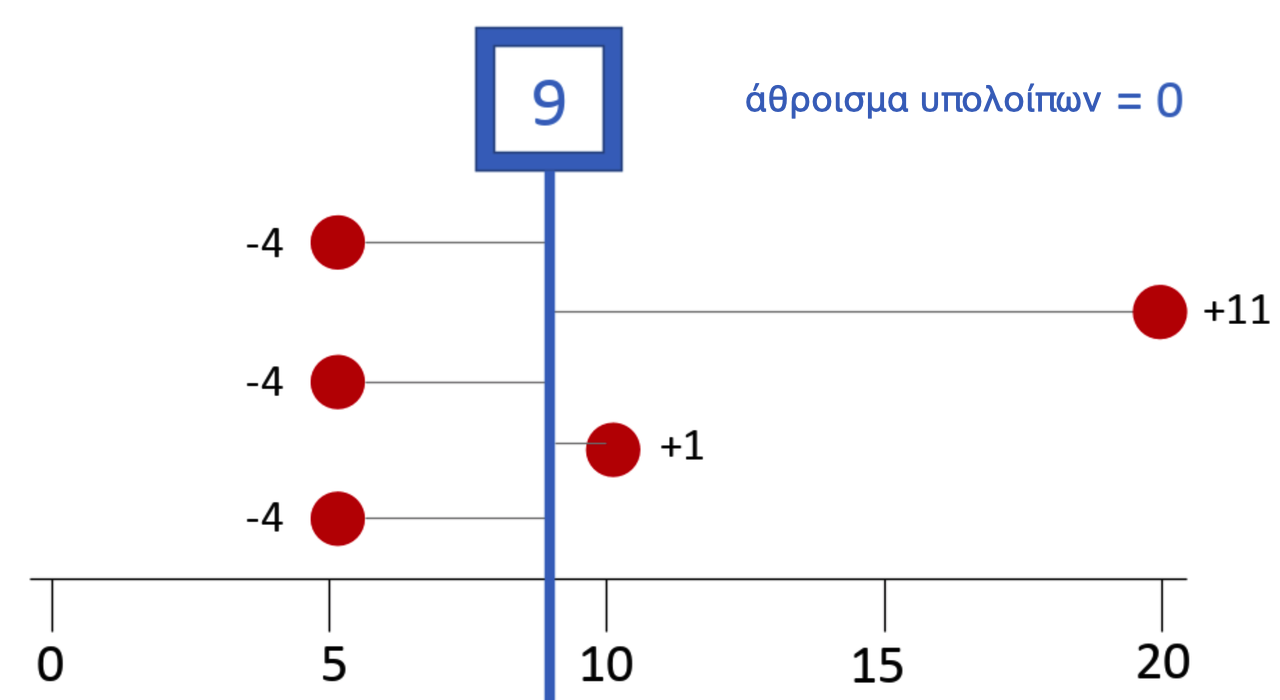
Αποδεικνύεται ότι κανένας άλλος αριθμός εκτός από τον μέσο όρο (ούτε το 8, ούτε το 8,5, ούτε το 9,1!) δεν θα εξισορροπήσει τέλεια τα υπόλοιπα πάνω από τον μέσο όρο με εκείνα κάτω από τον μέσο όρο. Ενώ το μέγεθος μιας τιμής—ειδικά μιας ακραίας τιμής—δεν θα επηρεάσει απαραίτητα τη διάμεσο, θα επηρεάσει τον μέσο όρο επειδή το μεγάλο υπόλοιπο από μια ακραία τιμή πρέπει να εξισορροπηθεί με τα υπόλοιπα από τις άλλες τιμές. Κάθε τιμή της κατανομής λαμβάνεται υπόψη κατά τον υπολογισμό του μέσου όρου.

Θυμηθείτε ότι μιλήσαμε για την εύρεση κάποιων απλών σχημάτων που «ταιριάζουν» καλύτερα στο πιο λεπτομερές σχήμα του Ν. Καβάλας; Θέλαμε να βρούμε σχήματα που δεν ήταν ούτε πολύ μεγάλα ούτε πολύ μικρά, σχήματα που θα ελαχιστοποιούσαν το σφάλμα γύρω από το μοντέλο, ορισμένο ως τα μέρη του Ν. Καβάλας που δεν καλύπτονταν από το μοντέλο, και τα μέρη του μοντέλου που κάλυπταν και πράγματα εκτός του Νομού.

Ο μέσος όρος είναι ένα μοντέλο που δεν είναι ούτε πολύ μεγάλο ούτε πολύ μικρό. Ο μέσος όρος τραβιέται και προς τις δύο κατευθύνσεις (μεγαλύτερη και μικρότερη) ταυτόχρονα και εγκαθίσταται ακριβώς στη μέση. Ο μέσος όρος είναι η τιμή που εξισορροπεί τα υπόλοιπα πάνω και κάτω από αυτόν, αποδίδοντας το ίδιο ποσό σφάλματος πάνω από αυτόν όσο και κάτω από αυτόν. Είναι ενδιαφέρον ότι αυτή η διαδικασία της πρόσθεσης όλων των τιμών και της διαίρεσης του αθροίσματος με το πλήθος των τιμών οδηγεί σε αυτό το σημείο ισορροπίας.

Το να σκεφτόμαστε τον μέσο όρο με αυτόν τον τρόπο μας βοηθάει επίσης να σκεφτούμε το ΔΕΔΟΜΕΝΑ = ΜΟΝΤΕΛΟ + ΣΦΑΛΜΑ με πιο συγκεκριμένο τρόπο. Αν ο μέσος όρος είναι το μοντέλο, κάθε τιμή μπορεί τώρα να θεωρηθεί ως το άθροισμα του μοντέλου (9 στη μεταβλητή μας outcome) συν το υπόλοιπό του από το μοντέλο. Έτσι το 20 μπορεί να αναλυθεί στο τμήμα του μοντέλου (9) και το σφάλμα από το μοντέλο (+11). Και το 5 μπορεί να αναλυθεί σε 9 (μοντέλο) και -4 (σφάλμα).

Τι σημαίνει ότι η διάμεσος είναι “η μεσαία τιμή” της κατανομής;

Αν όλες οι τιμές στην κατανομή είναι τοποθετημένες με αύξουσα σειρά, υπάρχει ίσος αριθμός παρατηρήσεων κάτω και πάνω από τη διάμεσο:

ΝαιΌχι

Αν όλες οι τιμές στην κατανομή είναι τοποθετημένες με αύξουσα σειρά, υπάρχει ίσος αριθμός μεταβλητών κάτω και πάνω από τη διάμεσο:

ΝαιΌχι

Το άθροισμα των τιμών κάτω από τη διάμεσο είναι ίσο με το άθροισμα των τιμών πάνω από τη διάμεσο:

ΝαιΌχι

Η διάμεσος εξισορροπεί το ποσό του σφάλματος κάτω και πάνω από αυτήν:

ΝαιΌχι

Οι αποκλίσεις πάνω και κάτω από τη διάμεσο πάντα αθροίζουν στο 0:

ΝαιΌχι

Επεξήγηση για τη Διάμεσο

Σωστές απαντήσεις: Α και Δ

Α - Ίσος αριθμός σημείων - ΣΩΣΤΟ: - Αυτός είναι ο ορισμός της διαμέσου - 50% κάτω, 50% πάνω

Β - Μεταβλητές - ΛΑΘΟΣ: - Δεν έχει νόημα

Γ - Άθροισμα τιμών - ΛΑΘΟΣ: - Παράδειγμα: {1,2,10,11,12} → διάμεσος=10, αθροίσματα: 3 vs 23

Δ - Εξισορρόπηση σφάλματος - ΣΩΣΤΟ: - Ελαχιστοποιεί Σ|xi - διάμεσος|

Ε - Αθροίζουν στο 0 - ΛΑΘΟΣ: - Αυτό ισχύει για το μέσο όρο

---

Τι σημαίνει ότι ο μέσος όρος είναι το “κέντρο” της κατανομής; (Επιλέξτε όλα όσα ισχύουν)

Αν όλες οι τιμές στην κατανομή είναι τοποθετημένες με αύξουσα σειρά, υπάρχει ίσος αριθμός παρατηρήσεων κάτω και πάνω από το μέσο όρο:

ΝαιΌχι

Αν όλες οι τιμές στην κατανομή είναι τοποθετημένες με αύξουσα σειρά, υπάρχει ίσος αριθμός μεταβλητών κάτω και πάνω από το μέσο όρο:

ΝαιΌχι

Το άθροισμα των τιμών κάτω από το μέσο όρο είναι ίσο με το άθροισμα των τιμών πάνω από το μέσο όρο:

ΝαιΌχι

Ο μέσος όρος εξισορροπεί το ποσό του σφάλματος κάτω και πάνω από αυτόν:

ΝαιΌχι

Οι αποκλίσεις κάτω και πάνω από το μέσο όρο πάντα αθροίζουν στο 0:

ΝαιΌχι

Επεξήγηση για το Μέσο Όρο

Σωστές απαντήσεις: Δ και Ε

Α - Ίσος αριθμός σημείων - ΛΑΘΟΣ: - Παράδειγμα: {1,2,3,100} → μέσος=26.5 - 3 κάτω, 1 πάνω

Β - Μεταβλητές - ΛΑΘΟΣ: - Δεν έχει νόημα

Γ - Άθροισμα τιμών - ΛΑΘΟΣ: - {1,2,7,8} → μέσος=4.5 - Κάτω: 3, Πάνω: 15

Δ - Εξισορρόπηση σφάλματος - ΣΩΣΤΟ: - Ελαχιστοποιεί το Σ(xi - μέσος όρος)²

Ε - Αποκλίσεις=0 - ΣΩΣΤΟ: - Θεμελιώδης ιδιότητα - Σ(xi - μέσος όρος) = 0 πάντα

6.5 Προσαρμογή του Κενού Μοντέλου

Αυτή η ενότητα μπορεί να σας φανεί υπερβολικά δύσκολη στην αρχή, αλλά θα αποτελέσει τη βάση για την κατανόηση νέων εννοιών. Το απλό μοντέλο με το οποίο ξεκινήσαμε—η χρήση του μέσου όρου για τη μοντελοποίηση της κατανομής μιας ποσοτικής μεταβλητής—ονομάζεται μερικές φορές και κενό μοντέλο ή μηδενικό μοντέλο. Στο πλαίσιο της μελέτης του μήκους αντίχειρα, θα μπορούσαμε να διατυπώσουμε το κενό μοντέλο με μια λεκτική εξίσωση όπως αυτή:

Μήκος αντίχειρα = Μέσος Όρος + Σφάλμα

Σημειώστε ότι το μοντέλο είναι «κενό» επειδή δεν περιέχει ακόμη καμία ανεξάρτητη μεταβλητή. Το κενό μοντέλο δεν εξηγεί κανένα μέρος της μεταβλητότητας· απλώς αποκαλύπτει τη μεταβλητότητα της εξαρτημένης μεταβλητής (το Σφάλμα) που θα μπορούσε δυνητικά να εξηγηθεί από άλλες μεταβλητές. Αυτό το κενό μοντέλο θα χρησιμεύσει ως ένα είδος μοντέλου αναφοράς με το οποίο μπορούμε να συγκρίνουμε πιο πολύπλοκα μοντέλα στη συνέχεια.

Αν ο μέσος όρος είναι το μοντέλο μας, τότε η προσαρμογή του μοντέλου στα δεδομένα σημαίνει απλώς τον υπολογισμό του μέσου όρου της κατανομής, κάτι που θα μπορούσαμε να κάνουμε με τη χρήση της favstats().

favstats(~ Thumb, data = Fingers) 
min Q1 median Q3 max     mean       sd   n missing
 39 55     60 65  90 60.10366 8.726695 157       0

Γιατί ο μέσος όρος είναι μια λογική τιμή πρόβλεψης του μήκους του αντίχειρα ενός φοιτητή;

Όταν προσαρμόζουμε ένα μοντέλο βρίσκουμε τον συγκεκριμένο αριθμό που ελαχιστοποιεί περισσότερο το σφάλμα· αυτό εννοούμε με τη φράση «καλύτερα προσαρμοσμένο μοντέλο» (best-fitting model). Ο μέσος όρος μιας κατανομής είναι αυτός ο αριθμός επειδή εξισορροπεί τα σφάλματα (υπόλοιπα). Σε επόμενα κεφάλαια, θα συζητήσουμε περισσότερο γιατί η τιμή του μέσου όρου είναι η καλύτερα προσαρμοσμένη τιμή.

Είναι εύκολο, λοιπόν, να προσαρμόσουμε το κενό μοντέλο στα δεδομένα—είναι απλώς ο μέσος όρος (60,1 σε αυτήν την περίπτωση). Αλλά αργότερα θα μάθετε να προσαρμόζετε πιο πολύπλοκα μοντέλα στα δεδομένα σας. Θα μάθετε έναν τρόπο προσαρμογής μοντέλων στην R που μπορείτε να χρησιμοποιήσετε τώρα για την προσαρμογή του κενού μοντέλου, αλλά που θα λειτουργεί επίσης αργότερα για την προσαρμογή πιο πολύπλοκων μοντέλων.

Η συνάρτηση της R που θα χρησιμοποιήσουμε είναι η lm(), που σημαίνει «γραμμικό μοντέλο» (linear model). (Θα πούμε περισσότερα για το γιατί λέγεται έτσι σε επόμενο κεφάλαιο.) Παρακάτω δίνεται ο κώδικας που χρησιμοποιούμε για να προσαρμόσουμε το κενό μοντέλο, ακολουθούμενος από το αποτέλεσμα.

lm(Thumb ~ NULL, data = Fingers) 

Call:
lm(formula = Thumb ~ NULL, data = Fingers)

Coefficients:
(Intercept)
       60.1

Αν και το αποτέλεσμα μπορεί να φαίνεται λίγο περίεργο, με όρους όπως “Coefficients” (Συντελεστές) και “Intercept” (Σταθερός Όρος), η συνάρτηση lm() επιστρέφει τελικά τον μέσο όρο της κατανομής (60.1), όπως περιμέναμε. Με αυτόν τον τρόπο, η lm() «προσαρμόζει» το κενό μοντέλο στα δεδομένα, βρίσκοντας την καλύτερα προσαρμοσμένη τιμή για το μοντέλο μας. Η λέξη "NULL" απλώς δηλώνει το «κενό» (όπως στο «κενό μοντέλο»).

Είναι χρήσιμο να αποθηκεύουμε τα αποτελέσματα μιας προσαρμογής μοντέλου σε ένα αντικείμενο της R. Στο παρακάτω παράδειγμα, χρησιμοποιούμε τη συνάρτηση lm() για να προσαρμόσουμε το κενό μοντέλο και αποθηκεύουμε τα αποτελέσματα σε ένα αντικείμενο που ονομάζεται empty_model:

empty_model <- lm(Thumb ~ NULL, data = Fingers)

Αν θέλετε να δείτε τα περιεχόμενα του μοντέλου, μπορείτε απλώς να πληκτρολογήσετε το όνομα του αντικειμένου της R όπου το αποθηκεύσατε (δηλαδή, empty_model). Δοκιμάστε το παρακάτω.

Όταν αποθηκεύουμε το αποτέλεσμα της lm() στο empty_model, δημιουργούμε ένα νέο τύπο αντικειμένου στην R, το οποίο ονομάζεται model (μοντέλο) και διαφέρει από τα πλαίσια δεδομένων (data frames) ή τα διανύσματα (vectors). Ένα αντικείμενο μοντέλου περιέχει πληροφορίες σχετικά με την ανάλυση, τις οποίες δεν θα εξετάσουμε λεπτομερώς εδώ, αλλά ορισμένες συναρτήσεις που θα δούμε στη συνέχεια απαιτούν ως είσοδο συγκεκριμένα αντικείμενα τύπου μοντέλου.

Μία τέτοια συνάρτηση είναι η gf_model(), η οποία μας επιτρέπει να προβάλλουμε ένα μοντέλο (π.χ., το empty_model) επάνω σε διαφορετικά είδη διαγραμμάτων, συμπεριλαμβανομένων ιστογραμμάτων, boxplot, και διαγραμμάτων διασποράς.

Για παράδειγμα, δείτε πώς μπορείτε να προβάλετε τις τιμές πρόβλεψης του empty_model στο ιστόγραμμα μήκους αντίχειρα χρησιμοποιώντας τον τελεστή διοχέτευσης %>%.

gf_histogram(~ Thumb, data = Fingers) %>%
gf_model(empty_model)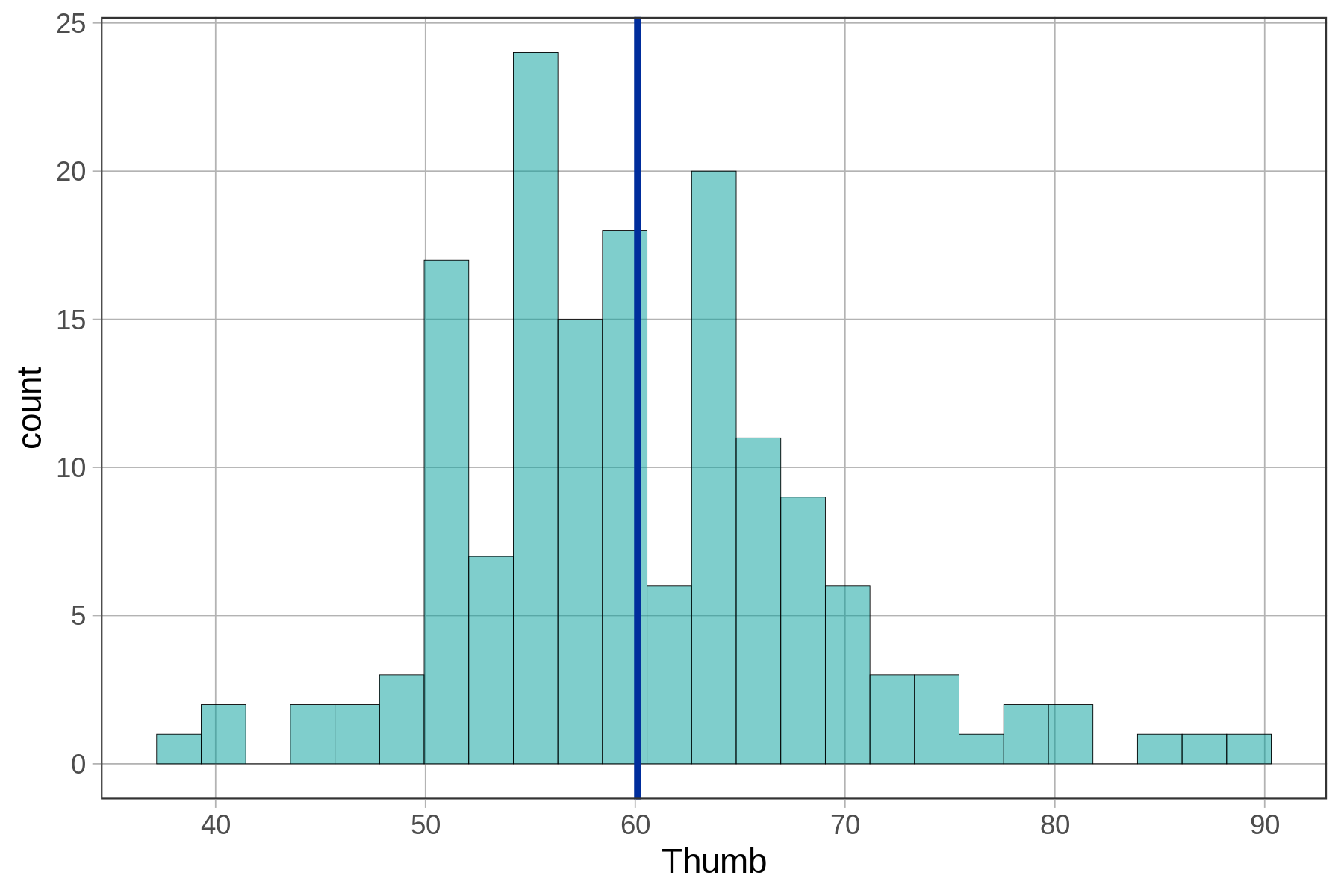

Σχήμα 6.15

Όπως γνωρίζουμε, το κενό μοντέλο προβλέπει για όλους τον μέσο όρο του μήκους αντίχειρα. Η πρόβλεψη αυτή απεικονίζεται με την ενιαία μπλε κατακόρυφη γραμμή στο 60.1 mm, που αντιστοιχεί στον μέσο όρο. Θα χρησιμοποιήσουμε την gf_model(empty_model) και σε άλλα διαγράμματα παρακάτω.

Αν προβάλλουμε το κενό μοντέλο του μήκους αντίχειρα σε ένα διάγραμμα διασποράς με το μήκος αντίχειρα (Thumb) στον άξονα y και το ύψος (Height) στον άξονα x, ποιο από τα παρακάτω θα συμβεί;

Το κενό μοντέλο θα εμφανιστεί ως μια κάθετη γραμμήΤο κενό μοντέλο θα εμφανιστεί ως μια οριζόντια γραμμήΤο κενό μοντέλο θα εμφανιστεί ως ένα σημείο

Επεξήγηση

Το κενό μοντέλο θα εμφανιστεί ως μια οριζόντια γραμμή είναι η σωστή απάντηση.

Τι είναι το κενό μοντέλο (empty model):

Το κενό μοντέλο είναι η απλούστερη πρόβλεψη που μπορούμε να κάνουμε:

μήκος αντίχειρα = μέσος όρος + σφάλμα

Όπου: - Καμία ανεξάρτητη μεταβλητή (όπως η Height) δεν χρησιμοποιείται στο μοντέλο - Προβλέπουμε την ίδια τιμή για όλους (τον μέσο όρο)

Γιατί είναι οριζόντια γραμμή:

Σε ένα διάγραμμα διασπορά με: - Άξονας x: Height (ύψος) - Άξονας y: Thumb (μήκος αντίχειρα)

Το κενό μοντέλο μας πληροφορεί: “Ανεξάρτητα από το ύψος σου (x), προβλέπω ότι το μήκος του αντίχειρά σου θα είναι ο μέσος όρος”

Αυτό σημαίνει: - Για κάθε τιμή του x (ύψος) - Η πρόβλεψη y (μήκος αντίχειρα) είναι η ίδια (mean(Thumb)) - Άρα η γραμμή είναι οριζόντια στο ύψος mean(Thumb)

Οπτική αναπαράσταση:

Thumb (y)
    ↑
    │
 70 │     ●        ●
    │          ●
 60 ├─────────────────────── ← Οριζόντια γραμμή (mean)
    │   ●            ●
 50 │        ●
    │
    └────────────────────→ Height (x)

Γιατί οι άλλες επιλογές είναι λάθος:

Α - Κάθετη γραμμή - ΛΑΘΟΣ: - Μια κάθετη γραμμή θα ήταν: x = σταθερά - Αυτό θα σήμαινε “για ένα συγκεκριμένο ύψος, όλες οι τιμές μήκους αντίχειρα” - Δεν είναι το κενό μοντέλο

Γ - Ένα σημείο - ΛΑΘΟΣ: - Ένα σημείο θα σήμαινε μία μόνο παρατήρηση - Το μοντέλο είναι μια πρόβλεψη για όλες τις τιμές x - Άρα είναι γραμμή, όχι σημείο

Μαθηματική εξήγηση:

Εξίσωση κενού μοντέλου:

ŷ = mean(Thumb)

Παράδειγμα: Αν mean(Thumb) = 60mm, τότε: - Για Height = 150cm → Πρόβλεψη Thumb = 60mm - Για Height = 160cm → Πρόβλεψη Thumb = 60mm - Για Height = 170cm → Πρόβλεψη Thumb = 60mm - Για Height = 180cm → Πρόβλεψη Thumb = 60mm

Όλες οι προβλέψεις στο ίδιο y → οριζόντια γραμμή

Πρακτική σημασία:

Η οριζόντια γραμμή του κενού μοντέλου: - Αντιπροσωπεύει τη βασική πρόβλεψη χωρίς να χρησιμοποιούμε πληροφορία - Είναι το μοντέλο αναφοράς για σύγκριση με πιο σύνθετα μοντέλα

Πότε χρησιμοποιούμε κενό μοντέλο: - Ως αρχική πρόβλεψη - Για σύγκριση με πιο πολύπλοκα μοντέλα - Όταν δεν έχουμε ανεξάρτητες μεταβλητές - Για να υπολογίσουμε το συνολικό σφάλμα (βλ. επόμενα κεφάλαια)

Δοκιμάστε να εκτελέσετε τον παρακάτω κώδικα και παρατηρήστε τα διαγράμματα που προκύπτουν. Στη συνέχεια χρησιμοποιούμε τον τελεστή διοχέτευσης (%>%) για να προβάλουμε την πρόβλεψη του κενού μοντέλου τόσο στο διάγραμμα διασποράς του μήκου αντίχειρα ανά ύψος όσο και στο διάγραμμα jitter του μήκους αντίχειρα ανά φύλο. (Το κενό μοντέλο έχει ήδη προσαρμοστεί στα δεδομένα και αποθηκευτεί ως empty_model.)

Στο ιστόγραμμα του μήκους του αντίχειρα, όπου η μεταβλητή Thumb βρίσκεται στον άξονα x, η πρόβλεψη του κενού μοντέλου εμφανίζεται ως μια κατακόρυφη γραμμή. Αντίθετα, στα διαγράμματα διασποράς και jitter, η μεταβλητή Thumb τοποθετείται στον άξονα y, με αποτέλεσμα η πρόβλεψη του κενού μοντέλου (δηλαδή, ο μέσος όρος της Thumb) να απεικονίζεται ως μια οριζόντια γραμμή στο 60.1 mm.

Αυτή η οριζόντια γραμμή στα παραπάνω διαγράμματα δείχνει ότι, σύμφωνα με το κενό μοντέλο, το προβλεπόμενο μήκος του αντίχειρα για κάθε φοιτητή παραμένει σταθερό (60.1 mm), ανεξάρτητα από το ύψος του.

Ο Μέσος Όρος ως Αμερόληπτος Εκτιμητής

Αν σας φαίνεται ότι δίνουμε μεγάλη σημασία στον υπολογισμό του μέσου όρου, έχετε δίκιο! Ο μέσος όρος είναι μια έννοια που θα εμφανίζεται συνεχώς σε αυτό το μάθημα και η κατανόησή σας για αυτόν και τις χρήσεις του θα βελτιώνεται με την πάροδο του χρόνου. Ένα κρίσιμο σημείο που πρέπει να τονίσουμε από τώρα είναι ότι ο απώτερος στόχος της στατιστικής είναι η κατανόηση της Διαδικασίας Παραγωγής Δεδομένων (ΔΠΔ). Σε αυτό το πλαίσιο, ο μέσος όρος του δείγματός μας είναι μια εκτίμηση του μέσου όρου του πληθυσμού που προκύπτει από τη ΔΠΔ. Αυτός ακριβώς είναι ο λόγος για τον οποίο οι τιμές που επιστρέφει η lm() ονομάζονται «εκτιμητές» ή «συντελεστές».

Φυσικά, ο μέσος όρος ενός δείγματος μπορεί να μην είναι μια τέλεια εκτίμηση — εξάλλου, βασίζεται σε έναν πεπερασμένο αριθμό παρατηρήσεων. Ωστόσο, είναι η καλύτερη δυνατή που έχουμε με βάση τα διαθέσιμα δεδομένα. Μια σημαντική ιδιότητά του είναι ότι είναι ένας αμερόληπτος εκτιμητής (unbiased estimator): αυτό σημαίνει ότι δεν έχει συστηματική τάση να υπερ- ή να υποεκτιμά την πραγματική τιμή του πληθυσμού, καθώς οι τυχαίες αποκλίσεις προς τα πάνω και προς τα κάτω ακυρώνουν η μία την άλλη μακροπρόθεσμα.

6.6 Δημιουργία Προβλέψεων από το Κενό Μοντέλο

Ο μέσος όρος του δείγματός μας αποτελεί την αμερόληπτη και βέλτιστη εκτίμηση για τον μέσο όρο του πληθυσμού. Αυτός ακριβώς είναι ο λόγος για τον οποίο τον υιοθετούμε ως βασικό μας μοντέλο για την περιγραφή του πληθυσμού. Συνεπώς, όταν θέλουμε να προβλέψουμε την τιμή μιας νέας, τυχαίας παρατήρησης χωρίς τη διαθεσιμότητα καμίας άλλης πληροφορίας, η πιο λογική επιλογή μας είναι ο μέσος όρος.

Στην πράξη, ο όρος «πρόβλεψη» στη στατιστική ανάλυση μπορεί να αναφέρεται σε δύο διακριτά σενάρια. Για παράδειγμα, στο σύνολο δεδομένων Fingers, όπου το μέσο μήκος αντίχειρα είναι 60.1 mm:

• Αν θέλαμε να προβλέψουμε το μήκος του αντίχειρα ενός νέου, άγνωστου φοιτητή, η βέλτιστη πρόβλεψη θα ήταν τα 60.1 mm.

• Παράλληλα, μπορούμε να εφαρμόσουμε το ίδιο μοντέλο και στα ήδη διαθέσιμα δεδομένα. Σε αυτήν την περίπτωση, το μοντέλο θα αντιστοιχούσε σε κάθε φοιτητή την ίδια προβλεπόμενη τιμή, τα 60.1 mm. Αυτή η «αναδρομική» εφαρμογή απαντά στο ερώτημα: Ποια τιμή θα μας έδινε το μοντέλο αν δεν γνωρίζαμε την πραγματική μέτρηση του φοιτητή;

Για τον αυτοματοποιημένο υπολογισμό αυτών των προβλέψεων, η R διαθέτει τη συνάρτηση predict(). Παρακάτω θα δούμε πώς μπορούμε να τη χρησιμοποιήσουμε για να λάβουμε τις προβλεπόμενες τιμές και για τους 157 μαθητές του πλαισίου δεδομένων Fingers. Υπενθυμίζεται ότι το κενό μοντέλο έχει ήδη προσαρμοστεί και αποθηκευτεί στο αντικείμενο empty_model.

predict(empty_model)

Δοκιμάστε να χρησιμοποιήσετε τη συνάρτηση predict() για να υπολογίσετε τα προβλεπόμενα μήκη αντίχειρα από το κενό μοντέλο, χρησιμοποιώντας τον παρακάτω κώδικα:

Αν εκτελέσετε τον κώδικα θα δείτε πολλές τιμές ίσες με 60.1 (μη στρογγυλοποιημένες). Πόσες είναι αυτές;

60157, μία προβλεπόμενη τιμή μήκους αντίχειρα για κάθε φοιτητή στο πλαίσιο δεδομένων FingersΆπειρος αριθμός, μπορούμε να προβλέψουμε οποιονδήποτε φοιτητή χρησιμοποιώντας το κενό μοντέλο

Επεξήγηση

157, μία προβλεπόμενη τιμή για κάθε φοιτητή είναι η σωστή απάντηση.

Τι συμβαίνει με το κενό μοντέλο:

Το μοντέλο:

empty_model <- lm(Thumb ~ NULL, data = Fingers)
predict(empty_model)

Τι κάνει η predict(): - Παίρνει το μοντέλο (που λέει: προβλέπω mean(Thumb) για όλους) - Εφαρμόζει την πρόβλεψη σε κάθε παρατήρηση στα δεδομένα - Επιστρέφει ένα διάνυσμα με μία τιμή για κάθε γραμμή

Αποτέλεσμα: - Το σύνολο δεδομένων έχει 157 γραμμές (157 φοιτητές) - Άρα η predict() επιστρέφει 157 τιμές - Όλες είναι η ίδια τιμή: mean(Thumb) ≈ 60.1mm - Αλλά υπάρχουν 157 αντίγραφα αυτής της τιμής

Γιατί οι άλλες επιλογές είναι λάθος:

Α - 60 τιμές - ΛΑΘΟΣ: - Το 60 δεν έχει ιδιαίτερη σημασία εδώ - Χρειαζόμαστε μία πρόβλεψη ανά παρατήρηση - Ο αριθμός των παρατηρήσεων είναι 157, όχι 60

Γ - Άπειρος αριθμός - ΕΝ ΜΕΡΕΙ-ΣΩΣΤΟ αλλά ΛΑΘΟΣ πλαίσιο: - Τεχνικά αληθές: Θα μπορούσαμε να χρησιμοποιήσουμε το μοντέλο για άπειρες προβλέψεις - Αλλά η ερώτηση είναι: Πόσες προβλέψεις έχουμε στο αποτέλεσμα της predict() - Η predict() χωρίς την παράμετρο newdata επιστρέφει προβλέψεις μόνο για τα υπάρχοντα δεδομένα - Άρα 157, όχι άπειρες

Βλέπουμε ότι παίρνουμε 5 τιμές (όσες οι παρατηρήσεις), όλες ίσες με το mean(Thumb) = 60.

Στο σύνολο δεδομένων Fingers: - 157 φοιτητές - mean(Thumb) ≈ 60.1mm - predict() επιστρέφει: [60.1, 60.1, 60.1, ..., 60.1] (157 φορές)

Μπορεί να αναρωτηθείτε: γιατί να θέλουμε να δημιουργήσουμε προβλεπόμενα μήκη αντίχειρα για αυτούς τους 157 φοιτητές, αφού ήδη γνωρίζουμε τα πραγματικά μήκη τους; Θα εξετάσουμε αυτό το ζήτημα πιο αναλυτικά στο επόμενο κεφάλαιο. Εν συντομία όμως, ο λόγος είναι ότι έτσι μπορούμε να δούμε πόσο απέχουν οι προβλέψεις του μοντέλου από τα πραγματικά δεδομένα. Με άλλα λόγια, αυτό μας δίνει μια πρώτη εικόνα για το σφάλμα γύρω από τις προβλέψεις του μοντέλου, δηλαδή για το πόσο καλά το μοντέλο προσαρμόζεται στα δεδομένα μας.

Για να χρησιμοποιήσουμε τις προβλεπόμενες τιμές ως μέτρο του σφάλματος, πρέπει πρώτα να αποθηκεύσουμε την πρόβλεψη για κάθε φοιτητή στο σύνολο δεδομένων. Όταν υπάρχει μόνο μία κοινή πρόβλεψη για όλους, όπως συμβαίνει με το κενό μοντέλο, αυτό ίσως φαίνεται περιττό.

Ωστόσο, όσο προχωράμε, θα δούμε πόσο χρήσιμο είναι να αποθηκεύουμε τις ατομικές προβλέψεις. Για παράδειγμα, αν δημιουργήσουμε μια νέα μεταβλητή με το όνομα Predict, που περιέχει την τιμή πρόβλεψης για κάθε φοιτητή, τότε μπορούμε να υπολογίσουμε τη διαφορά ανάμεσα στο πραγματικό και στο προβλεπόμενο μήκος αντίχειρα. Έτσι, μπορούμε να δούμε πόσο αποκλίνει η πρόβλεψη του μοντέλου για κάθε φοιτητή.

Στο παρακάτω παράθυρο κώδικα, χρησιμοποιήστε τη συνάρτηση predict() για να αποθηκεύσετε τα προβλεπόμενα μήκη αντίχειρα των 157 φοιτητών σε μια νέα μεταβλητή του συνόλου δεδομένων Fingers. Έχουμε επίσης προσθέσει κώδικα που εμφανίζει αυτές τις προβλέψεις πάνω σε ένα διάγραμμα διασποράς (Thumb με Height) που είδαμε προηγουμένως.

Όπως φαίνεται από το τμήμα του πλαισίου δεδομένων που εμφανίζει η head(), κάθε φοιτητής λαμβάνει την ίδια προβλεπόμενη τιμή (60.1 mm) από το κενό μοντέλο, ανεξάρτητα από το πραγματικό μήκος του αντίχειρά του. Αυτό οφείλεται στη φύση του κενού μοντέλου, το οποίο παράγει μία μόνο πρόβλεψη: τον μέσο όρο του δείγματος.

Παρά το γεγονός ότι στο διάγραμμα διασποράς παρατηρείται μια σχέση μεταξύ του μήκους του αντίχειρα και του ύψους, το κενό μοντέλο αγνοεί πλήρως αυτή τη σχέση. Καθώς δεν λαμβάνει υπόψη καμία ανεξάρτητη μεταβλητή, θα αναθέσει την ίδια προβλεπόμενη τιμή σε όλους τους φοιτητές. Αυτή ακριβώς είναι η αιτία που οι προβλέψεις (Fingers$Predict) σχηματίζουν μια οριζόντια γραμμή στο διάγραμμα.

Σε αντίθεση με αυτή την απλή προσέγγιση, τα πολύπλοκα μοντέλα που θα μελετήσουμε στη συνέχεια (π.χ. με την προσθήκη ανεξάρτητων μεταβλητών όπως το φύλο ή το ύψος φοιτητή) θα παράγουν διαφορετικές προβλέψεις για διαφορετικούς φοιτητές, αντανακλώντας έτσι τις υποκείμενες σχέσεις στα δεδομένα.

6.7 Σκέψεις για το Σφάλμα

Έχουμε δει ότι ο μέσος όρος αποτελεί το απλούστερο (ή «κενό») μοντέλο για την περιγραφή μιας ποσοτικής μεταβλητής. Αυτή η ιδέα μπορεί να εκφραστεί με την ακόλουθη θεμελιώδη εξίσωση:

ΔΕΔΟΜΕΝΑ = ΜΟΝΤΕΛΟ + ΣΦΑΛΜΑ

Στο πλαίσιο του κενού μοντέλου, αυτό μεταφράζεται σε:

ΔΕΔΟΜΕΝΑ = ΜΕΣΟΣ ΟΡΟΣ + ΣΦΑΛΜΑ

Αν αναδιατάξουμε αυτή την εξίσωση, μπορούμε να ορίσουμε το σφάλμα για κάθε παρατήρηση ως:

ΣΦΑΛΜΑ = ΔΕΔΟΜΕΝΑ - ΜΕΣΟΣ ΟΡΟΣ

Για παράδειγμα, με μέσο μήκος αντίχειρα 60.1mm:

• Ένας φοιτητής με μήκος αντίχειρα 62mm θα έχει θετικό σφάλμα (62 - 60.1 ≈ +1.9 mm)

• Ένας φοιτητής με μήκος αντίχειρα 58mm θα έχει αρνητικό σφάλμα (58 - 60.1 ≈ -2.1 mm)

Αυτό το υπολογιζόμενο σφάλμα ονομάζεται υπόλοιπο (residual) - δηλαδή, η διαφορά μεταξύ της πραγματικής τιμής και της πρόβλεψης του μοντέλου. Η ορολογία «υπόλοιπο» είναι ενδεικτική, καθώς εκφράζει την υπολειπόμενη μεταβλητότητα στα δεδομένα μας αφού αφαιρέσουμε την επίδραση του μοντέλου.

Για τον υπολογισμό των υπολοίπων στην R, αρκεί να αφαιρέσουμε τον μέσο όρο από κάθε παρατήρηση. Για παράδειγμα, για το σύνολο δεδομένων Fingers:

Fingers$Thumb - Fingers$Predict

Αν εκτελέσουμε τον κώδικα Fingers$Thumb - Fingers$Predict, τι νομίζετε ότι θα συμβεί;

H R θα υπολογίσει μια τιμή υπολοίπου για έναν μελλοντικό φοιτητή.Η R θα δημιουργήσει μια λίστα με τιμές υπολοίπων, μία για κάθε φοιτητή στο πλαίσιο δεδομένων Fingers.Η R θα κάνει μια πρόβλεψη για κάθε φοιτητή στο πλαίσιο δεδομένων Fingers.Η R θα δημιουργήσει μια λίστα από 157 ίδιες τιμές επειδή όλα αυτά τα υπόλοιπα πρέπει να είναι ίδια.

Επεξήγηση

Η R θα δημιουργήσει μια λίστα με τιμές υπολοίπων, μία για κάθε φοιτητή είναι η σωστή απάντηση.

Τι κάνει ο κώδικας:

Fingers$Thumb - Fingers$Predict

Αναλύοντας: - Fingers$Thumb: Διάνυσμα με 157 πραγματικές τιμές αντίχειρα - Fingers$Predict: Διάνυσμα με 157 προβλεπόμενες τιμές (όλες 60.1) - Η αφαίρεση γίνεται element-wise (τιμή προς τιμή)

Αποτέλεσμα: Διάνυσμα με 157 διαφορές: [Thumb₁ - 60.1, Thumb₂ - 60.1, ..., Thumb₁₅₇ - 60.1]

Αυτό είναι ακριβώς ο ορισμός των υπολοίπων (residuals):

υπόλοιπο = παρατηρούμενη τιμή - τιμή πρόβλεψης 

Γιατί οι άλλες επιλογές είναι λάθος:

Α - Μία τιμή υπολοίπου για μελλοντικό φοιτητή - ΛΑΘΟΣ: - Δεν υπάρχει μελλοντικός φοιτητής στον κώδικα - Χρησιμοποιούμε τα υπάρχοντα δεδομένα (Fingers) - Υπολογίζουμε τα υπόλοιπα για όλους τους 157 φοιτητές στο πλαίσιο δεδομένων

Γ - Θα κάνει πρόβλεψη - ΛΑΘΟΣ: - Η πρόβλεψη ήδη έγινε (Fingers$Predict) - Τώρα αφαιρούμε για να βρούμε τα σφάλματα - Αυτό είναι υπολογισμός υπολοίπων, όχι πρόβλεψη

Δ - 157 ίδιες τιμές - ΛΑΘΟΣ: - Οι τιμές των υπολοίπων δεν είναι ίδιες - Κάθε φοιτητής έχει διαφορετική πραγματική τιμή μήκους αντίχειρα - Άρα: Thumb - 60.1 θα δώσει διαφορετική τιμή υπολοίπου

Ιδιότητες των υπολοίπων από το κενό μοντέλο:

Τι είναι αληθές: - Υπάρχουν 157 υπόλοιπα (ένα ανά φοιτητή) - Είναι διαφορετικά μεταξύ τους - Το άθροισμά τους = 0 (ιδιότητα του μέσου όρου) - Ο μέσος όρος τους = 0

Τι ΔΕΝ είναι αληθές: - Δεν είναι όλα ίδια - Δεν είναι όλα μηδέν

Κώδικας R για επαλήθευση:

# Υπολογισμός residuals
residuals <- Fingers$Thumb - Fingers$Predict

# Πόσα residuals;
length(residuals)
# [1] 157

# Είναι όλα ίδια?
all(residuals == residuals[1])
# [1] FALSE

# Αθροίζουν στο 0;
sum(residuals)
# [1] 0 (ή πολύ κοντά, λόγω στρογγυλοποίησης)

# Μέσος όρος;
mean(residuals)
# [1] 0 (ή πολύ κοντά)

Γιατί είναι σημαντικό:

Τα υπόλοιπα ή κατάλοιπα μας λένε: - Πόσο λάθος κάνει το μοντέλο για κάθε άτομο - Προς ποια κατεύθυνση είναι το λάθος (θετικό = υπερεκτίμηση, αρνητικό = υποεκτίμηση) - Πόσο καλό είναι το μοντέλο συνολικά (μικρές τιμές υπολοίπων = καλό μοντέλο)

Για το κενό μοντέλο, τα υπόλοιπα δείχνουν πόσο κάθε φοιτητής αποκλίνει από τον μέσο όρο.

Αν εκτελέσουμε τον κώδικα, η R θα υπολογίσει τα 157 υπόλοιπα, αλλά δεν θα τα αποθηκεύσει εκτός αν της το ζητήσουμε. Τροποποιήστε τον παρακάτω κώδικα για να αποθηκεύσετε τα υπόλοιπα σε μια νέα μεταβλητή στο πλαίσιο δεδομένων Fingers που ονομάζεται Resid.

Τα υπόλοιπα (ή κατάλοιπα) είναι τόσο σημαντικά στη στατιστική μοντελοποίηση που υπάρχει ένας ακόμη πιο εύκολος τρόπος να τα υπολογίσουμε στην R. Η συνάρτηση resid(), όταν της δοθεί ένα μοντέλο (π.χ., empty_model), θα επιστρέψει όλα τα υπόλοιπα από τις προβλέψεις του μοντέλου.

resid(empty_model)

Τροποποιήστε τον ακόλουθο κώδικα για να αποθηκεύσετε τα υπόλοιπα που παίρνουμε χρησιμοποιώντας τη συνάρτηση resid() ως μεταβλητή στο πλαίσιο δεδομένων Fingers. Ονομάστε τη νέα μεταβλητή EasyResid.

Παρατηρήστε ότι οι τιμές των Resid και EasyResid είναι ίδιες για κάθε παρατήρηση. Θα χρησιμοποιούμε τη συνάρτηση resid() από εδώ και πέρα, απλώς επειδή είναι ευκολότερη, αλλά θέλουμε να γνωρίζετε τι κάνει η συνάρτηση αυτή στο παρασκήνιο.

Παρακάτω έχουμε σχεδιάσει μερικά από τα υπόλοιπα για το σύνολο δεδομένων Fingers στο διάγραμμα διασποράς Thumb ανά Height. Οπτικά, τα υπόλοιπα μπορούν να θεωρηθούν ως η κάθετη απόσταση ανάμεσα στις παρατηρούμενες τιμές (τα πραγματικά μήκη αντίχειρα των φοιτητών) και του προβλεπόμενου μήκους αντίχειρα του μοντέλου μας (60.1).

Παρατηρήστε ότι μερικές φορές τα υπόλοιπα είναι αρνητικά (βρίσκονται κάτω από το κενό μοντέλο) και μερικές φορές θετικά (πάνω από το κενό μοντέλο). Επειδή το κενό μοντέλο είναι ο μέσος όρος, γνωρίζουμε ότι αυτά τα υπόλοιπα εξισορροπούνται στο σύνολο των 157 φοιτητών.

Σχήμα 6.16

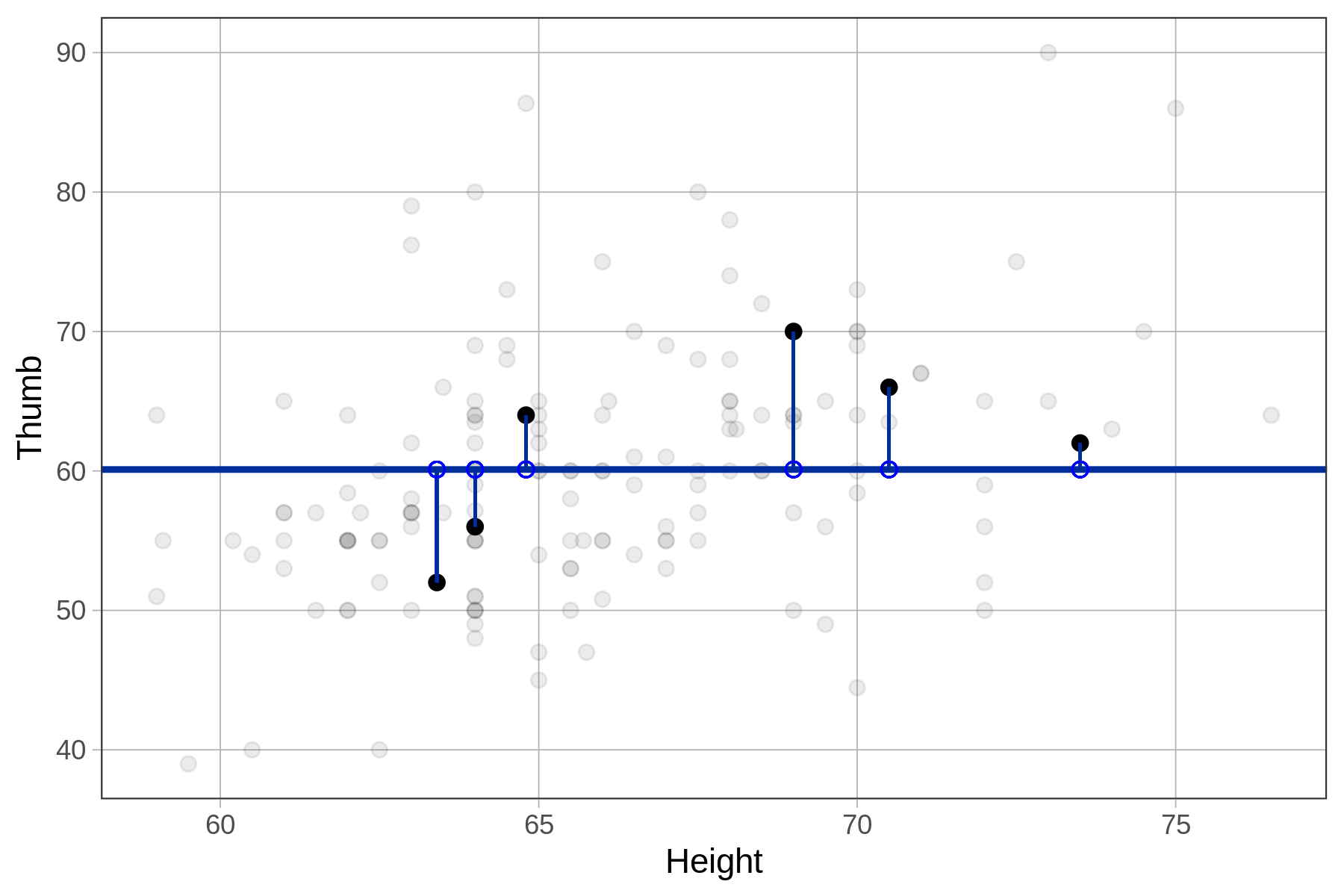
Επειδή ο μέσος όρος εξισορροπεί τα υπόλοιπα, αν χρησιμοποιήσουμε τον κώδικα sum(Fingers$Resid), ποιο αποτέλεσμα να περιμένουμε;

0Τον μέσο όρο (60.1)157 (ίδιο με τον αριθμό των φοιτητών)

Επεξήγηση

0 είναι η σωστή απάντηση.

Θεμελιώδης ιδιότητα του μέσου όρου:

Όταν χρησιμοποιούμε το μέσο όρο ως πρόβλεψη (όπως στο κενό μοντέλο), τα υπόλοιπα πάντα αθροίζουν στο μηδέν:

• Ο μέσος όρος είναι το σημείο ισορροπίας
• Οι θετικές αποκλίσεις (πάνω από το μέσο) εξουδετερώνουν τις αρνητικές (κάτω από το μέσο)
• Αυτό είναι ορισμός - ο μέσος όρος κατασκευάζεται έτσι ώστε να συμβαίνει αυτό

Παράδειγμα:

Μήκος αντίχειρα: 58, 62, 59, 61, 60
Μέσος όρος: 60

Υπόλοιπα:
58 - 60 = -2
62 - 60 =  2
59 - 60 = -1
61 - 60 =  1
60 - 60 =  0

Άθροισμα: (-2) + 2 + (-1) + 1 + 0 = 0 ✓

Γιατί οι άλλες επιλογές είναι λάθος:

Β - Ο μέσος όρος (60.1) - ΛΑΘΟΣ: - Το άθροισμα των υπολοίπων δεν είναι ο μέσος όρος - Ο μέσος όρος των υπολοίπων είναι 0 - Το άθροισμα των υπολοίπων είναι επίσης 0

Γ - 157 - ΛΑΘΟΣ: - Ο αριθμός των φοιτητών δεν σχετίζεται με το άθροισμα - Το άθροισμα είναι 0 ανεξάρτητα από το n (αριθμό παρατηρήσεων)

Σημαντική σημείωση: Στην πράξη μπορεί να δείτε κάτι σαν 2.84e-14 αντί για ακριβώς 0. Αυτό οφείλεται σε: - Σφάλματα στρογγυλοποίησης στους υπολογισμούς κινητής υποδιαστολής - Είναι ουσιαστικά μηδέν (0.0000000000000284)

Γενίκευση:

Αυτή η ιδιότητα ισχύει πάντα όταν: - Χρησιμοποιούμε το μέσο όρο ως πρόβλεψη - Υπολογίζουμε τα υπόλοιπα ως: observed - mean - Αθροίζουμε όλα τα υπόλοιπα

Δεν ισχύει για: - Διάμεσο ως πρόβλεψη (τότε Σ(residuals) ≠ 0 γενικά) - Άλλα μοντέλα που δεν βασίζονται στο μέσο όρο

Πρακτική σημασία:

Το γεγονός ότι Σ(υπόλοιπα) = 0: - Σημαίνει ότι ο μέσος όρος είναι αμερόληπτος εκτιμητής (unbiased) - Δείχνει την εξισσορόπηση μεταξύ υπερεκτιμήσεων και υποεκτιμήσεων

Η Κατανομή των Υπολοίπων

Παρακάτω έχουμε σχεδιάσει τα ιστογράμματα των τριών μεταβλητών: Thumb, Predict και Resid.

Σχήμα 6.17

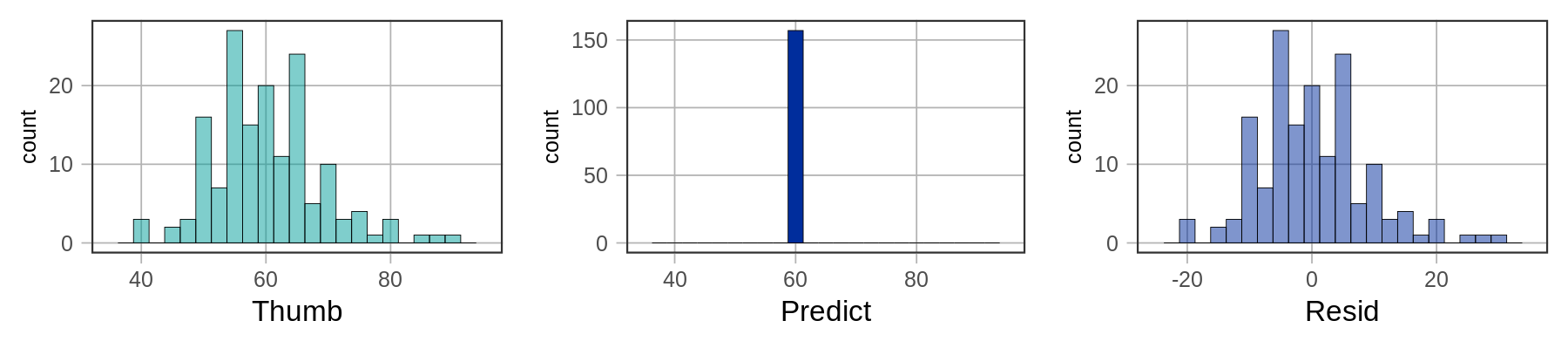
Εξετάστε τις παραπάνω κατανομές.

Πώς μοιάζει η κατανομή των δεδομένων του μήκους αντίχειρα;

Πώς θα σχολιάζατε την κατανομή της Predict (προβλέψεις του μοντέλου);

Τέλος, πώς θα σχολιάζατε την κατανομή της Resid (υπόλοιπα ή σφάλματα); Τι κοινό έχουν και σε τι διαφέρουν οι κατανομές των δεδομένων του μήκους αντίχειρα και οι κατανομές των σφαλμάτων;

Οι κατανομές των δεδομένων και των υπολοίπων έχουν το ίδιο σχήμα. Αλλά οι αριθμοί στον άξονα x διαφέρουν μεταξύ των δύο κατανομών. Η κατανομή του μήκους αντίχειρα (Thumb) είναι κεντραρισμένη στον μέσο όρο (60.1), ενώ η κατανομή των σφαλμάτων (Resid) είναι κεντραρισμένη στο 0. Μήκη αντίχειρα που είναι μικρότερα από τον μέσο όρο (όπως το μήκος αντίχειρα 50) έχουν αρνητικά υπόλοιπα (-10), αλλά μήκη αντίχειρα που είναι μεγαλύτερα από τον μέσο όρο (όπως το 70) έχουν θετικά υπόλοιπα (10).

Ας δούμε τι αποτέλεσμα θα παίρναμε αν αθροίζαμε όλες τις τιμές της μεταβλητής Fingers$Resid. Δοκιμάστε το στο παρακάτω παράθυρο κώδικα.

-2.060574e-12

Μερικές φορές η R εμφανίζει αριθμητικά αποτελέσματα σε επιστημονική σημειολογία. Για παράδειγμα, η τιμή -2.060574e-12 αντιστοιχεί στο \(-2.06 \times 10^{-12}\) - έναν εξαιρετικά μικρό αριθμό πολύ κοντά στο μηδέν (ο εκθέτης -12 δηλώνει μετατόπιση της υποδιαστολής 12 θέσεις προς τα αριστερά). Όταν συναντήσετε τέτοιες εκφράσεις με μεγάλο αρνητικό εκθέτη μετά το “e”, μπορείτε να τις ερμηνεύετε ως πρακτικά μηδενικές.

Τα υπόλοιπα (ή σφάλματα) γύρω από τον μέσο όρο πάντα αθροίζουν στο 0. Κατά συνέπεια, και ο μέσος όρος των σφαλμάτων θα είναι ακριβώς μηδέν, αφού το 0 διαιρεμένο με οποιοδήποτε \(n\) δίνει 0. Στην πράξη, λόγω αριθμητικών σφαλμάτων στρογγυλοποίησης, η R μπορεί να εμφανίζει τιμές πολύ κοντά στο μηδέν αντί για ακριβές μηδέν.

6.8 Μαθηματικές Αναπαραστάσεις

Μέχρι στιγμής, έχουμε αναπαραστήσει τα στατιστικά μας μοντέλα μέσω λεκτικών εξισώσεων, όπως: Μήκος αντίχειρα = Φύλο + Σφάλμα. Όλες αυτές ακολουθούν τη βασική δομή: ΔΕΔΟΜΕΝΑ = ΜΟΝΤΕΛΟ + ΣΦΑΛΜΑ. Ωστόσο, καθώς προχωράμε σε πιο πολύπλοκα μοντέλα, η συνεχής χρήση λεκτικών περιγραφών γίνεται κουραστική. Για το λόγο αυτό, οι στατιστικολόγοι έχουν αναπτύξει μαθηματικό συμβολισμό για την απόδοση αυτών των σχέσεων. Αν και δεν θα εμβαθύνουμε πολύ στη μαθηματική σημειολογία σε αυτό το μάθημα, θα παρουσιάσουμε ορισμένα βασικά σύμβολα. Ο συμβολισμός αυτός δεν αποτελεί μόνο έναν συνοπτικό και ακριβή τρόπο έκφρασης, αλλά βοηθάει στην καλύτερη κατανόηση των στατιστικών εννοιών και στη δομημένη σκέψη.

Αναπαράσταση του Μέσου Όρου

Έχετε μάθει πώς να υπολογίζετε τον αριθμητικό μέσο όρο στο δημοτικό σχολείο: πάρτε μια ομάδα τιμών, προσθέστε τους μεταξύ τους, και στη συνέχεια διαιρέστε το αποτέλεσμα με το πλήθος των τιμών. Θα μπορούσαμε να αναπαραστήσουμε αυτόν τον υπολογισμό ως εξής:

\[\textbf{μέσος όρος} = \frac{\textbf{άθροισμα όλων των τιμών}}{\textbf{πλήθος των τιμών}}\]

Όπως μπορείτε να διαπιστώσετε, στην παραπάνω έκφραση χρησιμοποιήσαμε άτυπο συμβολισμό, παρόμοιο με τις λεκτικές εξισώσεις που έχουμε χρησιμοποιήσει μέχρι στιγμής. Υποθέτοντας ότι γνωρίζετε ότι σε ένα κλάσμα η γραμμή του κλάσματος μπορεί να διαβαστεί ως «διαιρεμένο με» (όπως α/β σημαίνει «α διαιρέμενο με το β») τότε μπορείτε να δείτε σαφώς τι αντιπροσωπεύει η παραπάνω έκφραση: το άθροισμα μιας ομάδας τιμών διαιρεμένο με το πλήθος τους. Απλό.

Αν ξαναγράψουμε την άτυπη έκφραση με μαθηματικό συμβολισμό θα μπορούσαμε να τη γράψουμε ως εξής:

\[\bar{Y} = \frac{\sum Y_i}{n}\] Ας αναλύσουμε αυτήν την εξίσωση:

• Χρησιμοποιούμε το κεφαλαίο γράμμα \(Y\) για να συμβολίσουμε μια εξαρτημένη μεταβλητή, και θα το κάνουμε αυτό σε όλη τη διάρκεια του μαθήματος.

• Η τοποθέτηση της γραμμής πάνω από το \(Y\) (\(\bar{Y}\)) σημαίνει απλώς ο «μέσος όρος της Y».

• Το ελληνικό κεφαλαίο γράμμα \(\sum\) σημαίνει άθροισμα, και διαβάζεται ως «το άθροισμα των…».

• Το \(n\) είναι το γράμμα που χρησιμοποιείται για να εκφράσει το μέγεθος ενός δείγματος.

• Τέλος, χρησιμοποιούμε τον δείκτη \(i\) για να εκφράσουμε κάθε μεμονωμένη παρατήρηση στο δείγμα μας, ξεκινώντας από την παρατήρηση \(1\) και μετρώντας μέχρι την παρατήρηση \(n\).

Έτσι, στην παραπάνω εξίσωση, η έκφραση στα δεξιά του ίσον θα μπορούσε να διαβαστεί ως: το άθροισμα όλων των μεμονωμένων παρατηρήσεων της \(Υ\), από \(i=1\) έως \(i=n\), διαιρεμένο με \(n\) (το πλήθος των παρατηρήσεων).

Χρησιμοποιήσαμε αρκετά σύμβολα για να εκφράσουμε απλά και μόνο τον μέσο όρο ενός δείγματος. Αλλά, η εξίσωση αυτή περιλαμβάνει στοιχεία που θα γίνουν όλο και πιο χρήσιμα καθώς προχωράτε στο μάθημα. Και, αναμένεται να επιλύσουν ασάφειες που θα μπορούσαν να μας στοιχειώσουν αργότερα αν χρησιμοποιούμε απλώς άτυπες λεκτικές εξισώσεις. Για παράδειγμα, αν γράψουμε «το άθροισμα όλων των τιμών» σε ποιες ακριβώς τιμές αναφερόμαστε; Της εξαρτημένης μεταβλητής; Της ανεξάρτητης μεταβλητής; Η χρήση του συμβολισμού \(\sum Y_i\) το κάνει αυτό σαφές.

Ως μια μικρή παρέκκλιση, ας επιστρέψουμε σε μία από τις ιδιότητες του μέσου όρου που ανακαλύψαμε προηγουμένως χρησιμοποιώντας την R: αν προσθέσετε τις αποκλίσεις των τιμών σε μια κατανομή από τον μέσο όρο της κατανομής, θα πάρετε 0. Θα μπορούσαμε να χρησιμοποιήσουμε μαθηματικό συμβολισμό για να εκφράσουμε αυτήν την ιδέα ως εξής:

\[{\sum Y_i - \bar{Y}} = 0\]

Εξετάστε την παραπάνω εξίσωση. Ποια λεκτική δήλωση περιγράφει καλύτερα το νόημα της εξίσωσης;

Το άθροισμα των αποκλίσεων της τιμής κάθε παρατήρησης i, από το 1 έως το n, είναι ίσο με 0.Οποιαδήποτε τιμή διαιρεμένη με το 0 είναι ίση με 0.Το άθροισμα όλων των τιμών είναι ίσο με 0.Η απόκλιση του n από κάθε υπόλοιπο είναι ίση με 0.

Επεξήγηση

Το άθροισμα των αποκλίσεων της τιμής κάθε παρατήρησης i, από το 1 έως το n, είναι ίσο με 0 είναι η σωστή απάντηση.

Ανάλυση της εξίσωσης:

Σύμβολα: - Σ (σίγμα): Σύμβολο αθροίσματος - i=1 έως n: Δείκτης που διατρέχει από το 1ο άτομο έως το n-οστό (όλα τα άτομα) - Yᵢ: Η τιμή του ατόμου i - Ȳ (Y-παύλα): Ο μέσος όρος όλων των τιμών - Yᵢ - Ȳ: Η απόκλιση του ατόμου i από το μέσο όρο (το υπόλοιπο)

Με λόγια: “Πάρε κάθε παρατήρηση (από το 1 έως το n), υπολόγισε πόσο η τιμή της αποκλίνει από το μέσο όρο, και άθροισε όλες αυτές τις αποκλίσεις. Το αποτέλεσμα θα είναι 0.”

Γιατί οι άλλες επιλογές είναι λάθος:

Β - “Οποιαδήποτε τιμή διαιρεμένη με το 0 είναι ίση με 0” - ΛΑΘΟΣ: - Πρώτον, αυτό είναι μαθηματικά λάθος - η διαίρεση με 0 είναι απροσδιόριστη - Δεύτερον, στην εξίσωση δεν υπάρχει διαίρεση - Υπάρχει αφαίρεση (Yᵢ - Ȳ) και άθροιση Σ

Γ - “Το άθροισμα όλων των τιμών είναι ίσο με 0” - ΛΑΘΟΣ: - Πολύ ασαφές και ανακριβές - Δεν είναι το άθροισμα όλων των τιμών - Είναι το άθροισμα των αποκλίσεων από το μέσο όρο - Παράδειγμα: Αν Yᵢ = {58, 62, 60}, τότε ΣYᵢ = 180 ≠ 0 - Αλλά Σ(Yᵢ - 60) = -2 + 2 + 0 = 0 ✓

Δ - “Η απόκλιση του n από κάθε υπόλοιπο είναι ίση με 0” - ΛΑΘΟΣ: - Δεν έχει νόημα - το n είναι το πλήθος των παρατηρήσεων, όχι μια τιμή - Δεν μιλάμε για “απόκλιση του n” - Η εξίσωση αναφέρεται σε άθροισμα αποκλίσεων, όχι απόκλιση από κάτι

Λεπτομερής ανάλυση της σωστής απάντησης:

“Το άθροισμα των αποκλίσεων της βαθμολογίας κάθε ατόμου i”: - Κάθε άτομο i: Διατρέχουμε όλες τις παρατηρήσεις (i = 1, 2, 3, … n) - Βαθμολογία: Η τιμή Yᵢ για κάθε άτομο - Απόκλιση: Η διαφορά Yᵢ - Ȳ - Άθροισμα: Προσθέτουμε όλες τις αποκλίσεις

“από το 1 έως το n”: - Αναφέρεται στο εύρος του δείκτη i - Σημαίνει ότι συμπεριλαμβάνουμε όλες τις παρατηρήσεις

“είναι ίσο με 0”: - Το τελικό αποτέλεσμα του αθροίσματος - Θεμελιώδης ιδιότητα του μέσου όρου

Γιατί είναι σημαντικό:

Αυτή η εξίσωση εκφράζει: - Τον ορισμό του μέσου όρου ως σημείου ισορροπίας - Την ιδιότητα αμεροληψίας του μέσου όρου - Τη βάση της στατιστικής - οι θετικές και αρνητικές αποκλίσεις ακυρώνονται - Ότι ο μέσος όρος ελαχιστοποιεί το άθροισμα των τετραγωνικών αποκλίσεων

Δύο Σημαντικά Πράγματα για τη Μαθηματική Αναπαράσταση

Υπάρχουν δύο πράγματα που χρειάζεται να κατανοήσετε για τη μαθηματική αναπαράσταση—πράγματα που οι περισσότεροι φοιτητές δεν εκτιμούν πλήρως ποτέ αλλά οι μαθηματικοί γνωρίζουν καλά. Πρώτον, δεν υπάρχει ένας μόνο σωστός τρόπος χρήσης του μαθηματικού συμβολισμού. Έτσι, αν πέσουν στα χέρια σας διαφορετικά βιβλία στατιστικής, συχνά θα περιέχουν διαφορετικούς τύπους για δείκτες όπως ο μέσος όρος και η τυπική απόκλιση, καθώς και για οτιδήποτε άλλο. Πρέπει να δείξετε ευελιξία και να μην αγχώνεστε αν δείτε διαφορετικές μαθηματικές αναπαραστάσεις που βασικά σημαίνουν το ίδιο πράγμα.

Απλά και μόνο ως παράδειγμα, πολλοί θα έγραφαν την εξίσωση του μέσου όρου ως εξής:

\[\bar{Y} = \frac{\sum Y_i}{n}\]

Κάποια στιγμή, οι άνθρωποι κουράζονται να γράφουν ολόκληρο το τμήμα \(i = 1\) έως \(n\), και απλά συμφωνούν να το παραλείψουν επειδή όλοι γνωρίζουμε τι σημαίνει αυτό χωρίς αυτό: αθροίστε όλες τις μεμονωμένες τιμές της \(Y\) και διαιρέστε το αποτέλεσμα με το \(n\). Αυτό είναι μέρος του ζωντανού κόσμου του μαθηματικού συμβολισμού.

Επειδή οι διδάσκοντες θέλουν να χρησιμοποιείτε τα σύμβολα με συνέπεια, συχνά θα πουν στους φοιτητές να χρησιμοποιούν τον ακριβή συμβολισμό που χρησιμοποιείται στο συγκεκριμένο σύγγραμμα που χρησιμοποιείται στο μάθημα. Αλλά μην ξεγελαστείτε από αυτό: άλλα βιβλία θα γράφουν τα πράγματα διαφορετικά. Πρέπει να μπορείτε να διαβάσετε διαφορετικές εκδοχές μιας εξίσωσης ή ενός τύπου και να διαπιστώσετε ότι είναι πραγματικά το ίδιο πράγμα. (Αλλά ναι, πιθανώς πρέπει επίσης να θυμάστε την μία εκδοχή που οι δικοί σας καθηγητές περιμένουν να χρησιμοποιήσετε.)

Εξετάστε τις παρακάτω εξισώσεις. Ποιες από αυτές αντιπροσωπεύουν το μέσο όρο μιας μεταβλητής;

A: \(\bar{x} = \frac{\sum x_i}{n}\)

ΝαιΌχι

Β: \(\bar{Y} = \sum \frac{Y_i}{n}\)

ΝαιΌχι

Γ: \(\bar{Y} = \frac{\sum Y_i}{n}\)

ΝαιΌχι

Δ: \(\bar{y} = \frac{\text{sum}(y_1, y_2...y_n)}{n}\)

ΝαιΌχι

Ε: \(\bar{Y} = \frac{Y_i}{\sum n}\)

ΝαιΌχι

ΣΤ: \(\bar{Y} = \frac{\sum Y}{n}\)

ΝαιΌχι

Επεξήγηση

Σωστές απαντήσεις: Α, Β, Γ, Δ, ΣΤ

Ο ορισμός του μέσου όρου:

Ο μέσος όρος είναι το άθροισμα όλων των τιμών διαιρεμένο με το πλήθος τους:

\[\bar{x} = \frac{\sum_{i=1}^{n} x_i}{n} = \frac{x_1 + x_2 + \cdots + x_n}{n}\]

Ανάλυση κάθε εξίσωσης:

Α: \(\bar{x} = \frac{\sum x_i}{n}\) - ΣΩΣΤΟ ✓ - Η κλασική μορφή του τύπου του μέσου όρου - \(\sum x_i\) = άθροισμα όλων των τιμών \(x_1, x_2, ..., x_n\) - \(n\) = συνολικό πλήθος τιμών

Β: \(\bar{Y} = \sum \frac{Y_i}{n}\) - ΣΩΣΤΟ ✓ - Αλγεβρικά ισοδύναμη μορφή \(\sum \frac{Y_i}{n} = \frac{Y_1}{n} + \frac{Y_2}{n} + \cdots + \frac{Y_n}{n}\) \(= \frac{Y_1 + Y_2 + \cdots + Y_n}{n} = \frac{\sum Y_i}{n}\) ✓

Γ: \(\bar{Y} = \frac{\sum Y_i}{n}\) - ΣΩΣΤΟ ✓ - Ίδιο με το A, απλά χρησιμοποιεί το σύμβολο \(Y\) αντί για \(x\) - Εξίσου σωστό

Δ: \(\bar{y} = \frac{\text{sum}(y_1, y_2...y_n)}{n}\) - ΣΩΣΤΟ ✓ - Χρησιμοποιεί τη συνάρτηση sum() αντί για το σύμβολο \(\sum\) - Συνηθισμένη σημειολογία σε προγραμματισμό (π.χ., R) - Μαθηματικά ισοδύναμη

Ε: \(\bar{Y} = \frac{Y_i}{\sum n}\) - ΛΑΘΟΣ ✗ - Λάθος δομή: Το \(\sum\) βρίσκεται στο λάθος μέρος - \(\sum n\) δεν έχει νόημα - το \(n\) είναι σταθερά, όχι μεταβλητή με δείκτη - Θα έπρεπε να είναι: \(\frac{\sum Y_i}{n}\) - Επίσης, \(Y_i\) χωρίς άθροιση αναφέρεται σε μία παρατήρηση, όχι σε όλες

ΣΤ: \(\bar{Y} = \frac{\sum Y}{n}\) - ΣΩΣΤΟ ✓ - Συντομογραφία - Το \(\sum Y\) υπονοεί \(\sum Y_i\) (άθροισμα όλων των \(Y\)) - Συχνά χρησιμοποιείται όταν το πλαίσιο είναι σαφές

Σύνοψη:

Όλες οι παρακάτω είναι ισοδύναμες και σωστές:

\[\bar{x} = \frac{\sum x_i}{n} = \sum \frac{x_i}{n} = \frac{\sum x}{n} = \frac{x_1 + x_2 + \cdots + x_n}{n}\]

Η μόνη λάθος μορφή είναι η Ε, επειδή: 1. Έχει \(Y_i\) (μεμονωμένη τιμή) αντί για \(\sum Y_i\) (άθροισμα) 2. Έχει το \(\sum n\) που δεν έχει νόημα

Το άλλο πράγμα που χρειάζεται να γνωρίζετε για το μαθηματικό συμβολισμό είναι ότι υπάρχουν δύο διαφορετικοί τρόποι ερμηνείας του. Οι περισσότεροι φοιτητές σκέφτονται τον συμβολισμό (π.χ., την εξίσωση για τον μέσο όρο, παραπάνω) ως μια βήμα-προς-βήμα συνταγή για το πώς να πάρουν μια απάντηση. Έτσι, για να βρείτε τον μέσο όρο, πάρτε όλες τις τιμές, προσθέστε τις, και στη συνέχεια διαιρέστε με το \(n\).

Αλλά υπάρχει ένας πολύ πιο ισχυρός τρόπος να σκέφτεστε τον μαθηματικό συμβολισμό: είναι η αναπαράσταση μιας ποσότητας ή μιας σχέσης.

Για να δούμε ένα απλό παράδειγμα, ο συμβολισμός \(2+3\) θα μπορούσε να θεωρηθεί ως συνταγή: πάρτε τον αριθμό \(2\), προσθέστε σε αυτόν άλλα \(3\), και θα πάρετε την απάντηση. Αλλά θα μπορούσε επίσης να θεωρηθεί ως μια ποσότητα από μόνη της, η ποσότητα (\(2+3\)).

Μπορεί να μην πιστεύετε ότι κάνει μεγάλη διαφορά, αλλά τι γίνεται αν σας δώσουμε αντί αυτού την έκφραση \(x+3\). Αν το δείτε αυτό ως συνταγή, και αν δεν γνωρίζετε τι είναι το \(x\), έχετε κολλήσει. Αλλά αν το δείτε ως κάτι που αντιπροσωπεύει την ποσότητα \(x+3\) τότε δεν χρειάζεται να γνωρίζετε την τιμή του \(x\). Μπορείτε ακόμα να το σκεφτείτε ως μια ποσότητα που είναι κάτα \(3\) μεγαλύτερη από το \(x\), ανεξάρτητα από το αν μπορείτε να το υπολογίσετε.

Στη στατιστική, αν σκεφτείτε τον συμβολισμό με αυτόν τον δεύτερο τρόπο, ως αναπαράσταση ποσοτήτων και σχέσεων, θα καταλήξετε να μαθαίνετε και να κατανοείτε περισσότερα. Έτσι, όταν βλέπετε μια έκφραση για τον μέσο όρο, μην τη σκέφτεστε ως ένα βολικό σύνολο οδηγιών για το πώς να υπολογίσετε τον μέσο όρο. Και μην αρχίζετε να υπολογίζετε τον μέσο όρο. Πραγματικά δεν χρειάζεται να το κάνετε αυτό έτσι κι αλλιώς· ο υπολογιστής σας θα υπολογίσει τον μέσο όρο για εσάς (σκεφτείτε την favstats()), και δεν χρειάζεται να του πείτε πώς!

Αντ’ αυτού, σκεφτείτε το ως αναπαράσταση μιας σημαντικής σχέσης που ορίζει τι είναι ο μέσος όρος. Όταν βλέπετε μια εξίσωση, σκεφτείτε τι εκφράζει, αναζητήστε μοτίβα, και ούτω καθεξής.

6.9 ΔΕΔΟΜΕΝΑ = ΜΟΝΤΕΛΟ + ΣΦΑΛΜΑ: Μαθηματική Αναπαράσταση

Στο σημείο αυτό ας δούμε πώς χρησιμοποιείται η μαθηματική σημειολογία για να αναπαραστήσει το απλό (κενό) μοντέλο που παρουσιάσαμε προηγουμένως.

Μήκος αντίχειρα = Μέσος Όρος + Σφάλμα

Υπάρχουν ορισμένα πλεονεκτήματα στο να ξαναγράψουμε αυτήν την εξίσωση με μαθηματικά σύμβολα. Ορίστε μία μορφή που θα μπορούσε να πάρει:

\[Y_i = \bar{Y} + e_i\] Αυτή η εξίσωση αντιπροσωπεύει κυριολεκτικά αυτό που δείξαμε παραπάνω στη λεκτική μας εξίσωση. Μας λέει ότι κάθε τιμή του μήκους αντίχειρα (Thumb ή \(Y_i\)) στο σύνολο δεδομένων μας μπορεί να γραφεί ως το άθροισμα δύο μερών: του μέσου όρου όλων των τιμών της \(Y\) (\(\bar{Y}\), η πρόβλεψη του κενού μοντέλου), και του υπολοίπου της από αυτόν τον μέσο όρο (\(e_i\), ή σφάλμα). Αν προσθέσουμε αυτούς τους δύο αριθμούς μαζί (Μέσος Όρος + Σφάλμα) για μια συγκεκριμένη παρατήρηση, θα πάρουμε την αρχική της τιμή. Πολύ απλό, πολύ συγκεκριμένο.

Σημειολογία του Γενικού Γραμμικού Μοντέλου

Η αναπαράσταση του μέσου όρου με το σύμβολο \(\bar{Y}\) είναι αρκετά βολική για το κενό μοντέλο. Αλλά δεν πρόκειται να μας βοηθήσει να χτίσουμε πιο περίπλοκα μοντέλα αργότερα. Για να προετοιμαστούμε για κάτι τέτοιο, θα παρουσιάσουμε μια πιο γενική σημειολογία, που αναφέρεται ως το Γενικό Γραμμικό Μοντέλο (General Linear Model - GLM). Στη σημειολογία του GLM, το κενό μοντέλο εκφράζεται ως εξής:

\[Y_i = b_0 + e_i\]

Tι νομίζετε ότι μπορεί να εκφράζει το \(b_0\) στην παραπάνω εξίσωση;

Αυτή είναι μια πιο γενική εκδοχή της παραπάνω εξίσωσης, στην οποία έχουμε αντικαταστήσει τον μέσο όρο, \(\bar{Y}\) με τον όρο \(b_0\). Αυτό προς το παρόν δεν θα έχει πολύ νόημα, αλλά αργότερα θα μας βοηθήσει να προσθέσουμε πολυπλοκότητα στο μοντέλο μας (με όρους όπως \(b_1\), \(b_2\), και ούτω καθεξής). Κάτι βασικό που χρειάζεται να γνωρίζετε είναι ότι ο όρος \(b_0\) μπορεί να αντιπροσωπεύει τον μέσο όρο, όπως στην περίπτωση του κενού μοντέλου, αλλά δεν θα αντιπροσωπεύει πάντα τον μέσο όρο.

\[ \underbrace{Y_i}_{\text{Μήκος αντίχειρα}} = \underbrace{b_0}_{\text{Πρόβλεψη}} + \underbrace{e_i}_{\text{Υπόλοιπο}} \]

Πράγματι, αυτή η ευελιξία είναι που καθιστά το Γενικό Γραμμικό Μοντέλο γενικό. Όποτε βλέπετε μια έκφραση του μοντέλου GLM, χρειάζεται να σκέφτεστε προσεκτικά τι αντιπροσωπεύει κάθε σύμβολο στη συγκεκριμένη περίπτωση.

Στατιστικά και Παράμετροι

Εδώ είναι ένα καλό σημείο να υπενθυμίσουμε ότι ο στόχος μας όταν εξετάζουμε κατανομές δεδομένων είναι να μάθουμε περισσότερα για τη Διαδικασία Παραγωγής των Δεδομένων. Ο στόχος μας όταν εφαρμόζουμε στατιστικά μοντέλα είναι ο ίδιος: προσαρμόζουμε μοντέλα στα δεδομένα του δείγματος προκειμένου να βγάλουμε συμπεράσματα για τον πληθυσμό και τη ΔΠΔ.

Με τα δεδομένα μας, μπορούμε να υπολογίσουμε τον ακριβή μέσο όρο της κατανομής, και το ακριβές μέγεθος των σφαλμάτων. Όταν το κάνουμε αυτό, υπολογίζουμε ένα στατιστικό (statistic). Ένα στατιστικό είναι οτιδήποτε μπορείτε να υπολογίσετε για να συνοψίσετε κάτι σχετικά με τα δεδομένα σας· ο αριθμητικός μέσος όρος ήταν το πρώτο μας παράδειγμα στατιστικού.

Αλλά δεν μπορούμε να υπολογίσουμε τον μέσο όρο του πληθυσμού· η κατανομή του πληθυσμού είναι άγνωστη. Αντί αυτού χρησιμοποιούμε τον μέσο όρο που υπολογίζουμε από το δείγμα μας ως εκτιμητή του μέσου όρου του πληθυσμού—της κατανομής από την οποία προέρχονται τα δεδομένα μας.

Ο μέσος όρος του πληθυσμού είναι ένα παράδειγμα παραμέτρου (parameter). Μια παράμετρος είναι ένας αριθμός που συνοψίζει κάτι σχετικά με έναν πληθυσμό. Ενώ τα στατιστικά υπολογίζονται, οι παράμετροι εκτιμώνται. Χρησιμοποιούμε στατιστικά ως εκτιμητές επειδή γενικά δεν γνωρίζουμε ποιες είναι η πραγματικές τιμές των παραμέτρων.

Όταν χρησιμοποιούμε το μέσο όρο ως μοντέλο, γιατί τον ονομάζουμε εκτιμητή παραμέτρου (parameter estimate);

Επειδή δεν μπορούμε να υπολογίσουμε το μέσο όρο ενός δείγματος, πρέπει να τον εκτιμήσουμε.Επειδή δεν μπορούμε να υπολογίσουμε το μέσο όρο της ΔΠΔ (Διαδικασίας Παραγωγής Δεδομένων), πρέπει να τον εκτιμήσουμε.Επειδή όταν χρησιμοποιούμε την R για να υπολογίσουμε κάτι, το ονομάζουμε εκτίμηση.Επειδή ο τύπος υπολογισμού του μέσου όρου είναι πολύ περίπλοκος, τον ονομάζουμε εκτιμητή.

Επεξήγηση

Β - “Επειδή δεν μπορούμε να υπολογίσουμε το μέσο όρο της ΔΠΔ, πρέπει να τον εκτιμήσουμε” - ΣΩΣΤΟ

Βασικές έννοιες:

Διαδικασία Παραγωγής Δεδομένων (ΔΠΔ): - Η υποκείμενη διαδικασία που παράγει τα δεδομένα - Η πραγματική κατανομή του πληθυσμού - Περιλαμβάνει όλες τις πιθανές παρατηρήσεις - Παράδειγμα: Ο πραγματικός μέσος όρος μήκους αντίχειρα όλων των ανθρώπων στον κόσμο

Παράμετρος: - Μια σταθερή τιμή που περιγράφει τη ΔΠΔ - Συνήθως συμβολίζεται με ελληνικά γράμματα: \(\mu\) (μέσος όρος), \(\sigma\) (τυπική απόκλιση) - Άγνωστη - δεν μπορούμε να την υπολογίσουμε άμεσα

Στατιστικό: - Μια τιμή που υπολογίζουμε από το δείγμα - Συνήθως συμβολίζεται με λατινικά γράμματα: \(\bar{x}\) (δειγματικός μέσος), \(s\) (δειγματική τυπική απόκλιση) - Γνωστό - το υπολογίζουμε από τα δεδομένα μας

Εκτίμηση: - Χρησιμοποιούμε το στατιστικό του δείγματος για να εκτιμήσουμε την άγνωστη παράμετρο - Παράδειγμα: \(\bar{x} = 60.1\) mm είναι η εκτίμησή μας για το \(\mu\) (μέσος όρος πληθυσμού)

Γιατί οι άλλες επιλογές είναι λάθος:

Α - “Δεν μπορούμε να υπολογίσουμε το μέσο όρο του δείγματος” - ΛΑΘΟΣ: - Μπορούμε να υπολογίσουμε το μέσο όρο του δείγματος - Απλά με: \(\bar{x} = \frac{\sum x_i}{n}\) - Το πρόβλημα είναι ότι αυτός δεν είναι ο μέσος όρος του πληθυσμού

Γ - “Η R ονομάζει τα πάντα εκτιμήσεις” - ΛΑΘΟΣ: - Δεν είναι όλοι οι υπολογισμοί εκτιμήσεις - Μόνο όταν συμπεραίνουμε για την ΔΠΔ από το δείγμα

Δ - “Ο τύπος είναι περίπλοκος” - ΛΑΘΟΣ: - Ο τύπος του μέσου όρου είναι απλός - Η πολυπλοκότητα δεν είναι ο λόγος που τον ονομάζουμε εκτιμητή

Σε τι διαφέρει ένα μοντέλο των δεδομένων μας (του δείγματος) από ένα μοντέλο της ΔΠΔ;

Αυτό που θέλουμε είναι ένα καλό μοντέλο της ΔΠΔ. Επειδή δεν μπορούμε να το αναπτύξουμε απευθείας, πρέπει αντ' αυτού να αναπτύξουμε ένα μοντέλο βασισμένο σε δεδομένα δείγματος.Η βεβαιότητά μας για την ακρίβεια κάθε είδους μοντέλου είναι διαφορετική. Μπορούμε να είμαστε σίγουροι για τα στατιστικά του μοντέλου του δείγματός μας, αλλά ποτέ δεν γνωρίζουμε πραγματικά τις παραμέτρους στο μοντέλο της ΔΠΔ.Και τα δύο παραπάνω είναι σωστά.Κανένα από τα παραπάνω δεν είναι σωστό.

Επεξήγηση

Γ - “Και τα δύο παραπάνω είναι σωστά” - ΣΩΣΤΟ

Ανάλυση των διαφορών:

Διαφορά 1 - Στόχος vs Πραγματικότητα:

Τι θέλουμε: - Ένα μοντέλο της ΔΠΔ - τι ισχύει για τον πληθυσμό - Να γνωρίζουμε τις πραγματικές τιμές των παραμέτρων: \(\mu\), \(\sigma\), κλπ.

Τι έχουμε: - Ένα δείγμα από τη ΔΠΔ - Μπορούμε να χτίσουμε μόνο μοντέλο των δεδομένων μας - Το χρησιμοποιούμε για να βγάλουμε συμπεράσματα για τη ΔΠΔ

Διαφορά 2 - Βεβαιότητα:

Μοντέλο δεδομένων: - Γνωρίζουμε ακριβώς τα στατιστικά: \(\bar{x}\), \(s\) - Τα υπολογίζουμε από τα δεδομένα - 100% σίγουροι για τις τιμές (μέσα στα δεδομένα μας)

Μοντέλο ΔΠΔ: - Ποτέ δεν γνωρίζουμε τις πραγματικές παραμέτρους: \(\mu\), \(\sigma\) - Μόνο τις εκτιμούμε με αβεβαιότητα

Γιατί είναι σημαντικό:

Αυτή η διάκριση είναι θεμελιώδης στη στατιστική:

• Περιγραφική στατιστική: Μελετάμε το μοντέλο δεδομένων
  • “Ο μέσος όρος του δείγματός μου είναι 60.1 mm”
• Επαγωγική στατιστική: Χρησιμοποιούμε το μοντέλο δεδομένων για να βγάλουμε συμπεράσματα για το μοντέλο της ΔΠΔ
  • “Εκτιμώ ότι ο μέσος όρος του πληθυσμού είναι κοντά στα 60.1 mm”

Μερικές φορές οι φοιτητές πιστεύουν ότι ο βασικός σκοπός της στατιστικής ανάλυσης είναι να υπολογίσουν κάποιους δείκτες. Αλλά η στατιστική δεν αφορά κυρίως τους υπολογισμούς. Είναι κατά κύριο λόγο ένας τρόπος σκέψης για το πώς να ερμηνεύσουμε αυτούς τους υπολογισμούς. Στη στατιστική, η κατανόηση του τι προσπαθούμε να υπολογίσουμε μπορεί να είναι εξίσου σημαντική με τους ίδιους τους υπολογισμούς.

Η χρήση μαθηματικών συμβόλων είναι ένας τρόπος με τον οποίο κάνουμε τη σκέψη μας ξεκάθαρη σχετικά με το τι προσπαθούμε να υπολογίσουμε, και τι σημαίνουν τα αποτελέσματα των υπολογισμών μας. Επειδή η διάκριση μεταξύ στατιστικών (ή εκτιμητών) και παραμέτρων είναι κρίσιμη, χρησιμοποιούμε διαφορετικά σύμβολα για να τα διακρίνουμε.

Αν θέλουμε να εκφράσουμε το μέσο όρο που υπολογίζεται από τα δεδομένα (δείγμα), συνήθως χρησιμοποιούμε το σύμβολο \(\bar{Y}\) (ή, μερικές φορές, το \(\bar{X}\)). Για να εκφράσουμε το μέσο όρο του πληθυσμού, συνήθως χρησιμοποιούμε το ελληνικό γράμμα \(\mu\).

Η ίδια διάκριση εμφανίζεται και στη σημειολογία του Γενικού Γραμμικού Μοντέλου. Το κενό μοντέλο που έχουμε συζητήσει μέχρι στιγμής, το οποίο υπολογίζεται από τα δεδομένα, γράφεται ως εξής (όπως ήδη γνωρίζετε):

\[Y_i = b_0 + e_i\]

Το μοντέλο της ΔΠΔ που προσπαθούμε να εκτιμήσουμε όταν προσαρμόζουμε το κενό μοντέλο γράφεται ως εξής:

\[Y_i = \beta_0 + \epsilon_i\] Σημειώστε ότι σε αυτό το μοντέλο του πληθυσμού έχουμε αντικαταστήσει τους εκτιμητές \(b_0\) και \(e_i\) με τα ελληνικά γράμματα \(\beta_0\) και \(\epsilon_i\). Το \(b_0\) είναι ο εκτιμητής για το \(\beta_0\), το οποίο χρησιμοποιείται για να εκφράσει το μέσο όρο του πληθυσμού· και το \(e_i\) είναι ο εκτιμητής για το \(\epsilon_i\).

Όποτε βλέπετε ελληνικά γράμματα μπορείτε να είστε αρκετά σίγουροι ότι πρόκειται για παραμέτρους του πληθυσμού. Λατινικά γράμματα χρησιμοποιούνται γενικά για να εκφράσουν εκτιμητές που υπολογίζονται από τα δεδομένα. Τα μοντέλα συχνά αναφέρονται με τον αριθμό των παραμέτρων που εκτιμώνται. Το κενό μοντέλο μπορεί να αναφερθεί ως «μοντέλο μίας παραμέτρου» επειδή εκτιμάται μόνο μία παράμετρος (η \(\beta_0\)).

empty_model <- lm(Thumb ~ NULL, data = Fingers)
empty_model

Call:
lm(formula = Thumb ~ NULL, data = Fingers)

Coefficients:
(Intercept)  
       60.1

Όταν εκτελέσαμε τον παραπάνω κώδικα για να προσαρμόσουμε το κενό μοντέλο στα δεδομένα μας για τα μήκη αντίχειρα από το πλήρες σύνολο δεδομένων Fingers, τι ήταν ο αριθμός 60.1;

Στατιστικό;

ΝαιΌχι

Παράμετρος;

ΝαιΌχι

Εκτιμητής παραμέτρου;

ΝαιΌχι

Επεξήγηση

Σωστές απαντήσεις: Α (Στατιστικό) και Γ (Εκτιμητής παραμέτρου)

Ο αριθμός 60.1 είναι και στατιστικό και εκτιμητής παραμέτρου ταυτόχρονα, αλλά όχι παράμετρος.

Ανάλυση:

Α - Στατιστικό - ΣΩΣΤΟ ✓

Ο αριθμός 60.1 είναι στατιστικό επειδή: - Υπολογίστηκε από τα δεδομένα του δείγματος - Είναι ο δειγματικός μέσος όρος: \(\bar{x} = \frac{\sum x_i}{n}\) - Περιγράφει το δείγμα των 157 φοιτητών - Είναι γνωστό - το υπολογίσαμε από τα δεδομένα μας

Β - Παράμετρος - ΛΑΘΟΣ ✗

Ο αριθμός 60.1 δεν είναι παράμετρος επειδή: - Μια παράμετρος περιγράφει τη ΔΠΔ (πληθυσμό), όχι το δείγμα - Οι παράμετροι είναι άγνωστες και συμβολίζονται με ελληνικά γράμματα (\(\mu\), \(\sigma\)) - Η πραγματική παράμετρος \(\mu\) (μέσος όρος πληθυσμού) είναι άγνωστη - Ο αριθμός 60.1 είναι υπολογισμένος από το δείγμα, όχι η πραγματική τιμή του πληθυσμού

Γ - Εκτιμητής παραμέτρου - ΣΩΣΤΟ ✓

Ο αριθμός 60.1 είναι εκτίμηση της τιμής της παραμέτρου επειδή: - Χρησιμοποιούμε αυτή την τιμή για να εκτιμήσουμε την άγνωστη παράμετρο \(\mu\) - Συμβολίζεται ως \(\hat{\mu}\)$ - Είναι η καλύτερη εκτίμησή μας για τον πραγματικό μέσο όρο του πληθυσμού - Βασίζεται στο δείγμα για να βγάλουμε συμπεράσματα για τον πληθυσμό

Κατανοώντας τους ρόλους:

\[\begin{align} \text{Δειγματικός μέσος} &: \bar{x} = 60.1 \text{ mm} \quad \text{(Statistic)} \\ \text{Εκτιμητής παραμέτρου} &: \hat{\mu} = 60.1 \text{ mm} \quad \text{(Parameter estimate)} \\ \text{Άγνωστη παράμετρος} &: \mu = ? \quad \text{(Parameter)} \end{align}\]

Αναλογία:

Σκεφτείτε το ως: - Στατιστικό: “Στο δείγμα των 157 φοιτητών, ο μέσος όρος είναι 60.1 mm” - Εκτιμητής παραμέτρου: “Βάσει αυτού του δείγματος, εκτιμώ ότι ο μέσος όρος μήκους αντίχειρα όλων των φοιτητών είναι περίπου 60.1 mm” - Παράμετρος: “Ο πραγματικός μέσος όρος όλων των φοιτητών στον κόσμο (που δεν θα μάθουμε ποτέ)”

Στα αποτελέσματα της R:

Coefficients:
(Intercept)  
       60.1 

Αυτό σημαίνει: - Στατιστικό: Ο υπολογισμένος μέσος όρος από τα δεδομένα - Εκτίμηση: Η εκτίμησή μας για τον πληθυσμιακό μέσο - Μοντέλο: \(\text{Thumb} = 60.1 + \text{error}\)

Σημαντικό:

Ο ίδιος αριθμός (60.1) μπορεί να είναι: 1. Στατιστικό όταν τον βλέπουμε ως υπολογισμό από το δείγμα 2. Εκτίμηση παραμέτρου όταν τον χρησιμοποιούμε για να καταλήξουμε σε συμπεράσματα για τον πληθυσμό

Αυτό δεν είναι αντίφαση - είναι δύο διαφορετικές οπτικές του ίδιου αριθμού: - Περιγραφική στατιστική (στατιστικό): Τι βλέπουμε στα δεδομένα - Επαγωγική στατιστική (εκτίμηση): Τι συμπεραίνουμε για τον πληθυσμό

Παράδειγμα με θερμόμετρο: - Μέτρηση (στατιστικό): “Το θερμόμετρο δείχνει 23°C” - Εκτίμηση (εκτίμηση παραμέτρου): “Εκτιμώ ότι η πραγματική θερμοκρασία είναι περίπου 23°C” - Πραγματικότητα (παράμετρος): Η πραγματική θερμοκρασία (που δεν γνωρίζουμε με απόλυτη ακρίβεια)

Στη σημειολογία του GLM (Γενικευμένου Γραμμικού Μοντέλου), το 60.1 θα αναπαρασταθεί ως \(\beta_0\) ή ως \(b_0\);

\(\beta_0\) (παράμετρος πληθυσμού)\(b_0\) (εκτιμητής παραμέτρου)

Επεξήγηση

\(b_0\) (εκτιμητής παραμέτρου) είναι η σωστή απάντηση.

Διάκριση στη σημειολογία GLM:

\(\beta_0\) (ελληνικό γράμμα): - Η πραγματική, άγνωστη παράμετρος του πληθυσμού - Περιγράφει τη Διαδικασία Παραγωγής Δεδομένων (ΔΠΔ) - Σταθερή τιμή που δεν γνωρίζουμε ποτέ - Θεωρητική παράμετρος που θέλουμε να εκτιμήσουμε

\(b_0\) (λατινικό γράμμα): - Η εκτίμηση της παραμέτρου βάσει δείγματος - Υπολογισμένη τιμή από τα δεδομένα μας - Στατιστικό που χρησιμοποιείται για εκτίμηση του \(\beta_0\) - Γνωστή τιμή (60.1 στην περίπτωσή μας)

Γιατί το 60.1 είναι \(b_0\):

1. Προέρχεται από δείγμα: Υπολογίστηκε από τα δεδομένα των 157 φοιτητών
2. Είναι γνωστό: Το υπολογίσαμε με το R
3. Είναι εκτιμητής: Χρησιμοποιείται για να εκτιμήσει την άγνωστη παράμετρο \(\beta_0\)
4. Μεταβλητό: Αν πάρουμε διαφορετικό δείγμα, θα πάρουμε διαφορετική τιμή

Στο κενό μοντέλο:

Μοντέλο πληθυσμού (ΔΠΔ): \[Y_i = \beta_0 + \epsilon_i\] όπου το \(\beta_0\) είναι άγνωστο

Εκτιμημένο μοντέλο: \[\hat{Y_i} = b_0 = 60.1\] όπου \(b_0 = 60.1\) είναι η εκτίμησή μας

Παράδειγμα διάκρισης:

Πραγματικός μέσος όρος πληθυσμού:     β₀ = ? (άγνωστο)
Δειγματικός μέσος όρος:           b₀ = 60.1 mm (γνωστό)
Εκτίμηση για τον πληθυσμό:       b₀ = 60.1 ≈ β₀

Σημειολογία ελληνικά vs λατινικά:

Ελληνικά γράμματα (\(\alpha, \beta, \gamma, \mu, \sigma\)): - **Παράμετροι πληθυσμού* (άγνωστες) - Θεωρητικές τιμές της ΔΠΔ

Λατινικά γράμματα (\(a, b, c, \bar{x}, s\)): - Εκτιμήσεις και στατιστικά δείγματος (γνωστές) - Υπολογισμένες τιμές από δεδομένα

Στα αποτελέσματα της R:

Coefficients:
(Intercept)  
       60.1  

Αυτό το 60.1 είναι: - Η εκτιμημένη τιμή της παραμέτρου (\(b_0\)) - Όχι η πραγματική παράμετρος (\(\beta_0\))

Γιατί η διάκριση είναι σημαντική:

1. Σαφήνεια: Ξεκαθαρίζει τι γνωρίζουμε vs τι εκτιμούμε
2. Αβεβαιότητα: Υπενθυμίζει ότι υπάρχει σφάλμα εκτίμησης
3. Θεωρία: Διαχωρίζει το μοντέλο πληθυσμού από το εκτιμημένο μοντέλο
4. Επικοινωνία: Αποφεύγει σύγχυση μεταξύ παραμέτρων και εκτιμήσεων

Παραδείγματα αντιστοιχιών:

Παράμετρος πληθυσμού	Εκτίμηση δείγματος
\(\beta_0\)	\(b_0\)
\(\beta_1\)	\(b_1\)
\(\mu\)	\(\bar{x}\)
\(\sigma\)	\(s\)
\(\sigma^2\)	\(s^2\)

Σύνοψη:

\[\begin{align} \text{Πραγματικότητα (άγνωστη):} \quad & \text{Thumb} = \beta_0 + \epsilon \\ \text{Εκτίμηση (από δείγμα):} \quad & \text{Thumb} = b_0 + \text{residual} \\ & \text{όπου } b_0 = 60.1 \end{align}\]

Το 60.1 είναι η εκτιμησή μας (\(b_0\)) για την άγνωστη πραγματικότητα (\(\beta_0\)).

Όπως αποδεικνύεται, ελλείψει άλλων πληροφοριών για τα υποκείμενα μιας μελέτης, ο μέσος όρος του δείγματός μας είναι η καλύτερη εκτίμηση που έχουμε για τον πραγματικό μέσο όρο του πληθυσμού. Είναι εξίσου πιθανό να είναι πολύ υψηλός όσο και πολύ χαμηλός, καθιστώντας τον αμερόληπτο εκτιμητή της τιμής της παραμέτρου.

Επειδή είναι η καλύτερη εικασία μας για το ποια είναι η παράμετρος του πληθυσμού, η τιμή του είναι η καλύτερη πρόβλεψη που έχουμε για την τιμή μιας μελλοντικής παρατήρησης. Ενώ σίγουρα θα είναι λανθασμένος, ο μέσος όρος θα κάνει καλύτερη δουλειά από οποιονδήποτε άλλο αριθμό.

Αντιστοιχίστε κάθε έννοια με το σύμβολό της.

Μέσος όρος πληθυσμού:

\(e_i\)\(\epsilon_i\)\(\mu\)\(\bar{Y}\)

Σφάλμα γύρω από ένα μοντέλο πληθυσμού:

\(e_i\)\(\epsilon_i\)\(\mu\)\(\bar{Y}\)

Μέσος όρος δείγματος:

\(e_i\)\(\epsilon_i\)\(\mu\)\(\bar{Y}\)

Σφάλμα γύρω από ένα μοντέλο δείγματος:

\(e_i\)\(\epsilon_i\)\(\mu\)\(\bar{Y}\)

Επεξήγηση

Σωστές αντιστοιχίες:

Μέσος όρος πληθυσμού → \(\mu\) - Ελληνικό γράμμα μι - Παράμετρος πληθυσμού (άγνωστη) - Πραγματικός μέσος όρος της ΔΠΔ

Σφάλμα πληθυσμού → \(\epsilon_i\) (epsilon) - Ελληνικό γράμμα έψιλον - Θεωρητικό σφάλμα στο μοντέλο πληθυσμού - Η διαφορά μεταξύ πραγματικής τιμής και παραμέτρου

Μέσος όρος δείγματος → \(\bar{Y}\) (Y-bar) - Λατινικό γράμμα με παύλα πάνω - Υπολογισμένος από το δείγμα - Στατιστικό δείγματος (γνωστό)

Σφάλμα δείγματος → \(e_i\) - Λατινικό γράμμα e (error) - Υπόλοιπο - υπολογισμένο σφάλμα από το δείγμα - Διαφορά: παρατηρούμενη τιμή - προβλεπόμενη τιμή

Κανόνας διάκρισης:

Ελληνικά γράμματα → Πληθυσμός (άγνωστα) - \(\mu, \sigma, \beta, \epsilon\) - Θεωρητικές έννοιες

Λατινικά γράμματα → Δείγμα (γνωστά) - \(\bar{x}, s, b, e\) - Υπολογισμένες τιμές

Παράδειγμα:

Μοντέλο πληθυσμού: \[Y_i = \mu + \epsilon_i\]

Μοντέλο δείγματος: \[Y_i = \bar{Y} + e_i\] \[\text{όπου } e_i = Y_i - \bar{Y}\]

Συγκεκριμένα: - \(\mu\) ≈ άγνωστο (πραγματικός μέσος) - \(\bar{Y} = 60.1\) mm (υπολογισμένος από δείγμα) - \(\epsilon_i\) = θεωρητικό σφάλμα (άγνωστο) - \(e_i = Y_i - 60.1\) (υπολογισμένο υπόλοιπο)

Ποιο είναι το σωστό;

Περιγράφει ένα δείγμα:

ΠαράμετροςΣτατιστικό

Περιγράφει έναν πληθυσμό:

ΠαράμετροςΣτατιστικό

Επεξήγηση

Σωστές αντιστοιχίες:

Περιγράφει ένα δείγμα → Στατιστικό

Περιγράφει έναν πληθυσμό → Παράμετρος

Βασική διάκριση:

Παράμετρος: - Περιγράφει τον πληθυσμό - Άγνωστη τιμή - Σταθερή (δεν αλλάζει) - Συμβολίζεται με ελληνικά γράμματα: \(\mu\), \(\sigma\), \(\beta_0\) - Παράδειγμα: Ο μέσος όρος μήκους αντίχειρα όλων των ανθρώπων

Στατιστικό: - Περιγράφει το δείγμα (sample) - Γνωστή τιμή (υπολογισμένη) - Μεταβλητή (αλλάζει από δείγμα σε δείγμα) - Συμβολίζεται με λατινικά γράμματα: \(\bar{x}\), \(s\), \(b_0\) - Παράδειγμα: Ο μέσος όρος μήκους αντίχειρα των 157 φοιτητών στο δείγμα

Μνημονικός κανόνας:

• Παράμετρος → Πληθυσμός
• Στατιστικό → Δείγμα

Παραδείγματα:

Έννοια	Παράμετρος	Στατιστικό
Μέσος όρος	\(\mu\)	\(\bar{x}\)
Τυπική απόκλιση	\(\sigma\)	\(s\)
Διασπορά	\(\sigma^2\)	\(s^2\)
Αναλογία	\(p\)	\(\hat{p}\)
Σταθερός όρος	\(\beta_0\)	\(b_0\)

Στο πλαίσιο δεδομένων Fingers:

Παράμετρος (άγνωστη): - \(\mu\) = Ο πραγματικός μέσος όρος μήκους αντίχειρα στον πληθυσμό - Δεν τον γνωρίζουμε ποτέ με βεβαιότητα

Στατιστικό (γνωστό): - \(\bar{x} = 60.1\) mm = Ο μέσος όρος των 157 φοιτητών στο δείγμα - Τον υπολογίσαμε με ακρίβεια από τα δεδομένα μας

Σχέση μεταξύ τους:

Χρησιμοποιούμε το στατιστικό (γνωστό) για να εκτιμήσουμε την παράμετρο (άγνωστη):

\[\text{Στατιστικό} \rightarrow \text{εκτιμά την} \rightarrow \text{Παράμετρο}\] \[\bar{x} = 60.1 \rightarrow \text{εκτίμηση του} \rightarrow \mu ≈ 60.1\]

Γιατί είναι σημαντική η διάκριση:

1. Βεβαιότητα: Γνωρίζουμε τα στατιστικά, εκτιμούμε τις παραμέτρων
2. Μεταβλητότητα: Τα στατιστικά αλλάζουν, οι παράμετροι μένουν σταθερές
3. Στόχος: Θέλουμε να μάθουμε για τον πληθυσμό (παράμετροι) από το δείγμα (στατιστικά)
4. Αβεβαιότητα: Κάθε στατιστικό είναι μια εκτίμηση της αντίστοιχης παραμέτρου με σφάλμα

Ποια είναι η διαφορά ανάμεσα στο \(b_0\) και το \(\bar{Y}\);

Ποια είναι η διαφορά ανάμεσα στο \(b_0\) και το \(\beta_0\);

6.10 Ανακεφαλαίωση

Ας αφιερώσουμε μια στιγμή για να σκεφτούμε πόσο μακριά έχετε ήδη φτάσει σε αυτό το μάθημα. Ως αποτέλεσμα της σκληρής δουλειάς και της επιμονής σας, έχετε αποκτήσει γνώσεις για το πώς τα δεδομένα στον κόσμο μπορούν να οργανώνονται, να οπτικοποιούνται και να συνοψίζονται!

Μέχρι αυτό το κεφάλαιο, χρησιμοποιούσαμε την ιδέα ΔΕΔΟΜΕΝΑ = ΜΟΝΤΕΛΟ + ΣΦΑΛΜΑ με ποιοτικό τρόπο. Βασιστήκαμε σε αυτήν την ποιοτική προσέγγιση σε αυτό το κεφάλαιο για να εισάγουμε το πρώτο μας στατιστικό μοντέλο—το απλό (ή κενό) μοντέλο, το οποίο εκφράσαμε ως ΔΕΔΟΜΕΝΑ = ΜΕΣΟΣ ΟΡΟΣ + ΣΦΑΛΜΑ. Μόλις αντιλαμβανόμαστε ένα μοντέλο ως αριθμό, τότε μπορούμε να είμαστε πιο συγκεκριμένοι: μπορούμε να είμαστε συγκεκριμένοι για το ποιον αριθμό χρησιμοποιούμε για το μοντέλο μας, και πώς να τον υπολογίσουμε. Και, μπορούμε να είμαστε πιο συγκεκριμένοι για το νόημα του σφάλματος, ορίζοντάς το ως τη διαφορά μεταξύ της πρόβλεψης του μοντέλου μας και μιας πραγματικής παρατηρούμενης τιμής (δηλ., το υπόλοιπο).

Αλλά στη συνέχεια προχωρήσαμε και προσθέσαμε ένα σωρό σύμβολα, που φαίνεται να περιπλέκουν τα πάντα. Κατά μια έννοια, όντως περιπλέκουν τα πάντα. Αλλά κατά μια άλλη έννοια, απλοποιούν τα πάντα, ειδικά καθώς προχωράμε. Υπάρχουν μερικές βασικές ιδέες που πρέπει να κρατήσουμε ξεκάθαρες καθώς συνεχίζουμε να δουλεύουμε με μοντέλα, και η σημειολογία που παρουσιάσαμε θα μας βοηθήσει να το κάνουμε αυτό.

Θυμηθείτε: ο στόχος μας είναι να χρησιμοποιήσουμε μια κατανομή δεδομένων για να κατασκευάσουμε ένα στατιστικό μοντέλο της κατανομής του πληθυσμού.

	Δεδομένα	Πληθυσμός
	Μοντέλο που κατασκευάζεται βάσει δεδομένων	Μοντέλο που προσπαθούμε να εκτιμήσουμε
	(εκτιμημένο)	(άγνωστο)
Λεκτική εξίσωση	Μήκος αντίχειρα ατόμου \(i\) = μέσος όρος δείγματος + σφάλμα	Μήκος αντίχειρας ατόμου \(i\) = μέσος όρος πληθυσμού + σφάλμα
Σημειογραφία για μοντέλο μιας παραμέτρου που χρησιμοποιεί τον μέσο όρο	\(Y_i = \bar{Y} + e_i\)	\(Y_i = \mu + \varepsilon_i\)
	• \(Y_i\) είναι ο αντίχειρας του ατόμου \(i\)	• \(Y_i\) είναι ο αντίχειρας του ατόμου \(i\)
	• \(\bar{Y}\) είναι ο μέσος όρος του δείγματος	• \(\mu\) είναι ο μέσος όρος του πληθυσμού (άγνωστος)
	• \(e_i\) είναι η διαφορά μεταξύ του μήκους αντίχειρα του ατόμου \(i\) και του μέσου όρου του δείγματος	• \(\varepsilon_i\) είναι η διαφορά μεταξύ του μήκους αντίχειρα του ατόμου \(i\) και του μέσου όρου του πληθυσμού (άγνωστος)
Σημειογραφία για οποιοδήποτε μοντέλο μιας παραμέτρου	\(Y_i = b_0 + e_i\)	\(Y_i = \beta_0 + \varepsilon_i\)
	• Μπορεί να χρησιμοποιηθεί για να αντιπροσωπεύσει οποιοδήποτε μοντέλο μιας παραμέτρου όχι μόνο τον μέσο όρο	• Μπορεί να χρησιμοποιηθεί για να αντιπροσωπεύσει οποιοδήποτε μοντέλο μιας παραμέτρου του πληθυσμού, όχι μόνο τον μέσο όρο

6.11 Ερωτήσεις Επανάληψης Κεφαλαίου 6

1. Ποια είναι η μονάδα παρατήρησης στο παρακάτω πλαίσιο δεδομένων;

Δεδομένα BikeCommute: Ένα άτομο που μετακινείται στη δουλειά με ποδήλατο κάθε μέρα κρατούσε αρχείο διαφόρων μεταβλητών για 56 διαδρομές.

    Bike     Date Distance    Time Minutes AvgSpeed TopSpeed Seconds Month
1  Steel 20/01/10    27.20 1:55:04  115.07    14.10    31.50    6904  1Jan
2 Carbon 21/01/10    27.46 1:55:35  115.58    14.25    30.64    6935  1Jan
3  Steel 25/01/10    27.20 1:55:45  115.75    14.10    30.92    6945  1Jan
4 Carbon 26/01/10    27.52 1:53:56  113.93    14.49    33.02    6836  1Jan
5 Carbon 27/01/10    27.51 1:59:12  119.20    13.84    30.92    7152  2Feb
6  Steel 01/02/10    27.17 1:48:44  108.73    14.99    32.09    6524  2Feb

Ποδήλατα (Bikes)Γραμμές (Rows)Διαδρομές με ποδήλατο (Bike commutes)Ποδηλάτες (Bikers)

Επεξήγηση

Διαδρομές με ποδήλατο (Bike commutes) είναι η σωστή απάντηση.

Τι είναι η μονάδα παρατήρησης (observational unit):

Η μονάδα παρατήρησης είναι αυτό για το οποίο συλλέγουμε δεδομένα. Είναι η βασική οντότητα που περιγράφει κάθε γραμμή στο σύνολο δεδομένων.

Ανάλυση των δεδομένων:

Τι αντιπροσωπεύει κάθε γραμμή: - Κάθε γραμμή περιγράφει μία διαδρομή από το σπίτι στη δουλειά - Κάθε γραμμή έχει: ημερομηνία, απόσταση, χρόνος, ταχύτητα, τύπος ποδηλάτου - Συνολικά 56 γραμμές = 56 διαφορετικές διαδρομές - Όλες από τον ίδιο ποδηλάτη, αλλά διαφορετικές ημέρες/διαδρομές

Γιατί οι άλλες επιλογές είναι λάθος:

Α - Ποδήλατα (Bikes) - ΛΑΘΟΣ: - Υπάρχουν τουλάχιστον δύο τύποι ποδηλάτων (Steel και Carbon) - Αλλά έχουμε 56 παρατηρήσεις - Ο ίδιος τύπος ποδηλάτου χρησιμοποιείται σε πολλές διαδρομές Β - Γραμμές (Rows) - ΛΑΘΟΣ: - Πολύ γενικό και δεν περιγράφει το περιεχόμενο - Οι “γραμμές” είναι η δομή των δεδομένων, όχι η έννοια - Δεν μας λέει τι μετράμε

Δ - Ποδηλάτες (Bikers) - ΛΑΘΟΣ: - Υπάρχει μόνο ένας ποδηλάτης (το άτομο που κρατά το αρχείο) - Αλλά έχουμε 56 παρατηρήσεις - Αν η μονάδα ήταν “ποδηλάτες”, θα είχαμε μόνο 1 γραμμή

2. Ας πούμε ότι θέλουμε να γράψουμε μια λεκτική εξίσωση για να εξηγήσουμε τη μεταβλητότητα στον χρόνο που χρειάζεται για να πάει κάποιος με ποδήλατο στη δουλειά (Time). Πιστεύουμε ότι η μεταβλητή Distance (απόσταση) της διαδρομής είναι μια σημαντική ανεξάρτητη μεταβλητή. Ποια θα ήταν η λεκτική εξίσωση;

Άλλα πράγματα = Distance + TimeDistance = Time + άλλα πράγματαModel = Time + DistanceTime = Distance + άλλα πράγματα

Επεξήγηση

Time = Distance + άλλα πράγματα είναι η σωστή απάντηση.

Δομή λεκτικής εξίσωσης:

Μια λεκτική εξίσωση έχει τη μορφή:

Εξαρτημένη = Ανεξάρτητη + άλλα πράγματα

Αναγνώριση ρόλων:

Εξαρτημένη μεταβλητή: - Αυτό που θέλουμε να εξηγήσουμε - Στην ερώτηση: “τη μεταβλητότητα στον χρόνο που χρειάζεται” - Άρα: η Time είναι η εξαρτημένη

Ανεξάρτητη μεταβλητή: - Αυτό που χρησιμοποιούμε για εξήγηση - Στην ερώτηση: “η Distance είναι σημαντική ανεξάρτητη μεταβλητή” - Άρα: η Distance είναι η ανεξάρτητη

“άλλα πράγματα”: - Όλοι οι άλλοι παράγοντες που επηρεάζουν τον χρόνο - Παραδείγματα: άνεμος, κίνηση, κόπωση, κλίση δρόμου, καιρός

Λογική της εξίσωσης:

Time = Distance + άλλα πράγματα σημαίνει: “Ο χρόνος που χρειάζεται ο ποδηλάτος εξηγείται από την απόσταση συν άλλους παράγοντες”

Γιατί οι άλλες επιλογές είναι λάθος:

Α - άλλα πράγματα = Distance + Time - ΛΑΘΟΣ: - Τo “άλλα πράγματα” δεν είναι αυτό που θέλουμε να εξηγήσουμε - Είναι περίεργο να θέλουμε να εξηγήσουμε “τα άλλα πράγματα” - Δεν ταιριάζει με το ερώτημα

Β - Distance = Time + άλλα πράγματα - ΛΑΘΟΣ: - Αντίστροφη κατεύθυνση αιτιότητας - Θα σήμαινε: “η απόσταση εξηγείται από τον χρόνο” - Δεν έχει λογική - η απόσταση είναι σταθερή για κάθε διαδρομή - Ο χρόνος εξαρτάται από την απόσταση, όχι το αντίστροφο

Γ - Model = Time + Distance - ΛΑΘΟΣ: - Λάθος δομή - το “Model” δεν είναι μεταβλητή - Δεν διευκρινίζει ποια είναι η εξαρτημένη μεταβλητή - Δεν περιλαμβάνει το “άλλα πράγματα”

3. Ο μέσος όρος της απόστασης (Distance) που καλύπτουν οι διαδρομές αυτού του ποδηλάτη είναι λίγο πάνω από 27 μίλια. Φανταστείτε ότι ανακαλύψατε ότι μία από τις παρατηρήσεις σας έχει καταγραφεί λανθασμένα. Αντί για απόσταση γύρω στα 27 μίλια, η απόσταση για μία από τις διαδρομές είχε καταχωρηθεί ως 54 μίλια! Κάνετε τη διόρθωση στο πλαίσιο δεδομένων σας. Πώς θα επηρεάσει η διόρθωση το μέσο όρο;

Ο μέσος όρος δεν θα επηρεαστεί από τη διόρθωση.Ο μέσος όρος θα είναι χαμηλότερος λόγω της διόρθωσης.Ο μέσος όρος θα είναι υψηλότερος λόγω της διόρθωσης.Είναι αδύνατο να πούμε πώς θα επηρεαστεί ο μέσος όρος από τη διόρθωση.

Επεξήγηση

Ο μέσος όρος θα είναι χαμηλότερος λόγω της διόρθωσης είναι η σωστή απάντηση.

Ανάλυση της κατάστασης:

Πριν τη διόρθωση: - 55 παρατηρήσεις με ~27 μίλια - 1 λανθασμένη παρατήρηση με 54 μίλια - Η τιμή 54 είναι πολύ μεγαλύτερη από την πραγματική (~27)

Μετά τη διόρθωση: - 56 παρατηρήσεις με ~27 μίλια - Η τιμή 54 αντικαθίσταται με ~27

Επίδραση στο μέσο όρο:

Πώς επηρεάζει ο μέσος όρος: \[\bar{x} = \frac{\text{άθροισμα όλων των τιμών}}{n}\]

Αλλαγή στο άθροισμα: - Αφαιρούμε: 54 μίλια (λανθασμένη τιμή) - Προσθέτουμε: ~27 μίλια (σωστή τιμή) - Καθαρή αλλαγή: -27 μίλια (54 - 27 = 27 μίλια λιγότερα)

Επειδή το άθροισμα μειώνεται: \[\text{Νέος μέσος} = \frac{\text{Παλιό άθροισμα} - 27}{56} < \text{Παλιός μέσος}\]

Αριθμητικό παράδειγμα:

Υποθετικό σενάριο:

Πριν: 55 τιμές των ~27 + 1 τιμή των 54
Άθροισμα = 55 × 27 + 54 = 1485 + 54 = 1539
Μέσος = 1539 ÷ 56 = 27.48 μίλια

Μετά: 56 τιμές των ~27
Άθροισμα = 56 × 27 = 1512
Μέσος = 1512 ÷ 56 = 27.00 μίλια

Διαφορά: 27.48 - 27.00 = 0.48 μίλια λιγότερα

Γιατί οι άλλες επιλογές είναι λάθος:

Α - Δεν θα επηρεαστεί - ΛΑΘΟΣ: - Ο μέσος όρος πάντα επηρεάζεται από αλλαγές στις τιμές - Είναι ευαίσθητος σε κάθε παρατήρηση - Η αλλαγή από 54 σε 27 είναι μεγάλη και θα έχει επίδραση

Γ - Θα είναι υψηλότερος - ΛΑΘΟΣ: - Αντίθετη κατεύθυνση - Μειώνουμε μία μεγάλη τιμή (54) και την αντικαθιστούμε με μικρότερη (~27) - Αυτό μειώνει το άθροισμα, άρα και το μέσο όρο

Δ - Αδύνατο να προβλέψουμε - ΛΑΘΟΣ: - Μπορούμε να προβλέψουμε με βεβαιότητα - Γνωρίζουμε ότι 54 > 27, άρα η αντικατάσταση θα μειώσει το μέσο όρο - Η κατεύθυνση της αλλαγής είναι προβλέψιμη

Ευαισθησία του μέσου όρου:

Χαρακτηριστικά του μέσου όρου: - Ευαίσθητος σε ακραίες τιμές - Κάθε παρατήρηση επηρεάζει το αποτέλεσμα - Μεγάλες τιμές “τραβούν” το μέσο προς τα πάνω - Μικρές τιμές “τραβούν” το μέσο προς τα κάτω

Στην περίπτωσή μας: - Η λανθασμένη τιμή (54) ήταν ασυνήθιστη τιμή - “Τραβούσε” το μέσο προς τα πάνω - Με τη διόρθωση, αφαιρούμε αυτή την “τράβηγμα” - Ο μέσος “επιστρέφει” σε πιο φυσιολογικό επίπεδο

4. Πώς θα περιμέναμε αυτή η διόρθωση (αλλαγή από 54 πίσω σε 27) να επηρεάσει το μέσο όρο και τη διάμεσο;

Τόσο ο μέσος όρος όσο και η διάμεσος θα επηρεαστούν εξίσου από αυτή τη διόρθωση.Η διάμεσος θα επηρεαστεί πιθανότατα λιγότερο από ό,τι ο μέσος όρος.Η διάμεσος θα επηρεαστεί πιθανότατα περισσότερο από ό,τι ο μέσος όρος.Είναι αδύνατο να πούμε πώς θα επηρεαστεί η διάμεσος από τη διόρθωση.

Επεξήγηση

Η διάμεσος θα επηρεαστεί πιθανότατα λιγότερο από ό,τι ο μέσος όρος είναι η σωστή απάντηση.

Βασική διαφορά: Ευαισθησία σε outliers

Μέσος όρος: - Ευαίσθητος σε κάθε τιμή - Κάθε παρατήρηση επηρεάζει το αποτέλεσμα - Ακραίες τιμές έχουν μεγάλη επίδραση - Χρησιμοποιεί όλες τις τιμές στον υπολογισμό

Διάμεσος: - Ανθεκτική σε outliers - Εξαρτάται μόνο από τη μεσαία τιμή (ή τις δύο μεσαίες) - Δεν επηρεάζεται από τις ακραίες τιμές - Βασίζεται στη θέση, όχι στις τιμές

Ανάλυση της συγκεκριμένης κατάστασης:

Η ασυνήθιστη τιμή (54 μίλια): - Είναι διπλάσια από τις κανονικές τιμές (~27) - Είναι πολύ μεγαλύτερη από όλες τις άλλες παρατηρήσεις - Θα βρίσκεται στο τέλος της ταξινομημένης σειράς

Επίδραση στο μέσο όρο: \[\text{Αλλαγή στο μέσο} = \frac{27 - 54}{56} = \frac{-27}{56} ≈ -0.48 \text{ μίλια}\]

Επίδραση στη διάμεσο:

Με 56 παρατηρήσεις: - Διάμεσος = μέσος όρος της 28ης και 29ης τιμής (όταν είναι ταξινομημένες) - Το outlier (54) θα είναι η 56η τιμή (τελευταία) - Η 28η και 29η τιμή θα είναι και οι δύο περίπου 27 μίλια

Πριν τη διόρθωση:

Θέσεις: 1, 2, ..., 28, 29, ..., 55, 56
Τιμές:  27, 27, ..., 27, 27, ..., 27, 54
                    ↑   ↑
                   28η  29η → Διάμεσος ≈ 27

Μετά τη διόρθωση:

Θέσεις: 1, 2, ..., 28, 29, ..., 55, 56
Τιμές:  27, 27, ..., 27, 27, ..., 27, 27
                    ↑   ↑
                   28η  29η → Διάμεσος ≈ 27

Αποτέλεσμα: - Διάμεσος: Καμία αλλαγή (27 → 27) - Μέσος όρος: Σημαντική μείωση (~0.48 μίλια)

Γιατί συμβαίνει αυτό:

Η διάμεσος “δεν βλέπει” την ακραία τιμή: - Η ακραία τιμή είναι πάρα πολύ μακριά από το κέντρο - Η 28η και 29η τιμή δεν αλλάζουν - Η διάμεσος εξαρτάται μόνο από αυτές τις δύο τιμές

Ο μέσος όρος “βλέπει” όλα: - Κάθε τιμή συνεισφέρει στο άθροισμα - Το outlier “τραβάει” όλο το μέσο προς τα πάνω - Η αλλαγή του επηρεάζει άμεσα το αποτέλεσμα

Γενική αρχή:

Ανθεκτικά (robust) vs Μη ανθεκτικά (non-robust) στατιστικά:

Robust (ανθεκτικά): - Διάμεσος: Δεν επηρεάζεται από ακραίες τιμές - Interquartile Range (IQR): Ανθεκτικό στις ακραίες τιμές - Mode: Δεν επηρεάζεται από ακραίες τιμές

Non-robust (μη ανθετικά): - Μέσος όρος: Επηρεάζεται από κάθε τιμή - Τυπική απόκλιση: Ευαίσθητη σε ακραίες τιμές - Range: Εξαρτάται από τις ακραίες τιμές

Πρακτικό παράδειγμα:

Δεδομένα: 25, 26, 27, 27, 27, 27, 28, 28, 54

Μέσος όρος = (25+26+27+27+27+27+28+28+54)/9 = 269/9 ≈ 29.9
Διάμεσος = 27 (5η τιμή από 9)

Μετά τη διόρθωση: 25, 26, 27, 27, 27, 27, 27, 28, 28

Μέσος όρος = (25+26+27+27+27+27+27+28+28)/9 = 242/9 ≈ 26.9
Διάμεσος = 27 (5η τιμή από 9)

Αλλαγή: - Μέσος: 29.9 → 26.9 (μείωση 3.0) - Διάμεσος: 27 → 27 (καμία αλλαγή)

Πότε η διάμεσος επηρεάζεται:

Η διάμεσος θα επηρεαζόταν μόνο αν: - Η ακραία τιμή ήταν κοντά στο κέντρο της κατανομής - Αλλάζαμε μία από τις μεσαίες τιμές - Είχαμε πολύ μικρό δείγμα (π.χ., n=3)

Συμπέρασμα:

Αυτό το παράδειγμα δείχνει γιατί: - Η διάμεσος είναι καλύτερη όταν έχουμε ακραίες τιμές - Ο μέσος όρος μπορεί να παραπλανήσει με ακραίες τιμές - Το καθάρισμα των δεδομένων είναι κρίσιμο για τον μέσο όρο - Τα ανθετικά στατιστικά είναι πιο αξιόπιστα σε “μη τακτοποιημένα” δεδομένα

5. Πώς θα δημιουργούσατε ένα διάγραμμα για να εξετάσετε την κατανομή της Distance;

gf_histogram(~ Distance)gf_histogram(~ Distance, data = BikeCommute)gf_histogram(BikeCommute, Distance)gf_plot(~ Distance$BikeCommute)

Επεξήγηση

gf_histogram(~ Distance, data = BikeCommute) είναι η σωστή απάντηση.

Σωστή σύνταξη της gf_histogram:

Πλήρης μορφή:

gf_histogram(~ μεταβλητή, data = όνομα_πλαισίου_δεδομένων)

Στην περίπτωσή μας:

gf_histogram(~ Distance, data = BikeCommute)

Γιατί αυτή είναι η σωστή μορφή:

1. ~ (tilde): Δηλώνει τη μεταβλητή για την κατανομή
2. Distance: Η μεταβλητή που θέλουμε να εξετάσουμε
3. data = BikeCommute: Καθορίζει το πλαίσιο δεδομένων που περιέχει τη μεταβλητή

Γιατί οι άλλες επιλογές είναι λάθος:

Α - gf_histogram(~ Distance) - ΑΤΕΛΗΣ: - Λείπει το data = BikeCommute - Η R δεν θα ξέρει που να βρει τη μεταβλητή Distance - Θα δώσει σφάλμα: “object ‘Distance’ not found” - Θα λειτουργήσει μόνο αν έχουμε κάνει attach(BikeCommute) πρώτα (δεν συνιστάται)

Γ - gf_histogram(BikeCommute, Distance) - ΛΑΘΟΣ ΣΕΙΡΑ: - Λάθος σύνταξη - το πλαίσιο δεδομένων δεν μπαίνει πρώτο - Η gf_histogram() περιμένει πρώτα την εξίσωση, και μετά τα δεδομένα - Θα δώσει σφάλμα

Δ - gf_plot(~ Distance$BikeCommute) - ΠΟΛΛΑΠΛΑ ΛΑΘΗ: - Λάθος συνάρτηση: gf_plot() δεν υπάρχει - Λάθος σύνταξη: Distance$BikeCommute είναι ανάποδα - Θα έπρεπε να είναι BikeCommute$Distance αν θέλαμε αυτή τη μορφή - Αλλά ακόμα και έτσι, χρειαζόμαστε gf_histogram(), όχι gf_plot()

Εναλλακτικές σωστές μορφές:

1. Χρήση του $ operator:

gf_histogram(~ BikeCommute$Distance)

2. Με attach (δεν συνιστάται):

attach(BikeCommute)
gf_histogram(~ Distance)
detach(BikeCommute)

3. Χρήση with():

with(BikeCommute, gf_histogram(~ Distance))

Γιατί προτιμάμε το data =:

Πλεονεκτήματα: - Σαφήνεια: Φαίνεται ξεκάθαρα ποιο σύνολο δεδομένων χρησιμοποιούμε - Συνέπεια: Όλες οι gf_ συναρτήσεις δουλεύουν με αυτόν τον τρόπο - Ασφάλεια: Αποφεύγουμε τα προβλήματα του attach() - Αναγνωσιμότητα: Πιο εύκολο να καταλάβει κάποιος άλλος

Τι θα δείξει το ιστόγραμμα:

Για τη μεταβλητή Distance: - Κατανομή των αποστάσεων των 56 διαδρομών - Συχνότητα κάθε εύρους αποστάσεων - Σχήμα της κατανομής (κανονική, ασύμμετρη, κλπ.) - Ακραίες τιμές ή ασυνήθιστες τιμές - Κεντρική τάση και διασπορά

Αναμενόμενα χαρακτηριστικά: - Οι περισσότερες τιμές θα είναι γύρω στα 27 μίλια - Μικρή διασπορά (η διαδρομή είναι η ίδια) - Πιθανώς μια κορυφή γύρω στα 27 - Αν υπάρχει το ακραία τιμή (54), θα φαίνεται ως απομονωμένη μπάρα

Επιπλέον επιλογές:

Προσαρμογή του ιστογράμματος:

gf_histogram(~ Distance, data = BikeCommute, 
             bins = 20,                    # αριθμός bins
             fill = 'skyblue',            # χρώμα
             color = 'black',             # χρώμα περιγράμματος
             title = 'Κατανομή της Απόστασης')

6. Ποια από τις παρακάτω δηλώσεις είναι πάντα αληθής για το μέσο όρο, ανεξάρτητα από το σχήμα της κατανομής;

Ο μέσος όρος εξισορροπεί τις αποκλίσεις πάνω και κάτω από το μέσο όρο.Ο μέσος όρος εξισορροπεί τον αριθμό των τιμών πάνω και κάτω από το μέσο όρο.Ο μέσος όρος είναι το μέσο σημείο του εύρους.Όλα τα παραπάνω.

Επεξήγηση

Ο μέσος όρος εξισορροπεί τις αποκλίσεις πάνω και κάτω από το μέσο όρο είναι η σωστή απάντηση.

Θεμελιώδης ιδιότητα του μέσου όρου: \[\sum_{i=1}^{n}(x_i - \bar{x}) = 0\]

Αυτό ισχύει πάντα, ανεξάρτητα από το σχήμα της κατανομής: - Οι θετικές αποκλίσεις ακριβώς εξισορροπούν τις αρνητικές - Ο μέσος όρος είναι το σημείο ισορροπίας μαθηματικά - Αυτό δεν εξαρτάται από τη συμμετρία της κατανομής

Γιατί οι άλλες επιλογές είναι λάθος:

Β - “Εξισορροπεί τον αριθμό των τιμών” - ΛΑΘΟΣ: - Αυτό περιγράφει τη διάμεσο - Ο μέσος όρος δεν εξασφαλίζει ίσο αριθμό παρατηρήσεων εκατέρωθεν

Γ - “Είναι το μέσο σημείο του εύρους” - ΛΑΘΟΣ: - Διαφορετικός υπολογισμός: (min + max) / 2 ≠ Σ(xi) / n - Ειδικά σε ασύμμετρες κατανομές, αυτά διαφέρουν σημαντικά

Συμπέρασμα:

Η επιλογή Α είναι η μόνη μαθηματικά ακριβής από τις δοθείσες επιλογές. Παρόλο που ο μέσος όρος μπορεί να μη είναι το ιδανικό μοντέλο για μια ασύμμετρη κατανομή, η ιδιότητα της εξισορρόπησης των αποκλίσεων ισχύει πάντα και είναι ο βασικός λόγος για τον οποίο χρησιμοποιούμε το μέσο όρο ως μοντέλο.

7. Αυτός ο ποδηλάτης θεωρεί ότι ο τύπος του ποδηλάτου που χρησιμοποιεί επηρεάζει τη μέγιστη ταχύτητα που μπορεί να φτάσει. Για να πάρει μια ιδέα της κατανομής της μέγιστης ταχύτητας, κοιτάζει το παρακάτω αποτέλεσμα. Ποια συνάρτηση δημιούργησε αυτό το αποτέλεσμα;

   min   Q1 median      Q3 max     mean       sd  n missing
 29.58 32.4  33.59 34.7425  36 33.55571 1.478628 56       0

arrange()table()favstats()head()

Επεξήγηση

favstats() είναι η σωστή απάντηση.

Αναγνώριση του output:

Τι βλέπουμε: - min: 29.58 (ελάχιστη τιμή) - Q1: 32.4 (1ο τεταρτημόριο) - median: 33.59 (διάμεσος) - Q3: 34.7425 (3ο τεταρτημόριο) - max: 36 (μέγιστη τιμή) - mean: 33.55571 (μέσος όρος) - sd: 1.478628 (τυπική απόκλιση) - n: 56 (αριθμός παρατηρήσεων) - missing: 0 (αριθμός ελλειπουσών τιμών)

Αυτό είναι το χαρακτηριστικό αποτέλεσμα της favstats():

Η συνάρτηση favstats(): - Favorite statistics - αγαπημένα στατιστικά - Παρέχει συνοπτικά στατιστικά μιας μεταβλητής - Περιλαμβάνει όλα τα βασικά μέτρα: κεντρική τάση, διασπορά, θέση Σύνταξη:

favstats(~ TopSpeed, data = BikeCommute)
# ή
favstats(BikeCommute$TopSpeed)

Γιατί οι άλλες επιλογές είναι λάθος:

Α - arrange() - ΛΑΘΟΣ: - Η arrange() ταξινομεί τις γραμμές ενός πλαισίου δεδομένων - Δεν υπολογίζει στατιστικά - Το αποτέλεσμα θα ήταν το ταξινομημένο πλαίσιο δεδομένων, όχι αριθμητικά στατιστικά - Παράδειγμα αποτελέσματος: πλήρες πλαίσιο δεδομένων με τις παρατηρήσεις στη σειρά

Β - table() - ΛΑΘΟΣ: - Η table() μετράει παρατηρήσεις - Το αποτέλεσμα θα ήταν ένας πίνακας συχνοτήτων - Δεν υπολογίζει mean, sd, quartiles - Παράδειγμα αποτελέσματος: Steel: 28, Carbon: 28

Δ - head() - ΛΑΘΟΣ: - Η head() εμφανίζει τις πρώτες γραμμές ενός πλαισίου δεδομένων - Δεν υπολογίζει τίποτα - Το αποτέλεσμα θα ήταν οι πρώτες 6 γραμμές των δεδομένων - Παράδειγμα αποτελέσματος: γραμμές με Bike, Date, Distance, κ.λπ.

Σύγκριση με άλλες στατιστικές συναρτήσεις:

summary():

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max.
  29.58   32.40   33.59   33.56   34.74   36.00

Παρόμοιο, αλλά χωρίς sd, n, missing

mean(), median(), κ.λπ.:

[1] 33.55571

Μόνο μία τιμή κάθε φορά

describe() (από psych package): Διαφορετική μορφή με περισσότερες λεπτομέρειες

Πρακτική χρήση:

Για διερεύνηση δεδομένων:

# Γενική εικόνα
favstats(~ TopSpeed, data = BikeCommute)

# Ανά τύπο ποδηλάτου
favstats(TopSpeed ~ Bike, data = BikeCommute)

Τι μας λέει το αποτέλεσμα:

Για την TopSpeed: - Εύρος: 29.58 - 36.00 mph (εύρος ~6.4 mph) - Κεντρική τιμή: Median ≈ Mean (~33.6 mph) → σχεδόν συμμετρική - Διασπορά: sd = 1.48 → σχετικά χαμηλή μεταβλητότητα - Δεδομένα: Πλήρη (0 missing από 56 παρατηρήσεις)

IQR = Q3 - Q1 = 34.74 - 32.4 = 2.34 mph Το 50% των τιμών βρίσκεται σε εύρος 2.34 mph

8. Παρακάτω δίνεται το ιστόγραμμα της TopSpeed. Ποιος κώδικας δημιούργησε τη γραμμή που δείχνει το μέσο όρο;

gf_vline(xintercept = 33.6, color = "blue")gf_mean(mean = 33.6, color = "blue")gf_mean(33.6, color = "blue")Κανένα από τα παραπάνω

Επεξήγηση

gf_vline(xintercept = 33.6, color = "blue") είναι η σωστή απάντηση.

Τι βλέπουμε στο διάγραμμα: - Κάθετη μπλε γραμμή στη θέση ~33.6 στον άξονα x - Η γραμμή εκτείνεται από κάτω έως πάνω στο γράφημα - Βρίσκεται στη θέση του μέσου όρου (33.56 ≈ 33.6) - Κάθετη ως προς τον άξονα x (TopSpeed)

Η συνάρτηση gf_vline():

Σκοπός: - Vertical line = Κάθετη γραμμή - Προσθέτει κάθετες γραμμές σε ένα γράφημα - Χρησιμοποιείται για να επισημάνει συγκεκριμένες τιμές στον άξονα x

Σύνταξη:

gf_vline(xintercept = τιμή, color = χρώμα, linetype = τύπος)

Παράμετροι: - xintercept = 33.6: Η θέση στον άξονα x όπου θα σχεδιαστεί η γραμμή - color = "blue": Το χρώμα της γραμμής

Πλήρης κώδικας:

gf_histogram(~ TopSpeed, data = BikeCommute) %>%
  gf_vline(xintercept = 33.6, color = "blue")

Γιατί οι άλλες επιλογές είναι λάθος:

Β - gf_mean(mean = 33.6, color = "blue") - ΛΑΘΟΣ: - Δεν υπάρχει συνάρτηση gf_mean() στα πακέτα mosaic/ggformula - Αν υπήρχε, η σύνταξη θα ήταν διαφορετική - Θα έδινε σφάλμα: “could not find function ‘gf_mean’”

Γ - gf_mean(33.6, color = "blue") - ΛΑΘΟΣ: - Όπως και πάνω, η gf_mean() δεν υπάρχει - Η σύνταξη είναι επίσης λάθος

Δ - Κανένα από τα παραπάνω - ΛΑΘΟΣ: - Η επιλογή Α είναι σωστή

Πρακτική χρήση:

Γιατί προσθέτουμε τη γραμμή μέσου όρου: - Οπτική αναφορά: Βλέπουμε πού βρίσκεται το κέντρο - Σύγκριση: Σχετίζουμε τις τιμές με το μέσο όρο - Ερμηνεία: Καταλαβαίνουμε τη θέση της κατανομής - Ανάλυση: Εντοπίζουμε ασυμμετρίες ή ιδιαιτερότητες

Στο συγκεκριμένο γράφημα: - Η μπλε γραμμή (~33.6) φαίνεται να είναι λίγο αριστερά από την κορυφή - Αυτό υποδηλώνει ελαφρά αριστερή ασυμμετρία (left skew) - Ο μέσος όρος “τραβιέται” από τις χαμηλότερες τιμές στα αριστερά

9. Ποια από τις ακόλουθες δηλώσεις είναι αληθής για το κενό μοντέλο της μέγιστης ταχύτητας (TopSpeed);

Το μοντέλο θα ήταν ο καλύτερος τρόπος εξήγησης του πόσες μεταβλητές επηρεάζουν την TopSpeed (όπως η εποχή του έτους και ο τύπος ποδηλάτου).Το μοντέλο θα περιλάμβανε μόνο το μέσο όρο της TopSpeed.Το μοντέλο θα προέβλεπε διαφορετική τιμή της TopSpeed ανάλογα με την κατάσταση.Κανένα από τα παραπάνω.

Επεξήγηση

Το μοντέλο θα περιλάμβανε μόνο το μέσο όρο της TopSpeed είναι η σωστή απάντηση.

Τι είναι το κενό μοντέλο (Empty Model):

Ορισμός: Το κενό μοντέλο είναι το απλούστερο δυνατό μοντέλο που μπορούμε να δημιουργήσουμε:

Χαρακτηριστικά του κενού μοντέλου: - Δεν περιλαμβάνει καμία ανεξάρτητη μεταβλητή (όπως τύπος ποδηλάτου, εποχή) - Μία μόνο παράμετρος: ο μέσος όρος - Ίδια πρόβλεψη για όλες τις παρατηρήσεις - Μοντέλο αναφοράς για σύγκριση με πιο σύνθετα μοντέλα

**Ανάλυση κάθε επιλογής:**

**Α - "Καλύτερος τρόπος εξήγησης πολλών μεταβλητών" - ΛΑΘΟΣ:**
- Το κενό μοντέλο **δεν περιλαμβάνει** καμία εξηγητική μεταβλητή
- **Δεν εξηγεί** πώς άλλες μεταβλητές επηρεάζουν την TopSpeed
- Είναι το **απλούστερο**, όχι το καλύτερο για εξήγηση
- Αγνοεί εντελώς μεταβλητές όπως τύπος ποδηλάτου, καιρός, κλπ.

**Β - "Περιλαμβάνει μόνο το μέσο όρο" - ΣΩΣΤΟ:**
- Ακριβώς αυτό κάνει το κενό μοντέλο
- Περιλαμβάνει μόνο τον μέσο όρο $b_0 = 33.56$
- Καμία άλλη πληροφορία δεν χρησιμοποιείται
- Πρόβλεψη = μέσος όρος για όλους

**Γ - "Προβλέπει διαφορετική τιμή της TopSpeed ανάλογα με την κατάσταση" - ΛΑΘΟΣ:**
- Το κενό μοντέλο προβλέπει **πάντα την ίδια τιμή**
- Δεν "βλέπει" καμία κατάσταση (καιρός, ποδήλατο, κλπ.)
- Η πρόβλεψη είναι **σταθερή**: 33.56 για όλους

**Δ - "Κανένα από τα παραπάνω" - ΛΑΘΟΣ:**
- Η επιλογή Β είναι σωστή

**Πρακτικό παράδειγμα:**

**Κενό μοντέλο TopSpeed:**
```r
empty_model <- lm(TopSpeed ~ NULL, data = BikeCommute)
empty_model

# Output:
# Coefficients:
# (Intercept)
#      33.56

Προβλέψεις:

predict(empty_model)
# Όλες οι 56 προβλέψεις θα είναι 33.56

Συμπέρασμα: Το κενό μοντέλο είναι η απλούστερη μορφή μοντέλου που περιέχει μόνο το μέσο όρο. Δεν εξηγεί τίποτα για τους παράγοντες που επηρεάζουν την TopSpeed, αλλά αποτελεί ένα μοντέλο αναφοράς για την αξιολόγηση πιο σύνθετων μοντέλων.

10. Ποιον κώδικα θα χρησιμοποιούσατε για να προσαρμόσετε το κενό μοντέλο για την TopSpeed;

lm(TopSpeed ~ NULL, data = BikeCommute)gf(TopSpeed ~ NULL, data = BikeCommute)gf_histogram(NULL ~ TopSpeed, data = BikeCommute)NULL(TopSpeed, data = BikeCommute)

Επεξήγηση

lm(TopSpeed ~ NULL, data = BikeCommute) είναι η σωστή απάντηση.

Ανάλυση του σωστού κώδικα:

Η συνάρτηση lm(): - Linear Model - προσαρμόζει γραμμικά μοντέλα - Βασική συνάρτηση για της R - Χρησιμοποιείται για όλα τα μοντέλα του Γενικού Γραμμικού Μοντέλου

Η σύνταξη ~ NULL: - Σημειογραφία εξίσωσης στην R - TopSpeed ~ NULL σημαίνει: Η “TopSpeed εξαρτάται από τίποτα” - Το NULL υποδηλώνει καμία ανεξάρτητη μεταβλητή - Αυτό δημιουργεί το κενό μοντέλο (intercept-only model)

Παράμετρος data = BikeCommute: - Καθορίζει το πλαίσιο δεδομένων που περιέχει τη μεταβλητή TopSpeed - Απαραίτητο για να εντοπίσει η R τη μεταβλητή

Τι αποτέλεσμα θα δώσει:

empty_model <- lm(TopSpeed ~ NULL, data = BikeCommute)
empty_model

# Output:
# Call:
# lm(formula = TopSpeed ~ NULL, data = BikeCommute)
#
# Coefficients:
# (Intercept)
#      33.56

Γιατί οι άλλες επιλογές είναι λάθος:

Β - gf(TopSpeed ~ NULL, data = BikeCommute) - ΛΑΘΟΣ: - Δεν υπάρχει συνάρτηση gf() γενικά - Υπάρχουν gf_point(), gf_histogram(), κλπ., αλλά όχι απλό gf() - Οι gf_ συναρτήσεις δημιουργούν διαγράμματα, όχι μοντέλα - Θα έδινε σφάλμα: “could not find function ‘gf’”

Γ - gf_histogram(NULL ~ TopSpeed, data = BikeCommute) - ΛΑΘΟΣ: - Η gf_histogram() δημιουργεί ιστόγραμμα, όχι μοντέλο - Λάθος σύνταξη: Θα έπρεπε gf_histogram(~ TopSpeed, data = BikeCommute) - Το NULL ~ TopSpeed δεν έχει νόημα για ιστόγραμμα - Δεν “προσαρμόζει” τίποτα - απλά οπτικοποιεί

Δ - NULL(TopSpeed, data = BikeCommute) - ΛΑΘΟΣ: - Το NULL δεν είναι συνάρτηση - Είναι μια ειδική τιμή στην R που σημαίνει “τίποτα” - Θα έδινε σφάλμα: “attempt to apply non-function”

Εναλλακτικές σωστές μορφές:

1. Χρήση του 1 αντί για NULL:

lm(TopSpeed ~ 1, data = BikeCommute)
# Ισοδύναμο με ~ NULL
# Το 1 σημαίνει "μόνο intercept"

2. Χωρίς ορισμό του πλαισίου δεδομένων:

lm(BikeCommute$TopSpeed ~ NULL)
# Λιγότερο προτιμητέο

3. Με την attach() (δεν συνιστάται):

attach(BikeCommute)
lm(TopSpeed ~ NULL)
detach(BikeCommute)

Πλήρης ανάλυση του μοντέλου:

# Δημιουργία μοντέλου
empty_model <- lm(TopSpeed ~ NULL, data = BikeCommute)

# Βασικές πληροφορίες
summary(empty_model)

# Προβλέψεις (όλες ίδιες)
predictions <- predict(empty_model)
head(predictions)
# [1] 33.56 33.56 33.56 33.56 33.56 33.56

# Residuals
residuals <- resid(empty_model)
sum(residuals)  # Πάντα ≈ 0

Θεωρητική σημασία:

Το κενό μοντέλο αντιπροσωπεύει την απλούστερη υπόθεση: - “Όλες οι τιμές TopSpeed προέρχονται από την ίδια κατανομή” - “Δεν υπάρχει τίποτα που μπορεί να προβλέψει τη TopSpeed” - “Η καλύτερη πρόβλεψη για οποιονδήποτε είναι ο μέσος όρος”

Από εκεί, χτίζουμε προς τα πάνω προσθέτοντας ανεξάρτητες μεταβλητές που βελτιώνουν την πρόβλεψη.

11. Αν ο μέσος όρος για την TopSpeed είναι 33.6, τι θα προβλέψει το κενό μοντέλο για την TopSpeed κάθε παρατήρησης;

0Είναι αδύνατο να πούμε33.6Ένα εύρος τιμών γύρω από το 33.6

Επεξήγηση

33.6 είναι η σωστή απάντηση.

Θεμελιώδης αρχή του κενού μοντέλου:

Το κενό μοντέλο προβλέπει πάντα τον μέσο όρο

Αυτό σημαίνει: - Κάθε παρατήρηση παίρνει την ίδια πρόβλεψη - Ανεξάρτητα από οποιεσδήποτε άλλες πληροφορίες - Καμία διαφοροποίηση μεταξύ διαφορετικών καταστάσεων - Η πρόβλεψη είναι σταθερή: 33.6 για όλους

Γιατί οι άλλες επιλογές είναι λάθος:

Α - “0” - ΛΑΘΟΣ: - Το κενό μοντέλο δεν προβλέπει μηδέν - Προβλέπει το μέσο όρο των δεδομένων - Το 0 δεν έχει σχέση με τα δεδομένα TopSpeed

Β - “Αδύνατο να πούμε” - ΛΑΘΟΣ: - Είναι πολύ εύκολο να πούμε - Το κενό μοντέλο έχει προβλέψιμη συμπεριφορά - Πάντα προβλέπει τον μέσο όρο, χωρίς εξαιρέσεις

Δ - “Ένα εύρος τιμών γύρω από το 33.6” - ΛΑΘΟΣ: - Το κενό μοντέλο δεν δίνει εύρος τιμών - Το κενό μοντέλο δίνει ακριβώς μία τιμή: 33.6 - Δεν υπάρχει εύρος στην πρόβλεψη - Αυτή η επιλογή συγχέι την τιμή πρόβλεψης με το διάστημα εμπιστοσύνης

Πρακτικό παράδειγμα:

# Δημιουργία κενού μοντέλου
empty_model <- lm(TopSpeed ~ NULL, data = BikeCommute)

# Όλες οι προβλέψεις
predictions <- predict(empty_model)
head(predictions, 10)
#  1    2    3    4    5    6    7    8    9   10
# 33.6 33.6 33.6 33.6 33.6 33.6 33.6 33.6 33.6 33.6

# Έλεγχος ότι όλες είναι ίδιες
all(predictions == 33.6)
# [1] TRUE

# Αριθμός μοναδικών προβλέψεων
length(unique(predictions))
# [1] 1

Σύγκριση με άλλα μοντέλα:

Κενό μοντέλο:

Παρατήρηση 1: Πρόβλεψη = 33.6
Παρατήρηση 2: Πρόβλεψη = 33.6
....
Παρατήρηση 56: Πρόβλεψη = 33.6

Μοντέλο με ανεξάρτητη μεταβλητή:

Steel bike: Πρόβλεψη = 33.2
Carbon bike: Πρόβλεψη = 33.9

Στατιστική αιτιολόγηση: - Ο μέσος όρος είναι αμερόληπτος εκτιμητής της κεντρικής τάσης - Ελαχιστοποιεί τη μέση τετραγωνική απόκλιση - Είναι η καλύτερη σταθερή πρόβλεψη χωρίς πρόσθετες πληροφορίες

Residuals:

Παρόλο που η πρόβλεψη είναι πάντα 33.6, τα residuals διαφέρουν:

Παρατήρηση 1: TopSpeed = 31.5, Residual = 31.5 - 33.6 = -2.1
Παρατήρηση 2: TopSpeed = 35.8, Residual = 35.8 - 33.6 = +2.2
Παρατήρηση 3: TopSpeed = 33.6, Residual = 33.6 - 33.6 = 0

Ιδιότητες residuals: - Άθροισμα = 0 - Μέσος όρος = 0 - Διασπορά = μέτρο της μεταβλητότητας γύρω από το μέσο

12. Σκεφτείτε την ιδέα ότι DATA = MODEL + ERROR. Αν ο μέσος όρος της TopSpeed είναι 33.6 και μια δεδομένη παρατήρηση έχει TopSpeed 23.6, ποιο μέρος είναι τα δεδομένα (DATA);

-1033.657.223.6

Επεξήγηση

23.6 είναι η σωστή απάντηση.

Κατανόηση του τύπου DATA = MODEL + ERROR:

Ορισμοί: - DATA: Η παρατηρούμενη τιμή (αυτό που μετρήσαμε) - MODEL: Η πρόβλεψη του μοντέλου (για κενό μοντέλο = μέσος όρος) - ERROR: Το υπόλοιπο ή σφάλμα (η διαφορά μεταξύ δεδομένων και πρόβλεψης)

Στη συγκεκριμένη περίπτωση: - DATA = 23.6 (η παρατηρούμενη TopSpeed) - MODEL = 33.6 (η πρόβλεψη του κενού μοντέλου) - ERROR = DATA - MODEL = 23.6 - 33.6 = -10

Επαλήθευση: \[\text{DATA} = \text{MODEL} + \text{ERROR}\] \[23.6 = 33.6 + (-10)\] \[23.6 = 33.6 - 10 ✓\]

Γιατί οι άλλες επιλογές είναι λάθος:

Α - “-10” - ΛΑΘΟΣ: - Αυτό είναι το ERROR (residual), όχι τα DATA - ERROR = DATA - MODEL = 23.6 - 33.6 = -10 - Η ερώτηση ρωτάει για τα δεδομένα, όχι το σφάλμα

Β - “33.6” - ΛΑΘΟΣ: - Αυτό είναι το MODEL (η πρόβλεψη), όχι τα DATA - Είναι ο μέσος όρος που χρησιμοποιεί το κενό μοντέλο - Η ερώτηση ρωτάει για τα δεδομένα, όχι το μοντέλο

Γ - “57.2” - ΛΑΘΟΣ: - Αυτό θα ήταν MODEL + |ERROR| = 33.6 + 10 = 43.6 (όχι 57.2) - Ή ίσως 33.6 + 23.6 = 57.2, αλλά αυτό δεν έχει νόημα στο πλαίσιο - Δεν αντιστοιχεί σε κανέναν από τους όρους της εξίσωσης

Δ - “23.6” - ΣΩΣΤΟ: - Αυτή είναι η παρατηρούμενη τιμή - Είναι το δεδομένο που συλλέχθηκε - Αυτό που πραγματικά μετρήθηκε στη διαδρομή

Ερμηνεία της εξίσωσης:

DATA = MODEL + ERROR σημαίνει: “Η παρατηρούμενη τιμή αποτελείται από την πρόβλεψη του μοντέλου συν το σφάλμα πρόβλεψης”

Με λόγια: - Παρατηρούμενη TopSpeed = Μέσος όρος + Απόκλιση από το μέσο όρο - 23.6 = 33.6 + (-10)

Αυτή η διάσπαση είναι χρήσιμη επειδή: - Χωρίζει το προβλέψιμο μέρος (MODEL) από το απρόβλεπτο (ERROR) - Μας βοηθά να καταλάβουμε πόσο καλό είναι το μοντέλο - Δείχνει πού υπάρχουν ακόμη ανεξήγητες διαφορές

Ερμηνεία του αρνητικού υπολοίπου:

ERROR = -10 σημαίνει: - Η παρατηρούμενη τιμή είναι 10 μονάδες χαμηλότερη από την πρόβλεψη - Το μοντέλο υπερεκτίμησε την TopSpeed για αυτή τη διαδρομή - Αυτή η διαδρομή είχε ασυνήθιστα χαμηλή μέγιστη ταχύτητα

Σημαντική παρατήρηση: Τα DATA είναι πάντα το σημείο εκκίνησης. Αυτά συλλέγουμε πρώτα. Μετά χτίζουμε το MODEL και υπολογίζουμε το ERROR. Η εξίσωση DATA = MODEL + ERROR είναι ένας τρόπος να αναλύσουμε τα δεδομένα.

13. Αν ο μέσος όρος της TopSpeed είναι 33.6 και μια δεδομένη παρατήρηση έχει TopSpeed 23.6, ποιο είναι το σφάλμα (residual);

23.6-1057.233.6

Επεξήγηση

-10 είναι η σωστή απάντηση.

Ορισμός του υπολοίπου ή σφάλματος:

Σφάλμα = Παρατηρούμενη τιμή - Προβλεπόμενη τιμή

\[\text{Residual} = \text{Observed} - \text{Predicted}\]

Στη συγκεκριμένη περίπτωση: - Παρατηρούμενη τιμή (Observed) = 23.6 - Προβλεπόμενη τιμή (Predicted) = 33.6 (μέσος όρος από κενό μοντέλο)

Υπολογισμός: \[\text{Residual} = 23.6 - 33.6 = -10\]

Ερμηνεία του αποτελέσματος:

Residual = -10 σημαίνει: - Η παρατηρούμενη τιμή είναι 10 μονάδες χαμηλότερη από την πρόβλεψη - Το μοντέλο υπερεκτίμησε την TopSpeed για αυτή τη διαδρομή - Η πραγματική τιμή είναι κάτω από αυτό που περιμέναμε

Γιατί οι άλλες επιλογές είναι λάθος:

Α - “23.6” - ΛΑΘΟΣ: - Αυτή είναι η παρατηρούμενη τιμή, όχι το υπόλοιπο - Το υπόλοιπο είναι η διαφορά, όχι η αρχική τιμή

Γ - “57.2” - ΛΑΘΟΣ: - Αυτό θα ήταν 23.6 + 33.6 = 57.2 - Δεν υπάρχει λόγος να προσθέσουμε τις τιμές - Το υπόλοιπο είναι διαφορά, όχι άθροισμα

Δ - “33.6” - ΛΑΘΟΣ: - Αυτή είναι η προβλεπόμενη τιμή (μέσος όρος), όχι το υπόλοιπο - Το υπόλοιπο είναι πάντα μια διαφορά, όχι μια από τις αρχικές τιμές

Πρακτικό παράδειγμα:

# Δεδομένα
observed <- 23.6    # Παρατηρούμενη TopSpeed
predicted <- 33.6   # Πρόβλεψη κενού μοντέλου (μέσος όρος)

# Υπολογισμός υπολοίπου
residual <- observed - predicted
print(residual)
# [1] -10

# Με την R
empty_model <- lm(TopSpeed ~ NULL, data = BikeCommute)
# Residual για συγκεκριμένη παρατήρηση
specific_residual <- 23.6 - predict(empty_model)[1]
print(specific_residual)
# [1] -10

Σχέση με την εξίσωση DATA = MODEL + ERROR:

\[\text{DATA} = \text{MODEL} + \text{ERROR}\] \[23.6 = 33.6 + (-10)\]

Ανασυνταγμένη: \[\text{ERROR} = \text{DATA} - \text{MODEL}\] \[\text{ERROR} = 23.6 - 33.6 = -10\]

Στη στατιστική, ERROR = RESIDUAL

Ιδιότητες των υπολοίπων στο κενό μοντέλο:

Για όλες τις παρατηρήσεις: - Άθροισμα όλων των residuals = 0 - Μέσος όρος των residuals = 0 - Κάποια θετικά, κάποια αρνητικά residuals - Ισορροπία μεταξύ υπερεκτιμήσεων και υποεκτιμήσεων

Παράδειγμα με περισσότερες παρατηρήσεις:

Παρατήρηση 1: TopSpeed = 31.6, Residual = 31.6 - 33.6 = -2.0
Παρατήρηση 2: TopSpeed = 35.6, Residual = 35.6 - 33.6 = +2.0
Παρατήρηση 3: TopSpeed = 23.6, Residual = 23.6 - 33.6 = -10.0
Παρατήρηση 4: TopSpeed = 33.6, Residual = 33.6 - 33.6 = 0

Άθροισμα: -2.0 + 2.0 + (-10.0) + 0 + … = 0

Πρακτική σημασία του υπολοίπου:

Μέγεθος: - Μικρό residual (κοντά στο 0): Καλή πρόβλεψη - Μεγάλο residual (μακριά από το 0): Κακή πρόβλεψη

Πρόσημο residual: - Θετικό: Το μοντέλο υποεκτίμησε (observed > predicted) - Αρνητικό: Το μοντέλο υπερεκτίμησε (observed < predicted)

Στη συγκεκριμένη περίπτωση: - Residual = -10 είναι αρκετά μεγάλο - Υποδηλώνει ότι αυτή η διαδρομή είχε ασυνήθιστα χαμηλή TopSpeed - Πιθανώς υπήρχαν ειδικές συνθήκες που την επηρέασαν

14. Ας υποθέσουμε ότι φτιάχνετε τρία ιστογράμματα: ένα για την TopSpeed, ένα για τις τιμές πρόβλεψης βάσει του κενού μοντέλου για την TopSpeed, και ένα για τα υπόλοιπα του μοντέλου. Ποιες δύο κατανομές θα έχουν παρόμοιο σχήμα;

Της TopSpeed και των τιμών πρόβλεψηςΤων τιμών πρόβλεψης και των υπολοίπωνΤης TopSpeed και των υπολοίπωνΚαμία από αυτές τις κατανομές δεν θα έχει παρόμοιο σχήμα.

Επεξήγηση

Της TopSpeed και των υπολοίπων είναι η σωστή απάντηση.

Ανάλυση κάθε κατανομής:

1. Κατανομή της TopSpeed: - Ποικιλία τιμών: από ~29.6 έως ~36.0 - Σχήμα: Πιθανώς ελαφρώς ασύμμετρη ή περίπου κανονική - Κέντρο: γύρω στο 33.6 (μέσος όρος) - Διασπορά: sd ≈ 1.48

2. Κατανομή τιμών πρόβλεψης (κενό μοντέλο): - Μία μόνο τιμή: 33.6 - Σχήμα: Μία κάθετη γραμμή (όλες οι παρατηρήσεις στην ίδια θέση) - Καμία διασπορά: Όλες οι προβλέψεις είναι ίδιες - Ιστόγραμμα: Μία μόνο μπάρα στο 33.6

3. Κατανομή υπολοίπων: - Ποικιλία τιμών: από ~(29.6-33.6) έως ~(36.0-33.6) - Εύρος: από ~-4.0 έως ~+2.4 - Κέντρο: 0 (άθροισμα υπολοίπων = 0) - Σχήμα: Ίδιο με της TopSpeed, αλλά μετατοπισμένο

Μαθηματική σχέση:

\[\text{Residual} = \text{TopSpeed} - 33.6\]

Αυτό σημαίνει ότι τα υπόλοιπα είναι:

• Η κατανομή της TopSpeed μετατοπισμένη κατά -33.6 μονάδες

• Ίδιο σχήμα με την αρχική κατανομή

• Ίδια διασπορά με την αρχική κατανομή

• Διαφορετικό κέντρο (0 αντί για 33.6)

Γιατί οι άλλες επιλογές είναι λάθος:

Α - TopSpeed και τιμές πρόβλεψης - ΛΑΘΟΣ:

• TopSpeed: Ποικιλία τιμών με κάποια διασπορά

• Τιμές πρόβλεψης: Μία μόνο τιμή (33.6)

• Τελείως διαφορετικά σχήματα: Κανονική κατανομή vs μία γραμμή

Β - Τιμές πρόβλεψης και υπολοίπων - ΛΑΘΟΣ: - Τιμές πρόβλεψης: Μία τιμή (καμία διασπορά) - Υπόλοιπα: Κατανομή με διασπορά γύρω από το 0 - Αντίθετα σχήματα: Καμία διασπορά vs μεγάλη διασπορά

Δ - Καμία - ΛΑΘΟΣ: - Υπάρχει σαφής ομοιότητα μεταξύ της TopSpeed και των υπολοίπων

Θεωρητική εξήγηση:

Γραμμικός μετασχηματισμός: Όταν αφαιρούμε μια σταθερά (33.6) από κάθε τιμή: - Το σχήμα δεν αλλάζει - Η διασπορά δεν αλλάζει - Μόνο το κέντρο μετακινείται

Για μοντελοποίηση: - Η ομοιότητα σχήματος επιβεβαιώνει ότι το κενό μοντέλο απλά αφαιρεί το κέντρο - Δεν αλλάζει τη βασική δομή των δεδομένων - Τα υπόλοιπα διατηρούν όλη την πληροφορία για τη διασπορά

15. Ο μέσος όρος της TopSpeed είναι 33.6 και μια δεδομένη παρατήρηση έχει τιμή 23.6. Ποιο μέρος της παρακάτω εξίσωσης του Γενικού Γραμμικού Μοντέλου αντιπροσωπεύει το 23.6;

Εξίσωση: \(Y_i = \bar{Y} + e_i\)

\(Y_i\)\(\bar{Y}\)\(e_i\)Κανένα από τα παραπάνω

Επεξήγηση

\(Y_i\) είναι η σωστή απάντηση.

Ανάλυση της εξίσωσης GLM:

\(Y_i = \bar{Y} + e_i\)

Ορισμοί των συμβόλων:

• \(Y_i\): Η παρατηρούμενη τιμή για την παρατήρηση i

• \(\bar{Y}\): Ο μέσος όρος (η πρόβλεψη του κενού μοντέλου)

• \(e_i\): Το υπόλοιπο (σφάλμα) για την παρατήρηση i

Στη συγκεκριμένη περίπτωση:

• \(Y_i = 23.6\) (η παρατηρούμενη TopSpeed)

• \(\bar{Y} = 33.6\) (ο μέσος όρος)

• \(e_i = Y_i - \bar{Y} = 23.6 - 33.6 = -10\) (το υπόλοιπο)

Επαλήθευση:

\[Y_i = \bar{Y} + e_i\]

\[23.6 = 33.6 + (-10)\]

\[23.6 = 23.6 ✓\]

Γιατί οι άλλες επιλογές είναι λάθος:

Β - \(\bar{Y}\) - ΛΑΘΟΣ:

• Το \(\bar{Y} = 33.6\) είναι ο μέσος όρος

• Όχι η συγκεκριμένη παρατηρούμενη τιμή 23.6

Γ - \(e_i\) - ΛΑΘΟΣ: - Το \(e_i = -10\) είναι το υπόλοιπο

• Όχι η παρατηρούμενη τιμή 23.6

Δ - Κανένα από τα παραπάνω - ΛΑΘΟΣ:

• Το \(Y_i\) αντιπροσωπεύει ακριβώς το 23.6

Σημασία στη σημειογραφία GLM:

\(Y_i\) (παρατηρούμενη τιμή):

• Είναι τα πραγματικά δεδομένα που συλλέξαμε

• Αυτό που μετρήσαμε στην πραγματικότητα

• Το αποτέλεσμα της μέτρησης για κάθε παρατήρηση

\(\bar{Y}\) (μέσος όρος):

• Η πρόβλεψη του κενού μοντέλου

• Σταθερή τιμή για όλες τις παρατηρήσεις

• Το κέντρο της κατανομής

\(e_i\) (residual):

• Η διαφορά μεταξύ παρατηρούμενου και προβλεπόμενου

• Μεταβλητό για κάθε παρατήρηση

• Δείχνει πόσο το μοντέλο απέτυχε να προβλέψει την τιμή

16. Στη σημειογραφία του Γενικευμένου Γραμμικού Μοντέλου, ποιο από τα παρακάτω αντιπροσωπεύει το μοντέλο (ή την πρόβλεψη);

\(Y_i\)\(b_0\)\(e_i\)Κανένα από τα παραπάνω

Επεξήγηση

\(b_0\) είναι η σωστή απάντηση.

Μορφή GLM του κενού μοντέλου: \[Y_i = b_0 + e_i\]

όπου:

• \(Y_i\): Παρατηρούμενη τιμή (δεδομένα)

• \(b_0\): Εκτιμημένη παράμετρος (μοντέλο/πρόβλεψη)

• \(e_i\): Υπόλοιπο (σφάλμα)

Ρόλος κάθε όρου:

\(b_0\) - Το ΜΟΝΤΕΛΟ:

• Είναι η πρόβλεψη του μοντέλου

• Στο κενό μοντέλο: \(b_0 = \text{μέσος όρος}\)

• Σταθερή τιμή για όλες τις παρατηρήσεις

• Αυτό που το μοντέλο προβλέπει για κάθε παρατήρηση

Στο παράδειγμα της TopSpeed:

• \(b_0 = 33.6\) (ο μέσος όρος)

• Το μοντέλο προβλέπει 33.6 για κάθε παρατήρηση

Γιατί οι άλλες επιλογές είναι λάθος:

Α - \(Y_i\) - ΛΑΘΟΣ:

• Το \(Y_i\) είναι η παρατηρούμενη τιμή (δεδομένα)

• Όχι η πρόβλεψη του μοντέλου

• Αυτό που μετρήσαμε, όχι αυτό που προβλέπουμε

Γ - \(e_i\) - ΛΑΘΟΣ:

• Το \(e_i\) είναι το υπόλοιπο (σφάλμα)

• Η διαφορά μεταξύ παρατηρούμενου και προβλεπόμενου

• Όχι η πρόβλεψη του μοντέλου

Δ - Κανένα από τα παραπάνω - ΛΑΘΟΣ:

• Το \(b_0\) αντιπροσωπεύει ακριβώς το μοντέλο

Εννοιολογική κατανόηση:

Το μοντέλο λέει: “Η καλύτερη πρόβλεψή μου για οποιαδήποτε τιμή της TopSpeed είναι 33.6”

Αυτό το 33.6 είναι:

• Η εκτιμημένη παράμετρος \(b_0\)

• Η πρόβλεψη του μοντέλου

• Ο σταθερός όρος (intercept)

• Ο μέσος όρος των δεδομένων

Στη σημειογραφία του GLM, το μοντέλο είναι πάντα το μέρος της εξίσωσης που δεν περιλαμβάνει τον όρο σφάλματος. Για το κενό μοντέλο, αυτό είναι μόνο το \(b_0\).

17. Ποιο σύμβολο ΔΕΝ μπορεί να χρησιμοποιηθεί για να αντιπροσωπεύσει το μέσο όρο του δείγματος;

\(Y_i\)\(\beta_0\)\(\mu\)Όλα τα παραπάνω

Επεξήγηση

\(Y_i\) είναι η σωστή απάντηση.

Διάκριση συμβόλων:

Το \(Y_i\) - ΔΕΝ μπορεί να αντιπροσωπεύσει το μέσο όρο:

• Το \(Y_i\) αντιπροσωπεύει μια μεμονωμένη παρατήρηση

• Είναι η i-οστή τιμή στο δείγμα

• Όχι ο μέσος όρος όλων των παρατηρήσεων

• Παράδειγμα: \(Y_1, Y_2, Y_3, \ldots\) είναι μεμονωμένες τιμές

Το \(\beta_0\) - ΜΠΟΡΕΙ να αντιπροσωπεύσει το μέσο όρο:

• Στο κενό μοντέλο: \(\beta_0 = \text{μέσος όρος πληθυσμού}\)

• Παράμετρος πληθυσμού που εκτιμάται από το δειγματικό μέσο

• Θεωρητική τιμή που προσεγγίζεται από το δείγμα

\(\mu\) - ΜΠΟΡΕΙ να αντιπροσωπεύσει το μέσο όρο:

• Συμβολίζει τον μέσο όρο πληθυσμού

• Παράμετρος που εκτιμάται από το δειγματικό μέσο

• Θεωρητική τιμή της ΔΠΔ

Σύμβολα για το δειγματικό μέσο όρο:

Κύρια Σύμβολα: - \(\bar{Y}\) (Y-bar): Πιο κοινό

• \(\bar{x}\) (x-bar): Επίσης συχνό

• \(b_0\): Στο πλαίσιο του GLM (εκτιμημένη παράμετρος)

Διάκριση παραμέτρων vs στατιστικών:

Παράμετροι πληθυσμού (άγνωστες):

• \(\mu\) (μι): Μέσος όρος πληθυσμού

• \(\beta_0\) (βήτα): Παράμετρος μοντέλου πληθυσμού

• \(\sigma\) (σίγμα): Τυπική απόκλιση πληθυσμού

Στατιστικά δείγματος (υπολογισμένα): - \(\bar{Y}\) ή \(\bar{x}\): Δειγματικός μέσος όρος

• \(b_0\): Εκτιμημένη παράμετρος από δείγμα

• \(s\): Δειγματική τυπική απόκλιση

Γιατί τα άλλα ΜΠΟΡΟΥΝ να χρησιμοποιηθούν:

Β - \(\beta_0\) - ΣΩΣΤΟ σε ορισμένα πλαίσια:

• Στο κενό μοντέλο: \(Y_i = \beta_0 + \epsilon_i\)

• Η εκτίμηση του \(\beta_0\) είναι ο δειγματικός μέσος

• \(\hat{\beta_0} = \bar{Y}\) (η εκτίμηση της παραμέτρου)

Γ - \(\mu\) - ΣΩΣΤΟ ως στόχος εκτίμησης:

• Ο δειγματικός μέσος εκτιμά το \(\mu\)

• \(\bar{Y}\) είναι αμερόληπτος εκτιμητής του \(\mu\)

• Παρόλο που το \(\mu\) είναι άγνωστο, ο δειγματικός μέσος το προσεγγίζει

Δ - “Όλα τα παραπάνω” - ΛΑΘΟΣ: - Επειδή το \(Y_i\) ΔΕΝ μπορεί να αντιπροσωπεύσει το μέσο όρο

18. Ποια σύμβολα ΜΠΟΡΟΥΝ να χρησιμοποιηθούν για να αντιπροσωπεύσουν το μέσο όρο του πληθυσμού (Υπάρχουν περισσότερες από μία σωστές απαντήσεις.);

\(\beta_0\)\(\mu\)Κανένα από τα παραπάνω

Επεξήγηση

Και τα δύο παραπάνω είναι η σωστή απάντηση.

Ανάλυση κάθε συμβόλου:

Α - \(\beta_0\) - ΣΩΣΤΟ:

• Στο πλαίσιο του GLM

• Παράμετρος πληθυσμού που αντιστοιχεί στον σταθερό όρο

• Στο κενό μοντέλο: \(Y_i = \beta_0 + \epsilon_i\)

• Εδώ το \(\beta_0\) είναι ο μέσος όρος πληθυσμού

Β - \(\mu\) - ΣΩΣΤΟ: - Κλασική σημειογραφία για μέσο όρο πληθυσμού

• Χρησιμοποιείται ευρέως στη περιγραφική στατιστική

• Παράμετρος της κανονικής κατανομής: \(N(\mu, \sigma^2)\)

• Ο στόχος εκτίμησης από δειγματικό μέσο όρο

Γ - “Κανένα από τα παραπάνω” - ΛΑΘΟΣ: - Και τα δύο είναι έγκυρα σύμβολα

19. Ποιος είναι ο «πληθυσμός» που προσπαθούμε να κατανοήσουμε με το κενό μοντέλο της TopSpeed;

20. Ποιες από αυτές τις μεταβλητές—Bike, Distance, ή Month—πιστεύετε ότι θα βοηθούσαν στην εξήγηση της μεταβλητότητας που βλέπουμε στην TopSpeed; Δημιουργήστε μια λεκτική εξίσωση και περιγράψτε το διάγραμμα που θα δημιουργούσατε. Εξηγήστε τι θα αναζητούσατε στο διάγραμμά σας που θα έδειχνε ότι αυτή η μεταβλητή πράγματι εξηγεί μέρος της μεταβλητότητας στην TopSpeed.

Το πλαίσιο δεδομένων NutritionStudy περιέχει δεδομένα για 315 ασθενείς ενός νοσοκομείου που είχαν υποβληθεί σε αφαίρεση μη καρκινικού όγκου μέσω χειρουργικής επέμβασης. Περιλαμβάνει τις ακόλουθες μεταβλητές:

• Age - Ηλικία του ατόμου (σε έτη)
• Vitamin - Χρήση βιταμινών: 1=Τακτική, 2=Περιστασιακή, ή 3=Καμία
• Calories - Αριθμός θερμίδων που καταναλώνονται ημερησίως
• Fat - Γραμμάρια λίπους που καταναλώνονται ημερησίως
• Fiber - Γραμμάρια φυτικών ινών που καταναλώνονται ημερησίως
• Alcohol - Αριθμός αλκοολούχων ποτών που καταναλώνονται εβδομαδιαίως
• Cholesterol - Χοληστερόλη που καταναλώνεται ημερησίως, σε mg
• Gender - Κωδικοποιημένο ως Γυναίκα (Female) ή Άνδρας (Male)
• EverSmoke - Κατάσταση καπνίσματος: Ποτέ (Never), Πρώην (Former), ή Τωρινός (Current)

Δείγμα δεδομένων από head(NutritionStudy):

  Age Vitamin Calories  Fat Fiber Alcohol Cholesterol Gender EverSmoke
1  64       1   1298.8 57.0   6.3     0.0       170.3 Female    Former
2  76       1   1032.5 50.1  15.8     0.0        75.8 Female     Never
3  38       2   2372.3 83.6  19.1    14.1       257.9 Female    Former
4  40       3   2449.5 97.5  26.5     0.5       332.6 Female    Former
5  72       1   1952.1 82.6  16.2     0.0       170.8 Female     Never
6  40       3   1366.9 56.0   9.6     1.3       154.6 Female    Former

21. Ακόμα και στην παρακάτω έντονα ασύμμετρη κατανομή, ο μέσος όρος μπορεί να είναι ένα καλό μοντέλο. Γιατί;

Ο μέσος όρος εξισορροπεί τις αποκλίσεις πάνω και κάτω από το μέσο όρο.Ο μέσος όρος εξισορροπεί τον αριθμό των τιμών πάνω και κάτω από το μέσο όρο.Ο μέσος όρος είναι ο πιο συχνός αριθμός σε αυτή την κατανομή.Όλα τα παραπάνω είναι λόγοι για τους οποίους ο μέσος όρος είναι ένα καλό μοντέλο.

Επεξήγηση

Ο μέσος όρος εξισορροπεί τις αποκλίσεις πάνω και κάτω από το μέσο όρο είναι η σωστή απάντηση.

Ανάλυση της κατανομής της Alcohol:

Χαρακτηριστικά της κατανομής:

• Έντονα ασύμμετρη στα δεξιά (right-skewed)

• Πολλά μηδενικά: ~180 άτομα δεν πίνουν καθόλου

• Μικρός αριθμός υψηλών τιμών (heavy drinkers)

• Μακριά δεξιά ουρά: Ορισμένοι πίνουν 30+ ποτά/εβδομάδα

Γιατί η επιλογή Α είναι σωστή:

Θεμελιώδης ιδιότητα του μέσου όρου:

\[\sum_{i=1}^{n}(x_i - \bar{x}) = 0\]

Αυτό ισχύει ΠΑΝΤΑ, ανεξάρτητα από το σχήμα κατανομής:

Στην ασύμμετρη κατανομή της Alcohol:

• Πολλές μικρές αρνητικές αποκλίσεις: 0 - μέσος όρος (για τους μη-πότες)

• Λίγες μεγάλες θετικές αποκλίσεις: 30 - μέσος όρος (για τους heavy drinkers)

• Ακριβής ισορροπία: Άθροισμα όλων των αποκλίσεων = 0

Γιατί οι άλλες επιλογές είναι λάθος:

Β - “Εξισορροπεί τον αριθμό τιμών” - ΛΑΘΟΣ:

• Αυτό περιγράφει τη διάμεσο, όχι το μέσο όρο

• Στο διάγραμμα: ~180 άτομα πίνουν κάτω από το μέσο, ~135 πάνω από το μέσο

• Ο μέσος όρος ΔΕΝ εξισορροπεί τον αριθμό παρατηρήσεων

Γ - “Είναι ο πιο συχνός αριθμός” - ΛΑΘΟΣ:

• Αυτό περιγράφει την επικρατούσα τιμή (mode)

• Η επικρατούσα τιμή εδώ είναι 0 (πιο συχνή τιμή)

• Ο μέσος όρος (~3-4) δεν είναι η πιο συχνή τιμή

Δ - “Όλα τα παραπάνω” - ΛΑΘΟΣ:

• Επειδή οι Β και Γ είναι λάθος

Γιατί ο μέσος όρος είναι ‘καλό μοντέλο’ παρά την ασυμμετρία:

1. Μαθηματική βέλτιστη ιδιότητα:

• Ελαχιστοποιεί το Άθροισμα Τετραγωνικών Σφαλμάτων (κάτι που θα δούμε στο επόμενο Κεφάλαιο)

• Αμερόληπτος εκτιμητής του πληθυσμιακού μέσου όρου

• Μοναδικό σημείο ισορροπίας των αποκλίσεων

2. Στατιστική χρησιμότητα: - Βάση για πολλές στατιστικές τεχνικές - Συγκρίσιμος μεταξύ δειγμάτων

3. Πρακτική ερμηνεία: - Μέσο ‘φορτίο’ για την κοινωνία από την κατανάλωση αλκοόλ - Προγραμματισμός υπηρεσιών υγείας - Οικονομικές προβλέψεις (φόροι, κόστη)

Πότε ο μέσος όρος δεν είναι καλό μοντέλο:

Παρόλη την εξισορρόπηση των αποκλίσεων, ο μέσος όρος μπορεί να παραπλανήσει: - Δεν είναι αντιπροσωπευτικός της τυπικής κατάστασης - Οι περισσότεροι πίνουν λιγότερο από το μέσο όρο - Επηρεάζεται από ακραίες τιμές (outliers)

Συμπέρασμα:

Παρόλο που η κατανομή είναι έντονα ασύμμετρη, ο μέσος όρος διατηρεί την θεμελιώδη μαθηματική του ιδιότητα: εξισορροπεί πάντα τις αποκλίσεις. Αυτό τον κάνει μαθηματικά ορθό και στατιστικά χρήσιμο μοντέλο, ακόμα και αν δεν είναι πάντα ο πιο ερμηνεύσιμος για την τυπική κατάσταση στην κατανομή.

Η εξισορρόπηση των αποκλίσεων είναι η μόνη απόλυτα αληθής δήλωση που ισχύει για κάθε κατανομή, ανεξάρτητα από το σχήμα της.

22. Να δημιουργήσετε το ιστόγραμμα της μεταβλητής Alcohol στο πλαίσιο δεδομένων NutritionStudy. Τι αναπαρίσταται στον άξονα y;

Η καταμέτρηση αλκοολούχων ποτώνΟ αριθμός των μεταβλητώνΟ αριθμός των ασθενώνΟ αριθμός ποτών που καταναλώνονται εβδομαδιαίως

Επεξήγηση

Αριθμός ασθενών είναι η σωστή απάντηση.

Κατανόηση του ιστογράμματος:

Τι δείχνει ένα ιστόγραμμα:

• Άξονας x: Η μεταβλητή που μελετάμε (Alcohol - ποτά/εβδομάδα)

• Άξονας y: Η συχνότητα (count) κάθε εύρους τιμών

• Κάθε μπάρα: Δείχνει πόσες παρατηρήσεις υπάρχουν σε κάθε διάστημα τιμών (bin)

Για το ιστόγραμμα της Alcohol:

Ερμηνεία των αξόνων:

• Άξονας x (Alcohol): Αριθμός ποτών ανά εβδομάδα (0, 1, 2, 3, … 35)

• Άξονας y (count): Πόσοι ασθενείς καταναλώνουν αυτόν τον αριθμό ποτών

Γιατί οι άλλες επιλογές είναι λάθος:

Α - “Καταμέτρηση αλκοολούχων ποτών” - ΛΑΘΟΣ:

• Ο άξονας y δεν δείχνει πόσα ποτά υπάρχουν συνολικά

• Δείχνει πόσοι άνθρωποι πίνουν κάθε ποσότητα

• Σύγχυση μεταξύ τιμής μεταβλητής και συχνότητας

Β - “Αριθμός μεταβλητών” - ΛΑΘΟΣ:

• Μελετάμε μία μεταβλητή (Alcohol)

• Ο άξονας y δεν σχετίζεται με τον αριθμό μεταβλητών

• Σύγχυση του ιστογράμματος με άλλους τύπους γραφημάτων

Δ - “Αριθμός ποτών που καταναλώνονται εβδομαδιαίως” - ΛΑΘΟΣ:

• Αυτό είναι ο άξονας x, όχι ο άξονας x

• Ο άξονας y δείχνει συχνότητα, όχι την τιμή της μεταβλητής

Κώδικας για δημιουργία ιστογράμματος:

gf_histogram(~ Alcohol, data = NutritionStudy)
# ή
hist(NutritionStudy$Alcohol)

Συμπέρασμα:

Ο άξονας y σε ένα ιστόγραμμα πάντα αντιπροσωπεύει τη συχνότητα - δηλαδή πόσες παρατηρήσεις (ασθενείς στην περίπτωσή μας) έχουν τιμές σε κάθε εύρος τιμών του άξονα x.

23. Δίνονται τα στατιστικά για την Alcohol. Ο μέσος αριθμός ποτών ανά εβδομάδα είναι 3.28 αλλά η διάμεσος είναι 0.3. Η μέγιστη τιμή σε αυτή την κατανομή είναι 203 - αυτά είναι πολλά αλκοολούχα ποτά την εβδομάδα (σχεδόν 30 την ημέρα)! Αυτή η τιμή μάλλον είναι εσφαλμένη. Ποιο από τα παρακάτω θα άλλαζε περισσότερο αν αφαιρούσαμε αυτή τη μέγιστη τιμή από την ανάλυση;

min Q1 median  Q3 max     mean       sd   n missing
  0  0    0.3 3.2 203 3.279365 12.32288 315       0

Η διάμεσοςΤο ελάχιστοΟ μέσος όροςΌλες αυτές οι τιμές (διάμεσος, ελάχιστο, και μέσος όρος) θα αλλάξουν πολύ.

Επεξήγηση

Ο μέσος όρος είναι η σωστή απάντηση.

Ανάλυση της ακραίας τιμής:

Το πρόβλημα:

• Τιμή: 203 ποτά/εβδομάδα ≈ 29 ποτά/ημέρα

• Αδύνατη τιμή: Πιθανότατα σφάλμα στα δεδομένα

• Ακραία τιμή: Πολύ μακριά από την υπόλοιπη κατανομή

• Επίδραση: Διαστρεβλώνει τα στατιστικά

Γιατί οι άλλες επιλογές είναι λάθος:

Α - “Η διάμεσος” - ΛΑΘΟΣ:

• Η διάμεσος δεν επηρεάζεται από ακραίες τιμές

• Εξαρτάται μόνο από τη θέση, όχι από την τιμή

• Η αφαίρεση μίας τιμής δεν αλλάζει σημαντικά τη μεσαία θέση

Β - “Η ελάχιστη τιμή” - ΛΑΘΟΣ:

• Η ελάχιστη τιμή είναι 0 και θα παραμείνει 0

• Η αφαίρεση της μέγιστης τιμής δεν επηρεάζει την ελάχιστη

• Καμία αλλαγή στην ελάχιστη τιμή

Δ - “Όλες θα αλλάξουν πολύ” - ΛΑΘΟΣ:

• Μόνο ο μέσος όρος θα αλλάξει σημαντικά

• Η διάμεσος και η ελάχιστη τιμή θα παραμείνουν σχεδόν ίδιες

Συμπέρασμα:

Ο μέσος όρος είναι το πιο ευαίσθητο στατιστικό σε ακραίες τιμές και θα αλλάξει σημαντικά αν αφαιρέσουμε την ακραία τιμή 203. Αντίθετα, η διάμεσος και το ελάχιστο θα παραμείνουν σχεδόν αμετάβλητα, επιβεβαιώνοντας την ανθεκτικότητά τους σε ακραίες τιμές.

24. Ποια από τις παρακάτω λεκτικές εξισώσεις αντιπροσωπεύει την υπόθεση ότι το κάπνισμα εξηγεί ένα μέρος της μεταβλητότητας στην κατανάλωση λίπους;

Κατανάλωση λίπους = ΚάπνισμαΚάπνισμα = Κατανάλωση λίπουςΚάπνισμα = Κατανάλωση λίπους + άλλα πράγματαΚατανάλωση λίπους = Κάπνισμα + άλλα πράγματα

Επεξήγηση

Κατανάλωση λίπους = Κάπνισμα + άλλα πράγματα είναι η σωστή απάντηση.

Κατανόηση της λεκτικής εξίσωσης:

Βασική αρχή:

Σε ένα μοντέλο:

Εξαρτημένη μεταβλητή = Ανεξάρτητη μεταβλητή + Σφάλμα

Στην περίπτωσή μας:

• Outcome (εξαρτημένη μεταβλητή): Κατανάλωση λίπους

• Predictor (ανεξάρτητη μεταβλητή): Κάπνισμα

• “Άλλα πράγματα”: Error term + άλλοι παράγοντες

Γιατί η Δ είναι σωστή:

“Το κάπνισμα εξηγεί ένα μέρος της μεταβλητότητας”:

• Θέλουμε να προβλέψουμε την κατανάλωση λίπους

• Χρησιμοποιούμε το κάπνισμα ως ανεξάρτητη μεταβλητή

• Αναγνωρίζουμε ότι υπάρχουν άλλοι παράγοντες που επηρεάζουν την κατανάλωση λίπους

Γιατί οι άλλες επιλογές είναι λάθος:

Α - “Κατανάλωση λίπους = Κάπνισμα” - ΛΑΘΟΣ:

• Υποθέτει τέλεια συσχέτιση

• Δεν αναγνωρίζει την ύπαρξη άλλων παραγόντων

• Μη ρεαλιστικό - κανένα μοντέλο δεν εξηγεί 100% της μεταβλητότητας

Β - “Κάπνισμα = Κατανάλωση λίπους” - ΛΑΘΟΣ:

• Αντίστροφη κατεύθυνση της αιτιότητας

• Θέλουμε το κάπνισμα να εξηγεί το λίπος, όχι το αντίθετο

• Λάθος outcome variable

Γ - “Κάπνισμα = Κατανάλωση λίπους + άλλα πράγματα” - ΛΑΘΟΣ:

• Αντίστροφη κατεύθυνση και πάλι

• Προσπαθεί να εξηγήσει το κάπνισμα από το λίπος

• Δεν αντιστοιχεί στην υπόθεση της ερώτησης

Συμπέρασμα:

Η λεκτική εξίσωση “Κατανάλωση λίπους = Κάπνισμα + άλλα πράγματα” αντικατοπτρίζει σωστά:

1. Την κατεύθυνση της υπόθεσης (κάπνισμα → λίπος)

2. Την αναγνώριση ότι υπάρχουν πολλαπλοί παράγοντες

3. Την ρεαλιστική προσέγγιση ότι κανένας μεμονωμένος παράγοντας δεν εξηγεί τα πάντα

25. Τι ισχύει για το κενό μοντέλο της κατανάλωσης λίπους (Fat);

Το μοντέλο είναι ο καλύτερος τρόπος εξήγησης του πόσες μεταβλητές επηρεάζουν την κατανάλωση λίπους (όπως η κατάσταση καπνίσματος και το φύλο).Το μοντέλο προβλέπει διαφορετική τιμή για την Fat για κάθε άτομο, ανάλογα με τις τιμές τους σε άλλες μεταβλητές.Το μοντέλο προβλέπει 0 γραμμάρια κατανάλωσης λίπους για κάθε άτομο.Το μοντέλο κάνει την ίδια πρόβλεψη (το μέσο όρο της Fat) για κάθε άτομο ανεξάρτητα από τις τιμές τους σε άλλες μεταβλητές.

Επεξήγηση

Το μοντέλο κάνει την ίδια πρόβλεψη (το μέσο όρο της Fat) για κάθε άτομο ανεξάρτητα από τις τιμές τους σε άλλες μεταβλητές είναι η σωστή απάντηση.

Ορισμός και χαρακτηριστικά του κενού μοντέλου:

Μαθηματική μορφή:

\[\text{Fat}_i = b_0 + e_i\]

όπου:

• \(b_0\) = μέσος όρος της Fat (σταθερός για όλους)

• \(e_i\) = υπόλοιπο του μοντέλου για κάθε άτομο i

Βασικά χαρακτηριστικά:

1. Μία μόνο παράμετρος: ο μέσος όρος

2. Καμία ανεξάρτητη μεταβλητή: δεν χρησιμοποιεί το κάπνισμα, το φύλο, την ηλικία, κτλ.

3. Ίδια πρόβλεψη για όλους: \(\hat{\text{Fat}} = \bar{\text{Fat}}\)

Γιατί οι άλλες επιλογές είναι λάθος:

Α - “Καλύτερος τρόπος εξήγησης πολλών μεταβλητών” - ΛΑΘΟΣ:

• Το κενό μοντέλο δεν περιλαμβάνει καμία ανεξάρτητη μεταβλητή

• Δεν εξηγεί πώς κάπνισμα ή φύλο επηρεάζουν το Fat

• Είναι το απλούστερο, όχι το καλύτερο για εξήγηση

Β - “Διαφορετική τιμή ανάλογα με άλλες μεταβλητές” - ΛΑΘΟΣ:

• Το κενό μοντέλο αγνοεί όλες τις άλλες μεταβλητές

• Η πρόβλεψη είναι ίδια για όλους

Γ - “Θα προέβλεπε 0 γραμμάρια” - ΛΑΘΟΣ:

• Το κενό μοντέλο προβλέπει τον μέσο όρο, όχι το μηδέν

• Για διατροφικά δεδομένα, ο μέσος όρος θα είναι θετικός (π.χ., 60-100g)

Συμπέρασμα:

Το κενό μοντέλο είναι το απλούστερο δυνατό μοντέλο που χρησιμοποιεί μόνο τον μέσο όρο ως πρόβλεψη για όλους. Παρόλο που δεν είναι ιδιαίτερα χρήσιμο για την κατανόηση παραγόντων που επηρεάζουν την κατανάλωση λίπους, είναι απαραίτητο ως μοντέλο βάσης για την αξιολόγηση πιο σύνθετων μοντέλων.

26. Ο μέσος όρος της Alcohol είναι 3.279 ποτά ανά εβδομάδα. Ένας συγκεκριμένος ασθενής καταναλώνει 2 ποτά ανά εβδομάδα. Ποιο από τα παρακάτω σύμβολα θα χρησιμοποιούνταν για να αντιπροσωπεύσει την τιμή 2 στη σημειογραφία του Γενικού Γραμμικού Μοντέλου;

\(Y_i\)\(b_0\)\(e_i\)Κανένα από τα παραπάνω

Επεξήγηση

\(Y_i\) είναι η σωστή απάντηση.

Ανάλυση της κατάστασης:

Δεδομένα:

• Μέσος όρος Alcohol = 3.279 ποτά/εβδομάδα

• Συγκεκριμένος ασθενής = 2 ποτά/εβδομάδα

• Ερώτηση: Τι αντιπροσωπεύει το “2” στη σημειογραφία GLM;

Εξίσωση του κενού μοντέλου:

\[Y_i = b_0 + e_i\]

όπου:

• \(Y_i\): Παρατηρούμενη τιμή για τον ασθενή i

• \(b_0\): Εκτιμημένη παράμετρος (μέσος όρος)

• \(e_i\): Υπόλοιπο για τον ασθενή i

Στη συγκεκριμένη περίπτωση:

• \(Y_i = 2\) (παρατηρούμενη κατανάλωση)

• \(b_0 = 3.279\) (μέσος όρος)

• \(e_i = Y_i - b_0 = 2 - 3.279 = -1.279\) (υπόλοιπο)

Συμπέρασμα:

Η τιμή 2 ποτά ανά εβδομάδα αντιστοιχεί στο σύμβολο \(Y_i\) στη σημειογραφία του GLM, καθώς είναι η παρατηρούμενη τιμή της μεταβλητής Alcohol για αυτόν τον συγκεκριμένο ασθενή.

27. Ποιο από τα παρακάτω ΔΕΝ μπορεί να υπολογιστεί από το σύνολο δεδομένων NutritionStudy;

Μια εκτίμησηΜια παράμετροςΈνα απλό μοντέλοΈνα στατιστικό

Επεξήγηση

Μια παράμετρος είναι η σωστή απάντηση.

Θεμελιώδης διάκριση: Παράμετροι vs Στατιστικά

Παράμετροι (Parameters):

• Χαρακτηρίζουν τον πληθυσμό

• Είναι άγνωστες και σταθερές τιμές

• ΔΕΝ μπορούν να υπολογιστούν άμεσα από δεδομένα

• Παραδείγματα: μ (μέσος όρος πληθυσμού), σ (τυπική απόκλιση πληθυσμού)

Στατιστικά (Statistics):

• Υπολογίζονται από το δείγμα

• Είναι γνωστές τιμές που προκύπτουν από δεδομένα

• Εκτιμούν τις άγνωστες παραμέτρους

• Παραδείγματα: x̄ (δειγματικός μέσος), s (δειγματική τυπική απόκλιση)

Γιατί η Β είναι σωστή:

Παράμετρος - ΔΕΝ μπορεί να υπολογιστεί:

• Οι πραγματικές παράμετροι του πληθυσμού είναι άγνωστες

• Το NutritionStudy είναι δείγμα 315 ασθενών, όχι ολόκληρος πληθυσμός

• Μπορούμε να εκτιμήσουμε παραμέτρους, αλλά όχι να τις υπολογίσουμε ακριβώς

Γιατί οι άλλες επιλογές είναι λάθος:

Α - “Μια εκτίμηση” - ΛΑΘΟΣ (μπορεί να υπολογιστεί):

Γ - “Ένα απλό μοντέλο” - ΛΑΘΟΣ (μπορεί να υπολογιστεί):

Δ - “Ένα στατιστικό” - ΛΑΘΟΣ (μπορεί να υπολογιστεί):

Συμπέρασμα:

Με τα δεδομένα NutritionStudy μπορούμε να υπολογίσουμε στατιστικά, εκτιμήσεις, και να προσαρμόσουμε μοντέλα. Ωστόσο, δεν μπορούμε να υπολογίσουμε τις πραγματικές παραμέτρους του πληθυσμού - μόνο να τις εκτιμήσουμε με κάποιο βαθμό αβεβαιότητας.

28. Χρησιμοποιήστε την lm() για να προσαρμόσετε το κενό μοντέλο για την κατανάλωση λίπους (Fat) στο πλαίσιο δεδομένων NutritionStudy. Ποιος είναι ο συντελεστής;

77.24757.065.12Κανένα από τα παραπάνω

Επεξήγηση

77.247 είναι η σωστή απάντηση.

Κώδικας για το κενό μοντέλο:

# Προσαρμογή κενού μοντέλου για Fat
empty_model <- lm(Fat ~ 1, data = NutritionStudy)
# ή ισοδύναμα:
empty_model <- lm(Fat ~ NULL, data = NutritionStudy)

# Εμφάνιση συντελεστή
coef(empty_model)
# (Intercept)
#    77.247

# Ή με summary
summary(empty_model)

Τι αντιπροσωπεύει ο συντελεστής:

Στο κενό μοντέλο:

\[\text{Fat}_i = b_0 + e_i\]

• \(b_0 = 77.247\) είναι ο σταθερός όρος (intercept)

• Αντιπροσωπεύει τον μέσο όρο της μεταβλητής Fat

• Είναι η πρόβλεψη του μοντέλου για κάθε άτομο

Ερμηνεία του αποτελέσματος:

77.247 γραμμάρια λίπους ανά ημέρα:

• Αυτός είναι ο μέσος όρος κατανάλωσης λίπους στο δείγμα

• Η καλύτερη πρόβλεψη για οποιονδήποτε ασθενή χωρίς άλλες πληροφορίες

• Μοντέλο αναφοράς για σύγκριση με πιο σύνθετα μοντέλα

Γιατί οι άλλες επιλογές είναι λάθος:

Β - “57.0” - ΛΑΘΟΣ:

• Όχι ο μέσος όρος όλων των παρατηρήσεων

Γ - “65.12” - ΛΑΘΟΣ:

• Όχι ο μέσος όρος όλων των παρατηρήσεων

Δ - “Κανένα από τα παραπάνω” - ΛΑΘΟΣ:

• Η επιλογή Α (77.247) είναι σωστή

Συμπέρασμα:

Το κενό μοντέλο για το Fat έχει συντελεστή 77.247, που αντιπροσωπεύει τον μέσο όρο κατανάλωσης λίπους (σε γραμμάρια ανά ημέρα) για τους 315 ασθενείς του δείγματος. Αυτή είναι η πρόβλεψη που κάνει το μοντέλο για κάθε άτομο, ανεξάρτητα από άλλα χαρακτηριστικά του.

Το StudentSurvey είναι ένα πλαίσιο δεδομένων με 362 παρατηρήσεις στις ακόλουθες 17 μεταβλητές:

• Year: Έτος σπουδών

• Gender: Φύλο φοιτητή: F ή M

• Smoke: Καπνιστής; No ή Yes

• Award: Προτίμηση για βραβείο: Academy, Nobel, ή Olympic

• HigherSAT: Ποια επίδοση στη δοκιμασία SAT είναι υψηλότερη; Math ή Verbal

• Exercise: Ώρες άσκησης ανά εβδομάδα

• TV: Ώρες παρακολούθησης τηλεόρασης ανά εβδομάδα

• Height: Ύψος (σε ίντσες)

• Weight: Βάρος (σε λίβρες)

• Siblings: Αριθμός αδελφών

• BirthOrder: Σειρά γέννησης, 1 = μεγαλύτερο

• VerbalSAT: Βαθμολογία στη δοκιμασία Verbal SAT

• MathSAT: Βαθμολογία στη δοκιμασία Math SAT

• SAT: Σύνθετη βαθμολογία Verbal + Math SAT

• GPA: Βαθμός πτυχίου

• Pulse: Σφυγμός (χτύποι ανά λεπτό)

• Piercings: Αριθμός piercing στο σώμα

29. Χρησιμοποιήστε την lm() για να προσαρμόσετε το κενό μοντέλο για τη μεταβλητή TV στο πλαίσιο δεδομένων StudentSurvey. Τι μπορείτε να ισχυριστείτε με βάση το αποτέλεσμα; (Υπάρχουν περισσότερες από μία σωστές απαντήσεις.)

Ο μέσος όρος της κατανομής των ωρών που περνούν οι φοιτητές βλέποντας τηλεόραση είναι 6.504.Η καλύτερα προσαρμοσμένη τιμή για το κενό μοντέλο είναι 6.504.Το 6.504 είναι μια αμερόληπτη εκτίμηση.

Επεξήγηση

Όλα τα παραπάνω είναι η σωστά.

Κενό μοντέλο για TV:

# Προσαρμογή κενού μοντέλου
empty_model_tv <- lm(TV ~ NULL, data = StudentSurvey)
coef(empty_model_tv)
# (Intercept)
#     6.504155

Ανάλυση κάθε δήλωσης:

Α - “Ο μέσος όρος… είναι 6.504” - ΣΩΣΤΟ:

• Ο σταθερός όρος του κενού μοντέλου ισούται πάντα με το δειγματικό μέσο όρο

• \(b_0 = \bar{TV} = 6.504\) ώρες/εβδομάδα

Β - “Η καλύτερα προσαρμοσμένη τιμή είναι 6.504” - ΣΩΣΤΟ:

• Ο μέσος όρος είναι η βέλτιστη σταθερή πρόβλεψη

Γ - “Το 6.504 είναι αμερόληπτη εκτίμηση” - ΣΩΣΤΟ:

• Ο δειγματικός μέσος όρος είναι αμερόληπτος εκτιμητής του πληθυσμιακού μέσου

30. Χρησιμοποιήστε την lm() για να προσαρμόσετε το κενό μοντέλο για το βαθμό πτυχίου (GPA). Αποθηκεύστε τα αποτελέσματα σε ένα αντικείμενο της R με όνομα empty_model_GPA. Τι περιέχει το αντικείμενο empty_model_GPA;

Τον “σταθερό όρο”3.158Τον μέσο όρο του GPA

Επεξήγηση

Όλα τα παραπάνω είναι σωστά.

Κενό μοντέλο για TV:

# Προσαρμογή κενού μοντέλου
empty_model_GPA <- lm(GPA ~ NULL, data = StudentSurvey)
coef(empty_model_GPA)
# (Intercept)
#     3.158

Ανάλυση της απάντησης:

Όταν εμφανίζετε το περιεχόμενο του empty_model_GPA, βλέπετε:

Α - “Τον σταθερό όρο (intercept)” - ΣΩΣΤΟ:

• Αυτός είναι ο σταθερός όρος του μοντέλου

• Στο κενό μοντέλο, είναι η μόνη παράμετρος

Β - “3.158” - ΣΩΣΤΟ:

• Αυτή είναι η αριθμητική τιμή του συντελεστή

• Η εκτιμημένη τιμή του σταθερού όρου

Γ - “Ο μέσος όρος του GPA” - ΣΩΣΤΟ:

• Ο σταθερός όρος του κενού μοντέλου ισούται πάντα με το δειγματικό μέσο όρο

• Στατιστικά: \(b_0 = \bar{GPA} = 3.158\)

• Μπορεί να επαληθευθεί με: mean(StudentSurvey$GPA, na.rm = TRUE)

31. Αν εμφανίσετε τα υπόλοιπα για το empty_model_GPA, τι αποτέλεσμα θα δείτε;

3.158Για κάθε συμμετέχοντα στη μελέτη, το μοντέλο (δηλαδή, ο μέσος όρος) για το GPAΤο GPA κάθε συμμετέχοντα στη μελέτηΓια κάθε συμμετέχοντα στη μελέτη, τη διαφορά μεταξύ του GPA του/της και του μέσου GPA

Επεξήγηση

Για κάθε συμμετέχοντα στη μελέτη, τη διαφορά μεταξύ του GPA του/της και του μέσου GPA είναι η σωστή απάντηση.

Ορισμός των υπολοίπων (residuals):

Υπόλοιπο = Παρατηρούμενη τιμή - Προβλεπόμενη τιμή

Στο κενό μοντέλο:

• Προβλεπόμενη τιμή = μέσος όρος = 3.158 για όλους

• Υπόλοιπο για φοιτητή i = \(\text{GPA}_i - 3.158\)

Κώδικας για εμφάνιση υπολοίπων:

# Εμφάνιση
residuals(empty_model_GPA)
# ή
resid(empty_model_GPA)

Ερμηνεία:

Θετικά υπόλοιπα:

• Παράδειγμα: Υπόλοιπο = +0.542

• Ερμηνεία: Ο φοιτητής έχει GPA = 3.158 + 0.542 = 3.700

• Συμπέρασμα: Αποδίδει καλύτερα από το μέσο όρο

Αρνητικά υπόλοιπα:

• Παράδειγμα: Υπόλοιπο = -0.658

• Ερμηνεία: Ο φοιτητής έχει GPA = 3.158 - 0.658 = 2.500

• Συμπέρασμα: Αποδίδει χειρότερα από το μέσο όρο

Μηδενικό υπόλοιπο:

• Residual = 0: GPA ακριβώς ίσο με το μέσο όρο (3.158)

Γιατί οι άλλες επιλογές είναι λάθος:

Α - “3.158” - ΛΑΘΟΣ:

• Αυτός είναι ο σταθερός όρος του μοντέλου, όχι τα υπόλοιπα

• Τα υπόλοιπα είναι πολλές τιμές (μία για κάθε φοιτητή), όχι μία τιμή

Β - “Το μοντέλο για κάθε συμμετέχοντα” - ΛΑΘΟΣ:

• Το μοντέλο (πρόβλεψη) είναι 3.158 για όλους

• Τα υπόλοιπα δεν είναι το μοντέλο, αλλά η απόκλιση από το μοντέλο

Γ - “Το GPA κάθε συμμετέχοντα” - ΛΑΘΟΣ:

• Τα υπόλοιπα δεν είναι οι παρατηρούμενες τιμές GPA

• Είναι οι διαφορές από τον μέσο όρο

Συμπέρασμα:

Τα υπόλοιπα του κενού μοντέλου δείχνουν πόσο διαφέρει το GPA κάθε φοιτητή από το μέσο όρο GPA όλων των φοιτητών (3.158). Είναι ένα μέτρο του πόσο “συνηθισμένη” ή “ασυνήθιστη” είναι η επίδοση κάθε φοιτητή σε σχέση με τους υπόλοιπους στα δεδομένα.

32. Δημιουργήστε ένα διαιρεμένο ιστόγραμμα για το βάρος (Weight) ανά φύλο (Gender) στο πλαίσιο δεδομένων StudentSurvey. Για ποιο φύλο είναι πιθανότατα καλύτερο μοντέλο ο μέσος όρος;

Ένα ιστόγραμμα δεν μπορεί να χρησιμοποιηθεί για να απαντήσει σε αυτή την ερώτηση.Ο μέσος όρος είναι εξίσου καλό μοντέλο για άνδρες και γυναίκες.ΓυναίκεςΆνδρες

Επεξήγηση

Γυναίκες είναι η σωστή απάντηση.

Δημιουργία διαιρεμένου ιστογράμματος:

# Διαιρεμένο ιστόγραμμα Weight ανά Gender
gf_histogram(~ Weight | Gender, data = StudentSurvey, bins = 15) %>%
  gf_labs(title = "Κατανομή Βάρους Ανά Φύλο",
          x = "Βάρος (pounds)",
          y = "Συχνότητα")

Γιατί ο μέσος όρος είναι καλύτερο μοντέλο για τις γυναίκες:

Μικρότερη διασπορά:

• Οι γυναίκες έχουν λιγότερη μεταβλητότητα στο βάρος

• Ο μέσος όρος είναι πιο αντιπροσωπευτικός

Γιατί οι άλλες επιλογές είναι λάθος:

Α - “Ιστόγραμμα δεν μπορεί να απαντήσει” - ΛΑΘΟΣ:

• Το ιστόγραμμα μπορεί να δείξει τη διασπορά

• Η οπτική επιθεώρηση της κατανομής είναι πολύτιμη

• Μπορούμε να δούμε ποια ομάδα έχει πιο συμπαγή κατανομή

Β - “Εξίσου καλό για αμφότερα” - ΛΑΘΟΣ:

• Υπάρχουν σαφείς διαφορές στη διασπορά

• Οι κατανομές δεν είναι ίδιες

Δ - “Άνδρες” - ΛΑΘΟΣ:

• Οι άνδρες έχουν μεγαλύτερη διασπορά

• Περισσότερες ακραίες τιμές και ασυμμετρία

• Ο μέσος όρος είναι λιγότερο αντιπροσωπευτικός

Στατιστική αρχή:

Ένας μέσος όρος είναι καλύτερο μοντέλο όταν έχουμε:

• Μικρή διασπορά γύρω από το κέντρο

• Συμμετρική κατανομή

• Λίγες ακραίες τιμές

• Ομοιογενή πληθυσμό

Αυτά τα κριτήρια ικανοποιούνται καλύτερα για τις γυναίκες στην κατανομή βάρους.

33. Χρησιμοποιήστε την lm() για να προσαρμόσετε το κενό μοντέλο για τη μεταβλητή SAT. Τι είναι η τιμή 1204;

Μια αμερόληπτη εκτίμηση της βαθμολογίας SATΗ εκτίμηση της βαθμολογίας SAT που έχει το μικρότερο σφάλμαΟ μέσος όρος της βαθμολογίας SAT

Επεξήγηση

Όλα τα παραπάνω είναι σωστά.

Κώδικας για το κενό μοντέλο της SAT:

# Προσαρμογή κενού μοντέλου για SAT
empty_model_SAT <- lm(SAT ~ NULL, data = StudentSurvey)

# Εμφάνιση του συντελεστή
coef(empty_model_SAT)
# (Intercept) 
#      1204 

# Επαλήθευση με μέσο όρο
mean(StudentSurvey$SAT, na.rm = TRUE)
# [1] 1204

Ανάλυση της τιμής 1204:

Α - “Αμερόληπτη εκτίμηση της βαθμολογίας SAT” - ΣΩΣΤΟ:

• Ο δειγματικός μέσος όρος είναι αμερόληπτος εκτιμητής του πληθυσμιακού μέσου

• Αν πάρουμε πολλά δείγματα, ο μέσος όρος των δειγματικών μέσων θα είναι ο πραγματικός μέσος όρος

Β - “Η εκτίμηση με το μικρότερο σφάλμα” - ΣΩΣΤΟ:

• Καμία άλλη σταθερή τιμή δεν δίνει μικρότερο σφάλμα

Γ - “Ο μέσος όρος της βαθμολογίας SAT” - ΣΩΣΤΟ:

• Στο κενό μοντέλο, ο σταθερός όρος ισούται πάντα με το δειγματικό μέσο όρο

• Οι τρεις παραπάνω δηλώσεις περιγράφουν διαφορετικές ιδιότητες της ίδιας τιμής

Στατιστική ερμηνεία:

Το 1204 αντιπροσωπεύει:

• Κεντρική τιμή: Η “τυπική” βαθμολογία SAT στο δείγμα

• Πρόβλεψη: Η καλύτερη εκτίμηση για έναν άγνωστο φοιτητή

• Μοντέλο αναφοράς: Σημείο αναφοράς για άλλα μοντέλα

Ιδιότητες αμεροληψίας:

Τι σημαίνει “αμερόληπτος εκτιμητής”:

• Αν επαναλάβουμε την έρευνα πολλές φορές

• Ο μέσος όρος των εκτιμήσεων θα είναι ο πραγματικός μέσος όρος

• Δεν υπερεκτιμά ή υποεκτιμά συστηματικά

Συμπέρασμα:

Το 1204 είναι ταυτόχρονα:

1. Αμερόληπτη εκτίμηση του πληθυσμιακού μέσου όρου της βαθμολογίας SAT

2. Η εκτίμηση με το μικρότερο σφάλμα

3. Ο δειγματικός μέσος όρος της SAT

Αυτές οι τρεις ιδιότητες συνυπάρχουν και περιγράφουν διαφορετικές πτυχές της ίδιας στατιστικής έννοιας - του σταθερού όρου στο κενό μοντέλο.