7 Κεφάλαιο: Ποσοτικοποίηση του Σφάλματος
Μια κατά προσέγγιση απάντηση στο σωστό πρόβλημα αξίζει πολύ περισσότερο από μια σωστή απάντηση σε ένα κατά προσέγγιση πρόβλημα.
— John Tukey
7.1 Ποσοτικοποίηση του Συνολικού Σφάλματος ενός Μοντέλου
Μέχρι στιγμής έχουμε αναπτύξει την ιδέα ότι ένα στατιστικό μοντέλο μπορεί να θεωρηθεί ως ένας αριθμός—μία τιμή της εξαρτημένης μεταβλητής. Στην ουσία προσπαθούμε να μοντελοποιήσουμε τη Διαδικασία Παραγωγής Δεδομένων (ΔΠΔ). Επειδή όμως δεν μπορούμε να έχουμε απευθείας πρόσβαση στη ΔΠΔ, προσαρμόζουμε ένα μοντέλο στα δεδομένα που διαθέτουμε και εκτιμούμε τις παραμέτρους του.
Με βάση τη λεκτική εξίσωση ΔΕΔΟΜΕΝΑ = ΜΟΝΤΕΛΟ + ΣΦΑΛΜΑ, έχουμε ορίσει το σφάλμα ως το υπόλοιπο που παραμένει αφότου αφαιρέσουμε το μοντέλο από τα δεδομένα. Στην περίπτωση του απλού μας μοντέλου για μια ποσοτική εξαρτημένη μεταβλητή, το μοντέλο είναι ο μέσος όρος, και το σφάλμα—ή υπόλοιπο—είναι η απόκλιση κάθε τιμής πάνω ή κάτω από το μέσο όρο.
Αναπαριστούμε το κενό μοντέλο με τη σημειολογία του Γενικού Γραμμικού Μοντέλου:
\[Y_i = b_0 + e_i\]
Αυτή η εξίσωση αναπαριστά κάθε τιμή στα δεδομένα μας ως το άθροισμα δύο μερών: του μέσου όρου της κατανομής (αναπαρίσταται από το \(b_0\)), και της απόκλισης της τιμής πάνω ή κάτω από το μέσο όρο (αναπαρίσταται ως \(e_i\)). Με άλλα λόγια, ΔΕΔΟΜΕΝΑ = ΜΟΝΤΕΛΟ + ΣΦΑΛΜΑ.
Σε αυτό το κεφάλαιο, θα εμβαθύνουμε στο ΣΦΑΛΜΑ. Συγκεκριμένα, θα αναπτύξουμε μεθόδους για την ποσοτικοποίηση του συνολικού σφάλματος γύρω από ένα μοντέλο, και για τη μοντελοποίηση της κατανομής του σφάλματος αυτού καθαυτού.
Η ποσοτικοποίηση του συνολικού σφάλματος θα μας βοηθήσει να συγκρίνουμε μοντέλα για να δούμε ποιο εξηγεί περισσότερη μεταβλητότητα. Η μοντελοποίηση της κατανομής του σφάλματος θα μας βοηθήσει να κάνουμε πιο λεπτομερείς προβλέψεις για μελλοντικές παρατηρήσεις και πιο ακριβείς δηλώσεις για τη ΔΠΔ.
Εξαρχής, αξίζει να υπενθυμίσουμε την πεμπτουσία της στατιστικής ανάλυσης: την εξήγηση της μεταβλητότητας. Αφού δημιουργήσουμε ένα μοντέλο, μπορούμε να σκεφτούμε την εξήγηση της μεταβλητότητας με έναν νέο τρόπο: ως μείωση του σφάλματος γύρω από τις προβλέψεις του μοντέλου.
Έχουμε δει στο προηγούμενο κεφάλαιο ότι ο μέσος όρος είναι το καλύτερο μοντέλο μιας ποσοτικής εξαρτημένης μεταβλητής όταν η διασπορά της κατανομής είναι μικρότερη παρά όταν είναι μεγαλύτερη. Όταν η διασπορά είναι μικρότερη, τα υπόλοιπα από το μοντέλο είναι μικρότερα. Η ποσοτικοποίηση του συνολικού σφάλματος γύρω από ένα μοντέλο θα μας βοηθήσει να γνωρίζουμε πόσο καλά είναι τα μοντέλα μας, και ποια μοντέλα είναι καλύτερα από άλλα.
Άθροιση των Υπολοίπων
Τα παρακάτω ιστογράμματα δείχνουν την κατανομή του μήκους αντίχειρα φοιτητών (Thumb) και την κατανομή των υπολοίπων (Resid) για το σύνολο δεδομένων μας. Όπως εξηγήθηκε προηγουμένως, αυτές οι κατανομές έχουν ακριβώς το ίδιο σχήμα, αλλά διαφορετικούς μέσους όρους.
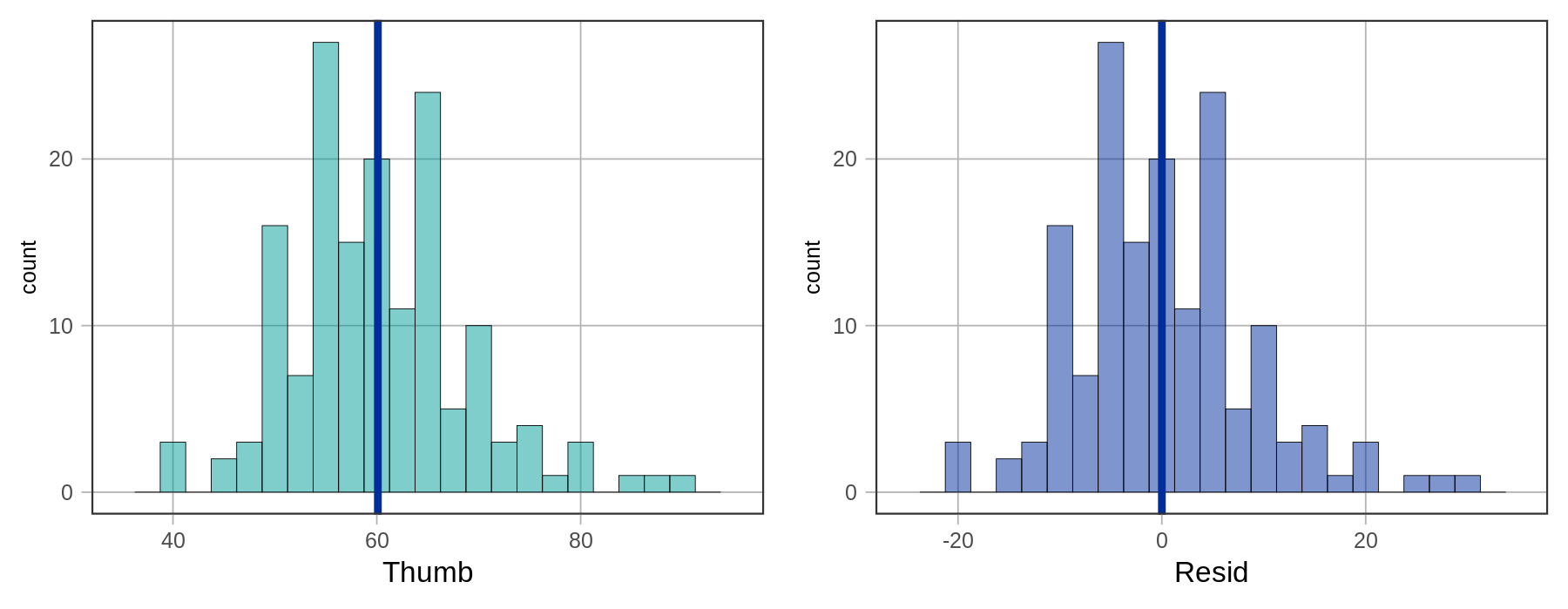
Όπως φαίνεται, έχει νόημα να χρησιμοποιήσουμε τα υπόλοιπα για την ανάλυση του σφάλματος του μοντέλου. Αν θέλουμε να ποσοτικοποιήσουμε το συνολικό σφάλμα, γιατί να μην αθροίσουμε απλώς όλα τα υπόλοιπα; Τα χειρότερα μοντέλα αναμένεται να έχουν μεγαλύτερο σφάλμα, άρα το άθροισμα όλων των σφαλμάτων θα πρέπει να αναπαριστά το «συνολικό» σφάλμα. Το πρόβλημα με αυτήν την προσέγγιση, όπως συζητήθηκε προηγουμένως, είναι ότι το άθροισμα των υπολοίπων γύρω από το μέσο όρο θα είναι πάντα 0. Ο παρακάτω κώδικας θα προσθέσει όλα τα υπόλοιπα από ένα κενό μοντέλο (empty_model).
Γιατί το άθροισμα των υπολοίπων ισούται με 0;
Επειδή ο μέσος όρος εξισορροπεί τα υπόλοιπα είναι η σωστή απάντηση.
Μαθηματική απόδειξη:
Στο κενό μοντέλο:
\[Y_i = b_0 + e_i\]
όπου \(b_0 = \bar{Y}\) (μέσος όρος)
Το υπόλοιπο για κάθε παρατήρηση:
\[e_i = Y_i - b_0 = Y_i - \bar{Y}\]
Άθροισμα όλων των υπολοίπων:
\[\sum_{i=1}^{n} e_i = \sum_{i=1}^{n} (Y_i - \bar{Y})\]
\[= \sum_{i=1}^{n} Y_i - \sum_{i=1}^{n} \bar{Y}\]
\[= \sum_{i=1}^{n} Y_i - n\bar{Y}\]
Αφού \(\bar{Y} = \frac{1}{n}\sum_{i=1}^{n} Y_i\), έχουμε \(n\bar{Y} = \sum_{i=1}^{n} Y_i\):
\[\sum_{i=1}^{n} e_i = \sum_{i=1}^{n} Y_i - \sum_{i=1}^{n} Y_i = 0\]
Αυτό ισχύει ΠΑΝΤΑ στο κενό μοντέλο, ανεξάρτητα από το μέγεθος των δεδομένων ή την πολυπλοκότητα.
Γιατί οι άλλες επιλογές είναι λάθος:
Α - “Μικρό σύνολο δεδομένων” - ΛΑΘΟΣ:
Το μέγεθος του δείγματος δεν επηρεάζει αυτή την ιδιότητα
Ισχύει για n=3 όσο και για n=10,000
Είναι μαθηματική ιδιότητα του μέσου όρου
Β - “Λανθασμένος υπολογισμός” - ΛΑΘΟΣ:
Τα υπόλοιπα υπολογίζονται σωστά ως \(Y_i - \bar{Y}\)
Το άθροισμα 0 είναι αναμενόμενο, όχι σφάλμα
Αν το άθροισμα ΔΕΝ ήταν 0, τότε θα υπήρχε σφάλμα
Δ - “Πολύ απλό μοντέλο” - ΛΑΘΟΣ:
Η ιδιότητα ισχύει σε όλα τα γραμμικά μοντέλα που περιλαμβάνουν τον σταθερό όρο
Ακόμα και σε πολύπλοκα μοντέλα: \(\sum e_i = 0\)
Δεν σχετίζεται με την πολυπλοκότητα του μοντέλου
Εννοιολογική εξήγηση:
Ο μέσος όρος ως σημείο ισορροπίας:
Ο μέσος όρος είναι το κέντρο βάρους των δεδομένων
Θετικές αποκλίσεις (πάνω από το μέσο) εξισορροπούνται από αρνητικές (κάτω από το μέσο)
Το άθροισμα των αποκλίσεων είναι πάντα μηδέν
Οι στατιστικολόγοι έχουν διερευνήσει διάφορες μεθόδους για τον ποσοτικό προσδιορισμό του σφάλματος γύρω από έναν μέσο όρο. Δύο από τις πιο συνηθισμένες, τις οποίες θα συζητήσουμε εδώ, είναι το Άθροισμα των Απόλυτων Αποκλίσεων (Sum of Absolute Deviations - SAD) και το Άθροισμα Τετραγώνων των Αποκλίσεων (Sum of Squared Deviations - SS). Ας δούμε καθεμία από αυτές.
Άθροισμα Απόλυτων Αποκλίσεων
Το άθροισμα των απόλυτων απχοκλίσεων ξεπερνά το πρόβλημα ότι οι αποκλίσεις γύρω από το μέσο όρο πάντα αθροίζουν στο 0, υπολογίζοντας την απόλυτη τιμή των αποκλίσεων πριν τις αθροίσει.
\[\sum_{i=1}^{n} |Y_i - \bar{Y} |\]
Ποια από τις παρακάτω μαθηματικές εκφράσεις αντιπροσωπεύει τις αποκλίσεις (deviations);
Για να υπολογίσετε το Άθροισμα των Απόλυτων Αποκλίσεων, ποια είναι η σωστή σειρά των πράξεων;
Σε αυτό το πλαίσιο, οι «αποκλίσεις από το μέσο όρο» είναι το ίδιο με τα «υπόλοιπα από το κενό μοντέλο», δεδομένου ότι ο μέσος όρος είναι το μοντέλο μας. Έχουμε ήδη τις αποκλίσεις του μήκους κάθε αντίχειρα από το μέσο όρο στη στήλη Resid του πλαισίου δεδομένων Fingers.
Μπορούμε να υπολογίσουμε την απόλυτη τιμή κάθε απόκλισης από το μέσο όρο με τη συνάρτηση abs() .
Αυτό θα εμφανίσει την απόλυτη τιμή όλων των υπολοίπων (υπάρχουν 157 από αυτά). Για να υπολογίσουμε το άθροισμα, μπορούμε να χρησιμοποιήσουμε τη συνάρτηση sum() γύρω από την abs(Fingers$Resid). Δοκιμάστε το στον παρακάτω κώδικα.
1052.437Αν έπρεπε να γράψετε μία γραμμή κώδικα για να εκφράσετε το Άθροισμα των Απόλυτων Αποκλίσεων (SAD), ποια θα ήταν;
sum(abs(resid(empty_model))) είναι η σωστή απάντηση.
Ανάλυση της μαθηματικής έκφρασης:
Η μαθηματική έκφραση είναι: \(\sum_{i=1}^{n}|Y_i - \bar{Y}|\)
Αναλύοντας από μέσα προς τα έξω:
-
\(Y_i - \bar{Y}\): Αποκλίσεις (deviations)
Στην R:
resid(empty_model)Τα υπόλοιπα είναι ακριβώς αυτό: παρατηρούμενες τιμές μείον μέσος όρος
-
\(|Y_i - \bar{Y}|\): Απόλυτες αποκλίσεις (absolute deviations)
Στην R:
abs(resid(empty_model))Η
abs()παίρνει την απόλυτη τιμή κάθε υπολοίπου
-
\(\sum_{i=1}^{n}|Y_i - \bar{Y}|\): Άθροισμα απόλυτων αποκλίσεων
Στην R:
sum(abs(resid(empty_model)))Η
sum()αθροίζει όλες τις απόλυτες τιμές των αποκλίσεων
Γιατί οι άλλες επιλογές είναι λάθος:
Β - abs(sum(resid(empty_model))) - ΛΑΘΟΣ:
Λάθος σειρά: Πρώτα αθροίζει, μετά παίρνει απόλυτη τιμή
Αφού \(\sum resid = 0\), το
abs(0) = 0Δεν υπολογίζει το άθροισμα των απόλυτων αποκλίσεων
Γ - sum(resid(abs(empty_model))) - ΛΑΘΟΣ:
Συντακτικό σφάλμα: Η
abs()δεν μπορεί να εφαρμοστεί στο μοντέλοΗ
abs()χρειάζεται αριθμητικά δεδομένα, όχι αντικείμενο μοντέλουΗ R θα εμφανίσει σφάλμα
Δ - resid(abs(sum(empty_model))) - ΛΑΘΟΣ:
Πολλαπλά σφάλματα στη σύνταξη
Η
sum()δεν εφαρμόζεται σε αντικείμενο μοντέλουΗ
resid()δεν εφαρμόζεται σε αριθμόΕντελώς λανθασμένη λογική
Τι μετράει το SAD:
Άθροισμα Απόλυτων Αποκλίσεων (SAD):
Συνολική απόκλιση από το μέσο όρο
Μέτρο διασποράς: Πόσο “διεσπαρμένα” είναι τα δεδομένα
Συμπέρασμα:
Η σωστή σειρά των υπολογισμών είναι:
Υπολογισμός αποκλίσεων:
resid(empty_model)Απόλυτη τιμή:
abs(...)Άθροισμα:
sum(...)
Αυτό δίνει: sum(abs(resid(empty_model))) - η μόνη επιλογή που ακολουθεί τη σωστή μαθηματική σειρά και σύνταξη.
Άθροισμα Τετραγώνων των Αποκλίσεων
Ένας άλλος τρόπος να ποσοτικοποιήσουμε το συνολικό σφάλμα είναι υψώσουμε τις αποκλίσεις (δηλαδή, τα υπόλοιπα) στο τετράγωνο και στη συνέχεια να τα αθροίσουμε. (Επειδή η ύψωση στο τετράγωνο θα έχει ως αποτέλεσμα έναν θετικό αριθμό ανεξάρτητα από το πρόσημο της αρχικής τιμής, δεν είναι απαραίτητο να υπολογίσουμε πρώτα την απόλυτη τιμή.)
\[\sum_{i=1}^{n} (Y_i - \bar{Y})^2\]
Έχουμε ήδη υπολογίσει τα υπόλοιπα και τα έχουμε αποθηκεύσει σε μια στήλη-μεταβλητή με το όνομα Resid. Για να τετραγωνίσουμε τα υπόλοιπα, μπορούμε να χρησιμοποιήσουμε τον παρακάτω κώδικα. (Σημειώστε ότι στην R χρησιμοποιούμε το σύμβολο ^ για να αναπαραστήσουμε εκθέτες, το οποίο συνήθως βρίσκεται πάνω από το 6 σε ένα τυπικό πληκτρολόγιο.)
Fingers$Resid^2Η εκτέλεση του παραπάνω κώδικα θα παράγει μια λίστα με 157 τιμές υπολοίπων στο τετράγωνο. Τροποποιήστε τον παρακάτω κώδικα με τη χρήση της sum() για να λάβετε το άθροισμα τετραγώνων των υπολοίπων.
11880.21Αν έπρεπε να γράψετε μία γραμμή κώδικα για να εκφράσετε το άθροισμα τετραγώνων των υπολοίπων, ποια θα ήταν;
sum(resid(empty_model)^2) είναι η σωστή απάντηση.
Ανάλυση της μαθηματικής έκφρασης:
Η μαθηματική έκφραση είναι: \(\sum_{i=1}^{n}(Y_i - \bar{Y})^2\)
Αναλύοντας βήμα προς βήμα:
-
\((Y_i - \bar{Y})\): Αποκλίσεις (deviations)
- Στην R:
resid(empty_model)
- Στην R:
-
\((Y_i - \bar{Y})^2\): τετραγωνικές αποκλίσεις (squared deviations)
- Στην R:
resid(empty_model)^2
- Στην R:
-
\(\sum_{i=1}^{n}(Y_i - \bar{Y})^2\): Άθροισμα τετραγώνων των αποκλίσεων
- Στην R:
sum(resid(empty_model)^2)
- Στην R:
Γιατί οι άλλες επιλογές είναι λάθος:
Α - sum(resid(empty_model))^2 - ΛΑΘΟΣ:
Λάθος σειρά: Πρώτα αθροίζει τα υπόλοιπα, μετά υψώνει στο τετράγωνο
Αφού \(\sum resid = 0\), το \((0)^2 = 0\)
Δεν υπολογίζει το άθροισμα των τετραγώνων
Β - sum(abs(empty_model)^2) - ΛΑΘΟΣ:
Συντακτικό σφάλμα: Η
abs()και το^2δεν μπορούν να εφαρμοστούν στο μοντέλοΤο
empty_modelείναι αντικείμενο μοντέλου, όχι αριθμητικά δεδομέναΜη έγκυρη σύνταξη στην R
Δ - resid(sum(empty_model))^2 - ΛΑΘΟΣ:
Εντελώς λανθασμένη λογική
Η
sum()δεν εφαρμόζεται σε αντικείμενο μοντέλουΗ
resid()δεν εφαρμόζεται σε αριθμό
Τι μετράει το SS:
Άθροισμα Τετραγώνων των Υπολοίπων (SS):
Μέτρο συνολικής διασποράς των δεδομένων
Βάση για υπολογισμό του δείκτη της διακύμανσης
Συμπέρασμα:
Για να υπολογίσουμε το Άθροισμα Τετραγώνων των Υπολοίπων, χρειαζόμαστε:
Τα υπόλοιπα:
resd(empty_model)Ύψωση στο τετράγωνο:
...^2Άθροισμα:
sum(...)
Η μόνη επιλογή που ακολουθεί τη σωστή σειρά είναι: sum(resid(empty_model)^2)
Αν χρησιμοποιήσουμε το μέγεθος ενός υπολοίπου για να δημιουργήσουμε ένα τετράγωνο, η περιοχή αυτού του τετραγώνου αναπαριστά το μέγεθος του τετραγωνισμένου υπολοίπου (βλ. παρακάτω Διάγραμμα). Ενώ τα μήκη αντίχειρα στα δεδομένα Fingers μετρώνται σε χιλιοστά, τα τετραγωνικά υπόλοιπα μετρώνται σε τετραγωνικά χιλιοστά.
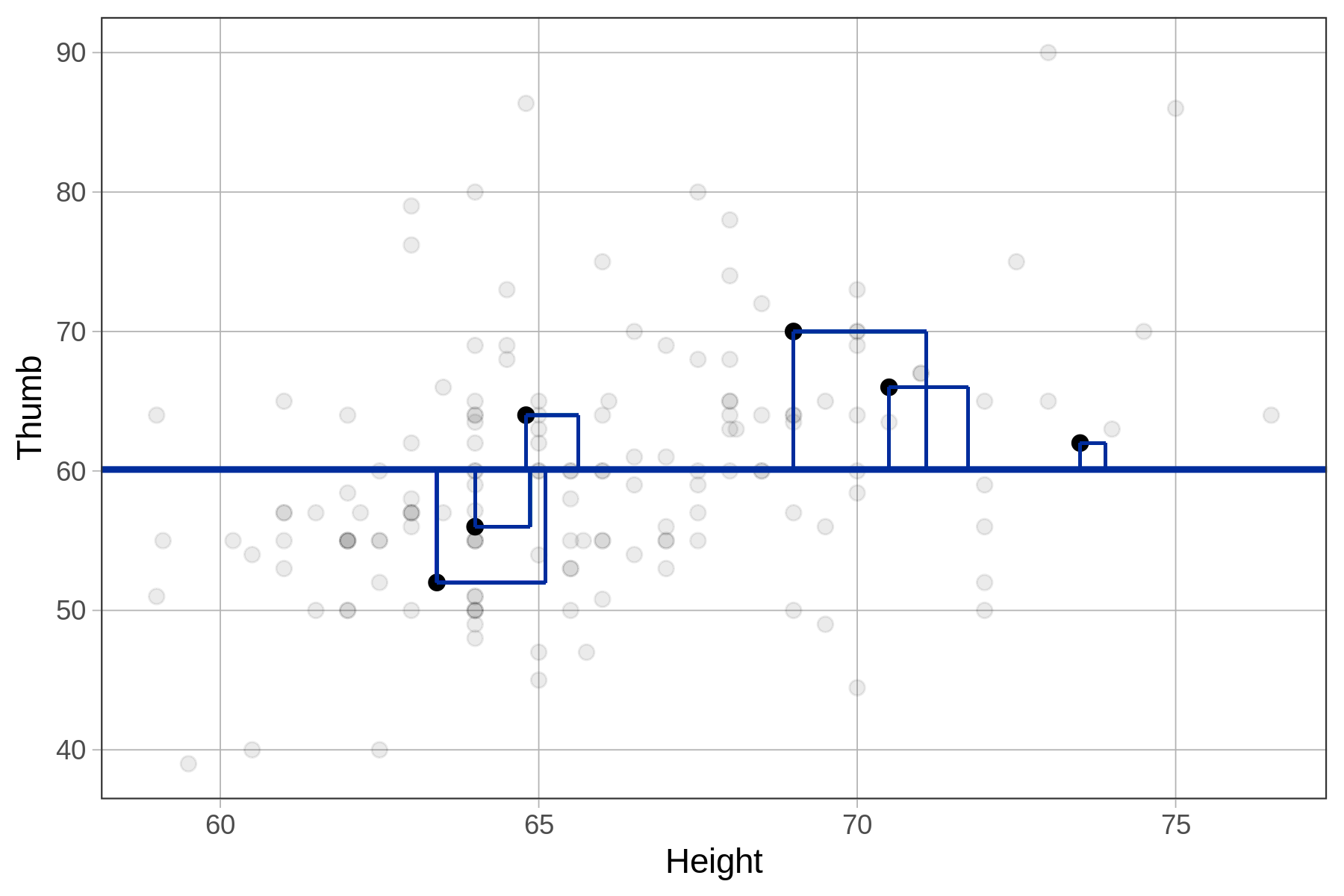
Μπορούμε να σκεφτούμε το Άθροισμα Τετραγώνων (SS) ως το συνολικό εμβαδόν των τετραγώνων για όλα τα υπόλοιπα στο σύνολο δεδομένων. Το Άθροισμα Τετραγώνων είναι ένας σημαντικός δείκτης της ποσότητας του σφάλματος που υπάρχει γύρω από τις προβλέψεις ενός μοντέλου.
7.2 Η Ομορφιά του Αθροίσματος Τετραγώνων
Όπως αποδεικνύεται, το Άθροισμα Τετραγώνων (SS) έχει μια ειδική σχέση με το μέσο όρο. Στο προηγούμενο κεφάλαιο παρουσιάσαμε αναλυτικά τις αρετές του μέσου όρου. Τώρα είναι η ώρα να αρχίσουμε να εκτιμάμε την ομορφιά του αθροίσματος τετραγώνων!
Το Άθροισμα Τετραγώνων Ελαχιστοποιείται στο Μέσο Όρο
Το πλεονέκτημα του αθροίσματος τετραγώνων των αποκλίσεων ως μέτρου του συνολικού σφάλματος είναι ότι ελαχιστοποιείται ακριβώς στο μέσο όρο. Και επειδή ο στόχος μας στη στατιστική μοντελοποίηση είναι να μειώσουμε το σφάλμα όσο το δυνατόν περισσότερο, αυτό είναι καλό.
Ας εξετάσουμε αυτόν τον ισχυρισμό για να διαπιστώσουμε αν πραγματικά στέκει. Ας θυμηθούμε ότι αν χρησιμοποιήσουμε το μέσο όρο των 60.1mm για να προβλέψουμε το μήκος αντίχειρα, και στη συνέχεια πάρουμε τα υπόλοιπα από το μέσο όρο, τα υψώσουμε στο τετράγωνο και τα αθροίσουμε για όλες τις γραμμές του συνόλου δεδομένων Fingers, παίρνουμε την τιμή 11880.21.
Όταν λέμε ότι το άθροισμα τετραγώνων ελαχιστοποιείται στο μέσο όρο, εννοούμε ότι αν υπολογίζαμε τις αποκλίσεις των τιμών από οποιονδήποτε άλλο αριθμό εκτός από το μέσο όρο, το συνολικό άθροισμα τετραγώνων θα ήταν μεγαλύτερο από 11880.21. Είναι αλήθεια αυτό;
Τι πιστεύετε; Αν χρησιμοποιούσαμε το 60.0 ως μοντέλο του μήκους αντίχειρα αντί του 60.1, τι θα συνέβαινε στο Άθροισμα Τετραγώνων;
Θα ήταν μεγαλύτερο από 11880.21 είναι η σωστή απάντηση.
Θεμελιώδης αρχή:
Ο μέσος όρος ελαχιστοποιεί το Άθροισμα Τετραγώνων των Αποκλίσεων. Οποιαδήποτε άλλη τιμή θα δώσει μεγαλύτερο άθροισμα.
Εννοιολογική εξήγηση:
Ο μέσος όρος ως σημείο ισορροπίας:
Ο μέσος όρος (60.1) είναι το βέλτιστο σημείο
Οποιαδήποτε απόκλιση από αυτό αυξάνει το συνολικό σφάλμα
Η αλλαγή από 60.1 σε 60.0 είναι απόκλιση κατά 0.1
Γιατί οι άλλες επιλογές είναι λάθος:
Β - “Θα ήταν μικρότερο” - ΛΑΘΟΣ:
Αντίθετο της θεμελιώδους ιδιότητας του μέσου όρου
Ο μέσος όρος πάντα δίνει το ελάχιστο άθροισμα τετραγώνων των αποκλίσεων
Οποιαδήποτε άλλη τιμή δίνει μεγαλύτερο
Γ - “Δεν μπορούμε να ξέρουμε” - ΛΑΘΟΣ:
Μπορούμε να ξέρουμε με βάση τη θεωρία
Είναι μαθηματικά αποδεδειγμένο ότι ο μέσος ελαχιστοποιεί το άθροισμα τετραγώνων των αποκλίσεων
Δεν χρειάζεται υπολογισμός για να γνωρίζουμε την κατεύθυνση
Πρακτικές συνέπειες:
Για μοντελοποίηση:
Χωρίς άλλες μεταβλητές, ο μέσος όρος είναι η καλύτερη επιλογή
Οποιαδήποτε άλλη σταθερή τιμή θα δώσει χειρότερη προσαρμογή
Αυτό δικαιολογεί τη χρήση του μέσου όρου στο κενό μοντέλο
Συμπέρασμα:
Η αλλαγή από 60.1 (μέσος όρος) σε 60.0 θα αυξήσει το Άθροισμα Τετραγώνων των Αποκλίσεων. Αυτό προκύπτει από τη θεμελιώδη ιδιότητα ότι ο μέσος όρος ελαχιστοποιεί το άθροισμα αυτό - οποιαδήποτε άλλη τιμή, όσο κοντά κι αν είναι, θα δώσει μεγαλύτερο άθροισμα.
Στο παρακάτω πλαίσιο κώδικα, έχουμε θέσει το μέσο όρο του μήκους αντίχειρα (Thumb) ως την τιμή πρόβλεψης του μοντέλου (model <- 60.1). Εκτελέστε τον κώδικα για να δείτε ότι θα πάρετε 11880.21 ως τιμή του αθροίσματος τετραγώνων.
Στη συνέχεια, αλλάξτε την τιμή του μοντέλου από 60.1 σε 60.0 και εκτελέστε ξανά τον κώδικα. Τι συμβαίνει στο άθροισμα τετραγώνων; Αν το άθροισμα όντως ελαχιστοποιείται στο μέσο όρο, τότε θα πρέπει να είναι μεγαλύτερο από 11880.21 όταν δοκιμάζετε οποιονδήποτε άλλο αριθμό εκτός από το μέσο όρο.
Δοκιμάστε να χρησιμοποιήσετε μερικούς άλλους αριθμούς ως τιμές μοντέλου για να δείτε αν μπορείτε να κάνετε το Άθροισμα Τετραγώνων ακόμα μικρότερο. Εμείς δοκιμάσαμε μερικές τιμές και τις παρουσιάζουμε στο παρακάτω διάγραμμα.
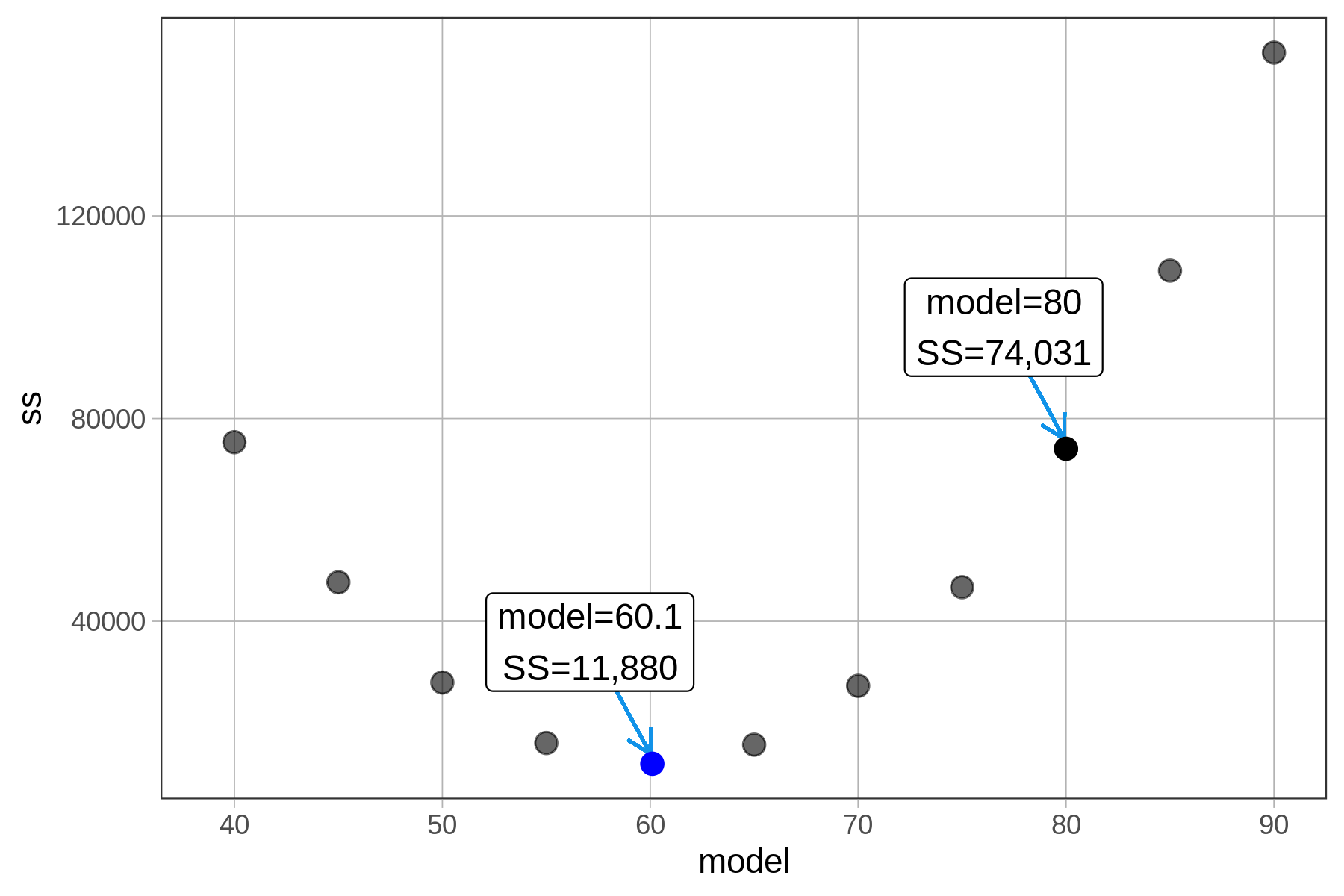
Οι τιμές του αθροίσματος τετραγώνων σχηματίζουν ένα μοτίβο—ένα είδος παραβολής. Στην πραγματικότητα, μπορεί να αποδειχθεί αλγεβρικά ότι το άθροισμα τετραγώνων δεν μπορεί ποτέ να είναι μικρότερο για οποιονδήποτε άλλο αριθμό πέρα από το μέσο όρο της κατανομής. (Μια εξομαλυμένη εκδοχή της συνάρτησης παρουσιάζεται στο παρακάτω διάγραμμα.)
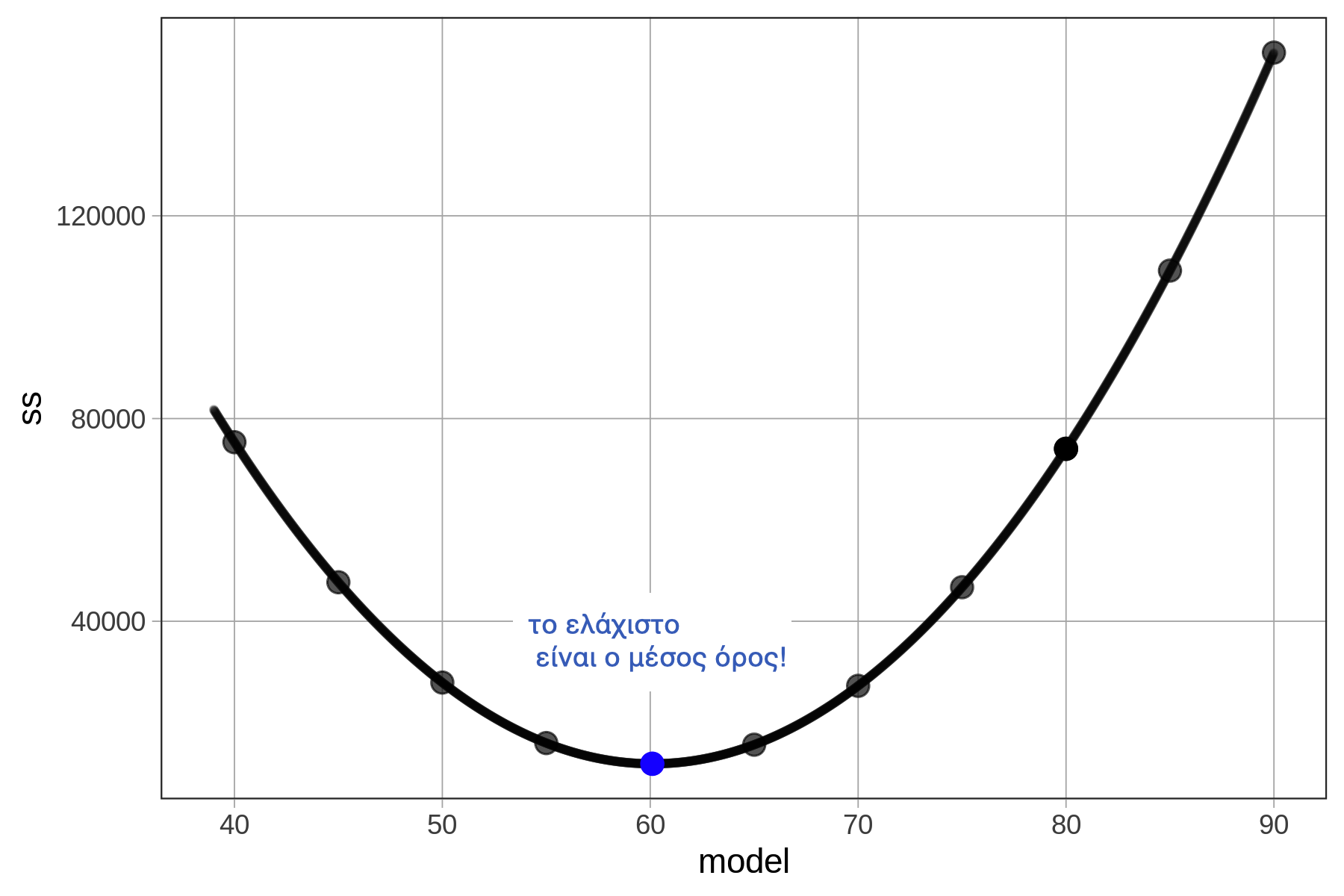
Ο Μέσος Όρος και το Άθροισμα Τετραγώνων Ταιριάζουν
Επειδή το Άθροισμα Τετραγώνων ελαχιστοποιείται στο μέσο όρο, είναι ένα χρήσιμο μέτρο του σφάλματος όταν το μοντέλο μας είναι ο μέσος όρος. Αν επιλέγαμε έναν άλλο αριθμό, όπως τη διάμεσο, για να μοντελοποιήσουμε μια κατανομή, πιθανότατα θα επιλέγαμε ένα διαφορετικό μέτρο σφάλματος—προφανώς ένα που ελαχιστοποιείται στη διάμεσο. Σε αυτό το μάθημα εστιάζουμε κυρίως στο μέσο όρο, οπότε θα επιλέξουμε το Άθροισμα Τετραγώνων των αποκλίσεων από το μέσο όρο ως το προτιμώμενο μέτρο του σφάλματος.
Με μια πρώτη ματιά, πολλές έννοιες της στατιστικής φαίνονται σαν να είναι μέρος μιας ατελείωτης λίστας άσχετων μεταξύ τους μαθηματικών τύπων—ο μέσος όρος, το άθροισμα τετραγώνων, τα γραμμικά μοντέλα. Αλλά ελπίζουμε ότι αρχίζετε να αντιλαμβάνεστε ότι όλα αυτά κάπως ταιριάζουν μεταξύ τους. Η σχέση μεταξύ του μέσου όρου και του Αθροίσματος Τετραγώνων είναι στην πραγματικότητα μόνο ένα παράδειγμα των σχέσεων που συνδέουν όλες αυτές τις έννοιες. Το άθροισμα τετραγώνων θα συνδεθεί και με άλλες ιδέες της στατιστικής στη συνέχεια.
Κάτι αντίστοιχο ισχύει για το Πυθαγόρειο Θεώρημα. Μάθαμε στο σχολείο ότι το τετράγωνο της υποτείνουσας ενός ορθογώνιου τριγώνου ισούται με το άθροισμα των τετραγώνων των δύο καθέτων πλευρών. Δηλαδή, \(\gamma^2 = \alpha^2 + \beta^2\). Η χρήση των τετραγώνων κάνει τα πάντα να αθροίζουν και να ταιριάζουν μεταξύ τους. Αν δεν υψώσουμε στο τετράγωνο, το θεώρημα δεν ισχύει πια: \(\gamma \neq \alpha + \beta\). Έτσι και όταν χρησιμοποιούμε το άθροισμα τετραγώνων για την ποσοτικοποίηση του συνολικού σφάλματος, πολλά πράγματα θα ταιριάξουν μεταξύ τους που διαφορετικά δεν θα ταίριαζαν.
Εύρεση Αθροίσματος Τετραγώνων
Ελπίζουμε ότι σας έχουμε πείσει ότι το Άθροισμα Τετραγώνων και ο μέσος όρος ταιριάζουν μεταξύ τους. Γενικότερα, θα χρησιμοποιήσουμε το Άθροισμα Τετραγώνων ως ένα δείκτη προσαρμογής ενός μοντέλου—και θα επιδιώκουμε να το ελαχιστοποιήσουμε—για όλα τα μοντέλα που θα δούμε στο πλαίσιο του Γενικού Γραμμικού Μοντέλου (GLM). Μέχρι στιγμής, έχουμε εξετάσει μόνο ένα μοντέλο—το κενό μοντέλο \((Y_i = b_0 + e_i\))—στο οποίο το \(b_0\) αντιπροσωπεύει το δειγματικό μέσο όρο (που είναι και η εκτίμησή μας για την τιμή της αντίστοιχης παραμέτρου, του πληθυσμιακού μέσου όρου).
Καθώς προχωράμε στην προσαρμογή πιο σύνθετων μοντέλων στα δεδομένα, θα βασιστούμε σε πίνακες ANOVA για να υπολογίσουμε τα αθροίσματα τετραγώνων. (Το ANOVA σημαίνει Aνάλυση Διακύμανσης—ANalysis Of VAriance.) Σε αυτό το βιβλίο θα χρησιμοποιήσουμε τη συνάρτηση supernova() στην R για να δημιουργήσουμε πίνακες ANOVA. Ας δούμε πώς λειτουργεί για το κενό μοντέλο του μήκους αντίχειρα (Thumb).
supernova(empty_model)Στο παρακάτω πλαίσιο κώδικα, αποθηκεύστε τα αποτελέσματα του κενού μοντέλου για το μήκος αντίχειρα (Thumb) ως empty_model. Έπειτα δοκιμάστε τη συνάρτηση supernova() δίνοντας ως είσοδο το empty_model .
Analysis of Variance Table (Type III SS)
Model: Thumb ~ NULL
SS df MS F PRE p
----- ----------------- --------- --- ------ --- --- ---
Model (error reduced) | --- --- --- --- --- ---
Error (from model) | --- --- --- --- --- ---
----- ----------------- --------- --- ------ --- --- ---
Total (empty model) | 11880.211 156 76.155 Όπως μπορείτε να διαπιστώσετε, τα περισσότερα κελιά σε αυτόν τον πίνακα ANOVA είναι κενά· θα αρχίσουμε να τα γεμίζουμε αργότερα καθώς μαθαίνουμε πώς να προσαρμόζουμε πιο σύνθετα μοντέλα. Προς το παρόν, θα εστιάσουμε στην τελευταία γραμμή του πίνακα, με τίτλο Total (empty model), και τη στήλη με τίτλο SS.
Στον πίνακα, το SS για το κενό μοντέλο είναι ίσο με 11880.211, η ίδια τιμή που πήραμε προηγουμένως υπολογίζοντας τα υπόλοιπα, τετραγωνίζοντάς τα, και στη συνέχεια αθροίζοντάς τα σε κάθε γραμμή του συνόλου δεδομένων.
Υπολογίστηκε ένα Άθροισμα Τετραγώνων (SS) περίπου ίσο με 11880. Ποια είναι η μονάδα μέτρησης αυτού του αριθμού;
Τετραγωνικά χιλιοστά είναι η σωστή απάντηση.
Ανάλυση των μονάδων:
Αν το μήκος αντίχειρα μετριέται σε χιλιοστά (mm):
Sum of Squares (SS):
\[SS = \sum_{i=1}^{n}(x_i - \bar{x})^2\]
Μονάδες κάθε όρου:
\(x_i\): Μέτρηση σε mm
\(\bar{x}\): Μέσος όρος σε mm
\((x_i - \bar{x})\): Απόκλιση σε mm
\((x_i - \bar{x})^2\): Απόκλιση στο τετράγωνο σε mm²
\(\sum(x_i - \bar{x})^2\): Άθροισμα τετραγώνων των αποκλίσεων σε mm²
Γιατί οι άλλες επιλογές είναι λάθος:
Α - “Ίντσες” - ΛΑΘΟΣ:
Οι ίντσες είναι γραμμικές μονάδες, όχι τετραγωνικές
Αν τα δεδομένα ήταν σε ίντσες, το SS θα ήταν σε ίντσες στο τετράγωνο (in²)
Β - “Δεν είναι δυνατό να γνωρίζουμε” - ΛΑΘΟΣ:
Μπορούμε να το προσδιορίσουμε
Αν τα αρχικά δεδομένα είναι σε mm, το SS είναι σε mm²
Η μαθηματική πράξη (ύψωση στο τετράγωνο) καθορίζει τη μονάδα
Γ - “Χιλιοστά” - ΛΑΘΟΣ:
Τα χιλιοστά είναι η μονάδα των αρχικών μετρήσεων
Το Sum of Squares είναι άθροισμα τετραγώνων, άρα mm²
Η πράξη της ύψωσης στο τετράγωνο αλλάζει τη διάσταση
Συμπέρασμα:
Το Άθροισμα Τετραγώνων (Sum of Squares) έχει τετραγωνικές μονάδες επειδή προκύπτει από την ύψωση των αποκλίσεων στο τετράγωνο. Αν οι αρχικές μετρήσεις είναι σε χιλιοστά, το SS είναι σε τετραγωνικά χιλιοστά (mm²). Αυτό είναι αποτέλεσμα του μαθηματικού κανόνα: όταν υψώνουμε μια ποσότητα στο τετράγωνο, το ίδιο συμβαίνει και στη μονάδα της.
7.3 Διακύμανση
Το άθροισμα τετραγώνων είναι ένα καλό μέτρο της συνολικής μεταβλητότητας σε μια εξαρτημένη μεταβλητή όταν χρησιμοποιούμε το μέσο όρο ως μοντέλο. Έχει όμως ένα σημαντικό μειονέκτημα.
Εξετάστε αυτές τις δύο κατανομές.
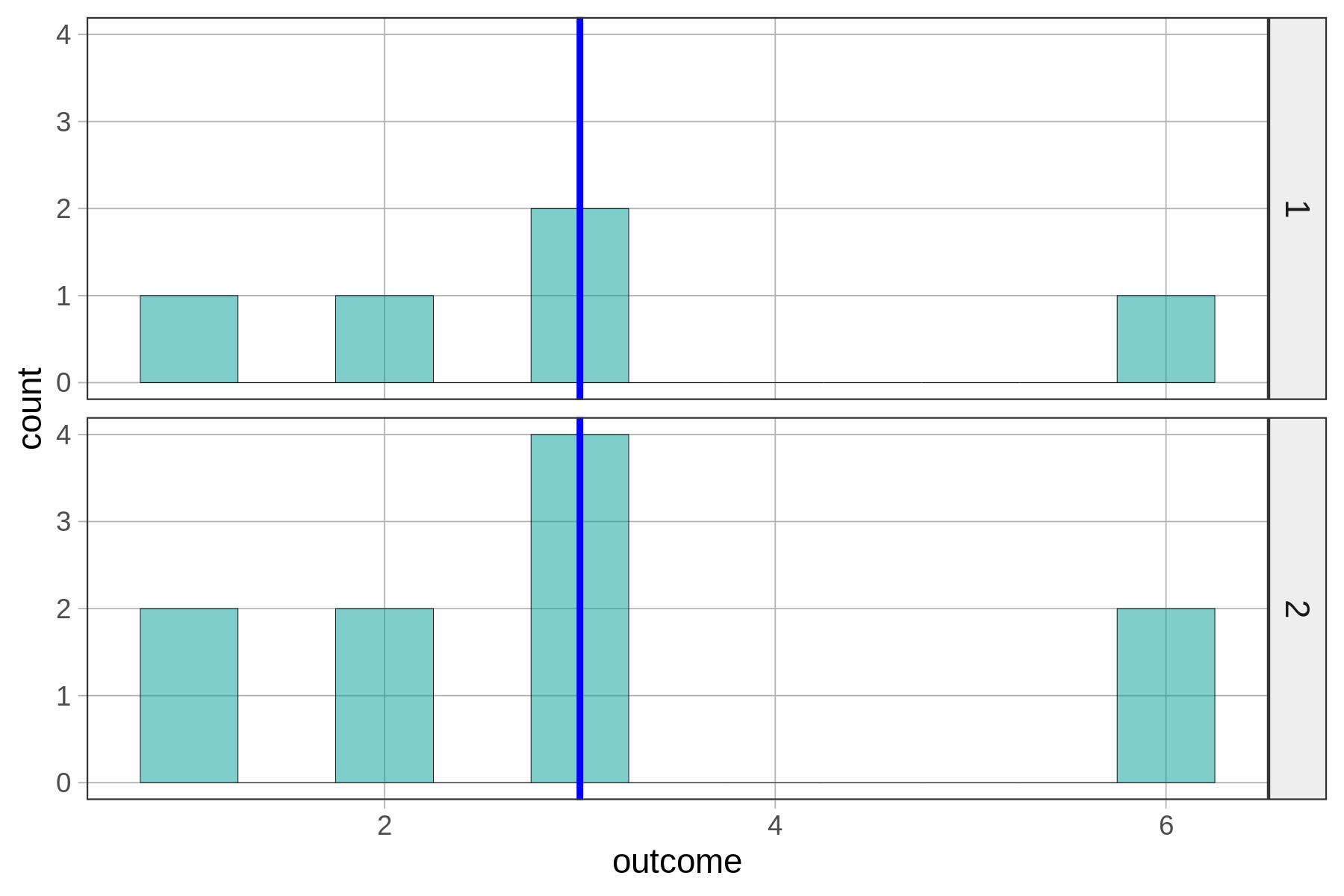
Ποια κατανομή σας φαίνεται πιο διεσπαρμένη;
Από τις παραπάνω κατανομές, ποια νομίζετε ότι θα έχει το μεγαλύτερο Άθροισμα Τετραγώνων Υπολοίπων (SS);
Άθροισμα Τετραγώνων Υπολοίπων (`SS`) για το Μέσο Όρο της Κατανομής 1: 14
Άθροισμα Τετραγώνων Υπολοίπων (`SS`) για το Μέσο Όρο της Κατανομής 2: 28Αν και στα παραπάνω διαγράμματα η μεταβλητότητα των τιμών γύρω από το μέσο όρο οπτικά δε φαίνεται να διαφέρει, η Κατανομή 2 έχει τελικά διπλάσιο Άθροισμα Τετραγώνων από την Κατανομή 1.
Ας δούμε και ένα ακόμη πιο χαρακτηριστικό παράδειγμα.
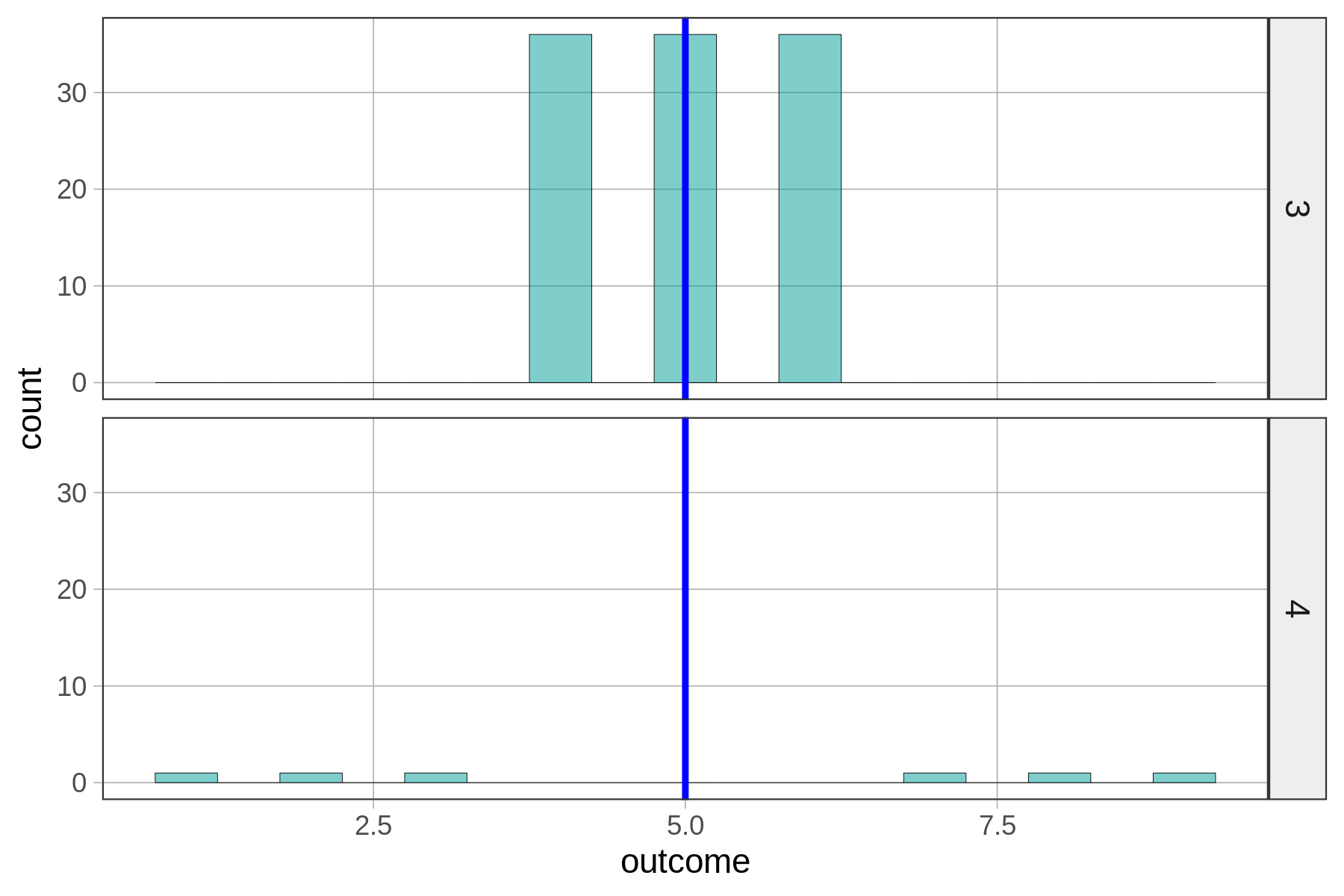
Ποια κατανομή σας φαίνεται πιο διεσπαρμένη;
Από τις παραπάνω κατανομές, για ποια πιστεύετε ότι ο μέσος όρος θα ήταν καλύτερο μοντέλο;
Για την πρώτη ερώτηση: Κατανομή 4 (πιο διεσπαρμένη)
Για τη δεύτερη ερώτηση: Κατανομή 3 (ο μέσος όρος είναι καλύτερο μοντέλο)
Ανάλυση των κατανομών από τα ιστογράμματα:
Κατανομή 3 (συμπαγής, συμμετρική):
Όλες οι τιμές συγκεντρωμένες γύρω από το μέσο (5)
Τρεις στήλες: μία στο ~4.5, μία στο ~5 (ψηλότερη), μία στο ~5.5
Πολύ μικρό εύρος τιμών
Συμμετρική κατανομή
Μικρή διασπορά από το μέσο όρο
Κατανομή 4 (διεσπαρμένη, ασύμμετρη):
Τιμές σε όλο το εύρος (από ~1.5 έως ~9)
Πολλές μικρές στήλες διάσπαρτες
Μεγάλο εύρος τιμών
Ασύμμετρη κατανομή με πιθανές ακραίες τιμές
Μεγάλη διασπορά από το μέσο όρο
Γιατί η Κατανομή 4 είναι πιο διεσπαρμένη:
Οπτικά κριτήρια:
Εύρος δεδομένων: Κατανομή 4 καλύπτει ~7-8 μονάδες, Κατανομή 3 μόνο ~1 μονάδα
Απόσταση από μέσο: Στην Κατανομή 4 υπάρχουν τιμές που απέχουν 3-4 μονάδες από το μέσο
Ομοιογένεια: Κατανομή 3 πολύ συμπαγής, Κατανομή 4 διάσπαρτη
Γιατί ο μέσος είναι καλύτερο μοντέλο για την Κατανομή 3:
1. Μικρή διασπορά:
Όλες οι τιμές είναι πολύ κοντά στο μέσο (5)
Τα υπόλοιπα (αποκλίσεις) είναι πολύ μικρά (±0.5 το πολύ)
Μικρό Άθροισμα Τετραγώνων Υπολοίπων σε σχέση με το μέγεθος του δείγματος
2. Συμμετρία:
Ισορροπημένη κατανομή γύρω από το μέσο
Μέσος ≈ Διάμεσος ≈ Επικρατούσα τιμή
Ο μέσος όρος είναι αντιπροσωπευτικός
3. Προβλεπτική ισχύς:
Αν προβλέψουμε 5 για οποιαδήποτε νέα παρατήρηση, θα κάνουμε πολύ μικρό λάθος
Το σφάλμα πρόβλεψης είναι συνήθως < 0.5
Γιατί ο μέσος είναι χειρότερο μοντέλο για την Κατανομή 4:
1. Μεγάλη διασπορά:
Οι τιμές είναι παντού (1.5 έως 9)
Τα υπόλοιπα (αποκλίσεις) είναι πολύ μεγάλα (έως ±4)
Μεγάλο Άθροισμα Τετραγώνων Υπολοίπων ανά παρατήρηση
2. Ασυμμετρία/Ακραίες τιμές:
Μη ομοιόμορφη κατανομή
Πιθανές ακραίες τιμές που τραβούν το μέσο
Ο μέσος όρος δεν είναι αντιπροσωπευτικός
3. Αναξιόπιστες προβλέψεις:
Αν προβλέψουμε 5, μπορεί η πραγματική τιμή να είναι 2 ή 8
Μεγάλο σφάλμα πρόβλεψης
Ο μέσος όρος δεν είναι χρήσιμος ως πρόβλεψη
Συμπέρασμα:
Η Κατανομή 4 είναι πολύ πιο διεσπαρμένη (μεγάλο εύρος, μεγάλη διασπορά), γι’ αυτό και ο μέσος όρος είναι κακό μοντέλο για αυτήν.
Η Κατανομή 3 είναι συμπαγής (μικρό εύρος, μικρή διασπορά), γι’ αυτό και ο μέσος όρος είναι εξαιρετικό μοντέλο για αυτήν.
Γενικός κανόνας: Όσο πιο διεσπαρμένα τα δεδομένα, τόσο χειρότερο μοντέλο είναι ο μέσος όρος!
Άθροισμα Τετραγώνων Υπολοίπων (`SS`) για το Μέσο Όρο της Κατανομής 3: 72
Άθροισμα Τετραγώνων Υπολοίπων (`SS`) για το Μέσο Όρο της Κατανομής 4: 58Γιατί, όμως, το
SSείναι τόσο μεγαλύτερο για την Κατανομή 3 σε σχέση με την Κατανομή 4;
Το άθροισμα τετραγώνων των υπολοίπων (ή των αποκλίσεων από το μέσο όρο) είναι καλός τρόπος μέτρησης του σφάλματος γύρω από το μέσο όρο, και σύγκρισης του σφάλματος ανάμεσα σε δύο κατανομές. Αλλά αυτό ισχύει μόνο όταν και οι δύο κατανομές έχουν το ίδιο μέγεθος δείγματος.
Ο λόγος γι’ αυτό είναι ότι κάθε φορά που προσθέτετε μια επιπλέον παρατήρηση στην κατανομή του δείγματος σας, στην ουσία προσθέτετε μία ακόμη τετραγωνική απόκλιση από το μέσο όρο στο συνολικό άθροισμα. Έτσι, ακόμη κι αν δύο κατανομές φαίνεται να μοντελοποιούνται εξίσου καλά από τους αντίστοιχους μέσους όρους τους, μπορεί να έχουν πολύ διαφορετικό SS. Το SS πάντα θα αυξάνεται καθώς αυξάνεται ο αριθμός των παρατηρήσεων, ανεξάρτητα από το μέγεθος της μεταβλητότητας.
Μπορείτε να σκεφτείτε έναν τρόπο μέτρησης του σφάλματος που δεν θα επηρεαζόταν από το μέγεθος του δείγματος; Υπόδειξη: Τι θα μπορούσατε να κάνετε για να αποτρέψετε την αύξηση του
SSκάθε φορά που προσθέτετε μία παρατήρηση;
Αυτό το πρόβλημα λύνεται με δύο νέους στατιστικούς δείκτες στην εργαλειοθήκη μας: τη διακύμανση (variance) και την τυπική απόκλιση (standard deviation). Για να υπολογίσουμε τη διακύμανση, αρχικά υπολογίζουμε το SS, ή συνολικό σφάλμα, αλλά στη συνέχεια το διαιρούμε με το μέγεθος του δείγματος για να καταλήξουμε σε ένα μέτρο του μέσου σφάλματος γύρω από το μέσο όρο—το μέσο όρο των τετραγώνων των αποκλίσεων.
Επειδή η διακύμανση είναι κι αυτή ένας μέσος όρος, δεν επηρεάζεται από το μέγεθος του δείγματος, και συνεπώς, μπορεί να χρησιμοποιηθεί για να συγκρίνουμε την ποσότητα σφάλματος ανάμεσα σε δύο δείγματα διαφορετικού μεγέθους. Μπορείτε να σκεφτείτε τη διακύμανση ως ένα μέτρο της μέσης μεταβλητότητας ανά μονάδα δείγματος στο σύνολο δεδομένων.
Ο τύπος για τη διακύμανση, που συνήθως συμβολίζεται με \(s^2\), είναι ο εξής:
\[s^2 = \frac{\sum_{i=1}^{n}(Y_i - \bar{Y})^2}{n-1}\]
Μπορείτε εύκολα να διαπιστώσετε ότι ο αριθμητής είναι το άθροισμα τετραγώνων των αποκλίσεων από το μέσο όρο. Αν και για να υπολογίσουμε έναν πραγματικό μέσο όρο θα διαιρούσαμε τον αριθμητή με το \(n\), στην περίπτωση αυτή διαιρούμε με το \(n-1\). Αυτό το κάνουμε διότι η διαίρεση με το \(n-1\) μας δίνει μια καλύτερη εκτίμηση της πραγματικής διακύμανσης του πληθυσμού. Αυτό μπορεί να φανεί αν προσομοιώσουμε πολλαπλά τυχαία δείγματα από έναν πληθυσμό με γνωστή διακύμανση και στη συνέχεια εξετάσουμε ποιες εκτιμήσεις είναι καλύτερες—αυτές που προκύπτουν διαιρώντας με το \(n\), ή αυτές που προκύπτουν διαιρώντας με το \(n-1\).
Υπάρχει, φυσικά, και μια μαθηματική απόδειξη γι’ αυτό. Αλλά είναι χρήσιμο να το σκεφτόμαστε ως εξής: όταν έχετε ένα μικρό δείγμα, οι πιο ακραίες τιμές σε έναν πληθυσμό είναι απίθανο να εμφανιστούν στο δείγμα. Έτσι, αν διαιρούσαμε με το \(n\) θα υποεκτιμούσαμε ελαφρώς την πραγματική διακύμανση του πληθυσμού, ειδικά σε μικρότερα δείγματα. Η διαίρεση με το \(n-1\) διορθώνει αυτή την μεροληψία, μεγαλώνοντας λιγάκι την εκτίμηση της διακύμανσης. Και, καθώς το δείγμα μεγαλώνει, η διαφορά μεταξύ \(n\) και \(n-1\) θα γίνεται ολοένα και μικρότερη.
Το βασικό που πρέπει να γνωρίζετε είναι ότι η διαίρεση του SS (αθροίσματος τετραγώνων) με το \(n-1\) προσεγγίζει τη μέση τετραγωνική απόκλιση. Επιπρόσθετα, να σημειωθεί ότι το \(n-1\), που εμφανίζεται στον παρονομαστή, αποκαλείται συχνά βαθμοί ελευθερίας (degrees of freedom) ή df. Η έννοια αυτή θα εξεταστεί αναλυτικότερα σε επόμενη ενότητα.

Στο παραπάνω διάγραμμα, ποιος είναι ο οπτικός ορισμός του Αθροίσματος Τετραγώνων των Υπολοίπων;
Ποιος είναι ο οπτικός ορισμός της διακύμανσης (variance);
Για SS: Το άθροισμα του εμβαδού όλων των τετραγώνων
Για Διακύμανση: Ο μέσος όρος του εμβαδού των τετραγώνων
Ας δούμε τι αναπαριστούν τα μπλε τετράγωνα στο διάγραμμα:
Κάθε τετράγωνο έχει πλευρά ίση με την απόκλιση από το μέσο όρο της Thumb (υπόλοιπο)
Εμβαδόν κάθε τετραγώνου = (απόκλιση)² = υπόλοιπο στο τετράγωνο
Οριζόντια γραμμή (y = 60) = μέσος όρος της Thumb
Μαθηματική σύνδεση:
Άθροισμα Τετραγώνων (SS):
\[SS = \sum_{i=1}^{n}(Y_i - \bar{Y})^2\]
Οπτικά:
Κάθε σημείο έχει ένα τετράγωνο με πλευρά = \(|Y_i - \bar{Y}|\)
Εμβαδόν τετραγώνου = \((Y_i - \bar{Y})^2\)
SS = άθροισμα όλων των εμβαδών
Διακύμανση:
\[s^2 = \frac{SS}{n-1} = \frac{\sum_{i=1}^{n}(Y_i - \bar{Y})^2}{n-1}\]
Οπτικά:
Διακύμανση = μέσο εμβαδόν των τετραγώνων
Παίρνουμε το SS και το διαιρούμε με (n-1)
Δίνει το τυπικό/μέσο μέγεθος τετραγώνου
Διαγραμματική ερμηνεία:
SS (Συνολικό εμβαδόν):
Αν προσθέσουμε όλα τα μπλε τετράγωνα
Παίρνουμε το συνολικό εμβαδόν = SS
Μεγαλύτερα τετράγωνα → μεγαλύτερο SS → μεγαλύτερη διασπορά
Διακύμανση (Μέσο εμβαδόν):
Αν κατά μέσο όρο φτιάχναμε ένα τετράγωνο ανά παρατήρηση
Πόσο μεγάλο θα ήταν;
Διακύμανση = το τυπικό μέγεθος τετραγώνου
Γιατί οι άλλες επιλογές είναι λάθος:
“Ο αριθμός των τετραγώνων” - ΛΑΘΟΣ:
Ο αριθμός τετραγώνων = αριθμός παρατηρήσεων (n)
Δεν μετράει τη διασπορά, μόνο το μέγεθος δείγματος
“Το άθροισμα των πλευρών” - ΛΑΘΟΣ:
Άθροισμα πλευρών = \(\sum|Y_i - \bar{Y}|\) (Άθροισμα Απόλυτων Διαφορών)
Αυτό είναι διαφορετικό μέτρο διασποράς
“Το άθροισμα των περιμέτρων” - ΛΑΘΟΣ:
Περίμετρος = \(4 \times |Y_i - \bar{Y}|\)
Απλά πολλαπλασιάζει το άθροισμα πλευρών επί 4
Δεν σχετίζεται με το SS ή τη διακύμανση
Πρακτική χρήση της οπτικοποίησης:
Για κατανόηση:
Μεγάλα τετράγωνα = μεγάλες αποκλίσεις = κακό μοντέλο
Μικρά τετράγωνα = μικρές αποκλίσεις = καλό μοντέλο
Διαγραμματική σύγκριση μοντέλων
Συμπέρασμα:
Η οπτικοποίηση με τετράγωνα κάνει την έννοια του “Αθροίσματος Τετραγώνων των Υπολοίπων” συγκεκριμένη:
SS = συνολική επιφάνεια όλων των τετραγώνων
Διακύμανση = μέση επιφάνεια ανά τετράγωνο
Τετράγωνα αναπαριστούν γεωμετρικά την ποσότητα \((Y_i - \bar{Y})^2\)
Αυτή η οπτικοποίηση βοηθά να καταλάβουμε γιατί ονομάζεται “Άθροισμα Τετραγώνων**“!
Για να υπολογίσουμε τη διακύμανση στην R μπορούμε να χρησιμοποιήσουμε τη συνάρτηση var(). Στο παρακάτω πλαίσιο, να υπολογίσετε τη διακύμανση του μήκους αντίχειρα (Thumb) από το πλαίσιο δεδομένων Fingers.
var(Fingers$Thumb)Μπορείτε επίσης να υπολογίσετε τη διακύμανση με την εκτέλεση της συνάρτησης supernova() για το κενό μοντέλο (empty_model).
76.155Analysis of Variance Table (Type III SS)
Model: Thumb ~ NULL
SS df MS F PRE p
----- ----------------- --------- --- ------ --- --- ---
Model (error reduced) | --- --- --- --- --- ---
Error (from model) | --- --- --- --- --- ---
----- ----------------- --------- --- ------ --- --- ---
Total (empty model) | 11880.211 156 76.155Μπορείτε εύκολα να διαπιστώσετε ότι η τιμή της διακύμανσης της Thumb είναι η ίδια, είτε παράγεται από τη συνάρτηση var() είτε από τη συνάρτηση supernova(). Στον πίνακα ANOVA, ωστόσο, η διακύμανση βρίσκεται στη στήλη MS. Το MS σημαίνει Mean Square, δηλαδή «μέσο άθροισμα τετραγώνων». Αν διαιρέσετε το συνολικό άθροισμα τετραγώνων (11880.211) με το \(n-1\) (156), θα πάρετε το μέσο άθροισμα τετραγώνων, ή με άλλα λόγια τη διακύμανση της μεταβλητής Thumb (76.155).
Ποια είναι η σωστή ερμηνεία της τιμής 76.155;
Η μέση τετραγωνική απόκλιση σε αυτή την κατανομή είναι περίπου 76 τετραγωνικά χιλιοστά είναι η σωστή απάντηση.
Τι είναι η Μέση Τετραγωνική Απόκλιση (MS - Mean Square):
Mean Square = Variance = Διακύμανση
\[MS = \frac{SS}{df} = \frac{SS}{n-1} = \frac{11880.211}{156} = 76.155\]
Ερμηνεία:
MS = Mean (μέσος όρος) of the Squared (τετραγωνικών) deviations (αποκλίσεων)
Είναι η διακύμανση (variance)
Μετράει τη μέση τετραγωνική απόκλιση από το μέσο όρο
Μαθηματική ανάλυση:
Βήμα προς βήμα:
Αποκλίσεις: \((Thumb_i - \bar{Thumb})\) (σε mm)
Τετραγωνικές αποκλίσεις: \((Thumb_i - \bar{Thumb})^2\) (σε mm²)
Άθροισμα: \(SS = \sum(Thumb_i - \bar{Thumb})^2 = 11880.211\)mm²
Μέση τετραγωνική απόκλιση: \(MS = \frac{SS}{n-1} = 76.155\)mm²
Μονάδες μέτρησης:
Thumb μετριέται σε mm
Απόκλιση \((Thumb_i - \bar{Thumb})\) σε mm
Τετραγωνική απόκλιση \((Thumb_i - \bar{Thumb})^2\) σε mm²
MS (variance) σε mm² (τετραγωνικά χιλιοστόμετρα)
Γιατί οι άλλες επιλογές είναι λάθος:
Α - “76 αντίχειρες μεγαλύτεροι από το μέσο” - ΛΑΘΟΣ:
Το 76.155 είναι μέτρο διασποράς, όχι πλήθος
Ο αριθμός αντίχειρων πάνω από το μέσο είναι περίπου n/2 ≈ 78-79
Δεν σχετίζεται με την τιμή 76.155
Β - “76 αντίχειρες διαφορετικοί από το μέσο” - ΛΑΘΟΣ:
Όλοι οι αντίχειρες είναι διαφορετικοί από το μέσο (εκτός από τυχαία ακριβή ταύτιση)
Το 76.155 δεν είναι πλήθος
Σύγχυση μεταξύ τιμής διακύμανσης και αριθμού παρατηρήσεων
Δ - “Μέση απόκλιση 76mm” - ΛΑΘΟΣ:
Αυτό θα ήταν η Μέση Απόλυτη Απόκλιση - Mean Absolute Deviation (MAD)
MAD = \(\frac{\sum|Thumb_i - \bar{Thumb}|}{n}\) (σε mm, όχι mm²)
Το 76.155 είναι τετραγωνική απόκλιση (mm²), όχι γραμμική (mm)
Ε - “Μέσος αντίχερας 76” - ΛΑΘΟΣ:
Ο μέσος όρος του μήκους αντίχειρα δεν είναι 76 mm
Το 76.155 είναι η διακύμανση, όχι ο μέσος όρος
Εντελώς διαφορετικά μεγέθη!
Πρακτική ερμηνεία του MS = 76.155:
Τι σημαίνει;
Αν πάρουμε κάθε μήκος αντίχειρα και υπολογίσουμε \((Thumb_i - \bar{Thumb})^2\)
Και μετά υπολογίσουμε το μέσο όρο αυτών των τετραγώνων
Παίρνουμε 76.155mm²
Οπτικά (από την προηγούμενη εξήγηση):
Αν σχεδιάσουμε τετράγωνα με πλευρά = απόκλιση
Το μέσο εμβαδόν αυτών των τετραγώνων είναι 76.155mm²
Συμπέρασμα:
Το MS = 76.155 ερμηνεύεται ως: “Η μέση τετραγωνική απόκλιση του μήκους αντίχειρα από το μέσο όρο είναι 76.155 τετραγωνικά χιλιοστά.”
7.4 Τυπική Απόκλιση
Η τυπική απόκλιση (standard deviation) συμβολίζεται με \(s\) και είναι απλά η τετραγωνική ρίζα της διακύμανσης. Γενικά προτιμούμε να σκεφτόμαστε το σφάλμα με όρους τυπικής απόκλισης επειδή είναι μια τιμή σε μονάδες της αρχικής κλίμακας μέτρησης.
Για παράδειγμα, αν μοντελοποιήσουμε το σωματικό βάρος σε kg:
- Η διακύμανση θα εκφράζει το σφάλμα σε τετραγωνικά kg (μια μονάδα μέτρησης που δεν είμαστε συνηθισμένοι να σκεφτόμαστε)
- Η τυπική απόκλιση θα εκφράζει το σφάλμα σε kg (πολύ πιο κατανοητό!)
Υπάρχουν δύο ισοδύναμοι τύποι που αναπαριστούν την τυπική απόκλιση:
\[s = \sqrt{s^2} = \sqrt{\frac{\sum_{i=1}^{n}(Y_i - \bar{Y})^2}{n-1}}\]
Ή απλούστερα:
\[s = \sqrt{\text{Διακύμανση}}\]
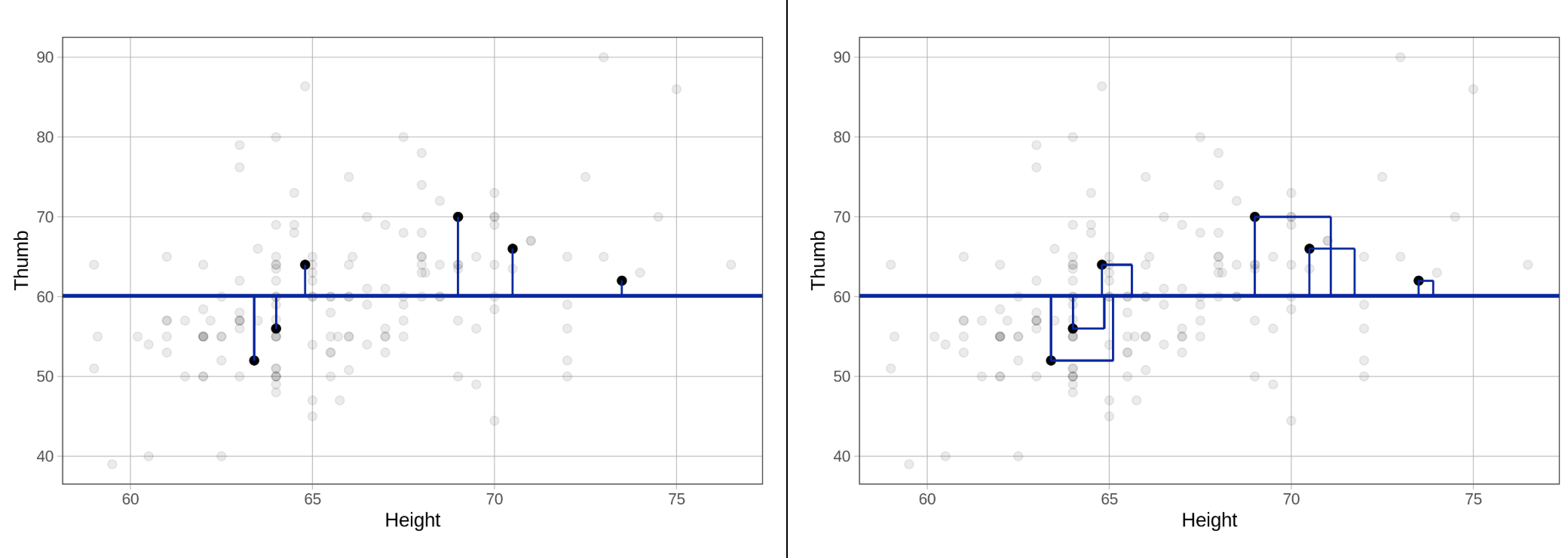
Ποιος είναι ο οπτικός ορισμός της τυπικής απόκλισης; (Υπάρχουν περισσότερες από μία σωστές απαντήσεις.)
Θυμηθείτε ότι η διακύμανση του μήκους αντίχειρα (Thumb) ήταν περίπου ίση με 76. Ποια από τις παρακάτω είναι μια καλή εκτίμηση για την τυπική απόκλιση του μήκους αντίχειρα;
Για την πρώτη ερώτηση: Α, Β είναι σωστές
Για τη δεύτερη ερώτηση: 9 (Γ)
Ανάλυση της τυπικής απόκλισης:
Τυπική απόκλιση (Standard Deviation):
\[SD = \sqrt{variance} = \sqrt{MS} = \sqrt{76} \approx 8.72 \approx 9\]
Οπτικοί ορισμοί της τυπικής απόκλισης:
Α - “Μέση απόλυτη απόκλιση από το μοντέλο” - ΣΩΣΤΟ:
Η τυπική απόκλιση είναι περίπου η μέση απόλυτη απόκλιση
Από το διάγραμμα 1: οι κάθετες γραμμές δείχνουν αποκλίσεις
Τυπική Απόκλιση ≈ μέση απόλυτη τιμή αυτών των αποκλίσεων
Β - “Μέση κάθετη απόσταση από το μέσο” - ΣΩΣΤΟ:
Οι μπλε κάθετες γραμμές στο αριστερό διάγραμμα δείχνουν την κάθετη απόσταση
Από κάθε σημείο στον οριζόντιο μέσο όρο (y = 60)
Η τυπική απόκλιση είναι περίπου ο μέσος όρος αυτών των αποστάσεων
Γ - “Μέσο εμβαδόν τετραγώνων” - ΛΑΘΟΣ:
Το μέσο εμβαδόν των τετραγώνων (διάγραμμα στα δεξιά) είναι η διακύμανση (76mm²)
Η τυπική απόκλιση είναι η ρίζα του μέσου εμβαδού, όχι το εμβαδόν
Τυπική απόκλιση = √(μέσο εμβαδόν) = √76 ≈ 9mm
Δ - “Αριθμός τετραγώνων” - ΛΑΘΟΣ:
Ο αριθμός τετραγώνων = αριθμός παρατηρήσεων (n)
Δεν σχετίζεται με τη μεταβλητότητα
Είναι απλά το μέγεθος του δείγματος
Υπολογισμός τυπικής απόκλισης:
# Δεδομένη διακύμανση
variance <- 76 # mm²
# Τυπική απόκλιση = ρίζα της διακύμανσης
SD <- sqrt(variance)
print(SD)
# [1] 8.717798
# Στρογγυλοποίηση
round(SD)
# [1] 9Γιατί η απάντηση είναι 9:
Έλεγχος όλων των επιλογών:
70: Πολύ κοντά στη διακύμανση (76), όχι στην τυπική απόκλιση
16: √256 = 16, πολύ μεγάλο
9: √81 = 9, πολύ κοντά στο √76 ≈ 8.72 ✓
4: √16 = 4, πολύ μικρό
1: √1 = 1, εξαιρετικά μικρό
Σχέση διακύμανσης και τυπικής απόκλισης:
# Αν SD = 9
SD_estimate <- 9
variance_from_SD <- SD_estimate^2
# 81 (κοντά στο 76)
# Αν SD = 8.72 (ακριβές)
SD_exact <- sqrt(76)
variance_check <- SD_exact^2
# 76 (ακριβώς!)Οπτική επαλήθευση από τα διαγράμματα:
Διάγραμμα στα αριστερά - Κάθετες γραμμές:
Οι περισσότερες αποκλίσεις φαίνονται να είναι 5-15mm
Μερικές πολύ μικρές (2-3mm)
Μερικές μεγάλες (15-20mm)
Μέση απόσταση ≈ 8-9mm ✓
Διάγραμμα στα δεξιά - Τετράγωνα:
Διαφορετικά μεγέθη τετραγώνων
Αν το μέσο εμβαδόν είναι 76mm²
Τότε η πλευρά του μέσου τετραγώνου είναι √76 ≈ 9mm ✓
Σύγκριση μέτρων διασποράς:
Μέτρο | Τιμή | Μονάδα | Ερμηνεία
------------------ | ------ | ------ | ---------
SS | 11.880 | mm² | Συνολική διασπορά
Variance (MS) | 76 | mm² | Μέση τετραγ. απόκλιση
Std Deviation (SD) | 9 | mm | Τυπική απόκλισηΓιατί χρησιμοποιούμε την τυπική απόκλιση αντί για τη διακύμανση:
1. Ίδιες μονάδες με τα δεδομένα:
Διακύμανση σε mm² (τετραγωνικά χιλιοστά)
Τυπική απόκλιση σε mm (χιλιοστά) - πιο κατανοητό
2. Άμεση ερμηνεία:
“Η τυπική απόκλιση είναι 9mm” = κατανοητή μονάδα μέτρησης
“Η διακύμανση είναι 76mm²” = δύσκολο να την κατανοήσουμε
Τετράγωνα που βοηθούν την κατανόηση:
Φανταστείτε ένα τετράγωνο με εμβαδόν 76mm²
Ποια είναι η πλευρά του; √76 ≈ 9mm
Αυτή η πλευρά είναι η τυπική απόκλιση!
Συμπέρασμα:
Η τυπική απόκλιση οπτικά είναι:
Περίπου η μέση κάθετη απόσταση από το μέσο όρο (διάγραμμα στα αριστερά)
Η πλευρά του μέσου τετραγώνου απόκλισης (διάγραμμα στα δεξιά)
Με διακύμανση = 76mm², η τυπική απόκλιση είναι √76 ≈ 9mm, που αντιπροσωπεύει την τυπική απόσταση κάθε μήκους αντίχειρα από το μέσο όρο.
Για να υπολογίσουμε την τυπική απόκλιση στην R, μπορούμε να χρησιμοποιήσουμε τη συνάρτηση sd().
sd(Fingers$Thumb) Εναλλακτικά, μπορούμε να συνδυάσουμε τη συνάρτηση var() με τη συνάρτηση sqrt(). Ένας τρίτος τρόπος είναι η χρήση της συνάρτησης favstats(), η οποία περιλαμβάνει την τυπική απόκλιση στα αποτελέσματά της.
Μπορείτε να δοκιμάσετε και τους τρεις τρόπους στο παρακάτω πλαίσιο κώδικα για να υπολογίσετε την τυπική απόκλιση της Thumb στο πλαίσιο δεδομένων Fingers.
8.726695
8.726695
min Q1 median Q3 max mean sd n missing
39 55 60 65 90 60.10366 8.726695 157 0Ποια είναι η σωστή ερμηνεία της τιμής 8.73;
Η μέση απόκλιση σε αυτή την κατανομή είναι περίπου 8.73mm είναι η σωστή απάντηση.
Τι είναι το 8.73:
Τυπική απόκλιση (Standard Deviation):
\[SD = \sqrt{variance} = \sqrt{76.155} \approx 8.73 \text{mm}\]
Ερμηνεία:
Η τυπική απόκλιση μετράει την τυπική/μέση απόσταση των παρατηρήσεων από το μέσο όρο
8.73mm = η τυπική απόκλιση του μήκους αντίχειρα από το μέσο όρο
Ένα αντιπροσωπευτικό μέτρο του πόσο διασκορπισμένα είναι τα δεδομένα
Γιατί οι άλλες επιλογές είναι λάθος:
Α - “8.73 αντίχειρες διαφορετικοί από το μέσο” - ΛΑΘΟΣ:
Το 8.73 είναι μέτρο απόστασης (mm), όχι πλήθος
Όλα τα μήκη αντίχειρα είναι (σχεδόν) διαφορετικά από το μέσο
Β - “Μέση τετραγωνική απόκλιση 8.73mm²” - ΛΑΘΟΣ:
Η μέση τετραγωνική απόκλιση είναι η διακύμανση = 76.155mm²
Το 8.73² = 76.15 (η διακύμανση)
Το 8.73 είναι η ρίζα της μέσης τετραγωνικής απόκλισης
Επίσης, οι μονάδες είναι mm, όχι mm²
Δ - “Μέσο μήκος αντίχειρα 8.73mm” - ΛΑΘΟΣ:
Ο μέσος όρος του μήκους αντίχειρα δεν είναι 8.73mm (πολύ μικρό!)
Ο μέσος όρος του μήκους αντίχειρα είναι περίπου 60mm
Το 8.73 είναι η διασπορά γύρω από το μέσο, όχι ο μέσος
Ε - “Άθροισμα υπολοίπων 8.73mm” - ΛΑΘΟΣ:
Το άθροισμα των υπολοίπων είναι πάντα 0
\(\sum(Y_i - \bar{Y}) = 0\) (θεμελιώδης ιδιότητα)
Το 8.73 δεν σχετίζεται με άθροισμα των υπολοίπων
Συμπέρασμα:
Το 8.73mm είναι η τυπική απόκλιση του μήκους αντίχειρα, που ερμηνεύεται ως “η μέση απόκλιση είναι περίπου 8.73mm”. Αυτό σημαίνει ότι το μήκος ενός τυπικού αντίχειρα απέχει περίπου 8.73mm από το μέσο όρο, και είναι το πιο κοινό μέτρο για την περιγραφή της διασποράς σε γραμμικές μονάδες (mm).
Άθροισμα Τετραγώνων, Διακύμανση και Τυπική Απόκλιση
Έχουμε συζητήσει τρεις δείκτες για την ποσοτικοποίηση του σφάλματος γύρω από ένα μοντέλο. Όλοι ξεκινούν με τα υπόλοιπα (αποκλίσεις από το μοντέλο), αλλά τα αθροίζουν με διαφορετικούς τρόπους για να συνοψίσουν το συνολικό σφάλμα.
Και οι τρεις ελαχιστοποιούνται στο μέσο όρο, και συνεπώς όλοι είναι χρήσιμοι όταν ο μέσος όρος είναι το μοντέλο για μια ποσοτική μεταβλητή.
Τι σημαίνει ότι αυτά τα τρία μέτρα σφάλματος (άθροισμα τετραγώνων, διακύμανση, και τυπική απόκλιση) ελαχιστοποιούνται στο μέσο όρο;
Αυτά τα μέτρα λαμβάνουν τη μικρότερη τιμή τους όταν το μοντέλο είναι ο μέσος όρος. είναι η σωστή απάντηση.
Τι σημαίνει “ελαχιστοποιούνται στο μέσο όρο”:
Θεμελιώδης ιδιότητα του μέσου όρου:
Ο μέσος όρος είναι η τιμή που ελαχιστοποιεί το Άθροισμα Τετραγώνων (και κατά συνέπεια και τη διακύμανση και την τυπική απόκλιση).
Γιατί οι άλλες επιλογές είναι λάθος:
Β - “Όλα εξίσου μικρά και ίσα” - ΛΑΘΟΣ:
Τα τρία μέτρα δεν είναι ίσα μεταξύ τους
SS = 11,880, Variance = 76, SD = 8.73
Έχουν διαφορετικές κλίμακες και μονάδες
Απλά όλα ελαχιστοποιούνται στην ίδια τιμή (μέσος όρος)
Γ - “Καλύτερο μέτρο για κάθε μοντέλο” - ΛΑΘΟΣ:
Υπάρχουν και άλλα μέτρα του σφάλματος: MAD, Εύρος, IQR κ.λπ.
Το “καλύτερο” μέτρο εξαρτάται από το πλαίσιο
Η δήλωση αφορά ποια τιμή ελαχιστοποιεί αυτά τα μέτρα, όχι ποιο μέτρο είναι καλύτερο
Δ - “Μικρότερα από άλλα μέτρα” - ΛΑΘΟΣ:
Δεν μπορούμε να συγκρίνουμε διαφορετικά μέτρα απευθείας (διαφορετικές κλίμακες)
Π.χ. SS = 11880mm², MAD ≈ 7mm - δεν συγκρίνονται!
Η δήλωση δεν αφορά σύγκριση μεταξύ μέτρων, αλλά ελαχιστοποίηση εντός μέτρου
Μαθηματική σχέση των τριών μέτρων:
Όλα σχετίζονται με το SS:
Άθροισμα Τετραγώνων Υπολοίπων = \(\sum(Y_i - \bar{Y})^2\) = συνολικό σφάλμα
Διακύμανση = SS / (n-1) = μέσο σφάλμα ανά παρατήρηση
Τυπική απόκλιση = √Διακύμανση = σφάλμα σε αρχικές μονάδες
Αφού όλα προέρχονται από το SS, και το SS ελαχιστοποιείται στο μέσο:
→ Όλα ελαχιστοποιούνται στο μέσο
Συμπέρασμα:
Όταν λέμε ότι τα τρία μέτρα “ελαχιστοποιούνται στο μέσο όρο”, εννοούμε:
→ Ο μέσος όρος είναι η τιμή που κάνει αυτά τα μέτρα όσο το δυνατόν μικρότερα
→ Οποιαδήποτε άλλη τιμή (μοντέλο) θα δώσει μεγαλύτερες τιμές SS, διακύμανσης, και τυπικής απόκλισης
→ Αυτό δικαιολογεί τη χρήση του μέσου όρου ως το μοντέλου βάσης στη στατιστική ανάλυση
Είναι μια θεμελιώδης ιδιότητα του μέσου όρου που τον κάνει το φυσικό σημείο αναφοράς για τη μέτρηση της μεταβλητότητας και του σφάλματος μοντέλου.
Εφαρμογή: Σκέψεις για την Ποσοτικοποίηση Σφάλματος στο StudentSurvey
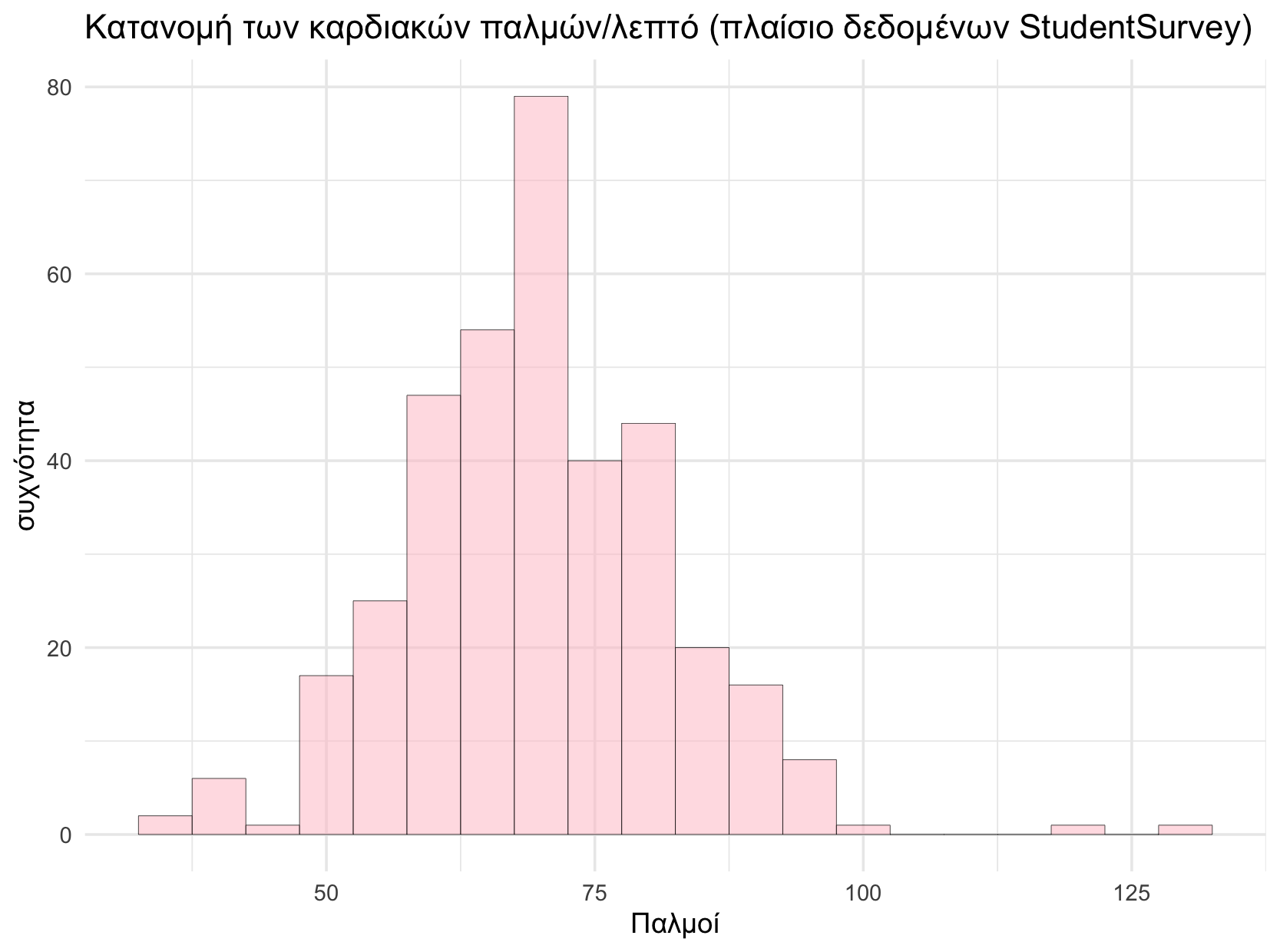
Χρησιμοποιήστε την R για να δημιουργήσετε το κενό μοντέλο των καρδιακών παλμών (Pulse) φοιτητή. Θυμίζουμε ότι στην έρευνα συμμετείχαν 362 φοιτητές. Ονομάστε το μοντέλο empty_model. Έπειτα υπολογίστε το SS, τη διακύμανση, και την τυπική απόκλιση αυτού του μοντέλου.
Υπάρχουν πολλοί τρόποι να υπολογίσουμε αυτά τα στατιστικά στην R, αλλά τα αποτελέσματα θα είναι τα ίδια: SS = 53776.486, Διακύμανση (MS) = 148.965, και Τυπική Απόκλιση = 12.20514.
Ποιες από τις παρακάτω εντολές θα σας βοηθούσαν να υπολογίσετε το SS για τους καρδιακούς παλμούς (Pulse); (Υπάρχουν περισσότερες από μία σωστές απαντήσεις.)
Σωστές απαντήσεις: Α και Δ
Α - var(StudentSurvey$Pulse) * (362 - 1) - ΣΩΣΤΟ:
Μαθηματική σχέση:
\[Variance = \frac{SS}{n-1}\]
\[SS = Variance \times (n-1)\]
# Υπολογισμός SS από τη διακύμανση
variance <- var(StudentSurvey$Pulse, na.rm = TRUE)
n <- 362 # μέγεθος δείγματος
SS <- variance * (n - 1)
# Ή σε μία γραμμή
SS <- var(StudentSurvey$Pulse, na.rm = TRUE) * (362 - 1)Γιατί λειτουργεί:
Η
var()υπολογίζει τη διακύμανση: \(s^2 = \frac{\sum(x_i - \bar{x})^2}{n-1}\)Πολλαπλασιάζοντας με \((n-1)\) παίρνουμε: \(SS = s^2 \times (n-1) = \sum(x_i - \bar{x})^2\)
Δ - supernova(empty_model) - ΣΩΣΤΟ:
Γιατί οι άλλες επιλογές είναι λάθος:
Β - SS(Pulse) - ΛΑΘΟΣ:
Δεν υπάρχει συνάρτηση
SS()στη βασική RΘα δώσει σφάλμα: “could not find function ‘SS’”
Το SS πρέπει να υπολογιστεί με άλλο τρόπο
Γ - sum(abs(resid(empty_model))) - ΛΑΘΟΣ:
Αυτό υπολογίζει το Άθροισμα των Απόλυτων Αποκλίσεων (SAD), όχι το SS
SAD = \(\sum|Y_i - \bar{Y}|\) (απόλυτες τιμές)
SS = \(\sum(Y_i - \bar{Y})^2\) (τετράγωνα)
# Αυτό είναι λάθος για SS
sum(abs(resid(empty_model))) # SAD, όχι SS
# Το σωστό για SS είναι
sum(resid(empty_model)^2) # SSΕ - SS(empty_model) - ΛΑΘΟΣ:
Παρόμοια με το Β, δεν υπάρχει συνάρτηση
SS()Ακόμα κι αν υπήρχε, η σύνταξη θα ήταν διαφορετική
Συμπέρασμα:
Για να υπολογίσετε το SS για Pulse, οι δύο σωστοί τρόποι είναι:
var(StudentSurvey$Pulse) * (362 - 1)- Πολλαπλασιάζει τη διακύμανση με το n - 1 (τους βαθμούς ελευθερίας)supernova(empty_model)- Εμφανίζει τον πίνακα ANOVA που περιλαμβάνει το SS
Και οι δύο μέθοδοι θα δώσουν το ίδιο αποτέλεσμα, απλά με διαφορετικό τρόπο παρουσίασης.
Ποιες από τις παρακάτω εντολές R θα σας βοηθούσαν να υπολογίσετε τη διακύμανση των καρδιακών παλμών (‘Pulse’);
Σωστή απάντηση: Μόνο Γ (var(StudentSurvey$Pulse))
Γ - var(StudentSurvey$Pulse) - ΣΩΣΤΟ:
Γιατί λειτουργεί:
Η
var()είναι η σωστή συνάρτηση στην R για τη διακύμανσηStudentSurvey$Pulse σωστά αναφέρεται στη στήλη Pulse του πλαισίου δεδομένων
Υπολογίζει: \(s^2 = \frac{\sum(x_i - \bar{x})^2}{n-1}\)
Γιατί οι άλλες επιλογές είναι λάθος:
Α - Var(Pulse) - ΛΑΘΟΣ:
Κεφαλαίο V: Η συνάρτηση είναι
var()με μικρό v, όχιVar()Η R είναι case-sensitive (διακρίνει πεζά/κεφαλαία)
Θα δώσει σφάλμα: “could not find function ‘Var’”
Β - var(Pulse) - ΛΑΘΟΣ:
Λείπει το πλαίσιο δεδομένων: Το αντικείμενο Pulse δεν υπάρχει ως αυτόνομο, αλλά μέσα στο πλαίσιο δεδομένων
Χρειάζεται να προσδιορίσουμε από ποιο πλαίσιο δεδομένων προέρχεται
Θα δώσει σφάλμα: “object ‘Pulse’ not found”
# ΛΑΘΟΣ - δεν ξέρει που να βρει το αντικείμενο Pulse
var(Pulse)
# Error: object 'Pulse' not found
# ΣΩΣΤΟ - προσδιορίζει το πλαίσιο δεδομένων
var(StudentSurvey$Pulse)Εξαίρεση για Β:
Το var(Pulse) θα δούλευε μόνο αν:
# 1. Έχουμε κάνει attach
attach(StudentSurvey)
var(Pulse) # Τώρα δουλεύει
detach(StudentSurvey)
# 2. Ή χρησιμοποιούμε with
with(StudentSurvey, var(Pulse))
# 3. Ή έχουμε δημιουργήσει ξεχωριστό διάνυσμα
Pulse <- StudentSurvey$Pulse
var(Pulse) # Τώρα δουλεύειΑλλά χωρίς αυτά, το var(Pulse) δεν δουλεύει.
Δ - variance(StudentSurvey$Pulse) - ΛΑΘΟΣ:
Δεν υπάρχει συνάρτηση
variance()στη βασική RΗ σωστή συνάρτηση είναι
var(), όχιvariance()Θα δώσει σφάλμα: “could not find function ‘variance’”
Πρόσθετοι τρόποι υπολογισμού διακύμανσης:
1. Από το SS (όπως στην προηγούμενη ερώτηση):
# Αν έχουμε το SS
SS <- sum((StudentSurvey$Pulse - mean(StudentSurvey$Pulse, na.rm = TRUE))^2, na.rm = TRUE)
n <- length(na.omit(StudentSurvey$Pulse))
variance <- SS / (n - 1)2. Από τον πίνακα ANOVA:
empty_model <- lm(Pulse ~ NULL, data = StudentSurvey)
anova_table <- supernova(empty_model)
variance <- anova_table$MS[1] # MS = Mean Square = Variance3. Από την τυπική απόκλιση:
4. Βήμα-βήμα:
Ποιες από τις παρακάτω εντολές της R θα σας βοηθούσαν να υπολογίσετε την τυπική απόκλιση για των καρδιακών παλμών; (Υπάρχουν περισσότερες από μία σωστές απαντήσεις.)
Σωστές απαντήσεις: Α, Δ, και Ε
Α - favstats(~ Pulse, data = StudentSurvey) - ΣΩΣΤΟ:
Παράδειγμα αποτελεσμάτων:
min Q1 median Q3 max mean sd n missing
-5.0 0 2 4 10 2.133333 3.456789 75 0Γιατί λειτουργεί:
Η
favstats()από το πακέτο mosaic εμφανίζει πολλά στατιστικάΣτη στήλη sd βρίσκεται η τυπική απόκλιση
Δ - sd(StudentSurvey$Pulse) - ΣΩΣΤΟ:
Γιατί λειτουργεί:
Η
sd()είναι η βασική συνάρτηση για τυπική απόκλιση στην RΣωστή αναφορά στο πλαίσιο δεδομένων:
StudentSurvey$PulseΥπολογίζει: \(s = \sqrt{\frac{\sum(x_i - \bar{x})^2}{n-1}}\)
Ε - sqrt(var(StudentSurvey$Pulse)) - ΣΩΣΤΟ:
Γιατί λειτουργεί:
Μαθηματική σχέση: \(SD = \sqrt{Variance}\)
Η
var()δίνει τη διακύμανσηΗ
sqrt()παίρνει την τετραγωνική ρίζαΙσοδύναμο με
sd()
Γιατί οι άλλες επιλογές είναι λάθος:
Β - sd(Pulse) - ΛΑΘΟΣ:
Λείπει το πλαίσιο δεδομένων: Το Pulse δεν υπάρχει ως αυτόνομο αντικείμενο της R
Χρειάζεται
StudentSurvey$PulseΘα δώσει σφάλμα: “object ‘Pulse’ not found”
# ΛΑΘΟΣ - χωρίς πλαίσιο δεδομένων
sd(Pulse)
# Error: object 'Pulse' not found
# ΣΩΣΤΟ
sd(StudentSurvey$Pulse)Εξαίρεση: Θα δούλευε μόνο με attach(), with(), ή αν το Pulse υπάρχει ως αυτόνομο διάνυσμα της R.
Γ - SD(StudentSurvey$Pulse) - ΛΑΘΟΣ:
Κεφαλαίο SD: Η συνάρτηση είναι
sd()με μικρά γράμματαΗ R είναι case-sensitive
Θα δώσει σφάλμα: “could not find function ‘SD’”
# ΛΑΘΟΣ - κεφαλαία γράμματα
SD(StudentSurvey$Pulse)
# Error: could not find function "SD"
# ΣΩΣΤΟ - μικρά γράμματα
sd(StudentSurvey$Pulse)Επαλήθευση ισοδυναμίας:
# Μέθοδος 1: Άμεση με sd()
SD1 <- sd(StudentSurvey$Pulse, na.rm = TRUE)
# Μέθοδος 2: Από variance
SD2 <- sqrt(var(StudentSurvey$Pulse, na.rm = TRUE))
# Μέθοδος 3: Από favstats
stats <- favstats(~ Pulse, data = StudentSurvey)
SD3 <- stats$sd
# Έλεγχος
all.equal(SD1, SD2, SD3)
# TRUE - όλες δίνουν το ίδιο!Πρόσθετοι τρόποι υπολογισμού SD:
1. Από SS:
SS <- sum((StudentSurvey$Pulse - mean(StudentSurvey$Pulse, na.rm = TRUE))^2, na.rm = TRUE)
n <- sum(!is.na(StudentSurvey$Pulse))
SD <- sqrt(SS / (n - 1))2. Από ANOVA table:
empty_model <- lm(Pulse ~ NULL, data = StudentSurvey)
anova_table <- supernova(empty_model)
SD <- sqrt(anova_table$MS[1]) # MS = variance3. Βήμα-βήμα:
Ταιριάξτε κάθε μέτρο σφάλματος με τη σωστή ερμηνεία του.
SS (Άθροισμα Τετραγώνων):
Διακύμανση (Variance):
Τυπική απόκλιση (Standard Deviation)):
Σωστές αντιστοιχίσεις:
SS → Άθροισμα τετραγωνικών αποκλίσεων από το μέσο όρο, σε τετραγωνικά χιλιόμετρα
Διακύμανση → Μέση τετραγωνική απόκλιση από το μέσο όρο, σε τετραγωνικά χιλιόμετρα
Τυπική απόκλιση → Μέση απόκλιση από το μέσο όρο, σε χιλιόμετρα
Αναλυτική εξήγηση:
SS (Άθροισμα Τετραγώνων):
\[SS = \sum_{i=1}^{n}(x_i - \bar{x})^2\]
Ερμηνεία:
Σύνολο (άθροισμα, όχι μέσος όρος)
Τετραγωνικές αποκλίσεις
Μονάδες: τετραγωνικά χιλιόμετρα (km²)
Διακύμανση:
\[s^2 = \frac{SS}{n-1} = \frac{\sum_{i=1}^{n}(x_i - \bar{x})^2}{n-1}\]
Ερμηνεία:
Μέση (μέσος όρος τετραγωνικών αποκλίσεων)
Τετραγωνική απόκλιση
Μονάδες: τετραγωνικά χιλιόμετρα (km²)
Τυπική απόκλιση:
\[s = \sqrt{s^2} = \sqrt{\frac{\sum_{i=1}^{n}(x_i - \bar{x})^2}{n-1}}\]
Ερμηνεία:
Μέση (μέσος όρος)
Απόκλιση, όχι στο τετράγωνο
Μονάδες: χιλιόμετρα (km)
Μαθηματικές σχέσεις:
Σύμβολα για Μέσο Όρο, Διακύμανση και Τυπική Απόκλιση
Τέλος, χρησιμοποιούμε διαφορετικά σύμβολα για να αναπαραστήσουμε τη διακύμανση και την τυπική απόκλιση ενός δείγματος από τη μία πλευρά, και του πληθυσμού (ή της ΔΠΔ) από την άλλη.
Τα δειγματικά στατιστικά ονομάζονται επίσης εκτιμητές επειδή στο πλαίσιο της στατιστικής μοντελοποίησης χρησιμοποιούνται ως εκτιμήσεις των παραμέτρων της ΔΠΔ. Έχουμε συνοψίσει αυτά τα σύμβολα στον παρακάτω πίνακα (η προφορά των συμβόλων αναγράφεται σε παρένθεση).
| Στατιστικό Μέτρο | Δείγμα (ή Εκτιμητής) | ΔΠΓ (ή Πληθυσμός) |
|---|---|---|
| Μέσος Όρος | \(\bar{Y}\) (y παύλα) | \(\mu\) (μι) |
| Διακύμανση | \(s^2\) (s τετράγωνο) | \(\sigma^2\) (σίγμα τετράγωνο) |
| Τυπική Απόκλιση | \(s\) (s) | \(\sigma\) (σίγμα) |
Σημειώσεις:
- Τα λατινικά γράμματα (\(\bar{Y}\), \(s\), \(s^2\)) αναφέρονται στο δείγμα
- Τα ελληνικά γράμματα (\(\mu\), \(\sigma\), \(\sigma^2\)) αναφέρονται στον πληθυσμό
Όπως προαναφέρθηκε, υπάρχουν συχνά πολλοί διαφορετικοί όροι που αντιπροσωπεύουν τις ίδιες ιδέες στη στατιστική. Θα συναντήσετε συχνά τον όρο «μέσο τετραγωνικό σφάλμα». Σε ποιο από τα παρακάτω πιστεύετε ότι αναφέρεται;
Διακύμανση είναι η σωστή απάντηση.
Ανάλυση του όρου “Mέσο Τετραγωνικό Σφάλμα (Mean Square ή Mean Squared Error)” (MSE):
Αναλύοντας τις λέξεις:
Mean = Μέσος όρος
Squared = Τετραγωνικό
Error = Σφάλμα/Απόκλιση
Άρα: Mean Squared Error = Μέσος όρος τετραγώνων των σφαλμάτων
Μαθηματική σύνδεση:
Διακύμανση:
\[s^2 = \frac{\sum(x_i - \bar{x})^2}{n-1}\]
Αυτό είναι:
Μέσος όρος
Τετραγώνων
Σφαλμάτων/αποκλίσεων από το μέσο
Επομένως, διακύμανση = μέσο τετραγωνικό σφάλμα!
Γιατί οι άλλες επιλογές είναι λάθος:
Α - Μέσος όρος - ΛΑΘΟΣ:
Ο μέσος όρος είναι απλά: \(\bar{x} = \frac{\sum x_i}{n}\)
Δεν περιλαμβάνει “τετράγωνα” ή “σφάλματα”
Δεν είναι μέτρο διασποράς
Γ - Τυπική απόκλιση - ΛΑΘΟΣ:
SD = \(\sqrt{variance}\) = ρίζα του μέσου τετραγωνικού σφάλματος
Είναι η “τετραγωνική ρίζα του μέσου τετραγωνικού σφάλματος”, όχι το “μέσο τετραγωνικό σφάλμα”
Δεν είναι στο τετράγωνο - έχει γραμμικές μονάδες
7.5 Τυποποιημένες Τιμές (Τιμές z)
Έχουμε εξετάσει το μέσο όρο ως μοντέλο και έχουμε δει μερικούς τρόπους ποσοτικοποίησης του συνολικού σφάλματος γύρω από το μέσο όρο, καθώς και μερικούς καλούς λόγους για να το κάνουμε αυτό. Υπάρχει όμως και ένας άλλος λόγος να εξετάσουμε μαζί το μέσο όρο και το σφάλμα. Μερικές φορές, συνδυάζοντας τις δύο αυτές ιδέες, μπορούμε να κατανοήσουμε καλύτερα πού βρίσκεται μια συγκεκριμένη τιμή σε μια κατανομή.
Μια φοιτήτρια (ας την ονομάσουμε Σοφία) έχει μήκος αντίχειρα 65.1mm. Τι σημαίνει αυτό; Είναι ένας μεγάλος αντίχειρας; Πώς μπορούμε να το γνωρίζουμε αυτό; Ίσως αρχίζετε να αντιλαμβάνεστε ότι το να γνωρίζετε μόνο μια μεμονωμένη τιμή της μεταβλητής δεν σας λέει πολλά.
Για να ερμηνεύσουμε το νόημα μιας μεμονωμένης τιμής, βοηθάει να γνωρίζουμε και κάτι για την κατανομή από την οποία προέρχεται η τιμή. Συγκεκριμένα, είναι σημαντικό να γνωρίζουμε κάτι για το σχήμα, το κέντρο και τη διασπορά της.
Ας πούμε ότι εκτός από το ότι γνωρίζουμε ότι το μήκος του αντίχειρα της Σοφίας είναι 65.1mm, γνωρίζουμε επίσης ότι ο μέσος όρος της κατανομής των μηκών αντίχειρα είναι 60.1mm. Τι μας δείχνει αυτό που δεν γνωρίζαμε πριν μάθουμε το μέσο όρο;
Τώρα γνωρίζουμε πόσο μακρύς είναι αυτός ο αντίχειρας σε σχέση με τους άλλους αντίχειρες στο δείγμά μας είναι η σωστή απάντηση.
Τι γνωρίζαμε πριν:
Μόνο η μεμονωμένη τιμή: Μήκος αντίχειρα Σοφίας = 65.1mm
Δεν είχαμε πλαίσιο σύγκρισης
Δεν ξέραμε αν αυτό είναι μεγάλο, μικρό, ή μεσαίο μέγεθος
Τι γνωρίζουμε τώρα:
Μεμονωμένη τιμή: 65.1mm
Μέσος όρος: 60.1mm
Σχετική θέση: 65.1 - 60.1 = +5mm πάνω από το μέσο όρο
Η σημασία του μέσου όρου:
Ο μέσος όρος δίνει σημείο αναφοράς:
Μπορούμε να υπολογίσουμε: Απόκλιση = 65.1 - 60.1 = +5mm
Ξέρουμε ότι ο αντίχειρας της Σοφίας είναι πάνω από το κέντρο της κατανομής
Μπορούμε να την τοποθετήσουμε σε σχέση με άλλους
Γιατί οι άλλες επιλογές είναι λάθος ή ανακριβείς:
Β - “Σε σχέση με άλλους μεγάλους αντίχειρες” - ΛΑΘΟΣ:
Ο μέσος όρος δεν δείχνει κάτι για τους “μεγάλους” αντίχειρες συγκεκριμένα
Δείχνει το κέντρο όλων των αντιχείρων
Χρειαζόμαστε περισσότερες πληροφορίες (π.χ. Q3, max) για σύγκριση με μεγάλους
Γ - “Ένας από τους μακρύτερους” - ΛΑΘΟΣ:
Δεν μπορούμε να το ξέρουμε μόνο από το μέσο όρο
-
65.1mm είναι 5mm πάνω από το μέσο, αλλά:
Αν η διακύμανση είναι μικρή, μπορεί να είναι στο ανώτερο 10%
Αν η διακύμανση είναι μεγάλη, μπορεί να είναι μόνο στο 60ο εκατοστημόριο
Χρειαζόμαστε την τυπική απόκλιση ή την κατανομή για να το ξέρουμε
Δ - “Μεγαλύτερος από το μέσο και αυτό είναι όλο” - ΑΝΕΠΑΡΚΕΣ:
Αυτό είναι μερικώς σωστό αλλά ελλιπές
-
Όχι μόνο ξέρουμε ότι είναι μεγαλύτερος, αλλά ξέρουμε:
Πόσο μεγαλύτερος (+5mm)
Τη σχετική του θέση στην κατανομή
Πώς συγκρίνεται με τον τυπικό αντίχειρα
Συμπέρασμα:
Γνωρίζοντας τον μέσο όρο μετατρέπουμε την απόλυτη τιμή “65.1mm” σε σχετική πληροφορία: “5mm πάνω από το μέσο όρο του δείγματος”.
Αυτό μας δίνει ένα πλαίσιο σύγκρισης - τώρα μπορούμε να:
Τοποθετήσουμε τον αντίχειρα της Σοφίας σε σχέση με άλλους στο δείγμα
Καταλάβουμε ότι είναι πάνω από το κέντρο της κατανομής
Υπολογίσουμε την απόκλιση (+5mm)
Χωρίς το μέσο όρο, το “65.1mm” είναι απλά ένας αριθμός χωρίς νόημα. Με το μέσο όρο, καταλαβαίνουμε πού βρίσκεται αυτή η τιμή στο πλαίσιο όλων των άλλων μετρήσεων.
Γνωρίζουμε ότι ο αντίχειρας αυτής της φοιτήτριας είναι περίπου 5mm μεγαλύτερος από το μέσο όρο. Αλλά επειδή δεν έχουμε ιδέα για τη διασπορά της κατανομής, εξακολουθούμε να μην έχουμε πολύ σαφή εικόνα για το πώς να χαρακτηρίσουμε το μήκος αντίχειρα 65.1mm. Είναι τα 5mm αρκετά κοντά στο μέσο όρο, ή είναι μακριά; Είναι δύσκολο να το πούμε αυτό χωρίς να γνωρίζουμε πώς είναι η διασπορά των μηκών αντίχειρα.
Ποιο από τα παρακάτω μέτρα διασποράς θα μπορούσε να είναι πιο χρήσιμο για τη μέτρηση του πόσο μακριά είναι το 65.1mm από το μέσο όρο;
Τυπική απόκλιση, μέσο σφάλμα: 8.726695 είναι η σωστή απάντηση.
Γιατί η Τυπική απόκλιση είναι η πιο χρήσιμη:
1. Ίδιες μονάδες με την απόκλιση:
Μήκος αντίχειρα της Σοφίας: 65.1mm
Μέσος όρος: 60.1mm
Απόκλιση: 65.1 - 60.1 = 5mm
Τυπική απόκλιση: 8.73mm (στις ίδιες μονάδες!)
Μπορούμε να συγκρίνουμε άμεσα:
Η απόκλιση της Σοφίας (5mm) vs τυπική απόκλιση (8.73mm)
Η Σοφία είναι 5/8.73 ≈ 0.57 τυπικές αποκλίσεις πάνω από το μέσο
2. Άμεση ερμηνεία:
# Υπολογισμός τιμής z
deviation <- 65.1 - 60.1 # 5mm
SD <- 8.73 #mm
z_score <- deviation / SD
# z = 5 / 8.73 ≈ 0.57
# Ερμηνεία: Ο αντίχειρας της Σοφίας είναι
# 0.57 τυπικές αποκλίσεις πάνω από το μέσο
# Αυτό είναι λίγο πάνω από το μέσο, αλλά όχι εξαιρετικά3. Κατανοητή κλίμακα:
SD = 8.73mm λέει: “Η τυπική απόσταση από το μέσο είναι ~9mm”
Η Σοφία με +5mm είναι εντός μιας SD
Άρα είναι σχετικά κοντά στο μέσο όρο
Γιατί οι άλλες επιλογές είναι λιγότερο χρήσιμες:
Α - SS (11880.21) - ΛΙΓΟΤΕΡΟ ΧΡΗΣΙΜΟ:
Προβλήματα:
Τετραγωνικές μονάδες: 11880.21mm² vs 5mm (δεν συγκρίνονται)
Συνολικό μέγεθος: Το SS είναι άθροισμα για όλο το δείγμα, όχι για ένα άτομο
Εξαρτάται από n: Μεγαλύτερο δείγμα → μεγαλύτερο SS (ακόμα και με ίδια διασπορά)
# Δεν μπορούμε να συγκρίνουμε
deviation <- 5 # mm
SS <- 11880.21 # mm²
# Τι κάνουμε με αυτά; Δεν έχει νόημα!Β - Διακύμανση (76.1552) - ΛΙΓΟΤΕΡΟ ΧΡΗΣΙΜΟ:
Προβλήματα:
Τετραγωνικές μονάδες: 76.16mm² vs 5mm (δεν συγκρίνονται άμεσα)
Δύσκολη ερμηνεία: Τι σημαίνει “76.16 τετραγωνικά mm” στην πράξη;
Χρειάζεται μετατροπή: Πρέπει να πάρουμε √variance για χρήσιμη σύγκριση
# Μη φυσική σύγκριση
deviation <- 5 # mm
variance <- 76.16 # mm²
# Πρέπει να μετατρέψουμε σε SD πρώτα
SD <- sqrt(variance) # 8.73 mm
z <- deviation / SD # Τώρα έχει νόημα!Σύγκριση των τριών μέτρων:
Μέτρο | Τιμή | Μονάδες | Σύγκριση με 5mm | Χρησιμότητα
---------- | --------- | ------- | --------------- | -----------
SS | 11,880.21 | mm² | Αδύνατη | Χαμηλή
Variance | 76.16 | mm² | Αδύνατη | Μέτρια
SD | 8.73 | mm | 5/8.73 = 0.57 | ΥψηλήΣυμπέρασμα:
Η Τυπική απόκλιση (8.73mm) είναι το πιο χρήσιμο μέτρο επειδή:
Ίδιες μονάδες με την απόκλιση (mm) - άμεση σύγκριση
Επιτρέπει υπολογισμό της τιμής z: deviation/SD = 5/8.73 = 0.57
Άμεση ερμηνεία: “Ο αντίχειρας της Σοφίας είναι 0.57 τυπικές αποκλίσεις πάνω από το μέσο - σχετικά κοντά στο κέντρο”
Τα SS και Διακύμανση, με τετραγωνικές μονάδες, δεν μπορούν να συγκριθούν άμεσα με μια απόκλιση σε γραμμικές μονάδες.
Αν και το SS θα είναι πολύ χρήσιμο αργότερα, για αυτόν τον σκοπό είναι άχρηστο. Οι αριθμοί 65.1 και 11880 δεν φαίνεται να ανήκουν στο ίδιο σύμπαν! Η διακύμανση θα είναι χρήσιμη σε κάποιες περιπτώσεις, αλλά οι μονάδες της είναι κάπως δύσκολο να ερμηνευτούν. Είναι δύσκολο να χρησιμοποιήσουμε τα τετραγωνικά χιλιοστά ως μονάδα όταν προσπαθούμε να κατανοήσουμε απλά χιλιοστά.
Η τυπική απόκλιση, από την άλλη πλευρά, είναι πραγματικά χρήσιμη. Γνωρίζουμε ότι ο αντίχειρας της Σοφίας είναι περίπου 5mm μεγαλύτερος από το μέσο αντίχειρα. Αλλά τώρα γνωρίζουμε επίσης ότι, κατά μέσο όρο, οι αντίχειρες απέχουν 8.7mm από το μέσο όρο, τόσο προς τα πάνω όσο και προς τα κάτω. Αν και ο αντίχειρας της Σοφίας είναι πάνω από το μέσο όρο σε μήκος, σίγουρα δεν είναι ένας από τους μεγαλύτερους αντίχειρες στην κατανομή. Ας εξετάσουμε το παρακάτω ιστόγραμμα για να δούμε αν αυτή η ερμηνεία υποστηρίζεται.
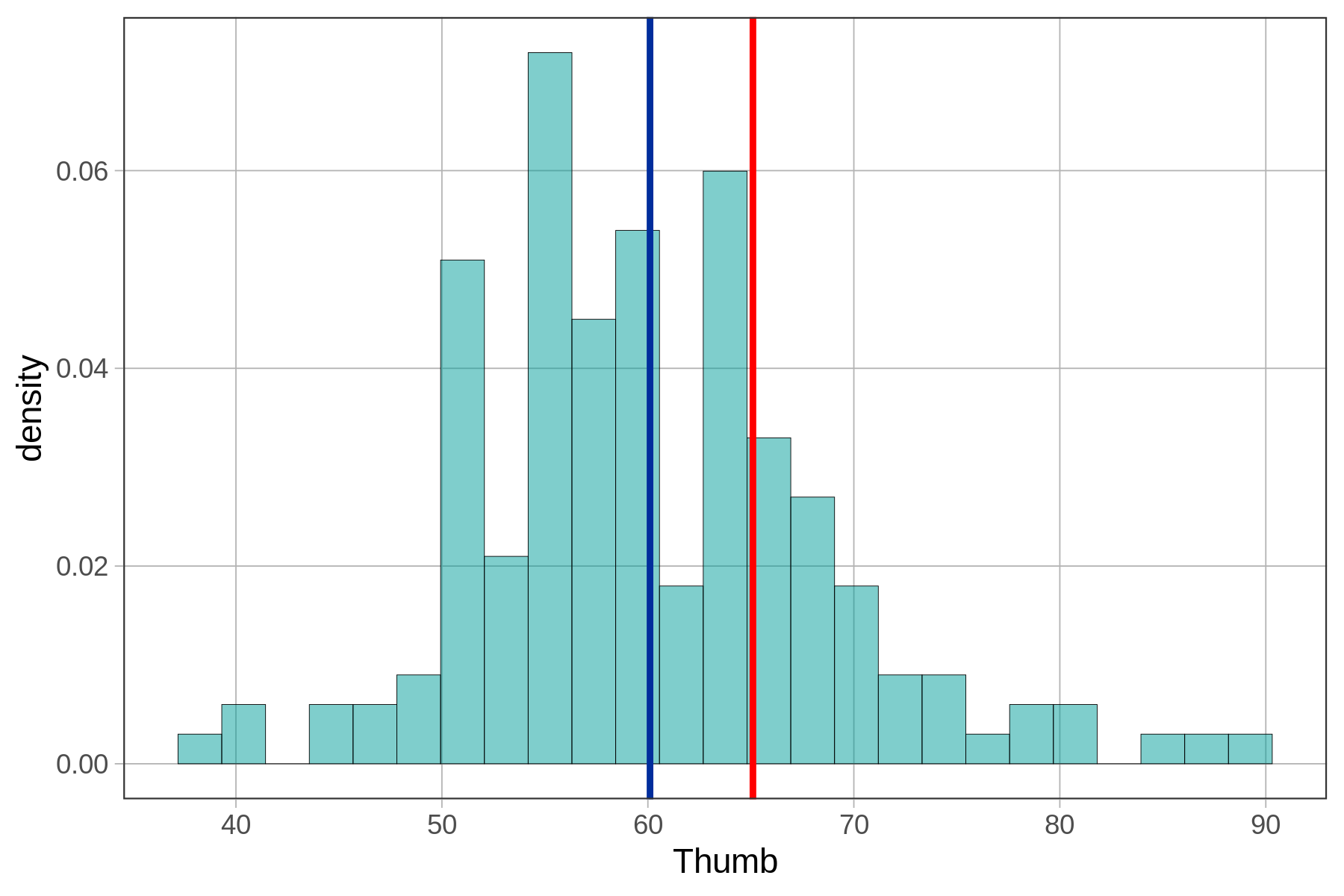
Ο μέσος όρος του μήκους αντίχειρα εμφανίζεται με μπλε, και ο αντίχειρας της Σοφίας (65.1mm) εμφανίζεται με κόκκινο.
Συνδυασμός Μέσου Όρου και Τυπικής Απόκλισης
Στην περίπτωση του μήκους αντίχειρα (Thumb), βρίσκουμε χρήσιμο να συνδυάσουμε το μέσο όρο και την τυπική απόκλιση για να ερμηνεύσουμε το νόημα μιας μεμονωμένης τιμής. Στο σημείο αυτό, ας εισάγουμε ένα μέτρο που θα συνδυάσει αυτές τις δύο πληροφορίες σε μία μόνο τιμή: την τιμή z (τυποποιημένη τιμή).
Ένας φίλος σας έχει συγκεντρώσει 37.000 πόντους σε ένα βιντεοπαιχνίδι που ονομάζεται Kargle. Είναι καλό σκορ; Πώς το γνωρίζετε αυτό; Τι άλλο θα θέλατε να μάθετε για να απαντήσετε σε αυτήν την ερώτηση;
Ας υποθέσουμε ότι γνωρίζετε ότι ο μέσος όρος του σκορ όλων των παικτών είναι 35.000. Θα σας βοηθούσε αυτό; Σαφώς θα βοηθούσε. Θα γνωρίζατε ότι το σκορ 37.000 είναι πάνω από το μέσο όρο κατά 2.000 πόντους. Αλλά ακόμα κι αν σας βοηθάει να ερμηνεύσετε το 37.000, δεν είναι αρκετό. Αυτό που δεν σας λέει είναι πόσο πάνω από το μέσο όρο είναι οι 37.000 πόντοι σε σχέση με ολόκληρη την κατανομή.
Τι κοινό έχουν οι 37.000 πόντοι στην περίπτωση του Kargle και το 65.1mm στην περίπτωση του μήκους αντίχειρα;
Ας υποθέσουμε ότι η κατανομή των σκορ στο Kargle αναπαρίσταται από ένα από τα παρακάτω ιστογράμματα. Και οι δύο κατανομές έχουν μέσο όρο 35.000 πόντους. Αλλά:
Κατανομή #1: Τυπική απόκλιση = 1.000 πόντοι
Κατανομή #2: Τυπική απόκλιση = 5.000 πόντοι
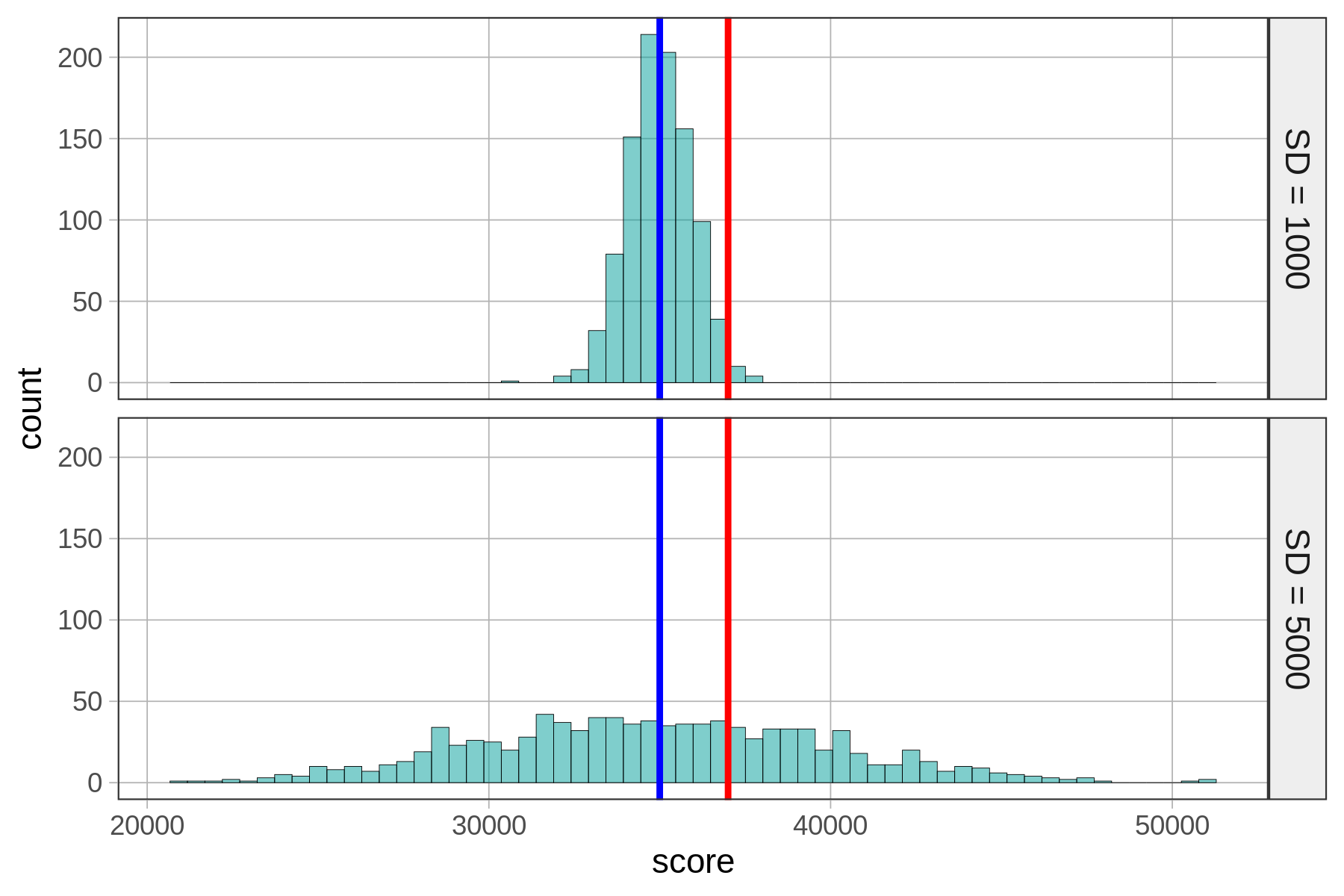
Αν η πραγματική κατανομή των πόντων στο Kargle ήταν αυτή που βρίσκεται στο πάνω μέρος, τι θα σκεφτόσασταν για το σκορ 37.000 πόντων του φίλου σας;
Τι θα γινόταν αν η πραγματική κατανομή των πόντων στο Kargle ήταν αυτή που βρίσκεται στο κάτω μέρος; Τώρα, τι θα σκεφτόσασταν για το σκορ 37.000 πόντων του φίλου σας;
Σε ποια από αυτές τις δύο κατανομές θα λέγατε ότι η βαθμολογία 37.000 είναι καλύτερη; Γιατί;
Σαφώς ο φίλος σας θα ήταν εξαιρετικός παίκτης αν η Κατανομή 1 ήταν η πραγματική. Αλλά αν ήταν η Κατανομή 2, το σκορ του θα βρισκόταν απλά λίγο πάνω πάνω από το μέσο όρο.
Μπορούμε να δούμε αυτό διαγραμματικά αν παρατηρήσουμε τα δύο ιστογράμματα. Αλλά υπάρχει κάποιος τρόπος να ποσοτικοποιήσουμε τη διαίσθησή μας; Ένας τρόπος είναι να μετασχηματίσουμε την τιμή που προσπαθούμε να ερμηνεύσουμε σε τιμή z με τον παρακάτω τύπο:
\[z = \frac{Y_i - \bar{Y}}{s}\]
Ποιος είναι ο αριθμητής στον παραπάνω τύπο;
Απόκλιση είναι η σωστή απάντηση.
Ανάλυση του τύπου υπολογισμού της τιμής z:
\[z_i = \frac{Y_i - \bar{Y}}{s}\]
Αριθμητής (Numerator): \(Y_i - \bar{Y}\)
Παρονομαστής (Denominator): \(s\)
Τι είναι ο αριθμητής:
\(Y_i - \bar{Y}\) = Απόκλιση
\(Y_i\) = η συγκεκριμένη παρατήρηση (π.χ. μήκος αντίχειρα της Σοφίας)
\(\bar{Y}\) = ο δειγματικός μέσος όρος
\(Y_i - \bar{Y}\) = η απόκλιση της παρατήρησης από το μέσο όρο
Γιατί οι άλλες επιλογές είναι λάθος:
Β - Άθροισμα τετραγώνων - ΛΑΘΟΣ:
SS = \(\sum(Y_i - \bar{Y})^2\) (άθροισμα τετραγώνων όλων των αποκλίσεων)
Ο αριθμητής είναι μία απόκλιση, όχι άθροισμα
Ο αριθμητής δεν είναι υψωμένος στο τετράγωνο
Γ - Δειγματικός μέσος όρος - ΛΑΘΟΣ:
Ο δειγματικός μέσος όρος (\(\bar{Y}\)) είναι μέρος του αριθμητή, όχι ο αριθμητής
Αριθμητής = \(Y_i - \bar{Y}\) (η διαφορά), όχι μόνο το \(\bar{Y}\)
Δ - Πληθυσμιακός μέσος όρος - ΛΑΘΟΣ:
Ο τύπος χρησιμοποιεί \(\bar{Y}\) (δειγματικό μέσο όρο), όχι \(\mu\) (πληθυσμιακό μέσο όρο)
Για την τιμή z του πληθυσμού: \(z = \frac{Y_i - \mu}{\sigma}\)
Εδώ έχουμε δειγματικό στατιστικό (s), όχι πληθυσμιακό (σ)
Ε - Δειγματική τυπική απόκλιση - ΛΑΘΟΣ:
Η τυπική απόκλιση (s) είναι ο παρονομαστής, όχι ο αριθμητής
Βρίσκεται κάτω από τη γραμμή κλάσματος
Ονοματολογία των μερών:
Y_i - Ȳ ← Αριθμητής (Numerator) = Απόκλιση
z_i = ─────────
s ← Παρονομαστής (Denominator) = Τυπική απόκλισηΛεπτομερής ανάλυση:
Τι μετράει ο αριθμητής:
Απόλυτη απόσταση από το μέσο όρο
Κατεύθυνση: θετική (πάνω από μέσο) ή αρνητική (κάτω από μέσο)
Μονάδες: ίδιες με την αρχική μεταβλητή (mm, kg), κλπ)
Τι μετράει ο παρονομαστής:
Τυπική κλίμακα της διασποράς
Δίνει πλαίσιο για το πόσο μεγάλη είναι η απόκλιση
Μονάδες: ίδιες με την αρχική μεταβλητή
Τι μετράει η τιμή z (ολόκληρο το κλάσμα):
Σχετική απόσταση σε τυπικές αποκλίσεις
Xωρίς μονάδες
Δείχνει πόσο ασυνήθιστη είναι η παρατήρηση
Ιδιότητες του αριθμητή (απόκλιση):
1. Μπορεί να είναι θετικός, αρνητικός, ή μηδέν:
Θετικός (+): \(Y_i > \bar{Y}\) (πάνω από μέσο)
Αρνητικός (-): \(Y_i < \bar{Y}\) (κάτω από μέσο)
Μηδέν (0): \(Y_i = \bar{Y}\) (ακριβώς στο μέσο)
2. Άθροισμα όλων των αποκλίσεων = 0:
\[\sum(Y_i - \bar{Y}) = 0\]
3. Διατηρεί μονάδες:
Αν Y σε mm, απόκλιση σε mm
Αν Y σε kg απόκλιση σε kg
Συμπέρασμα:
Ο αριθμητής στον τύπο της τιμής z:
\[z_i = \frac{Y_i - \bar{Y}}{s}\]
είναι το \(Y_i - \bar{Y}\), που ονομάζεται Απόκλιση.
Αυτό αντιπροσωπεύει την απόσταση της συγκεκριμένης παρατήρησης από το μέσο όρο του δείγματος, σε αρχικές μονάδες. Όταν διαιρεθεί με την τυπική απόκλιση (s), μετατρέπεται σε τυποποιημένη τιμή που δείχνει πόσες τυπικές αποκλίσεις μακριά από το μέσο βρίσκεται η παρατήρηση.
Και ποιος είναι ο παρονομαστής;
Δειγματική τυπική απόκλιση είναι η σωστή απάντηση.
Ανάλυση του τύπου:
\[z_i = \frac{Y_i - \bar{Y}}{s}\]
Αριθμητής: \(Y_i - \bar{Y}\) (απόκλιση)
Παρονομαστής: \(s\) (δειγματική τυπική απόκλιση)
Τι είναι το s:
\[s = \sqrt{\frac{\sum(Y_i - \bar{Y})^2}{n-1}}\]
s = δειγματική τυπική απόκλιση
Μετράει την τυπική διασπορά των δεδομένων γύρω από το μέσο
Είναι η κλίμακα με την οποία μετράμε τις αποκλίσεις
Γιατί οι άλλες επιλογές είναι λάθος:
Α - Απόκλιση - ΛΑΘΟΣ:
Η απόκλιση (\(Y_i - \bar{Y}\)) είναι ο αριθμητής, όχι ο παρονομαστής
Βρίσκεται πάνω από τη γραμμή κλάσματος
Β - Άθροισμα τετραγώνων - ΛΑΘΟΣ:
SS = \(\sum(Y_i - \bar{Y})^2\) δεν εμφανίζεται στον τύπο της τιμής z
Το SS χρησιμοποιείται για να υπολογίσουμε το s, αλλά δεν είναι ο παρονομαστής
Γ - Δειγματικός μέσος όρος - ΛΑΘΟΣ:
Ο δειγματικός μέσος όρος (\(\bar{Y}\)) είναι μέρος του αριθμητή, όχι ο παρονομαστής
Χρησιμοποιείται για να υπολογίσουμε την απόκλιση
Δ - Πληθυσμιακός μέσος όρος - ΛΑΘΟΣ:
Ο πληθυσμιακός μέσος όρος (\(\mu\)) δεν εμφανίζεται σε αυτόν τον τύπο
Αυτός ο τύπος χρησιμοποιεί δειγματικά στατιστικά (s και \(\bar{Y}\)), όχι παραμέτρους του πληθυσμού
Ρόλος του παρονομαστή:
Γιατί διαιρούμε με s:
-
Standardization (Τυποποίηση):
Μετατρέπει τις αποκλίσεις σε κοινή κλίμακα
Επιτρέπει σύγκριση μεταξύ διαφορετικών μεταβλητών
-
Σχετικό μέγεθος:
Μια απόκλιση 5mm είναι μεγάλη ή μικρή;
Αν s = 2mm: 5/2 = 2.5 SD (μεγάλη!)
Αν s = 10mm: 5/10 = 0.5 SD (μικρή)
-
Αποτέλεσμα χωρίς μονάδες μέτρησης:
- Η τιμή z δεν έχει μονάδες
Συμπέρασμα:
Ο παρονομαστής στον τύπο υπολογισμού της τιμής z:
\[z_i = \frac{Y_i - \bar{Y}}{s}\]
είναι η s (δειγματική τυπική απόκλιση).
Αυτό:
Τυποποιεί την απόκλιση σε κοινή κλίμακα
Δίνει πλαίσιο για το πόσο μεγάλη είναι η απόκλιση
Μετατρέπει το την τιμή z σε μέτρο χωρίς διαστάσεις
Επιτρέπει σύγκριση μεταξύ διαφορετικών μεταβλητών και κατανομών
Χωρίς τον παρονομαστή (s), θα είχαμε μόνο την απόκλιση, που δεν μας δείχνει αν είναι μεγάλη ή μικρή σε σχέση με τη συνολική διασπορά των δεδομένων.
Ας εφαρμόσουμε αυτόν τον τύπο στο σκορ των 37.000 πόντων με βάση καθεμία από τις δύο υποθετικές κατανομές (1 και 2).
Σας παρουσιάζουμε τον κώδικα τον υπολογισμό της τιμής z για την αρχική τιμή \(37.000\), εάν ισχύει η κατανομή 1. Γράψτε παρόμοιο κώδικα για τον υπολογισμό της τιμής z, εάν ισχύει η κατανομή 2.
Τι τιμές z λάβατε για τις δύο κατανομές;
Και στις δύο περιπτώσεις, ο αριθμητής είναι ο ίδιος: \(37.000\) (το ατομικό σκορ) μείον το μέσο όρο της κατανομής, που ισούται με \(2.000\). Οι παρονομαστές για τα δύο τιμές z είναι διαφορετικοί, επειδή οι κατανομές έχουν διαφορετικές τυπικές αποκλίσεις:
Κατανομή #1:
\(s = 1.000\)
\(z_1 = 2.000 / 1.000 = +2\)
Κατανομή #2:
\(s = 5.000\)
\(z_2 = 2.000 / 5.000 = +0.4\)
Να συγκρίνετε τις δύο τιμές z (+2 έναντι +0.4). Ποια επίδοση είναι πιο εντυπωσιακή, αυτή ενός παίκτη με σκορ z = +2 ή ένός παίκτη με σκορ z = +0.4; Γιατί;
Μια τιμή z ίση με +2 είναι πιο εντυπωσιακή—βρίσκεται δύο τυπικές αποκλίσεις πάνω από το μέσο όρο. Είναι σαφώς πιο δύσκολο κανείς να βρίσκεται δύο τυπικές αποκλίσεις πάνω από το μέσο όρο παρά να βρίσκεται 0.4 (ή λιγότερο από μισή) τυπική απόκλιση πάνω από το μέσο όρο.
7.6 Ερμηνεία και Χρήση των Τιμών z
Ποια είναι η διαφορά ανάμεσα σε μια τιμή z και στην τυπική απόκλιση;
Η τυπική απόκλιση (SD) είναι κατά προσέγγιση η μέση απόκλιση όλων των τιμών από το μέσο όρο. Μπορεί να θεωρηθεί ως δείκτης της διασποράς της κατανομής. Μια τιμή z χρησιμοποιεί την SD ως ένα είδος χάρακα για τη μέτρηση του πόσο μακριά βρίσκεται μια μεμονωμένη τιμή πάνω ή κάτω από το μέσο όρο.
Μια τιμή z δείχνει πόσες τυπικές αποκλίσεις απέχει μια τιμή από το μέσο όρο της κατανομής της, αλλά δεν δείχνει ποια είναι η τυπική απόκλιση (ούτε ποιος είναι ο μέσος όρος). Ένας άλλος τρόπος να σκέφτεστε την τιμή z είναι ως τη σύγκριση της απόκλισης μίας τιμής (ο αριθμητής) με την τυπική απόκλιση της κατανομής (ο παρονομαστής).
Ας χρησιμοποιήσουμε τιμές z για να κατανοήσουμε καλύτερα τα δεδομένα του μήκους αντίχειρα (Thumb). Υπολογίστε την τιμή z ενός αντίχειρα μήκους 65.1mm.
0.5725349Ποια είναι η σωστή ερμηνεία της τιμής z = +0.57;
Αυτός ο αντίχειρας έχει μήκος \(0.57\) τυπικές αποκλίσεις (λιγότερο από 1 τυπική απόκλιση) πάνω από το μέσο όρο είναι η σωστή απάντηση.
Τι σημαίνει \(z = 0.57\):
\[z = 0.57 = \frac{Y_i - \bar{Y}}{s}\]
Ερμηνεία:
Η παρατήρηση είναι \(0.57\) τυπικές αποκλίσεις πάνω από το μέσο όρο
Αυτό είναι λιγότερο από \(1\) τυπική απόκλιση (άρα σχετικά κοντά στο μέσο)
Η θετική τιμή z σημαίνει “πάνω από το μέσο”
Γιατί οι άλλες επιλογές είναι λάθος:
Α - “Μεγαλύτερος από \(0.57\) όλων των αντιχείρων” - ΛΑΘΟΣ:
Η τιμή z δεν δείχνει το εκατοστημόριο στο οποίο βρίσκεται η αρχική τιμή
Αν κατανομή είναι κανονική, για \(z = 0.57\), το εκατοστημόριο είναι περίπου 71.6% (όχι 57%)
Χρειάζεται μετατροπή μέσω κανονικής κατανομής
Β - “\(0.57\)m μήκος” - ΛΑΘΟΣ:
Η τιμή z δεν έχει μονάδες
Δεν μετράει μήκος, αλλά σχετική θέση
\(0.57\)m = 570mm (εξωφρενικά μεγάλος αντίχειρας!)
Γ - “Πιθανότητα \(0.57\) για μεγαλύτερο” - ΛΑΘΟΣ:
- Η τιμή z δεν είναι πιθανότητα
Δ - “\(0.57\)mm μεγαλύτερος” - ΛΑΘΟΣ:
Η τιμή z μετράει σε τυπικές αποκλίσεις, όχι σε mm
Η απόκλιση σε mm είναι: απόκλιση = \(z \times s\)
Διαγραμματική αναπαράσταση:
|←─ 1 SD ─→|←─ 1 SD ─→|
| | |
--------|-----------|----------|---------
μ-σ μ μ+σ
51.4 60.1 68.8
↑
z=0.57
(65.1mm)
Η Σοφία βρίσκεται στο $0.57$ του δρόμου από μέσο όρο ($60.1$) προς τη $1$ τυπική απόκλιση ($68.8$)Συμπέρασμα:
Το \(z = 0.57\) ερμηνεύεται ως:
“Ο αντίχειρας είναι \(0.57\) τυπικές αποκλίσεις πάνω από το μέσο όρο”
Αυτό σημαίνει:
Θετική τιμή z → πάνω από το μέσο
\(0.57\) τυπικές αποκλίσεις → λιγότερο από \(1\) τυπική απόκλιση
Ερμηνεία: Σχετικά κοντά στο μέσο όρο, όχι ασυνήθιστη τιμή
Η τιμή z είναι ένα μέτρο σχετικής θέσης χωρίς μονάδες που δείχνει πόσες τυπικές αποκλίσεις μακριά από το μέσο βρίσκεται μια παρατήρηση, όχι την απόλυτη απόσταση σε mm ή το εκατοστημόριο απευθείας.
Μια μεμονωμένη τιμή z δείχνει πόσες τυπικές αποκλίσεις απέχει αυτός ο συγκεκριμένος αντίχειρας των \(65.1\)mm από το μέσο όρο. Επειδή η τυπική απόκλιση είναι κατά προσέγγιση η μέση απόσταση όλων των τιμών από το μέσο όρο, είναι πιο πιθανό οι περισσότερες τιμές να συγκεντρώνονται μεταξύ μίας τυπικής απόκλισης πάνω από το μέσο όρο και μίας τυπικής απόκλισης κάτω από το μέσο όρο. Είναι λιγότερο πιθανό να συναντήσουμε τιμές που απέχουν δύο ή τρεις τυπικές αποκλίσεις από το μέσο όρο. Οι τιμές z μας επιτρέπουν να χαρακτηρίσουμε τις αρχικές τιμές με πιο λεπτομερή τρόπο από το να πούμε απλά ότι είναι «μεγαλύτερες» ή «μικρότερες» από το μέσο όρο.
Χρήση Τιμών z για Σύγκριση Τιμών από Διαφορετικές Κατανομές
Μια επιπλέον χρήση της τιμής z είναι για τη σύγκριση τιμών που προέρχονται από διαφορετικές κατανομές, ακόμα κι αν οι μεταβλητές μετρώνται σε διαφορετικές κλίμακες.
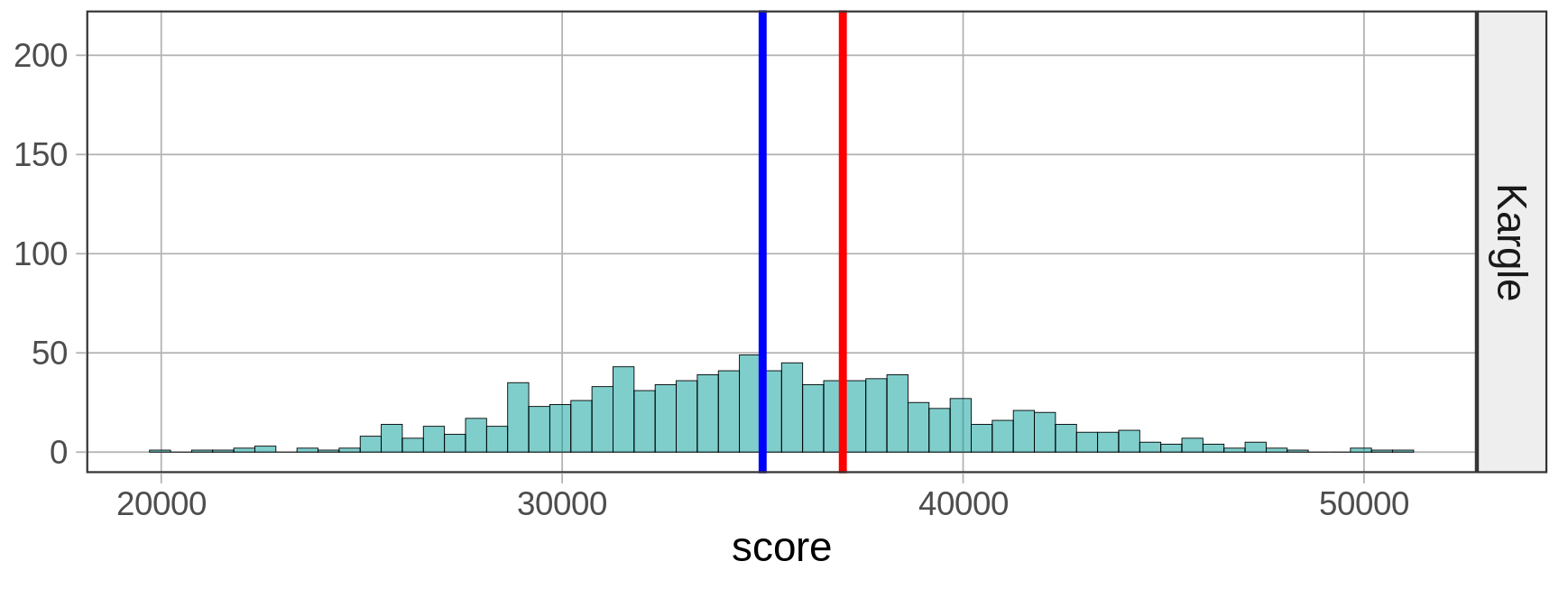
Ας δούμε ξανά την κατανομή των τιμών για όλους τους παίκτες του βιντεοπαιχνιδιού Kargle. Γνωρίζουμε ότι η κατανομή είναι κατά προσέγγιση κανονική, με μέσο όρο \(35.000\) και τυπική απόκλιση \(5.000\).
Μια φίλη σας συγκέντρωσε \(45.000\) πόντους στο παιχνίδι Kargle. Ποια είναι η αντίστοιχη τιμή z;
Η φίλη σας έχει συγκεντρώσει \(45.000\) πόντους. Η τιμή z είναι \(+2\). Εντυπωσιακό! Το σκορ της βρίσκεται δύο τυπικές αποκλίσεις πάνω από το μέσο όρο! Δεν υπάρχουν πολλά σκορ τόσο ψηλά.
Ας υποθέσουμε ότι έχετε και μια άλλη φίλη που δεν παίζει καθόλου Kargle. Παίζει όμως ένα παρόμοιο παιχνίδι—το Bargle!
Το Bargle μπορεί να είναι παρόμοιο, αλλά έχει εντελώς διαφορετικό σύστημα βαθμολόγησης. Η κατανομή της βαθμολογίας του είναι κατά προσέγγιση κανονική, ο μέσος όρος είναι \(50\) και η τυπική απόκλιση είναι \(5\) πόντοι. Η φίλη σας έχει συγκεντρώσει \(65\) πόντους.
Ποια φίλη από τις δύο είναι καλύτερη gamer; Αυτή που παίζει Kargle ή αυτή που παίζει Bargle; Αυτή είναι μια δύσκολη ερώτηση και υπάρχουν πολλοί τρόποι για να την απαντήσουμε. Ο υπολογισμός των τιμών z είναι ένας από αυτούς.
Έχουμε συνοψίσει τις τιμές z για τις δύο φίλες σας στον παρακάτω πίνακα.
| Παιχνίδι | Σκορ Παίκτριας | Μέσος Όρος | Τυπική Απόκλιση | Τιμή z |
|---|---|---|---|---|
| Kargle | \(45.000\) | \(35.000\) | \(5.000\) | +2 |
| Bargle | \(65\) | \(50\) | \(5\) | +3 |
Η εξέταση των τιμών z μας βοηθά να συγκρίνουμε τις ικανότητες των δύο παικτριών, παρόλο που παίζουν παιχνίδια με διαφορετικά συστήματα βαθμολόγησης. Με βάση τις τιμές z, θα μπορούσαμε να πούμε ότι η παίκτρια του Bargle είναι καλύτερη, επειδή σκόραρε τρεις τυπικές αποκλίσεις πάνω από το μέσο όρο, σε σύγκριση με μόνο δύο τυπικές αποκλίσεις πάνω από το μέσο όρο για την παίκτρια του Kargle.
Με ποια έννοια είναι η παίκτρια του Bargle καλύτερη; Πώς αυτό αποτυπώνεται με την τιμή z;
Μπορείτε να σκεφτείτε έναν λόγο για τον οποίο, παρά την καλύτερη τιμή z, η παίκτρια του Bargle μπορεί τελικά να μην είναι καλύτερη gamer;
Φυσικά, τίποτα δεν είναι σίγουρο με αυτές τις συγκρίσεις. Κάποιος θα μπορούσε να υποστηρίξει ότι το Bargle είναι πολύ πιο εύκολο παιχνίδι, και έτσι οι περισσότεροι παίκτες του τείνουν να είναι αρχάριοι. Ίσως η παίκτρια του Kargle να είναι καλύτερη gamer από αυτήν του Bargle, επειδή παρόλο που η τιμή z της είναι μικρότερη, συγκρίνεται τελικά με πιο έμπειρους παίκτες!
7.7 Μοντελοποίηση του Σχήματος της Κατανομής του Σφάλματος
Είδαμε προηγουμένως ότι η ποσοτικοποίηση του σφάλματος δείχνει πόσο καλά προσαρμόζεται το μοντέλο μας στα δεδομένα. Όταν το μοντέλο μας είναι ο μέσος όρος, οι υπολογισμοί του Αθροίσματος Τετραγώνων (SS), της διακύμανσης και της τυπικής απόκλισης είναι χρήσιμοι επειδή όλα αυτά τα μέτρα ελαχιστοποιούνται στο μέσο όρο. Και η ελαχιστοποίηση του σφάλματος είναι η πρώτη μας προτεραιότητα. Όσο λιγότερο σφάλμα, τόσο περισσότερη μεταβλητότητα εξηγείται από το μοντέλο.
Η ποσοτικοποίηση του σφάλματος μας δίνει επίσης έναν τρόπο να εξετάσουμε τις αποκλίσεις υπό ένα διαφορετικό πρίσμα. Ανεξάρτητα από την κλίμακα μέτρησης μιας εξαρτημένης μεταβλητής, η τυπική απόκλιση είναι ένας βολικός τρόπος εκτίμησης του πόσο μακριά βρίσκονται συγκεκριμένες τιμές πάνω ή κάτω από το μέσο όρο—ειδικά όταν λαμβάνεται υπόψη στον υπολογισμό των τιμών z.
Αλλά όσο χρήσιμο κι αν είναι να ποσοτικοποιούμε την ποσότητα του σφάλματος που υπάρχει, είναι επίσης χρήσιμο να μοντελοποιούμε το σχήμα της κατανομής του σφάλματος—ειδικά αν θέλουμε να κάνουμε καλύτερες προβλέψεις για μελλοντικές, τυχαία επιλεγμένες παρατηρήσεις.
Αν και ο μέσος όρος είναι η καλύτερη σημειακή εκτίμηση του μέσου όρου της ΔΠΔ, και η καλύτερη πρόβλεψη μιας μελλοντικής παρατήρησης αν θα έπρεπε να επιλέξουμε ένα μόνο αριθμό, μπορούμε να κάνουμε ακόμα πιο ακριβείς προβλέψεις αν είμαστε διατεθειμένοι να κάνουμε κάποιες υποθέσεις για το σχήμα της κατανομής του σφάλματος στον πληθυσμό.
Για παράδειγμα, αν είμαστε διατεθειμένοι να υποθέσουμε ότι η κατανομή μιας μεταβλητής στον πληθυσμό είναι συμμετρική γύρω από το μέσο όρο, τότε μπορούμε να προβλέψουμε ότι υπάρχει πιθανότητα \(0.5\) (ή \(50\%\)) η τιμή της επόμενης παρατήρησης να είναι πάνω από το μέσο όρο, και πιθανότητα \(0.5\) να είναι κάτω από το μέσο όρο.
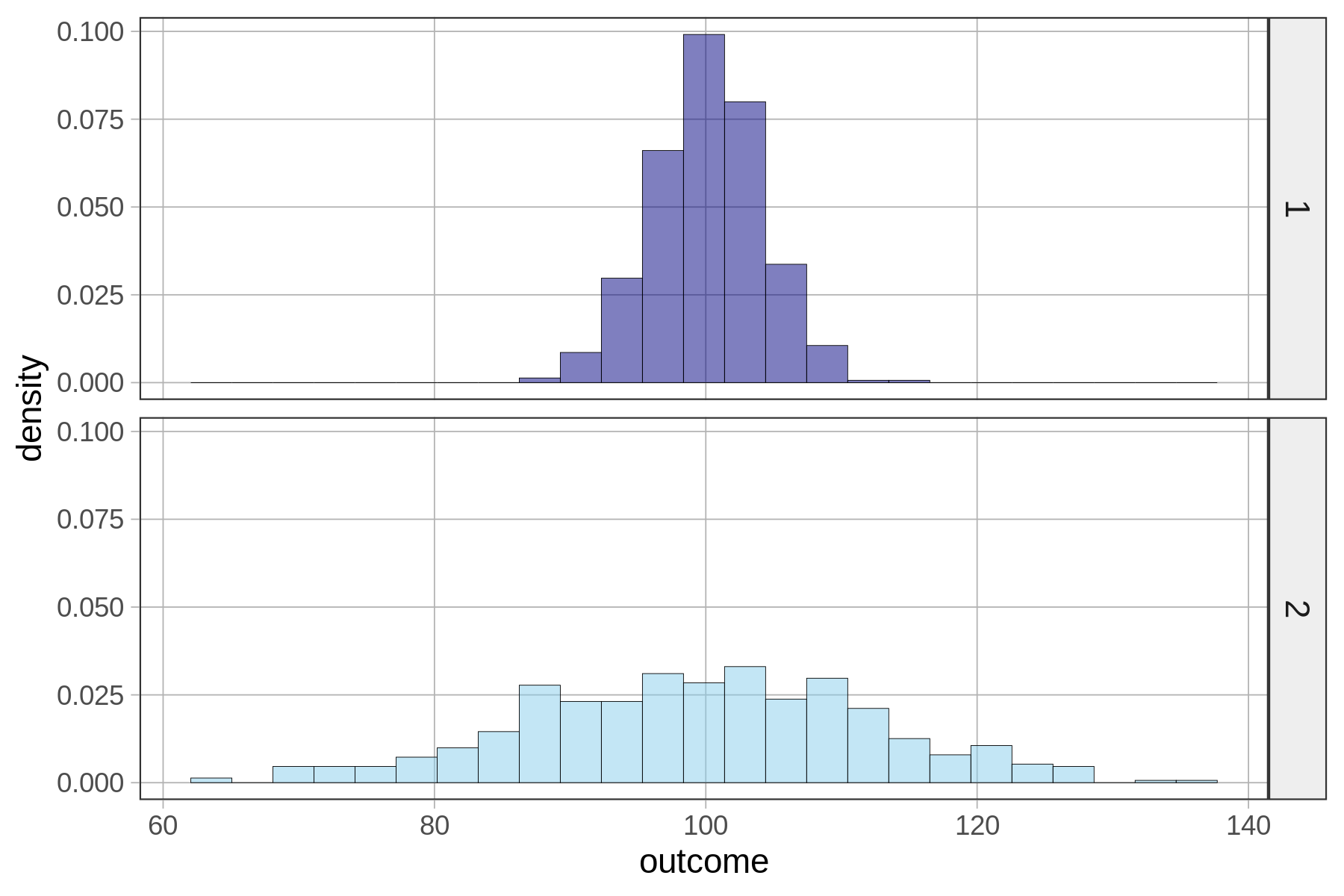
Εξετάστε τις δύο δειγματικές κατανομές στο παραπάνω διάγραμμα. Ο μέσος όρος και των δύο κατανομών είναι το \(100\). Επειδή και οι δύο φαίνονται περίπου συμμετρικές, ας υποθέσουμε ότι η ΔΠΔ που παρήγαγε κάθε κατανομή θα παρήγαγε, μακροπρόθεσμα, μια τέλεια συμμετρική κατανομή πληθυσμού.
Τώρα επιχειρήστε να κάνετε μια πρόβλεψη: Αν μία νέα, τυχαία επιλεγμένη παρατήρηση προστεθεί σε καθένα από αυτά τα δείγματα, ποια ΔΠΔ είναι πιο πιθανό να δώσει τιμή μεγαλύτερη από το μέσο όρο (δηλαδή \(> 100\));
Και οι δύο είναι εξίσου πιθανές είναι η σωστή απάντηση.
Θεμελιώδης αρχή:
Για οποιαδήποτε συμμετρική κατανομή γύρω από το μέσο όρο:
\[P(X > \mu) = 0.5 = 50\%\]
Αυτό ισχύει ανεξάρτητα από τη διασπορά!
Ανάλυση των δύο κατανομών:
Δείγμα 1 (πάνω διάγραμμα):
Συμπαγής, συμμετρική κατανομή γύρω από το 100
Μικρή διασπορά)
P(X > 100) = 0.5
Δείγμα 2 (κάτω διάγραμμα):
Διεσπαρμένη, συμμετρική κατανομή γύρω από το 100
Μεγάλη διασπορά
P(X > 100) = 0.5
Γιατί η διασπορά δεν επηρεάζει την πιθανότητα:
Το κλειδί είναι η συμμετρία:
Διαγραμματική κατανόηση:
Δείγμα 1 (μικρή τυπική απόκλιση):
|←50%→|←50%→|
----****100****----
94 97 100 103 106
Ο μέσος όρος (100) χωρίζει την κατανομή
σε δύο ίσα μέρηΔείγμα 2 (μεγάλη τυπική απόκλιση):
|←────50%────→|←────50%────→|
----****100****----
60 80 100 120 140
Και εδώ ο μέσος όρος (100) χωρίζει
την κατανομή σε δύο ίσα μέρηΓιατί οι άλλες επιλογές είναι λάθος:
Α - Η ΔΠΔ του Δείγματος 1 - ΛΑΘΟΣ:
Η μικρότερη διασπορά δεν αυξάνει την πιθανότητα
Συμμετρία → P(X > 100) = 0.5, όπως και στο Δείγμα 2
Β - Η ΔΠΔ του Δείγματος 2 - ΛΑΘΟΣ:
Η μεγαλύτερη διασπορά δεν αυξάνει την πιθανότητα
Συμμετρία → P(X > 100) = 0.5, όπως και στο Δείγμα 1
Συνήθης παρανόηση:
ΛΑΘΟΣ σκεπτικό: “Το Δείγμα 2 έχει μεγαλύτερο εύρος, άρα περισσότερες τιμές πάνω από 100”
ΣΩΣΤΟ: Ναι, έχει περισσότερες τιμές πάνω από 100 (σε απόλυτους αριθμούς), αλλά και περισσότερες κάτω από 100! Το ποσοστό παραμένει 50%-50%.
Πότε η πιθανότητα ΔΕΝ είναι 0.5:
Μόνο αν η κατανομή είναι ασύμμετρη:
Ασυμμετρία στα δεξιά:
Μέσος > Διάμεσος
P(X > μέσος) < 0.5
Ασυμμετρία στα αριστερά:
Μέσος < Διάμεσος
P(X > μέσος) > 0.5
Συμπέρασμα:
Και οι δύο ΔΠΔ έχουν ακριβώς την ίδια πιθανότητα (50%) να παράγουν τιμή > 100, επειδή:
Και οι δύο είναι συμμετρικές γύρω από το μέσο όρο 100
Για συμμετρική κατανομή, ο μέσος όρος χωρίζει την κατανομή στα δύο ίσα μέρη
Η διασπορά δεν επηρεάζει αυτήν την πιθανότητα - επηρεάζει μόνο πόσο μακριά μπορούν να πέσουν οι τιμές από το μέσο
P(X > μέσος) = 0.5 για το Δείγμα 1 (μικρή τυπική απόκλιση) και το Δείγμα 2 (μεγάλη τυπική απόκλιση)
Αν υποθέσουμε ότι και οι δύο ΔΠΔ παράγουν συμμετρικές κατανομές, τότε και οι δύο είναι εξίσου πιθανό να παράγουν μια επόμενη παρατήρηση που είναι μεγαλύτερη από το μέσο όρο. Κάποιοι μπορεί να ισχυριστούν ότι η ΔΠΔ για το Δείγμα 2 είναι πιο πιθανό να παράγει μια παρατήρηση πάνω από το μέσο όρο, επειδή συτή η ΔΠΔ είναι πιο πιθανό να παράγει ένα μεγαλύτερο αριθμό από τη ΔΠΔ για το Δείγμα 1. Αλλά προσέξτε: είναι επίσης πιο πιθανό να παράγει ένα μικρότερο αριθμό από τη ΔΠΔ για το Δείγμα 1. Και οι δύο κατανομές έχουν 50% πιθανότητα να παράγουν μια επόμενη παρατήρηση πάνω από το μέσο όρο.
Αν είμαστε διατεθειμένοι να κάνουμε πιο συγκεκριμένες υποθέσεις για τα σχήματα των κατανομών, μπορούμε να χρησιμοποιήσουμε αυτές τις υποθέσεις για να υπολογίσουμε την ακριβή πιθανότητα όχι μόνο να είναι η τιμή της επόμενης παρατήρησης πάνω ή κάτω από το μέσο όρο, αλλά και την πιθανότητα η τιμή της επόμενης παρατήρησης να είναι μεγαλύτερη ή μικρότερη από οποιαδήποτε άλλη τιμή—όχι μόνο από το μέσο όρο.
Ας θέσουμε μια διαφορετική ερώτηση: Σε ποια από τις δύο ΔΠΔ, αυτή που παρήγαγε το Δείγμα 1 ή αυτή που παρήγαγε το Δείγμα 2 παραπάνω, είναι πιο πιθανό η τιμή της επόμενης παρατήρησης να είναι μεγαλύτερη από 110; Να εξηγήσετε την απάντησή σας.
Αυτή τη φορά η απάντηση θα είναι διαφορετική. Θα ήσασταν περισσότεροι βέβαιοι ότι θα πάρετε μια τιμή μεγαλύτερη από 110 αν η κατανομή των δεδομένων σας ήταν αυτή στο κάτω μέρος, ακριβώς επειδή υπάρχει μεγαλύτερο σφάλμα (και μεγαλύτερη διασπορά) στο Δείγμα 2. Ένα αρκετά μεγάλο ποσοστό τιμών στο Δείγμα 2 είναι πάνω από 110, ενώ ένα πολύ μικρότερο ποσοστό είναι πάνω από 110 στο Δείγμα 1.
Αλλά τι θα κάνατε αν θέλατε να υπολογίσετε την ακριβή πιθανότητα η τιμή της επόμενης παρατήρησης να είναι μεγαλύτερη από 110;
Πώς θα μπορούσατε να υπολογίσετε αυτή την πιθανότητα; Προσπαθήστε να βρείτε έναν τρόπο. Περιγράψτε την προσέγγισή σας.
Για να απαντήσουμε σε αυτή την ερώτηση, πρέπει να μοντελοποιήσουμε το σχήμα της κατανομής του σφάλματος. Συγκεκριμένα, χρειαζόμαστε μια κατανομή πιθανότητας—κάτι που θα μας επιτρέψει να εκτιμήσουμε την πιθανότητα ενός συγκεκριμένου γεγονότος, όπως ακριβώς τα ορθογώνια και τα τρίγωνα μας έδωσαν έναν τρόπο να εκτιμήσουμε το εμβαδόν της περιφέρειας του Νομού Καβάλας.
Υπολογισμός Πιθανοτήτων από την Κατανομή του Δείγματος
Ένας τρόπος να αποκτήσουμε αυτή την κατανομή πιθανότητας είναι να χρησιμοποιήσουμε την κατανομή του δείγματος. Θυμηθείτε ότι χρησιμοποιήσαμε την τιμή του μέσου όρου μιας κατανομής δείγματος ως εκτίμηση της τιμής του μέσου όρου της κατανομής του πληθυσμού. Με παρόμοιο τρόπο, μπορούμε να χρησιμοποιήσουμε το ποσοστό των παρατηρήσεων που εμπίπτουν σε μια συγκεκριμένη περιοχή στα δεδομένα του δείγματος για να εκτιμήσουμε την πιθανότητα η ΔΠΔ να παράγει μια επόμενη παρατήρηση σε αυτήν την περιοχή.
Ας χρησιμοποιήσουμε την R για να μετρήσουμε το ποσοστό των παρατηρήσεων σε καθένα από τα παραπάνω δείγματα (1 και 2) με τιμές στην εξαρτημένη μεταβλητή μεγαλύτερες από 110. Αρχικά, δημιουργούμε μια μεταβλητή TRUE ή FALSE (τύπου Boolean) για να καταγράψουμε αν κάθε τιμή στην εξαρτημένη μεταβλητή είναι μεγαλύτερη από 110.
Δίνεται ο κώδικας για να το κάνουμε αυτό για ένα πλαίσιο δεδομένων που ονομάζεται sample_2 και περιέχει τα δεδομένα για το Δείγμα 2 του ιστογράμματος που παρουσιάστηκε παραπάνω.
sample_2$greater_than_110 <- sample_2$outcome > 110Θα χρησιμοποιήσουμε ένα συνδυασμό συναρτήσεων για να δούμε μερικές γραμμές του πλαισίου δεδομένων sample_2, εστιάζοντας μόνο στις στήλες outcome και greater_than_110.
head(select(sample_2, outcome, greater_than_110))
outcome greater_than_110
1 75.37310 FALSE
2 82.63074 FALSE
3 113.97732 TRUE
4 121.12801 TRUE
5 117.30387 TRUE
6 89.91760 FALSEΕίναι πάντα καλή ιδέα να εξετάζετε τα δεδομένα για να βεβαιωθείτε ότι ο κώδικάς σας έκανε αυτό που περιμένατε ότι θα κάνει. Στην περίπτωση αυτή, φαίνεται ότι το έκανε. Μπορείτε να δείτε ότι για τη γραμμή 1, η τιμή της outcome ήταν \(75.37310\), που είναι μικρότερη από \(110\), και η τιμή της greater_than_110 είναι FALSE. Αυτό είναι σωστό. Η γραμμή 5 έχει τιμή outcome που είναι μεγαλύτερη από 110, και πράγματι, έχει τιμή TRUE στην greater_than_110.
Στη συνέχεια, θα μετρήσουμε αυτές τις τιμές TRUE και FALSE. Γράφουμε κώδικα για να υπολογίσουμε την απόλυτη και τη σχετική συχνότητα των τιμών της greater_than_110.
# Καταμέτρηση των τιμών της greater_than_110 στο sample_2
table(sample_2$greater_than_110)
# Αναλογία τιμών
prop.table(table(sample_2$greater_than_110))greater_than_110
TRUE FALSE
101 399
greater_than_110
TRUE FALSE
0.202 0.798Μπορούμε να δούμε από το αποτέλεσμα ότι περίπου το \(0.20\) (\(20\%\)) των τιμών του Δείγματος 2 είναι μεγαλύτερες του 110. Με βάση αυτό, θα μπορούσαμε να ισχυριστούμε ότι η ποσοστιαία πιθανότητα μια επόμενη παρατήρηση να ανήκει σε αυτή την περιοχή θα είναι περίπου \(20\%\).
Εφαρμογή στα Δεδομένα Fingers
Ας εφαρμόσουμε αυτές τις ιδέες στο κενό μοντέλο (empty_model) που δημιουργήσαμε προηγουμένως από το πλαίσιο δεδομένων Fingers. Σε αυτό το κενό μοντέλο, μοντελοποιήσαμε τα μήκη αντίχειρα ως το μέσο όρο (\(60.1\)mm) συν το σφάλμα. Όπως είδαμε, το σφάλμα μπορεί να μοντελοποιηθεί είτε ως τα υπόλοιπα γύρω από το μέσο όρο, είτε ως η μεταβλητότητα γύρω από τον μέσο όρο. Και στις δύο περιπτώσεις, το σχήμα της κατανομής είναι το ίδιο, με τη διαφορά ότι όταν μοντελοποιούμε τα υπόλοιπα, ο μέσος όρος τους θα είναι 0.
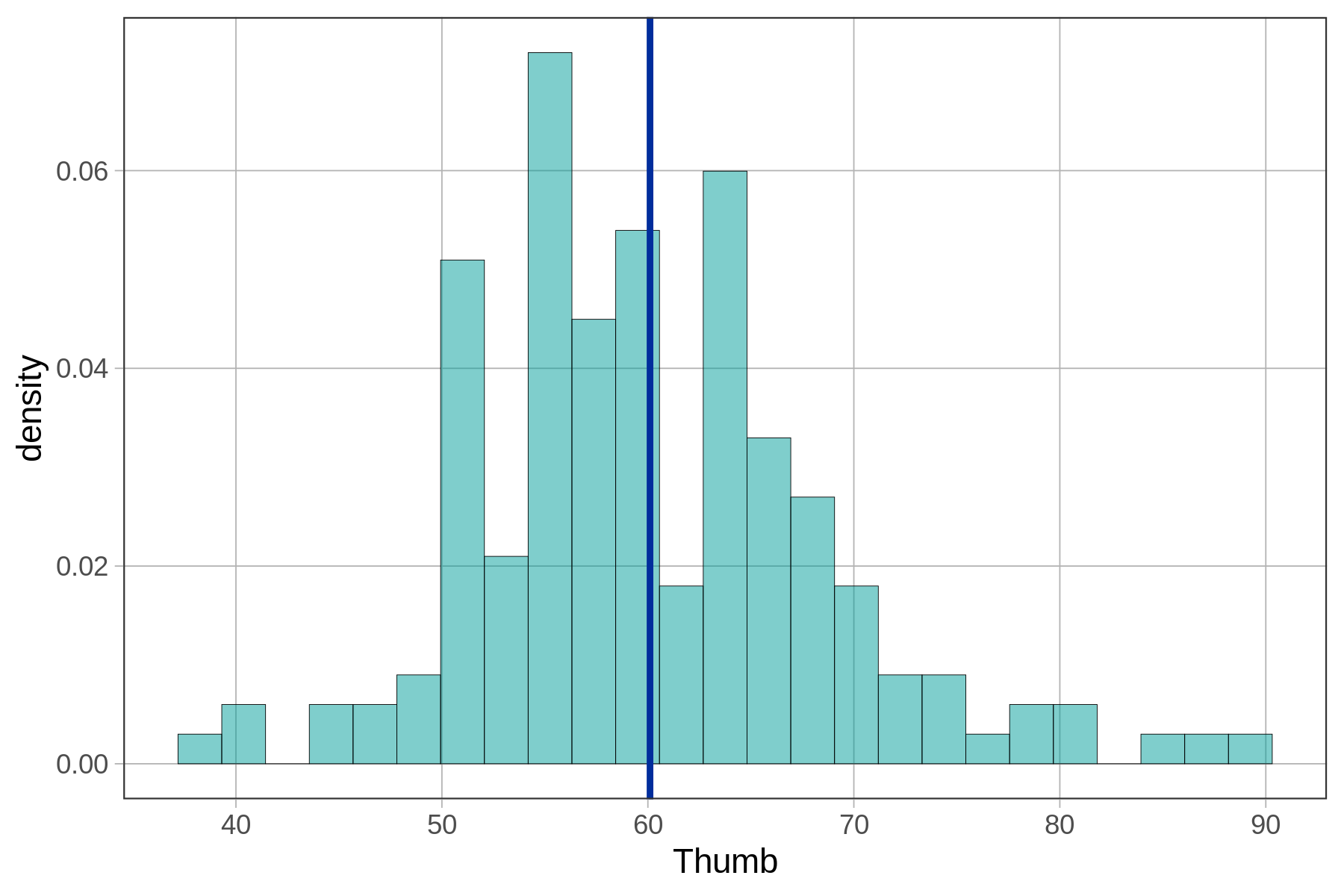
Χρησιμοποιήστε την κατανομή του μήκους αντίχειρα (Thumb) ως μοντέλο της κατανομής πιθανότητας της ΔΠΔ. Στη συνέχεια, γράψτε κώδικα για να υπολογίσετε την πιθανότητα ένας φοιτητής να έχει μήκος αντίχειρα μεγαλύτερο από \(65.1\)mm.
FALSE TRUE
0.8025478 0.1974522 Μπορούμε να δούμε από το αποτέλεσμα ότι περίπου το \(0.20\) (\(20\%\)) των φοιτητών έχουν μήκος αντίχειρα μεγαλύτερο από \(65.1\)mm. Με βάση αυτό, θα εκτιμούσαμε ότι αν μια νέα τυχαία παρατήρηση (μήκος αντίχειρα φοιτητή) προστίθονταν σε αυτό το σύνολο δεδομένων, η πιθανότητα το μήκος αντίχειρα να είναι μεγαλύτερο από \(65.1\) θα ήταν \(0.20\) (ή \(20\%\)).
7.8 Μοντελοποίηση του Σφάλματος με την Κανονική Κατανομή
Η Έννοια μιας Θεωρητικής Κατανομής Πιθανότητας
Ο υπολογισμός πιθανοτήτων από τη δειγματική σας κατανομή λειτουργεί αρκετά καλά, ειδικά αν έχετε πολλά δεδομένα. Αλλά αν έχετε μικρότερη ποσότητα δεδομένων, το σχήμα της κατανομής μπορεί να είναι πολύ ακανόνιστο. Θυμάστε στο Κεφάλαιο 4 όταν εξετάζαμε την κατανομή των ρίψεων ζαριού; Προσομοιώσαμε ένα τυχαίο δείγμα 24 ρίψεων ζαριού, και καταλήξαμε σε μια κατανομή που έμοιαζε κάπως έτσι:
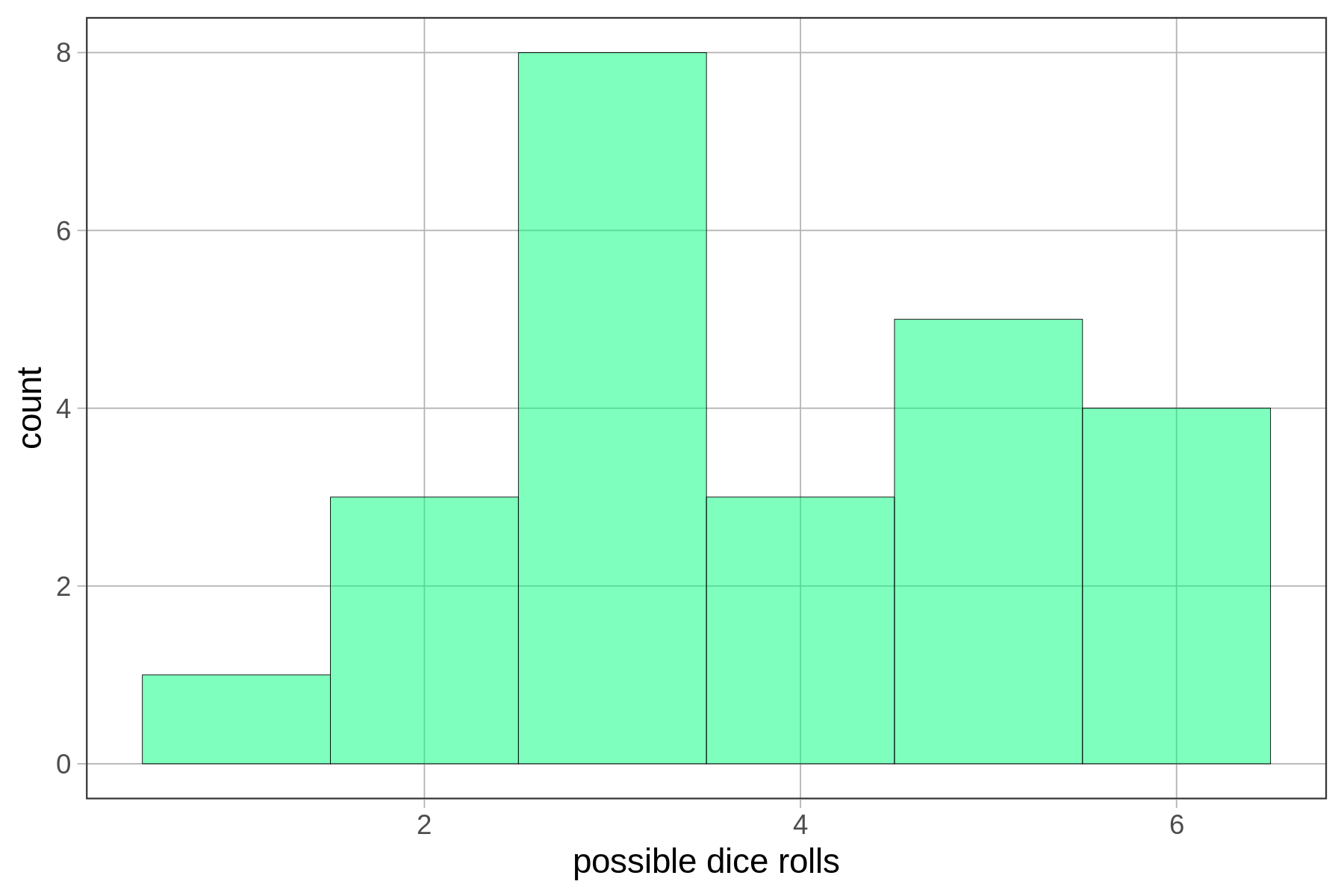
Δεν έχει νόημα να χρησιμοποιήσουμε αυτή την κατανομή για να υπολογίσουμε την πιθανότητα το επόμενο ζάρι να έρθει 3. Γιατί;
Δε θα θέλαμε να χρησιμοποιήσουμε αυτή την κατανομή για να υπολογίσουμε την πιθανότητα η επόμενη ρίψη ζαριού να έρθει 3 επειδή μπορούμε και καλύτερα. Γνωρίζουμε, σε αυτή την περίπτωση, ότι η πιθανότητα να έρθει 3 είναι μία στις έξι, επειδή έχουμε μια καλή εικόνα για το πώς είναι η πραγματική ΔΠΔ (η κατανομή του πληθυσμού).
Παρόλο που η δειγματική μας κατανομή των 24 προσομοιωμένων ρίψεων ζαριού δεν φαίνεται ομοιόμορφη, είμαστε αρκετά σίγουροι ότι στην πραγματικότητα προήλθε από μια ομοιόμορφη κατανομή στην οποία καθεμία από τις έξι πλευρές του ζαριού έχει ίδια πιθανότητα να εμφανιστεί.
Το αναφέρουμε αυτό επειδή παρόλο που τις περισσότερες φορές για πραγματικά δεδομένα δε γνωρίζουμε πώς είναι το σχήμα της κατανομής του πληθυσμού, μπορούμε να είμαστε σχεδόν βέβαιοι ότι δεν θα μοιάζει ακριβώς με τη δειγματική μας κατανομή. Γι’ αυτόν τον λόγο, και επίσης για να διευκολύνουμε τον υπολογισμό πιθανοτήτων, συνήθως μοντελοποιούμε την κατανομή του σφάλματος με μια πιο ομαλή θεωρητική κατανομή πιθανότητας. Η ομοιόμορφη κατανομή, την οποία χρησιμοποιήσαμε στην περίπτωση των ρίψεων ζαριού, είναι ένα παράδειγμα θεωρητικής κατανομής πιθανότητας.
Συνάθροιση Κατανομών και η Κανονική Κατανομή Πιθανότητας
Η πιο συνηθισμένη θεωρητική κατανομή πιθανότητας που χρησιμοποιείται για τη μοντελοποίηση του σφάλματος είναι η κανονική κατανομή (συχνά αναφέρεται και ως κατανομή με σχήμα καμπάνας ή κατανομή του Gauss). Ακόμα κι αν η κατανομή του σφάλματος στα δεδομένα μας δεν μοιάζει ακριβώς με κανονική, υπάρχουν καλοί θεωρητικοί λόγοι να υποθέσουμε ότι στον πληθυσμό η κατανομή του σφάλματος μπορεί να προσεγγίζει την κανονική, υπό ορισμένες προϋποθέσεις.
Αυτό βασίζεται σε ένα θεμελιώδες μαθηματικό θεώρημα, γνωστό ως Κεντρικό Οριακό Θεώρημα (ΚΟΘ). Σύμφωνα με το ΚΟΘ, όταν αθροίζουμε ένα μεγάλο αριθμό ανεξάρτητων τυχαίων μεταβλητών, η κατανομή του (τυποποιημένου) αθροίσματός τους συγκλίνει σε μια κανονική κατανομή, ανεξάρτητα από τις κατανομές των επιμέρους μεταβλητών που συμμετέχουν στο άθροισμα. Με άλλα λόγια, όσο περισσότερες ανεξάρτητες τυχαίες μεταβλητές αθροίζουμε, τόσο πιο κοντά πλησιάζει η κατανομή του αθροίσματος σε μια κανονική κατανομή, ανεξάρτητα από το σχήμα που έχουν οι αρχικές κατανομές.
Ας το σκεφτούμε αυτό εστιάζοντας στο ΣΦΑΛΜΑ (στην εξίσωση ΔΕΔΟΜΕΝΑ = ΜΟΝΤΕΛΟ + ΣΦΑΛΜΑ). Αν το σφάλμα μιας μεταβλητής προκύπτει από πολλές ανεξάρτητες πηγές που προστίθενται μεταξύ τους, τότε η κατανομή του σφάλματος τείνει να προσεγγίζει μια κανονική κατανομή. Ας δώσουμε ένα παράδειγμα: όταν μετράμε το ύψος ενός ατόμου, η μέτρησή μας επηρεάζεται από πολλές μικρές και ανεξάρτητες πηγές σφάλματος (π.χ. ακρίβεια του οργάνου μέτρησης, στάση σώματος, ώρα της ημέρας).Κάθε μία από αυτές τις πηγές σφάλματος συνεισφέρει μια μικρή τυχαία απόκλιση στο τελικό αποτέλεσμα. Για παράδειγμα, το όργανο μέτρησης μπορεί να έχει μια μικρή απόκλιση λόγω βαθμονόμησης, η στάση του ατόμου μπορεί να αλλάζει ελαφρώς τη μέτρηση, και η ώρα της ημέρας μπορεί να επηρεάζει το ύψος λόγω μικρών διακυμάνσεων στη σπονδυλική στήλη. Όταν όλες αυτές οι μικρές, ανεξάρτητες αποκλίσεις αθροίζονται, το Κεντρικό Οριακό Θεώρημα μας δείχνει ότι η συνολική κατανομή του σφάλματος θα μοιάζει με κανονική κατανομή, με σχήμα καμπάνας, που βρίσκεται γύρω από το 0 (αν θεωρήσουμε ότι το μοντέλο μας είναι ο μέσος όρος). Αυτό μας επιτρέπει να χρησιμοποιούμε την κανονική κατανομή για να κάνουμε προβλέψεις σχετικά με την πιθανότητα συγκεκριμένων σφαλμάτων ή αποκλίσεων από το μοντέλο μας, όπως για παράδειγμα την πιθανότητα το ύψος που μετρήσαμε να είναι εντός ενός συγκεκριμένου εύρους από την πραγματική τιμή.
Ας δώσουμε ένα άλλο παράδειγμα: στη ψυχολογική έρευνα, όταν προσπαθούμε να προβλέψουμε μια συμπεριφορά, όπως το επίπεδο άγχους ενός ατόμου, με βάση γνωστούς παράγοντες (π.χ. ηλικία, φύλο, επίπεδο κοινωνικής υποστήριξης, προηγούμενο ιστορικό ψυχικών διαταραχών) η διαφορά μεταξύ της πραγματικής τιμής του άγχους και της τιμής που προβλέπει το μοντέλο μας θεωρείται σφάλμα. Αυτό το σφάλμα προκύπτει από μια ποικιλία μικρών, ανεξάρτητων και συχνά μη μετρήσιμων παραγόντων που δεν μπορούμε να συμπεριλάβουμε στο μοντέλο μας (π.χ. μια τυχαία καλή διάθεση λόγω μιας καλής μέρας, μια απρόσμενη συζήτηση με έναν φίλο, ή μικρές αλλαγές στη σωματική υγεία, όπως κόπωση ή ενέργεια). Κάθε ένας από αυτούς τους παράγοντες θεωρούμε ότι συνεισφέρει μια μικρή, τυχαία ποσότητα στο συνολικό σφάλμα. Σύμφωνα με το Κεντρικό Οριακό Θεώρημα, το άθροισμα όλων αυτών των μικρών και ανεξάρτητων πηγών διακύμανσης τείνει να ακολουθεί μια κανονική κατανομή. Αυτός είναι ο λόγος για τον οποίο η υπόθεση της κανονικότητας του σφάλματος είναι τόσο θεμελιώδης για πολλές στατιστικές μεθόδους.
Επίδειξη της Διαδικασίας της Συνάθροισης
Μπορούμε να δείξουμε τη δύναμη του ΚΟΘ με μια απλή προσομοίωση. Ας προσομοιώσουμε ένα σύνολο δεδομένων με 1.000 παρατηρήσεις και 10 μεταβλητές, καθεμία δημιουργημένη τυχαία από μια ομοιόμορφη κατανομή, με πιθανές τιμές από -3 έως +3.
Θα ξεκινήσουμε με την προσομοίωση μίας μεταβλητής με τον παρακάτω κώδικα:
var1 <- resample(-3:3, 1000)Η resample() πραγματοποιεί τυχαία δειγματοληψία με επανατοποθέτηση, όπου κάθε τιμή έχει ίση πιθανότητα να επιλεγεί. Μπορείτε να εκτελέστε τον παρακάτω κώδικα για να δημιουργήσετε την πρώτη μεταβλητή, var1. Ας την αποθηκεύσουμε σε ένα πλαίσιο δεδομένων που ονομάζεται somedata.
Για να το κάνουμε αυτό θα χρησιμοποιήσουμε τη συνάρτηση data.frame(). Αυτή η συνάρτηση μας επιτρέπει να πάρουμε ένα ή περισσότερα διανύσματα ίδιου μεγέθους και να τα συνδυάσουμε σε ένα πλαίσιο δεδομένων στο οποίο κάθε διάνυσμα γίνεται μια μεταβλητή.
Πώς πιστεύετε ότι θα μοιάζει η κατανομή της var1;
Ποια είναι η Διαδικασία Δημιουργίας των Δεδομένων (ΔΠΔ) της var1;
Για την πρώτη ερώτηση: Περίπου επίπεδη, σαν ομοιόμορφη κατανομή
Για τη δεύτερη ερώτηση: Η ΔΠΔ είναι η συνάρτηση resample()
Ανάλυση του κώδικα:
Τι κάνει αυτός ο κώδικας:
-3:3δημιουργεί το διάνυσμα: -3, -2, -1, 0, 1, 2, 3 (7 τιμές)resample()επιλέγει τυχαία με επανατοποθέτηση από αυτές τις 7 τιμέςΕπιλέγει 1000 φορές, άρα n = 1000
Κάθε τιμή έχει ίση πιθανότητα 1/7 ≈ 14.3% να επιλεγεί
Αναμενόμενη κατανομή:
Ομοιόμορφη:
Το ιστόγραμμα θα δείξει 7 στήλες με περίπου ίδιο ύψος → επίπεδη/uniform κατανομή
Γιατί οι άλλες επιλογές είναι λάθος:
Β - Κωδωνοειδής/Κανονική - ΛΑΘΟΣ:
Η κανονική κατανομή έχει περισσότερες τιμές κοντά στο μέσο
Εδώ όλες οι τιμές έχουν ίση πιθανότητα
Δεν υπάρχει “κορυφή” στο κέντρο
Γ/Δ - Ασύμμετρη - ΛΑΘΟΣ:
Η κατανομή είναι συμμετρική γύρω από το 0
Ίδια πιθανότητα για θετικές και αρνητικές τιμές
Δεν υπάρχουν “ακραίες” τιμές - όλες είναι μεταξύ -3 και 3
Ε - Δεν μπορούμε να πούμε - ΛΑΘΟΣ:
Το n = 1000 είναι μεγάλο δείγμα
Με τον Νόμο των Μεγάλων Αριθμών, η εμπειρική κατανομή θα προσεγγίσει την ομοιόμορφη
Μπορούμε να προβλέψουμε με σιγουριά ότι θα είναι επίπεδη
ΔΠΔ (Διαδικασία Παραγωγής Δεδομένων):
Τι είναι η ΔΠΔ:
Η ΔΠΔ είναι η διαδικασία που δημιουργεί τα δεδομένα. Στην περίπτωσή μας:
Περιγραφή:
Διακριτή Ομοιόμορφη Κατανομή από το σύνολο {-3, -2, -1, 0, 1, 2, 3}
Κάθε τιμή επιλέγεται με πιθανότητα 1/7
Με επανατοποθέτηση (replacement)
Γιατί το Δ είναι σωστό:
Περιγράφει ακριβώς τι κάνει ο κώδικας
Η
resample()επιλέγει τυχαία από τους αριθμούς -3 έως 3Αυτή είναι η πραγματική ΔΠΔ
Γιατί οι άλλες επιλογές είναι λάθος:
Α - Άγνωστη - ΛΑΘΟΣ:
Η ΔΠΔ είναι γνωστή - έχουμε τον κώδικα!
Ξέρουμε ακριβώς πώς δημιουργούνται τα δεδομένα
Β - Κανονική κατανομή - ΛΑΘΟΣ:
Για κανονική χρησιμοποιούμε τη συνάρτηση
rnorm()Εδώ χρησιμοποιούμε την
resample()
Γ - Εξισορροπεί τα υπόλοιπα - ΛΑΘΟΣ:
Η ΔΠΔ δεν “προσπαθεί” να κάνει τίποτα
Απλά επιλέγει τυχαία
Δεν υπάρχει μηχανισμός “εξισορρόπησης”
Συμπέρασμα:
Η κατανομή της var1 θα είναι περίπου επίπεδη/ομοιόμορφη επειδή:
Κάθε τιμή από -3 έως 3 έχει ίση πιθανότητα επιλογής
Με μεγάλο δείγμα (n=1000), κάθε τιμή θα εμφανιστεί περίπου τον ίδιο αριθμό φορών
Το ιστόγραμμα θα είναι περίπου επίπεδο με 7 στήλες ίδιου ύψους
Η ΔΠΔ είναι η συνάρτηση resample() επειδή:
Αυτή είναι η ακριβής διαδικασία που δημιουργεί τα δεδομένα
Επιλέγει τυχαία με επανατοποθέτηση από το σύνολο {-3, -2, -1, 0, 1, 2, 3}
Δημιουργεί μια διακριτή ομοιόμορφη κατανομή
Στη συνέχεια, δημιουργήστε το ιστόγραμμα της var1.
Ο παρακάτω κώδικας θα δημιουργήσει τις άλλες εννέα μεταβλητές (var2 έως var10), και στη συνέχεια θα αποθηκεύσει τις 10 προσομοιωμένες μεταβλητές στο πλαίσιο δεδομένων somedata.
Να εμφανίσετε τις πρώτες έξι γραμμές του somedata, και στη συνέχεια να δημιουργήσετε τα 10 ιστογράμματα, ένα για καθεμία από τις 10 μεταβλητές.
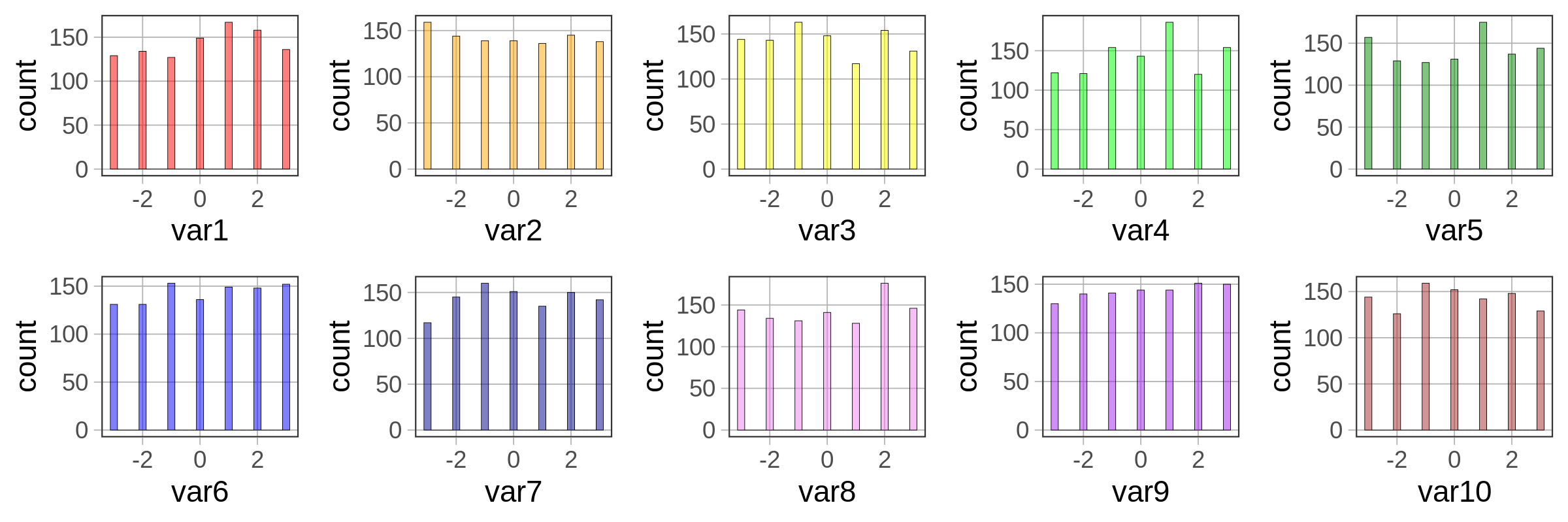
Μοιάζουν με Κανονικές κάποιες από τις προσομοιωμένες κατανομές (var1 έως var10);
ΟΧΙ, οι περισσότερες δεν μοιάζουν με καμπύλες κανονικής κατανομής είναι η σωστή απάντηση.
Ανάλυση των διαγραμμάτων:
Όλες οι μεταβλητές (var1-var10) δείχνουν:
Επίπεδη/Ομοιόμορφη κατανομή
Όλες οι στήλες έχουν περίπου το ίδιο ύψος
Γιατί όλες είναι περίπου ομοιόμορφες:
# Όλες οι μεταβλητές φαίνεται ότι δημιουργούνται
# με τον ίδιο τρόπο:
var1 <- resample(-3:3, 1000)
var2 <- resample(-3:3, 1000)
var3 <- resample(-3:3, 1000)
# ... κλπ
# Όλες είναι ΑΝΕΞΑΡΤΗΤΑ δείγματα από ομοιόμορφη κατανομήΣυμπέρασμα:
ΟΧΙ, καμία κατανομή δεν μοιάζει με καμπύλη κανονικής κατανομής.
Επειδή προσομοιώσαμε 10 μεγάλα δείγματα, και επειδή επιλέξαμε τυχαία κάθε τιμή τους από μια ομοιόμορφη κατανομή, μπορούμε να δούμε στο αντίστοιχο ιστόγραμμα ότι κάθε κατανομή μοιάζει περίπου ομοιόμορφη.
Μπορούμε επίσης να δούμε από τα ιστογράμματα ότι ο μέσος όρος κάθε μεταβλητής είναι κοντά στο 0, κάτι που ήταν αναμενόμενο με βάση τον κώδικα που χρησιμοποιήσαμε για να προσομοιώσουμε τις μεταβλητές. Μπορείτε να χρησιμοποιήσετε τη συνάρτηση summary() για να πάρετε μια γρήγορη σύνοψη όλων των μεταβλητών στο somedata. Αυτή η συνάρτηση είναι παρόμοια με την favstats(), με τη διαφορά ότι η favstats θα συνοψίσει μόνο μία μεταβλητή τη φορά, ενώ η summary θα συνοψίσει όλες τις μεταβλητές που βρίσκονται σε ένα πλαίσιο δεδομένων. Δοκιμάστε τη στο παρακάτω πλαίσιο κώδικα.
Τώρα ας δούμε τι συμβαίνει αν φτιάξουμε μια νέα, σύνθετη μεταβλητή που είναι το άθροισμα των 10 μεταβλητών για κάθε γραμμή-παρατήρηση στο σύνολο δεδομένων somedata.
Ας γράψουμε κώδικα που αθροίζει τις 10 μεταβλητές και αποθηκεύει το άθροισμά τους ως μια νέα μεταβλητή στο somedata. Ας δημιουργήσουμε το ιστόγραμμα αυτής της μεταβλητής (μπορούμε να την ονομάσουμε total).
Αν βλέπετε κενά στο ιστόγραμμα, αυτό σημαίνει ότι ο προεπιλεγμένος αριθμός ράβδων (bins) είναι πολύ μεγάλος. Η προεπιλεγμένη τιμή στην R είναι bins = 30. Μπορείτε να δοκιμάσετε να ορίσετε περισσότερα ή λιγότερα bins ώστε να παρατηρήσετε ποιο είναι το γενικό σχήμα της κατανομής που είναι κοινό σε αυτούς τους διαφορετικούς τρόπους παρουσίασης των ίδιων δεδομένων.
Πώς μοιάζει γενικά η κατανομή της σύνθετης μεταβλητής total;
Κανονική είναι η σωστή απάντηση.
Ανάλυση των διαγραμμάτων:
Παράδειγμα 1: 10 bins:
Έχει κωδωνοειδές σχήμα
Υψηλότερη ράβδο στο κέντρο (γύρω στο 0)
Χαμηλότερες ράβδοι στα άκρα
Περίπου συμμετρική
Αλλά με λίγα bins, το σχήμα είναι χονδροειδές
Παράδειγμα 2: 75 bins:
Δείχνει ξεκάθαρα καμπύλη κανονικής κατανομής 🔔
Ομαλή κορυφή στο κέντρο
Συμμετρικές ουρές αριστερά και δεξιά
Κλασική κανονική κατανομή
Με περισσότερα bins, η κανονικότητα γίνεται εμφανής
Γιατί οι άλλες επιλογές είναι λάθος:
Α - Ομοιόμορφη - ΛΑΘΟΣ:
Ομοιόμορφη = επίπεδη κατανομή
Εδώ βλέπουμε κορυφή στο κέντρο, όχι επίπεδη
Οι στήλες δεν έχουν ίδιο ύψος
Γ - Ασύμμετρη - ΛΑΘΟΣ:
Εδώ η κατανομή είναι συμμετρική
Αριστερή και δεξιά πλευρά είναι καθρέφτες
Δ - Άλλο - ΛΑΘΟΣ:
Η κατανομή έχει ξεκάθαρα σχήμα καμπάνας
Δεν είναι κάτι “άλλο” - είναι κλασική κανονική
Συμπέρασμα:
Η κατανομή της μεταβλητής total είναι κανονική (Normal), όπως φαίνεται καθαρά στο διάγραμμα με 75 bins. Αυτό είναι αποτέλεσμα του Κεντρικού Οριακού Θεωρήματος: όταν η total δημιουργείται ως άθροισμα πολλών (10) ανεξάρτητων ομοιόμορφων μεταβλητών (var1-var10), η κατανομή του αθροίσματος τείνει στην κανονική, με:
Κωδωνοειδές σχήμα με κορυφή στο κέντρο
Συμμετρία γύρω από το μέσο όρο (0)
Ομαλές ουρές που φθίνουν προς τα άκρα
Όσο περισσότερα bins χρησιμοποιούμε στο ιστόγραμμα, τόσο πιο καθαρά φαίνεται η κανονική καμπύλη.
Όπως μπορείτε να διαπιστώσετε, αθροίζοντας πολλές μεταβλητές μαζί η κατανομή που προκύπτει είναι περίπου κανονική, παρόλο που καμία από τις 10 αρχικές μεταβλητές που αθροίσατε δεν είχε κανονική κατανομή—όλες ήταν περίπου ομοιόμορφες. Αλλά το άθροισμά τους έχει το σχήμα μιας περίπου κανονικής κατανομής.
Ας προσπαθήσουμε να κατανοήσουμε γιατί προκύπτει αυτό το σχήμα της κανονικής κατανομής. Ορισμένες από τις τυχαία δημιουργημένες τιμές θα μετακινήσουν το άθροισμα προς τα πάνω, ενώ άλλες θα το μετακινήσουν προς τα κάτω. Τα περισσότερα αθροίσματα, ωστόσο, θα συγκεντρώνονται γύρω από το κέντρο (σε αυτή την περίπτωση, την τιμή 0). Σκεφτείτε πόσοι πολλοί τρόποι υπάρχουν να πάρουμε ένα συνολικό άθροισμα από τις 10 αρχικές τιμές μας (που κινούνται στο εύρος -3 έως +3) που να είναι γύρω από το 0, και πόσοι λιγότεροι υπάρχουν να πάρουμε ένα πολύ μικρό ή ένα πολύ μεγάλο άθροισμα, π.χ. κοντά στο -30 ή στο +30.
Αυτή, λοιπόν, η ιδιότητα που απορρέει από το Κεντρικό Οριακό Θεώρημα είναι που μας οδηγεί στο να υποθέτουμε συνήθως ότι η κατανομή των σφαλμάτων είναι κανονική. Και όπως θα δείτε αργότερα στο μάθημα, αυτή η ιδέα της συνάθροισης είναι επίσης η βάση των μεθόδων που χρησιμοποιούμε για την αξιολόγηση και σύγκριση στατιστικών μοντέλων.
Ας σκεφτούμε πώς αυτό μπορεί να εφαρμοστεί σε δεδομένα που έχουμε ήδη εξετάσει. Αν μας ενδιαφέρει γιατί οι άνθρωποι έχουν συγκεκριμένο μήκος αντίχειρα, το σφάλμα γύρω από το μέσο όρο πιθανώς προκύπτει από πολλές διαφορετικές ανεξάρτητες πηγές τυχαίας διακύμανσης (γενετικοί παράγοντες, διατροφή, μέτρηση, κτλ.). Όταν αυτές οι πολλές ανεξάρτητες επιδράσεις προστίθενται μεταξύ τους (και καμία δεν κυριαρχεί), η κατανομή του σφάλματος θα τείνει να είναι κανονική - υπάρχουν πολύ περισσότεροι τρόποι να προκύψουν σφάλματα στη μέση παρά στα άκρα της κατανομής.
7.9 Χρήση του Μοντέλου της Κανονικής Κατανομής για Πρόβλεψη
Ας επιστρέψουμε τώρα στην ερώτηση που θέσαμε νωρίτερα: Δεδομένης της κατανομής του μήκους του αντίχειρα, ποια είναι η πιθανότητα ο επόμενος τυχαία επιλεγμένος φοιτητής να έχει μήκος αντίχειρα τουλάχιστον 65.1 χιλιοστά; (Η φράση «τουλάχιστον» υποδηλώνει μήκος αντίχειρα 65.1 χιλιοστά ή μεγαλύτερο!) Πώς μπορούμε να χρησιμοποιήσουμε το μοντέλο της κανονικής κατανομής για να απαντήσουμε σε αυτή την ερώτηση;
Προσαρμογή του Μοντέλου της Κανονικής Κατανομής στην Κατανομή των Δεδομένων
Αρχικά, χρειάζεται να προσαρμόσουμε το μοντέλο της εξομαλυμένης κανονικής κατανομής στην κατανομή του μήκους του αντίχειρα στο δείγμα μας (κατά τον ίδιο τρόπο που προσαρμόσαμε απλά γεωμετρικά σχήματα πάνω από το ακανόνιστο σχήμα του Ν. Καβάλας). Παρακάτω παρουσιάζεται η ακανόνιστη κατανομή του μήκους του αντίχειρα. Έχουμε αναπαραστήσει το κενό μοντέλο (το μέσο όρο της κατανομής, \(60.1\)) με μια μπλε γραμμή για να χρησιμεύσει ως σημείο αναφοράς.
empty_model <- lm(Thumb ~ NULL, data = Fingers)
gf_dhistogram(~ Thumb, data = Fingers) %>%
gf_model(empty_model)
Η κανονική κατανομή είναι στην πραγματικότητα μια ομάδα θεωρητικών κατανομών, καθεμία με διαφορετικό μέσο όρο και διαφορετική τυπική απόκλιση. Οποιαδήποτε κανονική κατανομή μπορεί να περιγραφεί με τις τιμές αυτών των δύο παραμέτρων, το μέσο όρο και την τυπική απόκλιση. Για να βρούμε την κανονική κατανομή που προσαρμόζεται καλύτερα στα δεδομένα μας, πρέπει να βρούμε τις τιμές του μέσου όρου και της τυπικής απόκλισης για την καλύτερα προσαρμοσμένη καμπύλη, δηλαδή την καμπύλη που ελαχιστοποιεί τα τετραγωνικά υπόλοιπα των τιμών μας από το μοντέλο.
Η παρακάτω εικόνα μπορεί να σας δώσει μια αίσθηση του πώς οι κανονικές κατανομές μπορεί να διαφέρουν μεταξύ τους, ανάλογα με τους μέσους όρους και τις τυπικές αποκλίσεις τους. Σημειώστε ότι τρεις από τις τέσσερις κατανομές που απεικονίζονται έχουν τον ίδιο μέσο όρο, που είναι 0, αλλά αρκετά διαφορετικό σχήμα καμπύλης. Η τέταρτη καμπύλη κανονικής κατανομής έχει μέσο όρο μικρότερο από τις άλλες τρεις.
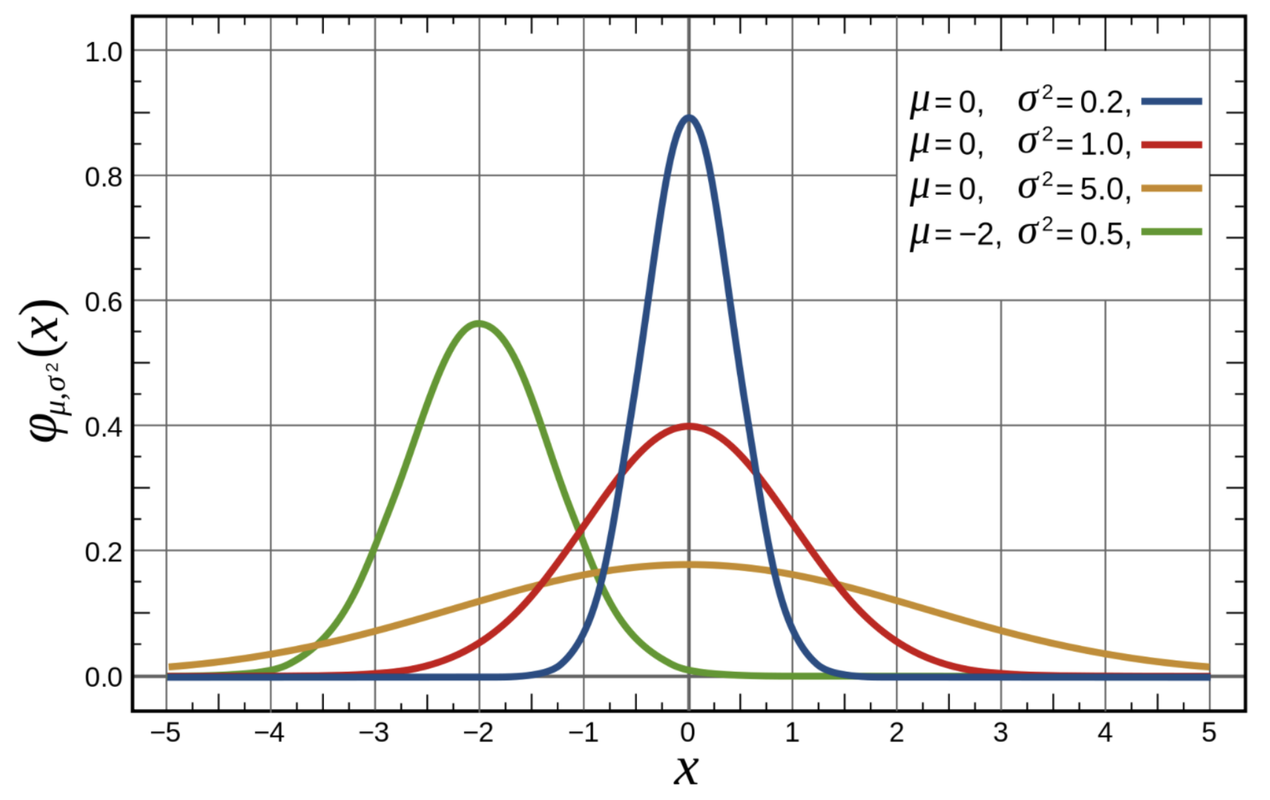
Η εύρεση της καμπύλης κανονικής κατανομής που προσαρμόζεται καλύτερα στην κατανομή των δεδομένων μας είναι αρκετά απλή υπόθεση. Πρώτα, χρησιμοποιούμε το δειγματικό μέσο όρο και τη δειγματική τυπική απόκλιση τυπική απόκλιση (\(\bar{Y}\) και \(s\)) ως εκτιμήσεις του πληθυσμιακού μέσου όρου και της πληθυσμιακής τυπικής απόκλισης (\(\mu\) και \(\sigma\)). Στη συνέχεια, με αυτές τις τιμές ως εκτιμήσεις, μπορούμε να χρησιμοποιήσουμε τη συνάρτηση gf_fitdistr() για να προβάλλουμε το καλύτερα προσαρμοσμένο μοντέλο κανονικής κατανομής στην κατανομή των δεδομένων μας.
Η συνάρτηση gf_fitdistr() προβάλει σε ιστογράμματα διαφορετικές θεωρητικές κατανομές πιθανοτήτων. Η προεπιλεγμένη κατανομή είναι η κανονική κατανομή (αυτή η συνάρτηση υπολογίζει αυτόματα το μέσο όρο και την τυπική απόκλιση του δείγματος για να σχεδιάσει την αντίστοιχη καμπύλη κανονικής κατανομής).
gf_dhistogram(~ Thumb, data = Fingers) %>%
gf_model(empty_model) %>%
gf_fitdistr()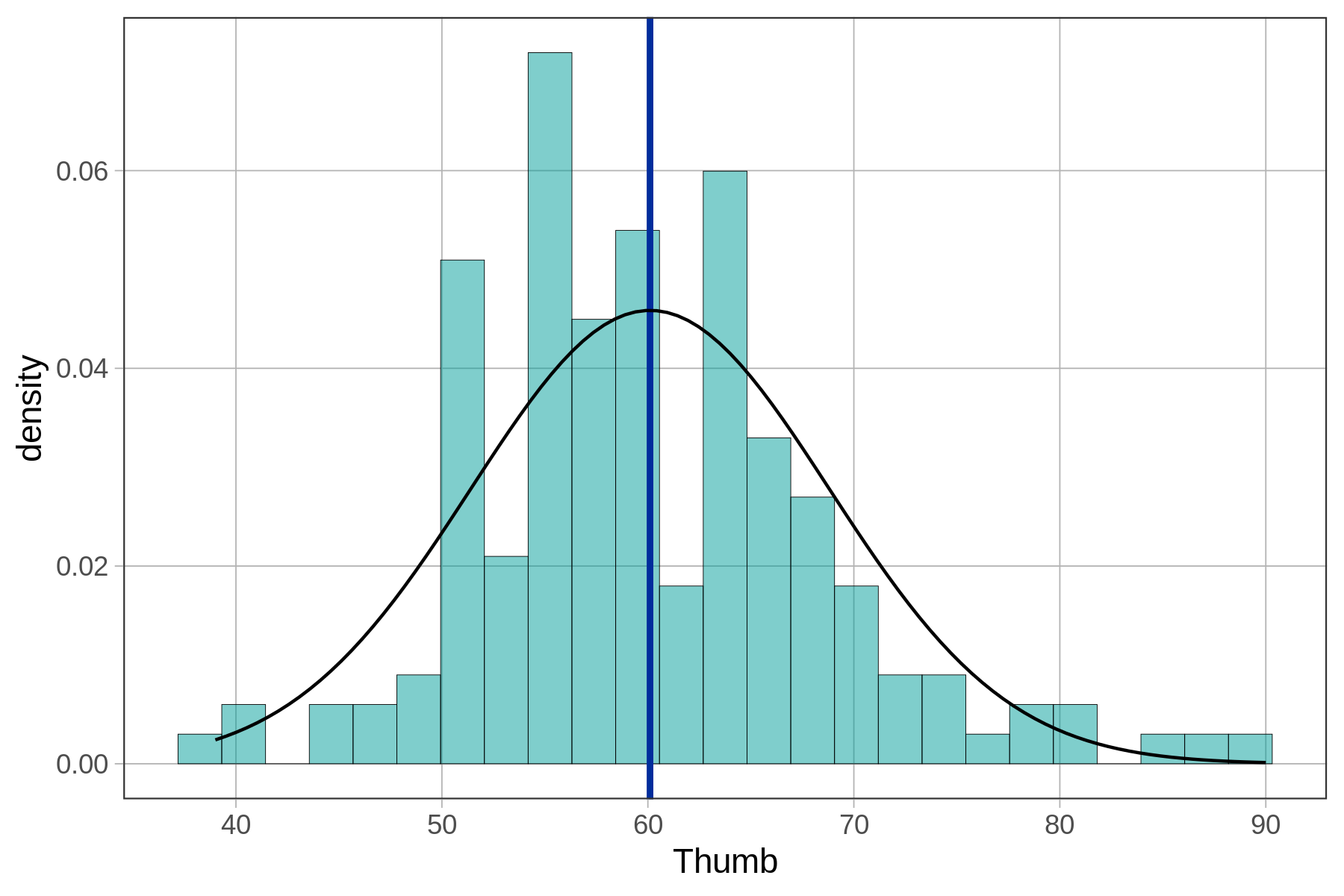
Ίσως σκέφτεστε ότι η καμπύλη κανονική κατανομής που προέκυψ δεν προσαρμόζεται και τόσο καλά στα δεδομένα μας. Έχετε δίκιο! Αλλά θυμηθείτε ότι ο στόχος μας δεν είναι μόνο να μοντελοποιήσουμε τα δεδομένα του δείγματός μας, αλλά να μοντελοποιήσουμε τα μακροπρόθεσμα αποτελέσματα της Διαδικασίας Παραγωγής των Δεδομένων μας (ΔΠΔ). Ακόμα κι όταν τα δεδομένα μας φαίνονται ακανόνιστα, η κατανομή του πληθυσμού μπορεί να μην είναι.
Επιπλέον, ο στόχος ενός μοντέλου δεν είναι να προσαρμόζεται απόλυτα στα δεδομένα, αλλά να συνδυάζει την προσαρμογή του μοντέλου με την απλότητα και την κομψότητα του μοντέλου. Όταν μοντελοποιούμε το σφάλμα με την καμπύλη της κανονική κατανομής, στην ουσία ανταλλάσουμε την πολυπλοκότητα 157 ακανόνιστων τιμών με ένα κομψό μοντέλο δύο παραμέτρων—την καμπύλη της κανονικής κατανομής.
Τέλος, ας θυμηθούμε την αρχική μας ερώτηση; Θέλαμε να μάθουμε την ακριβή πιθανότητα ο επόμενος τυχαία επιλεγμένος φοιτητής να έχει μήκος αντίχειρα μεγαλύτερο από 65.1 χιλιοστά. Για να βοηθήσουμε στη διαγραμματική αναπαράσταση αυτής της ερώτησης, ας προσθέσουμε ακόμα ένα στοιχείο στο διάγραμμα: μια κόκκινη γραμμή για να εντοπίσουμε στην κατανομή τα 65.1 χιλιοστά.
gf_dhistogram(~ Thumb, data = Fingers) %>%
gf_model(empty_model) %>%
gf_fitdistr() %>%
gf_vline(xintercept = 65.1, color = "red") 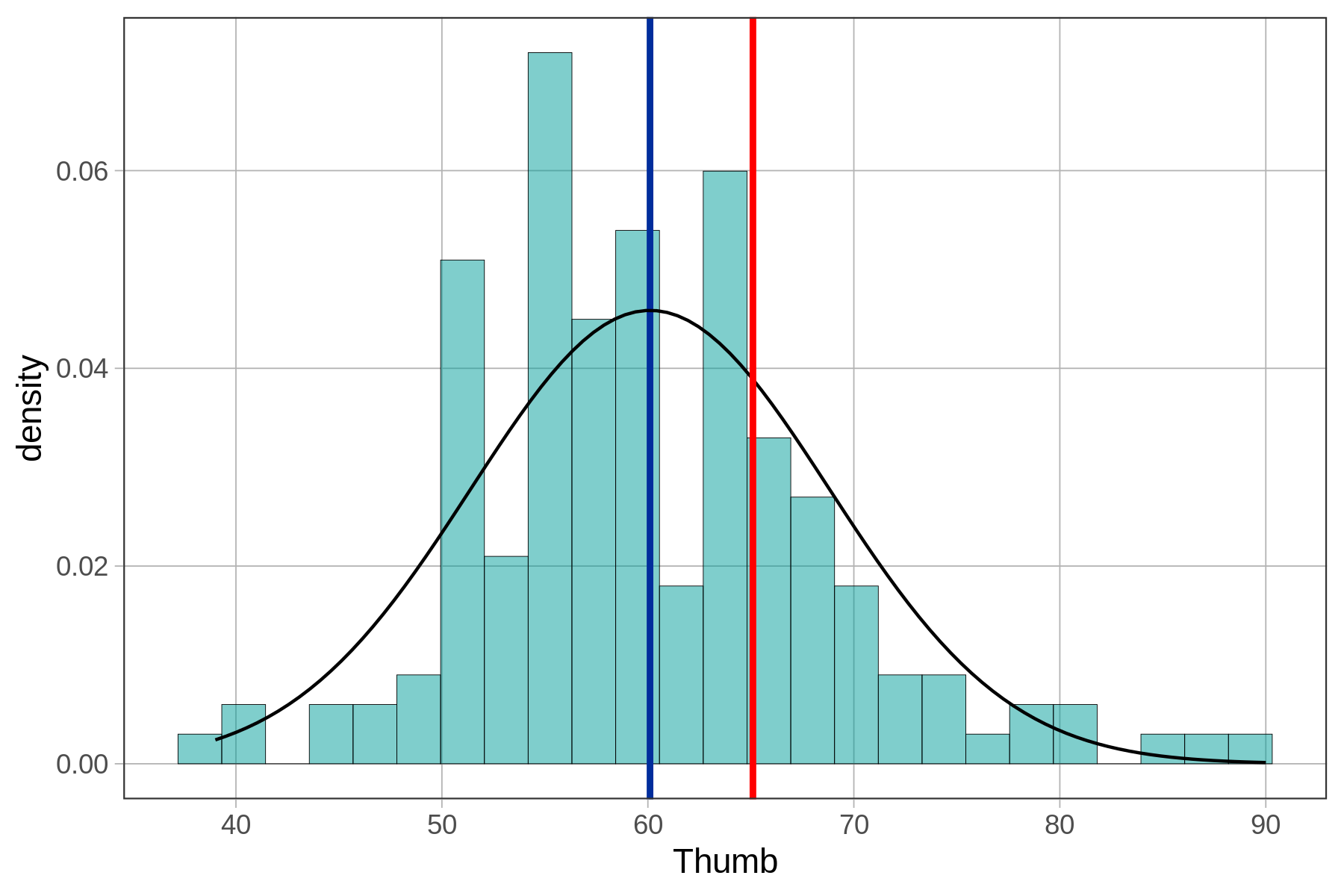
Με τη βοήθεια αυτού του διαγράμματος, μπορούμε να επαναδιατυπώσουμε την ερώτησή μας ως εξής: Τι ποσοστό της περιοχής κάτω από την μαύρη καμπύλη της κανονικής κατανομής βρίσκεται δεξιά από την κόκκινη κατακόρυφη γραμμή; Αυτό το ποσοστό, το οποίο θα υπολογίσουμε παρακάτω, εκφράζει την πιθανότητα ότι ο επόμενος τυχαία επιλεγμένος φοιτητής να έχει μήκος αντίχειρα μεγαλύτερο από 65.1 χιλιοστά.
Χρήση της Κανονικής Κατανομής για Υπολογισμό Τιμών Πιθανότητας
Αφού προσαρμόσουμε μια εξομαλυμένη καμπύλη κανονικής κατανομής στα δεδομένα μας, μπορούμε να χρησιμοποιήσουμε τις μαθηματικές της ιδιότητες (μην ανησυχείτε, αυτό θα το κάνει η R!) για να βρούμε την πιθανότητα οι τιμές να βρίσκονται σε συγκεκριμένες περιοχές. Αυτό είναι παρόμοιο με ό,τι κάναμε όταν χρησιμοποιήσαμε ορθογώνια για να προσεγγίσουμε την επιφάνεια του Ν. Καβάλας: μόλις σχεδιάσαμε το ορθογώνιο, μπορούσαμε απλά να χρησιμοποιήσουμε τον τύπο για το εμβαδόν ενός ορθογωνίου.
Στο παρακάτω διάγραμμα, έχουμε αφαιρέσει την κατανομή των δεδομένων και έχουμε αφήσει μόνο την καλύτερα προσαρμοσμένη καμπύλη κανονικής κατανομής. Η απάντηση στην ερώτηση, «Ποια είναι η πιθανότητα ο επόμενος φοιτητής να έχει μήκος αντίχειρα μεγαλύτερο από 65.1 χιλιοστά;», αναπαρίσταται από την πράσινη σκιασμένη περιοχή κάτω από την καμπύλη. Εάν βρούμε το ποσοστό της συνολικής περιοχής που είναι σκιασμένο με πράσινο, μπορούμε να χρησιμοποιήσουμε αυτό το ποσοστό ως την εκτίμησή μας για την πιθανότητα η επόμενη παρατήρηση να είναι μεγαλύτερη από 65.1.
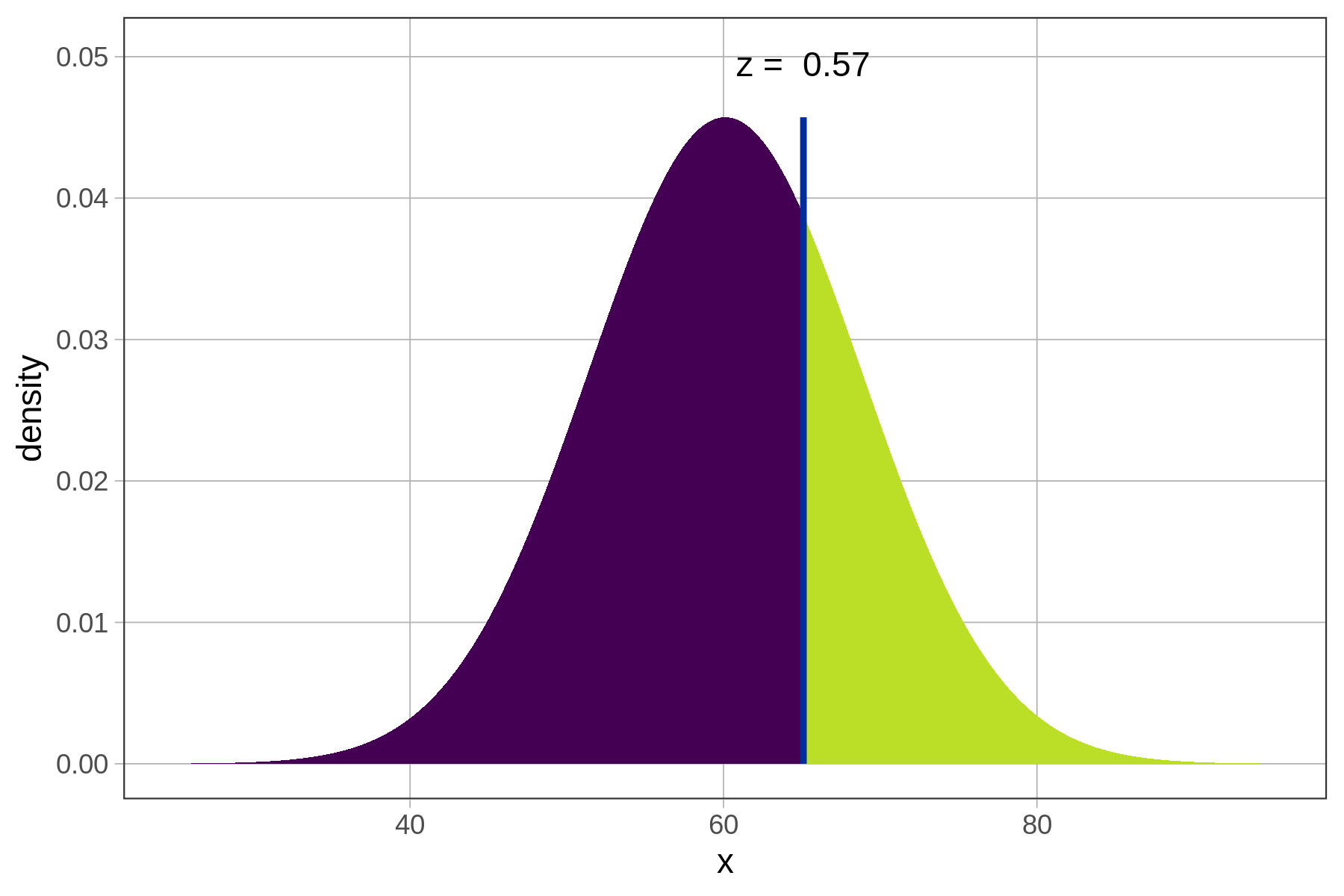
Ποια τιμή της Thumb αντιπροσωπεύεται από την μπλε, κάθετη γραμμή στο παραπάνω διάγραμμα;
Βάσει αυτού του διαγράμματος, εκτιμήστε με το μάτι το ποσοστό των αντιχείρων που μπορεί να είναι τουλάχιστον 65.1.
Ανάλυση του διαγράμματος:
Κανονική κατανομή (κωδωνοειδής καμπύλη)
άξονας x: Τιμές μήκους αντίχειρα (40 έως 80+)
Μπλε κάθετη γραμμή: Στο x ≈ 65.1
z = 0.57: Η τιμή z του μήκους αντίχειρα της Σοφίας
Μωβ περιοχή: Αριστερά της μπλε γραμμής (~70% της κατανομής)
Πράσινη περιοχή: Δεξιά της μπλε γραμμής (~30% της κατανομής)
Ερώτηση: Τι αντιπροσωπεύει η μπλε γραμμή;
Η μπλε γραμμή αντιπροσωπεύει την τιμή 65.1 χιλιοστά (μήκος αντίχειρα της Σοφίας)
Γιατί οι άλλες επιλογές είναι λάθος:
Β - Μέσος όρος - ΛΑΘΟΣ:
Ο μέσος όρος είναι στο κέντρο της καμπύλης
Το κέντρο φαίνεται να είναι γύρω στο 60
Η μπλε γραμμή βρίσκεται δεξιά του κέντρου
Γ - Ποσοστό μεγαλύτερων - ΛΑΘΟΣ:
Το ποσοστό είναι περιοχή (πράσινη), όχι γραμμή
Η γραμμή δείχνει τιμή, όχι ποσοστό
Δ - Ποσοστό μικρότερων - ΛΑΘΟΣ:
Το ποσοστό είναι η μωβ περιοχή
Η γραμμή είναι το όριο (65.1 mm)
Ερώτηση: Ποσοστό μηκών αντίχειρα ≥ 65.1
Η πράσινη περιοχή ≈ 30% της συνολικής καμπύλης
Διαγραμματική εκτίμηση:
Κοιτάζοντας το διάγραμμα:
Η πράσινη περιοχή (δεξιά της γραμμής) φαίνεται να είναι περίπου 1/3 της συνολικής καμπύλης
Η μωβ περιοχή (αριστερά) είναι περίπου 2/3
Άρα: ~30% του μήκους αντίχειρα ≥ 65.1
Γιατί οι άλλες επιλογές είναι λάθος:
Α - .10 (10%) - ΛΑΘΟΣ:
Η πράσινη περιοχή είναι πολύ μεγαλύτερη από 10%
10% θα ήταν μια πολύ μικρή ουρά
Θα αντιστοιχούσε σε z ≈ 1.28
Γ - .50 (50%) - ΛΑΘΟΣ:
50% θα σήμαινε ότι η γραμμή είναι στο κέντρο
Αλλά η γραμμή βρίσκεται δεξιά του κέντρου
Η πράσινη περιοχή είναι μικρότερη από τη μωβ
Δ - .75 (75%) - ΛΑΘΟΣ:
Αυτό θα ήταν το ποσοστό αριστερά της γραμμής
Όχι δεξιά (≥ 65.1)
P(X ≤ 65.1) ≈ 72%, όχι P(X ≥ 65.1)
Ε - .85 (85%) - ΛΑΘΟΣ:
Πολύ μεγάλο ποσοστό
Η πράσινη περιοχή είναι σαφώς μικρότερη από 85%
Συμπέρασμα:
Ερώτηση: Η μπλε κάθετη γραμμή αντιπροσωπεύει την τιμή 65.1mm (το μήκος του αντίχειρα της Σοφίας), που αντιστοιχεί σε z = 0.57 τυπικές αποκλίσεις πάνω από το μέσο όρο.
Ερώτηση: Βάσει του διαγράμματος, περίπου 30% (.30) των αντιχείρων είναι τουλάχιστον 65.1 mm. Αυτό φαίνεται από το μέγεθος της πράσινης περιοχής δεξιά της μπλε γραμμής, που αντιπροσωπεύει περίπου 1/3 της συνολικής καμπύλης.
Επειδή η κανονική κατανομή έχει εξομαλυμένο σχήμα που ορίζεται εύκολα από δύο παραμέτρους, μπορούμε να υπολογίσουμε την ακριβή πιθανότητα χρησιμοποιώντας τη μαθηματική συνάρτηση της κανονικής κατανομής. Φυσικά, δεν θα το κάνουμε με το χέρι. Υπάρχει μια συνάρτηση της R που ονομάζεται xpnorm() που μπορεί να το κάνει αυτό με μόλις τρεις πληροφορίες: το όριο που σας ενδιαφέρει, και το μέσο όρο και την τυπική απόκλιση της κανονικής κατανομής.
Σημειώστε ότι μπορείτε επίσης να συμπεριλάβετε στην xpnorm() τα ονόματα των παραμέτρων, mean = και sd =, κάτι που σας δίνει την ευελιξία να τις τοποθετήσετε σε διαφορετική σειρά, όπως π.χ.: xpnorm(65.1, sd = sd(Fingers$Thumb), mean = mean(Fingers$Thumb)).
Μπορείτε να εκτελέσετε τη συνάρτηση στο παρακάτω πλαίσιο κώδικα. Θα δημιουργήσει τόσο το παραπάνω διάγραμμα όσο και κάποια αποτελέσματα στα οποία μπορείτε να διαβάσετε την ακριβή πιθανότητα που ψάχνετε. Όπως θα διαπιστώσετε, η πιθανότητα αυτή είναι \(0.2835\) ή \(28.35%\). Μπορείτε να δοκιμάσετε διαφορετικές τιμές ορίου για να δείτε πώς αλλάζει το αποτέλεσμα (π.χ. δοκιμάστε τις τιμές \(60.11\), \(44\) και \(91\)).
Όταν μοντελοποιούμε το σφάλμα με την κανονική κατανομή, φέρνουμε στο μυαλό μας την εικόνα μιας εξομαλυμένης καμπύλης πάνω στα ακανόνιστα δεδομένα μας. Αν μας ενδιαφέρει η πιθανότητα ένας φοιτητής να έχει αντίχειρα μεγαλύτερο από 65.1mm, ποια περιοχή του παραπάνω διαγράμματος πρέπει να κοιτάξουμε;
Σύμφωνα με το μοντέλο της κανονικής κατανομής, ποια είναι η πιθανότητα ένας φοιτητής να έχει αντίχειρα μεγαλύτερο από 65.1;
Πιθανώς παρατηρήσατε ότι το όριο (η μαύρη γραμμή που αντιπροσωπεύει τα 65.1mm) δεν έχει ετικέτα 65.1. Αντίθετα, έχει ετικέτα z = 0.57. Τι σημαίνει αυτή η τιμή z;
Πρώτη ερώτηση: Η πράσινη περιοχή
Δεύτερη ερώτηση: .28
Τρίτη ερώτηση: Ο αριθμός των τυπικών αποκλίσεων μεταξύ του μέσου όρου και των 65.1mm
Πρώτη ερώτηση: Ποια περιοχή δείχνει την P(Thumb > 65.1);
Η πράσινη περιοχή (δεξιά της κάθετης γραμμής)
Εξήγηση:
Μωβ περιοχή: P(Thumb ≤ 65.1) - μικρότεροι από 65.1
Πράσινη περιοχή: P(Thumb > 65.1) - μεγαλύτεροι από 65.1 ✓
Το εμβαδόν της πράσινης περιοχής = πιθανότητα
Γιατί οι άλλες είναι λάθος:
Α - Μωβ - ΛΑΘΟΣ: Δείχνει P(Thumb ≤ 65.1), όχι >
Β - Όριο - ΛΑΘΟΣ: Η γραμμή δείχνει την τιμή 65.1, όχι πιθανότητα
Γ - άξονας x - ΛΑΘΟΣ: Δείχνει τιμές του μήκους αντίχειρα, όχι πιθανότητες
Δ - άξονας y - ΛΑΘΟΣ: Δείχνει πυκνότητα πιθανότητας, όχι αθροιστική πιθανότητα
Δεύτερη ερώτηση: Ποια είναι η πιθανότητα;
P(Thumb > 65.1) = .28 (28%)
Δίνεται παραπάνω από την xpnorm(). Ένας εναλλακτικός τρόπος υπολογισμού:
# Δεδομένα
thumb <- 65.1
mean_thumb <- 60.1
sd_thumb <- 8.73
# Τιμή z
z <- (thumb - mean_thumb) / sd_thumb
# z = 0.573
# P(Z > 0.57) = 1 - P(Z ≤ 0.57)
p_greater <- 1 - pnorm(z)
# 0.284 ≈ 0.28Τρίτη ερώτηση: Τι σημαίνει z = 0.57;
Ο αριθμός των τυπικών αποκλίσεων μεταξύ μέσου όρου και 65.1 mm
Εξήγηση:
z = (X - μ) / σ
z = (65.1 - 60.1) / 8.73
z = 5.0 / 8.73
z = 0.57
# Ερμηνεία:
# "Το 65.1 βρίσκεται 0.57 τυπικές αποκλίσεις
# πάνω από το μέσο όρο (60.1)"Διαγραμματικά:
|←─── 0.57 SD ────→|
| |
────────●───────────────────●────────
60.1 65.1
(μέσος) (Σοφία)
Απόσταση = 5.0 mm
SD = 8.73 mm
z = 5.0/8.73 = 0.57 SDΓιατί οι άλλες είναι λάθος:
Α - Πιθανότητα ακριβώς 65.1 - ΛΑΘΟΣ:
Για μια συνεχή κατανομή, P(X = ακριβώς 65.1) = 0
Η τιμή z δεν είναι πιθανότητα
Β - Πιθανότητα ≥ 65.1 - ΛΑΘΟΣ:
Η πιθανότητα είναι 0.28, όχι 0.57
Η τιμή z και η πιθανότητα διαφέρουν
Συμπέρασμα:
Πρώτη ερώτηση: Κοιτάμε την πράσινη περιοχή (δεξιά της κάθετης γραμμής), που αντιπροσωπεύει το εμβαδόν για τιμές > 65.1.
Δεύτερη ερώτηση: Η πιθανότητα είναι 0.28 (28%), υπολογισμένη ως 1 - pnorm(0.57).
Τρίτη ερώτηση: Τιμή z = 0.57 σημαίνει ότι το 65.1mm είναι 0.57 τυπικές αποκλίσεις πάνω από το μέσο όρο. Η τιμή z είναι μέτρο σχετικής θέσης, όχι πιθανότητα.
7.10 Εξοικείωση με την Κανονική Κατανομή
Μέχρι στιγμής, έχουμε παρουσιάσει γιατί οι κανονικές κατανομές είναι συχνά καλά μοντέλα για το σφάλμα (η δύναμη του Κεντρικού Οριακού Θεωρήματος!) και πώς μπορείτε να τις χρησιμοποιήσετε για να κάνετε προβλέψεις. Αλλά γιατί κατανομές που φαίνονται πολύ διαφορετικές μεταξύ τους ονομάζονται όλες «κανονικές»; Το σχήμα της κανονικής κατανομής μοιάζει διαισθητικά με «καμπάνα», αλλά ας εξετάσουμε τι σημαίνει αυτό.
Για να γίνουμε πιο συγκεκριμένοι, ας επιστρέψουμε στο Kargle, το αγαπημένο μας βιντεοπαιχνίδι.
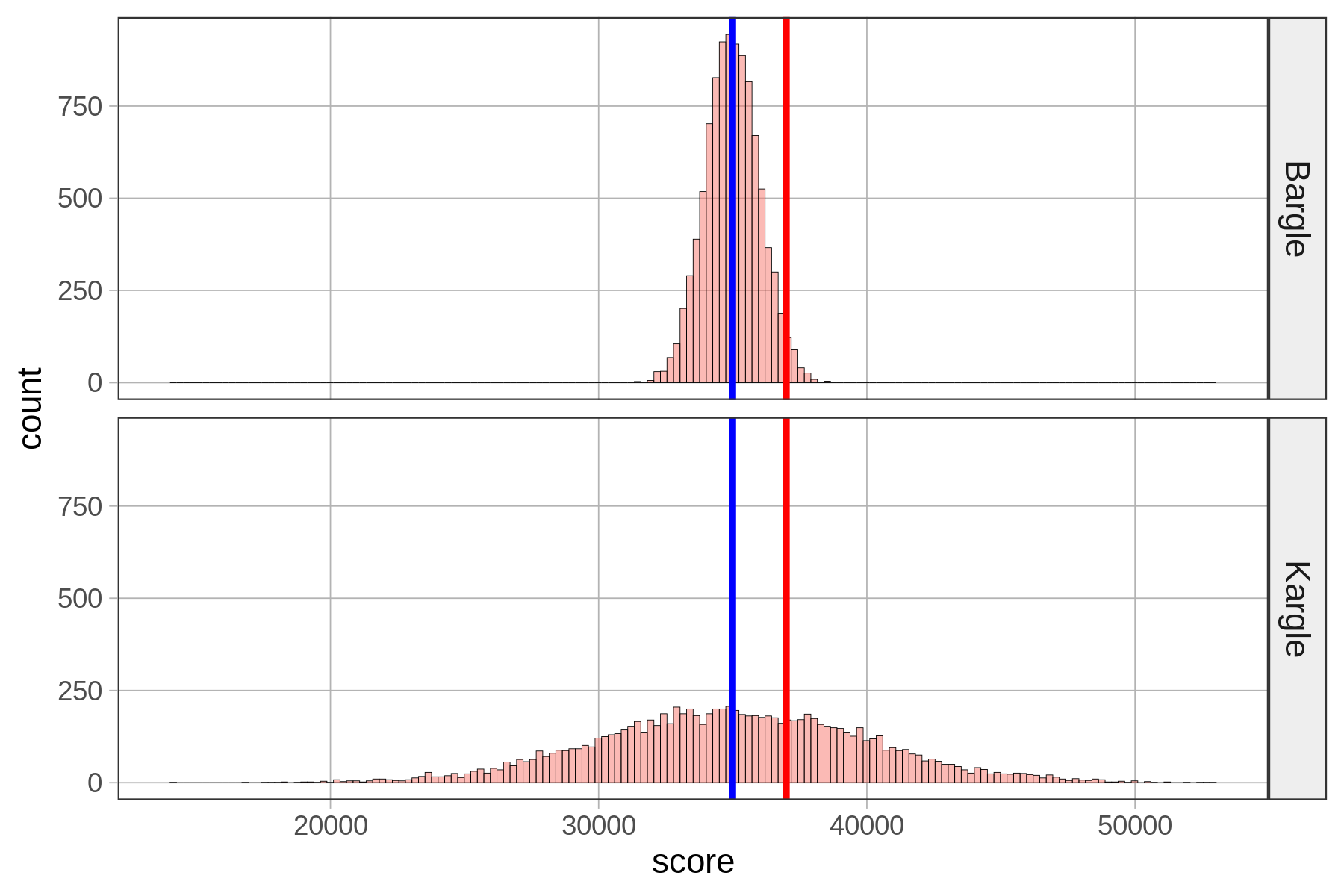
Θυμηθείτε ότι είχαμε ένα φίλο που σκόραρε 37.000 πόντους στο Kargle (υποδεικνύεται με κόκκινη γραμμή στο παραπάνω διάγραμμα) και προσπαθούσαμε να αξιολογήσουμε πόσο ικανός παίκτης ήταν. Όταν διαπιστώσαμε ότι η πραγματική κατανομή της βαθμολογίας του Kargle ήταν αυτή του ιστογράμματος που βρίσκεται στο κάτω μέρος (όπου η τυπική απόκλιση είναι περίπου 5.000), εντυπωσιαστήκαμε λιγότερο από ό,τι όταν νομίζαμε ότι ήταν αυτή που βρίσκεται στο επάνω μέρος. Όπως τελικά αποδείχθηκε, η κατανομή που βρίσκεται στο επάνω μέρος (με τυπική απόκλιση περίπου 1.000) προέρχεται από ένα άλλο παιχνίδι που ονομάζεται Bargle.
Αυτές οι δύο κατανομές μοιάζει να είναι αρκετά διαφορετικές μεταξύ τους. Αλλά και οι δύο θα μπορούσαν να χαρακτηριστούν ως περίπου κανονικές. Τι είναι αυτό που μας οδηγεί να τις χαρακτηρίσουμε έτσι;
Οι κανονικές κατανομές έχουν κατά προσέγγιση «σχήμα καμπάνας», καθώς υπάρχουν πολύ περισσότερες τιμές στο κέντρο παρά στις ουρές. Είναι επίσης συμμετρικές ως προς το κέντρο τους. Αλλά απ’ ό,τι φαίνεται οι κανονικές κατανομές έχουν ακόμη περισσότερα κανονικά και ποσοτικοποιήσιμα χαρακτηριστικά από την παραπάνω περιγραφή.
Για να δείξουμε την κανονικότητα αυτού του σχήματος, ας σκεφτούμε τους παίκτες και των δύο παιχνιδιών, Kargle και Bargle, που βρίσκονται εντός ±1 τυπικής απόκλισης από το μέσο όρο. Ας ονομάσουμε προς το παρόν αυτή την περιοχή της κατανομής «Ζώνη 1». Αυτοί είναι οι παίκτες με τα λιγότερο ακραία σκορ.
Αν ο μέσος όρος της βαθμολογίας στο Bargle είναι 35.000 και η τυπική απόκλιση είναι 1.000, ποιο είναι το εύρος της βαθμολογίας στη Ζώνη 1 της κανονικής κατανομής; Υπόδειξη: ίσως σας βοηθήσει να σχεδιάσετε το σχήμα μιας κανονικής κατανομής και να γραμμοσκιάσετε την περιοχή που ψάχνετε.
Αν ο μέσος όρος της βαθμολογίας στο Kargle είναι 35.000 και η τυπική απόκλιση είναι 5.000, ποιο είναι το εύρος της βαθμολογίας στη Ζώνη 1 της κανονικής κατανομής;
Διαίρεση της Κατανομής σε Ζώνες με Βάση την Τυπική Απόκλιση
Δημιουργήσαμε μια νέα μεταβλητή που ονομάζεται zone, η οποία απλώς υποδεικνύει αν το σκορ κάθε ατόμου βρίσκεται εντός της Ζώνης 1 (με τιμή «1») ή εκτός αυτής (με τιμή «outside»).
Για να το κάνουμε αυτό, πρώτα μετατρέψαμε το αρχικό σκορ κάθε ατόμου σε τιμή z (που, όπως ίσως θυμάστε, υποδεικνύει πόσες τυπικές αποκλίσεις απέχει ένα αρχικό σκορ από τη μέση τιμή). Στη συνέχεια, στη μεταβλητή zone θέσαμε την τιμή «1» για κάθε παίκτη του οποίου η τιμή z ήταν ανάμεσα στο \(-1\) και το \(1\). (Μην ανησυχείτε για το πώς γίνεται αυτό στην R· μπορείτε να το μάθετε αργότερα αν θέλετε.)
Στα παρακάτω ιστογράμματα, έχουμε χρωματίσει τη Ζώνη 1 με κόκκινο και οτιδήποτε εκτός της Ζώνης 1 με μωβ.
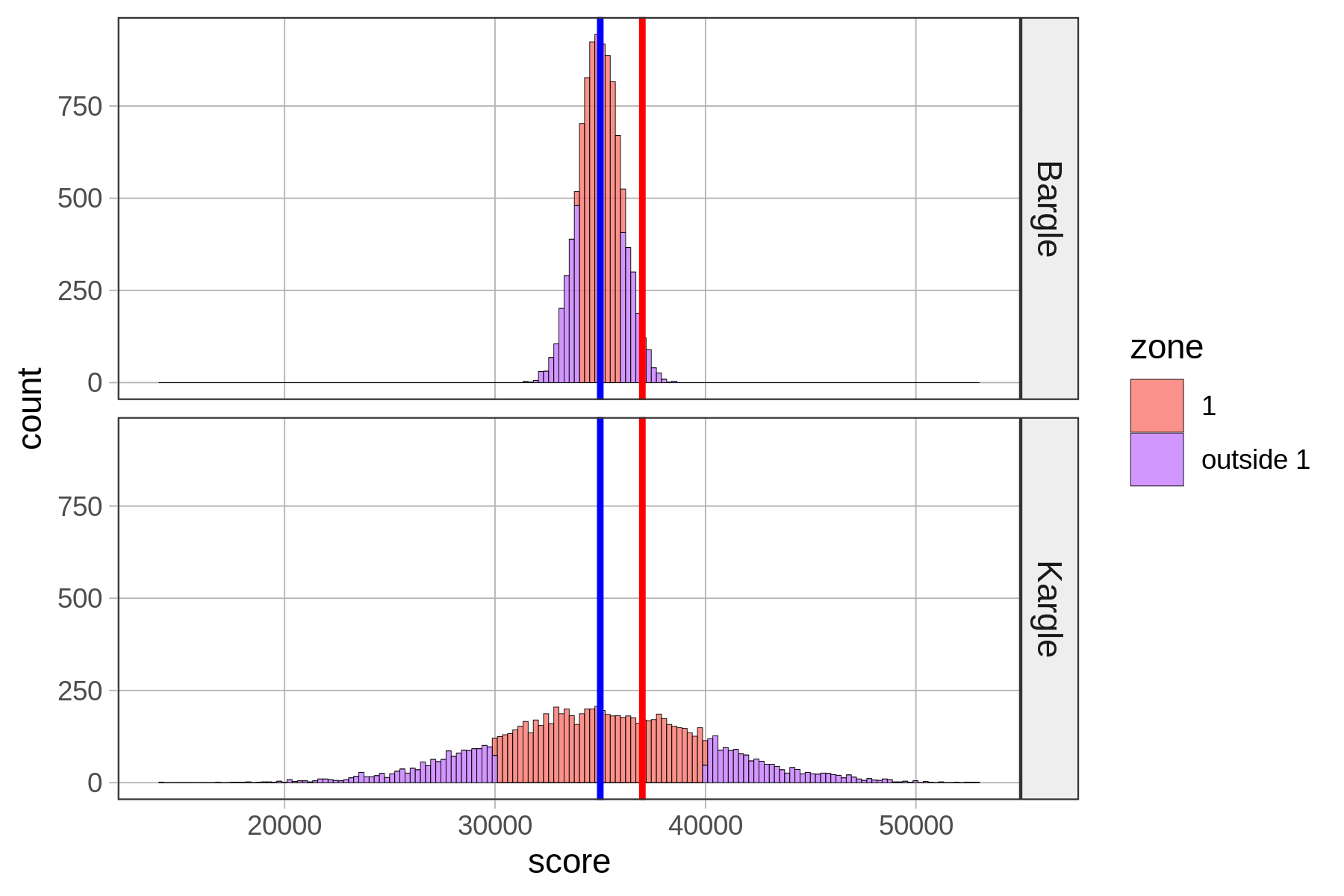
Παρατηρήστε ότι ο φίλος μας που πέτυχε 37.000 πόντους βρίσκεται εντός της Ζώνης 1 για το Kargle, αλλά αν αυτό ήταν το σκορ του στο Bargle, θα βρισκόταν εκτός της Ζώνης 1. Αφήνοντας το φίλο μας για λίγο, ποιο είναι το ποσοστό των παικτών που βρίσκονται εντός της Ζώνης 1 στο Bargle και το Kargle, αντίστοιχα; Ας κάνουμε μια καταμέτρηση των τιμών της zone για να το μάθουμε.
prop.table(table(VideoGame$zone, VideoGame$game))
game
zone Bargle Kargle
1 0.6844 0.6822
outside 1 0.3156 0.3178Το ποσοστό των τιμών που βρίσκεται εντός της Ζώνης 1, δηλαδή εντός μίας τυπικής απόκλισης από το μέσο όρο της κατανομής, είναι παρόμοιο για τα δύο παιχνίδια (περίπου 0.68 ή 68%)! Είναι ενδιαφέρον ότι περισσότερο από το ήμισυ της κατανομής βρίσκεται εντός μίας τυπικής απόκλισης από το μέσο όρο.
Ποιο είναι το εύρος των τιμών z για τις παρατηρήσεις που βρίσκονται στη Ζώνη 1;
Αν βρισκόμαστε μία τυπική απόκλιση προς τα θετικά, η τιμή z θα είναι 1. Αν βρισκόμαστε μία τυπική απόκλιση προς τα αρνητικά, η τιμή z θα είναι -1. Έτσι, η Ζώνη 1 (±1 τυπική απόκλιση), θα περιλαμβάνει όλες τις παρατηρήσεις για τις οποίες οι αντίστοιχες τιμές z βρίσκονται μεταξύ του -1 και του 1.
Τώρα ας εξετάσουμε τους παίκτες και των δύο παιχνιδιών, Kargle και Bargle, που βρίσκονται ±2 τυπικές αποκλίσεις από το μέσο όρο. Θα ονομάσουμε αυτή την περιοχή Ζώνη 2.
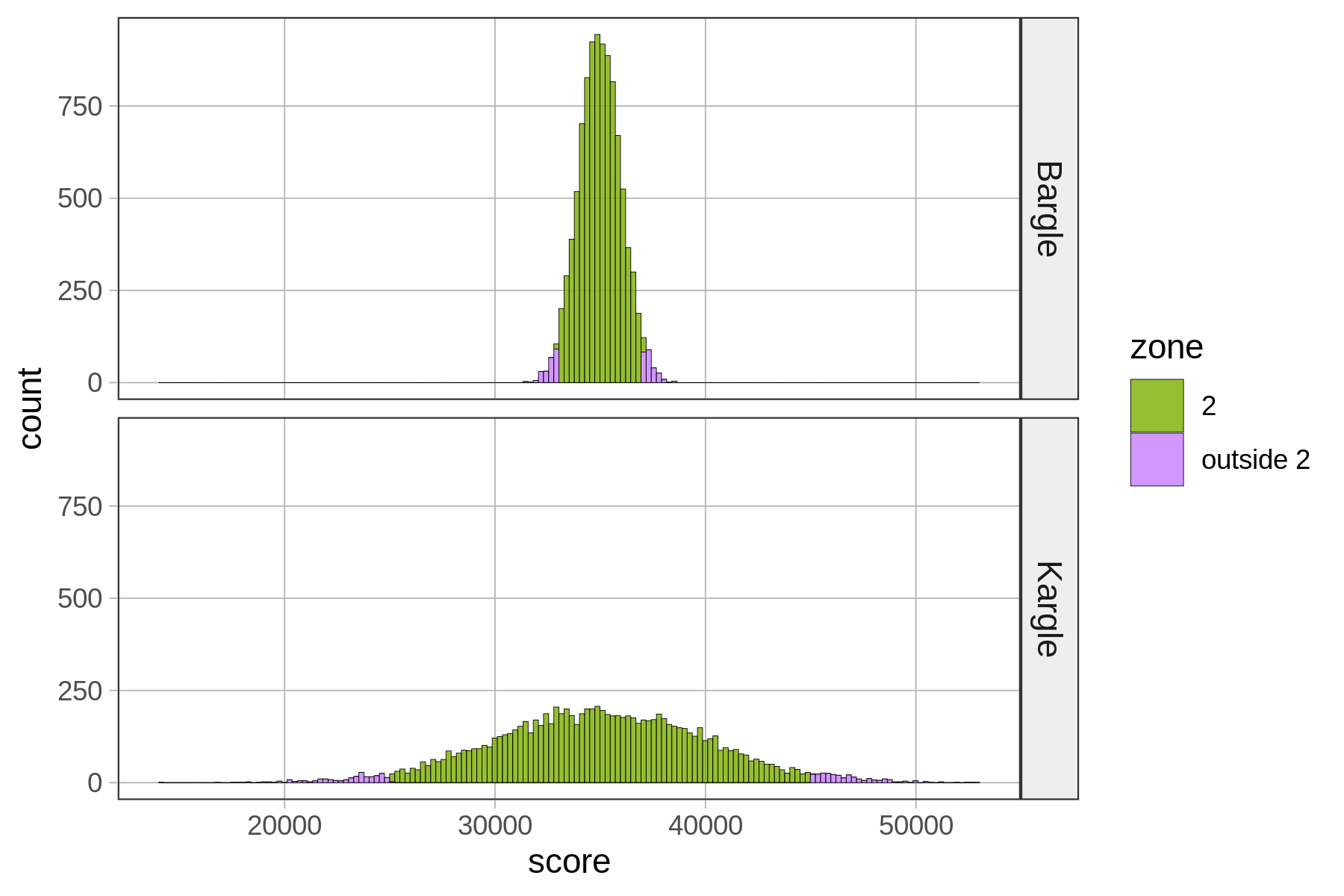
Παρατηρήστε ότι η Ζώνη 2 αποτελεί το μεγαλύτερο μέρος των κατανομών των Bargle και Kargle. Ποιο πιστεύετε ότι μπορεί να είναι το ποσοστό των σκορ στη Ζώνη 2;
game
zone Bargle Kargle
2 0.9518 0.9487
outside 2 0.0482 0.0513 Βασικά, το 0.95 (ή 95%) των σκορ βρίσκονται εντός δύο τυπικών αποκλίσεων από το μέσο όρο. Σε μια κανονική κατανομή, τα σκορ είναι τόσο συγκεντρωμένα στο κέντρο που αν μετακινηθείτε μόλις δύο τυπικές αποκλίσεις από το κέντρο, έχετε καλύψει σχεδόν ολόκληρη την κατανομή σας!
Τι νομίζω ότι μπορεί να συμβαίνει στις ±3 τυπικές αποκλίσεις μακριά από το μέσο όρο;
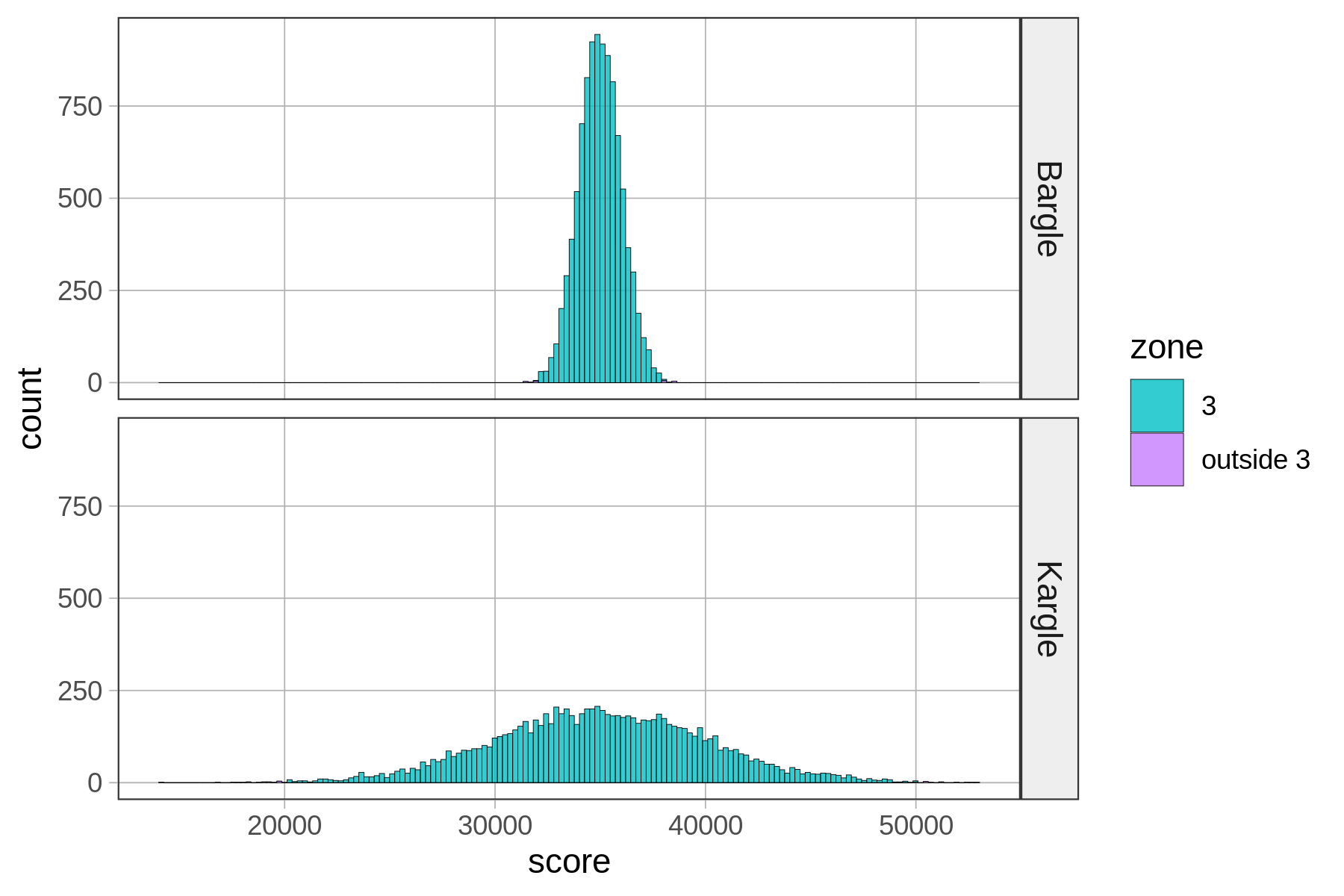
zone Bargle Kargle
1 1 0.6844 0.6822
2 2 0.9518 0.9487
3 3 0.9982 0.9972
4 outside 3 0.0018 0.0028Η Ζώνη 3, που βρίσκεται εντός τριών τυπικών αποκλίσεων από το μέσο όρο, φαίνεται να καλύπτει σχεδόν ολόκληρη την κατανομή. Αν παρατηρήσετε τα αποτελέσματα της καταμέτρησης (ή κοιτάξετε πολύ, πολύ προσεκτικά τα ιστογράμματα), μπορείτε να δείτε ότι υπάρχει ένα μικροσκοπικό ποσοστό τιμών εκτός της Ζώνης 3.
7.11 Ο Εμπειρικός Κανόνας
Το εντυπωσιακό με τις κανονικές κατανομές είναι ότι όλες ακολουθούν, κατά βάση, το ίδιο μοτίβο. Στην εξομαλυμένη, «τέλεια» εκδοχή της κανονικής κατανομής (δηλαδή, στη θεωρητική κατανομή πιθανότητας), η Ζώνη 1 καλύπτει περίπου το 68%, η Ζώνη 2 καλύπτει το 95% και η Ζώνη 3 καλύπτει το 99.7%. Αυτό το μοτίβο 68-95-99.7 ονομάζεται εμπειρικός κανόνας.
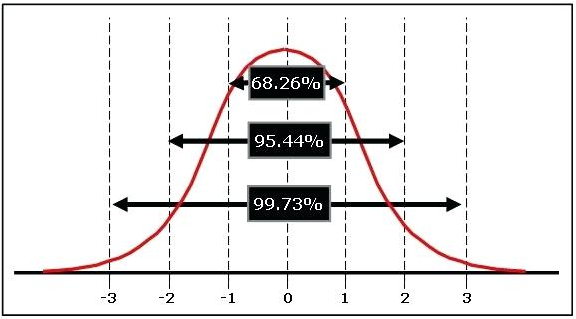
Σύμφωνα με τον εμπειρικό κανόνα 68-95-99.7:
- Περίπου το 68% των τιμών σε μια κανονική κατανομή βρίσκονται εντός μίας τυπικής απόκλισης, συν ή πλην, από το μέσο όρο.
- Περίπου το 95% των τιμών βρίσκονται εντός δύο τυπικών αποκλίσεων.
- Περίπου το 99.7% των τιμών βρίσκονται εντός τριών τυπικών αποκλίσεων από το μέσο όρο (με άλλα λόγια, σχεδόν όλες).
Η εξομαλυμένη μορφή της κανονικής κατανομής είναι κάτι τόσο «τέλειο» που, στην πραγματικότητα, δεν υπάρχει. Είναι ένα μαθηματικό αντικείμενο, παρόμοιο με την ευθεία γραμμή. Όπως ακριβώς μια ευθεία είναι ένα θεωρητικό αντικείμενο, χωρίς προεξοχές που εκτείνεται στο άπειρο, έτσι και η κανονική κατανομή είναι μια θεωρητική κατασκευή με:
- Τέλεια συμμετρία γύρω από το μέσο όρο
- Άπειρη έκταση (οι ουρές της ποτέ δεν αγγίζουν το μηδέν)
- Απόλυτη ομαλότητα χωρίς διακυμάνσεις ή ανωμαλίες
Στην πραγματικότητα, οι κατανομές που παρατηρούμε είναι προσεγγίσεις της κανονικής - χρήσιμες επειδή πολλά φαινόμενα τείνουν προς αυτό το σχήμα, αλλά ποτέ δεν το επιτυγχάνουν πλήρως.
Οι ουρές της κανονικής κατανομής δεν αγγίζουν ποτέ ακριβώς στο 0, αλλά συνεχίζουν επ’ άπειρον. Αυτός είναι ο λόγος που η κανονική κατανομή ονομάζεται μερικές φορές ασυμπτωτική. Αυτή η ιδιότητα είναι σημαντική, επειδή μας επιτρέπει να προβλέψουμε τις πολύ μικρές πιθανότητες πολύ σπάνιων γεγονότων, όπως το να έχει κάποιος αντίχειρα μήκους 1.000 χιλιοστών.
Πιθανότατα δεν έχετε ακούσει ποτέ για έναν τόσο μακρύ αντίχειρα. Ωστόσο, αν υποθέσουμε την κανονική κατανομή πιθανοτήτων, μπορούμε να ποσοτικοποιήσουμε ακριβώς πόσο χαμηλή θα ήταν η πιθανότητα να συναντήσουμε ένα τόσο σπάνιο γεγονός.
Μπορείτε να δοκιμάσετε να δημιουργήσετε μια δική σας τυπική απόκλιση για ένα φανταστικό παιχνίδι (ας το ονομάσουμε Zargle) και να εκτελέσετε τον κώδικα. Θα σας δείξει τα ιστογράμματα και τις αναλογίες για τις τρεις ζώνες. Δοκιμάστε διαφορετικές τυπικές αποκλίσεις για να δείτε αν μπορείτε να «σπάσετε» τον εμπειρικό κανόνα.
Αυτό είναι το αποτέλεσμα που θα παίρναμε για την κατανομή του Zargle αν η τυπική απόκλιση ήταν 3.500.
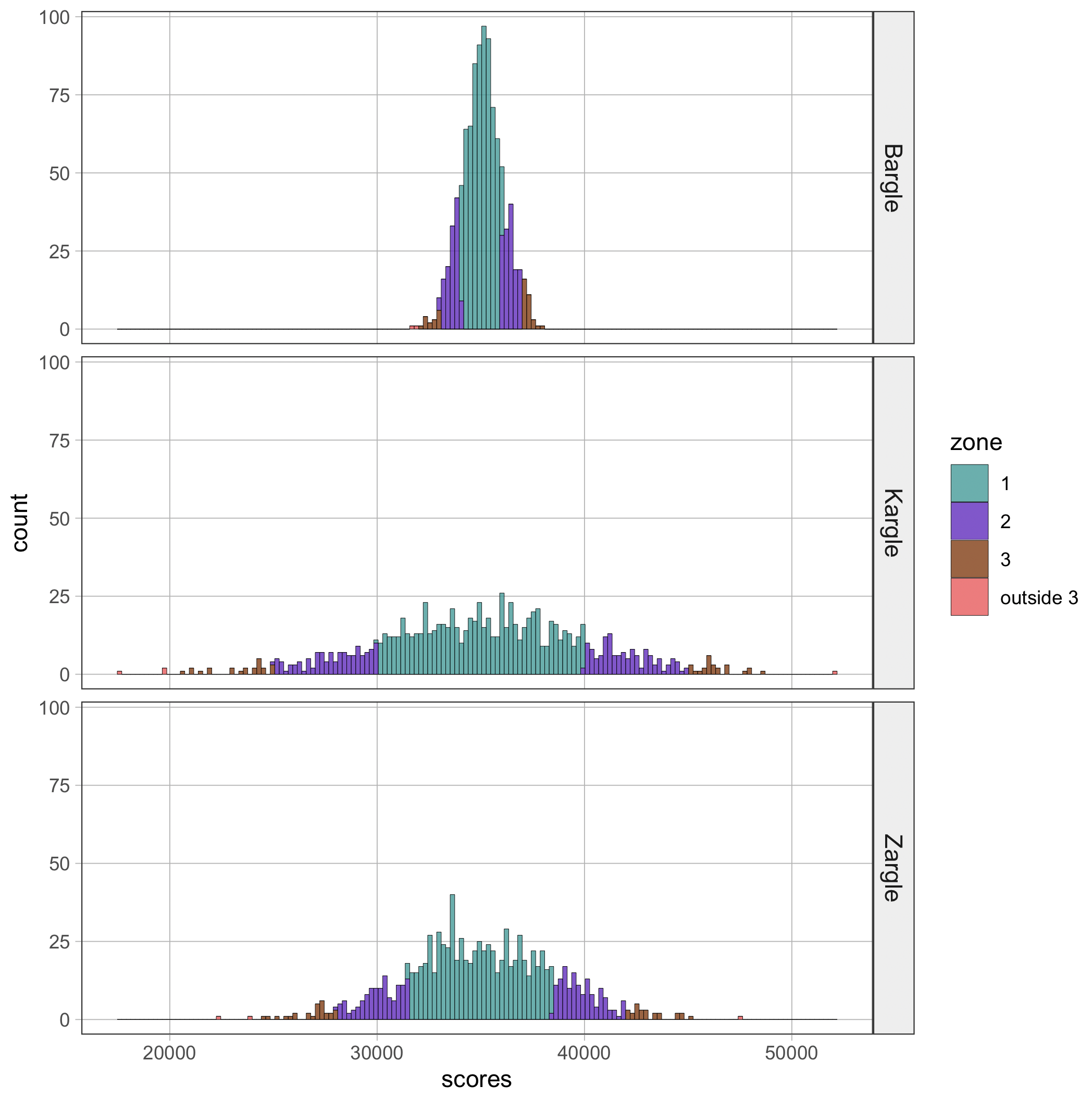
zone Bargle Kargle Zargle
1 0.678 0.665 0.697
2 0.953 0.957 0.952
3 0.999 0.996 0.998
outside 3 0.001 0.004 0.002Ο εμπειρικός κανόνας μπορεί να είναι πολύ χρήσιμος όταν προσπαθούμε να ερμηνεύσουμε γρήγορα μία συγκεκριμένη τιμή. Αν μια μητέρα πει ότι το μωρό της γεννήθηκε με μήκος 54 εκατοστά, πώς θα ερμηνεύατε αυτή τη μέτρηση; Ως έμπειροι αναλυτές δεδομένων, θα πρέπει να ρωτήσετε: ποιος είναι ο μέσος όρος και ποια είναι η τυπική απόκλιση της κατανομής του μήκους των μωρών κατά τη γέννηση;
Ας υποθέσουμε ότι το μέσο μήκος των μωρών είναι περίπου 50 εκατοστά, και η τυπική απόκλιση είναι 2 εκατοστά. Χρησιμοποιώντας τον εμπειρικό κανόνα, θα λέγατε: «Ουάου! Το μωρό σου βρίσκεται δύο τυπικές αποκλίσεις πάνω από το μέσο όρο! Είναι τεράστιο μωρό! Μόνο το 5% των μωρών είναι μεγαλύτερα από 54 εκατοστά (ο μέσος όρος συν δύο τυπικές αποκλίσεις).»
Στην πραγματικότητα, θα κάνατε ένα μικρό λάθος. (Συγγνώμη, ξέρουμε ότι σας βάλαμε σε αυτή τη θέση!) Σύμφωνα με τον εμπειρικό κανόνα, το 95% των τιμών σε μια κανονική κατανομή βρίσκονται εντός ±2 τυπικών αποκλίσεων από το μέσο όρο. Από αυτό προκύπτει ότι το 5% των τιμών είναι πιο ακραίες, δηλαδή εκτός των ±2 τυπικών αποκλίσεων.
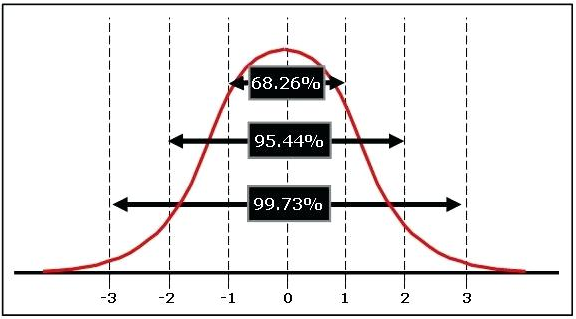
Αλλά παρατηρήστε, στην εικόνα, ότι αν το 0.05 (ή 5%) των τιμών βρίσκεται εκτός των ±2 τυπικών αποκλίσεων, το μισό από αυτό (δηλαδή το 2.5%) αναμένεται να βρίσκεται πάνω από δύο τυπικές αποκλίσεις από το μέσο όρο, και το άλλο μισό κάτω από δύο τυπικές αποκλίσεις από το μέσο όρο.
Άρα, μόνο το 0.025 (ή 2.5%) των τιμών θα είναι μεγαλύτερες από δύο τυπικές αποκλίσεις πάνω από το μέσο όρο. Αυτό το μωρό είναι ακόμα πιο εντυπωσιακό από ό,τι νομίζαμε! Είναι μεγαλύτερο από το 97.5% όλων των μωρών!
Τι Θεωρείται Απίθανο;
Έχουμε δει με ποιον τρόπο η μοντελοποίηση της κατανομής του σφάλματος (στην περίπτωση του κενού μοντέλου η κατανομή των τιμών γύρω από το μέσο όρο) μπορεί να μας βοηθήσει να υπολογίσουμε πιθανότητες και να κάνουμε προβλέψεις. Το πρόβλημα με την πιθανότητα, ωστόσο, είναι ότι είναι απλώς ένας αριθμός. Δεν μας δείχνει τι να κάνουμε μετά. Χρειάζεται να συνεχίσουμε να σκεφτόμαστε για το υπό μελέτη φαινόμενο, ακόμα και μετά από όλους τους περίπλοκους υπολογισμούς μας με την R.
Για παράδειγμα, αν επιθυμούσα να χρησιμοποιήσουμε το μοντέλο για τα μήκη των δαχτύλων για να σχεδιάσουμε ελαστικά γάντια ενιαίου μεγέθους, πόσο μεγάλα θα έπρεπε να τα κάνουμε; Εξάλλου, παρόλο που οι πολύ μακριοί αντίχειρες είναι απίθανοι, παραμένουν πιθανοί. Αλλά αν κάνουμε αυτά τα γάντια πολύ μεγάλα, τότε θα αποκλείσουμε τα άτομα με κοντά δάχτυλα.
Ποιο θα ήταν το σωστό μέγεθος γαντιών; Για να απαντήσουμε σε τέτοιες ερωτήσεις, πρέπει να προσδιορίσουμε ποια είναι τα πιο πιθανά μήκη των δαχτύλων των ανθρώπων, και αυτό σημαίνει ότι πρέπει να προσδιορίσουμε τι σημαίνει «πιθανό» και τι «απίθανο». Μπορεί να συμφωνήσουμε για τον καλύτερο τρόπο εκτίμησης μιας πιθανότητας, αλλά οι απόψεις θα διαφέρουν ως προς το τι θεωρείται «απίθανο».
Για παράδειγμα, κάποιος που είναι πολύ τολμηρός μπορεί να κοιτάξει μια πιθανότητα ίση με 0.01 (ή 1%) και να ισχυριστεί: «Ε, τουλάχιστον κι αυτό είναι κάπως πιθανό!» Αλλά κάποιος που προτιμά να είναι πολύ σίγουρος μπορεί να πει: «Ακόμα και το 0.40 είναι απίθανο, γιατί είναι λιγότερο πιθανό από το να φέρεις κορώνα ή γράμματα!» Έτσι, ως μέρος μιας στατιστικής κοινότητας, είναι χρήσιμο να υπάρχει συμφωνία για το τι θεωρείται απίθανο.
Οι στατιστικολόγοι, ως κοινότητα, έχουν αποφασίσει ότι τιμές πιθανότητας ίσες με 0,05 ή μικρότερες θεωρούνται απίθανες. Έτσι, στην περίπτωση μιας Διαδικασίας Παραγωγής Δεδομένων (ΔΠΔ) που παράγει μια αρκετά κανονική κατανομή πληθυσμού, θα θεωρούσαμε τις τιμές που βρίσκονται εκτός της Ζώνης 2 (±2 τυπικές αποκλίσεις από το μέσο όρο) ως απίθανες, και τις τιμές εντός της Ζώνης 2 ως πιθανές. Σημειώστε ότι αυτή η απόφαση δεν προκύπτει από κάποιον υπολογισμό. Οι στατιστικολόγοι απλώς συμφωνούν ότι το 0.05 είναι αρκετά μικρή πιθανότητα.
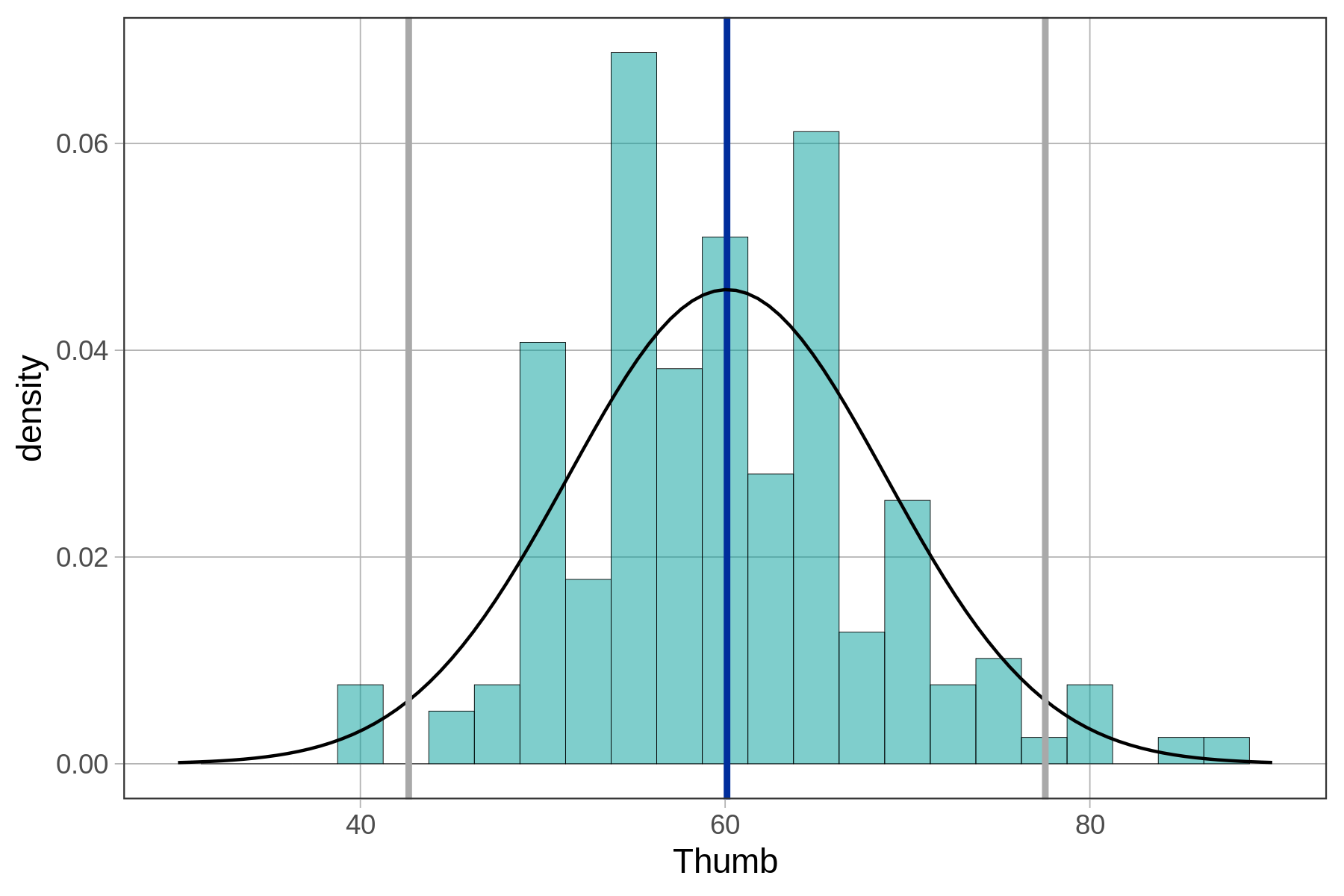
Επιλέξτε όλα τα απίθανα μήκη αντιχείρων (±2 τυπικές αποκλίσεις μακριά από το μέσο όρο). (Υπάρχουν περισσότερες από μία σωστές απαντήσεις.)
Σωστές απαντήσεις: 38mm, 82mm, 90mm
Ζώνη 2 (εντός ±2 τυπικές αποκλίσεις): Περίπου 40-80mm
Απίθανα (εκτός Ζώνης 2):
38mm: < 40mm (εκτός αριστερά)
82mm: > 80mm (εκτός δεξιά)
90mm: > 80mm (πολύ εκτός δεξιά)
Πιθανά (εντός Ζώνης 2): 48, 53, 64, 71, 75, 80 mm
Τιμές εκτός ±2 τυπικές αποκλίσεις αντιπροσωπεύουν το 5% των παρατηρήσεων και θεωρούνται στατιστικά ασυνήθιστες.
Αυτή η «απίθανη» περιοχή είναι το 0.05 (ή 5%) που απέχει περισσότερο από το μέσο όρο (τόσο προς τα αριστερά όσο και προς τα δεξιά).
Με βάση το παραπάνω διαγράμμα κανονικής κατανομής, ποια από τις παρακάτω αναλογίες αντιστοιχούν στις μπλε σκιασμένες περιοχές (ουρές);
Ποια από τις παρακάτω αναλογίες αντιστοιχεί στη συνολική περιοχή των δύο ουρών μαζί;
Ποια από τις παρακάτω αναλογίες αντιστοιχεί στην κεντρική περιοχή (μεταξύ των δύο ουρών);
Ερώτηση: 0.025 (για κάθε ουρά)
Ερώτηση: 0.05
Ερώτηση: 0.95
Ανάλυση του διαγράμματος:
Δομή κανονικής κατανομής:
Κεντρική περιοχή: Περιοχή με λευκό χρώμα μεταξύ των ουρών
Αριστερή ουρά: Μπλε σκιασμένη περιοχή αριστερά
Δεξιά ουρά: Μπλε σκιασμένη περιοχή δεξιά
Τυπικά ποσοστά για α = 0.05:
Κάθε ουρά (μπλε περιοχές):
α/2 = 0.05/2 = 0.025 = 2.5% για κάθε ουρά
Συνολικά οι δύο ουρές: 2 × 2.5% = 5%
Κεντρική περιοχή (λευκή):
- 1 - α = 1 - 0.05 = 0.95 = 95%
Στατιστική σημασία:
Το α = 0.05 είναι το τυπικό επίπεδο σημαντικότητας:
95% των δεδομένων στην κεντρική περιοχή (“αποδεκτό”)
5% στις ουρές (“απίθανο” ή “σημαντικό”)
2.5% σε κάθε ουρά
Συμπέρασμα:
Το διάγραμμα δείχνει την τυπική α = 0.05 κανονική κατανομή όπου:
Κάθε μπλε ουρά: 2.5% (0.025)
Συνολικές ουρές: 5% (0.05)
Κεντρική λευκή περιοχή: 95% (0.95)
7.12 Ερωτήσεις Επανάληψης Κεφαλαίου 7
Θα αναφερόμαστε σε ένα πλαίσιο δεδομένων που ονομάζεται mpg. Περιέχει ένα υποσύνολο από τα δεδομένα κατανάλωσης καυσίμου αυτοκινήτων που διατίθενται από την EPA (Environmetal Protection Agency) στο fueleconomy.gov. Περιλαμβάνει μόνο τα νέα μοντέλα αυτοκινήτων που κυκλοφόρησαν κάθε χρονιά από το 1999 έως το 2008. Παρακάτω παρουσιάζεται ένα τμήμα των δεδομένων, μαζί με τους ορισμούς των μεταβλητών που περιέχει.
manufacturer model displ year cyl trans drv cty hwy fl class
1 audi a4 1.80 1999 4 auto(l5) f 18 29 p comp~
2 audi a4 1.80 1999 4 manual(m5) f 21 29 p comp~
3 audi a4 2.00 2008 4 manual(m6) f 20 31 p comp~
4 audi a4 2.00 2008 4 auto(av) f 21 30 p comp~
5 audi a4 2.80 1999 6 auto(l5) f 16 26 p comp~
6 audi a4 2.80 1999 6 manual(m5) f 18 26 p comp~
Ορισμοί μεταβλητών:
`manufacturer`: Κατασκευαστής / μάρκα
`model`: Όνομα μοντέλου αυτοκινήτου
`displ`: Κυβισμός κινητήρα, σε λίτρα
`year`: Έτος κατασκευής
`cyl`: Αριθμός κυλίνδρων
`trans`: Τύπος κιβωτίου ταχυτήτων
`drv`: f = κίνηση στους εμπρός τροχούς, r = κίνηση στους πίσω τροχούς, 4 = τετρακίνηση
`cty`: Μίλια ανά γαλόνι στην πόλη
`hwy`: Μίλια ανά γαλόνι στον αυτοκινητόδρομο
`fl`: Τύπος καυσίμου. e = αιθανόλη, d = ντίζελ, r = απλή βενζίνη, p = σούπερ βενζίνη, c = φυσικό αέριο
`class`: Ο «τύπος» του αυτοκινήτου 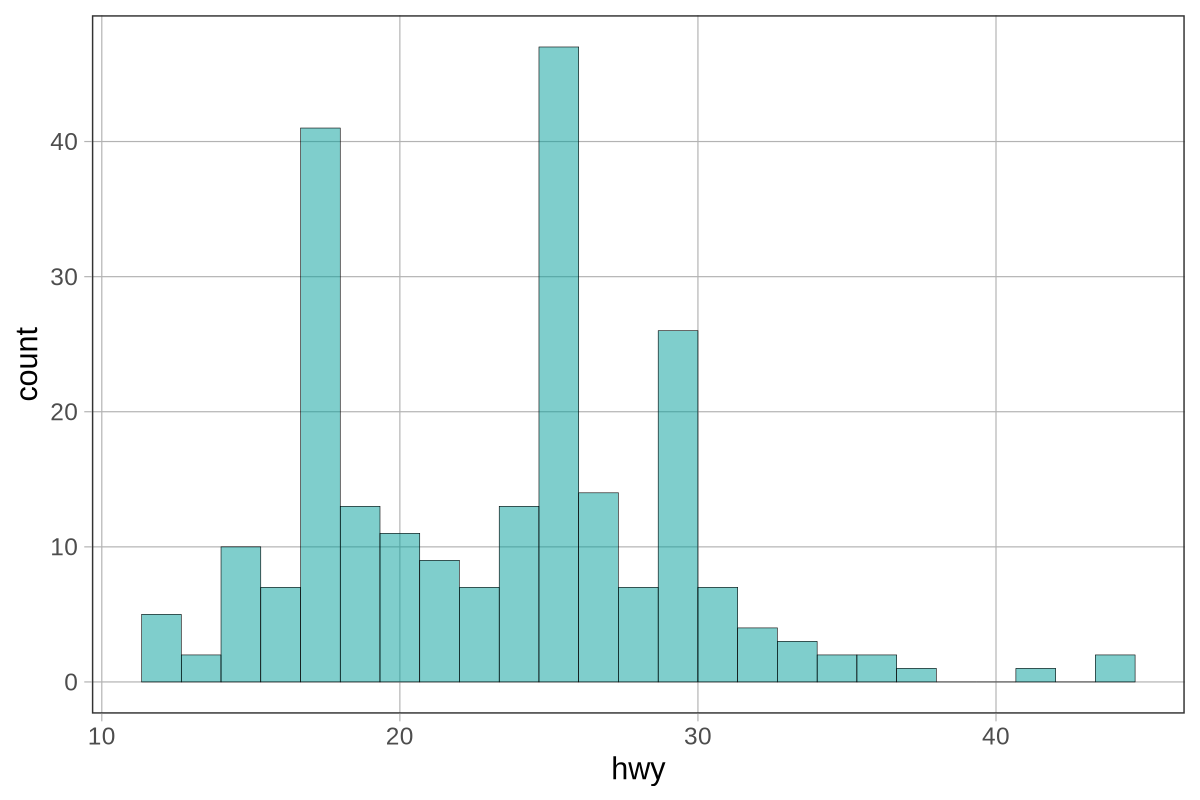
1. Τι αντιπροσωπεύουν οι αριθμοί στον άξονα y του παραπάνω ιστογράμματος;
Συγκεκριμένα αυτοκίνητα είναι η σωστή απάντηση.
Ανάλυση του ιστογράμματος:
Τι δείχνει ο άξονας y:
Τίτλος: “count” (πλήθος/συχνότητα)
Συχνότητα: 0, 10, 20, 30, 40, 50
Σημασία: Πόσα αυτοκίνητα (παρατηρήσεις) υπάρχουν σε κάθε διάστημα τιμών
Τι δείχνει ο άξονας x:
Ετικέτα: “hwy” (Μίλια ανά γαλόνι στον αυτοκινητόδρομο )
Τιμές: 12-44 μίλια ανά γαλόνι
Bins: Κάθε στήλη αντιπροσωπεύει ένα εύρος τιμών
Ερμηνεία του γραφήματος:
Κάθε στήλη δείχνει:
Πόσα αυτοκίνητα έχουν μίλια ανά γαλόνι σε συγκεκριμένο εύρος
Π.χ. η ψηλότερη στήλη (συχνότητα ~46) δείχνει ότι περίπου 46 αυτοκίνητα έχουν γύρω στα 26-27 μίλια ανά γαλόνι στον αυτοκινητόδρομο
Γιατί οι άλλες επιλογές είναι λάθος:
Α - Έτη κατασκευής - ΛΑΘΟΣ:
Η
yearείναι μεταβλητή στο σύνολο δεδομένων (1999-2008)Αλλά ο άξονας y δείχνει πλήθος, όχι έτη
Τα έτη θα βρίσκονταν στον άξονα x αν αυτή ήταν η μεταβλητή
Β - Τύποι κινητήρων - ΛΑΘΟΣ:
Ο τύπος κινητήρα θα ήταν κατηγορική μεταβλητή
Ο άξονας y δείχνει συχνότητα εμφάνισης τιμών
Γ - Μάρκες αυτοκινήτων - ΛΑΘΟΣ:
Η μάρκα αυτοκινήτου είναι κατηγορική μεταβλητή (audi, ford, κλπ)
Ο άξονας y δείχνει πλήθος, όχι μάρκα
Τι είναι ιστόγραμμα:
Ένα ιστόγραμμα δείχνει:
άξονας x: Τιμές μιας συνεχούς μεταβλητής (εδώ hwy mpg)
άξονας y: Συχνότητα/πλήθος παρατηρήσεων σε κάθε bin
Στήλες: Αντιπροσωπεύουν πόσες παρατηρήσεις πέφτουν σε κάθε εύρος
Σε αυτή την περίπτωση:
# Κάθε παρατήρηση = ένα αυτοκίνητο
# άξονας y = πόσα αυτοκίνητα
# άξονας x = μίλια ανά γαλόνι
# Παράδειγμα:
# "Περίπου 47 αυτοκίνητα διανύουν στον αυτοκινητόδρομο περίπου 26-27 μίλια ανά γαλόνι"
# "Περίπου 13 αυτοκίνητα διανύουν στον αυτοκινητόδρομο περίπου 17-18 μίλια ανά γαλόνι"Συμπέρασμα:
Οι αριθμοί στον άξονα y (0, 10, 20, 30, 40, 50) αντιπροσωπεύουν το πλήθος των συγκεκριμένων αυτοκινήτων που έχουν τιμές μιλίων ανά γαλόνι σε κάθε εύρος. Κάθε μονάδα στον άξονα y αντιστοιχεί σε ένα αυτοκίνητο από το σύνολο δεδομένων των 234 αυτοκινήτων.
Αυτή είναι η τυπική δομή ενός ιστογράμματος: ο άξονας x δείχνει την κατανομή μιας συνεχούς μεταβλητής, και ο άξονας y δείχνει πόσες παρατηρήσεις (εδώ αυτοκίνητα) έχουν τιμές σε κάθε εύρος.
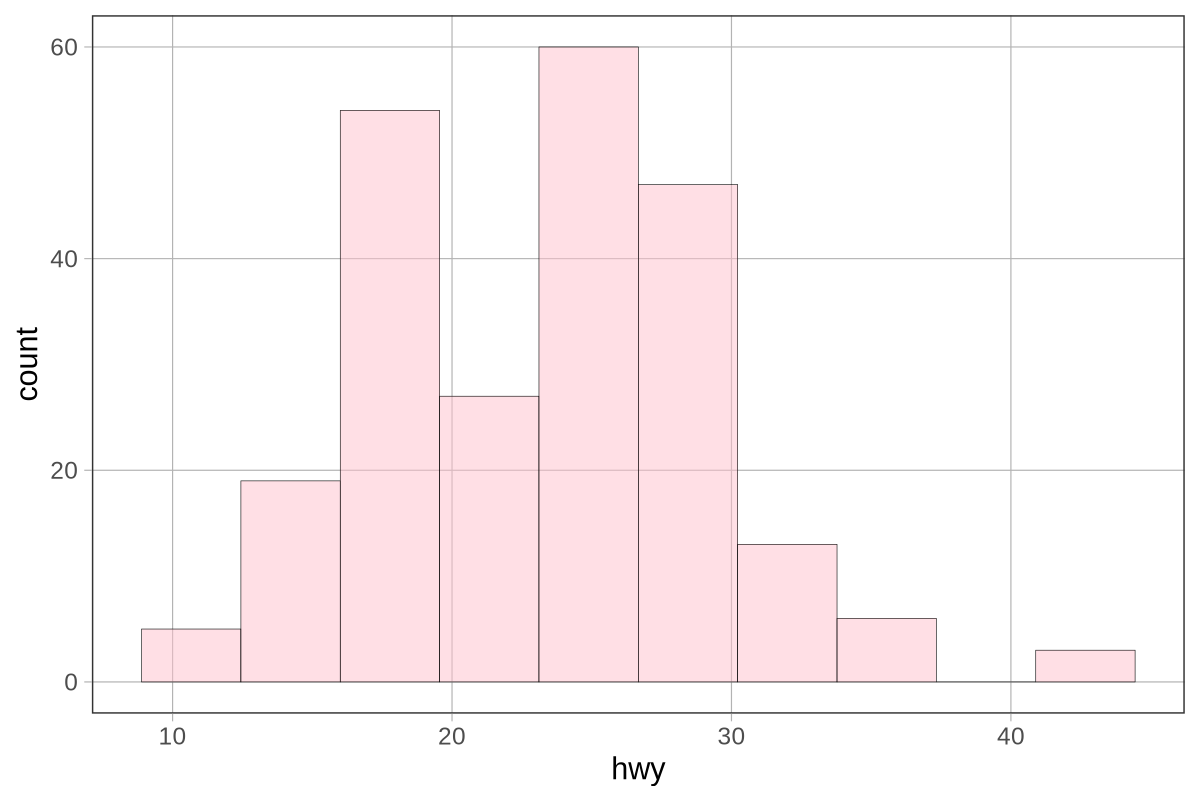
2. Το παραπάνω ιστόγραμμα δημιουργήθηκε με τον κώδικα gf_histogram(~ hwy, data = mpg, fill = "pink", bins = 10). Γιατί αυτό το ιστόγραμμα φαίνεται διαφορετικό από αυτό στην προηγούμενη ερώτηση;
Επειδή οι τιμές της hwy τοποθετήθηκαν σε λιγότερα bins είναι η σωστή απάντηση.
Ανάλυση της διαφοράς:
Κλειδί στον κώδικα:
bins = 10καθορίζει ότι το ιστόγραμμα θα έχει 10 ράβδουςΤο προηγούμενο ιστόγραμμα είχε περισσότερα bins (πιθανώς 20-30)
Τι σημαίνει λιγότερα bins:
Με περισσότερα bins (π.χ. 25):
Κάθε στήλη καλύπτει μικρό εύρος τιμών (π.χ. 1 mpg)
Περισσότερες λεπτομέρειες στη μορφή της κατανομής
Πιο “ακανόνιστο” ιστόγραμμα
Μπορεί να δείξει μικρές κορυφές και κοιλάδες
Με λιγότερα bins (10):
Κάθε στήλη καλύπτει μεγαλύτερο εύρος τιμών (π.χ. 3-4 mpg)
Πιο ομαλή εμφάνιση
Λιγότερες λεπτομέρειες, περισσότερη γενίκευση
Πιο απλό, “εξομαλυμένο” σχήμα
Γιατί οι άλλες επιλογές είναι λάθος:
Β - “Μη συμμετρική κατανομή” - ΛΑΘΟΣ:
Η σχήμα της κατανομής παραμένει το ίδιο
Αν η κατανομή είναι ασύμμετρη, θα είναι ασύμμετρη και στα δύο γραφήματα
Τα bins δεν αλλάζουν τη βασική μορφή της κατανομής
Γ - “Οι μεταβλητές τοποθετήθηκαν σε 10 bins” - ΛΑΘΟΣ:
Μόνο η μεταβλητή
hwyχρησιμοποιείται στο ιστόγραμμαΌχι “όλες οι μεταβλητές”
Ιστόγραμμα = μία μεταβλητή μόνο
Δ - “Λιγότερα αυτοκίνητα (μόνο 10)” - ΛΑΘΟΣ:
Το ίδιο πλαίσιο δεδομένων (mpg) με 234 αυτοκίνητα
Το
bins = 10αναφέρεται στον αριθμό στηλών, όχι αυτοκινήτωνΤα δεδομένα παραμένουν τα ίδια
Πρακτικό παράδειγμα:
# Ίδια δεδομένα, διαφορετικά bins
# Πολλά bins (λεπτομερές)
gf_histogram(~ hwy, data = mpg, bins = 25)
# Λίγα bins (απλό)
gf_histogram(~ hwy, data = mpg, bins = 10)
# Ακόμα λιγότερα bins (πολύ απλό)
gf_histogram(~ hwy, data = mpg, bins = 5)Αποτέλεσμα του αριθμού bins:
Bins = 5: Πολύ γενικό, χάνει λεπτομέρειες
Bins = 10: Καλή ισορροπία
Bins = 25: Πολλές λεπτομέρειες, μπορεί να είναι θορυβώδες
Bins = 50: Πάρα πολλές λεπτομέρειες, δύσκολο να διαβαστεί
Στην πράξη:
5-15 bins: Συνήθως καλό για πρώτη διερεύνηση
Περισσότερα bins: Για λεπτομερή ανάλυση
Δοκιμάστε διαφορετικούς αριθμούς να δείτε ποιος δουλεύει καλύτερα
Τι δεν αλλάζει:
Τα δεδομένα (ίδια 234 αυτοκίνητα)
Η βασική μορφή της κατανομής
Ο μέσος όρος και η διακύμανση
Το εύρος των τιμών (min-max)
Τι αλλάζει:
Η ανάλυση του διαγράμματος
Πόσες στήλες βλέπουμε
Πόσες λεπτομέρειες μπορούμε να διακρίνουμε
Συμπέρασμα:
Το ιστόγραμμα μοιάζει διαφορετικό επειδή χρησιμοποιεί 10 bins αντί για περισσότερα. Αυτό σημαίνει ότι οι τιμές του hwy ομαδοποιούνται σε 10 ευρύτερες κατηγορίες αντί για περισσότερες στενότερες κατηγορίες. Το αποτέλεσμα είναι ένα πιο απλό και εξομαλυμένο ιστόγραμμα που δείχνει τη γενική μορφή της κατανομής χωρίς πολλές λεπτομέρειες.
Τα ίδια δεδομένα μπορούν να φαίνονται διαφορετικά ανάλογα με τον αριθμό των bins που επιλέγουμε - αυτό είναι ένα σημαντικό σημείο στην οπτικοποίηση δεδομένων.
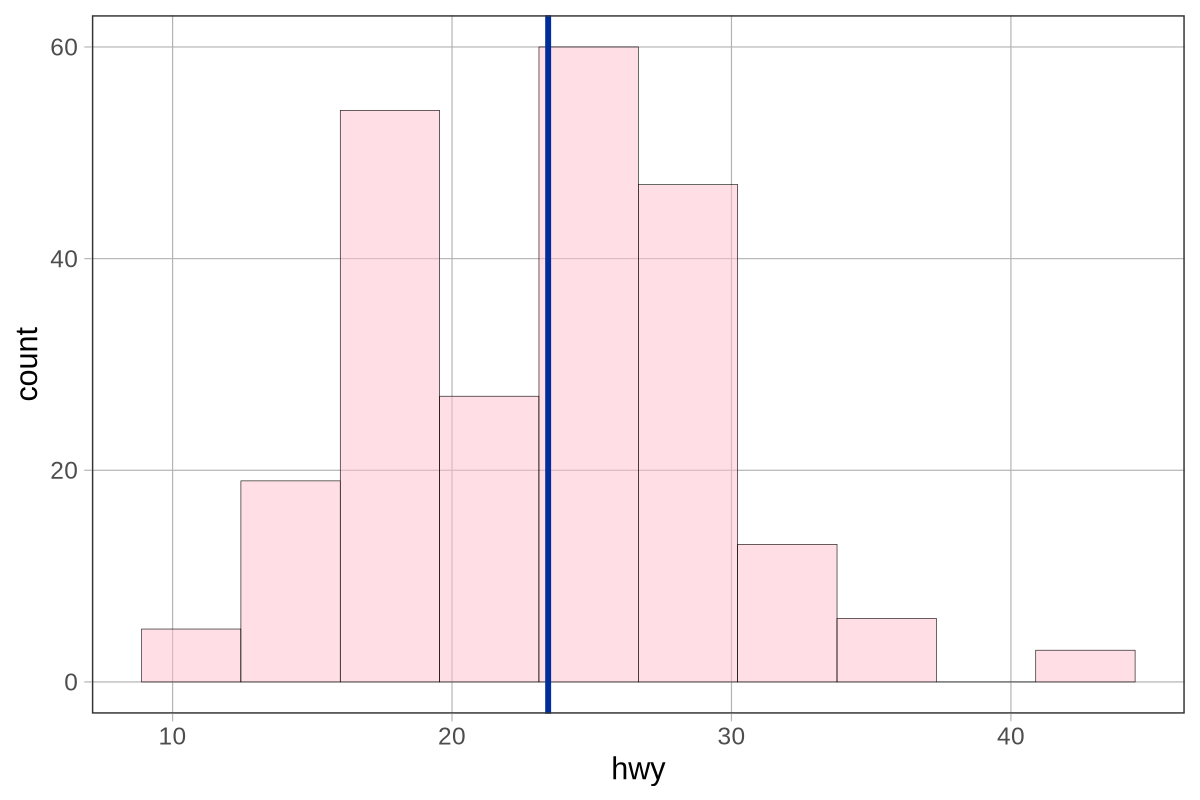
3. Στο παραπάνω ιστόγραμμα έχουμε αναπαραστήσει το μέσο όρο με μια κάθετη μπλε γραμμή. Γιατί ο μέσος όρος είναι ένα καλό μοντέλο για τη μεταβλητή hwy;
Ο μέσος όρος εξισορροπεί τα υπόλοιπα και ελαχιστοποιεί το SS (Άθροισμα Τετραγώνων)
Μαθηματική ιδιότητα: Ο μέσος όρος ικανοποιεί:
\(\sum(Y_i - \bar{Y}) = 0\) (άθροισμα υπολοίπων = 0)
\(\sum(Y_i - \bar{Y})^2\) = ελάχιστο (ελαχιστοποιεί το SS)
Αυτό τον καθιστά τη βέλτιστη επιλογή για πρόβλεψη όταν δεν έχουμε άλλες πληροφορίες.
Γιατί οι άλλες επιλογές είναι λάθος:
Β - “Καλύτερο για οπτικοποίηση” - ΛΑΘΟΣ:
Η οπτικοποίηση δεν καθορίζει ποιο μοντέλο είναι καλό
Για ασύμμετρες κατανομές, η διάμεσος μπορεί να είναι καλύτερη
Ο μέσος όρος είναι καλός λόγω μαθηματικών ιδιοτήτων, όχι οπτικοποίησης
Γ - “Καλύτερο για κατηγορικές” - ΛΑΘΟΣ:
H
hwyείναι συνεχής μεταβλητή, όχι κατηγορικήΓια κατηγορικές χρησιμοποιούμε την επικρατούσα τιμή (mode)
Ο μέσος όρος δεν έχει νόημα για κατηγορικές
Δ - “Μόνο πραγματικό μοντέλο” - ΛΑΘΟΣ:
Υπάρχουν πολλά έγκυρα στατιστικά μοντέλα
Ο μέσος όρος δεν είναι το “μόνο” - είναι ένα από πολλά
Διαφορετικά μοντέλα κατάλληλα για διαφορετικούς σκοπούς
4. Αν μια παρατήρηση βρίσκεται πολύ μακριά από το μέσο όρο, τι θα περιμένατε για την αντίστοιχη τιμή του υπολοίπου (residual);
Σωστή απάντηση: Β
Ορισμός υπολοίπου:
\[\text{residual} = Y_i - \bar{Y}\]
Όσο πιο μακριά από το μέσο όρο, τόσο μεγαλύτερο το |υπόλοιπο|:
Κοντά στο μέσο: μικρό |υπόλοιπο|
Μακριά από μέσο: μεγάλο |υπόλοιπο|
Πολύ μακριά: πολύ μεγάλο |υπόλοιπο|
Γιατί οι άλλες επιλογές είναι λάθος:
Α - “Πιο θετικό” - ΛΑΘΟΣ:
Μακριά κάτω από μέσο → αρνητικό υπόλοιπο
Μακριά πάνω από μέσο → θετικό υπόλοιπο
Το πρόσημο εξαρτάται από την κατεύθυνση, όχι την απόσταση
Γ - “Πιο μεταβλητό” - ΛΑΘΟΣ:
Το υπόλοιπο είναι μία τιμή, όχι κατανομή
Δεν έχει “μεταβλητότητα” - είναι σταθερό για κάθε παρατήρηση
Η φράση δεν έχει νόημα για μεμονωμένο υπόλοιπο
Δ - “Υπόλοιπο = 0” - ΛΑΘΟΣ:
Μόνο παρατηρήσεις ακριβώς στο μέσο έχουν υπόλοιπο = 0
Το γεγονός ότι \(\sum e_i = 0\) δεν σημαίνει κάθε \(e_i = 0\)
Μακριά από μέσο → μεγάλο υπόλοιπο, όχι μηδέν
5. Τι ισχύει για την κατανομή οποιασδήποτε μεταβλητής, αν το μοντέλο σας είναι ο μέσος όρος αυτής της μεταβλητής;
Σωστή απάντηση: Δ
Βασική σχέση:
\[e_i = Y_i - \bar{Y}\]
Τα υπόλοιπα είναι τα αρχικά δεδομένα μετατοπισμένα κατά \(\bar{Y}\)
Η μετατόπιση διατηρεί:
Σχήμα: Ίδιο
Διασπορά: \(Var(e) = Var(Y)\)
Τυπική απόκλιση: \(SD(e) = SD(Y)\)
Η μετατόπιση αλλάζει:
- Κέντρο: Από \(\bar{Y}\) στο 0
Γιατί οι άλλες επιλογές είναι λάθος:
Α - “Y πιο στενή” - ΛΑΘΟΣ:
Ίδια διασπορά: \(Var(e) = Var(Y)\)
Η μετατόπιση δεν αλλάζει τη διασπορά
Β - “Y κεντραρισμένη στο 0” - ΛΑΘΟΣ:
Η μεταβλητή Y κεντράρεται στο \(\bar{Y}\)
Τα υπόλοιπα κεντράρονται στο 0
Γ - “Y χαμηλότερα” - ΛΑΘΟΣ:
Κέντρο υπολοίπων = 0 (πάντα)
Κέντρο Y = \(\bar{Y}\) (μπορεί > ή < 0)
Όχι σταθερή σχέση
6. Αν εκτελέσετε τον παρακάτω κώδικα, ποια από τα παρακάτω μπορείτε να βρείτε στο αντικείμενο empty_model;
Σωστή απάντηση: Και οι τρεις απαντήσεις είναι σωστές.
Τι κάνει η lm(hwy ~ NULL):
Δημιουργεί το empty model (κενό μοντέλο):
\[\text{hwy}_i = b_0 + e_i\]
Όπου:
\(b_0\) = μέσος όρος της
hwy(εκτιμητής του \(\beta_0\))\(e_i\) = υπόλοιπο για παρατήρηση i
Αποτέλεσμα εξόδου:
Τι μπορούμε να βρούμε στο empty_model:
Β. Το μέσο όρο:
Ο σταθερός όρος
(Intercept) = 23.44είναι ο μέσος όρος τηςhwyΜπορούμε να κάνουμε επαλήθευση με:
mean(mpg$hwy) = 23.44
Γ. Το \(\beta_0\):
- Ο σταθερός όρος
(Intercept) = 23.44είναι το \(b_0\), που είναι και η εκτίμησή μας για το \(\beta_0\)
Α. Πόσο σφάλμα υπάρχει:
Με
sd(residuals(empty_model))ή με
summary(empty_model)βλέπουμε το τυπικό σφάλμα των υπολοίπων (Residual standard error)
Όλες οι πληροφορίες είναι διαθέσιμες στo αντικείμενο empty_model!
7. Αν εκτελέσετε τον παρακάτω κώδικα, ποια από τα παρακάτω μπορείτε να βρείτε στα αποτελέσματα;
Όλες οι επιλογές είναι σωστές
Τα αποτελέσματα της supernova() για το κενό μοντέλο δείχνουν:
Analysis of Variance Table (Type III SS)
Model: hwy ~ NULL
SS df MS
Total (empty model) | 8261.662 233 35.4581. Σφάλμα γύρω από το κενό μοντέλο:
MS (Mean Square) = 35.458
SD = √MS = √35.458 ≈ 5.95 mpg
Αυτό δείχνει το σφάλμα γύρω από το μέσο όρο
2. Άθροισμα τετραγώνων υπολοίπων:
Total SS = 8261.662
Για το καινό μοντέλο: SS = άθροισμα τετραγώνων υπολοίπων
\(SS = \sum(Y_i - \bar{Y})^2\)
3. Βαθμοί ελευθερίας:
df = 233
df = n - 1 = 234 - 1 = 233
Όλες αυτές οι πληροφορίες είναι διαθέσιμες στα αποτελέσματα!
8. Το άθροισμα τετραγώνων αυξάνεται όταν:
Όλες οι επιλογές είναι σωστές
Ορισμός Αθροίσματος Τετραγώνων (Sum of Squares):
\[SS = \sum_{i=1}^{n}(Y_i - \bar{Y})^2\]
Τρεις παράγοντες που αυξάνουν το SS:
Α. Αυξάνεται η διακύμανση:
\[SS = (n-1) \times s^2\]
Μεγαλύτερη διακύμανση (\(s^2\)) → μεγαλύτερο SS
Όταν οι τιμές είναι πιο “διεσπαρμένες”
Γ. Διασπορά κατανομής αυξάνεται:
Η “διασπορά” και η “διακύμανση” είναι στενά συνδεδεμένες
Μεγαλύτερη διασπορά = μεγαλύτερες αποκλίσεις από μέσο
Άρα μεγαλύτερο SS
Β. Μέγεθος δείγματος αυξάνεται:
Το SS είναι άθροισμα n όρων
Περισσότερες παρατηρήσεις (n) → περισσότεροι όροι → μεγαλύτερο άθροισμα
Ακόμα κι όταν η διακύμανση μένει σταθερή
Παραδείγματα:
1. Επίδραση διακύμανσης (σταθερό n):
# Μικρή διασπορά
y1 <- c(10, 11, 12, 13, 14) # n=5, s²≈2.5
SS1 <- sum((y1 - mean(y1))^2) # 10
# Μεγάλη διασπορά
y2 <- c(5, 10, 15, 20, 25) # n=5, s²≈62.5
SS2 <- sum((y2 - mean(y2))^2) # 250
# SS2 > SS1 (μεγαλύτερη διασπορά)2. Επίδραση μεγέθους δείγματος (σταθερή διακύμανση):
# Μικρό δείγμα
set.seed(123)
y1 <- rnorm(10, mean=100, sd=10) # n=10
SS1 <- sum((y1 - mean(y1))^2) # ≈900
# Μεγάλο δείγμα (ίδια κατανομή)
y2 <- rnorm(100, mean=100, sd=10) # n=100
SS2 <- sum((y2 - mean(y2))^2) # ≈9900
# SS2 ≈ 10×SS1 (10 φορές μεγαλύτερο n)3. Συνδυασμός και των δύο:
# Μικρό δείγμα, μικρή διασπορά
y1 <- rnorm(10, mean=100, sd=5) # SS ≈ 225
# Μεγάλο δείγμα, μεγάλη διασπορά
y2 <- rnorm(100, mean=100, sd=20) # SS ≈ 39600
# Τεράστια διαφορά!Γιατί αυτό έχει σημασία:
Πρόβλημα με SS:
Το SS εξαρτάται από το n
Δεν μπορούμε να συγκρίνουμε SS από διαφορετικά μεγέθη δείγματος
Λύση - Mean Square (ή διακύμανση):
\[MS = \frac{SS}{n-1} = s^2\]
Το MS δεν εξαρτάται από το n
Μπορούμε να συγκρίνουμε MS από διαφορετικά δείγματα
Συμπέρασμα:
Το Άθροισμα Τετραγώνων (Sum of Squares) αυξάνεται όταν:
Αυξάνεται η διακύμανση - τα δεδομένα πιο διεσπαρμένα
Αυξάνεται το μέγεθος δείγματος - περισσότεροι όροι στο άθροισμα
Αυξάνεται η διασπορά - ίδιο με τη διακύμανση
Γι’ αυτό χρησιμοποιούμε για συγκρίσεις το συνολικό μέσο τετραγωνικό σφάλμα ή διακύμανση, όχι το SS.
9. Ας υποθέσουμε ότι έχετε υπολογίσει το άθροισμα τετραγώνων για την hwy. Ποιο θα ήταν το πλεονέκτημα να διαιρέσετε αυτόν τον αριθμό με το \(n-1\) (δηλαδή, να το διαιρέσετε με τους βαθμούς ελευθερίας, df);
Σωστή απάντηση: Β
Τι υπολογίζουμε:
\[Total MS = \frac{SS}{n-1} = \frac{\sum(Y_i - \bar{Y})^2}{n-1} = s^2\]
Αυτό είναι η δειγματική διακύμανση (sample variance)
Γιατί το Β είναι σωστό:
Το μειονέκτημα του SS:
Το SS εξαρτάται από το μέγεθος δείγματος (n)
Μεγαλύτερο n → μεγαλύτερο SS (ακόμα κι αν η διασπορά ίδια)
Δεν μπορούμε να συγκρίνουμε SS από διαφορετικά n
Λύση - Mean Square (MS):
Διαιρώντας με \(n-1\) → ανεξάρτητο από n
Το MS δείχνει μέση τετραγωνική απόκλιση
Συγκρίσιμο μεταξύ δειγμάτων
Παράδειγμα:
# Δύο δείγματα με ΙΔΙΑ διασπορά αλλά διαφορετικό n
set.seed(123)
small <- rnorm(10, mean=100, sd=10) # n=10
large <- rnorm(100, mean=100, sd=10) # n=100
# Sum of Squares - ΔΙΑΦΟΡΕΤΙΚΑ (δεν συγκρίνονται)
SS_small <- sum((small - mean(small))^2)
SS_large <- sum((large - mean(large))^2)
# SS_small ≈ 900
# SS_large ≈ 9900
# Mean Square - ΠΑΡΟΜΟΙΑ (συγκρίνονται!)
MS_small <- SS_small / (10-1)
MS_large <- SS_large / (100-1)
# MS_small ≈ 100
# MS_large ≈ 100
# Ή απευθείας:
var(small) # ≈ 100
var(large) # ≈ 100Γιατί οι άλλες επιλογές είναι λάθος:
Α - “Μετατρέπει σε μέτρο διασποράς” - ΑΝΑΚΡΙΒΕΣ:
Το SS ήδη είναι μέτρο διασποράς
Απλά δεν είναι κανονικοποιημένο ως προς το n
Το MS είναι καλύτερο μέτρο, όχι ότι το SS δεν είναι μέτρο
Η απάντηση Β είναι πιο ακριβής για το κύριο πλεονέκτημα
Γ - “Διακύμανση πληθυσμού” - ΛΑΘΟΣ:
Υπολογίζουμε τη δειγματική διακύμανση (\(s^2\)), όχι την πληθυσμιακή (\(\sigma^2\))
Η \(s^2\) είναι εκτιμητής της \(\sigma^2\)
Δεν ξέρουμε την πραγματική τιμή της \(\sigma^2\) (είναι άγνωστη παράμετρος)
Δ - “Κανένα πλεονέκτημα” - ΛΑΘΟΣ:
Υπάρχει τεράστιο πλεονέκτημα
Χωρίς διαίρεση δεν μπορούμε να συγκρίνουμε δείγματα
Γιατί \(n-1\) και όχι \(n\):
Διαιρούμε με \(n-1\) (όχι \(n\)) για να έχουμε αμερόληπτο εκτιμητή
Το \(s^2\) με \(n-1\) είναι αμερόληπτος εκτιμητής του \(\sigma^2\)
Συμπέρασμα:
Το κύριο πλεονέκτημα της διαίρεσης SS με \(n-1\) είναι ότι δημιουργεί μια κανονικοποιημένη μετρική (Mean Square ή διακύμανση) που:
Δεν εξαρτάται από το μέγεθος δείγματος
Μπορεί να συγκριθεί μεταξύ δειγμάτων διαφορετικών μεγεθών
Αντιπροσωπεύει τη μέση τετραγωνική απόκλιση ανά παρατήρηση
Αυτό κάνει τη διακύμανση (και την τυπική απόκλιση) χρήσιμα εργαλεία για τη σύγκριση της διασποράς σε διαφορετικά σύνολα δεδομένων.
10. Ποια από αυτές τις γραμμές κώδικα θα υπολογίσει τη διακύμανση του hwy;
Σωστή απάντηση: Β (var(mpg$hwy))
Γιατί η Β είναι σωστή:
Η συνάρτηση var() υπολογίζει απευθείας τη δειγματική διακύμανση:
\[s^2 = \frac{\sum(Y_i - \bar{Y})^2}{n-1}\]
Γιατί οι άλλες επιλογές είναι λάθος:
Α - favstats(~ hwy, data = hwy) - ΛΑΘΟΣ:
Λάθος dataset: Πρέπει
data = mpg, όχιdata = hwyΤο
hwyείναι μεταβλητή, όχι data frameΣωστό:
favstats(~ hwy, data = mpg)Το
favstats()δείχνει πολλά στατιστικά (min, Q1, median, mean, Q3, max, sd, n, missing) αλλά όχι τη διακύμανση
Γ - lm(hwy ~ var, data = mpg) - ΛΑΘΟΣ:
Η
lm()δημιουργεί γραμμικό μοντέλοΤο
varδεν είναι μεταβλητή στο mpg datasetΑυτό θα δώσει σφάλμα: “object ‘var’ not found”
Δεν υπολογίζει διακύμανση
Δ - anova(mpg, data = hwy) - ΛΑΘΟΣ:
Λάθος σύνταξη - το
anova()δεν έχειdata =argumentΤο
anova()χρειάζεται αντικείμενο μοντέλου ως είσοδο, όχι πλαίσιο δεδομένωνΣωστό:
anova(model)ήanova(model1, model2)
Εναλλακτικοί τρόποι υπολογισμού διακύμανσης:
# Μέθοδος 1: Απευθείας με var()
var(mpg$hwy) # 35.46 ✓
# Μέθοδος 2: Από τυπική απόκλιση
sd(mpg$hwy)^2 # 35.46 ✓
# Μέθοδος 3: Βήμα-βήμα από τον ορισμό
mean_hwy <- mean(mpg$hwy)
SS <- sum((mpg$hwy - mean_hwy)^2)
variance <- SS / (length(mpg$hwy) - 1)
# 35.46 ✓
# Μέθοδος 4: Με την supernova()
empty_model <- lm(hwy ~ NULL, data = mpg)
result <- supernova(empty_model)
MS <- result$MS[3] # Mean Square = διακύμανση
# 35.46 ✓Συμπέρασμα:
Για να υπολογίσετε τη διακύμανση της hwy, χρησιμοποιήστε:
Αυτή είναι η πιο άμεση και απλή μέθοδος στην R.
11. Ποιος κώδικας θα εμφανίσει την τυπική απόκλιση της hwy;
Όλες οι επιλογές είναι σωστές.
Α. sd(mpg$hwy) - ΣΩΣΤΟ:
Η πιο άμεση μέθοδος - υπολογίζει απευθείας την τυπική απόκλιση.
Β. sqrt(var(mpg$hwy)) - ΣΩΣΤΟ:
Υπολογίζει τη διακύμανση και παίρνει την τετραγωνική ρίζα:
\[SD = \sqrt{\text{Variance}} = \sqrt{s^2} = s\]
Γ. favstats(~ hwy, data = mpg) - ΣΩΣΤΟ:
favstats(~ hwy, data = mpg)
# min Q1 median Q3 max mean sd n missing
# 12 18 24 27 44 23.44 5.954 234 0
# ↑
# Τυπική απόκλιση!Η favstats() εμφανίζει πολλά στατιστικά, συμπεριλαμβανομένης της τυπικής απόκλισης (sd).
Σύγκριση των μεθόδων:
# Μέθοδος 1: Απευθείας
sd(mpg$hwy) # 5.954
# Μέθοδος 2: Από διακύμανση
sqrt(var(mpg$hwy)) # 5.954
# Μέθοδος 3: Από favstats (μαζί με άλλα)
favstats(~ hwy, data = mpg)$sd # 5.954
# Όλες δίνουν το ίδιο αποτέλεσμα!Πότε να χρησιμοποιήσετε κάθε μέθοδο:
sd(mpg$hwy):
Όταν θέλετε μόνο την τυπική απόκλιση
Πιο απλό και άμεσο
Προτιμότερο για γρήγορους υπολογισμούς
sqrt(var(mpg$hwy)):
Όταν έχετε ήδη τη διακύμανση
Για εκπαιδευτικούς σκοπούς (δείχνει τη σχέση)
Λιγότερο συνηθισμένο στην πράξη
favstats(~ hwy, data = mpg):
Όταν θέλετε πολλά στατιστικά ταυτόχρονα
Για διερευνητική ανάλυση
Δίνει πλήρη εικόνα της κατανομής
Επιπλέον μέθοδοι:
12. Αν έχετε υπολογίσει την τυπική απόκλιση της hwy, τι έχετε βρει;
Σωστή απάντηση: Γ
Τι είναι η τυπική απόκλιση:
\[SD = \sqrt{\frac{\sum(Y_i - \bar{Y})^2}{n-1}}\]
Η τυπική απόκλιση είναι η τετραγωνική ρίζα της διακύμανσης, που τη φέρνει πίσω στις αρχικές μονάδες.
Για την hwy:
Ερμηνεία: Η τυπική (χαρακτηριστική) απόκλιση από το μέσο όρο είναι περίπου 5.95 mpg.
Γιατί οι άλλες επιλογές είναι λάθος:
Α - “Άθροισμα τετραγώνων των αποκλίσεων” - ΛΑΘΟΣ:
Αυτό είναι το Sum of Squares (SS)
SS = \(\sum(Y_i - \bar{Y})^2\) = 8261.662 mpg²
Όχι η τυπική απόκλιση
Μονάδες: mpg² (τετραγωνικά)
Β - “Μέση τετραγωνική απόκλιση” - ΛΑΘΟΣ:
Αυτό είναι η διακύμανση (variance)
Variance = \(\frac{SS}{n-1}\) = 35.458 mpg²
Όχι η τυπική απόκλιση
Μονάδες: mpg² (τετραγωνικά)
Γ - “Μέση απόκλιση” - ΣΩΣΤΟ:
“Περίπου” επειδή δεν είναι ακριβώς ο μέσος όρος των |αποκλίσεων|
Αυτό είναι η τυπική απόκλιση (SD)
SD = \(\sqrt{\text{Variance}}\) = 5.954 mpg
Μονάδες: mpg (αρχικές)
Σύγκριση μέτρων:
Μέτρο | Τύπος | Τιμή | Μονάδες
------------------ | ------------------------ | --------- | -------
Άθροισμα Τετραγώνων | Σ(Y-Ȳ)² | 8261.662 | mpg²
Διακύμανση | Σ(Y-Ȳ)²/(n-1) | 35.458 | mpg²
Τυπική απόκλιση | √[Σ(Y-Ȳ)²/(n-1)] | 5.954 | mpgΓιατί “περίπου” η μέση απόκλιση:
Η τυπική απόκλιση δεν είναι ακριβώς ο μέσος όρος των απόλυτων αποκλίσεων:
# Τυπική απόκλιση
sd(mpg$hwy) # 5.954
# Μέσος όρος απόλυτων αποκλίσεων (MAD)
mean(abs(mpg$hwy - mean(mpg$hwy))) # 4.703
# Διαφορετικό αποτέλεσμα! Αλλά συνήθως είναι κοντά.Η τυπική απόκλιση είναι μεγαλύτερη επειδή:
Τετραγωνίζει τις αποκλίσεις (δίνει μεγαλύτερο βάρος σε ακραίες τιμές)
Υπολογίζει τη ρίζα του μέσου των τετραγώνων
Πρακτική ερμηνεία:
Για το hwy με SD = 5.95 mpg:
mean(mpg$hwy) # 23.44 mpg
sd(mpg$hwy) # 5.95 mpg
# Ερμηνεία:
# Το "τυπικό" αυτοκίνητο καλύπτει στον αυτοκινητόδρομο αριθμό μιλίων ανά γαλόνι που αποκλίνει
# κατά ±5.95 mpg από το μέσο όρο των 23.44 mpg
# Περίπου 68% των αυτοκινήτων έχουν τιμή hwy μεταξύ:
# 23.44 - 5.95 = 17.49 mpg
# 23.44 + 5.95 = 29.39 mpgΓιατί οι μονάδες έχουν σημασία:
| Μέτρο | Μονάδες | Ερμηνεία |
|---|---|---|
| SS | mpg² | Δύσκολο να ερμηνευτεί |
| Variance | mpg² | Δύσκολο να ερμηνευτεί |
| SD | mpg | Εύκολο - ίδιες με αρχικά δεδομένα |
Συμπέρασμα:
Η τυπική απόκλιση (SD = 5.95 mpg) αντιπροσωπεύει την τυπική ή χαρακτηριστική απόκλιση από το μέσο όρο, μετρημένη στις ίδιες μονάδες με τα αρχικά δεδομένα (μίλια ανά γαλόνι). Είναι περίπου - αλλά όχι ακριβώς - η μέση απόκλιση, επειδή υπολογίζεται ως η τετραγωνική ρίζα της μέσης τετραγωνικής απόκλισης.
Η τυπική απόκλιση είναι το πιο χρήσιμο μέτρο διασποράς επειδή έχει τις ίδιες μονάδες με τα δεδομένα και μπορεί να ερμηνευτεί εύκολα.

13. Στο ιστόγραμμα της hwy (βλ. παραπάνω) τι θα πάρετε αν αθροίσετε το ύψος (το “count”) όλων των στηλών;
Σωστή απάντηση: Α
Τι δείχνει το ιστόγραμμα:
άξονας x: Τιμές της
hwy(μίλια ανά γαλόνι)άξονας y: Count (πλήθος/συχνότητα)
Κάθε στήλη: Πόσα αυτοκίνητα σε συγκεκριμένο εύρος τιμών της hwy
Άθροισμα όλων των υψών:
# Το άθροισμα όλων των counts
sum(counts) = Συνολικός αριθμός παρατηρήσεων
# Για το mpg dataset
nrow(mpg) # 234 αυτοκίνηταΓιατί:
Κάθε αυτοκίνητο εμφανίζεται ακριβώς μία φορά στο ιστόγραμμα, σε μία από τις στήλες (bins). Άρα:
\[\text{Άθροισμα counts} = \text{Συνολικός αριθμός αυτοκινήτων} = n = 234\]
Γιατί οι άλλες επιλογές είναι λάθος:
Β - “Άθροισμα τετραγώνων” - ΛΑΘΟΣ:
Το Άθροισμα Τετραγώνων (Sum of Squares - SS) = \(\sum(Y_i - \bar{Y})^2\) = 8261.662
Αυτό δεν σχετίζεται με το άθροισμα των υψών των στηλών
Το SS μετράει διασπορά, όχι πλήθος
Γ - “Αριθμός μιλίων ανά γαλόνι” - ΛΑΘΟΣ:
Το ιστόγραμμα δείχνει πόσα αυτοκίνητα έχουν κάθε τιμή της hwy
Όχι το συνολικό άθροισμα των τιμών της hwy
Για το άθροισμα:
sum(mpg$hwy)= 5485 (διαφορετικό!)
Δ - “Κανένα” - ΛΑΘΟΣ:
- Η Α είναι σωστή!
Επαλήθευση:
# Δημιουργία ιστογράμματος και εξαγωγή συχνοτήτων (counts)
hist_data <- hist(mpg$hwy, plot = FALSE)
counts <- hist_data$counts
# Άθροισμα όλων των συχνοτήτων
sum(counts)
# Αποτέλεσμα: 234
# Επιβεβαίωση
nrow(mpg)
# Αποτέλεσμα: 234
# Ταιριάζουν! ✓Διαγραμματική κατανόηση:
Από το διάγραμμα, αν μετρήσουμε κάθε στήλη:
~5 + ~2 + ~10 + ~7 + ~41 + ~13 + ~11 + ~9 + ~7 + ~13 + ~47 + ...
= 234 συνολικά αυτοκίνηταΣυμπέρασμα:
Το άθροισμα των υψών (counts) όλων των στηλών στο ιστόγραμμα ισούται με τον συνολικό αριθμό των παρατηρήσεων στο σύνολο δεδομένων, δηλαδή 234 αυτοκίνητα για το πλαίσιο δεδομένων mpg. Κάθε αυτοκίνητο καταμετράται ακριβώς μία φορά, στη στήλη που αντιστοιχεί στην τιμή της hwy.
14. Ο μέσος όρος της hwy είναι 23.44. Αν θέλατε να υπολογίσετε την τιμή z που αντιστοιχεί στην τιμή hwy = 27, πώς θα επηρεαζόταν το αποτέλεσμα από την τυπική απόκλιση της hwy;
Σωστή απάντηση: Γ
Τύπος υπολογισμού τιμής z:
\[z = \frac{X - \bar{X}}{SD}\]
Για το παράδειγμά μας:
X <- 27
mean <- 23.44
deviation <- 27 - 23.44 # 3.56 (σταθερό)
# Η z εξαρτάται από την τυπική απόκλιση
z <- deviation / SDΣχέση τυπικής απόκλισης και τιμής z:
Η απόκλιση (3.56) είναι σταθερή. Άρα:
Μεγάλη τυπική απόκλιση → Μικρή z
Μικρή τυπική απόκλιση → Μεγάλη z
Αντίστροφη σχέση!
Παράδειγμα:
# Σενάριο 1: Μικρή τυπική απόκλιση
SD1 <- 2
z1 <- 3.56 / 2 # 1.78 (μεγάλη z)
# Σενάριο 2: Μεγάλη τυπική απόκλιση
SD2 <- 10
z2 <- 3.56 / 10 # 0.356 (μικρή z)
# Μεγαλύτερη τυποκή απόκλιση → μικρότερη τιμή z ✓Γιατί η z είναι θετικό:
27 > 23.44 (πάνω από μέσο)
Άρα απόκλιση = +3.56 (θετική)
Διαίρεση θετικού με θετικό → θετική τιμή z
Γιατί οι άλλες επιλογές είναι λάθος:
Α - “Μεγάλη τυπική απόκλιση → μεγάλη τιμή |z|” - ΛΑΘΟΣ:
Το αντίθετο είναι αληθές
Μεγάλη SD → μικρή |z|
Το πρόσημο της z είναι προβλέψιμο (θετικό)
Β - “Δεν έχουν σχέση” - ΛΑΘΟΣ:
Η SD είναι στον παρονομαστή του τύπου της z
Άμεση μαθηματική σχέση
Η z ορίζεται με βάση την SD
Δ - “Μεγάλη SD → μεγάλη z” - ΛΑΘΟΣ:
Αντίστροφη σχέση
Μεγάλη SD → μικρή z
Διαισθητική εξήγηση:
Τι σημαίνει η τιμή z:
Η z μετράει “Πόσες τυπικές αποκλίσεις μακριά από το μέσο όρο βρίσκεται η αρχική τιμή;”
Παράδειγμα:
- Απόσταση από μέσο όρο: 3.56 mpg
Αν SD = 2mpg:
z = 3.56 / 2 = 1.78 τυπικές αποκλίσεις
Η απόσταση 3.56 είναι μεγάλη σε σχέση με την SD
Αν SD = 10 mpg:
z = 3.56 / 10 = 0.356 τυπικές αποκλίσεις
Η ίδια απόσταση είναι μικρή σε σχέση με την SD
Συμπέρασμα:
Όταν η τυπική απόκλιση είναι μεγάλη, το η τιμή z για 27 mpg θα είναι μικρή και θετική. Αυτό συμβαίνει επειδή:
Θετική: Το 27 > 23.44, άρα πάνω από μέσο
Μικρή: Μεγάλη τυπική απόκλιση στον παρονομαστή → μικρό κλάσμα
Αντίστροφη σχέση: z ∝ 1/SD
Μεγάλη τυπική απόκλιση σημαίνει ότι τα δεδομένα είναι πιο διεσπαρμένα, οπότε η απόσταση 3.56mpg από το μέσο όρο αντιστοιχεί σε λιγότερες τυπικές αποκλίσεις.
15. Αν η τιμή z για τα μίλια ανά γαλόνι που διανύει ένα αυτοκίνητο στον αυτοκινητόδρομο βρεθεί ίση με 0.6, τι σημαίνει αυτό;
Σωστή απάντηση: Β
Ερμηνεία z = 0.6:
Η τιμή z = 0.6 σημαίνει ότι το αυτοκίνητο διανύει μίλια ανά γαλόνι που είναι 0.6 τυπικές αποκλίσεις πάνω από το μέσο όρο.
Υπολογισμός:
mean_hwy <- 23.44
sd_hwy <- 5.954
z <- 0.6
# X = μέσος + (z × SD)
X <- 23.44 + (0.6 × 5.954)
# X ≈ 27 mpgΓιατί οι άλλες είναι λάθος:
Α: Η τιμή z δεν μπορεί να συγκριθεί άμεσα με mpg - είναι διαφορετικές κλίμακες.
Γ: z ≠ ποσοστό. Για τον υπολογισμό του εκατοστημορίου στο οποίο βρίσκεται το z = 0.6: pnorm(0.6) ≈ 73%, όχι 60%.
Δ: Η τιμή z μπορεί να είναι οποιοσδήποτε αριθμός, όχι μόνο ακέραιοι.
Η τιμή z = 0.6 είναι απολύτως έγκυρη και σημαίνει ότι το αυτοκίνητο διανύει περισσότερα μίλια ανά γαλόνι από περίπου το 73% των αυτοκινήτων στην κατανομή.
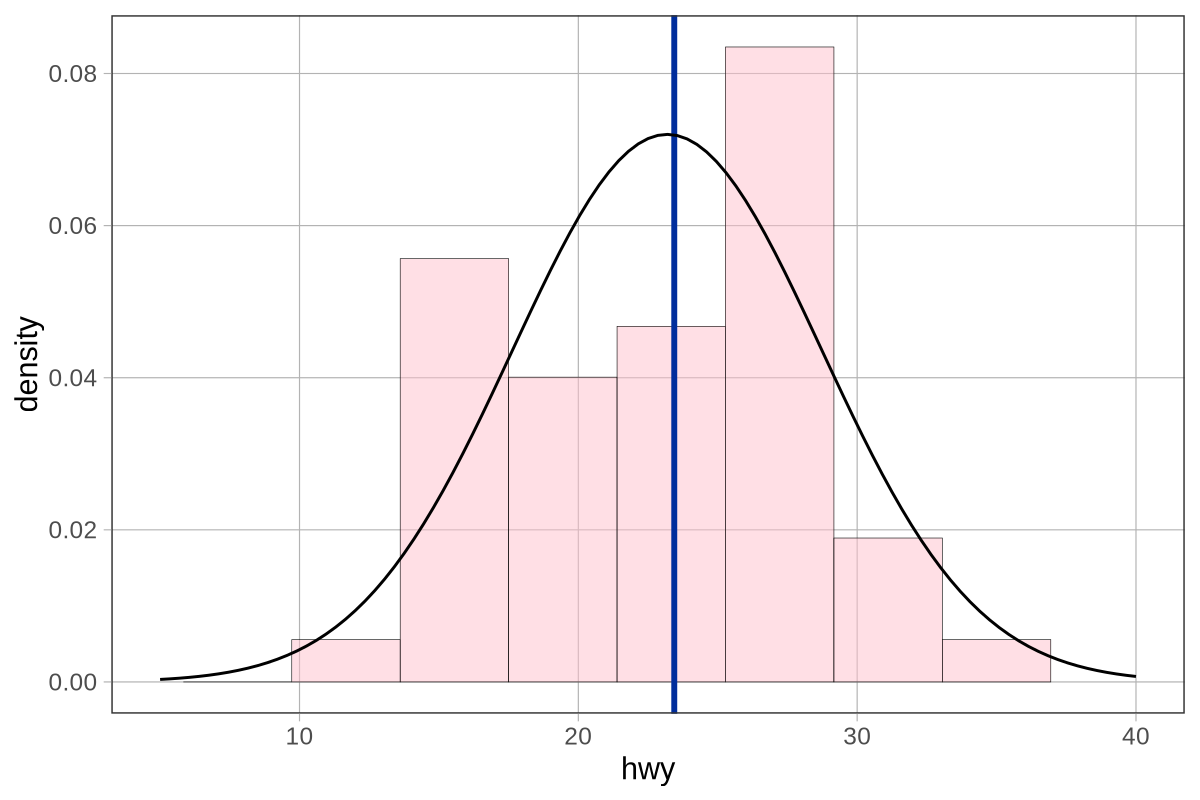
16. Αν προσαρμόσουμε μια καμπύλη κανονική κατανομής στη δειγματική κατανομή της hwy (δείτε το παραπάνω διάγραμμα), τι μοντελοποιούμε με αυτήν;
Σωστή απάντηση: Γ
Τι είναι το κενό μοντέλο:
\[\text{hwy}_i = \bar{\text{hwy}} + e_i\]
Όπου:
\(\bar{\text{hwy}}\) = μέσος όρος (23.44 mpg) - η μπλε γραμμή
\(e_i\) = υπόλοιπα που υποτίθεται ότι ακολουθούν κανονική κατανομή
Η κανονική καμπύλη μοντελοποιεί:
Την αναμενόμενη κατανομή των τιμών της hwy αν:
Το μόνο που ξέρουμε είναι ο μέσος όρος και η τυπική απόκλιση
Τα δεδομένα ακολουθούν κανονική κατανομή
Δεν υπάρχουν άλλες ανεξάρτητες μεταβλητές
Αυτό είναι το empty model με κανονικά κατανεμημένο σφάλμα.
Γιατί οι άλλες επιλογές είναι λάθος:
Α - “Δειγματικά στατιστικά” - ΑΝΑΚΡΙΒΕΣ:
Η μαύρη καμπύλη δείχνει το θεωρητικό μοντέλο
Η καμπύλη μοντελοποιεί την κατανομή, όχι τα στατιστικά του δείγματος
Β - “Τη διάμεσο” - ΛΑΘΟΣ:
Για την κανονική κατανομή ισχύει ότι μέσος = διάμεσος, αλλά εδώ μοντελοποιούμε το μέσο όρο
Η καμπύλη κανονικής κατανομής κεντράρεται στο μέσο όρο, όχι στη διάμεσο της κατανομής μας
Η μπλε γραμμή δείχνει το μέσο όρο (23.44)
Δ - “Σφάλμα γύρω από μοντέλο” - ΛΑΘΟΣ:
Η καμπύλη δείχνει την κατανομή των τιμών, όχι των σφαλμάτων
Τα σφάλματα θα ήταν: \(e_i = \text{hwy}_i - 23.44\)
Η κατανομή των σφαλμάτων είναι κεντραρισμένη στο 0, όχι στο 23.44
Συμπέρασμα:
Η κανονική καμπύλη που προσαρμόζεται στο ιστόγραμμα της hwy αντιπροσωπεύει το κενό μοντέλο - μια θεωρητική κατανομή που μοντελοποιεί την hwy χρησιμοποιώντας μόνο το μέσο όρο (23.44 mpg) και την τυπική απόκλιση (5.95 mpg), υποθέτοντας ότι τα δεδομένα ακολουθούν την κανονική κατανομή. Η μπλε γραμμή δείχνει το μέσο όρο, που είναι το “μοντέλο” μας για κάθε παρατήρηση όταν δεν έχουμε άλλες πληροφορίες.
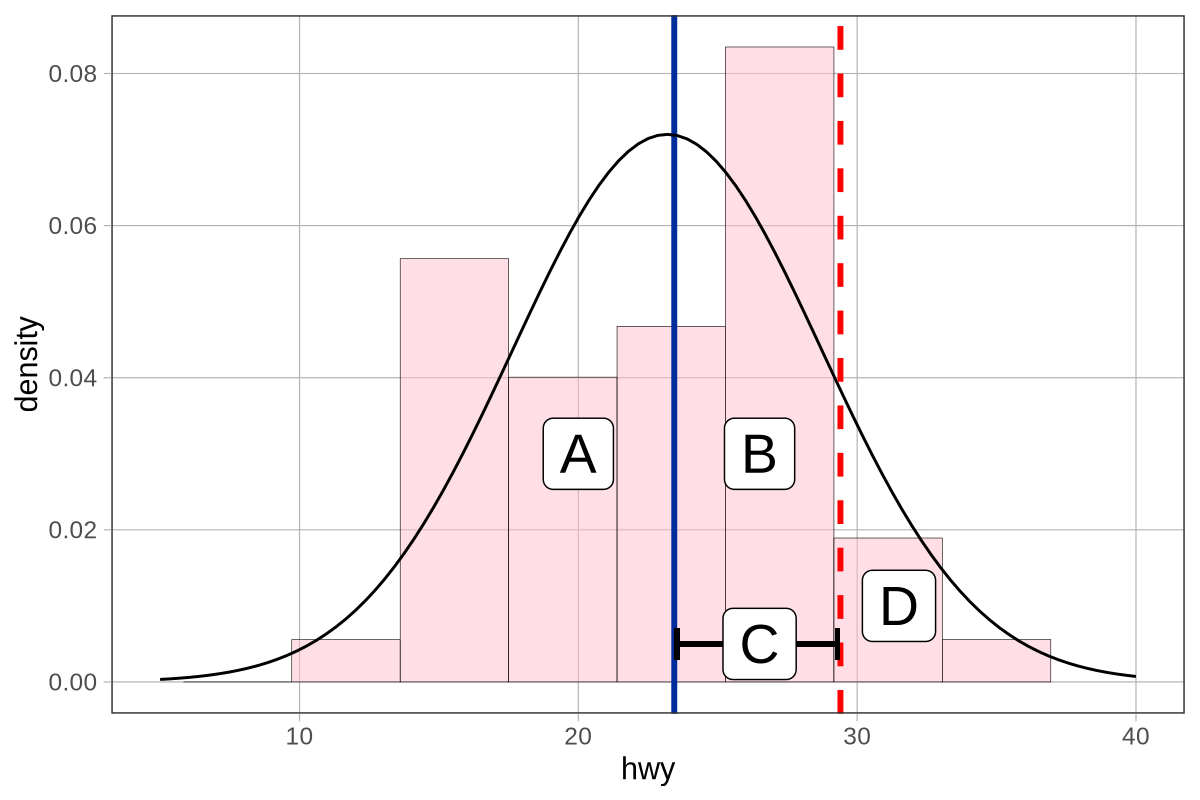
17. Στο παρακάτω διάγραμμα, ποιο μέρος αντιπροσωπεύει την πιθανότητα ένα αυτοκίνητο να έχει hwy πάνω από 29.4 (απεικονίζεται με κόκκινο); Ποιο μέρος αντιπροσωπεύει την απόκλιση της τιμής 29.4 από το μέσο όρο;
Σωστή απάντηση: Α (D και C)
Ανάλυση διαγράμματος:
Μπλε συμπαγής γραμμή: Μέσος όρος (23.44 mpg)
Κόκκινη διακεκομμένη γραμμή: Τιμή 29.4 mpg
A: Περιοχή αριστερά του μέσου όρου
B: Περιοχή μεταξύ μέσου όρου και 29.4
C: Οριζόντιο τμήμα στον άξονα x (από μπλε έως κόκκινη γραμμή)
D: Περιοχή δεξιά του 29.4
1. Πιθανότητα P(hwy > 29.4) = D:
Η πιθανότητα αντιπροσωπεύεται από το εμβαδόν κάτω από την καμπύλη δεξιά της κόκκινης γραμμής.
- Περιοχή D (σκιασμένη περιοχή δεξιά του 29.4)
2. Απόκλιση από το μέσο όρο = C:
Η απόκλιση αντιπροσωπεύεται από την οριζόντια απόσταση στον άξονα x από το μέσο όρο έως την τιμή 29.4.
Τμήμα C (οριζόντια γραμμή από 23.44 έως 29.4)
Μήκος: 29.4 - 23.44 = 5.96mpg
Σημείωση για τιμή z:
Το τμήμα C δείχνει την απόκλιση από το μέσο όρο (5.96 mpg). Για να βρούμε την τιμή z, διαιρούμε αυτή την απόκλιση με την τυπική απόκλιση:
\[z = \frac{\text{Απόκλιση}}{Τυπική Απόκλιση} = \frac{C}{5.95} = \frac{5.96}{5.95} \approx 1.0\]
Άρα το C αντιπροσωπεύει την απόκλιση, η οποία όταν τυποποιηθεί δίνει z ≈ 1.0.
Συνοπτικά:
D = Πιθανότητα (εμβαδόν)
C = Απόκλιση = 5.96 mpg (γραμμική απόσταση)
Απάντηση: D και C
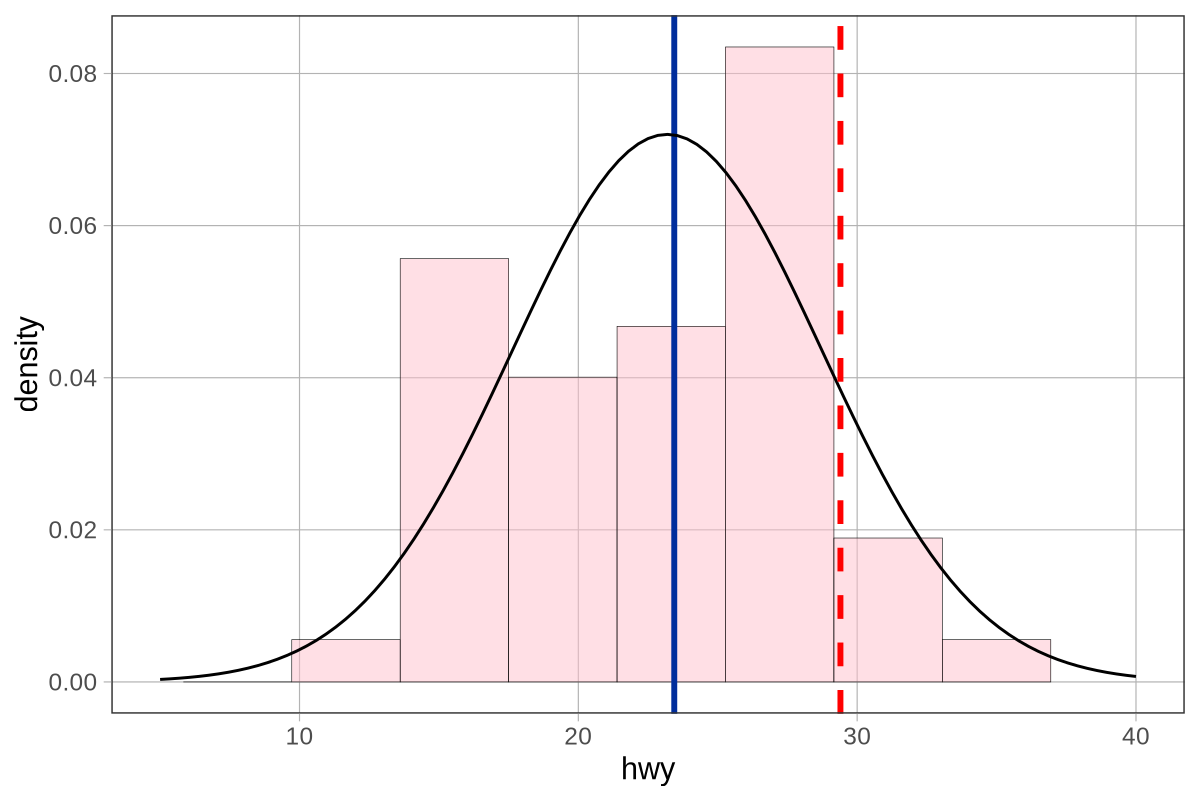
18. Δίνονται τα στατιστικά που αντιστοιχούν στο παραπάνω ιστόγραμμα της hwy. Με βάση τον Εμπειρικό Κανόνα (68-95-99.7), εκτιμήστε την πιθανότητα ένα αυτοκίνητο να έχει τιμή hwy πάνω από 29.4 (απεικονίζεται ως κόκκινη διακεκομμένη γραμμή).
min Q1 median Q3 max mean sd n missing
12 18 24 27 44 23.44017 5.954643 234 0Σημείωση: Αν και έχουμε αναπαραστήσει την αρχική κατανομή δεδομένων στο ιστόγραμμα, δεν χρειάζεται να χρησιμοποιήσετε τα δεδομένα. Απλά εκτιμήστε την πιθανότητα μιας τιμής μεγαλύτερης από 29.4 με βάση ένα μοντέλο της κανονικής κατανομής.
Σωστή απάντηση: Β (16%)
Εμπειρικός Κανόνας (68-95-99.7):
Για την κανονική κατανομή:
68% των δεδομένων εντός ±1 ΤΑ από μέσο
95% των δεδομένων εντός ±2 ΤΑ από μέσο
99.7% των δεδομένων εντός ±3 ΤΑ από μέσο
Υπολογισμός τιμής z:
mean_hwy <- 23.44
sd_hwy <- 5.95
x <- 29.4
z <- (x - mean_hwy) / sd_hwy
z <- (29.4 - 23.44) / 5.95
z ≈ 1.0Το 29.4 βρίσκεται ακριβώς 1 τυπική απόκλιση πάνω από το μέσο!
Εφαρμογή Εμπειρικού Κανόνα:
68% εντός ±1σ
|←────────────────→|
| |
────●──────────●───────●────
μ-1σ μ μ+1σ
17.5 23.44 29.4
32% αριστερά 34% δεξιά
από μ-1σ από μέσο
16% δεξιά
από μ+1σΛογική:
68% των δεδομένων είναι μεταξύ μ-1σ και μ+1σ
Άρα 32% είναι εκτός αυτής της ζώνης
Λόγω συμμετρίας: 16% κάτω από μ-1σ και 16% πάνω από μ+1σ
Το 29.4 είναι ακριβώς στο μ+1σ
Απάντηση: 16% των αυτοκινήτων έχουν hwy > 29.4
Γιατί οι άλλες είναι λάθος:
Α - 68% - ΛΑΘΟΣ:
Το 68% είναι το ποσοστό εντός ±1 SD, όχι εκτός
Αυτό θα ήταν P(-1 < z < 1), όχι P(z > 1)
Γ - 5.95% - ΛΑΘΟΣ:
Αυτό είναι το SD (5.95), όχι πιθανότητα
Σύγχυση μεταξύ SD και πιθανότητας
Δ - 32% - ΛΑΘΟΣ:
Αυτό είναι το ποσοστό εκτός ±1 SD (και στις δύο ουρές)
Θέλουμε μόνο τη δεξιά ουρά → 32% / 2 = 16%
Επαλήθευση με ακριβή υπολογισμό:
# Ακριβής πιθανότητα
1 - pnorm(29.4, mean = 23.44, sd = 5.95)
# 0.1587 ≈ 15.87% ≈ 16%
# Με z-score
1 - pnorm(1.0)
# 0.1587 ≈ 16%Ο Εμπειρικός Κανόνας δίνει εξαιρετική εκτίμηση!
Οπτικό διάγραμμα:
Κανονική κατανομή:
2.5% 13.5% 34% 34% 13.5% 2.5%
↓ ↓ ↓ ↓ ↓ ↓
────●──────●──────●──────●──────●──────●────
μ-3σ μ-2σ μ-1σ μ μ+1σ μ+2σ
23.44 29.4
P(z > 1) = 13.5% + 2.5% = 16% (περίπου)Χρήση Εμπειρικού Κανόνα:
Για z = 1.0 (ακριβώς 1 SD πάνω):
P(z > 1) = (100% - 68%) / 2
= 32% / 2
= 16%Συμπέρασμα:
Χρησιμοποιώντας τον Εμπειρικό Κανόνα:
Το 29.4 είναι 1 τυπική απόκλιση πάνω από το μέσο (z ≈ 1.0)
Ο Εμπειρικός Κανόνας λέει: 68% εντός ±1 Τυπική Απόκλιση
Άρα 32% εκτός, με 16% σε κάθε ουρά
Απάντηση: 16% των αυτοκινήτων έχουν hwy > 29.4
Αυτή η εκτίμηση είναι πολύ κοντά στην ακριβή τιμή (15.87%)!
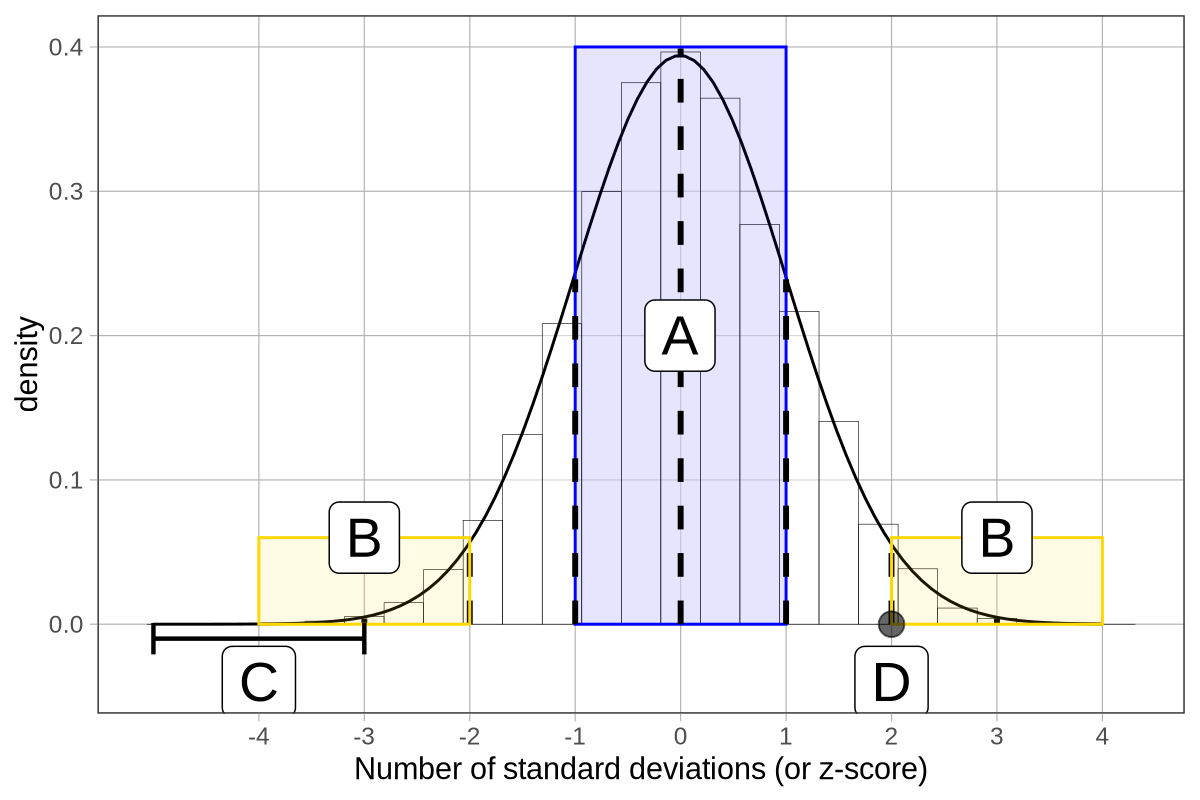
19. Παραπάνω δίνεται το μοντέλο της κανονικής κατανομής ενός πληθυσμού. Υπάρχουν περισσότερο ή λιγότερο πιθανές τιμές αυτής της μεταβλητής. Ποιο μέρος του πληθυσμού θα θεωρούνταν «απίθανο» να επιλεγεί τυχαία (σύμφωνα με τον ορισμό του απίθανου που έχει συμφωνηθεί από την κοινότητα των στατιστικολόγων);
Σωστή απάντηση: Β (οι περιοχές B)
Ορισμός του απίθανου στη στατιστική:
Στην κοινότητα των στατιστικολόγων, τιμές θεωρούνται απίθανες όταν βρίσκονται στα άκρα των ουρών της κατανομής, συγκεκριμένα:
Πέρα από ±2 τυπικές αποκλίσεις από το μέσο όρο
Αντιστοιχούν στο ακραίο 5% της κατανομής (από 2.5% σε κάθε ουρά)
Τιμές με |z| > 2
Ανάλυση διαγράμματος:
Στο διάγραμμα:
Άξονας x: Αριθμός τυπικών αποκλίσεων (τιμή z)
Διακεκομμένη γραμμή: Μέσος όρος (z = 0)
Μπλε περιοχή (A): Εντός ±1 τυπικής απόκλισης (68%)
Κίτρινες περιοχές (B): Μεταξύ 1-2 τυπικών αποκλίσεων και πέρα από 2 τυπικές αποκλήσεις (~27% + 5%)
C: Οριζόντιο τμήμα (απόσταση)
D: Σημείο στην τιμή z ≈ 2
Γιατί οι άλλες είναι λάθος:
Α - Μόνο η περιοχή A - ΛΑΘΟΣ:
Η περιοχή A (μπλε) περιέχει τις πιο συνηθισμένες τιμές (εντός ±1 τυπικές αποκλίσεις)
Αυτό είναι το 68% - αντίθετο του απίθανου
Οι απίθανες τιμές είναι εκτός αυτής της περιοχής
Γ - Το μήκος C - ΛΑΘΟΣ:
Το C δείχνει ένα οριζόντιο τμήμα, όχι περιοχή πιθανότητας
Δεν αντιπροσωπεύει πιθανότητες
Δ - Το σημείο D - ΛΑΘΟΣ:
Το D είναι ένα μεμονωμένο σημείο στο z ≈ 2
Δεν αντιπροσωπεύει μια περιοχή απίθανων τιμών
Οι απίθανες τιμές είναι πέρα από αυτό το σημείο (|z| > 2)
Γιατί ±2 τυπικές αποκλίσεις:
Από τον Εμπειρικό Κανόνα:
95% εντός ±2 τυπικών αποκλίσεων → “πιθανά”
5% εκτός ±2 τυπικών αποκλίσεων → “απίθανα”
Απίθανες τιμές: |z| > 2 (περιοχές B στα άκρα των ουρών)
Συμπέρασμα:
Οι κίτρινες περιοχές B (και στις δύο ουρές) αντιπροσωπεύουν τις απίθανες τιμές σύμφωνα με τη σύμβαση των στατιστικολόγων. Αυτές είναι οι τιμές με |z| > 2, που αντιστοιχούν στο εξωτερικό 5% της κατανομής (2.5% σε κάθε ουρά). Τέτοιες τιμές θεωρούνται ακραίες ή ασυνήθιστες και συχνά χρησιμοποιούνται ως κατώφλι για τον εντοπισμό ακραίων τιμών ή για τη λήψη στατιστικών αποφάσεων.
- Ποια είναι διαφορά ανάμεσα σε ένα υπόλοιπο (residual) και στην τυπική απόκλιση (standard deviation);
Η επόμενη ομάδα ερωτήσεων βασίζεται σε ένα πλαίσιο δεδομένων που ονομάζεται FatMice18, το οποίο περιέχει δεδομένα για 18 ποντίκια. Τα ποντίκια υποβλήθηκαν τυχαία σε μία από δύο θεραπείες με φως: LD (κύκλος φως/σκοτάδι) ή LL (φως κατά τη διάρκεια της ημέρας και φως τη νύχτα επίσης). Οι ερευνητές παρακολούθησαν το βάρος που έβαλε κάθε ποντίκι (σε γραμμάρια) κατά τη διάρκεια τεσσάρων εβδομάδων αυτής της παρέμβασης.
Οι μεταβλητές στο πλαίσιο δεδομένων είναι:
Light: Θεραπείες με φως: LD ή LLWgtGain4: Αύξηση βάρους σε γραμμάρια κατά τη διάρκεια τεσσάρων εβδομάδωνCageLoc: Η τοποθεσία του κλουβιού στο ερευνητικό εργαστήριο, στην επάνω σειρά (top row) ή την κάτω σειρά (bottom row)
Αποτέλεσμα της head(FatMice18):
Light WgtGain4 CageLoc
1 LL 10 top row
2 LL 10 top row
3 LL 11 bottom row
4 LL 9 bottom row
5 LL 12 top row
6 LL 9 bottom row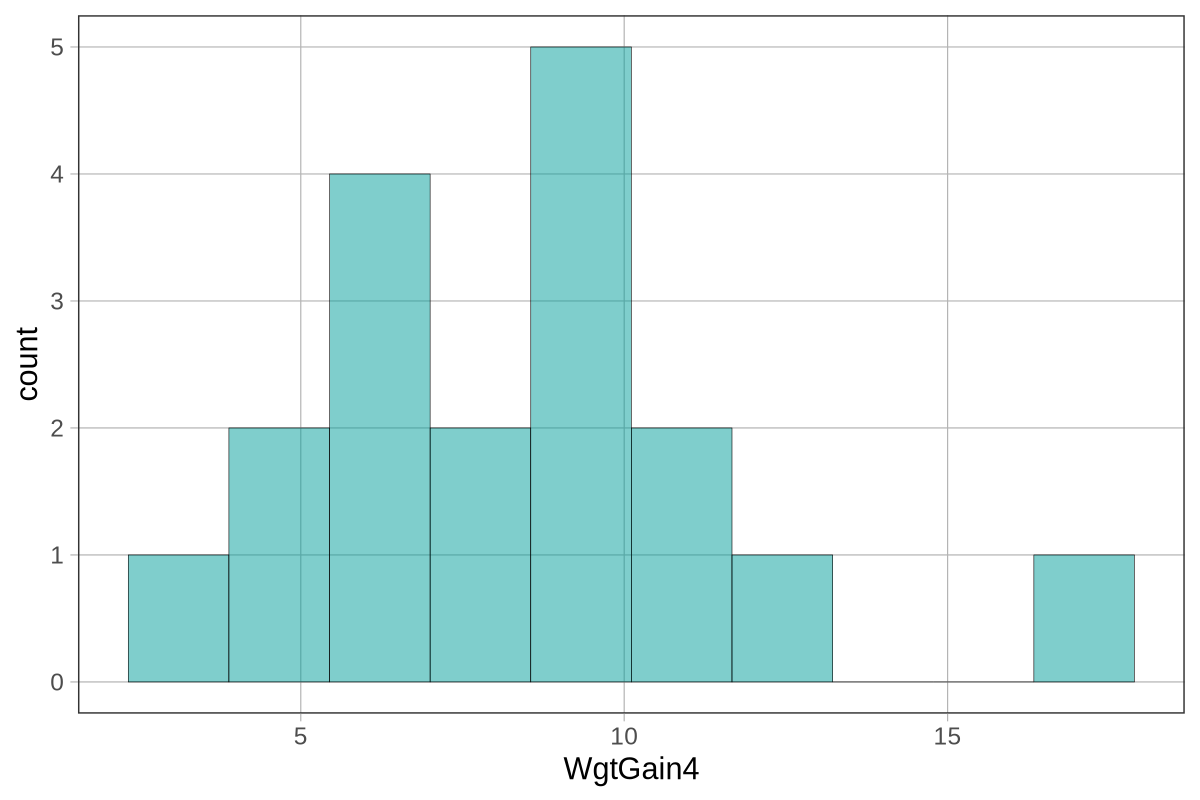
21. Δίνεται το ιστόγραμμα της μεταβλητής WgtGain4. Τι θα πάρετε αν αθροίσετε το ύψος (το “count”) όλων των στηλών;
Σωστή απάντηση: Β
Τι δείχνει το ιστόγραμμα:
άξονας x: Τιμές της
WgtGain4(αύξηση βάρους σε γραμμάρια)άξονας y: Count (πλήθος/συχνότητα)
Κάθε στήλη/ράβδος: Πόσα ποντίκια είχαν αύξηση βάρους σε συγκεκριμένο εύρος
Άθροισμα όλων των υψών:
Κάθε ποντίκι εμφανίζεται ακριβώς μία φορά στο ιστόγραμμα, σε μία από τις ράδβους.
\[\sum_{\text{all bins}} \text{count}_i = n = 18 \text{ ποντίκια}\]
Από το διάγραμμα:
Μετρώντας τις στήλες:
1 + 2 + 4 + 2 + 5 + 2 + 1 + 0 + 1 = 18 ποντίκιαΓιατί οι άλλες είναι λάθος:
Α - “Άθροισμα 0” - ΛΑΘΟΣ:
Το άθροισμα των counts είναι το n, όχι 0
Το άθροισμα των υπολοίπων είναι 0, όχι των counts
Γ - “Άθροισμα τετραγώνων” - ΛΑΘΟΣ:
Sum of Squares = \(\sum(Y_i - \bar{Y})^2\)
Αυτό δεν σχετίζεται με το άθροισμα των ύψη των στηλών
Δ - “Συνολική αύξηση βάρους” - ΛΑΘΟΣ:
Αυτό θα ήταν
sum(FatMice18$WgtGain4)Το ιστόγραμμα δείχνει πόσα ποντίκια σε κάθε διάστημα τιμών, όχι το άθροισμα των γραμμαρίων
Συμπέρασμα:
Το άθροισμα των υψών όλων των ράβδων στο ιστόγραμμα ισούται με τον συνολικό αριθμό ποντικιών στο σύνολο δεδομένων, δηλαδή 18. Αυτό ισχύει για κάθε ιστόγραμμα απολύτων συχνοτήτων - το άθροισμα των συχνοτήτων πάντα ισούται με το μέγεθος του δείγματος.
22. Με βάση τα δεδομένα (βλ. παραπάνω ιστόγραμμα), ποια είναι η καλύτερη εκτίμησή μας για την πιθανότητα ένα ποντίκι σε μελλοντική μελέτη να βάλει περισσότερα από 15 γραμμάρια βάρους;
Σωστή απάντηση: Γ (1/18)
Από το ιστόγραμμα:
Παρατηρώντας το διάγραμμα, βλέπουμε ότι 1 ποντίκι από τα 18 είχε αύξηση βάρους >15 γραμμάρια (φαίνεται στη στήλη στο ~17 γραμμάρια).
Εμπειρική πιθανότητα:
Η καλύτερη εκτίμηση βασισμένη στο δείγμα είναι η δειγματική αναλογία:
\[P(\text{WgtGain4} > 15) = \frac{\text{Αριθμός ποντικιών με WgtGain4 > 15}}{\text{Συνολικός αριθμός ποντικιών}} = \frac{1}{18}\]
Γιατί οι άλλες είναι λάθος:
Α - “0.001” - ΛΑΘΟΣ:
Αυτό θα ήταν 0.1% πιθανότητα
Πολύ μικρότερο από την πραγματική αναλογία 1/18 ≈ 5.56%
Δεν βασίζεται στα δεδομένα
Β - “Περισσότερο από δύο τυπικές αποκλίσεις” - ΛΑΘΟΣ:
Αυτό δεν είναι πιθανότητα, είναι περιγραφή απόστασης
Ακόμα και αν το 15 είναι >2 τυπικές αποκλίσεις, η πιθανότητα θα ήταν ~2.5%, όχι αυτή η φράση
Λάθος μορφή απάντησης
Δ - “15/WgtGain4” - ΛΑΘΟΣ:
Αυτό δεν έχει νόημα μαθηματικά
Δεν μπορείς να διαιρέσεις αριθμό με μεταβλητή
Δεν είναι έγκυρη πιθανότητα
Εμπειρική vs Θεωρητική πιθανότητα:
Εμπειρική (από δεδομένα):
Βασίζεται στο δείγμα: 1/18 ≈ 5.56%
Καλύτερη εκτίμηση με μικρό δείγμα
Θεωρητική (από μοντέλο):
# Αν υποθέσουμε κανονική κατανομή
mean_wgt <- mean(FatMice18$WgtGain4)
sd_wgt <- sd(FatMice18$WgtGain4)
1 - pnorm(15, mean = mean_wgt, sd = sd_wgt)
# Θα έδινε διαφορετική εκτίμησηΑλλά η ερώτηση ζητάει εκτίμηση βασισμένη στο δείγμα, όχι από μοντέλο.
Συμπέρασμα:
Η καλύτερη εκτίμηση για την πιθανότητα ένα ποντίκι να βάλει >15 γραμμάρια είναι η δειγματική αναλογία: 1/18 ≈ 0.0556 ή 5.56%. Αυτή είναι η πιο άμεση και απλή εκτίμηση βασισμένη στα παρατηρούμενα δεδομένα, όπου 1 από τα 18 ποντίκια στο δείγμα ξεπέρασε τα 15 γραμμάρια αύξησης βάρους.
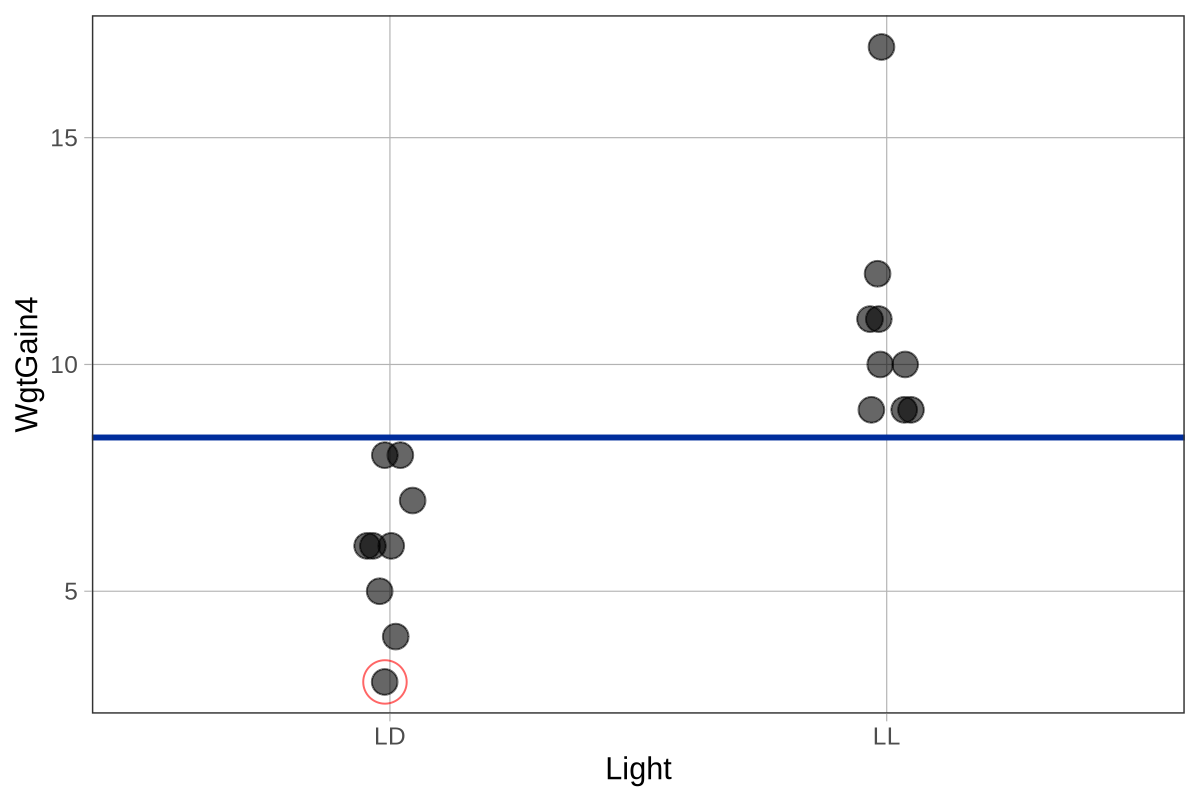
23. Εξετάστε το ποντίκι που έβαλε τη μικρότερη ποσότητα βάρους σε αυτή τη μελέτη (σημειώνεται με κόκκινο κύκλο στο παραπάνω διάγραμμα). Τι ισχύει για το υπόλοιπο (residual) της τιμής αυτού του ποντικιού από το κενό μοντέλο (empty model);
Σωστή απάντηση: Γ
Ανάλυση του διαγράμματος:
Μπλε οριζόντια γραμμή: Μέσος όρος της
WgtGain4για όλα τα ποντίκιαΚόκκινος κύκλος: Το ποντίκι με τη μικρότερη αύξηση βάρους (3 γραμμάρια)
Ομάδα LD: Αριστερά της κάθετης γραμμής
Υπολογισμός υπολοίπου:
\[\text{υπόλοιπο} = Y_i - \bar{Y}\]
Για το ποντίκι με τη μικρότερη αύξηση:
Y_min <- 3
mean_Y <- 8.4 # η μπλε γραμμή (εκτίμηση)
residual <- Y_min - mean_Y
# υπόλοιπο ≈ 3 - 8.4 = -5.4
# Απόλυτη τιμή
abs(residual) ≈ 5.4 # ΜΕΓΑΛΗ απόκλισηΓιατί η Γ είναι σωστή:
Το ποντίκι είναι πολύ μακριά από το μέσο όρο (μπλε γραμμή), άρα:
Το υπόλοιπο είναι αρνητικό (κάτω από μέσο)
Η απόλυτη τιμή |residual| είναι μεγάλη
Είναι πιθανή ακραία παρατήρηση
Γιατί οι άλλες είναι λάθος:
Α - “Το υπόλοιπο είναι έχει μεγαλύτερη μεταβλητότητα” - ΛΑΘΟΣ:
Ένα μεμονωμένο υπόλοιπο δεν είναι “μεταβλητό”
Η “μεταβλητότητα” αναφέρεται σε μια κατανομή υπολοίπων, όχι σε ένα σημείο
Το υπόλοιπο είναι απλά μεγάλο σε απόλυτη τιμή
Β - “Το υπόλοιπο θα πρέπει να είναι 0” - ΛΑΘΟΣ:
Το άθροισμα όλων των υπολοίπων είναι 0, όχι κάθε ένα ξεχωριστά
\[\sum e_i = 0\], αλλά \(e_i \neq 0\) για κάθε i
Αυτό το συγκεκριμένο υπόλοιπο είναι μεγάλο και αρνητικό (~-5.4)
Δ - “Το υπόλοιπο είναι μεγάλο και θετικό” - ΛΑΘΟΣ:
Το υπόλοιπο είναι μεγάλο αλλά αρνητικό, όχι θετικό
Το σημείο είναι κάτω από το μέσο → αρνητικό υπόλοιπο
Θετικό υπόλοιπο θα σήμαινε πάνω από το μέσο
Οπτική κατανόηση:
Μέσος (μπλε γραμμή) ≈ 8.4
═══════════════════════════
↑
|
| υπόλοιπο = -5.4
| (ΜΕΓΑΛΗ απόλυτη τιμή)
|
↓
⊗ ← Ποντίκι με min WgtGain = 3Σημασία:
Ένα υπόλοιπο με μεγάλη απόλυτη τιμή υποδηλώνει:
Το μοντέλο (μέσος όρος) δεν προβλέπει καλά αυτό το σημείο
Πιθανή ακραία ή ασυνήθιστη παρατήρηση
Μεγάλη απόκλιση από το μοντέλο
Συμπέρασμα:
Το ποντίκι που έβαλε τη μικρότερη ποσότητα βάρους (3g) βρίσκεται πολύ μακριά από το μέσο όρο (8.4g), με αποτέλεσμα ένα υπόλοιπο περίπου -5.4 γραμμαρίων. Η απόλυτη τιμή αυτού του υπολοίπου (=5.4) είναι σχετικά μεγάλη, καθιστώντας αυτό το ποντίκι πιθανά μια ακραία παρατήρηση στο σύνολο δεδομένων.
24. Αν έχετε υπολογίσει τη διακύμανση για το WgtGain4, τι έχετε βρει;
Σωστή απάντηση: Β
Τι είναι η διακύμανση:
\[\text{Variance} = s^2 = \frac{\sum(Y_i - \bar{Y})^2}{n-1} = \frac{\sum e_i^2}{n-1}\]
Είναι η μέση τετραγωνική απόκλιση από το μέσο όρο (ή από το empty model).
Για το empty model:
\[\text{WgtGain4}_i = \bar{\text{WgtGain4}} + e_i\]
Τα residuals είναι: \(e_i = \text{WgtGain4}_i - \bar{\text{WgtGain4}}\)
Η διακύμανση είναι ο μέσος όρος των τετραγώνων αυτών των residuals.
Γιατί οι άλλες είναι λάθος:
Α - “Άθροισμα των residuals” - ΛΑΘΟΣ:
Το άθροισμα των residuals είναι πάντα 0
\[\sum e_i = 0\]
Η διακύμανση δεν είναι 0
Γ - “Μέση απόκλιση σε γραμμάρια” - ΛΑΘΟΣ:
Αυτό θα ήταν η τυπική απόκλιση (SD), όχι η διακύμανση
SD = \(\sqrt{\text{Variance}}\)
Μονάδες: γραμμάρια (όχι τετραγωνικά)
Δ - “Συνολική τετραγωνική απόκλιση” - ΛΑΘΟΣ:
Αυτό θα ήταν το Sum of Squares (SS)
SS = \(\sum(Y_i - \bar{Y})^2\) (χωρίς διαίρεση)
Η διακύμανση = SS/(n-1), όχι SS
Σύγκριση μέτρων:
Μέτρο | Τύπος | Μονάδες | Ερμηνεία
------------------ | -------------- | -------------- | -----------
Sum of Squares | Σ(Y-Ȳ)² | g² | Συνολική
Variance | Σ(Y-Ȳ)²/(n-1) | g² | Μέση τετρ.
Standard Deviation | √[Σ(Y-Ȳ)²/(n-1)] | g | ΜέσηΠαράδειγμα υπολογισμού:
# Δεδομένα (υποθετικά)
WgtGain4 <- c(2.5, 4, 5, 6, 8, 9, 10, 11, 12, 17)
mean_wgt <- mean(WgtGain4) # 8.45
# Residuals
e <- WgtGain4 - mean_wgt
# Sum of Squares (Δ - λάθος)
SS <- sum(e^2) # 184.25 g²
# Variance (Β - σωστό)
variance <- SS / (length(WgtGain4) - 1)
# 184.25 / 9 = 20.47 g²
# Ή απευθείας
var(WgtGain4) # 20.47 g²
# Standard Deviation (Γ - λάθος)
SD <- sqrt(variance) # 4.52 g
sd(WgtGain4) # 4.52 gΓιατί “περίπου” μέση:
Λέμε “περίπου” επειδή:
Διαιρούμε με \(n-1\), όχι \(n\)
Είναι το Mean Square, όχι ακριβώς ο αριθμητικός μέσος όρος
Αλλά εννοιολογικά είναι η “χαρακτηριστική” τετραγωνική απόκλιση
Μονάδες - τετραγωνικά γραμμάρια:
# Αρχικά δεδομένα: γραμμάρια (g)
WgtGain4 # μονάδες: g
# Residuals: γραμμάρια
e <- WgtGain4 - mean(WgtGain4) # g
# Τετράγωνα residuals: τετραγωνικά γραμμάρια
e^2 # g²
# Variance: μέσος όρος τετραγώνων
var(WgtGain4) # g²
# Standard Deviation: ρίζα διακύμανσης
sd(WgtGain4) # g (πίσω στα γραμμάρια)Συμπέρασμα:
Η διακύμανση του WgtGain4 αντιπροσωπεύει περίπου τη μέση τετραγωνική απόκλιση από το empty model (μέσος όρος), μετρημένη σε τετραγωνικά γραμμάρια (g²). Είναι ο μέσος όρος των τετραγώνων των residuals, που δείχνει πόσο διασκορπισμένα είναι τα δεδομένα γύρω από το μέσο όρο. Οι μονάδες είναι τετραγωνικές επειδή τετραγωνίζουμε τις αποκλίσεις πριν υπολογίσουμε το μέσο όρο.
25. Αν η τιμή z της αύξησης του βάρους ενός ποντικιού είναι -0.7, τι σημαίνει αυτό;
Σωστή απάντηση: Γ
Ερμηνεία z = -0.7:
\[z = \frac{X - \bar{X}}{SD} = -0.7\]
Η αρνητική τιμη z σημαίνει ότι η τιμή βρίσκεται κάτω από το μέσο όρο.
Συγκεκριμένα: 0.7 τυπικές αποκλίσεις κάτω από το μέσο όρο.
Γιατί οι άλλες είναι λάθος:
Α - “Χαμηλότερη από 70%” - ΛΑΘΟΣ:
Η τιμή z δεν είναι εκατοστημόριο
Για εκατοστημόρια
pnorm(-0.7)≈ 24.2%Δηλαδή χαμηλότερη από ~76% του δείγματος, όχι 70%
Β - “70% χαμηλότερη” - ΛΑΘΟΣ:
z = -0.7 δεν σημαίνει 70% μείωση
Αυτό θα ήταν: X = 0.30 × μέσος (30% του μέσου)
Η z μετράει σε τυπικές αποκλίσεις, όχι ποσοστά
Δ - “Έχασε 0.7 γραμμάρια” - ΛΑΘΟΣ:
z = -0.7 δεν σημαίνει -0.7 γραμμάρια
Η z δεν έχει μονάδες
Η πραγματική απόκλιση: z × SD = -0.7 × 3.5 = -2.45 γραμμάρια
Επίσης, το ποντίκι δεν έχασε βάρος - έβαλε λιγότερο από μέσο όρο
Συμπέρασμα:
Η τιμή z= -0.7 σημαίνει ότι η αύξηση βάρους του ποντικιού είναι 0.7 τυπικές αποκλίσεις κάτω από το μέσο όρο. Αυτό είναι μια τυποποιημένη μέτρηση που μας δείχνει πόσο “μακριά” είναι η τιμή από το μέσο, μετρημένη σε μονάδες τυπικής απόκλισης. Το ποντίκι έβαλε λιγότερο βάρος από το μέσο όρο, αλλά όχι εξαιρετικά λιγότερο (|z| < 1 θεωρείται σχετικά συνηθισμένη τιμή).
26. Εκτελέστε την favstats() για τη WgtGain4 (πλαίσιο δεδομένων FatMice18). Σε ποια τιμή της θα είναι μικρότερο το άθροισμα των τετραγώνων των σφαλμάτων;
Σωστή απάντηση: Β (8.39)
Θεμελιώδης αρχή:
Το άθροισμα των τετραγώνων των σφαλμάτων (Sum of Squares) ελαχιστοποιείται όταν χρησιμοποιούμε το μέσο όρο ως τιμή πρόβλεψης:
\[SS = \sum_{i=1}^{n}(Y_i - c)^2\]
Όπου \(c\) είναι η σταθερή τιμή πρόβλεψης. Το SS είναι ελάχιστο όταν \(c = \bar{Y}\).
Για τη WgtGain4:
Μέσος όρος = 8.388889 ≈ 8.39
Αυτή η τιμή ελαχιστοποιεί το SS
Γιατί ο μέσος ελαχιστοποιεί το SS:
Αν πάρουμε την παράγωγο:
\[\frac{d}{dc}\sum(Y_i - c)^2 = -2\sum(Y_i - c) = 0\]
Λύνουμε ως προς \(c\):
\[\sum Y_i - nc = 0\] \[c = \frac{\sum Y_i}{n} = \bar{Y}\]
Γιατί οι άλλες είναι λάθος:
Α - “3” (ελάχιστη τιμή) - ΛΑΘΟΣ:
Το 3 είναι η ελάχιστη τιμή (minimum), όχι η τιμή που ελαχιστοποιεί το SS
Αν χρησιμοποιήσουμε το 3: το SS θα είναι πολύ μεγαλύτερο
Γ - “0” - ΛΑΘΟΣ:
Η τιμή 0 δεν βρίσκεται καν στο εύρος των δεδομένων (min = 3)
Θα έδινε τεράστιο SS
Συγχέει το SS (που ελαχιστοποιείται) με το άθροισμα των υπολοίπων (που είναι 0)
Δ - “Δεν μπορούμε να είμαστε σίγουροι” - ΛΑΘΟΣ:
Μπορούμε να είμαστε απολύτως σίγουροι
Είναι μαθηματικό θεώρημα: ο μέσος όρος ελαχιστοποιεί το SS
Δεν είναι εμπειρική εκτίμηση - είναι αλγεβρικό αποτέλεσμα
Συμπέρασμα:
Το άθροισμα τετραγώνων των σφαλμάτων (Sum of Squares) ελαχιστοποιείται στο μέσο όρο (8.39 γραμμάρια). Αυτή είναι θεμελιώδης ιδιότητα του μέσου όρου - ελαχιστοποιεί το άθροισμα των τετραγώνων των αποκλίσεων από αυτόν. Γι’ αυτό χρησιμοποιούμε το μέσο όρο ως το κενό μοντέλο (“empty model”) - είναι η καλύτερη σημειακή πρόβλεψη όταν δεν έχουμε άλλες πληροφορίες.
27. Προσαρμόστε το μηδενικό (NULL) ή κενό μοντέλο (empty model) της WgtGain4. Ποιο είναι το άθροισμα τετραγώνων γι’ αυτό το μοντέλο;
Σωστή απάντηση: Β (186.278)
Ανάγνωση των αποτελεσμάτων της supernova:
Από τον πίνακα ANOVA:
Total (empty model) | 186.278 17 10.958
↑ ↑ ↑
SS df MSΤο Sum of Squares (SS) είναι 186.278.
Τι σημαίνει αυτό:
\[SS = \sum_{i=1}^{18}(\text{WgtGain4}_i - \bar{\text{WgtGain4}})^2 = 186.278\]
Αυτό είναι η συνολική διακύμανση των δεδομένων γύρω από το μέσο όρο (8.389g).
Επαλήθευση των σχέσεων:
# Από supernova
SS <- 186.278
df <- 17
MS <- 10.958
# Έλεγχος: MS = SS/df
SS / df # 186.278 / 17 = 10.958 ✓
# Έλεγχος: SD = √MS
sqrt(MS) # √10.958 = 3.31 ✓Γιατί οι άλλες είναι λάθος:
Α - “10.958” - ΛΑΘΟΣ:
Αυτό είναι το Mean Square (MS) ή διακύμανση
MS = SS/df = μέση τετραγωνική απόκλιση
Γ - “17” - ΛΑΘΟΣ:
Αυτό είναι οι βαθμοί ελευθερίας (df)
df = n - 1 = 18 - 1 = 17
Δ - “0” - ΛΑΘΟΣ:
Το άθροισμα των υπολοίπων είναι 0: \(\sum e_i = 0\)
Το άθροισμα των τετραγώνων των υπολοίπων είναι 186.278: \(\sum e_i^2 = 186.278\)
Πλήρης πίνακας τιμών:
Μέτρο | Τιμή | Μονάδες
---------------------- | --------- | -------
Sum of Squares (SS) | 186.278 | g²
Degrees of Freedom | 17 | -
Mean Square (MS) | 10.958 | g²
Standard Deviation | 3.31 | gΣυμπέρασμα:
Το άθροισμα των τετραγώνων για το κενό μοντέλο είναι 186.278, όπως φαίνεται απευθείας στη στήλη SS του πίνακα της supernova.
28. Μόλις εκτελέσατε τον παρακάτω κώδικα:
Λάβατε το παρακάτω αποτέλεσμα:
FALSE TRUE
14 4
FALSE TRUE
0.7777778 0.2222222Τι μπορείτε να ισχυριστείτε;
Σωστή απάντηση: Γ (Και τα δύο παραπάνω)
Ανάλυση των αποτελεσμάτων:
# Συχνότητες
table(FatMice18$WgtGain4 > 10)
# FALSE: 14 ποντίκια (≤10g)
# TRUE: 4 ποντίκια (>10g)
# Αναλογίες
prop.table(table(FatMice18$WgtGain4 > 10))
# FALSE: 0.778 (77.8%)
# TRUE: 0.222 (22.2%)Α. Περίπου το 22% έβαλε >10g - ΣΩΣΤΟ ✓
Αυτή είναι η δειγματική αναλογία:
4 από 18 ποντίκια = 4/18 = 0.222 = 22.2%
Περιγραφή του δείγματος που έχουμε
Β. Πιθανότητα για νέο ποντίκι = 22% - ΣΩΣΤΟ ✓
Η δειγματική αναλογία είναι η καλύτερη εκτίμηση για την πιθανότητα:
Χρησιμοποιούμε την εμπειρική πιθανότητα από το δείγμα
P(WgtGain4 > 10) ≈ 0.222
Εκτίμηση για μελλοντική παρατήρηση
Γιατί και τα δύο είναι σωστά:
Δειγματική αναλογία (Α):
Περιγράφει το παρελθόν - τι συνέβη στο δείγμα
“22% των ποντικιών που παρατηρήσαμε”
Εκτιμώμενη πιθανότητα (Β):
Πρόβλεψη για το μέλλον - τι αναμένουμε
“22% πιθανότητα για νέο ποντίκι”
Η ίδια τιμή (22%) χρησιμοποιείται και για τα δύο!
Σχέση αναλογίας και πιθανότητας:
Δειγματική αναλογία → Εκτίμηση πιθανότητας
Παρελθόν (δεδομένα) Μέλλον (πρόβλεψη)
↓ ↓
22.2% → 22.2%
"τι είδαμε" "τι περιμένουμε"Συμπέρασμα:
Και οι δύο δηλώσεις είναι σωστές:
Α: Περιγραφική - το 22% του δείγματός μας
Β: Προβλεπτική - 22% πιθανότητα για νέα παρατήρηση
Η δειγματική αναλογία (0.222) χρησιμεύει ως η καλύτερη εκτίμησή μας τόσο για την περιγραφή του δείγματος όσο και για την πρόβλεψη μελλοντικών αποτελεσμάτων.
29. Ας υποθέσουμε ότι θέλουμε να συγκρίνουμε το μοντέλο WgtGain4 = Light + σφάλμα με το κενό μοντέλο (WgtGain4 = μέσος όρος + σφάλμα). Σε τι αναφέρεται ο «μέσος όρος» στην εξίσωση του κενού μοντέλου;
Σωστή απάντηση: Β
Το κενό μοντέλο:
\[\text{WgtGain4}_i = \text{μέσος όρος} + e_i\]
Ο “μέσος όρος” αναφέρεται στο γενικό μέσο όρο της WgtGain4 για όλα τα 18 ποντίκια, ανεξάρτητα από την ομάδα της Light.
Σύγκριση μοντέλων:
Κενό Μοντέλο:
WgtGain4 = 8.389 + σφάλμα
Μία πρόβλεψη για όλα τα ποντίκια
Αγνοεί τη μεταβλητή Light
Μοντέλο Light:
WgtGain4 = Light + σφάλμα
-
Διαφορετική πρόβλεψη για κάθε ομάδα:
ομάδα LD: μέσος όρος WgtGain4 για Light=LD
ομάδα LL: μέσος όρος WgtGain4 για Light=LL
Γιατί οι άλλες είναι λάθος:
Α - “Μέσος υπολοίπων” - ΛΑΘΟΣ:
Ο μέσος όρος των υπολοίπων είναι πάντα 0
\(\sum e_i = 0\) για κάθε μοντέλο
Δεν είναι χρήσιμη πρόβλεψη
Γ - “Μέσος όρος της Light” - ΛΑΘΟΣ:
Η
Lightείναι κατηγορική μεταβλητή (LD, LL)Δεν έχει αριθμητικό μέσο όρο
Δεν έχει νόημα: mean(“LD”, “LL”) = ?
Δ - “Μέσος όρος για πρώτη συνθήκη” - ΛΑΘΟΣ:
Το κενό μοντέλο χρησιμοποιεί τον γενικό μέσο
Όχι τον μέσο μιας υποομάδας
Παράδειγμα με δεδομένα:
# Κενό μοντέλο - ένας μέσος όρος για όλα
overall_mean <- mean(FatMice18$WgtGain4)
# 8.389 g
# Μοντέλο Light - διαφορετικοί μέσοι ανά ομάδα
mean_LD <- mean(FatMice18$WgtGain4[FatMice18$Light == "LD"])
mean_LL <- mean(FatMice18$WgtGain4[FatMice18$Light == "LL"])
# Προβλέψεις του κενού μοντέλου για όλες τις παρατηρήσεις:
# 8.389, 8.389, 8.389, ...
# Προβλέψεις του μοντέλου Light:
# LD ποντίκια: mean_LD, mean_LD, ...
# LL ποντίκια: mean_LL, mean_LL, ...Συμπέρασμα:
Ο “μέσος όρος” στο κενό μοντέλο αναφέρεται στο γενικό μέσο όρο της WgtGain4 για όλα τα 18 ποντίκια (8.389 γραμμάρια). Αυτή είναι η απλούστερη πρόβλεψη - χρησιμοποιούμε την ίδια τιμή για κάθε ποντίκι, ανεξάρτητα από την ομάδα θεραπείας που ανήκει (Light). Το μοντέλο που περιλαμβάνει τη μεταβλητή Light, αντίθετα, χρησιμοποιεί διαφορετικούς μέσους όρους για κάθε ομάδα (LD και LL).
30. Αν προσθέσουμε περισσότερα ποντίκια στη μελέτη, ποιο από τα παρακάτω σίγουρα ΔΕΝ θα επηρεαστεί;
Σωστή απάντηση: Α (\(\beta_0\))
Ερμηνεία ως τιμές:
Α. \(\beta_0\) (παράμετρος πληθυσμού) - ΔΕΝ ΕΠΗΡΕΑΖΕΤΑΙ ✓
Το \(\beta_0\) είναι η άγνωστη σταθερή παράμετρος του πληθυσμού
Αντιπροσωπεύει την πραγματική μέση τιμή στον πληθυσμό όλων των ποντικιών
Δεν αλλάζει όταν προσθέτουμε περισσότερα ποντίκια στο δείγμα
Είναι σταθερή, ανεξάρτητα από το μέγεθος του δείγματός μας
Β. \(b_0\) (εκτιμητής δείγματος) - ΕΠΗΡΕΑΖΕΤΑΙ ✗
Το \(b_0\) είναι ο δειγματικός μέσος όρος (εκτιμητής)
Η τιμή του θα αλλάξει με νέα δεδομένα
Γ. \(n\) (μέγεθος δείγματος) - ΕΠΗΡΕΑΖΕΤΑΙ ✗
- Προφανώς αλλάζει: 18 → 28 (αν προσθέσουμε 10 ποντίκια)
Δ. \(\bar{Y}\) (δειγματικός μέσος) - ΕΠΗΡΕΑΖΕΤΑΙ ✗
Το \(\bar{Y}\) είναι ίδιο με το \(b_0\) - ο δειγματικός μέσος
Η τιμή του θα αλλάξει με νέα δεδομένα
Κρίσιμη διάκριση:
ΠΑΡΑΜΕΤΡΟΣ vs ΕΚΤΙΜΗΤΗΣ
$\beta_0$$:
- Παράμετρος ΠΛΗΘΥΣΜΟΥ
- Άγνωστη αλλά ΣΤΑΘΕΡΗ τιμή
- Δεν αλλάζει με το μέγεθος του δείγματος
- Στο παράδειγμα: η πραγματική μέση αύξηση
βάρους για ΟΛΟΥΣ τους πιθανούς ποντικούς
$b_0$ (εκτιμητής):
- Εκτιμητής από ΔΕΙΓΜΑ
- Μεταβλητή τιμή (αλλάζει με δείγμα)
- Αλλάζει με νέα δεδομένα
- Παράδειγμα: 8.389 από αυτά τα 18 ποντίκιαΓιατί το \(\beta_0\) δεν αλλάζει:
Το \(\beta_0\) αντιπροσωπεύει μια ιδιότητα του πληθυσμού, όχι του δείγματος:
Όπως το “μέσο ύψος όλων των ενήλικων ανδρών” είναι σταθερό
Ακόμα κι αν μετρήσουμε 100 ή 1000 άτομα
Οι εκτιμήσεις μας (δειγματικοί μέσοι) αλλάζουν
Αλλά η πραγματική τιμή παραμένει σταθερή
Συμπέρασμα:
Το \(\beta_0\) είναι η μόνη τιμή που σίγουρα δεν επηρεάζεται από την προσθήκη περισσότερων ποντικιών, επειδή είναι μια σταθερή παράμετρος του πληθυσμού. Ενώ η τιμή του εκτιμητή μας \(b_0\) (ή \(\bar{Y}\)) αναμένεται να αλλάξει με νέα δεδομένα, η πραγματική υποκείμενη παράμετρος \(\beta_0\) που προσπαθούμε να εκτιμήσουμε παραμένει αμετάβλητη.
31. Εκτελέστε την favstats για τη μεταβλητή Siblings από το πλαίσιο δεδομένων StudentSurvey. Για ποια τιμή θα ήταν το άθροισμα τετραγώνων των σφαλμάτων (SS) μικρότερο;
Σωστή απάντηση: Α (1.7)
Θεμελιώδης αρχή:
Το Sum of Squares (SS) ελαχιστοποιείται στο μέσο όρο:
\[SS = \sum_{i=1}^{n}(Y_i - c)^2 \text{ είναι ελάχιστο όταν } c = \bar{Y}\]
Από τα αποτελέσματα της favstats():
> favstats(StudentSurvey$Siblings)
min Q1 median Q3 max mean sd n missing
0 1 1 2 8 1.726519 1.179142 362 0- Μέσος όρος = 1.726519 ≈ 1.7
Γιατί οι άλλες είναι λάθος:
Β - “2” (Q3) - ΛΑΘΟΣ:
Το 2 είναι το τρίτο τεταρτημόριο, όχι ο μέσος
Θα δώσει μεγαλύτερο SS από το 1.7
Γ - “1” (διάμεσος) - ΛΑΘΟΣ:
H διάμεσος ελαχιστοποιεί το άθροισμα των απόλυτων αποκλίσεων: \(\sum|Y_i - c|\)
Ο μέσος ελαχιστοποιεί το άθροισμα των τετραγώνων των αποκλίσεων: \(\sum(Y_i - c)^2\)
Δ - “0” (min) - ΛΑΘΟΣ:
Το 0 είναι η ελάχιστη τιμή στα δεδομένα
Θα δώσει πολύ μεγάλο SS
Συμπέρασμα:
Το Άθροισμα Τετραγώνων είναι χαμηλότερο στον μέσο όρο (1.7 αδέλφια). Αυτός είναι ο λόγος που χρησιμοποιούμε το μέσο όρο στο κενό μοντέλο - ελαχιστοποιεί το άθροισμα των τετραγώνων των σφαλμάτων.