9 Κεφάλαιο: Εμβαθύνοντας στα Mοντέλα Oμάδων

Όλα πρέπει να γίνονται όσο πιο απλά είναι δυνατόν, αλλά όχι απλούστερα.

— Albert Einstein

9.1 Επέκταση σε Μοντέλο Τριών Ομάδων

Μέχρι αυτό το σημείο έχετε μάθει πώς να ορίζετε ένα μοντέλο με μία ανεξάρτητη ποιοτική μεταβλητή που περιλαμβάνει δύο κατηγορίες (ομάδες). Η επέκταση αυτής της ιδέας σε μια ποιοτική ανεξάρτητη μεταβλητή με τρεις ομάδες είναι σχετικά απλή.

Ένα Νέο Μοντέλο Δύο Ομάδων

Ας χρησιμοποιήσουμε μια νέα ανεξάρτητη μεταβλητή για να εξηγήσουμε τη μεταβλητότητα στο μήκος του αντίχειρα: το Ύψος φοιτητή (Height). Στο πλαίσιο δεδομένων Fingers, το ύψος είναι μια ποσοτική μεταβλητή μετρημένη σε εκατοστά. Για εκπαιδευτικούς σκοπούς, μπορούμε να δημιουργήσουμε μια νέα μεταβλητή που μετατρέπει το ύψος σε ποιοτική μεταβλητή με δύο κατηγορίες: short (κοντοί) και tall (ψηλοί).

Μπορούμε να το επιτύχουμε αυτό με τη συνάρτηση ntile(). Ο παρακάτω κώδικας χωρίζει το δείγμα σε δύο ομάδες ίσου μεγέθους με βάση το ύψος (Height) και αποθηκεύει το αποτέλεσμα σε μια νέα μεταβλητή με το όνομα Height2Group.

Fingers$Height2Group <- ntile(Fingers$Height, 2)
head(select(Fingers, Thumb, Height, Height2Group), 10)

Χρησιμοποιήσαμε τις συναρτήσεις head() και select() για να εμφανίσουμε τις πρώτες 10 γραμμές των σχετικών μεταβλητών: Thumb, Height και Height2Group:

   Thumb  Height Height2Group
1  66.00 179.070            2
2  64.00 164.592            1
3  56.00 162.560            1
4  58.42 177.800            2
5  74.00 172.720            2
6  60.00 172.720            2
7  70.00 175.260            2
8  55.00 166.878            2
9  60.00 158.750            1
10 52.00 161.036            1

Στο παρακάτω πλαίσιο κώδικα, χρησιμοποιήστε τη συνάρτηση factor() για να προσθέσετε ετικέτες στη μεταβλητή Height2Group, ώστε η τιμή 1 να αντιστοιχεί στο short και η τιμή 2 στο tall:

   Thumb  Height Height2Group
1  66.00 179.070         tall
2  64.00 164.592        short
3  56.00 162.560        short
4  58.42 177.800         tall
5  74.00 172.720         tall
6  60.00 172.720         tall
7  70.00 175.260         tall
8  55.00 166.878         tall
9  60.00 158.750        short
10 52.00 161.036        short

Ακολουθούμε την ίδια προσέγγιση που ακολουθήσαμε για τη μεταβλητή Gender και γράφουμε το μοντέλο της Height2Group ως εξής:

\[\text{Thumb}_i = b_0 + b_1 \text{Height2Group}_i + e_i\]

Μπορείτε να προσαρμόσετε το μοντέλο με τη συνάρτηση lm() και να εμφανίσετε τις εκτιμήσεις των παραμέτρων και τον πίνακα ANOVA:

lm(formula = Thumb ~ Height2Group, data = Fingers)

Coefficients:
     (Intercept)  Height2Grouptall
          57.818             4.601

Η τιμή του $b_0$ είναι:

57.8184.601

Η τιμή του $b_1$ είναι:

57.8184.601

Επεξήγηση

Από τα αποτελέσματα της lm():

$b_0$ = 57.818 (Intercept)
$b_1$ = 4.601 (Height2Grouptall)

Το μοντέλο:

\[\text{Thumb}_i = 57.818 + 4.601 \times \text{Height2Group}_i\]

Ερμηνεία:

$b_0 = 57.818$ mm:

Ο μέσος όρος του μήκους αντίχειρα για την ομάδα αναφοράς (short)
Όταν Height2Group = 0 (short)

$b_1 = 4.601$ mm:

Η διαφορά στο μέσο μήκος αντίχειρα μεταξύ tall και short
Τα ψηλά άτομα έχουν κατά μέσο όρο 4.601mm μεγαλύτερο αντίχειρα

Υπολογισμοί:

# Short group (Height2Group = 0):
Thumb = 57.818 + 4.601×0 = 57.818mm

# Tall group (Height2Group = 1):
Thumb = 57.818 + 4.601×1 = 62.419mm

# Διαφορά:
62.419 - 57.818 = 4.601mm

Γιατί στα αποτελέσματα εμφανίζεται το όνομα Height2Grouptall (αντί απλά το Height2Group);

Αυτό είναι το μέσο ύψος κάποιου στην ομάδα tall.Αυτό είναι το μέσο μήκος αντίχειρα κάποιου στην ομάδα tall.Αυτή είναι η ποσότητα που προστίθεται για να πάρουμε το ύψος κάποιου στην ομάδα tall.Αυτή είναι η ποσότητα που προστίθεται για να πάρουμε το μήκος αντίχειρα κάποιου στην ομάδα tall.

Πώς θα γίνει από την lm η κωδικοποίηση της $X_i$ για να έχει νόημα αυτό το μοντέλο;

-1 για short και 1 για tall1 για short και 2 για tall-1 για short και 1 για tall0 για short και 1 για tall

Επεξήγηση

Πρώτη ερώτηση - Σωστή απάντηση: Δ

Γιατί Height2Grouptall:

Η R προσθέτει το όνομα της κατηγορίας στο όνομα της μεταβλητής για να δείξει ποιο επίπεδο κωδικοποιείται ως 1.

# Η μεταβλητή: Height2Group
# Οι κατηγορίες (levels): "short" και "tall"
# Ομάδα αναφοράς: "short" (κωδικοποιείται ως 0)
# Ομάδα σύγκρισης: "tall" (κωδικοποιείται ως 1)

# Άρα ο συντελεστής ονομάζεται: Height2Grouptall

Ερμηνεία του $b_1 = 4.601$:

Αυτή είναι η ποσότητα που προστίθεται στο μήκος αντίχειρα όταν κάποιος είναι στην ομάδα tall.

# Short: Thumb = 57.818 + 4.601×0 = 57.818 mm
# Tall:  Thumb = 57.818 + 4.601×1 = 62.419 mm

# Η ποσότητα που προστίθεται: +4.601mm για tall

Δεύτερη ερώτηση - Σωστή απάντηση: Δ

Κωδικοποίηση 0/1 (dummy coding):

X_i = 0  αν `short` (ομάδα αναφοράς)
X_i = 1  αν `tall` (ομάδα σύγκρισης)

Γιατί 0/1:

Αυτή είναι η προεπιλεγμένη κωδικοποίηση στην lm() για ποσοτικές μεταβλητές:

\[\text{Thumb} = 57.818 + 4.601 \times X_i\]

Όταν $X_i = 0$ (short): Thumb = 57.818 ✓
Όταν $X_i = 1$ (tall): Thumb = 57.818 + 4.601 = 62.419 ✓

Γιατί οι άλλες είναι λάθος:

Α & Γ (-1/1): Αυτή η κωδικοποίηση ονομάζεται κωδικοποίηση επίδρασης (effect coding)

Θα έδινε διαφορετικές εκτιμήσεις
Το Intercept θα ήταν ο γενικός μέσος όρος, όχι ο μέσος όρος της short

Β (1/2):

Δεν χρησιμοποιείται
Θα έδινε λάθος ερμηνεία του Intercept

Συμπέρασμα:

Η lm() χρησιμοποιεί ψευδομεταβλητή (0/1) όπου:

0 = ομάδα αναφοράς (short)
1 = ομάδα σύγκρισης (tall)
Το όνομα Height2Grouptall δείχνει ότι ο συντελεστής αναφέρεται στην κατηγορία tall

Analysis of Variance Table (Type III SS)
Model: Thumb ~ Height2Group

                               SS  df      MS      F    PRE     p
----- --------------- | --------- --- ------- ------ ------ -----
Model (error reduced) |   830.880   1 830.880 11.656 0.0699 .0008
Error (from model)    | 11049.331 155  71.286
----- --------------- | --------- --- ------- ------ ------ -----
Total (empty model)   | 11880.211 156  76.155

Τι είναι το SS Total; (Υπάρχουν περισσότερες από μία σωστές απαντήσεις.)

Το συνολικό σφάλμα τετραγώνων του μήκους αντίχειρα από το γενικό μέσο όροΤο άθροισμα τετραγώνων των υπολοίπων από το κενό μοντέλο του μήκους αντίχειραΤο συνολικό άθροισμα τετραγώνων των υπολοίπων που εξηγείται από το Height2Group_model του μήκους αντίχειραΤο άθροισμα τετραγώνων των σφαλμάτων από το κενό μοντέλο του μήκους αντίχειρα

Επεξήγηση

Σωστές απαντήσεις: Α, Β, Δ

Το SS$_{\text{Total}}$ είναι το ίδιο με το SS$_{\text{Error}}$ από το κενό μοντέλο.

Α. Συνολικό τετραγωνικό σφάλμα από το γενικό μέσο όρο - ΣΩΣΤΟ ✓

\[\text{SS}_{\text{Total}} = \sum_{i=1}^{n}(\text{Thumb}_i - \bar{\text{Thumb}})^2\]

Μετράει όλη τη μεταβλητότητα στα δεδομένα
Υπόλοιπα από το γενικό μέσο όρο (κενό μοντέλο)

Β. Το άθροισμα τετραγώνων των υπολοίπων από το κενό μοντέλο - ΣΩΣΤΟ ✓

Το κενό μοντέλο προβλέπει μόνο το γενικό μέσο όρο
Όλη η μεταβλητότητα είναι “σφάλμα” σε αυτό το μοντέλο

Δ. Το άθροισμα τετραγώνων των σφαλμάτων από το κενό μοντέλο - ΣΩΣΤΟ ✓

Αυτό είναι ακριβώς το ίδιο με το Β
SS Total = SS Error (από το κενό μοντέλο)

Γιατί οι άλλες είναι λάθος:

Γ. “Εξηγείται από Height2Group” - ΛΑΘΟΣ:

Αυτό είναι το SS Model (830.880), όχι το SS Total
SS Model = η μεταβλητότητα που εξηγείται

Σχέση:

\[\text{SS}_{\text{Total}} = \text{SS}_{\text{Model}} + \text{SS}_{\text{Error}}\]

\[11880.211 = 830.880 + 11049.331\]

Συμπέρασμα:

Το SS$_{\text{Total}}$ (11880.211) αντιπροσωπεύει:

Τη συνολική μεταβλητότητα στο μήκος αντίχειρα
Το σφάλμα (ή τη μεταβλητότητα που υπολείπεται) από το κενό μοντέλο
Το άθροισμα τετραγώνων των αποκλίσεων από το γενικό μέσο όρο

Ποια είναι η τιμή του PRE για το μοντέλο της Height2Group;

Τι δείχνει ο δείκτης PRE;

Την αναλογία της μεταβλητότητας που εξηγείται από το κενό μοντέλο.Τον αριθμό των τετραγωνικών mm που εξηγούνται από το μοντέλο της Height2Group.Την αναλογία της μεταβλητότητας που εξηγείται από το μοντέλο της Height2Group.Την αναλογία της μεταβλητότητας που δεν εξηγείται από το μοντέλο της Height2Group.Το άθροισμα τετραγώνων των σφαλμάτων που εξηγείται από το μοντέλο της Height2Group.

Επεξήγηση

Σωστή απάντηση: Γ

PRE = Αναλογική Μείωση του Σφάλματος (Proportional Reduction in Error)

\[\text{PRE} = \frac{\text{SS}_{\text{Model}}}{\text{SS}_{\text{Total}}} = \frac{830.880}{11880.211} = 0.0699\]

Ερμηνεία:

Το PRE = 0.0699 (ή 6.99%) σημαίνει ότι το μοντέλο της Height2Group εξηγεί περίπου το 7% της μεταβλητότητας του μήκους αντίχειρα.

Γιατί οι άλλες είναι λάθος:

Α. “Εξηγείται από το κενό μοντέλο” - ΛΑΘΟΣ:

Το κενό μοντέλο δεν εξηγεί μεταβλητότητα
Το PRE πάντα αναφέρεται στο σύνθετο μοντέλο

Β. “Αριθμός τετραγωνικών mm” - ΛΑΘΟΣ:

Αυτό θα ήταν το SS Model (830.880mm²)
Το PRE είναι αναλογία (0-1), όχι απόλυτη τιμή

Δ. “Ανεξήγητη μεταβλητότητα” - ΛΑΘΟΣ:

Αυτό θα ήταν: $1 - \text{PRE} = 1 - 0.0699 = 0.9301$ (93%)
Το PRE μετράει την εξηγούμενη, όχι την ανεξήγητη

Ε. “Άθροισμα σφαλμάτων” - ΛΑΘΟΣ:

Παράδοξο: τα σφάλματα δεν “εξηγούνται”
Το μοντέλο μειώνει το σφάλμα εξηγώντας μεταβλητότητα

Συμπέρασμα:

Το PRE είναι η αναλογία της μεταβλητότητας που εξηγείται από το μοντέλο της Height2Group - ένας δείκτης χωρίς μονάδες μέτρησης μεταξύ του 0 και του 1 που δείχνει πόσο καλά το μοντέλο εξηγεί τη μεταβλητότητα στα δεδομένα.

Ένα Μοντέλο Τριών Ομάδων

Ας εφαρμόσουμε τώρα την ίδια προσέγγιση, αυτή τη φορά χωρίζοντας το δείγμα σε τρεις ομάδες ύψους: short, medium και tall.

Τροποποιήστε τον παρακάτω κώδικα ώστε να δημιουργηθεί μια νέα μεταβλητή με όνομα Height3Group, η οποία θα ταξινομεί τους φοιτητές σε τρεις κατηγορίες με βάση το ύψος τους, καθεμία με ίσο αριθμό ατόμων. Κωδικοποιήστε τις κατηγορίες (1, 2, 3) ως short, medium και tall, αντίστοιχα.

   Thumb  Height Height3Group
1  66.00 179.070         tall
2  64.00 164.592       medium
3  56.00 162.560        short
4  58.42 177.800         tall
5  74.00 172.720         tall
6  60.00 172.720         tall
7  70.00 175.260         tall
8  55.00 166.878       medium
9  60.00 158.750        short
10 52.00 161.036        short

Υπολογίστε και εμφανίστε τους μέσους όρους για τις τρεις ομάδες ύψους.

  Height3Group   min    Q1 median    Q3   max     mean       sd  n missing
1        short 39.00 51.00     55 58.42 79.00 56.07113 7.499937 53       0
2       medium 45.00 55.00     60 64.00 86.36 60.22375 8.490406 52       0
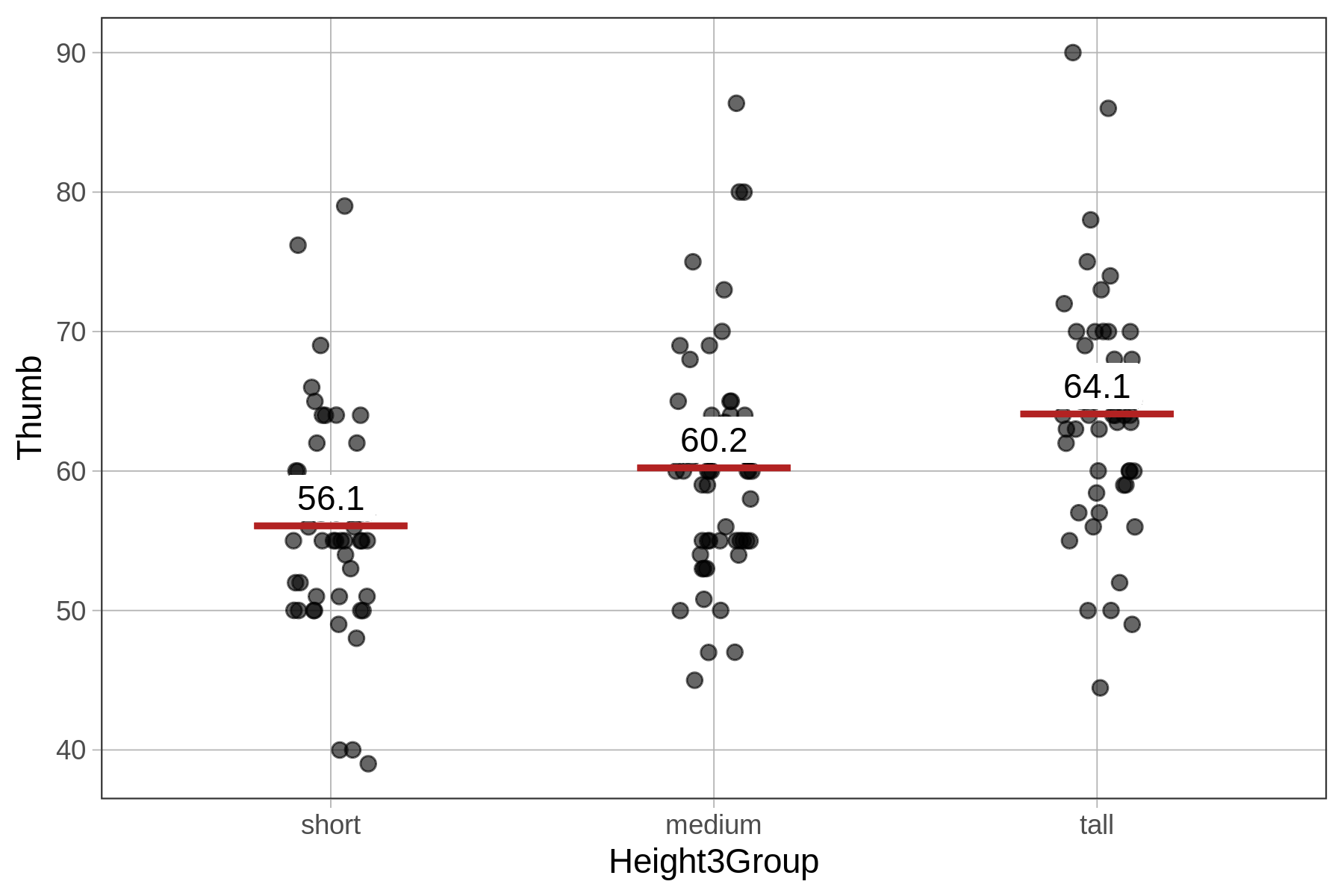
3         tall 44.45 59.75     64 68.25 90.00 64.09365 8.388113 52       0

Ποιο μοτίβο παρατηρείτε στους μέσους όρους, σύμφωνα με τα αποτελέσματα της favstats(), για τις τρεις ομάδες της μεταβλητής Height3Group;

Υπάρχουν περισσότεροι άνθρωποι καθώς οι ομάδες γίνονται μεγαλύτερες.Υπάρχουν ψηλότεροι άνθρωποι στην ομάδα tall.Οι ψηλότερες ομάδες τείνουν να έχουν μεγαλύτερους αντίχειρες.Η ομάδα medium έχει ελαφρώς μεγαλύτερους αντίχειρες από την ομάδα tall.

Επεξήγηση

Σωστή απάντηση: Γ

Το μοτίβο των μέσων:

short:  mean = 56.07 mm
medium: mean = 60.22 mm
tall:   mean = 64.09 mm

# Ξεκάθαρη αύξηση: 56 → 60 → 64

Καθώς το ύψος αυξάνεται, ο μέσος όρος του μήκους αντίχειρα επίσης αυξάνεται.

Γιατί οι άλλες είναι λάθος:

Α. “Περισσότεροι άνθρωποι” - ΛΑΘΟΣ:

Το n είναι παρόμοιο: 53, 52, 52
Όχι σαφές μοτίβο αύξησης
Η ερώτηση είναι για το μοτίβο των μέσων, όχι των μεγεθών δείγματος

Β. “Ψηλότεροι άνθρωποι στην tall” - ΛΑΘΟΣ:

Αυτός ο πίνακας δείχνει μήκος αντίχειρα (Thumb), όχι ύψος ατόμου
Οι ομάδες ορίζονται από ύψος, αλλά τα δεδομένα είναι για αντίχειρες
Η δήλωση είναι τετριμμένη (προφανώς η ομάδα “tall” έχει ψηλότερα άτομα)

Δ. “Medium > tall” - ΛΑΘΟΣ:

Το αντίθετο είναι αληθές
medium: 60.22 mm < tall: 64.09 mm

Συμπέρασμα:

Υπάρχει μια θετική συνάφεια μεταξύ ύψους και μήκους αντίχειρα: οι ψηλότερες ομάδες έχουν κατά μέσο όρο μεγαλύτερους αντίχειρες.

Ακολουθεί ένα διάγραμμα jitter που απεικονίζει την κατανομή του μήκους αντίχειρα για κάθε μία από τις τρεις ομάδες ύψους, μαζί με το μέσο όρο κάθε ομάδας. Στην επόμενη ενότητα θα δούμε πώς να προσαρμόσουμε ένα μοντέλο μήκους αντίχειρα βασισμένο στις τρεις αυτές ομάδες.

9.2 Προσαρμογή και Ερμηνεία του Μοντέλου Τριών Ομάδων

Τώρα μπορούμε να δημιουργήσουμε ένα μοντέλο που προσαρμόζει τις προβλέψεις ανάλογα με το αν οι φοιτητές είναι κοντοί, μετρίου ύψους ή ψηλοί (δηλαδή, με βάση τη μεταβλητή Height3Group). Ας δούμε πώς να προσαρμόσουμε αυτό το μοντέλο με την R και τη σημειολογία του GLM.

Προσαρμογή του Μοντέλου της `Height3Group`

Χρησιμοποιήστε τον παρακάτω κώδικα για να προσαρμόσετε το μοντέλο στα δεδομένα και να εμφανίσετε τις εκτιμήσεις των παραμέτρων:

lm(formula = Thumb ~ Height3Group, data = Fingers)

Coefficients:
       (Intercept)  Height3Groupmedium    Height3Grouptall
            56.071               4.153               8.023

Το μοντέλο τριών ομάδων μπορεί να εκφραστεί με τη σημειολογία του Γενικού Γραμμικού Μοντέλου (GLM) ως εξής:

\[Y_i = b_0 + b_1 X_{1i} + b_2 X_{2i} + e_i\]

Ενώ η προσαρμογή του μοντέλου δύο ομάδων περιλάμβανε δύο εκτιμήσεις παραμέτρων ($b_0$ και $b_1$), το μοντέλο τριών ομάδων προσθέτει μια τρίτη ($b_2$), η οποία αντιστοιχεί στη διαφορά του μέσου όρου της τρίτης ομάδας σε σχέση με την ομάδα αναφοράς.

Ποιοι αριθμοί από το μοντέλο της Height3Group αντιστοιχούν σε αυτές τις εκτιμήσεις παραμέτρων;

$b_0$ =

4.1538.02356.071

$b_1$ =

4.1538.02356.071

$b_2$ =

4.1538.02356.071

Επεξήγηση

Από τα αποτελέσματα της lm():

$b_0$ = 56.071 (Intercept)
$b_1$ = 4.153 (Height3Groupmedium)
$b_2$ = 8.023 (Height3Grouptall)

Το μοντέλο:

\[\text{Thumb}_i = 56.071 + 4.153 \times X_{1i} + 8.023 \times X_{2i}\]

όπου:

$X_{1i}$ = 1 αν medium, 0 διαφορετικά
$X_{2i}$ = 1 αν tall, 0 διαφορετικά

Ερμηνεία:

$b_0 = 56.071$ mm:

Ο μέσος όρος του μήκους αντίχειρα για την ομάδα αναφοράς (short)
Όταν $X_1 = 0$ και $X_2 = 0$ (short)

$b_1 = 4.153$ mm:

Η ποσότητα που προστίθεται για την ομάδα medium
Η διαφορά μεταξύ medium και short

$b_2 = 8.023$ mm:

Η ποσότητα που προστίθεται για την ομάδα tall
Η διαφορά μεταξύ tall και short

Υπολογισμοί των μέσων όρων:

# Short group (X1 = 0, X2 = 0):
Thumb = 56.071 + 4.153×0 + 8.023×0 = 56.071mm

# Medium group (X1 = 1, X2 = 0):
Thumb = 56.071 + 4.153×1 + 8.023×0 = 60.224mm

# Tall group (X1 = 0, X2 = 1):
Thumb = 56.071 + 4.153×0 + 8.023×1 = 64.094mm

Παρατήρηση:

Αυτές οι τιμές ταιριάζουν με τους μέσους όρους από την favstats():

short: 56.07mm ✓
medium: 60.22mm ✓
tall: 64.09mm ✓

Το $Y_i$ αντιστοιχεί σε:

Αν το άτομο ανήκει στην ομάδα mediumΑν το άτομο ανήκει στην ομάδα tallΤο μήκος του αντίχειρα του ατόμου

Το $X_{1i}$ αντιστοιχεί σε:

Αν το άτομο ανήκει στην ομάδα mediumΑν το άτομο ανήκει στην ομάδα tallΤο μήκος του αντίχειρα του ατόμου

Το $X_{2i}$ αντιστοιχεί σε:

Αν το άτομο ανήκει στην ομάδα mediumΑν το άτομο ανήκει στην ομάδα tallΤο μήκος του αντίχειρα του ατόμου

Επεξήγηση

Το μοντέλο τριών ομάδων:

\[Y_i = b_0 + b_1X_{1i} + b_2X_{2i} + e_i\]

Για το συγκεκριμένο μοντέλο:

\[\text{Thumb}_i = 56.071 + 4.153X_{1i} + 8.023X_{2i} + e_i\]

$Y_i$ = Το μήκος του αντίχειρα του ατόμου

Η εξαρτημένη μεταβλητή
Αυτό που προσπαθούμε να προβλέψουμε
Μετριέται σε χιλιοστά (mm)

$X_{1i}$ = Αν το άτομο ανήκει στην ομάδα medium

Ψευδομεταβλητή (dummy variable) για την ομάδα medium
$X_{1i} = 1$ αν το άτομο είναι medium
$X_{1i} = 0$ αν το άτομο δεν είναι medium (short ή tall)

$X_{2i}$ = Αν το άτομο ανήκει στην ομάδα tall

Ψευδομεταβλητή (dummy variable) για την ομάδα tall
$X_{2i} = 1$ αν το άτομο είναι tall
$X_{2i} = 0$ αν το άτομο δεν είναι tall (short ή medium)

Κωδικοποίηση ψευδομεταβλητών:

Ομάδα	$X_{1i}$	$X_{2i}$	Πρόβλεψη
short	0	0	56.071
medium	1	0	60.224
tall	0	1	64.094

Παρατηρήσεις:

Η ομάδα short είναι η ομάδα αναφοράς (reference group)
Δεν χρειάζεται ψευδομεταβλητή για την short γιατί αναπαρίσταται με $X_{1i} = 0$ και $X_{2i} = 0$
Για $k$ ομάδες χρειαζόμαστε $k-1$ ψευδομεταβλητές
Εδώ: 3 ομάδες → 2 ψευδομεταβλητές ($X_1$ και $X_2$)

Υπολογισμοί:

# Short: X1=0, X2=0
Thumb = 56.071 + 4.153(0) + 8.023(0) = 56.071 mm

# Medium: X1=1, X2=0
Thumb = 56.071 + 4.153(1) + 8.023(0) = 60.224 mm

# Tall: X1=0, X2=1
Thumb = 56.071 + 4.153(0) + 8.023(1) = 64.094 mm

Ερμηνεία του Μοντέλου της `Height3Group`

Το $b_0$ είναι ο μέσος όρος της ομάδας short. Το $b_1$ είναι η ποσότητα που πρέπει να προστεθεί στην ομάδα short για να πάρουμε το μέσο όρο της ομάδας medium. Και το $b_2$ είναι η ποσότητα που πρέπει να προστεθεί στην ομάδα short για να πάρουμε το μέσο όρο της ομάδας tall.

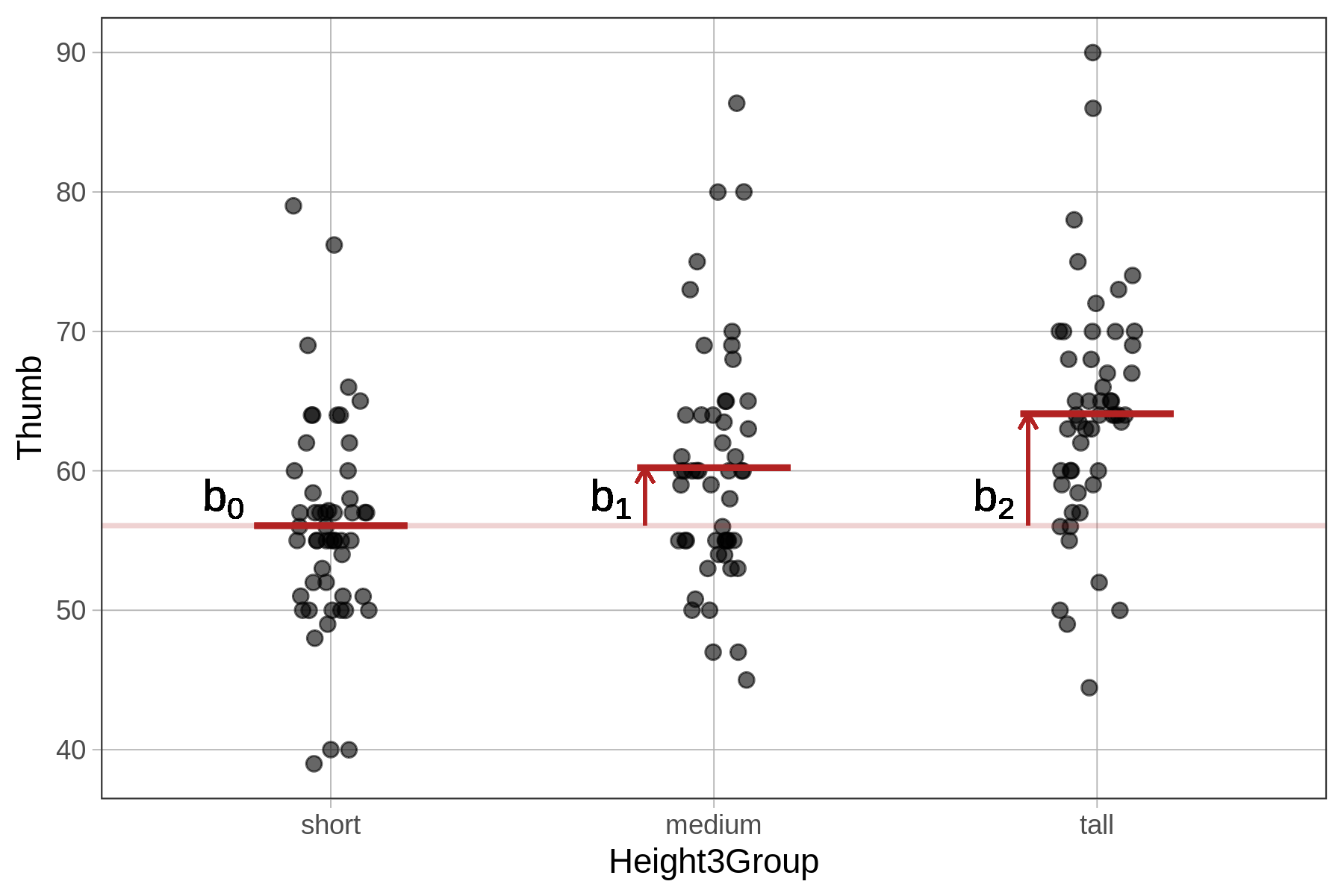
Μπορούμε να αντικαταστήσουμε τις εκτιμήσεις των παραμέτρων στην εξίσωση του μοντέλου, ως εξής:

\[\text{Thumb}_i = 56.071 + 4.153 X_{1i} + 8.023 X_{2i} + e_i\] Ή, πιο συγκεκριμένα, ως εξής:

\[\text{Thumb}_i = 56.071 + 4.153 \text{Height3Groupmedium}_i + 8.023 \text{Height3Grouptall}_i + e_i\] Όπως και πριν, είναι χρήσιμο να κατανοήσουμε πώς ακριβώς κωδικοποιούνται οι μεταβλητές $Χ$. Στο μοντέλο τριών ομάδων έχουμε τώρα δύο μεταβλητές αντί για μία, $X_{i1}$ και $X_{i2}$. Οι νέοι δείκτες (1 και 2) απλώς διακρίνουν μεταξύ αυτών των δύο μεταβλητών· αντί να τους δώσουμε διαφορετικά ονόματα, τις ονομάζουμε συνήθως medium και tall.

Ο δείκτης $i$ δείχνει ότι αυτές δεν είναι εκτιμήσεις παραμέτρων, αλλά μεταβλητές, που σημαίνει ότι κάθε παρατήρηση στο σύνολο δεδομένων θα έχει τις δικές της τιμές στις δύο μεταβλητές. Όπως και πριν, είναι λίγο δύσκολο να καταλάβουμε ποιες είναι οι πιθανές τιμές σε αυτές τις δύο μεταβλητές, και επίσης πώς αποδίδονται οι τιμές σε κάθε παρατήρηση.

Ποια είναι η διαφορά μεταξύ εκτίμησης παραμέτρου και μεταβλητής; (Υπάρχουν περισσότερες από μία σωστές απαντήσεις.)

Οι εκτιμήσεις παραμέτρων συνήθως συμβολίζονται με λατινικά γράμματα, ενώ οι μεταβλητές με ελληνικά γράμματα.Οι εκτιμήσεις παραμέτρων είναι οι ίδιες για κάθε άτομο σε ένα δείγμα, ενώ οι τιμές μιας μεταβλητής μπορεί να διαφέρουν ανάλογα με την ομάδα στην οποία ανήκει κάθε άτομο.Το μήκος του αντίχειρα κάθε ατόμου εξαρτάται από τις ίδιες εκτιμήσεις παραμέτρων, αλλά από διαφορετικές τιμές των μεταβλητών.Οι μεταβλητές έχουν δείκτη $i$ για να δείξουν ότι οι τιμές τους διαφέρουν από άτομο σε άτομο, ενώ οι εκτιμήσεις παραμέτρων δεν έχουν δείκτη $i$ επειδή είναι ίδιες για κάθε άτομο.

Επεξήγηση

Σωστές απαντήσεις: Β, Γ, και Δ

Το μοντέλο:

\[\text{Thumb}_i = b_0 + b_1X_{1i} + b_2X_{2i} + e_i\]

Β. Οι εκτιμήσεις παραμέτρων είναι οι ίδιες για κάθε άτομο - ΣΩΣΤΟ ✓

Εκτιμήσεις παραμέτρων (σταθερές για όλους):

$b_0 = 56.071$ mm
$b_1 = 4.153$ mm
$b_2 = 8.023$ mm

Μεταβλητές (διαφέρουν για κάθε άτομο):

$X_{1i}$: 0 ή 1 (ανάλογα με την ομάδα)
$X_{2i}$: 0 ή 1 (ανάλογα με την ομάδα)
$Y_i$: διαφορετικό μήκος αντίχειρα για κάθε άτομο

Γ. Το μήκος αντίχειρα αποτελείται από τις ίδιες εκτιμήσεις παραμέτρων αλλά διαφορετικές τιμές για τις μεταβλητές - ΣΩΣΤΟ ✓

Παράδειγμα:

# Άτομο 1 (short): X1=0, X2=0
Thumb₁ = 56.071 + 4.153(0) + 8.023(0) = 56.071 mm

# Άτομο 2 (medium): X1=1, X2=0
Thumb₂ = 56.071 + 4.153(1) + 8.023(0) = 60.224 mm

# Άτομο 3 (tall): X1=0, X2=1
Thumb₃ = 56.071 + 4.153(0) + 8.023(1) = 64.094 mm

Οι εκτιμήσεις παραμέτρων (56.071, 4.153, 8.023) είναι οι ίδιες και για τα τρία άτομα.

Οι τιμές των μεταβλητών ($X_1$, $X_2$) διαφέρουν για κάθε άτομο.

Δ. Οι μεταβλητές έχουν δείκτη i - ΣΩΣΤΟ ✓

Με δείκτη $i$ (μεταβλητές):

$Y_i$ - διαφορετικό για κάθε άτομο $i$
$X_{1i}$ - διαφορετικό για κάθε άτομο $i$
$X_{2i}$ - διαφορετικό για κάθε άτομο $i$
$e_i$ - διαφορετικό υπόλοιπο για κάθε άτομο $i$

Χωρίς δείκτη $i$ (εκτιμήσεις):

$b_0$ - σταθερό για όλους
$b_1$ - σταθερό για όλους
$b_2$ - σταθερό για όλους

Γιατί η Α είναι λάθος:

Α. “Παράμετροι με λατινικά, μεταβλητές με ελληνικά” - ΛΑΘΟΣ

Αυτό είναι ανάποδα:

Παράμετροι: $\beta_0, \beta_1, \beta_2$ (άγνωστες παράμετροι πληθυσμού)
Εκτιμήσεις παραμέτρων: $b_0, b_1, b_2$ (εκτιμήσεις από δείγμα)
Μεταβλητές: χρησιμοποιούν λατινικά γράμματα (X, Y)
- $Y_i$ - εξαρτημένη μεταβλητή
- $X_{1i}, X_{2i}$ - ανεξάρτητες μεταβλητές

Η συνάρτηση lm() στην R δεν χρησιμοποιεί απαραίτητα την ίδια κωδικοποίηση που έχετε επιλέξει εσείς για μια μεταβλητή. Στο μοντέλο της Height3Group δημιουργήσαμε μια ποιοτική ανεξάρτητη μεταβλητή (Height3Group), όπου η κατηγορία 1 αντιστοιχεί σε short, η κατηγορία 2 σε medium και η κατηγορία 3 σε tall. Ωστόσο, η lm() μετατρέπει αυτή τη μία μεταβλητή σε δύο νέες μεταβλητές, $X_1$ και $X_2$, οι οποίες είναι κωδικοποιημένες ως ψευδομεταβλητές (dummy variables). Αυτό σημαίνει ότι για κάθε παρατήρηση οι τιμές τους μπορούν να είναι μόνο 0 ή 1.

Ας δούμε πώς γίνεται η κωδικοποίηση των ψευδομεταβλητών:

Για ένα άτομο στην ομάδα short, το μοντέλο του αποδίδει την τιμή 56.07, που είναι ο μέσος όρος της ομάδας short. Αυτή η τιμή είναι το $b_0$. Η $X_1$ μπορεί να θεωρηθεί ως μια μεταβλητή που «ρωτάει» για κάθε άτομο: «Ανήκει αυτό το άτομο στην ομάδα medium;». Η τιμή 0 σημαίνει «όχι» και η τιμή 1 σημαίνει «ναι». Ομοίως, η $X_2$ δείχνει αν ένα άτομο ανήκει στην ομάδα tall. Για τα άτομα της ομάδας short, και οι δύο ψευδομεταβλητές $X_1$ και $X_2$ παίρνουν την τιμή 0, καθώς δεν ανήκουν ούτε στην medium ούτε στην tall.

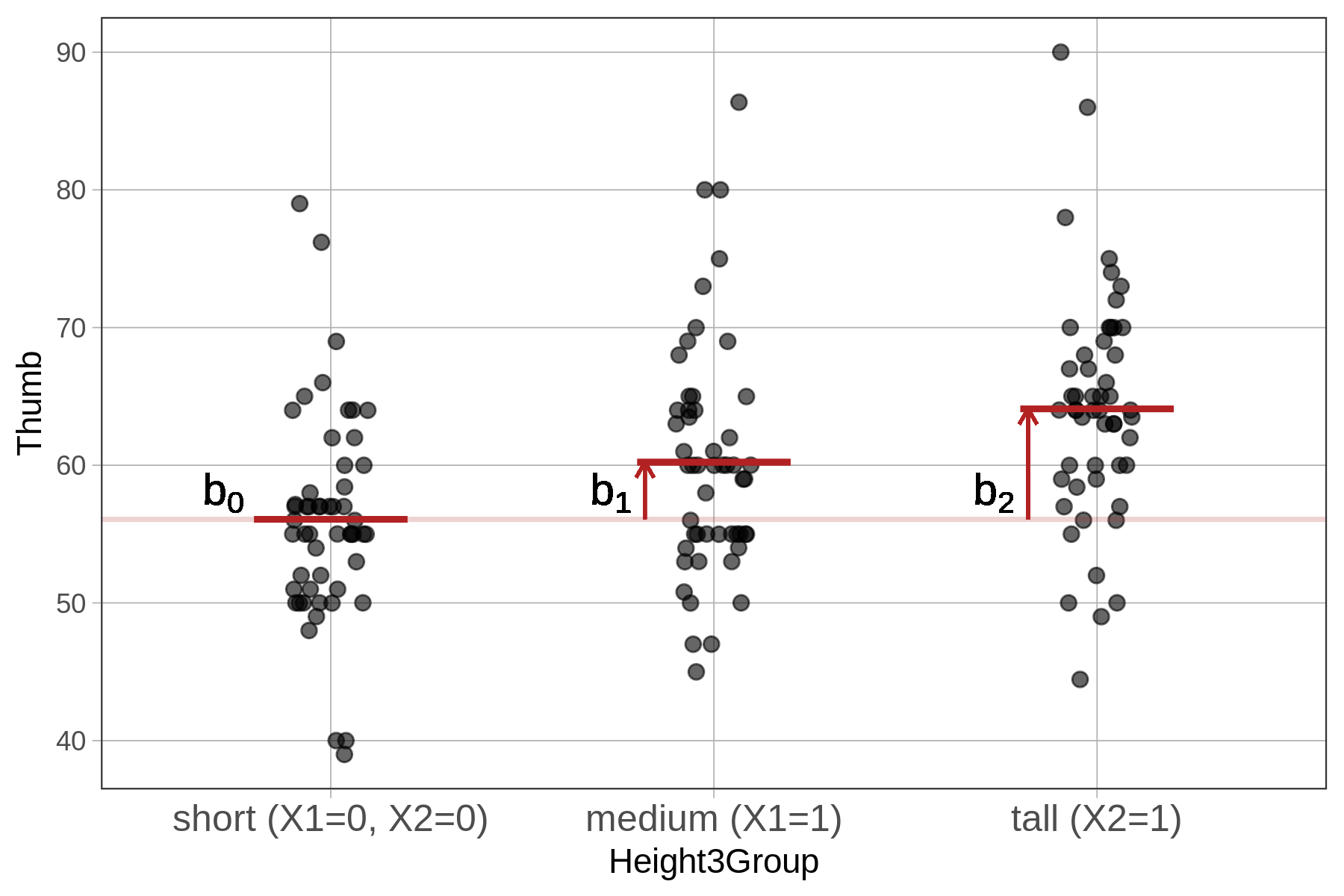
Ας υπολογίσουμε την εξίσωση για ένα άτομο στην ομάδα short.

\[Y_i = 56.07 + 4.15X_{1i} + 8.02X_{2i} + e_i\]

Ποια είναι η σωστή εξίσωση για ένα άτομο στην ομάδα short;

$56.07 + 4.15 \times 0 + 8.02 \times 0 + e_i$$56.07 \times 0 + 4.15 + 8.02 \times 0 + e_i$$56.07 + 4.15 + 8.02 \times 0 + e_i$$56.07 + 4.15 + 8.02 + e_i$

Επεξήγηση

Σωστή απάντηση: Α

Το μοντέλο:

\[Y_i = 56.07 + 4.15X_{1i} + 8.02X_{2i} + e_i\]

όπου:

$X_{1i}$ = 1 αν medium, 0 διαφορετικά
$X_{2i}$ = 1 αν tall, 0 διαφορετικά

Για κάποιον στην ομάδα short:

Η ομάδα short είναι η ομάδα αναφοράς (reference group), οπότε:

$X_{1i} = 0$ (δεν είναι medium)
$X_{2i} = 0$ (δεν είναι tall)

Αντικατάσταση στο μοντέλο:

\[Y_i = 56.07 + 4.15(0) + 8.02(0) + e_i\]

\[Y_i = 56.07 + 0 + 0 + e_i\]

\[Y_i = 56.07 + e_i\]

Άρα η πρόβλεψη για την ομάδα short είναι 56.07 mm (όταν $e_i = 0$).

Γιατί οι άλλες είναι λάθος:

Β. $56.07 \times 0 + 4.15 + 8.02 \times 0 + e_i$ - ΛΑΘΟΣ

Πολλαπλασιάζει το Intercept ($b_0 = 56.07$) με 0
Το Ιntercept είναι εκτίμηση παραμέτρου, όχι μεταβλητή - δεν πολλαπλασιάζεται με τίποτα
Το $b_0$ πάντα προστίθεται ως σταθερός όρος
Θα έδινε: $0 + 4.15 + 0 + e_i = 4.15 + e_i$ (εντελώς λάθος)

Γ. $56.07 + 4.15 + 8.02 \times 0 + e_i$ - ΛΑΘΟΣ

Ίδιο λάθος με το Β
Θα έδινε: $56.07 + 4.15 = 60.22$ mm (που είναι η τιμή για medium, όχι short)

Δ. $56.07 + 4.15 + 8.02 + e_i$ - ΛΑΘΟΣ

Αυτό υποθέτει ότι και τα δύο $X_{1i}$ και $X_{2i}$ είναι 1
Αλλά ένα άτομο δεν μπορεί να είναι ταυτόχρονα medium και tall
Θα έδινε: $56.07 + 4.15 + 8.02 = 68.24$ mm (που δεν αντιστοιχεί σε καμία ομάδα)

Σύνοψη - Κωδικοποίηση για τις τρεις ομάδες:

Ομάδα	$X_{1i}$	$X_{2i}$	Εξίσωση	Πρόβλεψη
`short`	0	0	$56.07 + 4.15(0) + 8.02(0) + e_i$	56.07 mm
`medium`	1	0	$56.07 + 4.15(1) + 8.02(0) + e_i$	60.22 mm
`tall`	0	1	$56.07 + 4.15(0) + 8.02(1) + e_i$	64.09 mm

Κλειδί: Για την ομάδα short, και οι δύο ψευδομεταβλητές είναι 0, οπότε απλά παίρνουμε το Ιntercept ($b_0 = 56.07$).

Ας υπολογίσουμε την εξίσωση για ένα άτομο στην ομάδα medium.

\[Y_i = 56.07 + 4.15X_{1i} + 8.02X_{2i} + e_i\]

Ποια είναι η σωστή εξίσωση για ένα άτομο στην ομάδα medium;

$56.07 + 4.15 \times 0 + 8.02 \times 0 + e_i$$56.07 + 4.15 + 8.02 \times 0 + e_i$$56.07 \times 0 + 4.15 + 8.02 \times 0 + e_i$$56.07 + 4.15 + 8.02 + e_i$

Επεξήγηση

Σωστή απάντηση: Β

Το μοντέλο:

\[Y_i = 56.07 + 4.15X_{1i} + 8.02X_{2i} + e_i\]

όπου:

$X_{1i}$ = 1 αν medium, 0 διαφορετικά
$X_{2i}$ = 1 αν tall, 0 διαφορετικά

Για κάποιον στην ομάδα medium:

$X_{1i} = 1$ (ναι, είναι medium)
$X_{2i} = 0$ (όχι, δεν είναι tall)

Αντικατάσταση στο μοντέλο:

\[Y_i = 56.07 + 4.15(1) + 8.02(0) + e_i\]

\[Y_i = 56.07 + 4.15 + 0 + e_i\]

\[Y_i = 60.22 + e_i\]

Άρα η πρόβλεψη για την ομάδα medium είναι 60.22 mm (όταν $e_i = 0$).

Γιατί οι άλλες είναι λάθος:

Α. $56.07 + 4.15 \times 0 + 8.02 \times 0 + e_i$ - ΛΑΘΟΣ

Αυτό υποθέτει $X_{1i} = 0$ και $X_{2i} = 0$ (ομάδα short)
Αλλά κάποιος στην medium έχει $X_{1i} = 1$
Θα έδινε: 56.07 mm (που είναι η τιμή για την short, όχι την medium)

Γ. $56.07 \times 0 + 4.15 + 8.02 \times 0 + e_i$ - ΛΑΘΟΣ

Πολλαπλασιάζει το Intercept ($b_0 = 56.07$) με 0
Το Intercept είναι εκτίμηση παράμετρου, όχι μεταβλητή - δεν πολλαπλασιάζεται με τίποτα
Το $b_0$ πάντα προστίθεται ως σταθερός όρος
Θα έδινε: $0 + 4.15 + 0 + e_i = 4.15 + e_i$ (εντελώς λάθος)

Δ. $56.07 + 4.15 + 8.02 + e_i$ - ΛΑΘΟΣ

Αυτό υποθέτει $X_{1i} = 1$ και $X_{2i} = 1$
Αλλά ένα άτομο δεν μπορεί να είναι ταυτόχρονα medium και tall
Για medium: $X_{2i} = 0$, άρα το 8.02 πολλαπλασιάζεται με 0
Θα έδινε: 68.24 mm (που δεν αντιστοιχεί σε καμία ομάδα)

Βήμα-βήμα υπολογισμός:

# Βήμα 1: Ταυτοποίηση των τιμών για `medium`
X1 = 1  # Είναι medium
X2 = 0  # Δεν είναι tall

# Βήμα 2: Αντικατάσταση στην εξίσωση
Y = 56.07 + 4.15*X1 + 8.02*X2 + e

# Βήμα 3: Υπολογισμός
Y = 56.07 + 4.15*(1) + 8.02*(0) + e
Y = 56.07 + 4.15 + 0 + e
Y = 60.22 + e

Σύνοψη - Κωδικοποίηση για τις τρεις ομάδες:

Ομάδα	$X_{1i}$	$X_{2i}$	Εξίσωση	Πρόβλεψη
short	0	0	$56.07 + 4.15(0) + 8.02(0) + e_i$	56.07 mm
medium	1	0	$56.07 + 4.15(1) + 8.02(0) + e_i$	60.22 mm
tall	0	1	$56.07 + 4.15(0) + 8.02(1) + e_i$	64.09 mm

Κλειδί: Για την ομάδα medium, το $X_1 = 1$ οπότε προσθέτουμε το 4.15, αλλά το $X_2 = 0$ οπότε δεν προσθέτουμε το 8.02.

Για ένα άτομο που ανήκει στην ομάδα medium, η τιμή της $X_1$ θα είναι 1 (επειδή ανήκει στην ομάδα medium), ενώ η τιμή της $X_2$ θα είναι 0 (επειδή δεν ανήκει στην ομάδα tall). Συνεπώς, το μοντέλο θα του αποδώσει προβλεπόμενο μήκος αντίχειρα ίσο με 56.07 + 4.15 = 60.22 χιλιοστά.

Παρατηρήστε ότι, σύμφωνα με τα αποτελέσματα της favstats() που ακολουθούν, ο μέσος όρος του μήκους του αντίχειρα για την ομάδα medium είναι πράγματι 60.22 χιλιοστά!

  Height3Group   min    Q1 median    Q3   max     mean      sd  n  missing
1        short 39.00 51.00     55 58.42 79.00 56.07113 7.499937 53       0
2       medium 45.00 55.00     60 64.00 86.36 60.22375 8.490406 52       0
3         tall 44.45 59.75     64 68.25 90.00 64.09365 8.388113 52       0

Η διαδικασία της δημιουργίας ψευδομεταβλητών μετατρέπει τις ποιοτικές μεταβλητές σε ένα σύνολο δυαδικών μεταβλητών (0/1). Όπως φαίνεται και στον παρακάτω πίνακα, αποδίδοντας σε κάθε άτομο την τιμή 0 ή την τιμή 1 στις $X_1$ και $X_2$, μπορούμε να το κατατάξουμε εύκολα σε μία από τις τρεις κατηγορίες: short, medium ή tall.

Κατηγορία (Ομάδα)	Κωδικοποίηση $X_1$	Κωδικοποίηση $X_2$
`short`	0	0
`medium`	1	0
`tall`	0	1

Ίσως αναρωτιέστε γιατί είναι απαραίτητο να γνωρίζετε όλες αυτές τις λεπτομέρειες σχετικά με το πώς η R κωδικοποιεί τις ψευδομεταβλητές για μια ποιοτική ανεξάρτητη μεταβλητή. Ο λόγος είναι ότι σας βοηθά να ερμηνεύετε σωστά τις παραμέτρους του μοντέλου. Για παράδειγμα, σας επιτρέπει να αντιληφθείτε πώς το μοντέλο υπολογίζει την τιμή πρόβλεψης για την τρίτη ομάδα, προσθέτοντας το $b_2$ στο $b_0$ (και όχι στο $b_1$). Σε αυτό το μάθημα, δεν θα σας ζητηθεί να υπολογίσετε αυτούς τους αριθμούς μόνοι σας· ο στόχος είναι να εστιάσετε στο νόημα των αριθμών και στο πώς αυτοί περιγράφουν τις διαφορές μεταξύ των ομάδων.

9.3 Σύγκριση της Προσαρμογής των Μοντέλων Δύο και Τριών Ομάδων

Εξέταση της Προσαρμογής του Μοντέλου Τριών Ομάδων

Μέχρι τώρα έχετε δημιουργήσει την ποιοτική ανεξάρτητη μεταβλητή Height3Group, εξετάσει τους μέσους όρους του μήκους αντίχειρα για κάθε ομάδα, προσαρμόσει το μοντέλο της Height3Group με τη συνάρτηση lm() και ερμηνεύσει τις εκτιμήσεις παραμέτρων, και μάθει πώς να αναπαριστάτε το μοντέλο τριών ομάδων με χρήση της σημειολογίας του GLM.

Το τελευταίο βήμα είναι να εξετάσετε τον πίνακα ANOVA για να συγκρίνετε την προσαρμογή του μοντέλου της Height3Group με το κενό μοντέλο. Μπορείτε να το κάνετε χρησιμοποιώντας τη συνάρτηση supernova(). Προσαρμόστε το μοντέλο της Height3Group και εμφανίστε τον πίνακα ANOVA.

Παρακάτω εμφανίζονται οι πίνακες ANOVA για τα δύο μοντέλα: πρώτα για το μοντέλο της Height2Group και στη συνέχεια για το μοντέλο της Height3Group, ώστε να μπορείτε να τα συγκρίνετε εύκολα.

Μοντέλο της `Height2Group`

Analysis of Variance Table (Type III SS)
Model: Thumb ~ Height2Group

                               SS  df      MS      F    PRE     p
----- --------------- | --------- --- ------- ------ ------ -----
Model (error reduced) |   830.880   1 830.880 11.656 0.0699 .0008
Error (from model)    | 11049.331 155  71.286
----- --------------- | --------- --- ------- ------ ------ -----
Total (empty model)   | 11880.211 156  76.155

Μοντέλο της `Height3Group`

Analysis of Variance Table (Type III SS)
Model: Thumb ~ Height3Group

                               SS  df      MS      F    PRE     p
----- --------------- | --------- --- ------- ------ ------ -----
Model (error reduced) |  1690.440   2 845.220 12.774 0.1423 .0000
Error (from model)    | 10189.770 154  66.167
----- --------------- | --------- --- ------- ------ ------ -----
Total (empty model)   | 11880.211 156  76.155

Παρατηρήστε τον πίνακα ANOVA για το μοντέλο της Height3Group. Ποια αναλογία της μεταβλητότητας στο μήκος αντίχειρα εξηγείται από αυτό το μοντέλο;

PRE (.1423)$SS_{Model}$(1690.4)$SS_{Error}$(10189.8)$SS_{Total}$(11880.2)

Επεξήγηση

Σωστή απάντηση: Α - PRE (0.1423)

Τι σημαίνει PRE;

PRE = Proportional Reduction in Error (Αναλογική Μείωση του Σφάλματος)

Το PRE μετράει την αναλογία της μεταβλητότητας που εξηγείται από το μοντέλο.

Ο τύπος:

\[\text{PRE} = \frac{\text{SS}_{\text{Model}}}{\text{SS}_{\text{Total}}} = \frac{1690.440}{11880.211} = 0.1423\]

Ερμηνεία:

PRE = 0.1423 ή 14.23%
Το μοντέλο της Height3Group εξηγεί περίπου το 14% της μεταβλητότητας στο μήκος αντίχειρα
Το υπόλοιπο 86% παραμένει ανεξήγητο (οφείλεται σε άλλους παράγοντες)

Εναλλακτικοί υπολογισμοί:

Μπορείτε επίσης να το υπολογίσετε ως μείωση του σφάλματος:

\[\text{PRE} = \frac{\text{SS}_{\text{Total}} - \text{SS}_{\text{Error}}}{\text{SS}_{\text{Total}}} = \frac{11880.2 - 10189.8}{11880.2} = \frac{1690.4}{11880.2} = 0.1423\]

Γιατί οι άλλες είναι λάθος:

Β. $SS_{Model}$ (1690.4) - ΛΑΘΟΣ

Αυτό είναι το άθροισμα τετραγώνων που εξηγείται από το μοντέλο
Έχει μονάδες μέτρησης (mm²)
Η ερώτηση ζητάει αναλογία (χωρίς μονάδες, 0-1)

Γ. $SS_{Error}$ (10189.8) - ΛΑΘΟΣ

Αυτό είναι η ανεξήγητη μεταβλητότητα
Όχι η εξηγούμενη μεταβλητότητα
Αντιπροσωπεύει το σφάλμα που απομένει μετά το μοντέλο

Δ. $SS_{Total}$ (11880.2) - ΛΑΘΟΣ

Αυτό είναι η συνολική μεταβλητότητα
Όχι η αναλογία που εξηγείται
Είναι το άθροισμα: $SS_{Model} + SS_{Error}$

Συμπέρασμα:

Το PRE = 0.1423 είναι η σωστή απάντηση γιατί:

Είναι αναλογία (0-1), όχι απόλυτη τιμή
Μετράει την εξηγούμενη μεταβλητότητα
Υπολογίζεται ως $\frac{SS_{Model}}{SS_{Total}}$
Απαντάει άμεσα στην ερώτηση: «Ποια αναλογία εξηγείται;»

Συγκρίνετε τους πίνακες ANOVA για τα μοντέλα της Height3Group και της Height2Group. Γιατί το συνολικό Άθροισμα Τετραγώνων (Total SS) είναι το ίδιο και για τα δύο μοντέλα;

Και τα δύο έχουν την ίδια ανεξάρτητη μεταβλητή.Και τα δύο περιλαμβάνουν μια ποιοτική ανεξάρτητη μεταβλητή.Και τα δύο περιλαμβάνουν μια ποσοτική μεταβλητή.Και τα δύο έχουν την ίδια εξαρτημένη μεταβλητή.

Επεξήγηση

Σωστή απάντηση: Δ - Και τα δύο έχουν την ίδια εξαρτημένη μεταβλητή

Τι είναι το SS$_{\text{Total}}$;

\[\text{SS}_{\text{Total}} = \sum_{i=1}^{n}(Y_i - \bar{Y})^2\]

Το SS$_{\text{Total}}$ μετράει τη συνολική μεταβλητότητα της εξαρτημένης μεταβλητής από το γενικό μέσο όρο.

Και τα δύο μοντέλα:

Height2Group: Thumb ~ Height2Group
Height3Group: Thumb ~ Height3Group

προσπαθούν να εξηγήσουν το μήκος αντίχειρα.

Γιατί το SS$_{\text{Total}}$ είναι το ίδιο (11880.211);

Ίδια εξαρτημένη μεταβλητή: Και τα δύο μοντέλα χρησιμοποιούν την ίδια μεταβλητή $Y$ (Thumb)
Ίδια δεδομένα: Και τα δύο χρησιμοποιούν το ίδιο σύνολο δεδομένων (n = 157 άτομα)
Ίδιος γενικός μέσος όρος: Ο μέσος όρος του μήκους αντίχειρα είναι ο ίδιος

Το SS$_{\text{Total}}$ δεν εξαρτάται από το μοντέλο - εξαρτάται μόνο από:

Τη μεταβλητότητα της $Y$ (Thumb)
Τον αριθμό των παρατηρήσεων

Γιατί οι άλλες είναι λάθος:

Α. “Ίδια ανεξάρτητη μεταβλητή” - ΛΑΘΟΣ

Οι ανεξάρτητες μεταβλητές είναι διαφορετικές:
- Height2Group: 2 κατηγορίες (short, tall)
- Height3Group: 3 κατηγορίες (short, medium, tall)
Και οι δύο βασίζονται στο ύψος (Height), αλλά με διαφορετική κατηγοριοποίηση

Β. “Ποιοτική ανεξάρτητη μεταβλητή” - ΛΑΘΟΣ

Ναι, και οι δύο χρησιμοποιούν ποιοτική μεταβλητή
Αλλά αυτός δεν είναι ο λόγος για τον οποίο το SS$_{\text{Total}}$ είναι ίδιο
Το SS$_{\text{Total}}$ θα ήταν ίδιο ακόμα και με ποσοτική ανεξάρτητη μεταβλητή

Γ. “Ποσοτική μεταβλητή” - ΛΑΘΟΣ

Και τα δύο χρησιμοποιούν ποιοτική ανεξάρτητη μεταβλητή (ομάδες ύψους)
Όχι ποσοτική
Αν και το Height (ύψος) είναι ποσοτική, οι Height2Group και Height3Group είναι ποιοτικές

Συμπέρασμα:

Το SS$_{\text{Total}}$ είναι το ίδιο επειδή και τα δύο μοντέλα εξηγούν την ίδια εξαρτημένη μεταβλητή (Thumb) χρησιμοποιώντας τα ίδια δεδομένα. Η συνολική μεταβλητότητα της $Y$ δεν αλλάζει - αλλάζει μόνο πόσο καλά την εξηγούμε.

Ποιο μοντέλο προσαρμόζεται καλύτερα στα δεδομένα;

Height3GroupHeight2Group

Πώς μπορείτε να καταλάβετε ποιο μοντέλο προσαρμόζεται καλύτερα στα δεδομένα; (Υπάρχουν περισσότερες από μία σωστές απαντήσεις.)

Το καλύτερο μοντέλο έχει μεγαλύτερο SS Total.Το καλύτερο μοντέλο έχει μεγαλύτερο PRE.Το καλύτερο μοντέλο έχει μεγαλύτερο SS Model.Το καλύτερο μοντέλο έχει μικρότερο SS Error (υπολειπόμενο σφάλμα).Το καλύτερο μοντέλο έχει μικρότερο SS Total.

Επεξήγηση

Πρώτη ερώτηση - Σωστή απάντηση: Α - Height3Group

Δεύτερη ερώτηση - Σωστές απαντήσεις: Β, Γ, και Δ

Πώς συγκρίνουμε μοντέλα;

Μέτρο	Height2Group	Height3Group	Καλύτερο
PRE	0.0699 (7%)	0.1423 (14%)	Height3Group ✓
SS$_{\text{Model}}$	830.880	1690.440	Height3Group ✓
SS$_{\text{Error}}$	11049.331	10189.770	Height3Group ✓
SS$_{\text{Total}}$	11880.211	11880.211	Ίδιο

Β. Μεγαλύτερο PRE - ΣΩΣΤΟ ✓

PRE = Proportional Reduction in Error
Μετράει την αναλογία της μεταβλητότητας που εξηγείται
Height3Group: PRE = 0.1423 (14.23%)
Height2Group: PRE = 0.0699 (6.99%)
Μεγαλύτερο PRE = καλύτερο μοντέλο

\[\text{PRE} = \frac{\text{SS}_{\text{Model}}}{\text{SS}_{\text{Total}}}\]

Γ. Μεγαλύτερο SS Model - ΣΩΣΤΟ ✓

SS$_{\text{Model}}$ = η μεταβλητότητα που εξηγείται από το μοντέλο
Height3Group: SS$_{\text{Model}}$ = 1690.440
Height2Group: SS$_{\text{Model}}$ = 830.880
Μεγαλύτερο SS$_{\text{Model}}$ = περισσότερη εξηγούμενη μεταβλητότητα = καλύτερο μοντέλο

Δ. Μικρότερο SS Error - ΣΩΣΤΟ ✓

SS$_{\text{Error}}$ = η μεταβλητότητα που δεν εξηγείται (υπολειπόμενο σφάλμα)
Height3Group: SS$_{\text{Error}}$ = 10189.770
Height2Group: SS$_{\text{Error}}$ = 11049.331
Μικρότερο SS$_{\text{Error}}$ = λιγότερο ανεξήγητο σφάλμα = καλύτερο μοντέλο

Γιατί οι άλλες είναι λάθος:

Α. “Μεγαλύτερο SS Total” - ΛΑΘΟΣ

Το SS$_{\text{Total}}$ είναι το ίδιο και για τα δύο μοντέλα (11880.211)
Εξαρτάται μόνο από τη μεταβλητότητα της εξαρτημένης μεταβλητής (Thumb)
Δεν αλλάζει με το μοντέλο

Ε. “Μικρότερο SS Total” - ΛΑΘΟΣ

Ίδιος λόγος με το Α
Το SS$_{\text{Total}}$ δεν σχετίζεται με την ποιότητα του μοντέλου

Η σχέση:

\[\text{SS}_{\text{Total}} = \text{SS}_{\text{Model}} + \text{SS}_{\text{Error}}\]

Αφού το SS$_{\text{Total}}$ είναι σταθερό:

Όταν το SS$_{\text{Model}}$ ↑ → το SS$_{\text{Error}}$ ↓
Καλύτερο μοντέλο = περισσότερη εξηγούμενη, λιγότερη ανεξήγητη μεταβλητότητα

Συμπέρασμα:

Το μοντέλο της Height3Group είναι καλύτερο μοντέλο επειδή:

Εξηγεί διπλάσια μεταβλητότητα (14% vs 7%)
Έχει μεγαλύτερο SS$_{\text{Model}}$ (1690 vs 831)
Έχει μικρότερο SS$_{\text{Error}}$ (10190 vs 11049)
Το SS$_{\text{Total}}$ δεν έχει σημασία - είναι το ίδιο για όλα τα μοντέλα με την ίδια εξαρτημένη μεταβλητή

Γιατί νομίζετε ότι αυτό το μοντέλο (της Height3Group) είναι καλύτερο;

Αυτό το μοντέλο είχε εξαρχής λιγότερη συνολική μεταβλητότητα να εξηγήσει.Αυτό το μοντέλο έδωσε πιο ακριβείς προβλέψεις του μήκους αντίχειρα, μειώνοντας έτσι τα υπόλοιπα.Αυτό το μοντέλο κάνει ένα εύρος προβλέψεων για κάθε άτομο· δεν κάνει απλά μία πρόβλεψη για κάθε άτομο.Όλα τα μοντέλα δύο ομάδων είναι καλύτερα από τα μοντέλα τριών ομάδων επειδή είναι απλούστερα.Επειδή απλά έτυχε.

Επεξήγηση

Σωστή απάντηση: Β - Πιο ακριβείς προβλέψεις, μικρότερα υπόλοιπα

Γιατί το μοντέλο της Height3Group είναι καλύτερο;

Το μοντέλο της Height3Group χωρίζει τα δεδομένα σε 3 ομάδες αντί για 2, επιτρέποντας:

Πιο εξειδικευμένες προβλέψεις
Καλύτερη προσαρμογή στα δεδομένα
Μικρότερα υπόλοιπα (residuals)

Σύγκριση:

Μοντέλο	Προβλέψεις	SS$_{\text{Error}}$	PRE
Height2Group	2 μέσοι όροι: • short: 57.82 mm • tall: 62.42 mm	11049.3	7%
Height3Group	3 μέσοι όροι: • short: 56.07 mm • medium: 60.22 mm • tall: 64.09 mm	10189.8	14%

Τι σημαίνει “πιο ακριβείς προβλέψεις”;

Με 3 ομάδες αντί για 2:

Τα άτομα μεσαίου ύψους παίρνουν τη δική τους πρόβλεψη (60.22 mm)
Δεν αναγκάζονται να ομαδοποιηθούν με τους κοντούς ή τους ψηλούς
Οι προβλέψεις είναι πιο κοντά στις πραγματικές τιμές

Μείωση υπολοίπων:

Μικρότερα υπόλοιπα = οι προβλέψεις είναι πιο κοντά στις πραγματικές τιμές
SS$_{\text{Error}}$ μειώθηκε από 11049 → 10189 (μείωση ~860 mm²)

Γιατί οι άλλες είναι λάθος:

Α. “Λιγότερη συνολική μεταβλητότητα” - ΛΑΘΟΣ

Το SS$_{\text{Total}}$ είναι το ίδιο και για τα δύο μοντέλα (11880.2)
Η συνολική μεταβλητότητα εξαρτάται από τα δεδομένα, όχι από το μοντέλο
Και τα δύο μοντέλα χρησιμοποιούν τα ίδια δεδομένα

Γ. “Εύρος προβλέψεων για κάθε άτομο” - ΛΑΘΟΣ

Κάθε μοντέλο κάνει μία πρόβλεψη ανά άτομο (το μέσο όρο της ομάδας του)
Δεν κάνει “εύρος” προβλέψεων

Δ. “Μοντέλα 2 ομάδων πάντα καλύτερα” - ΛΑΘΟΣ

Αυτό είναι το αντίθετο από αυτό που ισχύει
Τα πιο σύνθετα μοντέλα (με περισσότερες ομάδες) συχνά προσαρμόζονται καλύτερα στα δεδομένα
Η απλότητα ενός μοντέλου είναι επιθυμητή, αλλά όχι εις βάρος της ακρίβειας της πρόβλεψης
Εδώ, το μοντέλο της Height3Group έχει σαφώς καλύτερη προσαρμογή (PRE: 14% vs 7%)

Ε. “Έτυχε” - ΛΑΘΟΣ

Αυτό δεν είναι σύμπτωση
Υπάρχει συστηματική βελτίωση όταν προσθέτουμε μια ομάδα

Συμπέρασμα:

Το μοντέλο της Height3Group είναι καλύτερο επειδή παράγει πιο ακριβείς προβλέψεις με τη δημιουργία μιας ξεχωριστής ομάδας για τα άτομα μεσαίου ύψους. Αυτό μειώνει τα υπόλοιπα (SS$_{\text{Error}}$) και αυξάνει την εξηγούμενη μεταβλητότητα (PRE).

Σε επόμενο κεφάλαιο θα μάθουμε πώς να συγκρίνουμε άμεσα τα δύο μοντέλα μεταξύ τους. Προς το παρόν, θα περιοριστούμε στη σύγκριση κάθε μοντέλου με το κενό μοντέλο.

Βελτίωση Μοντέλων με την Προσθήκη Παραμέτρων

Όπως είδαμε παραπάνω, το μοντέλο της Height3Group εξηγεί μεγαλύτερο ποσοστό της μεταβλητότητας σε σχέση με το μοντέλο της Height2Group. Με άλλα λόγια, μειώνει περισσότερο το ανεξήγητο σφάλμα σε σύγκριση με το κενό μοντέλο. Αυτό φαίνεται καθαρά αν συγκρίνετε τις τιμές του PRE (.14 έναντι .07, αντίστοιχα).

Αν εξετάσετε τα παρακάτω ιστογράμματα και τα διαγράμματα jitter για το μοντέλο δύο ομάδων και το μοντέλο τριών ομάδων, αντίστοιχα, θα κατανοήσετε γιατί συμβαίνει αυτό. Όσο προσθέτουμε στο μοντέλο περισσότερες ομάδες ύψους, μειώνουμε τη μεταβλητότητα των υπολοίπων γύρω από το μέσο όρο του ύψους για κάθε ομάδα, κάτι που οδηγεί σε καλύτερη προσαρμογή του μοντέλου.

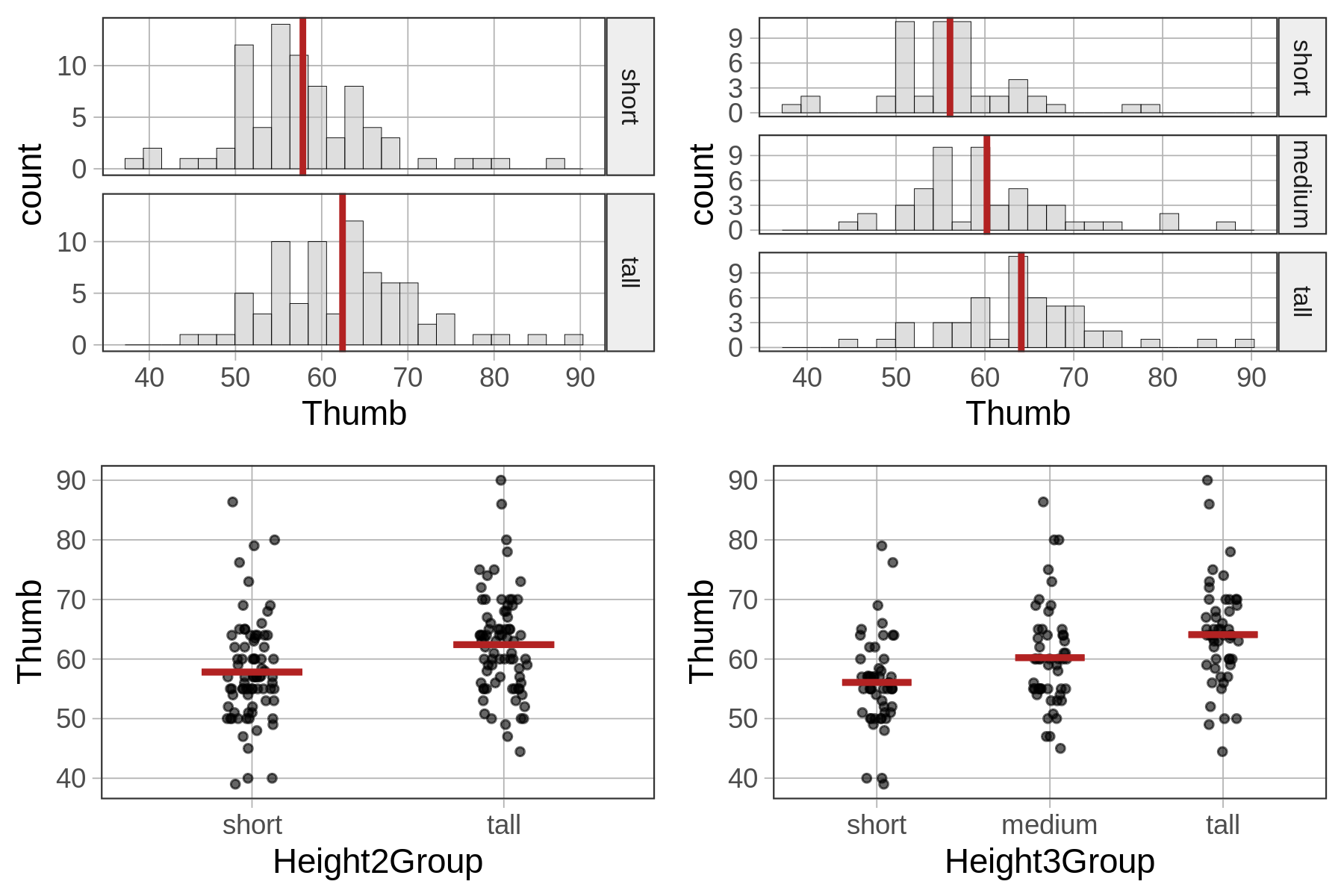
Γενικά, όσο περισσότερες παραμέτρους προσθέτουμε σε ένα μοντέλο, τόσο μικρότερο γίνεται το υπολειπόμενο σφάλμα μετά την αφαίρεση της επίδρασης του μοντέλου. Αν και αυτό δεν ισχύει πάντα, συνήθως τα πιο σύνθετα μοντέλα έχουν υψηλότερες τιμές PRE. Εφόσον ο στόχος μας είναι να μειώσουμε το σφάλμα, η αυξημένη πολυπλοκότητα φαίνεται αρχικά επιθυμητή — και πράγματι είναι, αλλά μόνο μέχρι ενός σημείου.

Ας κάνουμε ένα μικρό πείραμα σκέψης. Γνωρίζουμε ήδη ότι το μοντέλο τριών ομάδων εξηγεί περισσότερη μεταβλητότητα από το μοντέλο δύο ομάδων. Με την ίδια λογική, το μοντέλο τεσσάρων ομάδων θα εξηγούσε ακόμη περισσότερη, και ούτω καθεξής. Τι θα συνέβαινε, όμως, αν συνεχίζαμε να διαιρούμε τη μεταβλητή του ύψους σε όλο και περισσότερες ομάδες, μέχρι τελικά κάθε άτομο να ανήκει στη δική του ξεχωριστή ομάδα;

Αν το κάναμε αυτό, το σφάλμα θα μηδενιζόταν. Γιατί; Επειδή κάθε άτομο θα είχε τη δική του παράμετρο στο μοντέλο, και η τιμή πρόβλεψης για κάθε άτομο θα ήταν ακριβώς ίση με την πραγματική του τιμή. Δεν θα υπήρχε λοιπόν καμία διαφορά — κανένα υπόλοιπο — μεταξύ τιμής πρόβλεψης και πραγματικής τιμής. Με αυτόν τον τρόπο, όλη η μεταβλητότητα θα φαινόταν να εξηγείται από το μοντέλο.

Ωστόσο, αυτό οδηγεί σε δύο σημαντικά προβλήματα:

Πρώτον, αν και το μοντέλο θα προσαρμοζόταν τέλεια στα δεδομένα μας, δεν θα αναμενόταν να αποδώσει εξίσου καλά σε ένα νέο δείγμα, καθώς τα άτομα θα ήταν διαφορετικά.

Δεύτερον, ο σκοπός της αυξημένης πολυπλοκότητας είναι να μας βοηθήσει να κατανοήσουμε καλύτερα τη Διαδικασία Παραγωγής των Δεδομένων. Είναι λογικό να προσθέτουμε παραμέτρους όταν αυτό οδηγεί σε βαθύτερη κατανόηση του φαινομένου που μελετάμε. Αν, όμως, καταλήξουμε να έχουμε τόσες παραμέτρους όσες και παρατηρήσεις, τότε έχουμε προσθέσει πολυπλοκότητα χωρίς να έχουμε κερδίσει καμία ουσιαστική γνώση για τη διαδικασία που δημιουργεί τα δεδομένα.

Παρόλο που μπορούμε να βελτιώσουμε την προσαρμογή ενός μοντέλου προσθέτοντας περισσότερες παραμέτρους, υπάρχει πάντα ένας συμβιβασμός μεταξύ της μείωσης του σφάλματος, από τη μία πλευρά, και της διατήρησης της απλότητας, της ερμηνευσιμότητας και της κομψότητας του μοντέλου, από την άλλη.

Αυτός είναι και ένας βασικός περιορισμός του PRE ως μέτρου της επιτυχίας ενός μοντέλου στη μείωση του σφάλματος. Για παράδειγμα, μια τιμή PRE = .40 θα ήταν αρκετά εντυπωσιακή αν προέκυπτε με την προσθήκη μόνο μίας παραμέτρου. Αν όμως είχαμε το ίδιο αποτέλεσμα μετά την προσθήκη δέκα παραμέτρων, τότε η επίδοση αυτή δεν θα θεωρούνταν ιδιαίτερα αξιοσημείωτη. Αυτό το φαινόμενο είναι γνωστό στους στατιστικολόγους ως υπερπροσαρμογή (overfitting), δηλαδή η υπερβολική προσαρμογή ενός μοντέλου στα συγκεκριμένα δεδομένα του δείγματος, με αποτέλεσμα να χάνει τη γενικευσιμότητά του.

Ένα γνωμικό που αποδίδεται στον Αϊνστάιν συνοψίζει άψογα αυτή την ιδέα: «Όλα πρέπει να γίνονται όσο πιο απλά είναι δυνατόν, αλλά όχι απλούστερα.» Μια ορισμένη ποσότητα πολυπλοκότητας είναι αναπόφευκτη — τα μοντέλα μας πρέπει να αντικατοπτρίζουν, έστω και μερικώς, την πολυπλοκότητα του πραγματικού κόσμου. Ωστόσο, όσο μπορούμε να διατηρούμε τα μοντέλα μας απλά, χωρίς να χάνουμε τη δυνατότητα να κατανοούμε το φαινόμενο ή να κάνουμε επαρκώς ακριβείς προβλέψεις, τόσο το καλύτερο.

Ο στόχος της δημιουργίας ενός στατιστικού μοντέλου δεν είναι απλώς η μείωση του σφάλματος. Θέλουμε, φυσικά, να μειώσουμε το σφάλμα όσο το δυνατόν περισσότερο, αλλά αυτό δεν είναι ο μοναδικός μας σκοπός. Ποιοι άλλοι στόχοι πρέπει να μας καθοδηγούν όταν κατασκευάζουμε ένα μοντέλο;

Το μοντέλο μας βοηθά να κατανοήσουμε κάτι για τη ΔΠΔ (Διαδικασία Παραγωγής Δεδομένων).Το μοντέλο μας βοηθά να κάνουμε αρκετά καλές προβλέψεις.Το μοντέλο εξισορροπεί την απλότητα και την ακρίβεια.

Επεξήγηση

Σωστή απάντηση: Όλα τα Α, Β, Γ

Η δημιουργία ενός καλού στατιστικού μοντέλου απαιτεί την εξισορρόπηση πολλαπλών στόχων, όχι μόνο τη μείωση του σφάλματος.

Α. Κατανόηση της Διαδικασίας Παραγωγής των Δεδομένων - ΣΩΣΤΟ ✓

Τι είναι η ΔΠΔ;

Η Διαδικασία Παραγωγής Δεδομένων είναι ο υποκείμενος μηχανισμός που δημιουργεί τα δεδομένα που παρατηρούμε.

Παράδειγμα:

Ερώτημα: Γιατί τα ψηλότερα άτομα έχουν μεγαλύτερους αντίχειρες;
ΔΠΔ: Το ύψος και το μήκος αντίχειρα συσχετίζονται επειδή και τα δύο επηρεάζονται από γενετικούς παράγοντες, διατροφή, κλπ.
Το μοντέλο: Μας βοηθά να κατανοήσουμε αυτή τη σχέση

Γιατί είναι σημαντικό;

Θέλουμε να εξηγήσουμε φαινόμενα, όχι μόνο να προβλέψουμε
Κατανοώντας τη ΔΠΔ, μπορούμε να γενικεύσουμε σε νέες καταστάσεις
Μας βοηθά να λάβουμε αποφάσεις (π.χ., παρεμβάσεις)

Β. Καλές προβλέψεις - ΣΩΣΤΟ ✓

Γιατί χρειαζόμαστε προβλέψεις;

Ένα μοντέλο πρέπει να κάνει αρκετά καλές προβλέψεις για νέα δεδομένα.

Παράδειγμα:

Αν ξέρουμε ότι κάποιος είναι ψηλός, μπορούμε να προβλέψουμε ότι πιθανόν έχει μεγαλύτερο αντίχειρα
Το μοντέλο της Height3Group προβλέπει:
- short: 56.07 mm
- medium: 60.22 mm
- tall: 64.09 mm

Αλλά όχι τέλειες προβλέψεις:

Δεν χρειάζεται να έχουμε μηδενικό σφάλμα
Αρκεί να είναι χρήσιμες προβλέψεις (καλύτερες από την τύχη)
Υπερβολική ακρίβεια μπορεί να οδηγήσει σε υπερπροσαρμογή (overfitting)

Γ. Εξισορρόπηση απλότητας και ακρίβειας μοντέλου - ΣΩΣΤΟ ✓

Το δίλημμα:

Απλότητα ←──────────────────→ Ακρίβεια
(λίγες παράμετροι)      (πολλές παράμετροι)
Εύκολο να κατανοηθεί    Καλύτερη προσαρμογή
Γενικεύει καλά           Κίνδυνος υπερπροσαρμογής

Παράδειγμα:

Μοντέλο	Παράμετροι	PRE	Απλότητα vs Ακρίβεια
Κενό μοντέλο	1 ($b_0$)	0%	Πολύ απλό, καμία ακρίβεια
Height2Group	2 ($b_0, b_1$)	7%	Απλό, μέτρια ακρίβεια
Height3Group	3 ($b_0, b_1, b_2$)	14%	Πιο πολύπλοκο, καλύτερη ακρίβεια
Ατομικό μοντέλο	157 παράμετροι	100%	Πολύ πολύπλοκο, τέλεια προσαρμογή αλλά άχρηστο!

Γιατί όχι πάντα το πιο ακριβές μοντέλο;

Υπερπροσαρμογή: Ένα μοντέλο με μια παράμετρο για κάθε άτομο θα έχει μηδενικό σφάλμα, αλλά θα είναι άχρηστο για νέα, άγνωστα δεδομένα
Ερμηνευσιμότητα: Απλούστερα μοντέλα είναι πιο εύκολο να κατανοηθούν
Γενίκευση: Απλούστερα μοντέλα συχνά λειτουργούν καλύτερα σε νέα δεδομένα

Η αρχή της απλότητας (Parsimony / Occam’s Razor):

«Προτιμήστε το απλούστερο μοντέλο που κάνει αρκετά καλή δουλειά.»

Γιατί όλα τα παραπάνω;

Ένα καλό μοντέλο πρέπει να:

Εξηγεί την υποκείμενη διαδικασία (ΔΠΔ)
- Κατανοούμε γιατί υπάρχει η σχέση
- π.χ., «Το ύψος σχετίζεται με το μήκος αντίχειρα»
Προβλέπει αρκετά καλά
- Δίνει χρήσιμες εκτιμήσεις για νέες παρατηρήσεις
- π.χ., PRE = 14% σημαίνει ότι εξηγούμε μέρος της μεταβλητότητας
Εξισορροπεί απλότητα και ακρίβεια
- Όχι υπερβολικά απλό (χαμηλή ακρίβεια)
- Όχι υπερβολικά πολύπλοκο (υπερπροσαρμογή)
- π.χ., Height3Group: 3 παράμετροι = καλή ισορροπία

Παράδειγμα από τα δεδομένα μας:

Το μοντέλο της Height3Group ικανοποιεί και τους τρεις στόχους:

✓ Κατανόηση: Βλέπουμε ότι το ύψος συσχετίζεται θετικά με το μήκος αντίχειρα

✓ Πρόβλεψη: Εξηγεί 14% της μεταβλητότητας (αρκετά χρήσιμο)

✓ Ισορροπία: 3 παράμετροι = απλό αλλά όχι υπερβολικά απλό

Συμπέρασμα:

Η μοντελοποίηση δεν είναι μόνο για τη μείωση του σφάλματος. Χρειαζόμαστε μοντέλα που:

Μας βοηθούν να καταλάβουμε τον κόσμο (ΔΠΔ)
Κάνουν χρήσιμες προβλέψεις
Είναι αρκετά απλά για να γενικεύουν αλλά αρκετά πολύπλοκα για να είναι ακριβή

Όλοι αυτοί οι στόχοι είναι εξίσου σημαντικοί και πρέπει να λαμβάνονται ταυτόχρονα υπόψη!

Ποιο είναι το μειονέκτημα του PRE;

Κανένα. Είναι το τέλειο στατιστικό μέτρο.Το PRE δεν δείχνει πόσο σφάλμα έχει μειωθεί σε σχέση με το συνολικό σφάλμα.Το PRE είναι ένα από τα πολλά εναλλακτικά μέτρα που δείχνει πόσο σφάλμα έχει μειωθεί.Το PRE δεν δείχνει πόσο σφάλμα έχει μειωθεί σε σχέση με το πόση πολυπλοκότητα έχει προστεθεί στο μοντέλο.

Επεξήγηση

Σωστή απάντηση: Δ - Το PRE δεν λαμβάνει υπόψη την πολυπλοκότητα του μοντέλου

Το πρόβλημα με το PRE:

Το PRE μετράει πόσο καλά το μοντέλο προσαρμόζεται στα δεδομένα, αλλά δεν λαμβάνει υπόψη πόσο πολύπλοκο είναι το μοντέλο.

Παράδειγμα:

Μοντέλο	Παράμετροι	PRE	Πολυπλοκότητα
Κενό μοντέλο	1	0%	Πολύ απλό
Height2Group	2	7%	Απλό
Height3Group	3	14%	Μέτρια
Height10Group	10	25%	Πολύ πολύπλοκο
Ατομικό μοντέλο	157	100%	Άχρηστα πολύπλοκο!

Το πρόβλημα:

Αν συνεχίσουμε να προσθέτουμε παραμέτρους:

Το PRE θα συνεχίσει να αυξάνεται
Τελικά θα φτάσουμε σε 100% PRE (τέλεια προσαρμογή)
Αλλά το μοντέλο θα είναι υπερπροσαρμοσμένο (overfitted)
Δεν θα γενικεύεται σε νέα δεδομένα

Το PRE ΔΕΝ δείχνει:

Αν η βελτίωση στην προσαρμογή αξίζει την προσθήκη πολυπλοκότητας

Αν το μοντέλο θα λειτουργήσει καλά σε νέα δεδομένα

Αν έχουμε την καλύτερη ισορροπία μεταξύ απλότητας και ακρίβειας

Γιατί οι άλλες είναι λάθος:

Α. “Τέλειο στατιστικό” - ΛΑΘΟΣ

Κανένα στατιστικό δεν είναι τέλειο
Το PRE έχει σημαντικό μειονέκτημα: αγνοεί την πολυπλοκότητα

Β. “Δεν δείχνει πόσο σφάλμα μειώθηκε σε σχέση με το συνολικό” - ΛΑΘΟΣ

Αυτό είναι ακριβώς αυτό που κάνει το PRE!

\[\text{PRE} = \frac{\text{SS}_{\text{Model}}}{\text{SS}_{\text{Total}}} = \frac{\text{Μείωση σφάλματος}}{\text{Συνολικό σφάλμα}}\]

Π.χ., PRE = 0.14 σημαίνει ότι μειώσαμε το 14% του συνολικού σφάλματος

Γ. “Ένα από πολλά μέτρα” - ΜΕΡΙΚΩΣ ΣΩΣΤΟ αλλά όχι το χειρότερο

Ναι, υπάρχουν και άλλα μέτρα (AIC, BIC, Adjusted R², κλπ.)
Αλλά αυτό δεν είναι μειονέκτημα του PRE
Είναι καλό να έχουμε πολλά μέτρα!
Το πραγματικό πρόβλημα είναι η αγνόηση της πολυπλοκότητας

Παράδειγμα του προβλήματος:

Φανταστείτε ότι συγκρίνουμε:

Μοντέλο Α: 3 παράμετροι, PRE = 14%

Μοντέλο Β: 50 παράμετροι, PRE = 18%

Το PRE δείχνει ότι το Β είναι καλύτερο (18% > 14%).

Αλλά:

Το Β προσθέτει 47 επιπλέον παραμέτρους για μόνο 4% βελτίωση
Αξίζει την πολυπλοκότητα;
Το PRE δεν μας το δείχνει!

Λύσεις - Μέτρα που λαμβάνουν υπόψη την πολυπλοκότητα:

Adjusted R² (Διορθωμένο R²)
- “Τιμωρεί” μοντέλα με πολλές παραμέτρους
- Αυξάνεται μόνο αν η νέα παράμετρος βελτιώνει αρκετά την προσαρμογή
AIC (Akaike Information Criterion)
- Ισορροπεί καλή προσαρμογή με απλότητα
- Μικρότερο AIC = καλύτερο μοντέλο
BIC (Bayesian Information Criterion)
- Παρόμοιο με AIC αλλά “τιμωρεί” περισσότερο την πολυπλοκότητα

Συμπέρασμα:

Το μειονέκτημα του PRE είναι ότι:

Δε λαμβάνει υπόψη την πολυπλοκότητα του μοντέλου

Αυτό σημαίνει ότι:

Μπορεί να μας οδηγήσει σε υπερβολικά πολύπλοκα μοντέλα
Δεν μας βοηθά να βρούμε την καλύτερη ισορροπία μεταξύ απλότητας και ακρίβειας
Πρέπει να το χρησιμοποιούμε μαζί με άλλα μέτρα που λαμβάνουν υπόψη την πολυπλοκότητα

Για αυτό το λόγο:

Χρησιμοποιούμε το PRE για να κατανοήσουμε την ποσότητα της μεταβλητότητας που εξηγεί ένα μοντέλο, αλλά δεν μπορούμε να βασιστούμε σε αυτό για να επιλέξουμε μεταξύ μοντέλων διαφορετικής πολυπλοκότητας.

9.4 Το πηλίκο `F`

Στην προηγούμενη ενότητα συζητήσαμε τους περιορισμούς του PRE ως μέτρου προσαρμογής ενός μοντέλου. Ένα μοντέλο μπορεί να «υπερπροσαρμοστεί» αν προσθέσουμε υπερβολικά πολλές παραμέτρους, γεγονός που μειώνει μεν το σφάλμα, αλλά εις βάρος της γενικευσιμότητας. Το PRE, επομένως, από μόνο του δεν επαρκεί για να αξιολογήσουμε ουσιαστικά τη βελτίωση της προσαρμογής· μας δείχνει αν το σφάλμα μειώνεται, αλλά όχι με ποιο κόστος επιτυγχάνεται αυτή η μείωση.

Το πηλίκο F (F ratio) έρχεται να καλύψει αυτό το κενό, καθώς προσφέρει έναν δείκτη της μείωσης του σφάλματος που επιτυγχάνεται από ένα μοντέλο, λαμβάνοντας υπόψη τον αριθμό των παραμέτρων που απαιτήθηκαν για αυτή τη μείωση.

Για να κατανοήσουμε πώς υπολογίζεται το πηλίκο F, ας επιστρέψουμε στον πίνακα ANOVA για το μοντέλο Height2Group (που φαίνεται παρακάτω). Έχουμε ήδη εξηγήσει πώς ερμηνεύεται η στήλη SS. Τώρα, ας εξετάσουμε τις επόμενες τρεις στήλες: df, MS και F. Το df αναφέρεται στους βαθμούς ελευθερίας (degrees of freedom), το MS αντιστοιχεί στο Μέσο Άθροισμα Τετραγώνων (Mean Square), και το F είναι, φυσικά, το πηλίκο F.

Analysis of Variance Table (Type III SS)
Model: Thumb ~ Height2Group

                               SS  df      MS      F    PRE     p
----- --------------- | --------- --- ------- ------ ------ -----
Model (error reduced) |   830.880   1 830.880 11.656 0.0699 .0008
Error (from model)    | 11049.331 155  71.286
----- --------------- | --------- --- ------- ------ ------ -----
Total (empty model)   | 11880.211 156  76.155

Βαθμοί Ελευθερίας (`df`)

Τεχνικά, οι βαθμοί ελευθερίας είναι ο αριθμός των ανεξάρτητων πληροφοριών που χρησιμοποιούνται για τον υπολογισμό μιας εκτίμησης παραμέτρου (π.χ., των $b_0$ ή $b_1$). Ωστόσο, είναι συχνά πιο διαισθητικό να τους σκεφτόμαστε ως ένα «απόθεμα» (budget) που έχουμε στη διάθεσή μας. Όσο περισσότερες παρατηρήσεις διαθέτουμε (δηλαδή όσο μεγαλύτερο είναι το μέγεθος του δείγματος, $n$), τόσο περισσότερους βαθμούς ελευθερίας έχουμε για να εκτιμήσουμε περισσότερες παραμέτρους — με άλλα λόγια, για να δημιουργήσουμε πιο σύνθετα μοντέλα.

Στο σύνολο δεδομένων Fingers υπάρχουν 157 παρατηρήσεις (φοιτητές). Όταν εκτιμήσαμε τη μοναδική παράμετρο του κενού μοντέλου (την εκτίμηση $b_0$), χρησιμοποιήσαμε 1 βαθμό ελευθερίας (1 df), αφήνοντας 156 βαθμούς ελευθερίας διαθέσιμους — αυτό το σύνολο ονομάζεται df Total.

Το μοντέλο της Height2Group απαιτούσε την εκτίμηση μίας επιπλέον παραμέτρου (της εκτίμησης $b_1$), γεγονός που μας «κόστισε» έναν ακόμη βαθμό ελευθερίας. Γι’ αυτό, στον πίνακα ANOVA (γραμμή Model (error reduced)), βλέπουμε ότι το df Model είναι 1. Μετά την προσαρμογή του μοντέλου της Height2Group, απομένουν 155 βαθμοί ελευθερίας, οι οποίοι αντιστοιχούν στο df Error.

Κάθε επιπλέον παράμετρος σε ένα μοντέλο κοστίζει:

ένα επιπλέον σύνολο δεδομένωνέναν επιπλέον βαθμό ελευθερίαςμια μεταβλητή

Επεξήγηση

Σωστή απάντηση: Β - έναν επιπλέον βαθμό ελευθερίας

Τι είναι οι βαθμοί ελευθερίας;

Οι βαθμοί ελευθερίας είναι ο αριθμός των “ανεξάρτητων κομματιών πληροφορίας” που απομένουν μετά την εκτίμηση των παραμέτρων ενός μοντέλου.

Τύπος:

\[\text{df}_{\text{Error}} = n - k\]

όπου:

$n$ = αριθμός παρατηρήσεων (άτομα)
$k$ = αριθμός παραμέτρων στο μοντέλο

Παραδείγματα από τα μοντέλα μας:

Μοντέλο	Παράμετροι $(k)$	Παρατηρήσεις $(n)$	df Error
Κενό μοντέλο	1 ($b_0$)	157	$157 - 1 = 156$
Height2Group	2 ($b_0, b_1$)	157	$157 - 2 = 155$
Height3Group	3 ($b_0, b_1, b_2$)	157	$157 - 3 = 154$

Από τον πίνακα ANOVA:

Height2Group:
Error (from model)    | 11049.331  155  71.286
                                    ^^^  df = 155

Height3Group:
Error (from model)    | 10189.770  154  66.167
                                    ^^^  df = 154

Γιατί «κοστίζει» βαθμούς ελευθερίας;

Κάθε παράμετρος που εκτιμούμε:

“Χρησιμοποιεί” ένα μέρος των δεδομένων
- Για να εκτιμήσουμε το $b_0$, χρειαζόμαστε δεδομένα
- Για να εκτιμήσουμε το $b_1$, χρειαζόμαστε περισσότερα δεδομένα
- κλπ.
Μειώνει την “ελευθερία” των υπολοίπων
- Με περισσότερες παραμέτρους, τα υπόλοιπα έχουν λιγότερη ελευθερία να διαφέρουν
- Το μοντέλο είναι πιο “περιορισμένο”
Επηρεάζει την ακρίβεια της εκτίμησης
- Με λιγότερους df, οι εκτιμήσεις μας είναι λιγότερο ακριβείς

Γιατί οι άλλες είναι λάθος:

Α. “Επιπλέον σύνολο δεδομένων” - ΛΑΘΟΣ

Οι παράμετροι δεν χρειάζονται νέα δεδομένα
Χρησιμοποιούμε το ίδιο σύνολο δεδομένων για όλες τις παραμέτρους
Π.χ., Τα μοντέλα των Height2Group και Height3Group χρησιμοποιούν τα ίδια 157 άτομα

Γ. “Μια μεταβλητή” - ΛΑΘΟΣ

Οι παράμετροι και οι μεταβλητές είναι διαφορετικά πράγματα

Παράμετροι: - Σταθερές τιμές που εκτιμούμε ($b_0, b_1, b_2$)

Οι ίδιες για όλα τα άτομα

Μεταβλητές: - Δεδομένα που διαφέρουν ανά άτομο ($Y_i, X_{1i}, X_{2i}$)

Έχουν δείκτη $i$

Π.χ., στο μοντέλο της Height3Group:

3 παράμετροι: $b_0, b_1, b_2$
3 μεταβλητές: $Y_i$ (Thumb), $X_{1i}$ (medium), $X_{2i}$ (tall)
Αλλά οι παράμετροι κοστίζουν df, όχι μεταβλητές

Αναλυτική παρουσίαση:

Έχουμε 157 άτομα (n = 157)

Κενό μοντέλο: 1 παράμετρος
├─ Χρησιμοποιεί 1 df για το b₀
└─ Απομένουν: 157 - 1 = 156 df

Height2Group: 2 παράμετροι
├─ Χρησιμοποιεί 1 df για το b₀
├─ Χρησιμοποιεί 1 df για το b₁
└─ Απομένουν: 157 - 2 = 155 df

Height3Group: 3 παράμετροι
├─ Χρησιμοποιεί 1 df για το b₀
├─ Χρησιμοποιεί 1 df για το b₁
├─ Χρησιμοποιεί 1 df για το b₂
└─ Απομένουν: 157 - 3 = 154 df

Κάθε παράμετρος κοστίζει 1 df!

Συμπέρασμα:

Κάθε επιπλέον παράμετρος σε ένα μοντέλο κοστίζει έναν βαθμό ελευθερίας.

Για αυτό λέμε ότι η εκτίμηση επιπλέον παραμέτρων δεν είναι δωρεάν - έχει «κόστος» σε βαθμούς ελευθερίας!

Μέσα Αθροίσματα Τετραγώνων (`MS`)

Η στήλη με τίτλο MS, γνωστή και ως στήλη των διακυμάνσεων, περιέχει τα μέσα αθροίσματα τετραγώνων.

Analysis of Variance Table (Type III SS)
Model: Thumb ~ Height2Group

                               SS  df      MS      F    PRE     p
----- --------------- | --------- --- ------- ------ ------ -----
Model (error reduced) |   830.880   1 830.880 11.656 0.0699 .0008
Error (from model)    | 11049.331 155  71.286
----- --------------- | --------- --- ------- ------ ------ -----
Total (empty model)   | 11880.211 156  76.155

Κάθε τιμή MS υπολογίζεται διαιρώντας το άθροισμα τετραγώνων (SS) με τους αντίστοιχους βαθμούς ελευθερίας (df) για κάθε γραμμή του πίνακα.

\[\begin{align} \text{MS}_{\text{Model}} &= \frac{\text{SS}_{\text{Model}}}{\text{df}_{\text{Model}}} \\ \text{MS}_{\text{Error}} &= \frac{\text{SS}_{\text{Error}}}{\text{df}_{\text{Error}}} \\ \text{MS}_{\text{Total}} &= \frac{\text{SS}_{\text{Total}}}{\text{df}_{\text{Total}}} \end{align}\]

Ξεκινώντας από την τελευταία γραμμή, το MS Total δείχνει πόσο συνολικό σφάλμα υπάρχει στην εξαρτημένη μεταβλητή ανά βαθμό ελευθερίας, μετά την προσαρμογή του κενού μοντέλου. Αυτό, σε προηγούμενο κεφάλαιο, το ονομάσαμε διακύμανση της εξαρτημένης μεταβλητής. Το MS Error δείχνει πόσο σφάλμα παραμένει ανεξήγητο ανά βαθμό ελευθερίας, μετά την προσαρμογή του μοντέλου της Height2Group. Το MS Model εκφράζει τη μείωση του σφάλματος που πέτυχε το μοντέλο ανά βαθμό ελευθερίας που χρησιμοποιήθηκε πέρα από το κενό μοντέλο.

Ποιο από τα παρακάτω μέσα αθροίσματα τετραγώνων (MS) εκφράζει το συνολικό σφάλμα που υπολείπεται από το κενό μοντέλο ανά βαθμό ελευθερίας;

MS ModelMS ErrorMS Total

Επεξήγηση

Σωστή απάντηση: Γ - MS Total

Τι είναι το MS Total;

\[\text{MS}_{\text{Total}} = \frac{\text{SS}_{\text{Total}}}{\text{df}_{\text{Total}}}\]

Από τον πίνακα ANOVA:

\[\text{MS}_{\text{Total}} = \frac{11880.211}{156} = 76.155\]

Τι σημαίνει αυτό;

Το MS Total είναι το συνολικό σφάλμα από το κενό μοντέλο, διαιρεμένο με τους βαθμούς ελευθερίας που υπολείπονται στο κενό μοντέλο.

Αναλυτικά:

SS$_{\text{Total}}$ = 11880.211
- Η συνολική μεταβλητότητα του μήκους αντίχειρα
- Το σφάλμα από το κενό μοντέλο (που προβλέπει μόνο το γενικό μέσο όρο)
- \[\text{SS}_{\text{Total}} = \sum_{i=1}^{n}(Y_i - \bar{Y})^2\]
df$_{\text{Total}}$ = 156
- Οι βαθμοί ελευθερίας του κενού μοντέλου
- \[\text{df}_{\text{Total}} = n - 1 = 157 - 1 = 156\]
- Χάνουμε 1 df επειδή εκτιμούμε το γενικό μέσο όρο ($\bar{Y}$ ή $b_0$)
MS$_{\text{Total}}$ = 76.155
- Το μέσο σφάλμα ανά βαθμό ελευθερίας
- Πόσο σφάλμα έχουμε “κατά μέσο όρο” όταν χρησιμοποιούμε μόνο το γενικό μέσο όρο

Γιατί οι άλλες είναι λάθος:

Α. “MS Model” - ΛΑΘΟΣ

\[\text{MS}_{\text{Model}} = \frac{\text{SS}_{\text{Model}}}{\text{df}_{\text{Model}}} = \frac{830.880}{1} = 830.880\]

Αυτό αντιπροσωπεύει τη μεταβλητότητα που εξηγείται από το μοντέλο
Όχι το σφάλμα από το κενό μοντέλο
df$_{\text{Model}}$ = 1 (αριθμός ψευδομεταβλητών: $X_1$ για tall)

Β. “MS Error” - ΛΑΘΟΣ

\[\text{MS}_{\text{Error}} = \frac{\text{SS}_{\text{Error}}}{\text{df}_{\text{Error}}} = \frac{11049.331}{155} = 71.286\]

Αυτό αντιπροσωπεύει το σφάλμα που υπολείπεται μετά την προσαρμογή του μοντέλου της Height2Group
Όχι το σφάλμα από το κενό μοντέλο
df$_{\text{Error}}$ = 155 = 157 - 2 (χάσαμε 2 df για τις 2 παραμέτρους: $b_0, b_1$)

Σύγκριση των τριών MS:

Μέτρο	Τύπος	Τιμή	Ερμηνεία
MS Total	$\frac{SS_{Total}}{df_{Total}}$	$\frac{11880.2}{156} = 76.155$	Μέσο σφάλμα από κενό μοντέλο
MS Model	$\frac{SS_{Model}}{df_{Model}}$	$\frac{830.9}{1} = 830.880$	Μέση εξηγούμενη μεταβλητότητα
MS Error	$\frac{SS_{Error}}{df_{Error}}$	$\frac{11049.3}{155} = 71.286$	Μέσο σφάλμα από Height2Group

Παρατηρήσεις:

MS Total (76.155) > MS Error (71.286)
- Το μοντέλο της Height2Group μείωσε το μέσο σφάλμα!
- Από 76.155 → 71.286 mm²
MS Model (830.880) >> MS Error (71.286)

Γιατί είναι σημαντικό το MS Total;

Βάση για σύγκριση:
- Δείχνει πόσο σφάλμα έχουμε χωρίς μοντέλο
- Συγκρίνουμε το MS Error με το MS Total για να δούμε τη βελτίωση
Υπολογισμός του PRE:
- Μπορούμε να εκφράσουμε το PRE χρησιμοποιώντας το MS:
- Η μείωση από 76.155 → 71.286 αντιπροσωπεύει τη βελτίωση
Κατανόηση της βελτίωσης:
- MS Total = 76.155 mm² (ξεκινώντας)
- MS Error = 71.286 mm² (μετά το μοντέλο)
- Βελτίωση: $76.155 - 71.286 = 4.869$ mm² ανά df

Συμπέρασμα:

Το MS Total αντιπροσωπεύει το συνολικό σφάλμα από το κενό μοντέλο ανά βαθμό ελευθερίας. Είναι το σημείο αναφοράς που δείχνει πόσο σφάλμα έχουμε όταν δεν χρησιμοποιούμε καμία ανεξάρτητη μεταβλητή - απλά προβλέπουμε το γενικό μέσο όρο για όλους.

Ποιο από τα μέσα αθροίσματα τετραγώνων (MS) εκφράζει το σφάλμα που υπολείπεται από το σύνθετο μοντέλο ανά βαθμό ελευθερίας;

MS ModelMS ErrorMS Total

Επεξήγηση

Σωστή απάντηση: Β - MS Error

Τι είναι το MS Error;

\[\text{MS}_{\text{Error}} = \frac{\text{SS}_{\text{Error}}}{\text{df}_{\text{Error}}}\]

Από τον πίνακα ANOVA:

\[\text{MS}_{\text{Error}} = \frac{11049.331}{155} = 71.286\]

Τι σημαίνει αυτό;

Το MS Error είναι το σφάλμα που απομένει από το σύνθετο μοντέλο (της Height2Group), διαιρεμένο με τους βαθμούς ελευθερίας που απομένουν μετά την εκτίμηση των παραμέτρων του μοντέλου.

Αναλυτικά:

SS$_{\text{Error}}$ = 11049.331
- Η μεταβλητότητα που δεν εξηγείται από το μοντέλο της Height2Group
- Το άθροισμα των τετραγώνων των υπολοίπων:
- \[\text{SS}_{\text{Error}} = \sum_{i=1}^{n}(Y_i - \hat{Y}_i)^2\]
df$_{\text{Error}}$ = 155
- Οι βαθμοί ελευθερίας που απομένουν μετά την προσαρμογή του μοντέλου
- \[\text{df}_{\text{Error}} = n - k = 157 - 2 = 155\]
- Χάσαμε 2 df για τις 2 παραμέτρους: $b_0, b_1$
MS$_{\text{Error}}$ = 71.286
- Το μέσο σφάλμα ανά βαθμό ελευθερίας από το σύνθετο μοντέλο
- Πόσο σφάλμα απομένει “κατά μέσο όρο” μετά την εξήγηση από το μοντέλο της Height2Group

Γιατί λέγεται “σφάλμα από το σύνθετο μοντέλο”;

Το σύνθετο μοντέλο είναι:

\[\text{Thumb}_i = b_0 + b_1X_{1i} + e_i\]

όπου $X_1$ = 1 αν το άτομο είναι tall, 0 αν είναι short.

Το σφάλμα από το σύνθετο μοντέλο είναι το $e_i$ - η μεταβλητότητα που δεν μπόρεσε να εξηγήσει το μοντέλο.

Γιατί οι άλλες είναι λάθος:

Α. MS Model - ΛΑΘΟΣ

\[\text{MS}_{\text{Model}} = \frac{\text{SS}_{\text{Model}}}{\text{df}_{\text{Model}}} = \frac{830.880}{1} = 830.880\]

Αυτό αντιπροσωπεύει τη μεταβλητότητα που ΕΞΗΓΕΙΤΑΙ από το μοντέλο
Όχι το σφάλμα που απομένει
Μετράει την επιτυχία του μοντέλου, όχι το σφάλμα του

Γ. MS Total - ΛΑΘΟΣ

\[\text{MS}_{\text{Total}} = \frac{\text{SS}_{\text{Total}}}{\text{df}_{\text{Total}}} = \frac{11880.211}{156} = 76.155\]

Αυτό αντιπροσωπεύει το σφάλμα από το ΚΕΝΟ μοντέλο
Όχι από το σύνθετο μοντέλο (της Height2Group)
Είναι το σημείο αναφοράς πριν προσθέσουμε ανεξάρτητες μεταβλητές

Σύγκριση των τριών MS:

Μέτρο	Τύπος	Τιμή	Τι αντιπροσωπεύει
MS Total	$\frac{SS_{Total}}{df_{Total}}$	$\frac{11880.2}{156} = 76.155$	Σφάλμα από κενό μοντέλο
MS Error	$\frac{SS_{Error}}{df_{Error}}$	$\frac{11049.3}{155} = 71.286$	Σφάλμα από σύνθετο μοντέλο
MS Model	$\frac{SS_{Model}}{df_{Model}}$	$\frac{830.9}{1} = 830.880$	Μεταβλητότητα που εξηγείται

Πιο αναλυτικά:

ΔΙΑΔΙΚΑΣΙΑ ΜΟΝΤΕΛΟΠΟΙΗΣΗΣ:

Βήμα 1: ΚΕΝΟ ΜΟΝΤΕΛΟ
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
SS_Total = 11880.2 mm²
MS_Total = 76.155 mm²/df
(Όλο σφάλμα)

Βήμα 2: ΠΡΟΣΘΕΤΟΥΜΕ ΤΗΝ HEIGHT2GROUP
┌─────────────────┬──────────────────────────┐
│ ΕΞΗΓΕΙΤΑΙ       │ ΑΠΟΜΕΝΕΙ (ΣΦΑΛΜΑ)        │
│ SS_Model        │ SS_Error ← Αυτό!         │
│ 830.9           │ 11049.3                  │
│ MS = 830.880    │ MS = 71.286 ← Αυτό!      │
│                 │ (Σφάλμα από σύνθετο)     │
└─────────────────┴──────────────────────────┘

Το MS Error (71.286) είναι το μέσο σφάλμα
που ΑΠΟΜΕΝΕΙ μετά το μοντέλο της `Height2Group`

Η βελτίωση:

Πριν το μοντέλο: MS Total = 76.155 mm²/df
Μετά το μοντέλο: MS Error = 71.286 mm²/df
Μείωση: 76.155 - 71.286 = 4.869 mm²/df (6.4% μείωση)

Γιατί είναι σημαντικό το MS Error;

Μετράει την ποιότητα του μοντέλου:
- Μικρότερο MS Error = καλύτερο μοντέλο
- Λιγότερο σφάλμα ανά βαθμό ελευθερίας
Χρησιμοποιείται για στατιστικούς ελέγχους:
- Θα τους δούμε σε επόμενο κεφάλαιο
Εκτίμηση της διακύμανσης:
- Το MS Error εκτιμά τη διακύμανση $\sigma^2$ των υπολοίπων
- Χρησιμοποιείται για να υπολογίσουμε τυπικά σφάλματα (θα τα δούμε σε επόμενο κεφάλαιο)
Σύγκριση μοντέλων:

Μοντέλο	`MS Error`	Ερμηνεία
Κενό	76.155	Αρχικό σφάλμα ανά `df`
`Height2Group`	71.286	Λιγότερο

Παράδειγμα ερμηνείας:

Το MS Error = 71.286 mm² σημαίνει:

«Μετά την προσαρμογή του μοντέλου, το μέσο τετραγωνικό σφάλμα που απομένει είναι 71.286 mm². Αυτό σημαίνει ότι οι προβλέψεις μας έχουν τυπική απόκλιση περίπου $\sqrt{71.286} \approx 8.44$ mm.»

Συμπέρασμα:

Το MS Error αντιπροσωπεύει το σφάλμα που απομένει από το σύνθετο μοντέλο (Height2Group) ανά βαθμό ελευθερίας. Μετράει πόσο σφάλμα δεν μπόρεσε να εξηγήσει το μοντέλο - αυτό που παραμένει ακόμα και μετά την προσθήκη της ανεξάρτητης μεταβλητής.

Ποιο από αυτά τα μέσα αθροίσματα τετραγώνων (MS) εκφράζει το σφάλμα που μειώθηκε από το σύνθετο μοντέλο ανά βαθμό ελευθερίας που δαπανήθηκε;

MS ModelMS ErrorMS Total

Επεξήγηση

Σωστή απάντηση: Α - MS Model

Τι είναι το MS Model;

\[\text{MS}_{\text{Model}} = \frac{\text{SS}_{\text{Model}}}{\text{df}_{\text{Model}}}\]

Από τον πίνακα ANOVA:

\[\text{MS}_{\text{Model}} = \frac{830.880}{1} = 830.880\]

Τι σημαίνει αυτό;

Το MS Model αντιπροσωπεύει το σφάλμα που μειώθηκε (ή τη μεταβλητότητα που εξηγήθηκε) από το σύνθετο μοντέλο, διαιρεμένο με τους βαθμούς ελευθερίας που δαπανήθηκαν για να επιτευχθεί αυτή η μείωση.

Αναλυτικά:

SS$_{\text{Model}}$ = 830.880
- Το σφάλμα που μειώθηκε από το κενό μοντέλο
- Η μεταβλητότητα που εξηγήθηκε από το μοντέλο της Height2Group
- \[\text{SS}_{\text{Model}} = \text{SS}_{\text{Total}} - \text{SS}_{\text{Error}}\]
- \[830.880 = 11880.211 - 11049.331\]
df$_{\text{Model}}$ = 1
- Οι βαθμοί ελευθερίας που δαπανήθηκαν για το μοντέλο
- Αριθμός ψευδομεταβλητών (ανεξάρτητων μεταβλητών)
- 2 ομάδες → 1 ψευδομεταβλητή ($X_1$ για tall)
- Όχι 2, επειδή η ομάδα αναφοράς (short) δεν χρειάζεται ψευδομεταβλητή
MS$_{\text{Model}}$ = 830.880
- Το μέσο σφάλμα που μειώθηκε ανά df που δαπανήθηκε
- Πόσο σφάλμα μειώσαμε “κατά μέσο όρο” για κάθε παράμετρο που προσθέσαμε

Γιατί οι άλλες είναι λάθος:

Β. MS Error - ΛΑΘΟΣ

\[\text{MS}_{\text{Error}} = \frac{11049.331}{155} = 71.286\]

Αυτό αντιπροσωπεύει το σφάλμα που ΑΠΟΜΕΝΕΙ (όχι που μειώθηκε)
Είναι η ανεξήγητη μεταβλητότητα, όχι η εξηγούμενη

Γ. MS Total - ΛΑΘΟΣ

\[\text{MS}_{\text{Total}} = \frac{11880.211}{156} = 76.155\]

Αυτό αντιπροσωπεύει το συνολικό σφάλμα από το κενό μοντέλο
Δεν μετράει τη μείωση που επιτεύχθηκε από το σύνθετο μοντέλο

Η έννοια του “σφάλματος που μειώθηκε ανά df που δαπανήθηκε”:

ΚΕΝΟ ΜΟΝΤΕΛΟ:
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
SS_Total = 11880.2
(Όλο σφάλμα)

ΠΡΟΣΘΕΤΟΥΜΕ ΤΗΝ HEIGHT2GROUP:
Δαπανούμε 1 df (για X₁)

┌─────────────────┬──────────────────────────┐
│ ΜΕΙΩΣΗ ΣΦΑΛΜΑΤΟΣ│ ΥΠΟΛΟΙΠΟΜΕΝΟ ΣΦΑΛΜΑ      │
│ SS_Model        │ SS_Error                 │
│ 830.9           │ 11049.3                  │
│                 │                          │
│ Δαπανήθηκε 1 df │ Απομένουν 155 df         │
│                 │                          │
│ MS = 830.9/1    │ MS = 11049.3/155         │
│    = 830.880 ←──┼─ Αυτό!                   │
│                 │    = 71.286              │
└─────────────────┴──────────────────────────┘

MS Model = Πόσο σφάλμα μειώσαμε κατά μέσο όρο
           ανά παράμετρο που προσθέσαμε

Ερμηνεία:

Το MS Model = 830.880 mm² σημαίνει:

«Για τον έναν βαθμό ελευθερίας που δαπανήσαμε (την παράμετρο που προσθέσαμε), μειώσαμε το σφάλμα κατά 830.880 mm².»

Δαπανήσαμε 1 df (για $b_1$)
Μειώσαμε συνολικά 830.9 mm² σφάλμα
Κατά μέσο όρο: 830.9 mm² ανά df

Σύγκριση των τριών MS:

Μέτρο	Τύπος	Τιμή	Τι μετράει
`MS Total`	$\frac{SS_{Total}}{df_{Total}}$	$\frac{11880.2}{156} = 76.155$	Συνολικό σφάλμα (ανά `df`) πριν το μοντέλο
`MS Model`	$\frac{SS_{Model}}{df_{Model}}$	$\frac{830.9}{1} = 830.880$	Σφάλμα που μειώθηκε (ανά δαπανηθέν df)
`MS Error`	$\frac{SS_{Error}}{df_{Error}}$	$\frac{11049.3}{155} = 71.286$	Σφάλμα που απομένει (ανά `df` που απομένει)

Γιατί είναι σημαντικό το MS Model;

Μετράει την αποδοτικότητα του μοντέλου:
- Μεγάλο MS Model = πολύ σφάλμα μειώθηκε ανά παράμετρο
- Δείχνει ότι η παράμετρος “άξιζε” την επιπλέον πολυπλοκότητα
Αξιολόγηση κόστους-οφέλους:
- Κόστος: 1 df δαπανήθηκε
- Όφελος: 830.9 mm² μείωση ανά df
- Αξίζει; Ναι! Το MS Model >> MS Error

Οπτικοποίηση της έννοιας:

"Πόσο σφάλμα μειώνουμε ανά παράμετρο;"

Κάθε παράμετρος (df) "αγοράζει" μείωση σφάλματος:

Παράμετρος 1 (b₁):  ┌────────────┐
                    │ 830.9 mm²  │
                    │ μείωση     │
                    └────────────┘

Σύνολο: 1 df × 830.9 = 830.9 mm² (SS_Model)
Μέσος όρος: 830.9 mm²/df (MS_Model)

Συμπέρασμα:

Το MS Model αντιπροσωπεύει το σφάλμα που μειώθηκε από το σύνθετο μοντέλο ανά βαθμό ελευθερίας που δαπανήθηκε. Είναι μέτρο της αποδοτικότητας του μοντέλου - πόσο σφάλμα εξηγούμε κατά μέσο όρο για κάθε παράμετρο που προσθέτουμε. Μεγάλο MS Model σημαίνει ότι η παράμετρος “άξιζε” την πολυπλοκότητα που πρόσθεσε.

Το πηλίκο `F`

Ας περάσουμε τώρα στο πηλίκο F. Στον πίνακα που ακολουθεί παρουσιάζονται δύο διαφορετικές εκτιμήσεις διακύμανσης μετά την προσαρμογή του μοντέλου της Height2Group: το MS Model και το MS Error.

                               SS  df      MS      F    PRE     p
----- --------------- | --------- --- ------- ------ ------ -----
Model (error reduced) |   830.880   1 830.880 11.656 0.0699 .0008
Error (from model)    | 11049.331 155  71.286       
----- --------------- | --------- --- ------- ------ ------ -----
Total (empty model)   | 11880.211 156  76.155

Το MS Model εκφράζει τη διακύμανση των προβλέψεων που παράγει το μοντέλο της Height2Group, ενώ το MS Error εκφράζει τη διακύμανση των υπολοίπων —δηλαδή του σφάλματος που υπολείπεται αφού αφαιρεθεί το μοντέλο.

Το πηλίκο F υπολογίζεται ως ο λόγος αυτών των δύο ποσοτήτων:

\[F = \frac{\text{MS}_{\text{Model}}}{\text{MS}_{\text{Error}}} = \frac{\text{SS}_{\text{Model}}/\text{df}_{\text{Model}}}{\text{SS}_{\text{Error}}/\text{df}_{\text{Error}}}\]

Αυτός ο λόγος αποτελεί έναν εξαιρετικά χρήσιμο στατιστικό δείκτη.

Αν η μεταβλητή Height2Group έχει μικρή ή καθόλου επίδραση στο μήκος του αντίχειρα, τότε η διακύμανση των προβλέψεων του μοντέλου θα είναι περίπου ίση με τη διακύμανση των υπολοίπων, οπότε το πηλίκο F θα είναι κοντά στη μονάδα. Αντίθετα, όσο μεγαλύτερη είναι η διακύμανση των προβλέψεων σε σχέση με τη διακύμανση των υπολοίπων, τόσο μεγαλύτερο θα είναι το πηλίκο F και τόσο καλύτερη θεωρείται η προσαρμογή του μοντέλου.

Ένας άλλος τρόπος να το σκεφτούμε είναι ότι το F εκφράζει τον λόγο της διακύμανσης μεταξύ των ομάδων (καθώς οι μέσοι όροι των ομάδων αντιστοιχούν στις προβλέψεις του μοντέλου) προς τη διακύμανση εντός των ομάδων (δηλαδή τη διασπορά των παρατηρήσεων γύρω από τους μέσους όρους). Όταν η διακύμανση μεταξύ των ομάδων είναι σημαντικά μεγαλύτερη από τη διακύμανση εντός των ομάδων, το πηλίκο F υπερβαίνει τη μονάδα —υποδεικνύοντας ότι το μοντέλο εξηγεί ουσιαστικό μέρος της συνολικής μεταβλητότητας.

Το πηλίκο F για το μοντέλο της Height2Group είναι 11.66. Ποια είναι η σωστή ερμηνεία;

Υπάρχουν τουλάχιστον 11 άτομα των οποίων το μήκος αντίχειρα προβλέπεται καλύτερα γνωρίζοντας σε ποια ομάδα ύψους ανήκουν.Η Height2Group έχει μέγεθος επίδρασης 11.66 τυπικών αποκλίσεων.Η διακύμανση που εξηγείται από το μοντέλο είναι 11.66 φορές μεγαλύτερη από τη διακύμανση που παραμένει ανεξήγητη.Το άθροισμα τετραγώνων που εξηγείται από το μοντέλο είναι 11.66 φορές μεγαλύτερο από το άθροισμα τετραγώνων που υπολείπεται μετά την προσαρμογή του μοντέλου.

Επεξήγηση

Σωστή απάντηση: Γ - Η διακύμανση που εξηγείται είναι 11.66 φορές μεγαλύτερη από τη διακύμανση που παραμένει ανεξήγητη

Τι είναι το πηλίκο F;

Το πηλίκο F είναι ο λόγος δύο διακυμάνσεων:

\[F = \frac{\text{MS}_{\text{Model}}}{\text{MS}_{\text{Error}}}\]

Από τον πίνακα ANOVA:

\[F = \frac{830.880}{71.286} = 11.656 \approx 11.66\]

Τι δείχνει το F;

Το F συγκρίνει:

Αριθμητής (MS Model): Πόσο καλά το μοντέλο εξηγεί τη μεταβλητότητα (ανά βαθμό ελευθερίας)
Παρονομαστής (MS Error): Πόση μεταβλητότητα παραμένει ανεξήγητη (ανά βαθμό ελευθερίας)

Με απλά λόγια:

\[F = \frac{\text{Πόσο καλά δουλεύει το μοντέλο}}{\text{Πόσο σφάλμα απομένει}}\]

Ερμηνεία του F = 11.66:

«Η μεταβλητότητα που εξηγείται από την Height2Group (ανά βαθμό ελευθερίας) είναι 11.66 φορές μεγαλύτερη από τη μεταβλητότητα που παραμένει ανεξήγητη (ανά βαθμό ελευθερίας).»

«Η διακύμανση που εξηγείται από την Height2Group είναι 11.66 φορές μεγαλύτερη από τη διακύμανση που οφείλεται σε τυχαίο θόρυβο.»

Γιατί οι άλλες είναι λάθος:

Α. “11 άτομα προβλέπονται καλύτερα” - ΛΑΘΟΣ

Το F δεν μετράει αριθμό ατόμων
Είναι ένας λόγος διακυμάνσεων (χωρίς μονάδες μέτρησης)
Το μοντέλο δίνει προβλέψεις για όλα τα άτομα, όχι μόνο για 11

Β. “Μέγεθος επίδρασης 11.66 τυπικές αποκλίσεις” - ΛΑΘΟΣ

Το F δεν είναι μέγεθος επίδρασης σε τυπικές αποκλίσεις
Το F είναι χωρίς μονάδες
Για το μέγεθος επίδρασης μπορούμε να χρησιμοποιήσουμε το d του Cohen (βλ. επόμενη ενότητα)**

Δ. Το “SS Model είναι 11.66 φορές μεγαλύτερο από το SS Error” - ΛΑΘΟΣ

Ας το ελέγξουμε:

\[\frac{\text{SS}_{\text{Model}}}{\text{SS}_{\text{Error}}} = \frac{830.880}{11049.331} = 0.0752\]

Το SS Model είναι 0.075 φορές (όχι 11.66 φορές) το SS Error
Το SS Model είναι στην πραγματικότητα πολύ μικρότερο από το SS Error

Το F χρησιμοποιεί MS, όχι SS!

Η διαφορά μεταξύ SS και MS:

	Άθροισμα Τετραγώνων (SS)	Μέσο Τετραγωνικό Σφάλμα (MS)
Τύπος	Άθροισμα	Μέσος όρος (ανά `df`)
Model	830.880	830.880 / 1 = 830.880
Error	11049.331	11049.331 / 155 = 71.286
Πηλίκο	0.075	11.66

Γιατί η Γ είναι σωστή;

Το MS μετράει διακύμανση:

\[\text{MS} = \frac{\text{SS}}{\text{df}} = \text{μέση μεταβλητότητα ανά βαθμό ελευθερίας}\]

Ο υπολογισμός:

MS_Model = 830.880 / 1 = 830.880
MS_Error = 11049.331 / 155 = 71.286

F = MS_Model / MS_Error
  = 830.880 / 71.286
  = 11.656

# Ερμηνεία:
# Η εξηγούμενη μεταβλητότητα (ανά `df`) είναι
# 11.66 φορές η ανεξήγητη μεταβλητότητα (ανά `df`)

Τι σημαίνει αυτό στην πράξη;

Το μοντέλο είναι αποδοτικό:
- Κάθε βαθμός ελευθερίας που δαπανήσαμε (εδώ 1 για το $b_1$) εξηγεί 11.66 φορές περισσότερη μεταβλητότητα από όση θα περιμέναμε από τυχαία διακύμανση.
Σύγκριση με τυχαίο θόρυβο:
- Αν η Height2Group δεν είχε καμία πραγματική επίδραση, θα περιμέναμε F ≈ 1
- F = 11.66 >> 1, άρα η επίδραση είναι πολύ μεγαλύτερη από τυχαίες διακυμάνσεις.
- Όπως θα δούμε σε επόμενο κεφάλαιο, είναι εξαιρετικά απίθανο (πιθανότητα p = .0008) να δούμε τόσο μεγάλο F αν η ομάδα ύψους δεν επηρέαζε πραγματικά το μήκος αντίχειρα

Πλήρης ερμηνεία του F = 11.66:

«Το μοντέλο της Height2Group εξηγεί 11.66 φορές περισσότερη μεταβλητότητα στο μήκος αντίχειρα (ανά βαθμό ελευθερίας) σε σχέση με τη μεταβλητότητα που παραμένει ανεξήγητη. Αυτό σημαίνει ότι η γνώση της ομάδας ύψους (short vs tall) συμβάλει ουσιαστικά στην πρόβλεψη του μήκους αντίχειρα, πέρα από τον τυχαίο θόρυβο.»

Σύνδεση με άλλα μέτρα:

PRE = 0.0699 (7%): Το μοντέλο εξηγεί 7% της συνολικής μεταβλητότητας
F = 11.66: Η μεταβλητότητα που εξηγείται (ανά df) είναι 11.66× την ανεξήγητη (ανά df)

Όλα τα μέτρα μας δείχνουν το ίδιο πράγμα από διαφορετική οπτική: Η Height2Group έχει σημαντική επίδραση!

Συμπέρασμα:

Ένα πηλίκο F = 11.66 σημαίνει ότι η μεταβλητότητα που εξηγείται από το μοντέλο (ανά βαθμό ελευθερίας) είναι 11.66 φορές μεγαλύτερη από τη μεταβλητότητα που απομένει ανεξήγητη (ανά βαθμό ελευθερίας). Αυτό είναι η ουσία του πηλίκου F: συγκρίνει τη μέση εξηγούμενη με τη μέση ανεξήγητη μεταβλητότητα.

Όπως η διακύμανση προσαρμόζει το άθροισμα τετραγώνων (SS) ανάλογα με τους διαθέσιμους βαθμούς ελευθερίας, έτσι και το πηλίκο F λαμβάνει υπόψη του πόσους βαθμούς ελευθερίας «δαπανήσαμε» για να κάνουμε το μοντέλο πιο σύνθετο. Με άλλα λόγια, το F μάς δείχνει αν αυτή η «επένδυση» σε πολυπλοκότητα άξιζε τον κόπο — αν οι πρόσθετες παράμετροι συμβάλλουν ουσιαστικά στην εξήγηση της μεταβλητότητας ή αν απλώς βοηθούν το μοντέλο να προσαρμοστεί καλύτερα στον τυχαίο θόρυβο των δεδομένων.

Αν πάρουμε ένα διαφορετικό δείγμα 157 φοιτητών και τους ζητήσουμε μετρήσεις αντίχειρα και ύψους, θα πάρουμε την ίδια τιμή F;

Ναι, σίγουρα.Όχι, κάτι τέτοιο είναι απίθανο.

Επεξήγηση

Σωστή απάντηση: Β - Όχι, κάτι τέτοιο είναι απίθανο

Γιατί δεν θα πάρουμε την ίδια τιμή F;

Το πηλίκο F υπολογίζεται από δεδομένα δείγματος, οπότε εξαρτάται από την τυχαία δειγματοληπτική μεταβλητότητα (sampling variability).

Τι είναι η δειγματοληπτική μεταβλητότητα;

Κάθε φορά που παίρνουμε ένα νέο δείγμα από τον πληθυσμό:

Θα έχουμε διαφορετικά άτομα
Με διαφορετικές τιμές μήκους αντίχειρα και ύψους
Άρα διαφορετικά SS, MS, και F

Γιατί συμβαίνει αυτό;

Τυχαία δειγματοληψία:
- Κάθε δείγμα είναι μια τυχαία επιλογή από τον πληθυσμό
- Διαφορετικά δείγματα → διαφορετικοί μέσοι όροι, μεταβλητότητα
Μεταβλητότητα στις εκτιμήσεις:
- Οι παράμετροι $b_0, b_1$ αναμένεται να διαφέρουν
- Τα υπόλοιπα θα είναι διαφορετικά
- Άρα διαφορετικά SS, MS, F
Ατομικές διαφορές:
- Κάθε δείγμα θα έχει διαφορετικά άτομα
- Μερικά δείγματα μπορεί να έχουν πιο ακραίες τιμές
- Άλλα μπορεί να έχουν πιο “συνηθισμένες” τιμές

Οπτικοποίηση:

ΠΛΗΘΥΣΜΟΣ ΦΟΙΤΗΤΩΝ
(Όλοι οι φοιτητές)
         │
         ├─────┬─────┬─────┬─────┐
         │     │     │     │     │
     Δείγμα Δείγμα Δείγμα ... Δείγμα
        1      2      3           ∞
     ┌────┐ ┌────┐ ┌────┐     ┌────┐
     │F=  │ │F=  │ │F=  │ ... │F=  │
     │11.7│ │10.8│ │12.6│     │ ;  │
     └────┘ └────┘ └────┘     └────┘

Κάθε δείγμα δίνει διαφορετικό F!

Τι ΘΑ είναι παρόμοιο;

Αν και η τιμή του F θα διαφέρει, αναμένουμε:

Παρόμοιο μέγεθος F:
- Αν το πραγματικό F στον πληθυσμό είναι γύρω στο 11-12
- Τα περισσότερα δείγματα αναμένεται να δώσουν παρόμοιο F
Παρόμοια κατεύθυνση επίδρασης:
- Τα ψηλότερα άτομα θα έχουν μεγαλύτερους αντίχειρες
- Το πρόσημο των $b_1$ θα είναι θετικό

Αλλά το ΑΚΡΙΒΕΣ F = 11.656 είναι απίθανο να επαναληφθεί!

Γιατί η απάντηση “Ναι, σίγουρα” είναι λάθος:

Το “σίγουρα” υπονοεί:

100% βεβαιότητα ότι F = 11.656 ακριβώς
Αυτό είναι σχεδόν αδύνατο λόγω δειγματοληπτικής μεταβλητότητας
Ακόμα και αν το F του πληθυσμού είναι 11.656, τα δείγματα θα διαφέρουν

Συμπέρασμα:

Όχι, δεν θα πάρουμε το ίδιο F. Κάθε νέο δείγμα θα δώσει ελαφρώς διαφορετικές τιμές λόγω δειγματοληπτικής μεταβλητότητας. Ενώ αναμένουμε το F να είναι παρόμοιο και να δείχνει την ίδια γενική επίδραση, το ακριβές F = 11.656 είναι απίθανο να επαναληφθεί. Αυτή είναι η φύση της στατιστικής: εκτιμούμε παραμέτρους από δείγματα, αλλά οι εκτιμήσεις μας έχουν αβεβαιότητα.

Τι είναι το πηλίκο F;

Ένα στατιστικό δείγματοςΜια παράμετρος πληθυσμούΈνα μοντέλο

Επεξήγηση

Σωστή απάντηση: Α - Ένα στατιστικό δείγματος

Τι σημαίνει αυτό;

Το πηλίκο F είναι ένα στατιστικό επειδή:

Υπολογίζεται από δεδομένα δείγματος
- Χρησιμοποιούμε τις 157 παρατηρήσεις από το δείγμα μας
Διαφέρει από δείγμα σε δείγμα
- Κάθε δείγμα θα δώσει διαφορετικό F
- Υπόκειται σε δειγματοληπτική μεταβλητότητα
Χρησιμοποιείται για να εκτιμήσουμε κάτι για τον πληθυσμό
- Χρησιμοποιούμε το F για να βγάλουμε συμπεράσματα
- Ελέγχουμε αν υπάρχει πραγματική επίδραση στον πληθυσμό

Ορισμοί:

Στατιστικό (Statistic):

Μια αριθμητική τιμή που υπολογίζεται από δείγμα
Χρησιμοποιείται για να εκτιμήσει μια παράμετρο πληθυσμού
Παραδείγματα: $\bar{x}$, $s$, $b_0$, $b_1$, $F$, $t$

Παράμετρος πληθυσμού (Parameter):

Μια σταθερή τιμή που περιγράφει τον πληθυσμό
Συνήθως άγνωστη - προσπαθούμε να την εκτιμήσουμε
Παραδείγματα: $\mu$, $\sigma$, $\beta_0$, $\beta_1$

Γιατί το F είναι στατιστικό μέτρο;

\[F = \frac{\text{MS}_{\text{Model}}}{\text{MS}_{\text{Error}}}\]

Υπολογίζεται από:

SS Model = από τα δεδομένα του δείγματος
SS Error = από τα δεδομένα του δείγματος
df Model, df Error = από το μέγεθος δείγματος

Όλα προέρχονται από το δείγμα!

Σύγκριση:

	Στατιστικό (από δείγμα)	Παράμετρος (από πληθυσμό)
Μέσος όρος	$\bar{x}$	$\mu$
Τυπική απόκλιση	$s$	$\sigma$
Παράμετρος μοντέλου	$b_0, b_1$	$\beta_0, \beta_1$
πηλίκο F	$F$	—
Αλλάζει;	Ναι (κάθε δείγμα)	Όχι (σταθερό)
Γνωστό;	Ναι (υπολογίζεται)	Όχι (εκτιμάται)

Σημείωση για το F:

Δεν υπάρχει “F του πληθυσμού” με την ίδια έννοια
Το F είναι ένα στατιστικό που υπολογίζεται από δείγματα
Χρησιμοποιείται για να ελέγξουμε υποθέσεις για παραμέτρους του πληθυσμού

Γιατί οι άλλες είναι λάθος:

Β. “Παράμετρος πληθυσμού” - ΛΑΘΟΣ

Το F δεν είναι παράμετρος του πληθυσμού
Υπολογίζεται από δείγμα, όχι από πληθυσμό
Διαφέρει από δείγμα σε δείγμα

Οι πραγματικές παράμετροι πληθυσμού στο μοντέλο μας:

$\beta_0$: Ο πληθυσμιακός μέσος όρος της ομάδας αναφοράς
$\beta_1$: Η πληθυσμιακή διαφορά μεταξύ ομάδων
$\sigma^2$: Η πληθυσμιακή διακύμανση των σφαλμάτων

Αυτές είναι άγνωστες και τις εκτιμούμε με $b_0, b_1, MS_{Error}$.

Γ. “Μοντέλο” - ΛΑΘΟΣ

Το F δεν είναι το ίδιο το μοντέλο
Είναι ένα στατιστικό που χρησιμοποιείται για να αξιολογήσει το μοντέλο

Το μοντέλο:

\[Y_i = b_0 + b_1X_i + e_i\]

Το πηλίκο F:

\[F = \frac{MS_{Model}}{MS_{Error}}\]

Το F προέρχεται από το μοντέλο, αλλά δεν είναι το μοντέλο.

Οπτικοποίηση:

ΠΛΗΘΥΣΜΟΣ (άγνωστος)
┌─────────────────────────┐
│ Παράμετροι:             │
│ β₀, β₁, σ²              │
│ (άγνωστα)               │
└─────────────────────────┘
         ↓ δειγματοληψία
┌─────────────────────────┐
│ ΔΕΙΓΜΑ (n=157)          │
├─────────────────────────┤
│ Υπολογίζουμε:           │
│ • Στατιστικά: b₀, b₁    │
│ • Στατιστικά: MS, SS    │
│ • Στατιστικό: F = 11.66 │
└─────────────────────────┘
         ↓ συμπερασματολογία
┌─────────────────────────┐
│ ΣΥΜΠΕΡΑΣΜΑ για πληθυσμό:│
│ "Πιθανώς υπάρχει        │
│  πραγματική επίδραση"   │
└─────────────────────────┘

Συμπέρασμα:

Το πηλίκο F είναι ένα δειγματικό στατιστικό μέτρο επειδή:

Υπολογίζεται από δεδομένα δείγματος
Διαφέρει από δείγμα σε δείγμα
Χρησιμοποιείται για να βγάλουμε συμπεράσματα για παραμέτρους πληθυσμού
Υπόκειται σε δειγματοληπτική μεταβλητότητα

Γιατί θα ήταν απίθανο να πάρουμε την ίδια τιμή F από δείγμα σε δείγμα;

Επειδή το πηλίκο F είναι ένα στατιστικό μέτρο, όπως ο μέσος όρος ή το PRE. Ένα διαφορετικό δείγμα πιθανώς θα οδηγήσει σε διαφορετική τιμή του στατιστικού.Επειδή με τόσες πολλές παρατηρήσεις, μπορεί να γίνουν λάθη υπολογισμού.Επειδή το πηλίκο F είναι διαφορετικό για κάθε άτομο στη μελέτη σας. Θα παίρναμε ένα σύνολο 157 νέων πηλίκων F.Επειδή το πηλίκο F είναι διαφορετικό για κάθε ομάδα στη μελέτη μας. Θα παίρναμε μια τιμή F για την ομάδα short και μια διαφορετική τιμή για την ομάδα tall.Επειδή το df Total θα ήταν διαφορετικό σε κάθε νέο δείγμα.

Επεξήγηση

Σωστή απάντηση: Α - Το F είναι στατιστικό μέτρο που διαφέρει μεταξύ δειγμάτων

Γιατί αυτό είναι σωστό;

Το πηλίκο F είναι ένα δειγματικό στατιστικό μέτρο (sample statistic), όπως:

Ο μέσος όρος δείγματος ($\bar{x}$)
Η τυπική απόκλιση δείγματος ($s$)
Το PRE
Οι εκτιμήσεις παραμέτρων ($b_0, b_1$)

Χαρακτηριστικά στατιστικών μέτρων:

Υπολογίζονται από δεδομένα δείγματος
Διαφέρουν από δείγμα σε δείγμα (δειγματοληπτική μεταβλητότητα)
Χρησιμοποιούνται για να εκτιμήσουν παραμέτρους πληθυσμού

Όλα τα στατιστικά διαφέρουν μεταξύ δειγμάτων!

Γιατί οι άλλες είναι λάθος:

Β. “Λάθη υπολογισμού” - ΛΑΘΟΣ

Η διαφορά δεν οφείλεται σε σφάλματα υπολογισμού
Οφείλεται σε φυσική δειγματοληπτική μεταβλητότητα
Ακόμα και με τέλειους υπολογισμούς, τα δείγματα θα διαφέρουν

Αναλογία:

Αν ρίξουμε ένα νόμισμα 100 φορές, μπορεί να πάρουμε 48 φορές γράμματα.

Αν το ρίξουμε άλλες 100 φορές, μπορεί να πάρουμε 52 φορές γράμματα.

Αυτό δεν είναι “λάθος” - είναι τυχαία μεταβλητότητα!

Γ. “Διαφορετικό F για κάθε άτομο” - ΛΑΘΟΣ

Το F δεν υπολογίζεται ξεχωριστά για κάθε άτομο
Υπάρχει μία τιμή F για το όλο το μοντέλο
Το F συγκρίνει τη μεταβλητότητα σε επίπεδο δείγματος, όχι ατόμου

Δ. “Διαφορετικό F για κάθε ομάδα” - ΛΑΘΟΣ

Το F δεν υπολογίζεται ξεχωριστά για κάθε ομάδα
Υπάρχει μία τιμή F για το όλο το μοντέλο
Το F ελέγχει: “Έχουν όλες οι ομάδες μαζί επίδραση;”

Τι διαφέρει μεταξύ ομάδων:

Οι μέσοι όροι διαφέρουν: short = 57.82, tall = 62.42
Οι παράμετροι διαφέρουν: $b_1$ για tall
Αλλά το F είναι ένα για το συνολικό μοντέλο

Ε. “Το df Total θα ήταν διαφορετικό” - ΛΑΘΟΣ

Το df Total εξαρτάται από το μέγεθος του δείγματος (n)
\[df_{Total} = n - 1\]

Αν πάρουμε νέο δείγμα με το ΙΔΙΟ $n$:

Οι df είναι τα ίδιοι, αλλά το F διαφέρει!

Γιατί το F διαφέρει αν οι df είναι ίδιοι;

Επειδή τα SS (αθροίσματα τετραγώνων) διαφέρουν.

Οι df παραμένουν ίδιοι, αλλά τα SS αλλάζουν → το F αλλάζει!

Συμπέρασμα:

Θα ήταν απίθανο να πάρουμε το ίδιο πηλίκο F επειδή:

✓ Το F είναι δειγματικό στατιστικό μέτρο

✓ Όπως όλα τα στατιστικά μέτρα, διαφέρει μεταξύ δειγμάτων

✓ Κάθε δείγμα έχει διαφορετικά άτομα με διαφορετικές τιμές

✓ Αυτό οδηγεί σε διαφορετικά SS, MS, και τελικά F

Αυτή είναι η δειγματοληπτική μεταβλητότητα - ένα θεμελιώδες χαρακτηριστικό της στατιστικής συμπερασματολογίας. Χρησιμοποιούμε δείγματα για να εκτιμήσουμε τον πληθυσμό, αλλά οι εκτιμήσεις μας έχουν φυσική μεταβλητότητα.

Ποιος είναι ο τύπος υπολογισμού του F;

$F = \frac{MS_{Error}}{MS_{Total}}$$F = \frac{MS_{Total}}{MS_{Error}}$$F = \frac{MS_{Model}}{MS_{Error}}$$F = \frac{MS_{Model}}{MS_{Total}}$

Επεξήγηση

Σωστή απάντηση: Γ

\[F = \frac{MS_{Model}}{MS_{Error}}\]

Τι σημαίνει αυτός ο τύπος;

Το πηλίκο F συγκρίνει:

Αριθμητής (MS$_{Model}$): Η μεταβλητότητα που εξηγείται από το μοντέλο (ανά df)
Παρονομαστής (MS$_{Error}$): Η μεταβλητότητα που δεν εξηγείται (ανά df)

Γιατί αυτός ο τύπος έχει νόημα;

Το F μετράει:

«Πόσες φορές μεγαλύτερη είναι η εξηγούμενη μεταβλητότητα (ανά df) σε σχέση με την ανεξήγητη μεταβλητότητα (ανά df);»

Ερμηνεία:

F >> 1: Το μοντέλο εξηγεί πολύ περισσότερη μεταβλητότητα από την τυχαία μεταβλητότητα → καλό μοντέλο
F ≈ 1: Το μοντέλο εξηγεί περίπου όσο και η τυχαία μεταβλητότητα → μη σημαντικό μοντέλο
F < 1: Το μοντέλο εξηγεί λιγότερο από την τυχαία μεταβλητότητα → κακό μοντέλο

Στο παράδειγμά μας: F = 11.656 >> 1, άρα πολύ καλό μοντέλο!

Γιατί οι άλλες είναι λάθος:

Α. $F = \frac{MS_{Error}}{MS_{Total}}$ - ΛΑΘΟΣ

Ας το υπολογίσουμε:

\[F = \frac{71.286}{76.155} = 0.936\]

Προβλήματα:

Αυτό θα έδινε F < 1, που δεν έχει νόημα για καλό μοντέλο
Συγκρίνει το σφάλμα από το σύνθετο μοντέλο με το σφάλμα από το κενό μοντέλο - όχι τη σωστή σύγκριση
Δεν μετράει την εξηγούμενη μεταβλητότητα

Β. $F = \frac{MS_{Total}}{MS_{Error}}$ - ΛΑΘΟΣ

Ας το υπολογίσουμε:

\[F = \frac{76.155}{71.286} = 1.068\]

Προβλήματα:

Αυτό θα έδινε F ≈ 1 πάντα, ανεξάρτητα από το πόσο καλό είναι το μοντέλο
Συγκρίνει τη συνολική με την ανεξήγητη μεταβλητότητα - λείπει η εξηγούμενη μεταβλητότητα

Δ. $F = \frac{MS_{Model}}{MS_{Total}}$ - ΛΑΘΟΣ

Ας το υπολογίσουμε:

\[F = \frac{830.880}{76.155} = 10.911\]

Προβλήματα:

Αυτό συγκρίνει την εξηγούμενη μεταβλητότητα με τη συνολική
Δεν λαμβάνει υπόψη την ανεξήγητη μεταβλητότητα από το σύνθετο μοντέλο
Αυτό μοιάζει περισσότερο με το PRE (αλλά όχι ακριβώς):

\[PRE = \frac{SS_{Model}}{SS_{Total}} = \frac{830.880}{11880.211} = 0.0699\]

Σύγκριση όλων των τύπων:

Τύπος	Υπολογισμός	Αποτέλεσμα	Σωστό;
Α: $\frac{MS_{Error}}{MS_{Total}}$	$\frac{71.286}{76.155}$	0.936	✗
Β: $\frac{MS_{Total}}{MS_{Error}}$	$\frac{76.155}{71.286}$	1.068	✗
Γ: $\frac{MS_{Model}}{MS_{Error}}$	$\frac{830.880}{71.286}$	11.656	✓
Δ: $\frac{MS_{Model}}{MS_{Total}}$	$\frac{830.880}{76.155}$	10.911	✗

Μόνο η Γ δίνει το σωστό F = 11.656 από τον πίνακα ANOVA!

Η λογική πίσω από τον τύπο:

1. Τι θέλουμε να μετρήσουμε;

Θέλουμε να ελέγξουμε αν το μοντέλο εξηγεί σημαντικά περισσότερη διακύμανση από την τυχαία διακύμανση.

2. Πώς το κάνουμε;

Συγκρίνουμε:

Αριθμητής: Πόση διακύμανση εξηγεί το μοντέλο (MS$_{Model}$)
Παρονομαστής: Πόση διακύμανση δεν εξηγείται (MS$_{Error}$)

3. Τι δείχνει το αποτέλεσμα;

F = 11.66 σημαίνει: «Για κάθε μονάδα ανεξήγητης διακύμανσης, έχουμε 11.66 μονάδες εξηγούμενης διακύμανσης»
Αυτό είναι πολύ μεγαλύτερο από αυτό που θα αναμέναμε λόγω τυχαιότητας (που θα ήταν F ≈ 1)

Συμπέρασμα:

Ο σωστός τύπος είναι:

\[F = \frac{MS_{Model}}{MS_{Error}}\]

Αυτός ο τύπος συγκρίνει την εξηγούμενη μεταβλητότητα (ανά df που δαπανήθηκε) με την ανεξήγητη μεταβλητότητα (ανά df που απομένει), δίνοντάς μας ένα μέτρο του πόσο καλά το μοντέλο λειτουργεί σε σχέση με την τυχαία μεταβλητότητα.

Ένας Εναλλακτικός Τρόπος Έκφρασης του Πηλίκου `F`

Υπάρχει ένας διαφορετικός τρόπος να σκεφτούμε το πηλίκο F, ο οποίος καθιστά πιο σαφή τη σχέση του με το PRE. Η σχέση αυτή αποτυπώνεται στην ακόλουθη εναλλακτική εξίσωση:

\[F = \frac{\text{PRE} / \text{df}_{\text{Model}}}{(1 - \text{PRE}) / \text{df}_{\text{Error}}}\]

Η εξίσωση αυτή δίνει ακριβώς το ίδιο αριθμητικό αποτέλεσμα με τον προηγούμενο ορισμό του F, αλλά προσφέρει μια πιο διαισθητική κατανόηση του πώς συνδέεται το PRE με το F.

Ο αριθμητής δείχνει πόσο PRE επιτυγχάνεται από το μοντέλο ανά βαθμό ελευθερίας που χρησιμοποιήθηκε —δηλαδή, ανά εκτιμημένη παράμετρο πέρα από το κενό μοντέλο. Στην περίπτωση του μοντέλου της Height2Group, αυτό αντιστοιχεί απλώς στο PRE διαιρεμένο με 1, αφού το μοντέλο χρησιμοποίησε μόνο έναν επιπλέον βαθμό ελευθερίας σε σχέση με το κενό μοντέλο.

Ο παρονομαστής, αντίθετα, εκφράζει πόσο σφάλμα απομένει να εξηγηθεί (το ανεξήγητο σφάλμα, δηλαδή 1 − PRE) ανά διαθέσιμο βαθμό ελευθερίας στο σφάλμα (df Error). Με άλλα λόγια, δείχνει ποιο θα ήταν, κατά μέσο όρο, το PRE που θα μπορούσε να επιτευχθεί αν επιλέγαμε τυχαία μια παράμετρο προς εκτίμηση, αντί για εκείνη που συμπεριλάβαμε στο μοντέλο.

Έτσι, το πηλίκο F συγκρίνει την ποσότητα του PRE που πέτυχε το μοντέλο μας (ανά βαθμό ελευθερίας που χρησιμοποιήθηκε) με τη μέση ποσότητα σφάλματος που θα μπορούσε να μειωθεί αν χρησιμοποιούσαμε όλους τους υπόλοιπους διαθέσιμους βαθμούς ελευθερίας.

Με απλά λόγια, το πηλίκο F απαντά στο εξής ερώτημα:

Πόσες φορές μεγαλύτερη είναι η μείωση του σφάλματος που επιτεύχθηκε από το προσαρμοσμένο μοντέλο (ανά βαθμό ελευθερίας που χρησιμοποιήθηκε), σε σύγκριση με τη μείωση του σφάλματος που θα αναμέναμε τυχαία (επίσης ανά βαθμό ελευθερίας) αν χρησιμοποιούσαμε όλους τους υπόλοιπους διαθέσιμους βαθμούς ελευθερίας;

Δίνονται οι τύποι:

\[F = \frac{MS_{Model}}{MS_{Error}}\]

\[F = \frac{PRE/df_{model}}{(1-PRE)/df_{error}}\]

Ποια από τις παρακάτω δηλώσεις είναι ΨΕΥΔΗΣ;

Χρειαζόμαστε και τους δύο αυτούς τύπους επειδή μας δίνουν διαφορετικές τιμές για το στατιστικό F.Χρειαζόμαστε και τους δύο αυτούς τύπους επειδή εκφράζουν διαφορετικούς τρόπους σκέψης για το στατιστικό F.Χρειαζόμαστε και τους δύο αυτούς τύπους επειδή ο ένας δείχνει τη σχέση του F με τη διακύμανση, ενώ ο άλλος τη σχέση του F με το PRE.Και οι δύο τύποι δείχνουν πώς το στατιστικό F λαμβάνει υπόψη τους βαθμούς ελευθερίας.

Επεξήγηση

Σωστή απάντηση: Α - ΨΕΥΔΗΣ δήλωση

Γιατί η Α είναι ψευδής;

Οι δύο τύποι δίνουν την ΙΔΙΑ τιμή F - δεν δίνουν διαφορετικές τιμές!

Είναι μαθηματικά ισοδύναμοι - απλά εκφράζουν το F με διαφορετικό τρόπο.

Απόδειξη ότι δίνουν την ίδια τιμή:

Από το παράδειγμά μας (μοντέλο της Height2Group):

Τύπος 1: Χρησιμοποιώντας τα MS

\[F = \frac{MS_{Model}}{MS_{Error}} = \frac{830.880}{71.286} = 11.656\]

Τύπος 2: Χρησιμοποιώντας το PRE

Γνωρίζουμε: - PRE = 0.0699

df$_{model}$ = 1
df$_{error}$ = 155

\[F = \frac{PRE/df_{model}}{(1-PRE)/df_{error}} = \frac{0.0699/1}{(1-0.0699)/155}\]

\[F = \frac{0.0699}{0.9301/155} = \frac{0.0699}{0.006001} = 11.648\]

(Η μικρή διαφορά 11.648 vs 11.656 οφείλεται σε στρογγυλοποίηση του PRE)

Και οι δύο τύποι δίνουν F ≈ 11.66!

Γιατί οι άλλες είναι αληθείς;

Β. “Διαφορετικοί τρόποι σκέψης” - ΑΛΗΘΗΣ ✓

Ναι! Οι δύο τύποι εκφράζουν διαφορετικές οπτικές:

Τύπος 1: $F = \frac{MS_{Model}}{MS_{Error}}$

Σκέψη: «Πόσες φορές μεγαλύτερη είναι η εξηγούμενη διακύμανση από την ανεξήγητη διακύμανση;»
Οπτική της Διακύμανσης (variance)

Τύπος 2: $F = \frac{PRE/df_{model}}{(1-PRE)/df_{error}}$

Σκέψη: «Πόσο αποδοτική είναι η μείωση σφάλματος (PRE) ανά df που δαπανήθηκε;»
Οπτική της Αναλογικής μείωσης σφάλματος (proportional error reduction)

Γ. “Μία σχέση με διακύμανση, μία με PRE” - ΑΛΗΘΗΣ ✓

Ναι! Ακριβώς αυτό:

Δ. “Λαμβάνουν υπόψη τους df” - ΑΛΗΘΗΣ ✓

Ναι! Και οι δύο τύποι ενσωματώνουν τους βαθμούς ελευθερίας:

Και οι δύο τύποι λαμβάνουν υπόψη το κόστος της πολυπλοκότητας (df που δαπανήθηκαν)!

Συμπέρασμα:

Η δήλωση Α είναι ΨΕΥΔΗΣ επειδή:

Χρειαζόμαστε και τους δύο επειδή δίνουν διαφορετικές τιμές» - ΛΑΘΟΣ!

✓ Η αλήθεια: Οι δύο τύποι είναι μαθηματικά ισοδύναμοι και δίνουν την ίδια τιμή για το F. Τους χρειαζόμαστε επειδή:

Εκφράζουν διαφορετικές οπτικές γωνίες (διακύμανση vs αναλογική μείωση)
Δείχνουν διαφορετικές σχέσεις (με MS vs με PRE)
Και οι δύο λαμβάνουν υπόψη τους βαθμούς ελευθερίας

Εξετάστε την εξίσωση:

\[F = \frac{PRE / df_{model}}{(1 - PRE) / df_{error}}\]

Αν το πηλίκο F είναι ίσο με 1, τι σημαίνει αυτό;

Το PRE που εξηγείται από την επιπλέον παράμετρό μας είναι πολύ ιδιαίτερο, επειδή το 100% του PRE έχει εξηγηθεί από αυτήν την παράμετρο.Το PRE που εξηγείται από την επιπλέον παράμετρό μας είναι κάπως ιδιαίτερο, επειδή ο αριθμητής είναι ίσος με τον παρονομαστή, τυχαία.Το PRE που εξηγείται από την επιπλέον παράμετρό μας δεν είναι ιδιαίτερο, επειδή είναι περίπου ίσο με τη μέση ποσότητα PRE που θα μπορούσε να είχε εξηγηθεί από οποιαδήποτε άλλη παράμετρο.

Επεξήγηση

Σωστή απάντηση: Γ – Το PRE δεν είναι ιδιαίτερο

Όταν το F είναι ίσο με 1, αυτό σημαίνει ότι:

\[\frac{PRE/df_{model}}{(1-PRE)/df_{error}} = 1\]

Άρα:

\[PRE/df_{model} = (1 - PRE)/df_{error}\]

Ερμηνεία:

Η μείωση του σφάλματος ανά βαθμό ελευθερίας που χρησιμοποιήθηκε είναι ίση με τη μέση ποσότητα σφάλματος που απομένει να μειωθεί για κάθε διαθέσιμο βαθμό ελευθερίας.

Με άλλα λόγια, η επιπλέον παράμετρος που προσθέσαμε εξηγεί μια τυπική (μέση) ποσότητα μεταβλητότητας — δηλαδή, περίπου όση θα εξηγούσε μια τυχαία παράμετρος.

Πρακτικά:

Η παράμετρος δεν είναι χρήσιμη· δεν προσθέτει πραγματική εξηγηματική ισχύ.
Το μοντέλο μας δεν είναι καλύτερο από το κενό μοντέλο.

Παράδειγμα:

Αν df$_{model}$ = 1 και df$_{error}$ = 155, τότε:

\[1 = \frac{PRE / 1}{(1 - PRE) / 155}\]

\[PRE = \frac{1}{156} = 0.0064 \approx 0.64\%\]

Άρα η παράμετρος εξηγεί μόνο περίπου 0.64% της μεταβλητότητας — δηλαδή, όσο θα εξηγούσε τυχαία μια οποιαδήποτε παράμετρος.

Συνοψίζοντας:

Όταν F = 1:

Το PRE είναι μέσο/τυπικό.
Η παράμετρος δεν έχει πραγματική επίδραση.
Δεν αξίζει τους βαθμούς ελευθερίας που χρησιμοποιήθηκαν.

9.5 Μέτρα Μεγέθους Επίδρασης

Επανεξέταση της Μελέτης του Φιλοδωρήματος

Στο Κεφάλαιο 5 εξετάσαμε μια πειραματική μελέτη που διερεύνησε αν η σχεδίαση ενός χαμογελαστού προσώπου στην πίσω πλευρά του λογαριασμού θα οδηγούσε τους πελάτες εστιατορίων να αφήνουν υψηλότερα φιλοδωρήματα (Rind & Bordia, 1996).

Η μελέτη ήταν ένα τυχαιοποιημένο πείραμα που διεξήχθη σε πραγματικές συνθήκες. Μια σερβιτόρα σε συγκεκριμένο εστιατόριο κλήθηκε, σύμφωνα με μια προκαθορισμένη τυχαία διαδικασία, είτε να σχεδιάζει ένα χαμογελαστό προσωπάκι στο χαρτάκι του λογαριασμού είτε όχι για κάθε τραπέζι που εξυπηρετούσε.

Η εξαρτημένη μεταβλητή ήταν το ποσοστό φιλοδωρήματος από κάθε τραπέζι (Tip). Συνολικά, 44 τραπέζια κατανεμήθηκαν τυχαία σε δύο ομάδες (22 τραπέζια ανά συνθήκη, μεταβλητή Condition): μία που έλαβε λογαριασμό με χαμογελαστό προσωπάκι και μία που έλαβε λογαριασμό χωρίς αυτό.

Οι κατανομές του ποσοστού φιλοδωρήματος στις δύο πειραματικές συνθήκες παρουσιάζονται στο παρακάτω διάγραμμα. Στο ίδιο διάγραμμα προβάλλονται και οι εκτιμήσεις παραμέτρων του μοντέλου μέσω της gf_model().

Condition_model <- lm(Tip ~ Condition, data = TipExperiment)
gf_jitter(Tip ~ Condition, data = TipExperiment, width = .1) %>%
 gf_model(Condition_model)

Μια βασική ερώτηση που μπορούμε να θέσουμε για ένα στατιστικό μοντέλο είναι: Πόσο μεγάλη είναι η επίδραση; Όταν εξετάζουμε πώς μια μεταβλητή επηρεάζει μια άλλη — για παράδειγμα, πώς η συνθήκη (Condition) επηρεάζει το ποσοστό φιλοδωρήματος (Tip) — είναι φυσικό να θέλουμε να γνωρίζουμε το μέγεθος αυτής της επίδρασης.

Αυτό μας οδηγεί στη συζήτηση για το μέγεθος της επίδρασης (effect size) και τους τρόπους με τους οποίους μπορούμε να το μετρήσουμε. Αν και μέχρι τώρα δεν έχουμε χρησιμοποιήσει ρητά τον όρο «μέγεθος επίδρασης», στην πραγματικότητα έχουμε ήδη γνωρίσει δύο τέτοια μέτρα. Σε αυτή την ενότητα θα τα επανεξετάσουμε — και θα προσθέσουμε ένα τρίτο.

Διαφορά Μέσων Όρων (ή $b_1$)

Το πιο απλό μέτρο του μεγέθους της επίδρασης στο πλαίσιο ενός μοντέλου δύο ομάδων είναι η διαφορά των μέσων όρων της εξαρτημένης μεταβλητής μεταξύ των δύο ομάδων.

Παρακάτω παρουσιάζονται οι εκτιμήσεις των παραμέτρων από το μοντέλο, στο οποίο η ανεξάρτητη μεταβλητή είναι η συνθήκη (Condition) και η εξαρτημένη μεταβλητή το ποσοστό φιλοδωρήματος (Tip).

Call:
lm(formula = Tip ~ Condition, data = TipExperiment)

Coefficients:
         (Intercept)  ConditionSmiley Face
              27.000                 6.045

Ποια τιμή δείχνει τη διαφορά στο μέσο ποσοστό φιλοδωρήματος μεταξύ των δύο ομάδων;

Στο σύνολο δεδομένων TipExperiment, αυτό σημαίνει ότι το μέγεθος της επίδρασης της συνθήκης (Condition) είναι περίπου 6 ποσοστιαίες μονάδες: τα τραπέζια που έλαβαν λογαριασμό με χαμογελαστό προσωπάκι άφησαν, κατά μέσο όρο, περίπου 6% περισσότερο φιλοδώρημα σε σύγκριση με εκείνα που δεν έλαβαν χαμογελαστό προσωπάκι.

R: Η Συνάρτηση `b1()`

Οι προηγούμενες εκτιμήσεις παραμέτρων προήλθαν από την εκτέλεση της lm(Tip ~ Condition, data = TipExperiment). Υπάρχει όμως ένας πιο άμεσος τρόπος για να βρούμε το $b_1$ — δηλαδή τη διαφορά των μέσων όρων μεταξύ των δύο ομάδων — χρησιμοποιώντας τη συνάρτηση b1() από το πακέτο supernova.

Στο παρακάτω πλαίσιο, αντικαταστήστε την lm() με την b1() για να δείτε πώς λειτουργεί.

Η b1() επιστρέφει 6.045, που αντιστοιχεί στη διαφορά στο μέσο ποσοστό φιλοδωρήματος μεταξύ της ομάδας με το χαμογελαστό προσωπάκι (smiley face) και της ομάδας ελέγχου (control). Αυτή η τιμή είναι η εκτίμηση της παραμέτρου $b_1$.

Τώρα δοκιμάστε να αλλάξετε τη b1() σε b0() και εκτελέστε ξανά τον κώδικα. Η συνάρτηση b0() επιστρέφει την εκτίμηση του $b_0$, δηλαδή το μέσο ποσοστό φιλοδωρήματος της ομάδας ελέγχου.

PRE

Το PRE (Proportional Reduction in Error) αποτελεί ένα δεύτερο μέτρο μεγέθους επίδρασης. Όπως είδαμε προηγουμένως, εκφράζει την αναλογική μείωση του σφάλματος που επιτυγχάνεται όταν προσθέτουμε μια ανεξάρτητη μεταβλητή σε ένα κενό μοντέλο. Το PRE είναι ιδιαίτερα χρήσιμο ως μέτρο μεγέθους επίδρασης επειδή είναι σχετικό: δείχνει πόσο βελτιώνεται το μοντέλο με την προσθήκη της ανεξάρτητης μεταβλητής.

Όπως συμβαίνει με όλα τα στατιστικά μέτρα, το PRE ποικίλλει από δείγμα σε δείγμα και από μελέτη σε μελέτη. Το τι θεωρείται «μεγάλη» ή «σημαντική» επίδραση εξαρτάται από το πεδίο της έρευνας, και η αίσθηση αυτή αναπτύσσεται με την εμπειρία στην ανάλυση δεδομένων και τη δημιουργία μοντέλων.

Στις κοινωνικές επιστήμες υπάρχουν κάποιες γενικά αποδεκτές κατευθυντήριες γραμμές:

PRE = .25: Μεγάλη επίδραση
PRE = .09: Μέτρια επίδραση
PRE = .01: Μικρή επίδραση

Με βάση αυτές τις συμβάσεις, τα αποτελέσματα για το Condition_model (PRE = 0.07) δείχνουν μια μικρή έως μέτρια επίδραση του χαμογελαστού προσώπου στα φιλοδωρήματα. Αντίθετα, στο Height3Group_model, η ομάδα του ύψους είχε μέτρια ως μεγάλη επίδραση στο μήκος αντίχειρα (PRE = 0.14).

Προσοχή όμως: αυτές οι συμβάσεις δεν είναι απόλυτοι κανόνες. Το αν ένα μέγεθος επίδρασης είναι σημαντικό εξαρτάται από το πλαίσιο και το σκοπό της μελέτης. Για παράδειγμα, αν ένας διαδικτυακός λιανοπωλητής διαπιστώσει μια μικρή επίδραση στις πωλήσεις από την αλλαγή του χρώματος του κουμπιού «Αγορά» στον ιστότοπό του (π.χ. PRE = 0.01), μπορεί να επιλέξει να την εφαρμόσει. Αν και η επίδραση είναι μικρή, η αλλαγή είναι δωρεάν και εύκολη στην εφαρμογή, και μπορεί να οδηγήσει σε ουσιαστική αύξηση των πωλήσεων.

R: Η Συνάρτηση `pre()`

Όπως η συνάρτηση b1(), έτσι και η pre() επιστρέφει απευθείας μια συγκεκριμένη τιμή από το μοντέλο — σε αυτή την περίπτωση, το PRE.

Στο παρακάτω πλαίσιο κώδικα, εκτελέστε τη συνάρτηση supernova() στο Condition_model. Στον πίνακα ANOVA που θα εμφανιστεί, εντοπίστε την τιμή του PRE για να δείτε πόσο μειώνεται το σφάλμα με την προσθήκη της ανεξάρτητης μεταβλητής.

Στη συνέχεια, αντικαταστήστε τη supernova() με την pre() για να λάβετε απευθείας την ίδια τιμή. Αργότερα, όταν μελετήσουμε τις δειγματοληπτικές κατανομές, θα γίνει σαφές πόσο χρήσιμες είναι αυτές οι εξειδικευμένες συναρτήσεις, όπως οι b1() και pre().

Ο δείκτης d του Cohen

Ένα τρίτο μέτρο μεγέθους επίδρασης, ειδικά κατάλληλο για μοντέλα δύο ομάδων (όπως το Condition_model), είναι ο δείκτης $d$ του Cohen. Το $d$ εκφράζει το μέγεθος μιας διαφοράς μεταξύ ομάδων σε μονάδες τυπικής απόκλισης.

Για παράδειγμα, αντί να λέμε ότι η ομάδα με το χαμογελαστό προσωπάκι αφήνει 6% περισσότερο φιλοδώρημα από την ομάδα ελέγχου, μπορούμε να πούμε ότι τα ποσοστά φιλοδωρημάτων της ομάδας με το χαμογελαστό προσωπάκι είναι κατά μέσο όρο 0.55 τυπικές αποκλίσεις μεγαλύτερα από αυτά της ομάδας ελέγχου.

Ο δείκτης $d$ συνδέεται με την έννοια της τιμής $z$. Θυμηθείτε ότι οι τιμές $z$ δείχνουν πόσο μακριά βρίσκεται μια παρατήρηση από το μέσο όρο μιας κατανομής, μετρημένη σε τυπικές αποκλίσεις. Και οι δύο δείκτες — οι τιμές $z$ και ο δείκτης $d$ του Cohen — μας επιτρέπουν να αξιολογήσουμε το μέγεθος μιας διαφοράς ανεξάρτητα από τις αρχικές μονάδες μέτρησης.

\[d = \frac{\bar{Y_1}-{\bar{Y_2}}}{s}\]

Υπολογισμός του d του Cohen: Ποια Τυπική Απόκλιση να Χρησιμοποιήσουμε;

Όταν υπολογίζουμε το $d$ του Cohen, προκύπτει το ερώτημα: ποια τυπική απόκλιση πρέπει να χρησιμοποιήσουμε; Την τυπική απόκλιση της εξαρτημένης μεταβλητής για ολόκληρο το δείγμα, ή την τυπική απόκλιση εντός των δύο ομάδων; Αν οι μέσοι όροι των ομάδων απέχουν σημαντικά, η συνολική τυπική απόκλιση μπορεί να είναι σημαντικά μεγαλύτερη από την τυπική απόκλιση εντός κάθε ομάδας.

Συνήθως χρησιμοποιούμε την τυπική απόκλιση εντός των ομάδων, επειδή αυτή αντικατοπτρίζει καλύτερα τη μεταβλητότητα που δεν εξηγείται από το μοντέλο. Επειδή οι τυπικές αποκλίσεις συνήθως διαφέρουν μεταξύ των ομάδων, χρειαζόμαστε έναν τρόπο να τις συνδυάσουμε σε μία τιμή.

Μια πρώτη προσέγγιση είναι να πάρουμε τον απλό μέσο όρο των δύο τυπικών αποκλίσεων. Αυτό λειτουργεί καλά αν οι ομάδες έχουν το ίδιο μέγεθος, αλλά αν μια ομάδα έχει 100 παρατηρήσεις και η άλλη μόνο 10, ο απλός μέσος όρος θα έδινε την ίδια βαρύτητα και στις δύο, κάτι που δεν είναι σωστό. Η τιμή που βασίζεται στο μεγαλύτερο δείγμα θα πρέπει να έχει μεγαλύτερη βαρύτητα.

Η λύση είναι η «σταθμισμένη ή συγκεντρωτική τυπική απόκλιση» (pooled standard deviation), όπου τα βάρη καθορίζονται από τους βαθμούς ελευθερίας κάθε ομάδας. Η σταθμισμένη τυπική απόκλιση ($s_{\text{pooled}}$) υπολογίζεται ως εξής:

\[s_{\text{pooled}} = \sqrt{\frac{\text{df}_1 s_1^2 + \text{df}_2 s_2^2}{\text{df}_1 + \text{df}_2}}\]

Ένας πιο άμεσος τρόπος να βρούμε τη σταθμισμένη τυπική απόκλιση είναι να πάρουμε την τετραγωνική ρίζα του MS Error (Mean Square Error) από τον πίνακα ANOVA. Το MS Error είναι το SS Error διαιρεμένο με τους βαθμούς ελευθερίας του σφάλματος και δίνει μια εκτίμηση της διακύμανσης που βασίζεται αποκλειστικά στη μεταβλητότητα εντός των ομάδων. Στην περίπτωσή μας, η σταθμισμένη τυπική απόκλιση είναι η τετραγωνική ρίζα του 121.64, δηλαδή περίπου 11.

Analysis of Variance Table (Type III SS)
 Model: Tip ~ Condition

                               SS df      MS     F    PRE     p
 ----- --------------- | -------- -- ------- ----- ------ -----
 Model (error reduced) |  402.023  1 402.023 3.305 0.0729 .0762
 Error (from model)    | 5108.955 42 121.642
 ----- --------------- | -------- -- ------- ----- ------ -----
 Total (empty model)   | 5510.977 43 128.162

Μπορούμε να βελτιώσουμε τον υπολογισμό του $d$ του Cohen αντικαθιστώντας την απλή τυπική απόκλιση $s$ με τη σταθμισμένη τυπική απόκλιση $s_{\text{pooled}}$. Η εξίσωση γίνεται τότε:

\[d = \frac{b_1}{s_{\text{pooled}}}\] Αυτό σημαίνει ότι η διαφορά των μέσων όρων μεταξύ των ομάδων εκφράζεται σε μονάδες τυπικής απόκλισης που λαμβάνει υπόψη τη μεταβλητότητα εντός όλων των ομάδων.

R: Η Συνάρτηση `cohensD()`

Όπως και με τα άλλα στατιστικά μέτρα που είδαμε, υπάρχει συνάρτηση στην R για τον υπολογισμό του $d$ του Cohen.

cohensD(Tip ~ Condition, data = TipExperiment)

Δοκιμάστε να εκτελέσετε τον παρακάτω κώδικα.

0.5481351

Σε ποια μονάδα μέτρησης είναι αυτός ο αριθμός;

Επεξήγηση

Σωστή απάντηση: Γ - τυπικές αποκλίσεις (standard deviations)

Τι είναι το Cohen’s $d$;

Το $d$ του Cohen είναι ένα μέτρο μεγέθους επίδρασης (effect size) που εκφράζει τη διαφορά μεταξύ δύο ομάδων σε τυπικές αποκλίσεις.

Τύπος:

\[d = \frac{\bar{x}_1 - \bar{x}_2}{s_{pooled}}\]

όπου:

$\bar{x}_1 - \bar{x}_2$ = η διαφορά των μέσων όρων
$s_{pooled}$ = η σταθμισμένη τυπική απόκλιση (pooled standard deviation)

Ερμηνεία του αποτελέσματος:

\[d = 0.548\]

Αυτό σημαίνει:

«Η διαφορά μεταξύ των δύο συνθηκών (Condition) είναι 0.548 τυπικές αποκλίσεις.»

Με άλλα λόγια, οι δύο ομάδες διαφέρουν κατά περίπου μισή τυπική απόκλιση.

Γιατί είναι σε τυπικές αποκλίσεις;

Το $d$ του Cohen τυποποιεί τη διαφορά διαιρώντας με την τυπική απόκλιση:

Παρονομαστής = τυπική απόκλιση
- Διαιρούμε τη διαφορά με την τυπική απόκλιση
- Αυτό μετατρέπει τη διαφορά σε μονάδες τυπικών αποκλίσεων
Αποτέλεσμα = αδιάστατος αριθμός
- Το $d$ δεν έχει μονάδες (δολάρια, χιλιοστά, κλπ.)
- Εκφράζεται σε τυπικές αποκλίσεις
Πλεονέκτημα της τυποποίησης:
- Μπορούμε να συγκρίνουμε μεγέθη επίδρασης μεταξύ διαφορετικών μελετών
- Ακόμα και αν χρησιμοποιούν διαφορετικές μονάδες μέτρησης

Παράδειγμα:

Ας υποθέσουμε ότι στο TipExperiment:

Ομάδα 1 (π.χ., Smiley Face): μέσος όρος φιλοδωρήματος = $5.00, τυπική απόκλιση = $2.00
Ομάδα 2 (π.χ., Control): μέσος όρος φιλοδωρήματος = $3.90, τυπική απόκλιση = $2.00

Υπολογισμός:

\[d = \frac{5.00 - 3.90}{2.00} = \frac{1.10}{2.00} = 0.55\]

Ερμηνεία:

Η διαφορά είναι $1.10 (σε δολάρια)
Αλλά το $d$ = 0.55 (σε τυπικές αποκλίσεις)
Αυτό σημαίνει: η διαφορά είναι 0.55 τυπικές αποκλίσεις

Γιατί οι άλλες είναι λάθος:

Α. “ποσοστό” - ΛΑΘΟΣ

Το $d$ του Cohen δεν είναι ποσοστό
Τα ποσοστά κυμαίνονται από 0% έως 100%
Το $d$ μπορεί να είναι οποιοσδήποτε αριθμός (θετικός ή αρνητικός)

Μέτρα σε ποσοστό:

PRE (Proportional Reduction in Error)

Β. “ποσοστό στο τετράγωνο” - ΛΑΘΟΣ

Το $d$ του Cohen δεν είναι στο τετράγωνο
Είναι σε γραμμικές μονάδες (τυπικές αποκλίσεις), όχι τετραγωνικές

Μέτρα σε τετραγωνικές μονάδες:

Διακύμανση = SD²
Άθροισμα Τετραγώνων (SS)
Μέσο Άθροισμα Τετραγώνων (MS)

Δ. “τιμές z” - ΛΑΘΟΣ (αλλά συνδέεται στενά)

Το $d$ του Cohen δεν είναι το ίδιο με την τιμή $z$
Αλλά και τα δύο εκφράζονται σε τυπικές αποκλίσεις!

Διαφορές:

τιμή $z$: Πόσες τυπικές αποκλίσεις απέχει μια μεμονωμένη παρατήρηση από το μέσο όρο
- \[z = \frac{x - \mu}{\sigma}\]
$d$ του Cohen: Πόσες τυπικές αποκλίσεις διαφέρουν δύο ομάδες μεταξύ τους
- \[d = \frac{\bar{x}_1 - \bar{x}_2}{s_{pooled}}\]

Ε. “πίνακες” - ΛΑΘΟΣ

Αυτό δεν έχει νόημα
Το $d$ του Cohen είναι ένας αριθμός, όχι μονάδα μέτρησης

Σύγκριση με άλλα μέτρα:

Μέτρο	Μονάδα	Εύρος	Παράδειγμα
Διαφορά μέσων	Αρχικές μονάδες (π.χ., δολάρια)	-∞ έως +∞	1.10
d του Cohen	Τυπικές αποκλίσεις	-∞ έως +∞	0.548 SD
PRE	Αναλογία (0-1)	0 έως 1	0.07 (7%)
πηλίκο `F`	Αδιάστατος λόγος	0 έως +∞	11.66

Γιατί χρησιμοποιούμε τυπικές αποκλίσεις;

Τυποποίηση:
- Διαφορετικές μελέτες μπορούν να έχουν διαφορετικές κλίμακες
- Π.χ., φιλοδωρήματα σε δολάρια vs ικανοποίηση σε κλίμακα 1-10
- Το $d$ τις κάνει συγκρίσιμες!
Διαισθητική ερμηνεία:
- “Μισή τυπική απόκλιση” είναι εύκολο να κατανοηθεί
- Συνδέεται με την κανονική κατανομή
Σύνδεση με άλλα μέτρα:
- Μπορούμε να μετατρέψουμε μεταξύ τους τα $d$, $r$, $F$, κλπ.

Συμπέρασμα:

Το $d$ = 0.548 εκφράζεται σε μονάδες τυπικών αποκλίσεων. Αυτό σημαίνει ότι η διαφορά μεταξύ των δύο συνθηκών στο πείραμα του φιλοδωρήματος είναι 0.548 τυπικές αποκλίσεις - ένα μέτριο μέγεθος επίδρασης που υποδηλώνει μια ουσιαστική αλλά όχι τεράστια διαφορά μεταξύ των ομάδων.

Γνωρίζουμε ότι η διαφορά στο φιλοδώρημα κατά μέσο όρο μεταξύ των ομάδων smiley face και control είναι 6 ποσοστιαίες μονάδες, και η σταθμισμένη τυπική απόκλιση είναι περίπου 11. Χρησιμοποιώντας την τυπική απόκλιση (11) ως μονάδα μέτρησης, η διαφορά των μέσων όρων (6) αντιστοιχεί σε λίγο πάνω από μισή τυπική απόκλιση — ακριβώς 0.55 τυπικές αποκλίσεις.

Για τη μελέτη με τα φιλοδωρήματα, το να γνωρίζουμε ότι υπάρχει διαφορά περίπου 6 ποσοστιαίων μονάδων είναι αρκετά προφανές και κατανοητό. Όμως, για άλλες μεταβλητές — όπως το σκορ στα βιντεοπαιχνίδια Kargle και Spargle — οι άνθρωποι μπορεί διαισθητικά να μην αντιλαμβάνονται τι σημαίνει μια διαφορά π.χ. 6 πόντων. Σε τέτοιες περιπτώσεις, η έκφραση της διαφοράς σε τυπικές αποκλίσεις (με το $d$ του Cohen) είναι ιδιαίτερα χρήσιμη.

Αντιστοιχίστε κάθε μέτρο μεγέθους επίδρασης με τη μονάδα στην οποία μετριέται.

Σε ποια μονάδα μετριέται η διαφορά μέσων όρων;

Αρχικές μονάδεςΑρχικές μονάδες στο τετράγωνοΠοσοστό ή αναλογίαΤυπικές αποκλίσεις

Επεξήγηση

Σωστή απάντηση: Α - Αρχικές μονάδες

Τι είναι:

\[\text{Μέση διαφορά} = \bar{x}_1 - \bar{x}_2\]

Μονάδα: Οι αρχικές μονάδες μέτρησης της μεταβλητής

Παραδείγματα:

Μεταβλητή	Mean Difference	Μονάδα
Φιλοδώρημα	$1.10	Δολάρια
Μήκος αντίχειρα	4.60 mm	Χιλιοστά
Βαθμολογία τεστ	12.5	Βαθμοί
Ύψος	15 cm	Εκατοστά

Γιατί “αρχικές μονάδες”;

Η διαφορά μέσων όρων διατηρεί τις μονάδες των δεδομένων
Αν μετράμε σε δολάρια, η διαφορά είναι σε δολάρια
Αν μετράμε σε χιλιοστά, η διαφορά είναι σε χιλιοστά

Πλεονέκτημα: - Εύκολη ερμηνεία (π.χ., “$1.10 περισσότερο φιλοδώρημα”)

Μειονέκτημα: - Δεν μπορούμε να συγκρίνουμε μεταξύ διαφορετικών κλιμάκων

Σε ποια μονάδα μετριέται το PRE (Αναλογική Μείωση του Σφάλματος);

Αρχικές μονάδεςΑρχικές μονάδες στο τετράγωνοΠοσοστό ή αναλογίαΤυπικές αποκλίσεις

Επεξήγηση

Σωστή απάντηση: Γ - Ποσοστό ή αναλογία

Τι είναι:

\[PRE = \frac{SS_{Total} - SS_{Error}}{SS_{Total}} = \frac{SS_{Model}}{SS_{Total}}\]

Μονάδα: Ποσοστό (0% έως 100%) ή αναλογία (0 έως 1)

Παραδείγματα:

PRE (αναλογία)	PRE (ποσοστό)	Ερμηνεία
0.07	7%	Το μοντέλο εξηγεί 7% της διασποράς
0.14	14%	Το μοντέλο εξηγεί 14% της διασποράς
0.50	50%	Το μοντέλο εξηγεί 50% της διασποράς

Γιατί “ποσοστό ή αναλογία”;

Το PRE μετράει τι ποσοστό του σφάλματος μειώθηκε
Εύρος: 0 έως 1 (ή 0% έως 100%)
Αδιάστατο - δεν έχει μονάδες όπως δολάρια ή χιλιοστά

Ερμηνεία:

PRE = 0.14 σημαίνει:

«Το μοντέλο μείωσε το σφάλμα κατά 14% (ή αναλογία 0.14)»

Σχέση με R²:

PRE = R² (συντελεστής προσδιορισμού)
Και τα δύο εκφράζονται ως ποσοστό/αναλογία

Σε ποια μονάδα μετριέται το $d$ του Cohen;

Αρχικές μονάδεςΑρχικές μονάδες στο τετράγωνοΠοσοστό ή αναλογίαΤυπικές αποκλίσεις

Επεξήγηση

Σωστή απάντηση: Δ - Τυπικές αποκλίσεις

Τι είναι:

\[d = \frac{\bar{x}_1 - \bar{x}_2}{s_{pooled}}\]

Μονάδα: Τυπικές αποκλίσεις (standard deviations)

Παραδείγματα:

Cohen’s d	Ερμηνεία
0.2 SD	Μικρή διαφορά (0.2 τυπικές αποκλίσεις)
0.5 SD	Μέτρια διαφορά (0.5 τυπικές αποκλίσεις)
0.8 SD	Μεγάλη διαφορά (0.8 τυπικές αποκλίσεις)

Γιατί “τυπικές αποκλίσεις”;

Το d διαιρεί τη διαφορά μέσων με τη σταθμισμένη τυπική απόκλιση

\[d = \frac{\text{Διαφορά σε αρχικές μονάδες}}{\text{Σταθμισμένη Τυπική απόκλιση σε αρχικές μονάδες}} = \text{Αριθμός τυπικών αποκλίσεων}\]

Πλεονέκτημα: - Τυποποιημένο - μπορούμε να συγκρίνουμε τιμές d από διαφορετικές μελέτες

Ποια από τα παρακάτω μέτρα μεγέθους επίδρασης μπορεί να χρησιμοποιηθεί με ένα μοντέλο τριών ομάδων (ή ένα μοντέλο με περισσότερες ομάδες);

διαφορά μέσων όρωνPRE$d$ του Cohen

Επεξήγηση

Σωστή απάντηση: Β - PRE

Γιατί το PRE λειτουργεί με 3+ ομάδες;

Το PRE (Proportional Reduction in Error) μπορεί να χρησιμοποιηθεί με οποιονδήποτε αριθμό ομάδων επειδή:

Μετράει τη συνολική μείωση σφάλματος:

\[PRE = \frac{SS_{Total} - SS_{Error}}{SS_{Total}} = \frac{SS_{Model}}{SS_{Total}}\]

Δεν εξαρτάται από το πόσες ομάδες υπάρχουν
Συγκρίνει το συνολικό μοντέλο με το κενό μοντέλο

Υποθετικό παράδειγμα με διαφορετικούς αριθμούς ομάδων:

Μοντέλο	Αριθμός ομάδων	PRE	Ερμηνεία
Height2Group	2 (short, tall)	0.07	Εξηγεί 7% της μεταβλητότητας
Height3Group	3 (short, medium, tall)	0.14	Εξηγεί 14% της μεταβλητότητας
Height5Group	5 ομάδες	0.25	Εξηγεί 25% της μεταβλητότητας
Height10Group	10 ομάδες	0.40	Εξηγεί 40% της μεταβλητότητας

Το PRE μπορεί να χρησιμοποιηθεί ανεξάρτητα από τον αριθμό των ομάδων!

Γιατί οι άλλοι δείκτες ΔΕΝ έχουν νόημα με 3+ ομάδες;

Α. Διαφορά μέσων όρων - ΜΟΝΟ για 2 ομάδες

Πρόβλημα: Η “διαφορά μέσων όρων” υποθέτει δύο μέσους όρους

Με 2 ομάδες:

Ομάδα 1: μέσος = 57.82 mm
Ομάδα 2: μέσος = 62.42 mm
Διαφορά = 62.42 - 57.82 = 4.60 mm ✓

Με 3 ομάδες:

Ομάδα 1 (short):  μέσος = 56.07 mm
Ομάδα 2 (medium): μέσος = 60.22 mm
Ομάδα 3 (tall):   μέσος = 64.09 mm

Ποια διαφορά μέσων όρων υπολογίζουμε;
• 60.22 - 56.07 = 4.15 mm;
• 64.09 - 56.07 = 8.02 mm;
• 64.09 - 60.22 = 3.87 mm;

Συμπέρασμα: Δεν υπάρχει μία διαφορά μέσων όρων με 3+ ομάδες!

Τι μπορούμε να κάνουμε αντί αυτού;

Με 3+ ομάδες, μπορούμε να υπολογίσουμε:

Πολλαπλές συγκρίσεις κατά ζεύγη (pairwise comparisons)
- Short vs Medium: 4.15 mm
- Short vs Tall: 8.02 mm
- Medium vs Tall: 3.87 mm

Αλλά αυτό δεν είναι ένα μέτρο για το συνολικό μοντέλο!

Γ. d του Cohen - ΜΟΝΟ για 2 ομάδες

Πρόβλημα: Το d του Cohen σχεδιάστηκε για δύο ομάδες

Τύπος:

\[d = \frac{\bar{x}_1 - \bar{x}_2}{s_{pooled}}\]

Απαιτεί δύο μέσους όρους: $\bar{x}_1$ και $\bar{x}_2$
Υπολογίζει μία συγκεντρωτική τυπική απόκλιση από δύο ομάδες

Με 2 ομάδες:

# Λειτουργεί!
cohensD(Thumb ~ Height2Group, data = Fingers)
# d = 0.548

Με 3 ομάδες:

# ΔΕΝ λειτουργεί απευθείας!
cohensD(Thumb ~ Height3Group, data = Fingers)
# Σφάλμα ή απροσδιόριστο

Γιατί;

Με 3 ομάδες: - Ποιες δύο ομάδες να συγκρίνουμε;

Ποιες ομάδες να χρησιμοποιήσουμε για το $s_{pooled}$;

Τι μπορούμε να κάνουμε αντί αυτού;

Υπολογίζουμε το d του Cohen χωριστά για κάθε ζεύγος:

# Short vs Tall
cohensD(Thumb ~ Height, data = subset(Fingers, Height != "medium"))

# Short vs Medium
cohensD(Thumb ~ Height, data = subset(Fingers, Height != "tall"))

# Medium vs Tall
cohensD(Thumb ~ Height, data = subset(Fingers, Height != "short"))

Αλλά και πάλι, αυτό δίνει πολλαπλά d, όχι ένα συνολικό μέτρο!

Σύγκριση:

Μέτρο	2 Ομάδες	3 Ομάδες	4+ Ομάδες	Γιατί;
PRE	✓ Ναι	✓ Ναι	✓ Ναι	Μετράει συνολική μείωση σφάλματος
Mean Difference	✓ Ναι	✗ Όχι	✗ Όχι	Απαιτεί ακριβώς 2 μέσους όρους
Cohen’s d	✓ Ναι	✗ Όχι*	✗ Όχι*	Σχεδιασμένο για 2 ομάδες

*Μπορούμε να υπολογίσουμε πολλαπλά d ανά ζεύγη, αλλά όχι ένα συνολικό d

Εναλλακτικά μέτρα για 3+ ομάδες:

Εκτός από το PRE, μπορούμε να χρησιμοποιήσουμε (όπως θα δούμε σε επόμενα κεφάλαια):

1. η² (Eta squared) - Ίδιο με το PRE:

\[\eta^2 = \frac{SS_{Model}}{SS_{Total}} = PRE\]

Λειτουργεί για οποιονδήποτε αριθμό ομάδων

2. ω² (Omega squared) - Μια διορθωμένη εκδοχή του δείκτη η²:

\[\omega^2 = \frac{SS_{Model} - df_{Model} \times MS_{Error}}{SS_{Total} + MS_{Error}}\]

Λιγότερο μεροληπτικό από το η²
Λειτουργεί για οποιονδήποτε αριθμό ομάδων

3. πηλίκο F:

\[F = \frac{MS_{Model}}{MS_{Error}}\]

Όχι ακριβώς “μέγεθος επίδρασης”, αλλά κριτήριο στατιστικής σημαντικότητας (όπως θα δούμε σε επόμενο κεφάλαιο)
Λειτουργεί για οποιονδήποτε αριθμό ομάδων

Γιατί το PRE είναι τόσο ευέλικτο;

Το PRE:

Δεν εξαρτάται από συγκεκριμένες ομάδες:
- Μετράει τη συνολική μείωση σφάλματος
- Δεν χρειάζεται να επιλέξει ποιες ομάδες να συγκρίνει
Λειτουργεί με οποιοδήποτε μοντέλο:
- 2 ομάδες, 3 ομάδες, 10 ομάδες
- Ακόμα και με συνεχείς μεταβλητές
Απλή ερμηνεία:
- “Το μοντέλο εξηγεί X% της μεταβλητότητας”
- Ανεξάρτητα από τον αριθμό ομάδων

Συμπέρασμα:

Μόνο το PRE μπορεί να χρησιμοποιηθεί με μοντέλο τριών (ή περισσότερων) ομάδων επειδή:

✓ Μετράει τη συνολική μείωση σφάλματος από το μοντέλο

✓ Δεν απαιτεί σύγκριση μεταξύ δύο συγκεκριμένων ομάδων

✓ Λειτουργεί με οποιονδήποτε αριθμό ομάδων (2, 3, 4, …)

✓ Παρέχει ένα μέτρο για το συνολικό μοντέλο

Αντίθετα:

✗ Διαφορά μέσων όρων και d του Cohen σχεδιάστηκαν για ακριβώς 2 ομάδες

✗ Με 3+ ομάδες, θα χρειαζόμασταν πολλαπλά μέτρα (ένα για κάθε ζεύγος)

9.6 Μοντελοποίηση της ΔΠΔ

Έχουμε μάθει πώς να προσαρμόζουμε μοντέλα δύο και τριών ομάδων στα δεδομένα, καθώς και να αξιολογούμε πόσο σφάλμα μειώνεται όταν χρησιμοποιούμε ένα μοντέλο ομάδων σε σύγκριση με το κενό μοντέλο. Έχουμε επίσης δει πώς να ποσοτικοποιούμε αυτή τη μείωση του σφάλματος με διάφορα μέτρα μεγέθους επίδρασης, όπως το $b_1$, το PRE και το $d$ του Cohen.

Ωστόσο, αξίζει να θυμηθούμε ότι το κύριο ενδιαφέρον μας δεν είναι τα συγκεκριμένα δεδομένα που έχουμε συλλέξει, αλλά η Διαδικασία Παραγωγής των Δεδομένων (ΔΠΔ) — δηλαδή, η υποκείμενη διαδικασία που παρήγαγε αυτά τα δεδομένα.

Σκέψεις για τη ΔΠΔ των Φιλοδωρημάτων

Στο παρακάτω διάγραμμα παρατηρούμε ότι τα τραπέζια στην ομάδα με το χαμογελαστό προσωπάκι άφησαν, κατά μέσο όρο, υψηλότερα φιλοδωρήματα σε σχέση με την ομάδα ελέγχου. Παρ’ όλα αυτά, υπάρχει σημαντική επικάλυψη μεταξύ των δύο κατανομών.

Είναι πιθανό ότι η παρουσία του χαμογελαστού προσώπου στον λογαριασμό προκάλεσε μια μικρή αύξηση στα φιλοδωρήματα. Ταυτόχρονα, όμως, είναι εξίσου πιθανό η φαινομενική αυτή διαφορά να οφείλεται απλώς σε τυχαία δειγματοληπτική μεταβλητότητα.

Condition_model <- lm(Tip ~ Condition, data = TipExperiment)
gf_jitter(Tip ~ Condition, data = TipExperiment, width = .1) %>%
 gf_model(Condition_model)

Στο Κεφάλαιο 5, εξετάσαμε την πιθανότητα ότι η παρατηρούμενη διαφορά στα φιλοδωρήματα οφειλόταν σε τυχαία μεταβλητότητα χρησιμοποιώντας τη συνάρτηση shuffle(). Τότε, η προσέγγισή μας ήταν να δημιουργήσουμε πολλά τυχαία ανακατέματα των δεδομένων και να συγκρίνουμε τα διαγράμματα αυτών των τυχαίων δειγμάτων με το διάγραμμα των πραγματικών δεδομένων, ώστε να διαπιστώσουμε αν η παρατηρούμενη διαφορά ήταν ουσιαστική.

Τώρα που γνωρίζουμε πώς να προσαρμόζουμε ένα μοντέλο δύο ομάδων, μπορούμε να επανεξετάσουμε τη shuffle() με πιο προχωρημένο τρόπο. Όπως θα δούμε, οι έννοιες και οι διαδικασίες της στατιστικής μοντελοποίησης μας επιτρέπουν (α) να διατυπώσουμε το ερώτημά μας μέσα σε ένα πλαίσιο σύγκρισης μοντέλων και (β) να ποσοτικοποιήσουμε την ανάλυση των δεδομένων που παράγονται τυχαία.

Μοντελοποίηση των Δεδομένων

Ας ξεκινήσουμε επανεξετάζοντας το μοντέλο δύο ομάδων για τα φιλοδωρήματα (Tip) ανά συνθήκη (Condition):

\[\text{Tip}_i = b_0 + b_1 \text{Condition}_i + e_i\]

Όταν προσαρμόζουμε το μοντέλο με τη συνάρτηση lm(), λαμβάνουμε τις παρακάτω εκτιμήσεις παραμέτρων:

lm(formula = Tip ~ Condition, data = TipExperiment)

Coefficients:
         (Intercept)  ConditionSmiley Face
              27.000                 6.045

Ποια από τις δύο εκτιμήσεις παραμέτρων είναι το $b_1$;

276.045

Επεξήγηση

Σωστή απάντηση: Β - 6.045

Κατανόηση των αποτελεσμάτων της lm():

Το μοντέλο που εκτιμήθηκε είναι:

\[\text{Tip}_i = b_0 + b_1 \cdot X_{1i} + e_i\]

όπου $X_1$ = 1 αν Smiley Face, 0 αν Control

Από τα αποτελέσματα:

Coefficients:
    (Intercept)  ConditionSmiley Face
          27.000                 6.045

(Intercept) = 27.000 → Αυτό είναι το $b_0$
ConditionSmiley Face = 6.045 → Αυτό είναι το $b_1$

Γιατί η Α (27) είναι λάθος;

Το 27 είναι το $b_0$ (Intercept), όχι το $b_1$.

$b_0$ = 27.000: Το μέσο φιλοδώρημα στην ομάδα Control
$b_1$ = 6.045: Η διαφορά όταν περνάμε από την ομάδα Control στην ομάδα Smiley Face

Συμπέρασμα:

Το $b_1$ = 6.045 είναι η εκτίμηση που αντιστοιχεί στην ψευδομεταβλητή ConditionSmiley Face.

Ποια από τις παρακάτω είναι η καλύτερη ερμηνεία του $b_1$;

Το μέσο ποσό φιλοδωρήματος από τα τραπέζια στη συνθήκη control.Το μέσο ποσό φιλοδωρήματος από τα τραπέζια στη συνθήκη smiley face.Το μέσο φιλοδώρημα που κέρδισε κάθε σερβιτόρος ανά τραπέζι.Η ποσότητα που πρέπει να προστεθεί στο μέσο φιλοδώρημα στη συνθήκη control για να πάρουμε το μέσο φιλοδώρημα στη συνθήκη smiley face.

Επεξήγηση

Σωστή απάντηση: Δ - Η ποσότητα που πρέπει να προστεθεί στο μέσο φιλοδώρημα στη συνθήκη control για να πάρουμε το μέσο φιλοδώρημα στη συνθήκη smiley face.

Το μοντέλο:

\[\text{Tip}_i = b_0 + b_1 \cdot X_{1i}\]

όπου: - $X_1$ = 0 αν Control, 1 αν Smiley Face

$b_0$ = 27.000
$b_1$ = 6.045

Τι αντιπροσωπεύει το $b_1$;

Το $b_1$ είναι η διαφορά μεταξύ των δύο ομάδων:

\[b_1 = \bar{Y}_{\text{Smiley}} - \bar{Y}_{\text{Control}}\]

\[b_1 = 33.045 - 27.000 = 6.045\]

Ερμηνεία:

«Όταν προσθέτουμε 6.045 στο μέσο φιλοδώρημα της ομάδας ελέγχου (27.000), παίρνουμε το μέσο φιλοδώρημα της ομάδας με το χαμογελαστό προσωπάκι (33.045).»

Με άλλα λόγια:

«Το $b_1$ είναι η ποσότητα που προστίθεται όταν περνάμε από την ομάδα Control στην ομάδα Smiley Face.»

Γιατί οι άλλες είναι λάθος;

Α. “Το μέσο ποσό φιλοδωρήματος στη συνθήκη control” - ΛΑΘΟΣ

Αυτό είναι το $b_0$, όχι το $b_1$
$b_0$ = 27.000 = μέσο φιλοδώρημα στην Control

Β. “Το μέσο ποσό φιλοδωρήματος στη συνθήκη smiley face” - ΛΑΘΟΣ

Το μέσο φιλοδώρημα στην Smiley Face είναι $b_0 + b_1$, όχι μόνο $b_1$
Μέσο φιλοδώρημα στην Smiley Face = 27.000 + 6.045 = 33.045
Το $b_1$ = 6.045 είναι μόνο η διαφορά, όχι ο μέσος όρος

Γ. “Το μέσο φιλοδώρημα που κέρδισε κάθε σερβιτόρος ανά τραπέζι” - ΛΑΘΟΣ

Αυτό είναι πολύ ασαφές και δεν περιγράφει το $b_1$
Το $b_1$ δεν είναι ένα “μέσο φιλοδώρημα” - είναι μια διαφορά

Μαθηματική απόδειξη:

Για Control (X₁ = 0):

\[\text{Tip} = b_0 + b_1 \cdot 0 = b_0 = 27.000\]

Για Smiley Face (X₁ = 1):

\[\text{Tip} = b_0 + b_1 \cdot 1 = b_0 + b_1 = 27.000 + 6.045 = 33.045\]

Διαφορά:

\[\text{Smiley} - \text{Control} = (b_0 + b_1) - b_0 = b_1 = 6.045\]

Άρα, το $b_1$ είναι η διαφορά (ή αύξηση) μεταξύ των δύο ομάδων!

Γενική αρχή για ερμηνεία ψευδομεταβλητών:

Σε ένα μοντέλο με μία ψευδομεταβλητή:

\[Y_i = b_0 + b_1 \cdot X_{1i}\]

$b_0$: Ο μέσος όρος της ομάδας αναφοράς (όταν $X_1$ = 0)
$b_1$: Η διαφορά μεταξύ της ομάδας με $X_1$ = 1 και της ομάδας αναφοράς

Ερμηνεία του $b_1$:

«Η θετική ή αρνητική ποσότητα που προσθέτουμε στο $b_0$ όταν μεταβαίνουμε από την ομάδα αναφοράς στην άλλη ομάδα.»

Συμπέρασμα:

Η καλύτερη ερμηνεία του $b_1$ = 6.045 είναι:

«Η ποσότητα που πρέπει να προστεθεί στο μέσο φιλοδώρημα της συνθήκης control για να υπολογίσουμε το μέσο φιλοδώρημα της συνθήκης smiley face.»

Με απλά λόγια: Τα τραπέζια στη συνθήκη του χαμογελαστού προσώπου άφησαν κατά μέσο όρο περίπου 6 τοις εκατό επί του λογαριασμού μεγαλύτερο φιλοδώρημα από τα τραπέζια στη συνθήκη Control.

Στο παρακάτω διάγραμμα φαίνεται το ποσοστό φιλοδωρήματος ανά ομάδα, μαζί με τις τιμές πρόβλεψης του μοντέλου των δύο ομάδων (μέσοι όροι). Η εκτίμηση παραμέτρου $b_1$ δείχνει ότι η προσθήκη ενός χαμογελαστού προσώπου στον λογαριασμό οδηγεί σε αύξηση των φιλοδωρημάτων, κατά μέσο όρο, κατά 6 ποσοστιαίες μονάδες (είναι η απόσταση ανάμεσα στις δύο κόκκινες γραμμές).

Σύγκριση Δύο Μοντέλων της ΔΠΔ

Αφού προσαρμόσαμε το μοντέλο, μπορούμε να επανεξετάσουμε το ίδιο ερώτημα που θέσαμε στο Κεφάλαιο 5 — αυτή τη φορά όμως με πιο προχωρημένο τρόπο. Στο Κεφάλαιο 5 αναρωτηθήκαμε: είναι πιθανό η μικρή αύξηση στα φιλοδωρήματα μεταξύ των δύο ομάδων να οφείλεται μόνο σε τυχαία δειγματοληπτική μεταβλητότητα και όχι σε πραγματική επίδραση που υπάρχει στη ΔΠΔ;

Αν δεν υπήρχε επίδραση του χαμογελαστού προσώπου στα φιλοδωρήματα, ποια θα ήταν η τιμή της παραμέτρου $\beta_1$ στη ΔΠΔ;

6.045027Άγνωστο

Επεξήγηση

Σωστή απάντηση: Β - 0

Τι είναι η ΔΠΔ (Διαδικασία Παραγωγής Δεδομένων);

Η ΔΠΔ είναι η πραγματική, υποκείμενη διαδικασία που παράγει τα δεδομένα. Είναι το “αληθινό” μοντέλο που ισχύει στον πληθυσμό.

Το μοντέλο στη ΔΠΔ:

\[\text{Tip}_i = \beta_0 + \beta_1 \cdot X_{1i} + \epsilon_i\]

όπου:

$\beta_0, \beta_1$ = οι πραγματικές παράμετροι στον πληθυσμό (ΔΠΔ)
$b_0, b_1$ = οι εκτιμήσεις από το δείγμα
$X_1$ = 1 αν ανήκει στην ομάδα χαμογελαστού προσώπου, 0 αν ανήκει στην ομάδα ελέγχου

Τι σημαίνει “δεν υπάρχει επίδραση”;

Αν το χαμογελαστό προσωπάκι δεν έχει επίδραση στα φιλοδωρήματα, τότε:

«Το μέσο φιλοδώρημα είναι το ίδιο στις δύο συνθήκες.»

Αν δεν υπάρχει επίδραση, τότε:

\[\beta_0 = \beta_0 + \beta_1\]

\[\Rightarrow \beta_1 = 0\]

Συμπέρασμα:

Αν το χαμογελαστό προσωπάκι δεν έχει επίδραση, τότε $\beta_1 = 0$ στη ΔΠΔ.

Γιατί οι άλλες είναι λάθος;

Α. “6.045” - ΛΑΘΟΣ

Το 6.045 είναι η εκτίμηση παραμέτρου $b_1$ από το δείγμα, όχι η αληθινή τιμή $\beta_1$ στη ΔΠΔ
Αν δεν υπάρχει επίδραση στη ΔΠΔ ($\beta_1 = 0$), τότε το $b_1 = 6.045$ οφείλεται μόνο στην τυχαία δειγματοληπτική μεταβλητότητα

Σύγκριση:

Παράμετρος	Σύμβολο	Τιμή	Πού υπάρχει
Πραγματική παράμετρος	$\beta_1$	0 (αν δεν υπάρχει επίδραση)	ΔΠΔ (πληθυσμός)
Εκτίμηση από δείγμα	$b_1$	6.045	Δείγμα

Γ. “27” - ΛΑΘΟΣ

Το 27 είναι η εκτίμηση του $\beta_0$ (Intercept), όχι του $\beta_1$
Το $\beta_0$ αντιπροσωπεύει το μέσο φιλοδώρημα στην ομάδα ελέγχου
Ακόμα κι αν δεν υπάρχει επίδραση του χαμογελαστού προσώπου, το $\beta_0$ μπορεί να είναι οποιαδήποτε τιμή (π.χ., 27)

Δ. “Άγνωστο” - ΛΑΘΟΣ

Η τιμή του $\beta_1$ δεν είναι άγνωστη αν ξέρουμε ότι δεν υπάρχει επίδραση
“Δεν υπάρχει επίδραση” σημαίνει ακριβώς $\beta_1 = 0$

Η διαφορά μεταξύ ΔΠΔ και δείγματος:

ΔΠΔ (ΠΛΗΘΥΣΜΟΣ):
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
Πραγματικό μοντέλο:
Tip = β₀ + β₁·X₁ + ε

Αν δεν υπάρχει επίδραση:
β₁ = 0

        ↓ Παίρνουμε δείγμα

ΔΕΙΓΜΑ:
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
Εκτιμώμενο μοντέλο:
Tip = b₀ + b₁·X₁

Από τα δεδομένα:
b₀ = 27.000
b₁ = 6.045  ← Τυχαία μεταβλητότητα!

Ακόμα κι αν β₁ = 0 (ΔΠΔ),
το b₁ ≠ 0 λόγω τυχαίας δειγματοληπτικής μεταβλητότητας

Συμπέρασμα:

Αν δεν υπάρχει επίδραση του χαμογελαστού προσώπου στα φιλοδωρήματα, τότε:

\[\beta_1 = 0 \text{ στη ΔΠΔ}\]

Αυτό σημαίνει ότι:

Οι δύο συνθήκες έχουν το ίδιο μέσο φιλοδώρημα στον πληθυσμό
Η διαφορά που παρατηρούμε στο δείγμα ($b_1 = 6.045$) οφείλεται αποκλειστικά σε τυχαία δειγματοληπτική μεταβλητότητα
Το $\beta_1 = 0$ είναι ο ορισμός της “απουσίας επίδρασης” στη ΔΠΔ.

Αν και το προσαρμοσμένο μοντέλο εκτιμά την παράμετρο $\beta_1$ περίπου 6 ποσοστιαίες μονάδες, θα μπορούσε ένα τέτοιο αποτέλεσμα να είχε προκύψει από μια ΔΠΔ όπου η πραγματική τιμή της $\beta_1$ είναι 0;

Με άλλα λόγια, με βάση τα δεδομένα μας, ποιο μοντέλο θα προτιμήσουμε;

Το πιο σύνθετο μοντέλο, όπου η συνθήκη (Condition) περιλαμβάνεται ως ανεξάρτητη μεταβλητή και η $\beta_1$ εκτιμάται ίση με 6;
Ή το απλούστερο, κενό μοντέλο, στο οποίο η $\beta_1$ θεωρείται ίση με 0;

Μοντέλο Condition: $\text{Tip}_i = \beta_0 + \beta_1 \text{Condition}_i + \epsilon_i$

Κενό μοντέλο: $\text{Tip}_i = \beta_0 + \epsilon_i$

Σημειώστε ότι η μόνη διαφορά μεταξύ αυτών των δύο μοντέλων είναι ότι ο όρος $\beta_1 \text{Condition}_i$ δεν υπάρχει στο κενό μοντέλο. Αν η πραγματική τιμή της $\beta_1$ είναι 0, τότε αυτός ο όρος θα εξαλειφθεί.

9.7 Χρήση του Τυχαίου Ανακατέματος για Σύγκριση Μοντέλων της ΔΠΔ

Προσομοίωση του Κενού Μοντέλου με τη `shuffle()`

Αν στην πραγματικότητα δεν υπήρχε καμία επίδραση του χαμογελαστού προσώπου στα φιλοδωρήματα, τότε το κενό μοντέλο θα αποτελούσε καλή αναπαράσταση της ΔΠΔ (στην οποία $\beta_1 = 0$). Ωστόσο, ακόμη κι αν αυτή ήταν η πραγματική ΔΠΔ, δεν θα περιμέναμε η εκτίμηση της επίδρασης στο δείγμα μας ($b_1$) να είναι ακριβώς μηδέν. Ιδιαίτερα σε μικρά δείγματα, η εκτίμηση μπορεί να αποκλίνει λίγο προς τα πάνω ή προς τα κάτω. Το κρίσιμο ερώτημα είναι: πόσο μεγάλη μπορεί να είναι αυτή η απόκλιση;

Για να διερευνήσουμε αυτό το ερώτημα, μπορούμε να χρησιμοποιήσουμε τη συνάρτηση shuffle(). Τώρα όμως που γνωρίζουμε πώς να προσαρμόζουμε μοντέλα, μπορούμε να αξιοποιήσουμε το ανακάτεμα με πιο προχωρημένο τρόπο: αντί απλώς να ανακατεύουμε τις τιμές των φιλοδωρημάτων και να παρατηρούμε τα διαγράμματα των ομάδων, μπορούμε να προσαρμόζουμε ένα μοντέλο σε κάθε ανακατεμένο δείγμα και να υπολογίζουμε την εκτίμηση $b_1$ της παραμέτρου $\beta_1$ για κάθε ανακάτεμα.

Στην πράξη, δεν χρειάζεται καν να δημιουργούμε διαγράμματα. Μπορούμε να συνδυάσουμε τη συνάρτηση b1() με τη shuffle() για να υπολογίσουμε απευθείας το $b_1$ για κάθε ανακατεμένο δείγμα. Αν επαναλάβουμε αυτή τη διαδικασία πολλές φορές, αποκτούμε μια κατανομή των εκτιμήσεων $b_1$ υπό την υπόθεση ότι το κενό μοντέλο αντιπροσωπεύει την πραγματική ΔΠΔ — δηλαδή, ότι οποιαδήποτε διαφορά μεταξύ των ομάδων οφείλεται αποκλειστικά στην τύχη.

Στο παρακάτω πλαίσιο κώδικα, υπολογίζουμε την εκτίμηση $b_1$ της παραμέτρου $\beta_1$ από τα δεδομένα του δείγματος και, στη συνέχεια, εφαρμόζουμε το ανακάτεμα των τιμών των φιλοδωρημάτων για να υπολογίσουμε εκ νέου την εκτίμηση $b_1$ σε κάθε ανακατεμένο δείγμα.

Εκτελέστε τον κώδικα μερικές φορές και παρατηρήστε τα αποτελέσματα που προκύπτουν.

6.045
0.036

Έστω ότι πήραμε τα δύο παραπάνω αποτελέσματα εκτελώντας τον κώδικα. Η τιμή 6.045 μάς είναι ήδη γνωστή —είναι η εκτίμηση παραμέτρου $b_1$ που είχαμε υπολογίσει προηγουμένως από την προσαρμογή του μοντέλου στα πραγματικά δεδομένα με τη συνάρτηση lm(). Η τιμή 0.036 είναι η εκτίμηση $b_1$ που προέκυψε από τα ανακατεμένα δεδομένα.

Τι συμβαίνει κάθε φορά που εκτελείτε τον παραπάνω κώδικα; Παίρνετε το ίδιο αποτέλεσμα κάθε φορά; Γιατί ή γιατί όχι;

Κάθε φορά που εκτελείτε τον παραπάνω κώδικα, η εκτίμηση παραμέτρου $b_1$ αλλάζει, επειδή το ανακάτεμα είναι τυχαίο. Δεν θα πάρετε το ίδιο αποτέλεσμα κάθε φορά. Δοκιμάστε να εκτελέσετε τον κώδικα πολλές φορές για να δείτε τη μεταβλητότητα των αποτελεσμάτων.

Αν χρησιμοποιήσετε τη συνάρτηση do() πριν από τον κώδικα, μπορείτε να επαναλάβετε αυτόματα τη διαδικασία ανακατέματος όσες φορές θέλετε, ώστε να προκύψει μια νέα εκτίμηση $b_1$ για κάθε επανάληψη.

Για παράδειγμα, για να πραγματοποιήσετε 5 ανακατέματα, θα γράφατε:

do(5) * b1(shuffle(Tip) ~ Condition, data = TipExperiment)

Τροποποιήστε τον κώδικα στο παρακάτω πλαίσιο ώστε να εκτελέσετε 10 ανακατέματα των φιλοδωρημάτων μεταξύ των συνθηκών και να παραγάγετε 10 τυχαίες εκτιμήσεις του $b_1$.

           b1
1  -3.7727273
2  -2.6818182
3  -1.4090909
4  -2.6818182
5  -4.6818182
6   2.0454545
7  -0.1363636
8  -1.1363636
9   0.5909091
10  4.6818182

Οι δέκα εκτιμήσεις $b_1$ που προέκυψαν από την εκτέλεση του κώδικα δεν θα είναι ακριβώς ίδιες με αυτές που εμφανίζονται παραπάνω. Παρατηρήστε, ωστόσο, ότι μερικές από αυτές τις τιμές του $b_1$ είναι θετικές, άλλες αρνητικές· κάποιες απέχουν αρκετά από το 0 (π.χ. 4.68 και -3.77), ενώ άλλες είναι πολύ κοντά στο 0 (π.χ. -0.13). Εκτελέστε τον κώδικα μερικές φορές ακόμη, για να αποκτήσετε μια αίσθηση της μεταβλητότητας αυτών των εκτιμήσεων.

Αν συνεχίσουμε να δημιουργούμε τυχαίες εκτιμήσεις $b_1$, θα παρατηρήσουμε ότι, αν και σπάνια είναι ακριβώς ίσες με 0, τείνουν να συγκεντρώνονται γύρω από το 0 (για να το δείτε αυτό κατασκευάστε ένα ιστόγραμμα για 1000 τυχαίες εκτιμήσεις $b_1$). Αυτό συμβαίνει επειδή η συνάρτηση shuffle() προσομοιώνει μια Διαδικασία Παραγωγής Δεδομένων (ΔΠΔ) στην οποία δεν υπάρχει καμία πραγματική επίδραση του χαμογελαστού προσώπου στα φιλοδωρήματα — δηλαδή, το ποσοστό φιλοδωρήματος είναι ανεξάρτητο από τη συνθήκη.

Να θυμάστε: κάθε μία από αυτές τις εκτιμήσεις $b_1$ προκύπτει από μια καθαρά τυχαία διαδικασία, που δεν έχει καμία σχέση με το αν το τραπέζι έλαβε λογαριασμό με χαμογελαστό πρόσωπο ή όχι. Η συνάρτηση shuffle() μιμείται μια ΔΠΔ στην οποία η παράμετρος $\beta_1 = 0$. Μερικές φορές αυτή η ΔΠΔ αποκαλείται και «γονικός πληθυσμός» (parent population), επειδή οι εκτιμήσεις $b_1$ που παράγει — τα «παιδιά» (children) — τείνουν να μοιάζουν με το «γονέα» τους — συγκεντρώνονται δηλαδή γύρω από το μηδέν.

Χρήση Προσομοιωμένων $b_1$ για Καλύτερη Κατανόηση των Δεδομένων

Μπορούμε να αξιοποιήσουμε αυτές τις προσομοιωμένες εκτιμήσεις $b_1$ για να κατανοήσουμε καλύτερα τα δεδομένα μας. Ξεκινάμε συγκρίνοντας την εκτίμηση $b_1$ από τα πραγματικά δεδομένα της μελέτης (6.045) με τις 10 εκτιμήσεις $b_1$ που προέκυψαν από τα ανακατεμένα δεδομένα.

Οι εκτιμήσεις αυτές παρουσιάζονται ξανά παρακάτω, ταξινομημένες από τη μικρότερη προς τη μεγαλύτερη.

           b1
1  -3.7727273
2  -3.2272727
3  -1.6818182
4  -1.6818182
5  -1.5000000
6  -0.5000000
7   0.1363636
8   2.7727273
9   3.6818182
10  6.9545455

Θυμηθείτε ότι η τιμή $b_1$ του δείγματος ήταν περίπου 6. Που βρίσκεται αυτή η τιμή σε σχέση με τις προσομοιωμένες τιμές $b_1$;

Η τιμή $b_1$ του δείγματος είναι σχετικά μικρή.Η τιμή $b_1$ του δείγματος είναι σχετικά μεγάλη.Η τιμή $b_1$ του δείγματος βρίσκεται περίπου στη μέση αυτών των τυχαία παραχθέντων τιμών $b_1$.Επειδή η ακριβής τιμή $b_1$ του δείγματός μας δεν περιλαμβάνεται σε αυτό το σύνολο των προσομοιωμένων τιμών $b_1$, δεν μπορούμε να απαντήσουμε με βεβαιότητα σε αυτή την ερώτηση.

Επεξήγηση

Σωστή απάντηση: Β - Η τιμή $b_1$ του δείγματος είναι σχετικά μεγάλη.

Το πλαίσιο:

Στο πείραμα φιλοδωρημάτων: - Η $b_1$ του δείγματος ≈ 6.045

Αυτό αντιπροσωπεύει τη διαφορά μεταξύ των ομάδων Smiley Face και Control

Τι είναι οι προσομοιωμένες ή ανακατεμένες (shuffled) τιμές $b_1$;

Το ανακάτεμα (shuffling) είναι μια τεχνική για:

…να προσομοιώσουμε τη ΔΠΔ με $\beta_1 = 0$:
- Ανακατεύουμε τυχαία τις τιμές φιλοδωρήματος ανεξάρτητα από την ομάδα όπου ανήκουν (Smiley Face ή Control)
- Αυτό σπάει οποιαδήποτε πραγματική σχέση μεταξύ συνθήκης και ποσοστού φιλοδωρήματος
- Προσομοιώνει έναν κόσμο όπου $\beta_1 = 0$ (δεν υπάρχει επίδραση της συνθήκης)
…να υπολογίσουμε την τιμή $b_1$ για κάθε ανακάτεμα:
- Κάθε φορά που ανακατεύουμε, υπολογίζουμε μία νέα τιμή $b_1$
- Αυτές οι τιμές $b_1$ μας δείχνουν τι τιμές είναι πιθανό να προκύψουν λόγω τυχαιότητας

Παρατήρηση:

Η τιμή $b_1 = 6.045$ του δείγματος βρίσκεται πολύ μακριά από το κέντρο (0) της κατανομής των προσομοιωμένων τιμών $b_1$.

Αυτό σημαίνει ότι η τιμή $b_1 = 6.045$ είναι σχετικά μεγάλη σε σύγκριση με τις τιμές που λαμβάνουμε λόγω τυχαιότητας.

Γιατί οι άλλες είναι λάθος;

Α. “Η τιμή $b_1$ του δείγματος είναι σχετικά μικρή” - ΛΑΘΟΣ

Η $b_1 = 6.045$ δεν είναι μικρή
Βρίσκεται στη δεξιά ουρά της κατανομής των προσομοιωμένων τιμών $b_1$
Οι περισσότερες προσομοιωμένες τιμές είναι κοντά στο 0, όχι κοντά στο 6

Γ. “Η τιμή $b_1$ θα έπεφτε στη μέση” - ΛΑΘΟΣ

Η μέση των προσομοιωμένων $b_1$ είναι περίπου 0
Η τιμή $b_1 = 6.045$ είναι πολύ μακριά από τη μέση

Δ. “Δεν μπορώ να απαντήσω” - ΛΑΘΟΣ

Δεν χρειάζεται η ακριβής τιμή 6.045 να εμφανιστεί στις προσομοιωμένες τιμές
Μπορούμε να συγκρίνουμε το 6.045 με την κατανομή των προσομοιωμένων τιμών
Ρωτάμε: “Πού βρίσκεται η τιμή 6.045 σε σχέση με την υπόλοιπη κατανομή;”

Ερμηνεία:

«Μόνο μία από τις δέκα προσομοιωμένες τιμές $b_1$ είναι τόσο μεγάλη ή μεγαλύτερη από την τιμή 6.045. Αυτό σημαίνει ότι η εκτίμηση $b_1 = 6.045$ του δείγματός μας είναι σχετικά ακραία σε σχέση με ό,τι θα περιμέναμε αν το κενό μοντέλο ήταν αληθινό — επομένως, είναι μάλλον απίθανο να έχει προκύψει αποκλειστικά λόγω τυχαιότητας.»

Συμπέρασμα:

Η τιμή $b_1 = 6.045$ του δείγματος είναι σχετικά μεγάλη σε σύγκριση με τις προσομοιωμένες τιμές $b_1$ επειδή:

✓ Βρίσκεται πολύ μακριά από τη μέση (≈0) των προσομοιωμένων τιμών
✓ Βρίσκεται στη δεξιά ουρά της κατανομής
✓ Πολύ λίγες προσομοιωμένες τιμές είναι τόσο μεγάλες

Αυτό αποτελεί ένδειξη ότι το χαμογελαστό πρόσωπο έχει πραγματική επίδραση στα φιλοδωρήματα!

Αυτό που μπορούμε πλέον να διακρίνουμε —πολύ πιο καθαρά απ’ ό,τι όταν είχαμε μόνο τα διαγράμματα— είναι ότι μόνο μία από τις δέκα τυχαία παραγόμενες εκτιμήσεις $b_1$ είναι τόσο μεγάλη ή μεγαλύτερη από εκείνη που παρατηρήθηκε στη μελέτη. Από αυτό μπορούμε να συμπεράνουμε ότι υπάρχει πιθανότητα περίπου μία στις δέκα να παρατηρήσουμε μια εκτίμηση $b_1 = 6.045$, αν το κενό μοντέλο είναι πράγματι το σωστό μοντέλο της ΔΠΔ.

Με βάση αυτή την παρατήρηση, θεωρείτε ότι θα έπρεπε να απορρίψουμε το κενό μοντέλο ως την καλύτερη περιγραφή της ΔΠΔ;

Πρόκειται για μια δύσκολη απόφαση — στην οποία θα επανέλθουμε σε επόμενο κεφάλαιο. Προς το παρόν, αρκεί να σημειώσουμε ότι, συγκρίνοντας την παρατηρούμενη εκτίμηση $b_1$ με τις εκτιμήσεις που θα μπορούσαν να έχουν παραχθεί από το κενό μοντέλο, μαθαίνουμε να σκεφτόμαστε πιο κριτικά για το πώς ερμηνεύουμε τα αποτελέσματα της μελέτης των φιλοδωρημάτων.

9.8 Ασκήσεις Επανάληψης Κεφαλαίου 9

Το StudentSurvey είναι ένα πλαίσιο δεδομένων με 362 παρατηρήσεις στις ακόλουθες 17 μεταβλητές:

Year: Έτος σπουδών
Gender: Φύλο φοιτητή: F ή M
Smoke: Καπνιστής; No ή Yes
Award: Προτίμηση για βραβείο: Academy, Nobel, ή Olympic
HigherSAT: Ποια επίδοση στη δοκιμασία SAT είναι υψηλότερη; Math ή Verbal
Exercise: Ώρες άσκησης ανά εβδομάδα
TV: Ώρες παρακολούθησης τηλεόρασης ανά εβδομάδα
Height: Ύψος (σε ίντσες)
Weight: Βάρος (σε λίβρες)
Siblings: Αριθμός αδελφών
BirthOrder: Σειρά γέννησης, 1 = μεγαλύτερο
VerbalSAT: Βαθμολογία στη δοκιμασία Verbal SAT
MathSAT: Βαθμολογία στη δοκιμασία Math SAT
SAT: Σύνθετη βαθμολογία Verbal + Math SAT
GPA: Βαθμός πτυχίου
Pulse: Kαρδιακός ρυθμός ηρεμίας (χτύποι ανά λεπτό)
Piercings: Αριθμός piercing στο σώμα

Ας ρίξουμε μια ματιά στον αριθμό των ωρών που αφιερώνουν στην άσκηση κάθε εβδομάδα (μεταβλητή Exercise) οι φοιτητές αυτού του δείγματος.

gf_histogram(~ Exercise, data = StudentSurvey, bins = 8)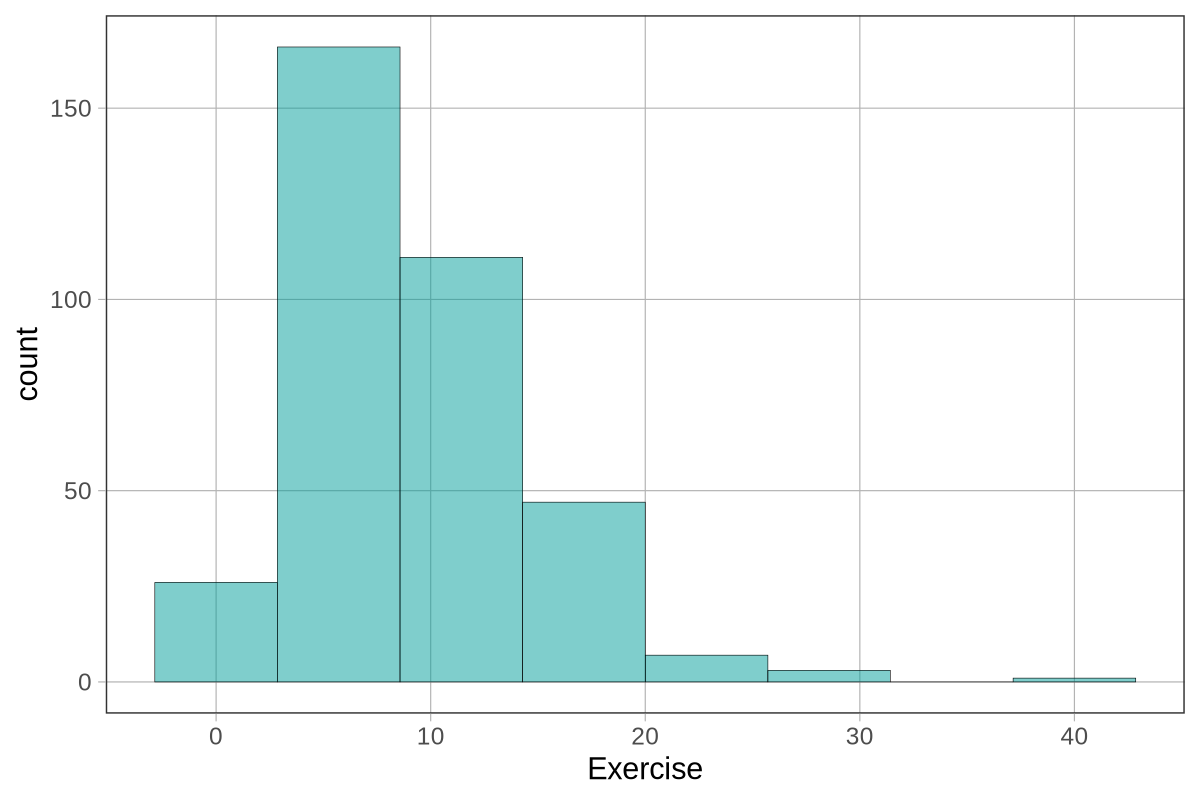

1. Γιατί ο μέσος όρος μπορεί να είναι ένα καλό απλό μοντέλο για την κατανομή της Exercise;

Επειδή ο μέσος όρος είναι ένα μοντέλο που εξισορροπεί τις αποκλίσεις από αυτό και ελαχιστοποιεί το άθροισμα τετραγώνων των υπολοίπων.Επειδή ο μέσος όρος είναι η μόνη στατιστικά αποδεκτή τιμή του $b_0$.Επειδή ο μέσος όρος είναι η πιο συχνή τιμή σε αυτή την κατανομή.Επειδή σε όλες τις ασύμμετρες κατανομές, ο μέσος όρος είναι το καλύτερο μοντέλο διότι διαφέρει από τη διάμεσο.

Επεξήγηση

Σωστή απάντηση: Α - Επειδή ο μέσος όρος είναι ένα μοντέλο που εξισορροπεί τις αποκλίσεις από αυτό και ελαχιστοποιεί το άθροισμα τετραγώνων των υπολοίπων.

Γιατί ο μέσος όρος είναι ένα καλό απλό μοντέλο;

Ο μέσος όρος $\bar{Y}$ είναι το βέλτιστο απλό μοντέλο (κενό μοντέλο) επειδή:

1. Ελαχιστοποιεί το Άθροισμα Τετραγώνων των Υπολοίπων (SS):

Για οποιοδήποτε μοντέλο με μία σταθερά:

\[Y_i = b_0 + e_i\]

Το άθροισμα τετραγώνων των υπολοίπων είναι:

\[SS = \sum_{i=1}^{n}(Y_i - b_0)^2\]

Το $SS$ ελαχιστοποιείται όταν $b_0 = \bar{Y}$ (ο μέσος όρος).

2. Εξισορροπεί τις αποκλίσεις:

Το άθροισμα των αποκλίσεων από το μέσο όρο είναι πάντα μηδέν:

\[\sum_{i=1}^{n}(Y_i - \bar{Y}) = 0\]

Αυτό σημαίνει ότι:

Οι θετικές αποκλίσεις (τιμές πάνω από το μέσο)
..εξισορροπούνται από τις αρνητικές αποκλίσεις (τιμές κάτω από το μέσο)

Γιατί οι άλλες είναι λάθος;

Β. “Ο μέσος όρος είναι η μόνη στατιστικά αποδεκτή τιμή του $b_0$” - ΛΑΘΟΣ

Ο μέσος όρος δεν είναι η “μόνη” αποδεκτή τιμή
Θα μπορούσαμε να χρησιμοποιήσουμε οποιαδήποτε τιμή ως $b_0$
Αλλά ο μέσος όρος είναι η βέλτιστη τιμή (ελαχιστοποιεί το SS)

Γ. “Ο μέσος όρος είναι η πιο συχνή τιμή” - ΛΑΘΟΣ

Η πιο συχνή τιμή είναι η επικρατούσα τιμή (mode), όχι ο μέσος όρος
Στην κατανομή της μεταβλητής Exercise, η επικρατούσα τιμή φαίνεται να είναι περίπου 5-7 ώρες
Ο μέσος όρος είναι πιθανώς περίπου 10-12 ώρες (μετατοπισμένος δεξιά λόγω της ασυμμετρίας)

Δ. “Σε ασύμμετρες κατανομές, ο μέσος είναι καλύτερος επειδή διαφέρει από τη διάμεσο” - ΛΑΘΟΣ

Η κατανομή της Exercise είναι ασύμμετρη. Η διαφορά μέσου όρου – διάμεσου είναι απλώς ένδειξη ασυμμετρίας, όχι αιτία για να επιλέξουμε το μέσο όρο.
Ο μέσος όρος είναι καλό απλό μοντέλο γιατί ελαχιστοποιεί τα τετράγωνα των αποκλίσεων από αυτόν, ακόμη και όταν η κατανομή είναι ασύμμετρη.

Συμπέρασμα:

Ο μέσος όρος είναι ένα καλό απλό μοντέλο για την κατανομή της Exercise επειδή:

✓ Ελαχιστοποιεί το άθροισμα τετραγώνων των υπολοίπων (SS)

✓ Εξισορροπεί τις αποκλίσεις - το άθροισμα των αποκλίσεων είναι μηδέν

✓ Παρέχει μια βέλτιστη σταθερή τιμή για να προβλέψουμε την Exercise χωρίς άλλες μεταβλητές

✓ Είναι η βάση για τη σύγκριση με πιο σύνθετα μοντέλα

Αυτές οι ιδιότητες κάνουν το μέσο όρο το μαθηματικά βέλτιστο απλό μοντέλο, ανεξάρτητα από το σχήμα της κατανομής (συμμετρική, ασύμμετρη, κλπ.).

2. Αν χρησιμοποιήσουμε αυτόν τον κώδικα για να προσαρμόσουμε το κενό μοντέλο:

empty_model <- lm(Exercise ~ NULL, data = StudentSurvey)

και στη συνέχεια χρησιμοποιήσουμε τη συνάρτηση predict() για να προβλέψουμε τον αριθμό ωρών άσκησης την εβδομάδα για κάθε φοιτητή, ποια θα ήταν η τιμή πρόβλεψης;

Η τιμή πρόβλεψης θα ήταν ο μέσος όρος των ωρών άσκησης αυτού του δείγματος και θα ήταν η ίδια για κάθε φοιτητή.Η τιμή πρόβλεψης εξαρτάται από το πόσο πραγματικά ασκήθηκαν οι φοιτητές.Δεν θα μπορούσαμε να προσδιορίσουμε την τιμή πρόβλεψης επειδή αναπαρίσταται από το $b_0$.Η τιμή πρόβλεψης θα ήταν ο μέσος όρος των ωρών άσκησης κάθε φοιτητή το συγκεκριμένο έτος και θα διέφερε για κάθε φοιτητή.

Επεξήγηση

Σωστή απάντηση: Α - Η τιμή πρόβλεψης θα ήταν ο μέσος όρος των ωρών άσκησης αυτού του δείγματος και θα ήταν η ίδια για κάθε φοιτητή.

Τι είναι το κενό μοντέλο;

Το κενό μοντέλο (empty model ή null model) είναι το απλούστερο μοντέλο που περιλαμβάνει μόνο μία σταθερά:

\[\text{Exercise}_i = b_0 + e_i\]

Όπου: - $b_0$ = ο σταθερός όρος (intercept)

$e_i$ = το υπόλοιπο (residual) για το φοιτητή $i$

Στην R:

empty_model <- lm(Exercise ~ NULL, data = StudentSurvey)

Exercise ~ NULL σημαίνει: “προβλέπουμε την Exercise χωρίς ανεξάρτητες μεταβλητές”
Αυτό εκτιμά μόνο το $b_0$, που είναι ο μέσος όρος της Exercise

Τι κάνει η συνάρτηση predict();

predictions <- predict(empty_model)

Η predict() επιστρέφει τις προβλέψεις του μοντέλου για κάθε παρατήρηση.

Για το κενό μοντέλο:

\[\hat{Y}_i = b_0\]

Επειδή δεν υπάρχουν ανεξάρτητες μεταβλητές, η πρόβλεψη είναι πάντα το $b_0$ (ο μέσος όρος).

Γιατί οι άλλες είναι λάθος;

Β. “Θα εξαρτιόταν από το πόσο πραγματικά ασκήθηκαν” - ΛΑΘΟΣ

Το κενό μοντέλο ΔΕΝ χρησιμοποιεί καμία πληροφορία για κάθε φοιτητή
Η πρόβλεψη είναι η ίδια για όλους, ανεξάρτητα από το πόσο πραγματικά ασκούνται

Γ. “Δεν θα μπορούσατε να προσδιορίσετε την τιμή επειδή αναπαρίσταται από το $b_0$” - ΛΑΘΟΣ

Μπορούμε εύκολα να προσδιορίσουμε το $b_0$!
Το $b_0$ εκτιμάται από το μοντέλο και είναι ο μέσος όρος της Exercise
Μπορούμε να το δούμε με:

coef(empty_model)      # Επιστρέφει b₀
mean(StudentSurvey$Exercise, na.rm = TRUE)  # Το ίδιο αποτέλεσμα

Δ. “Ο μέσος όρος ωρών άσκησης για κάθε φοιτητή εκείνο το έτος” - ΛΑΘΟΣ

Στο σύνολο δεδομένων δεν υπάρχει για κάθε φοιτητή ο μέσος όρος των ωρών άσκησης το συγκεκριμένο έτος, αλλά ο αριθμός των ωρών άσκησης την εβδομάδα
Η τιμή πρόβλεψης για κάθε φοιητή θα είναι η ίδια: ο μέσος όρος ολόκληρου του δείγματος

Γιατί όλες οι προβλέψεις είναι ίδιες;

Το κενό μοντέλο:

\[\text{Exercise}_i = b_0\]

Δεν περιλαμβάνει:

Καμία ανεξάρτητη μεταβλητή (π.χ., Gender, Height)
Καμία επιπλέον πληροφορία για το συγκεκριμένο φοιτητή

Άρα, η πρόβλεψη είναι: - Η ίδια για όλους

Βασισμένη μόνο στο συνολικό μέσο όρο

Αναλογία:

Αν αναρωτηθείτε “Πόσες ώρες ασκείται ένας τυχαία επιλεγμένος φοιτητής την εβδομάδα;” χωρίς να ξέρετε τίποτα γι’ αυτόν, η καλύτερη πρόβλεψή σας είναι ο μέσος όρος των ωρών άσκησης όλων των φοιτητών.

Σύγκριση με σύνθετο μοντέλο:

Κενό μοντέλο:

empty_model <- lm(Exercise ~ NULL, data = StudentSurvey)

Πρόβλεψη: 9.054 ώρες για όλους

Σύνθετο μοντέλο (με Gender):

gender_model <- lm(Exercise ~ Gender, data = StudentSurvey)

Πρόβλεψη για άνδρες: 9.876 ώρες
Πρόβλεψη για γυναίκες: 8.11 ώρες

Το σύνθετο μοντέλο δίνει διαφορετικές προβλέψεις ανάλογα με το φύλο (Gender)!

Υπόλοιπα (Residuals):

Επειδή όλες οι προβλέψεις είναι ίδιες στο κενό μοντέλο:

\[e_i = Y_i - \bar{Y}\]

Συμπέρασμα:

Όταν χρησιμοποιούμε τηνpredict() με το κενό μοντέλο:

empty_model <- lm(Exercise ~ NULL, data = StudentSurvey)
predict(empty_model)

Η τιμή που προβλέπεται είναι:

✓ Ο μέσος αριθμός ωρών άσκησης του δείγματος

✓ Η ίδια για κάθε φοιτητή (περίπου 9 ώρες)

✓ Δεν εξαρτάται από χαρακτηριστικά του φοιτητή (Gender, Height, κλπ.)

Αυτό συμβαίνει επειδή το κενό μοντέλο δεν έχει ανεξάρτητες μεταβλητές - χρησιμοποιεί μόνο τη συνολική μέση τιμή ως πρόβλεψη για όλους!

3. Το να έχεις χαμηλό καρδιακό ρυθμό ηρεμίας (καταγεγραμμένο για κάθε φοιτητή στη μεταβλητή Pulse) υποτίθεται ότι είναι ένδειξη καλής καρδιαγγειακής υγείας. Ας υποθέσουμε ότι θέλουμε να δημιουργήσουμε τρεις ομάδες της Pulse: 1 = low, 2 = medium, και 3 = high. Ποια από τις παρακάτω γραμμές κώδικα θα το έκανε αυτό και θα αποθήκευε τις τιμές σε μια νέα μεταβλητή που ονομάζεται Pulse3Group;

Pulse3Group <- ntile(3)StudentSurvey$Pulse3Group <- ntile(StudentSurvey$Pulse, 2)StudentSurvey$Pulse3Group <- ntile(StudentSurvey$Pulse, 3)StudentSurvey <- ntile(StudentSurvey$Pulse3Group)

Επεξήγηση

Σωστή απάντηση: Γ - StudentSurvey$Pulse3Group <- ntile(StudentSurvey$Pulse, 3)

Τι κάνει η συνάρτηση ntile();

Η συνάρτηση ntile() από το πακέτο dplyr διαιρεί μια μεταβλητή σε n ομάδες ίσου μεγέθους βάσει εκατοστημορίων.

Σύνταξη:

ntile(x, n)

Όπου:

x = η μεταβλητή που θέλουμε να διαιρέσουμε σε ομάδες
n = ο αριθμός των ομάδων

Τι επιστρέφει: - Ένα διάνυσμα με αριθμούς 1, 2, …, n που αντιπροσωπεύουν την ομάδα κάθε παρατήρησης

Ανάλυση της σωστής απάντησης:

StudentSurvey$Pulse3Group <- ntile(StudentSurvey$Pulse, 3)

Τι κάνει αυτός ο κώδικας;

StudentSurvey$Pulse: Επιλέγει τη μεταβλητή Pulse από το πλαίσιο δεδομένων StudentSurvey
ntile(..., 3): Διαιρεί την Pulse σε 3 ομάδες:
- Ομάδα 1: Χαμηλό Pulse (low) - κάτω 33%
- Ομάδα 2: Μέτριο Pulse (medium) - μεσαίο 33%
- Ομάδα 3: Υψηλό Pulse (high) - πάνω 33%
StudentSurvey$Pulse3Group <-: Αποθηκεύει το αποτέλεσμα σε μια νέα μεταβλητή Pulse3Group στο πλαίσιο δεδομένων StudentSurvey

Γιατί οι άλλες είναι λάθος;

Α. Pulse3Group <- ntile(3) - ΛΑΘΟΣ

Προβλήματα:

Λείπει το πρώτο όρισμα:
- Η ntile() χρειάζεται 2 ορίσματα: τη μεταβλητή και τον αριθμό ομάδων
- Αυτός ο κώδικας επιστρέφει μόνο τον αριθμό 3
Δεν αναφέρεται το πλαίσιο δεδομένων:
- Δεν ορίζει πού να αποθηκευτεί η νέα μεταβλητή
- Δημιουργεί ένα αντικείμενο στο περιβάλλον της R, όχι στο StudentSurvey
Θα δώσει σφάλμα:

Pulse3Group <- ntile(3)
# Error: argument "x" is missing, with no default

Β. StudentSurvey$Pulse3Group <- ntile(StudentSurvey$Pulse, 2) - ΛΑΘΟΣ

Πρόβλημα:

Χρησιμοποιεί n = 2 αντί για n = 3
Αυτό δημιουργεί 2 ομάδες (low και high), όχι 3 ομάδες (low, medium, high)

Αποτέλεσμα:

StudentSurvey$Pulse3Group <- ntile(StudentSurvey$Pulse, 2)
table(StudentSurvey$Pulse3Group)
#   1   2
# 181 181

# Μόνο 2 ομάδες, όχι 3!

Δ. StudentSurvey <- ntile(StudentSurvey$Pulse3Group) - ΛΑΘΟΣ

Προβλήματα:

Λανθασμένη σειρά ορισμάτων:
- Προσπαθεί να χρησιμοποιήσει Pulse3Group (που δεν υπάρχει ακόμα)
- Λείπει το δεύτερο όρισμα (αριθμός ομάδων)
Αντικαθιστά ολόκληρο το πλαίσιο δεδομένων:
- StudentSurvey <- θα αντικαταστήσει ολόκληρο το data frame
- Θα χάσουμε όλες τις άλλες μεταβλητές!
Θα δώσει σφάλμα:

StudentSurvey <- ntile(StudentSurvey$Pulse3Group)
# Επειδή δεν υπάρχει ακόμα

Σύγκριση όλων των επιλογών:

Επιλογή	Κώδικας	Σωστό;	Πρόβλημα
Α	`Pulse3Group <- ntile(3)`	✗	Λείπει η μεταβλητή x
Β	`StudentSurvey$Pulse3Group <- ntile(StudentSurvey$Pulse, 2)`	✗	Δημιουργεί 2 ομάδες, όχι 3
Γ	`StudentSurvey$Pulse3Group <- ntile(StudentSurvey$Pulse, 3)`	✓	Τέλειο!
Δ	`StudentSurvey <- ntile(StudentSurvey$Pulse3Group)`	✗	Λάθος σύνταξη, αντικαθιστά το πλαίσιο δεδομένων

Πλήρες παράδειγμα στην R:

# Δημιουργούμε 3 ομάδες βάσει Pulse
StudentSurvey$Pulse3Group <- ntile(StudentSurvey$Pulse, 3)

# Ελέγχουμε το αποτέλεσμα
table(StudentSurvey$Pulse3Group)
#   1   2   3
# 121 121 120

# Βλέπουμε το εύρος Pulse σε κάθε ομάδα
StudentSurvey %>%
  group_by(Pulse3Group) %>%
  summarise(
    min_pulse = min(Pulse, na.rm = TRUE),
    max_pulse = max(Pulse, na.rm = TRUE),
    mean_pulse = mean(Pulse, na.rm = TRUE)
  )

Αποτέλεσμα:

  Pulse3Group min_pulse max_pulse mean_pulse
1           1        35        65       56.9
2           2        65        74       69.3
3           3        74       130       82.6

Εναλλακτικός τρόπος με ετικέτες:

Αν θέλουμε να χρησιμοποιήσουμε ετικέτες low, medium, high αντί για 1, 2, 3:

# Δημιουργία με αριθμούς
StudentSurvey$Pulse3Group <- ntile(StudentSurvey$Pulse, 3)

# Μετατροπή σε ετικέτες
StudentSurvey$Pulse3Group <- factor(
  StudentSurvey$Pulse3Group,
  levels = c(1, 2, 3),
  labels = c("low", "medium", "high")
)

# Ή όλα μαζί με mutate και case_when:
library(dplyr)
StudentSurvey <- StudentSurvey %>%
  mutate(
    Pulse3Group = ntile(Pulse, 3),
    Pulse3Group = case_when(
      Pulse3Group == 1 ~ "low",
      Pulse3Group == 2 ~ "medium",
      Pulse3Group == 3 ~ "high"
    )
  )

Σημαντικές παρατηρήσεις:

1. Ίσα μεγέθη ομάδων:

Η ntile() προσπαθεί να δημιουργήσει ομάδες με περίπου ίσο πλήθος παρατηρήσεων
Όχι ομάδες με ίσα εύρη τιμών (π.χ., 0-33, 34-66, 67-100)

2. Χειρισμός ισοπαλιών (ties):

Αν πολλοί φοιτητές έχουν την ίδια τιμή Pulse, μπορεί να μην είναι ακριβώς 1/3 σε κάθε ομάδα

3. Χαμηλή τιμή Pulse = Καλή υγεία:

Ομάδα 1 (χαμηλή τιμή Pulse) = καλύτερη καρδιαγγειακή υγεία
Ομάδα 3 (υψηλή τιμή Pulse) = χειρότερη καρδιαγγειακή υγεία

Συμπέρασμα:

Ο σωστός κώδικας είναι:

StudentSurvey$Pulse3Group <- ntile(StudentSurvey$Pulse, 3)

Αυτός ο κώδικας:

✓ Επιλέγει τη σωστή μεταβλητή: StudentSurvey$Pulse

✓ Δημιουργεί 3 ομάδες: n = 3

✓ Αποθηκεύει το αποτέλεσμα στη νέα μεταβλητή: StudentSurvey$Pulse3Group

✓ Διατηρεί το πλαίσιο δεδομένων StudentSurvey με όλες τις άλλες μεταβλητές

✓ Δημιουργεί 3 ομάδες περίπου ίσου μεγέθους που αντιπροσωπεύουν low (1), medium (2), και high (3) Pulse

4. Ποια από αυτές τις παρακάτω εντολές θα μπορούσε να χρησιμοποιηθεί για να αναπαραστήσει διαγραμματικά τη σχέση μεταξύ της Exercise και της Pulse3Group;

gf_boxplot(Exercise ~ Pulse3Group, data = StudentSurvey)gf_histogram(~ Exercise, data = StudentSurvey) %>% gf_facet_grid(Pulse3Group ~ .)gf_point(Exercise ~ Pulse3Group, data = StudentSurvey)Όλα τα παραπάνω

Επεξήγηση

Σωστή απάντηση: Δ - Όλα τα παραπάνω

Και οι τρεις επιλογές μπορούν να απεικονίσουν τη σχέση μεταξύ της Exercise (συνεχής μεταβλητή) και της Pulse3Group (ποιοτική μεταβλητή με 3 επίπεδα).

Γιατί όλα τα παραπάνω είναι σωστά;

Κοινό χαρακτηριστικό:

Και οι τρεις μέθοδοι:

✓ Απεικονίζουν τη σχέση μεταξύ της Exercise (ποσοτική Y) και της Pulse3Group (ποιοτική X)

✓ Επιτρέπουν σύγκριση των τιμών της Exercise μεταξύ των τριών ομάδων της Pulse

✓ Χρησιμοποιούν τη σωστή σύνταξη της ggformula(): Y ~ X, data = ...

✓ Είναι κατάλληλες για αυτό το είδος δεδομένων (ποσοτική vs ποιοτική)

Διαφορετικές οπτικές γωνίες:

Boxplot: Συνοπτική σύγκριση (καλύτερο για μια γρήγορη σύγκριση)
Ιστόγραμμα: Λεπτομερής κατανομή (καλύτερο για να δούμε το σχήμα της κατανομής)
Διάγραμμα διασποράς: Ατομικά δεδομένα (καλύτερα για ατομικές παρατηρήσεις)

Πότε χρησιμοποιούμε κάθε διάγραμμα;

Χρησιμοποιούμε Boxplot όταν:

Θέλουμε γρήγορη σύγκριση μεταξύ ομάδων
Ενδιαφερόμαστε για διάμεσο και τεταρτημόρια
Θέλουμε να εντοπίσουμε ακραίες τιμές
Έχουμε πολλές ομάδες προς σύγκριση

Χρησιμοποιούμε Διαιρεμένο Ιστόγραμμα όταν:

Θέλουμε να δούμε το σχήμα της κατανομής (συμμετρία, ασυμμετρία)
Ενδιαφερόμαστε για συχνότητες ή πλήθη
Θέλουμε να εξετάσουμε λεπτομερώς την κατανομή σε κάθε ομάδα

Χρησιμοποιούμε Διάγραμμα Διασποράς όταν:

Θέλουμε να δούμε κάθε ατομική παρατήρηση
Ενδιαφερόμαστε για διασπορά εντός ομάδων
Θέλουμε να εντοπίσουμε μοτίβα ή συστάδες παρατηρήσεων
Θέλουμε να προσθέσουμε επιπλέον πληροφορίες (π.χ., χρώμα ανά Gender)

Συνδυασμός μεθόδων

Συχνά, η καλύτερη προσέγγιση είναι να συνδυάσουμε πολλαπλές οπτικοποιήσεις:

# Συνδυασμός boxplot + jitter
gf_boxplot(Exercise ~ Pulse3Group, data = StudentSurvey,
           fill = "lightblue", alpha = 0.5) %>%
  gf_jitter(width = 0.1, height = 0, alpha = 0.3)

Αυτό δίνει:

Συνοπτική πληροφορία (από το boxplot)
Ατομικά δεδομένα (από τα σημεία)

Συμπέρασμα

Και οι τρεις μέθοδοι οπτικοποίησης είναι σωστές για την αναπαράσταση της σχέσης μεταξύ της Exercise και της Pulse3Group:

✓ Boxplot - Συνοπτική, εύκολη σύγκριση

✓ Διαιρεμένο Ιστόγραμμα - Λεπτομερής κατανομή

✓ Διάγραμμα Διασποράς - Ατομικές παρατηρήσεις

Η επιλογή εξαρτάται από:

Το ερώτημα που θέλουμε να απαντήσουμε
Το κοινό που απευθυνόμαστε
Το επίπεδο λεπτομέρειας που χρειαζόμαστε

Συνήθως, η χρήση πολλαπλών οπτικοποιήσεων παρέχει την πιο πλήρη εικόνα των δεδομένων!

5. Επιθυμούμε να εξηγήσουμε τη μεταβλητότητα στις ώρες άσκησης την εβδομάδα (Exercise) με την ομαδοποιημένη καρδιαγγειακή υγεία (Pulse3Group).

Υποθέτουμε ότι το μοντέλο μας είναι το εξής:

Exercise = Pulse3Group + άλλα πράγματα

Αν γράψουμε το μοντέλο σε σημειογραφία GLM, ποια εξίσωση αντιπροσωπεύει αυτό το μοντέλο της Pulse3Group;

$Y_i = b_0 + e_i$$Y_i = b_0 + b_1X_i + e_i$$Y_i = b_0 + b_1X_{1i} + b_2X_{2i} + e_i$$\text{Pulse3Group}_i = b_0 + b_1\text{Exercise}_i + e_i$

Επεξήγηση

Σωστή απάντηση: Γ - $Y_i = b_0 + b_1X_{1i} + b_2X_{2i} + e_i$

Κατανόηση του προβλήματος:

Έχουμε:

Εξαρτημένη μεταβλητή (Y): Exercise (ποσοτική)
Ανεξάρτητη μεταβλητή (X): Pulse3Group (ποιοτική με 3 κατηγορίες: low, medium, high)

Πρόβλημα: Πώς εκφράζουμε μια ποιοτική μεταβλητή με 3 επίπεδα σε σημειογραφία GLM;

Κωδικοποίηση ποιοτικής μεταβλητής με 3 επίπεδα

Μια ποιοτική μεταβλητή με k επίπεδα χρειάζεται k - 1 ψευδομεταβλητές (dummy variables).

Για Pulse3Group με 3 επίπεδα:

Χρειαζόμαστε 3 - 1 = 2 ψευδομεταβλητές

Κωδικοποίηση:

Ας υποθέσουμε ότι η ομάδα αναφοράς είναι low:

Pulse3Group	$X_{1i}$	$X_{2i}$	Περιγραφή
`low` (1)	0	0	Ομάδα αναφοράς
`medium` (2)	1	0	$X_1$ = 1 για `medium`
`high` (3)	0	1	$X_2$ = 1 για `high`

Μοντέλο GLM:

\[Y_i = b_0 + b_1X_{1i} + b_2X_{2i} + e_i\]

Όπου:

$Y_i$ = Exercise για φοιτητή $i$
$X_{1i}$ = 1 αν medium, 0 διαφορετικά
$X_{2i}$ = 1 αν high, 0 διαφορετικά
$b_0$ = Μέσος όρος Exercise για low (ομάδα αναφοράς)
$b_1$ = Διαφορά: medium - low
$b_2$ = Διαφορά: high - low
$e_i$ = Υπόλοιπο (residual)

Πώς λειτουργεί το μοντέλο για κάθε ομάδα;

Για Low Pulse (ομάδα αναφοράς):

$X_{1i} = 0$, $X_{2i} = 0$

\[Y_i = b_0 + b_1(0) + b_2(0) + e_i = b_0 + e_i\]

μέσος όρος της low $= b_0$

Για Medium Pulse:

$X_{1i} = 1$, $X_{2i} = 0$

\[Y_i = b_0 + b_1(1) + b_2(0) + e_i = b_0 + b_1 + e_i\]

μέσος όρος της medium $= b_0 + b_1$

Για High Pulse:

$X_{1i} = 0$, $X_{2i} = 1$

\[Y_i = b_0 + b_1(0) + b_2(1) + e_i = b_0 + b_2 + e_i\]

μέσος όρος της high $= b_0 + b_2$

Ερμηνεία των εκτιμήσεων παραμέτρων

Εκτίμηση	Τι αντιπροσωπεύει	Ερμηνεία
$b_0$	Μέσος όρος `Exercise` για χαμηλό καρδιακό ρυθμό ηρεμίας, `low`	ομάδα αναφοράς (10.3802 ώρες/εβδομάδα)
$b_1$	Διαφορά Medium - Low	Πόσο λιγότερο ασκούνται αυτοί που έχουν μεσαίο καρδιακό ρυθμό ηρεμίας, `medium` (-0.8468 ώρες)
$b_2$	Διαφορά High - Low	Πόσο λιγότερο ασκούνται αυτοί που έχουν υψηλό καρδιακό ρυθμό ηρεμίας, `high` (-3.1427 ώρες)

Παράδειγμα αποτελεσμάτων:

lm(Exercise ~ Pulse3Group, data = StudentSurvey)

Coefficients:
                  Estimate
(Intercept)          10.3802  # b₀: Μέσος όρος για Low
Pulse3GroupMedium    -0.8468  # b₁: Medium - Low
Pulse3GroupHigh      -3.1427  # b₂: High - Low

Ερμηνεία: - Low Pulse: Μέσος όρος Exercise = 10.38 ώρες

Medium Pulse: Μέσος όρος Exercise = 10.38 - 0.8468 = 9.53 ώρες
High Pulse: Μέσος όρος Exercise = 10.38 - 3.14 = 7.24 ώρες

Γιατί οι άλλες είναι λάθος;

Α. $Y_i = b_0 + e_i$ - ΛΑΘΟΣ

Αυτό είναι το κενό μοντέλο (empty model)
Δεν περιλαμβάνει καμία ανεξάρτητη μεταβλητή
Δεν εξηγεί τη μεταβλητότητα με την Pulse3Group

Στην R:

lm(Exercise ~ NULL, data = StudentSurvey)  # ή lm(Exercise ~ 1)

Β. $Y_i = b_0 + b_1X_i + e_i$ - ΛΑΘΟΣ

Αυτό είναι για μια ανεξάρτητη μεταβλητή με 2 επίπεδα (μία ψευδομεταβλητή)
Η Pulse3Group έχει 3 επίπεδα, όχι 2
Χρειαζόμαστε 2 ψευδομεταβλητές, όχι 1

Παράδειγμα με 2 επίπεδα:

# Αν είχαμε μόνο 2 ομάδες (π.χ., Low vs High):
lm(Exercise ~ Gender, data = StudentSurvey)  # M vs F (2 επίπεδα)
# Μοντέλο: Y = b₀ + b₁X₁ + e

Δ. $\text{Pulse3Group}_i = b_0 + b_1\text{Exercise}_i + e_i$ - ΛΑΘΟΣ

Προβλήματα:

Λάθος εξαρτημένη μεταβλητή:
- Το μοντέλο προβλέπει την Pulse3Group (ποιοτική), όχι την Exercise (ποσοτική)
- Θέλουμε να εξηγήσουμε την Exercise, όχι την Pulse3Group
Λάθος κατεύθυνση:
- Η ερώτηση λέει: “εξηγούμε την Exercise με την Pulse3Group”
- Αυτό το μοντέλο κάνει το αντίθετο

Γενική εξίσωση για k επίπεδα

Για ποιοτική μεταβλητή με k επίπεδα:

Αριθμός ψευδομεταβλητών: k - 1

Μοντέλο GLM:

\[Y_i = b_0 + b_1X_{1i} + b_2X_{2i} + \cdots + b_{k-1}X_{(k-1)i} + e_i\]

Παραδείγματα:

Αριθμός επιπέδων (k)	Ψευδομεταβλητές (k-1)	Μοντέλο
2	1	$Y_i = b_0 + b_1X_{1i} + e_i$
3	2	$Y_i = b_0 + b_1X_{1i} + b_2X_{2i} + e_i$
4	3	$Y_i = b_0 + b_1X_{1i} + b_2X_{2i} + b_3X_{3i} + e_i$

Συμπέρασμα: Φοιτητές με χαμηλότερο καρδιακό ρυθμό ηρεμίας (καλύτερη καρδιαγγειακή υγεία) τείνουν να ασκούνται περισσότερο!

Επαλήθευση των μέσων όρων

# Υπολογισμός μέσων όρων ανά ομάδα
StudentSurvey %>%
  group_by(Pulse3Group) %>%
  summarise(mean_exercise = mean(Exercise, na.rm = TRUE))

  Pulse3Group mean_exercise
1 Low              10.4  ← b₀
2 Medium            9.53  ← b₀ + b₁
3 High              7.24  ← b₀ + b₂

Οι εκτιμήσεις του μοντέλου ταιριάζουν ακριβώς με τους μέσους όρους των ομάδων! ✓

Συμπέρασμα

Για να εξηγήσουμε την Exercise με την Pulse3Group (3 επίπεδα), το σωστό μοντέλο GLM είναι:

\[Y_i = b_0 + b_1X_{1i} + b_2X_{2i} + e_i\]

Επειδή:

✓ Η Pulse3Group έχει 3 επίπεδα → χρειαζόμαστε 2 ψευδομεταβλητές

✓ $X_{1i}$ = 1 για Medium, 0 διαφορετικά

✓ $X_{2i}$ = 1 για High, 0 διαφορετικά

✓ $b_0$ = μέσος όρος για Low (ομάδα αναφοράς)

✓ $b_1$ = διαφορά Medium - Low

✓ $b_2$ = διαφορά High - Low

✓ Το μοντέλο εξηγεί τη μεταβλητότητα της Exercise με βάση την καρδιαγγειακή υγεία

6. Επιθυμούμε να εξηγήσουμε τη μεταβλητότητα στις ώρες άσκησης την εβδομάδα (Exercise) με την ομαδοποιημένη καρδιαγγειακή υγεία (Pulse3Group).

Υποθέτουμε ότι το μοντέλο μας είναι το εξής:

Exercise = Pulse3Group + άλλα πράγματα

Αν γράψουμε το μοντέλο σε σημειογραφία GLM, τι αντιπροσωπεύει το $Y_i$;

Η τιμή των ωρών άσκησης για κάθε άτομοΟ μέσος όρος των ωρών άσκησης για όλους τους συμμετέχοντεςΗ απόκλιση μεταξύ των ωρών άσκησης κάθε ατόμου και του μέσου όρου των ωρών άσκησης όλων των συμμετεχόντωνΜπορεί να είναι οποιοδήποτε από τα παραπάνω, ανάλογα με την ερμηνεία που δίνουμε.

Επεξήγηση

Σωστή απάντηση: Α - Η τιμή της Exercise για κάθε άτομο

Το Μοντέλο GLM:

Για το μοντέλο Exercise ~ Pulse3Group, η σημειογραφία GLM είναι:

\[Y_i = b_0 + b_1X_{1i} + b_2X_{2i} + e_i\]

Τι αντιπροσωπεύει το $Y_i$;

Το $Y_i$ είναι η παρατηρούμενη τιμή της εξαρτημένης μεταβλητής για το άτομο $i$.

Στο πλαίσιο μας:

\[Y_i = \text{Exercise}_i\]

«Το $Y_i$ είναι ο πραγματικός αριθμός ωρών άσκησης την εβδομάδα για τον φοιτητή $i$.»

Ανατομία του μοντέλου GLM

Το πλήρες μοντέλο:

\[Y_i = b_0 + b_1X_{1i} + b_2X_{2i} + e_i\]

Κάθε όρος:

Σύμβολο	Τι αντιπροσωπεύει	Παράδειγμα
$Y_i$	Παρατηρούμενη τιμή της `Exercise` για άτομο $i$	10 ώρες
$b_0$	Μέσος όρος `Exercise` για ομάδα αναφοράς (Low)	10.38 ώρες
$b_1$	Διαφορά Medium - Low	-0.85 ώρες
$X_{1i}$	1 αν άτομο $i$ είναι Medium, 0 διαφορετικά	0 ή 1
$b_2$	Διαφορά High - Low	-3.14 ώρες
$X_{2i}$	1 αν άτομο $i$ είναι High, 0 διαφορετικά	0 ή 1
$e_i$	Υπόλοιπο (residual) για άτομο $i$	-0.38 ώρες

Γιατί οι άλλες είναι λάθος;

Β. “Ο μέσος όρος της Exercise για όλους τους συμμετέχοντες” - ΛΑΘΟΣ

Ο μέσος όρος όλων των συμμετεχόντων συμβολίζεται με $\bar{Y}$, όχι $Y_i$

Διαφορά:

Σύμβολο	Τι είναι	Τιμή	Σημείωση
$Y_i$	Ατομική τιμή	Διαφορετική για κάθε $i$	Π.χ., $Y_1=10$, $Y_2=4$
$\bar{Y}$	Μέσος όρος όλων	Μία τιμή για όλους	$\bar{Y}=10.38$

Γ. “Η απόκλιση μεταξύ της Exercise κάθε ατόμου και του μέσου όρου της Exercise” - ΛΑΘΟΣ

Το υπόλοιπο συμβολίζεται με $e_i$, όχι $Y_i$

Δ. “Μπορεί να είναι οποιοδήποτε από τα παραπάνω” - ΛΑΘΟΣ

Το $Y_i$ έχει μία και μόνη ερμηνεία στη σημειογραφία GLM
Πάντα αντιπροσωπεύει την παρατηρούμενη τιμή της εξαρτημένης μεταβλητής
Δεν αλλάζει ανάλογα με το πλαίσιο ή την ερμηνεία

Συμπέρασμα

Στο μοντέλο GLM:

\[Y_i = b_0 + b_1X_{1i} + b_2X_{2i} + e_i\]

Το $Y_i$ αντιπροσωπεύει:

Την παρατηρούμενη τιμή της Exercise για το άτομο $i$

Αυτό σημαίνει:

✓ Είναι η πραγματική μέτρηση από τα δεδομένα

✓ Είναι διαφορετική για κάθε άτομο

✓ Είναι το αριστερό μέρος της εξίσωσης - αυτό που προσπαθούμε να εξηγήσουμε

✓ Για παράδειγμα: $Y_1 = 10$ σημαίνει “ο φοιτητής 1 ασκείται 10 ώρες την εβδομάδα”

Αυτή είναι η μόνη σωστή ερμηνεία του $Y_i$ στη σημειογραφία GLM - δεν αλλάζει ανάλογα με το πλαίσιο!

7. Το παρακάτω διάγραμμα δείχνει τη σχέση μεταξύ της μεταβλητής Exercise και της Pulse3Group.

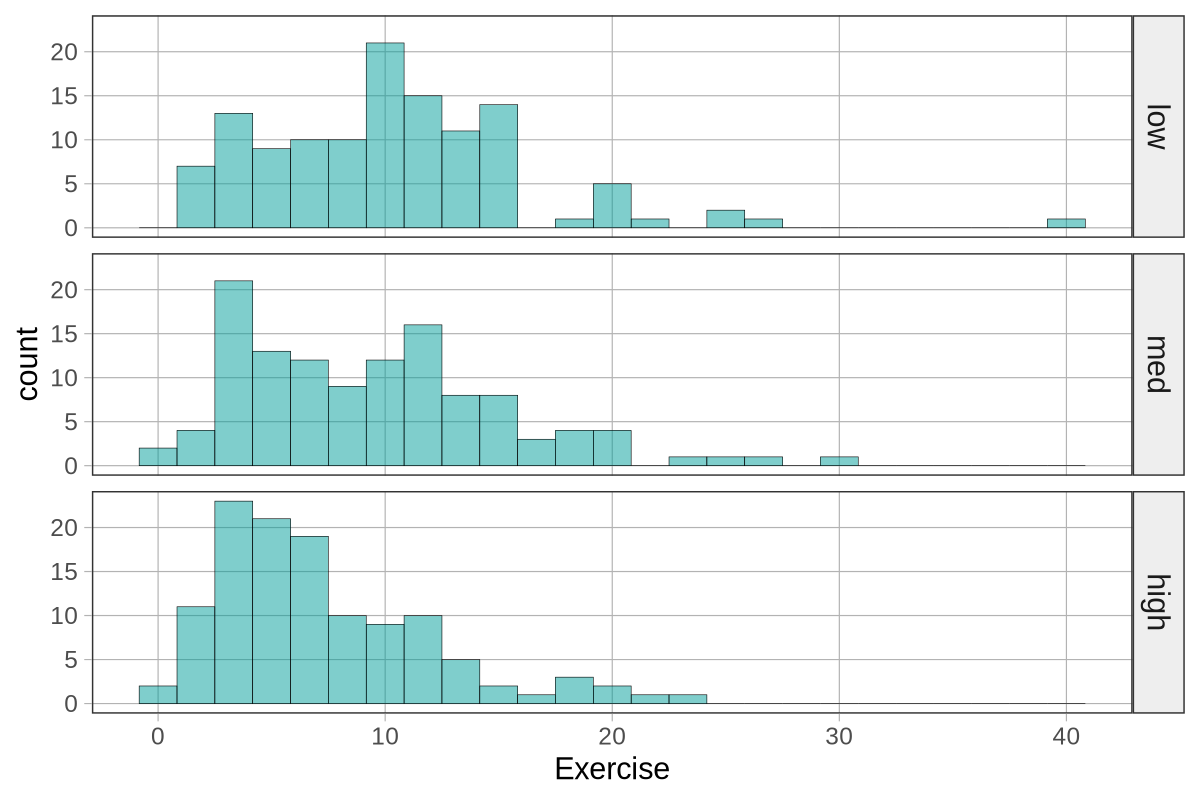
Όταν η Pulse3Group συμπεριλαμβάνεται ως ανεξάρτητη μεταβλητή στο μοντέλο πρόβλεψης της Exercise, προκύπτουν τα εξής αποτελέσματα από την εντολή lm(Exercise ~ Pulse3Group, data = StudentSurvey):

Call:
lm(formula = Exercise ~ Pulse3Group, data = StudentSurvey)

Coefficients:
       (Intercept)  Pulse3Groupmed  Pulse3Grouphigh  
           10.3802         -0.8468          -3.1427

Πώς ερμηνεύετε την τιμή -3.14;

Αντιπροσωπεύει τη διαφορά στο μέσο όρο ωρών άσκησης για άτομα με υψηλό σε σύγκριση με άτομα με χαμηλό καρδιακό ρυθμό ηρεμίας.Αντιπροσωπεύει το μέσο όρο ωρών άσκησης την εβδομάδα για την ομάδα υψηλού καρδιακού ρυθμού ηρεμίας.Είναι ο αριθμός των ατόμων, κατά μέσο όρο, που έχουν υψηλό καρδιακό ρυθμό ηρεμίας.Αντιπροσωπεύει τη διαφορά στο μέσο αριθμό ωρών άσκησης για άτομα με υψηλό σε σχέση με άτομα με μέτριο καρδιακό ρυθμό ηρεμίας.

Επεξήγηση

Σωστή απάντηση: Α - Αντιπροσωπεύει τη διαφορά στο μέσο όρο ωρών άσκησης για άτομα με υψηλό σε σύγκριση με άτομα με χαμηλό καρδιακό ρυθμό ηρεμίας.

Ανάλυση του μοντέλου:

Coefficients:
       (Intercept)  Pulse3Groupmed  Pulse3Grouphigh  
           10.3802         -0.8468          -3.1427

Μοντέλο GLM:

\[\text{Exercise}_i = b_0 + b_1 \cdot \text{Medium}_i + b_2 \cdot \text{High}_i + e_i\]

Όπου: - $b_0 = 10.38$ = Μέσος όρος Exercise για ομάδα low (ομάδα αναφοράς)

$b_1 = -0.85$ = Διαφορά: medium - low
$b_2 = -3.14$ = Διαφορά: high - low ← ΑΥΤΟ ΕΡΜΗΝΕΥΟΥΜΕ

Τι σημαίνει το $b_2 = -3.14$;

Το $b_2 = -3.14$ είναι ο συντελεστής για την ψευδομεταβλητή Pulse3Grouphigh.

Ερμηνεία: Άτομα στην ομάδα high ασκούνται κατά μέσο όρο 3.14 ώρες λιγότερο την εβδομάδα σε σχέση με άτομα στην ομάδα low (ομάδα αναφοράς).

Υπολογισμός μέσων όρων για κάθε ομάδα

Low Pulse (ομάδα αναφοράς):

\[b_0 = 10.38 \text{ ώρες}\]

Medium Pulse:

\[b_0 + b_1 = 10.38 + (-0.85) = 9.53 \text{ ώρες}\]

High Pulse:

\[b_0 + b_2 = 10.38 + (-3.14) = 7.24 \text{ ώρες}\]

Επαλήθευση της ερμηνείας

Διαφορά High - Low:

\[7.24 - 10.38 = -3.14\] ✓

Αυτό επιβεβαιώνει ότι το $b_2 = -3.14$ είναι η διαφορά μεταξύ high και low!

Γιατί οι άλλες είναι λάθος;

Β. “Ο μέσος όρος ωρών άσκησης για την ομάδα υψηλού καρδιακού ρυθμού ηρεμίας” - ΛΑΘΟΣ

Ο μέσος για την ομάδα high είναι: $b_0 + b_2 = 10.38 + (-3.14) = 7.24$ ώρες
Το $b_2 = -3.14$ δεν είναι ο μέσος όρος - είναι η διαφορά

Σύγκριση:

Τι	Τιμή	Τι αντιπροσωπεύει
$b_2$	-3.14	Διαφορά (High - Low)
$b_0 + b_2$	7.24	Μέσος όρος για High

Γ. “Ο αριθμός των ατόμων που έχουν υψηλό καρδιακό ρυθμό” - ΛΑΘΟΣ

Οι συντελεστές του μοντέλου αφορούν ώρες άσκησης, όχι πλήθος ατόμων
Ο αριθμός ατόμων στην ομάδα high είναι 120 (περίοπου 1/3 των 362)
Το -3.14 δεν έχει καμία σχέση με το πλήθος

Αν θέλαμε το πλήθος:

table(StudentSurvey$Pulse3Group)
# Low  Medium  High
# 121     121   120

Δ. “Η διαφορά σε σχέση με την ομάδα μέτριου καρδιακού ρυθμού ηρεμίας” - ΛΑΘΟΣ

Το $b_2 = -3.14$ αντιπροσωπεύει τη διαφορά High - Low, όχι High - Medium

Υπολογισμός High - Medium:

\[= (b_0 + b_2) - (b_0 + b_1)\]

\[= b_2 - b_1\]

\[= -3.14 - (-0.85)\]

\[= -3.14 + 0.85\]

\[= -2.29 \text{ ώρες}\]

Η διαφορά High - Medium είναι -2.29 ώρες, όχι -3.14!

Πίνακας όλων των διαφορών

Σύγκριση	Τύπος	Υπολογισμός	Τιμή
Medium - Low	$b_1$	$-0.85$	-0.85 ώρες
High - Low	$b_2$	$-3.14$	-3.14 ώρες ← ΑΥΤΟ!
High - Medium	$b_2 - b_1$	$-3.14 - (-0.85)$	-2.29 ώρες

Πλήρης ερμηνεία του μοντέλου

Exercise_i = 10.38 - 0.85·Medium_i - 3.14·High_i + e_i

Ερμηνείες:

$b_0 = 10.38$: > «Άτομα με χαμηλό καρδιακό ρυθμό (καλή καρδιαγγειακή υγεία) ασκούνται κατά μέσο όρο 10.38 ώρες την εβδομάδα.»
$b_1 = -0.85$: > «Άτομα με μέτριο καρδιακό ρυθμό ασκούνται κατά μέσο όρο 0.85 ώρες λιγότερο την εβδομάδα σε σχέση με άτομα με χαμηλό καρδιακό ρυθμό.»
$b_2 = -3.14$: ← ΑΥΤΟ ΕΡΜΗΝΕΥΟΥΜΕ > «Άτομα με υψηλό καρδιακό ρυθμό (χειρότερη καρδιαγγειακή υγεία) ασκούνται κατά μέσο όρο 3.14 ώρες λιγότερο την εβδομάδα σε σχέση με άτομα με χαμηλό καρδιακό ρυθμό.»

Επαλήθευση με την R

# Μέσοι όροι ανά ομάδα
StudentSurvey %>%
  group_by(Pulse3Group) %>%
  summarise(mean_exercise = mean(Exercise, na.rm = TRUE))

  Pulse3Group mean_exercise
1 low              10.38     ← b₀
2 med               9.53     ← b₀ + b₁ = 10.38 - 0.85
3 high              7.24     ← b₀ + b₂ = 10.38 - 3.14

Ουσιαστική ερμηνεία

Τι μας λέει το $b_2 = -3.14$;

Κατεύθυνση: Το αρνητικό πρόσημο σημαίνει ότι η ομάδα high ασκείται λιγότερο
Μέγεθος: Η διαφορά είναι 3.14 ώρες - αρκετά μεγάλη (περίπου 30% μείωση)
Σύγκριση: Η διαφορά είναι σε σχέση με την ομάδα αναφοράς (low pulse)
Αιτία; Πιθανώς:
- Άτομα που ασκούνται περισσότερο έχουν χαμηλότερο καρδιακό ρυθμό (καλύτερη φυσική κατάσταση)
- Ή άτομα με χαμηλό καρδιακό ρυθμό είναι πιο πιθανό να ασκούνται
- (Το μοντέλο δεν αποδεικνύει αιτιότητα!)

Συμπέρασμα

Το $b_2 = -3.14$ (συντελεστής του Pulse3Grouphigh) ερμηνεύεται ως:

«Η διαφορά στον μέσο αριθμό ωρών άσκησης για άτομα στην ομάδα υψηλού καρδιακού ρυθμού σε σχέση με την ομάδα χαμηλού καρδιακού ρυθμού.»

Συγκεκριμένα:

✓ Άτομα στην ομάδα high ασκούνται κατά μέσο όρο 3.14 ώρες λιγότερο την εβδομάδα

✓ Η σύγκριση είναι με την ομάδα αναφοράς (low)

✓ Αυτό είναι μια διαφορά μέσων, όχι ο ίδιος ο μέσος

✓ Το αρνητικό πρόσημο δείχνει ότι η ομάδα high έχει χαμηλότερο μέσο όρο στην Exercise

✓ Αυτό ταιριάζει με την ιδέα ότι καλύτερη καρδιαγγειακή υγεία (χαμηλότερος ρυθμός ηρεμίας) σχετίζεται με περισσότερη άσκηση

8. Στην εξίσωση $Y_i = 10.38 - 0.85X_{1i} - 3.14X_{2i} + e_i$, τι αντιπροσωπεύει το $X_{1i}$;

Μια μεταβλητή που καταγράφει τις ώρες άσκησης κάθε εβδομάδα.Μια μεταβλητή που παίρνει την τιμή 1 αν το άτομο ανήκει στην ομάδα με μέτριο καρδιακό ρυθμό ηρεμίας και 0 διαφορετικά.Μια μεταβλητή που παίρνει την τιμή 1 για άτομα με υψηλό καρδιακό ρυθμό ηρεμίας και 0 διαφορετικά.Την τιμή πρόβλεψης των ωρών άσκησης για άτομα με χαμηλό καρδιακό ρυθμό ηρεμίας.

Επεξήγηση

Σωστή απάντηση: Β — Η $X_{1i}$ παίρνει την τιμή 1 αν το άτομο ανήκει στην ομάδα με μέτριο καρδιακό ρυθμό ηρεμίας (Medium pulse group) και 0 διαφορετικά.

Ανάλυση του μοντέλου

Το μοντέλο είναι:

\[Y_i = 10.38 - 0.85X_{1i} - 3.14X_{2i} + e_i\]

Η μεταβλητή Pulse3Group έχει τρία επίπεδα (low, medium, high) και γι’ αυτό χρειάζονται δύο ψευδομεταβλητές:

$X_{1i}$ → δείχνει αν το άτομο ανήκει στην ομάδα medium
$X_{2i}$ → δείχνει αν το άτομο ανήκει στην ομάδα high
Η ομάδα low είναι η ομάδα αναφοράς (reference group)

Τι είναι το $X_{1i}$

Το $X_{1i}$ είναι μια ψευδομεταβλητή που παίρνει τις τιμές:

\[X_{1i} = \begin{cases} 1 & \text{αν το άτομο } i \text{ έχει μέτριο καρδιακό ρυθμό ηρεμίας} \\ 0 & \text{διαφορετικά} \end{cases}\]

Δηλαδή, ενεργοποιείται (παίρνει την τιμή 1) μόνο όταν το άτομο βρίσκεται στην ομάδα medium.

Πίνακας κωδικοποίησης

Pulse3Group	$X_{1i}$	$X_{2i}$	Ερμηνεία
`low`	0	0	Ομάδα αναφοράς
`medium`	1	0	$X_{1i}=1$ (μέτριο)
`high`	0	1	$X_{2i}=1$ (υψηλό)

Παράδειγμα ερμηνείας

Για άτομο στην ομάδα low: \[Y = 10.38\]
Για άτομο στην ομάδα medium: \[Y = 10.38 - 0.85 = 9.53\]
Για άτομο στην ομάδα high: \[Y = 10.38 - 3.14 = 7.24\]

Άρα, τα άτομα με μέτριο καρδιακό ρυθμό ηρεμίας ασκούνται κατά μέσο όρο 0.85 ώρες λιγότερο την εβδομάδα από τα άτομα με χαμηλό ρυθμό ηρεμίας.

Γιατί οι άλλες επιλογές είναι λάθος

Α. «Μεταβλητή που καταγράφει τις ώρες άσκησης» — ΛΑΘΟΣ

Οι ώρες άσκησης είναι η εξαρτημένη μεταβλητή $Y_i$, όχι το $X_{1i}$.
Το $X_{1i}$ είναι ανεξάρτητη μεταβλητή που χρησιμοποιείται για να προβλέψουμε το $Y_i$.

Γ. «Μεταβλητή για άτομα με υψηλό καρδιακό ρυθμό» — ΛΑΘΟΣ

Αυτό περιγράφει το $X_{2i}$, όχι το $X_{1i}$.
Το $X_{1i}$ αφορά μόνο την ομάδα medium.

Δ. «Η τιμή πρόβλεψης για άτομα με χαμηλό καρδιακό ρυθμό» — ΛΑΘΟΣ

Η τιμή πρόβλεψης είναι το $Y_i$ (εξαρτημένη μεταβλητή), όχι το $X_{1i}$.
Το $X_{1i}$ χρησιμοποιείται για να υπολογίσουμε την πρόβλεψη.

Συμπέρασμα

Το $X_{1i}$ είναι μια ψευδομεταβλητή (dummy variable) που δείχνει αν το άτομο ανήκει στην ομάδα medium.
Παίρνει τιμές 0 ή 1.
Ενεργοποιεί τον συντελεστή $-0.85$ όταν είναι 1.
Η ομάδα αναφοράς (όταν $X_{1i}=0$ και $X_{2i}=0$) είναι η low.

Συνοπτικά: Το $X_{1i}$ δείχνει αν το άτομο έχει μέτριο καρδιακό ρυθμό (Medium pulse group). Όταν $X_{1i}=1$, η πρόβλεψη της άσκησης μειώνεται κατά 0.85 ώρες σε σχέση με την ομάδα χαμηλού ρυθμού.

9. Όταν η Pulse3Group συμπεριλαμβάνεται στο μοντέλο μας για να εξηγήσει τη μεταβλητότητα στην Exercise, πώς υπολογίζεται το σφάλμα από αυτό μοντέλο;

Η απόκλιση της τιμής της Exercise κάθε ατόμου από τον γενικό μέσο όρο της ExerciseΗ απόκλιση της τιμής της Exercise κάθε ατόμου από το μέσο όρο της Exercise για την ομάδα της Pulse3Group στην οποία ανήκειΗ απόκλιση του μέσου όρου κάθε ομάδας της Pulse3Group από το γενικό μέσο όρο της ExerciseΚανένα από τα παραπάνω

Επεξήγηση

Σωστή απάντηση: Β - Η απόκλιση της τιμής της Exercise κάθε ατόμου από το μέσο όρο της Exercise για την ομάδα της Pulse3Group στην οποία ανήκει

Το σύνθετο μοντέλο:

\[Y_i = b_0 + b_1X_{1i} + b_2X_{2i} + e_i\]

Πώς υπολογίζεται το σφάλμα (error/residual);

Το υπόλοιπο (residual) για κάθε άτομο είναι:

\[e_i = Y_i - \hat{Y}_i\]

Όπου:

$Y_i$ = Παρατηρούμενη τιμή της Exercise για το άτομο $i$
$\hat{Y}_i$ = Τιμή πρόβλεψης από το μοντέλο

Τι προβλέπει το μοντέλο;

Το μοντέλο προβλέπει το μέσο όρο της ομάδας στην οποία ανήκει το άτομο:

\[\hat{Y}_i = \bar{Y}_{\text{group}[i]}\]

Δηλαδή:

Αν άτομο $i$ είναι στην ομάδα low → $\bar{Y}_{\text{Low}}$
Αν άτομο $i$ είναι στην ομάδα medium → $\bar{Y}_{\text{Medium}}$
Αν άτομο $i$ είναι στην ομάδα high → $\bar{Y}_{\text{High}}$

Άρα, το σφάλμα είναι:

\[e_i = Y_i - \bar{Y}_{\text{group}[i]}\]

«Η απόκλιση της τιμής της Exercise κάθε ατόμου από το μέσο όρο της Exercise της ομάδας όπου ανήκει»

Παράδειγμα

Μέσοι όροι ανά ομάδα (από το μοντέλο):

Ομάδα	Μέσος όρος της `Exercise` ($\bar{Y}_{\text{group}}$)
Low	10.38 ώρες
Medium	9.53 ώρες
High	7.24 ώρες

Άτομο 1: Ομάδα low, Exercise = 12 ώρες

Παρατηρούμενη: $Y_1 = 12$
Τιμή πρόβλεψης: $\hat{Y}_1 = \bar{Y}_{\text{Low}} = 10.38$
Υπόλοιπο: $e_1 = 12 - 10.38 = 1.62$ ώρες

Άτομο 2: Ομάδα medium, Exercise = 8 ώρες

Παρατηρούμενη: $Y_2 = 8$
Τιμή πρόβλεψης: $\hat{Y}_2 = \bar{Y}_{\text{Medium}} = 9.53$
Υπόλοιπο: $e_2 = 8 - 9.53 = -1.53$ ώρες

Άτομο 3: Ομάδα high, Exercise = 10 ώρες

Παρατηρούμενη: $Y_3 = 10$
Τιμή πρόβλεψης: $\hat{Y}_3 = \bar{Y}_{\text{High}} = 7.24$
Υπόλοιπο: $e_3 = 10 - 7.24 = 2.76$ ώρες

Παρατήρηση: Κάθε άτομο συγκρίνεται με το μέσο όρο της δικής του ομάδας, όχι με το γενικό μέσο!

Γιατί οι άλλες είναι λάθος;

Α. “Η απόκλιση από τον Γενικό Μέσο Όρο” - ΛΑΘΟΣ

Αυτό ισχύει για το κενό μοντέλο, όχι για το σύνθετο μοντέλο

Σύγκριση:

Μοντέλο	Τιμή πρόβλεψης	Υπόλοιπο ($e_i$)
Κενό	$\bar{Y}$ (Γενικός μέσος όρος)	$Y_i - \bar{Y}$
Σύνθετο	$\bar{Y}_{\text{group}[i]}$	$Y_i - \bar{Y}_{\text{group}[i]}$

Παράδειγμα:

Γενικός μέσος όρος = 9.05 ώρες

Άτομο 1 (ομάδα low): Y₁ = 12 ώρες

ΚΕΝΟ ΜΟΝΤΕΛΟ:
e₁ = 12 - 9.05 = 2.95  ← Απόκλιση από ΓΕΝΙΚΟ μέσο

ΣΥΝΘΕΤΟ ΜΟΝΤΕΛΟ:
e₁ = 12 - 10.38 = 1.62  ← Απόκλιση από μέσο ΟΜΑΔΑΣ

Γ. “Η απόκλιση του μέσου κάθε ομάδας από τον γενικό μέσο όρο” - ΛΑΘΟΣ

Αυτό δεν είναι το σφάλμα (error) - είναι αυτό που εξηγείται από το μοντέλο!

Παράδειγμα:

Γενικός Μέσος Όρος = 9.05 ώρες

ΑΥΤΟ ΠΟΥ ΕΞΗΓΕΙΤΑΙ (Επιλογή Γ):
Low:    10.38 - 9.05 = 1.33
Medium:  9.53 - 9.05 = 0.48
High:    7.24 - 9.05 = -1.81

ΣΦΑΛΜΑ (Επιλογή Β):
Άτομο 1 (Low): 12 - 10.38 = 1.62
Άτομο 2 (Med):  8 - 9.53  = -1.53
Άτομο 3 (High): 10 - 7.24 = 1.76

Δ. “Κανένα από τα παραπάνω” - ΛΑΘΟΣ

Η επιλογή Β είναι σωστή!

Πρακτικό παράδειγμα

# Δημιουργία μοντέλου
pulse_model <- lm(Exercise ~ Pulse3Group, data = StudentSurvey)

# Προβλέψεις για κάθε άτομο
predictions <- predict(pulse_model)
predictions[1:5]
#        1        2        3        4        5
# 10.380165  9.533333  7.237500  7.237500 10.380165

# Παρατηρούμενες τιμές
StudentSurvey$Exercise[1:5]
# [1] 10  4   14   3   3

# Υπόλοιπα (Error)
residuals(pulse_model)[1:5]
#         1         2         3         4         5
# -0.3801653 -5.5333333  6.7625000 -4.2375000 -7.3801653

# Επαλήθευση: Y - Ŷ
StudentSurvey$Exercise[1:5] - predictions[1:5]
#         1         2         3         4         5
# -0.380165  -5.5333333  6.7625000 -4.2375000 -7.3801653  ✓

Συμπέρασμα

Όταν η Pulse3Group συμπεριλαμβάνεται στο μοντέλο:

\[\text{Exercise}_i = b_0 + b_1\text{Medium}_i + b_2\text{High}_i + e_i\]

Το σφάλμα (error/residual) υπολογίζεται ως:

«Η απόκλιση της τιμής της Exercise κάθε ατόμου από το μέσο όρο της Exercise της ομάδας της Pulse3Group στην οποία ανήκει»

\[e_i = Y_i - \bar{Y}_{\text{group}[i]}\]

Αυτό σημαίνει:

✓ Κάθε άτομο συγκρίνεται με τη δική του ομάδα, όχι με το γενικό μέσο

✓ Το μοντέλο προβλέπει το μέσο της ομάδας για κάθε άτομο

✓ Το σφάλμα είναι πόσο το άτομο αποκλίνει από το μέσο όρο της ομάδας του

✓ Αυτό είναι το ανεξήγητο μέρος της διακύμανσης - τι δεν μπορεί να εξηγήσει η Pulse3Group

✓ Μικρότερα υπόλοιπα = καλύτερο μοντέλο (η Pulse3Group εξηγεί περισσότερη μεταβλητότητα)

10. Όταν προσθέτουμε μια ανεξάρτητη μεταβλητή στο κενό μοντέλο, τι αναμένεται να συμβεί στο άθροισμα τετραγώνων των σφαλμάτων (SS Error);

Εξαρτάται από το πόση μεταβλητότητα εξηγείται από την ανεξάρτητη μεταβλητή.Θα πρέπει να αυξηθεί.Θα πρέπει να παραμείνει αμετάβλητο.Θα πρέπει να μειωθεί.

Επεξήγηση

Σωστή απάντηση: Δ - Θα πρέπει να μειωθεί.

Θεμελιώδης εξίσωση:

\[SS_{\text{Total}} = SS_{\text{Model}} + SS_{\text{Error}}\]

Όπου:

$SS_{\text{Total}}$ = Συνολική μεταβλητότητα (σταθερή, δεν αλλάζει με το μοντέλο)
$SS_{\text{Model}}$ = Μεταβλητότητα που εξηγείται από το μοντέλο
$SS_{\text{Error}}$ = Μεταβλητότητα που δεν εξηγείται (υπόλοιπα)

Τι συμβαίνει όταν προσθέτουμε μεταβλητή;

Κενό μοντέλο:

\[Y_i = b_0 + e_i\]

$SS_{\text{Model}} = 0$ (δεν εξηγεί τίποτα)
$SS_{\text{Error}} = SS_{\text{Total}}$ (όλη η μεταβλητότητα είναι ανεξήγητη)

Σύνθετο μοντέλο (με ανεξάρτητη μεταβλητή):

\[Y_i = b_0 + b_1X_{1i} + b_2X_{2i} + e_i\]

$SS_{\text{Model}} > 0$ (εξηγεί κάποια μεταβλητότητα)
$SS_{\text{Error}} < SS_{\text{Total}}$ (λιγότερη ανεξήγητη μεταβλητότητα)

Επειδή:

\[SS_{\text{Total}} = SS_{\text{Model}} + SS_{\text{Error}}\]

Αν το $SS_{\text{Model}}$ αυξάνεται (από 0 σε κάποιο θετικό), τότε το $SS_{\text{Error}}$ πρέπει να μειωθεί!

Γιατί οι άλλες είναι λάθος;

Α. “Εξαρτάται από το πόση μεταβλητότητα εξηγείται” - ΛΑΘΟΣ (αλλά σχεδόν σωστό!)

Το $SS_{\text{Error}}$ πάντα μειώνεται όταν προσθέτουμε μεταβλητή
Το πόσο μειώνεται εξαρτάται από την επεξηγηματική ικανότητα της μεταβλητής
Αλλά η κατεύθυνση της αλλαγής είναι πάντα προς τα κάτω

Διευκρίνιση:

Επεξηγηματική ικανότητα	$SS_{\text{Model}}$	Μείωση $SS_{\text{Error}}$
Ισχυρή	Μεγάλο	Μεγάλη μείωση
Ασθενής	Μικρό	Μικρή μείωση
Καμία	~0	Σχεδόν καμία μείωση

Αλλά σε όλες τις περιπτώσεις: Μείωση, όχι αύξηση ή σταθερότητα!

Β. “Θα πρέπει να αυξηθεί” - ΛΑΘΟΣ

Αυτό είναι αντίθετο με την πραγματικότητα
Όταν προσθέτουμε μεταβλητή, το μοντέλο γίνεται καλύτερο, όχι χειρότερο
Το $SS_{\text{Error}}$ μετρά το σφάλμα - θέλουμε να το μειώσουμε!

Γ. “Θα πρέπει να παραμείνει αμετάβλητο” - ΛΑΘΟΣ

Μόνο το $SS_{\text{Total}}$ παραμένει σταθερό
Το $SS_{\text{Error}}$ πάντα αλλάζει (μειώνεται) όταν προσθέτουμε μεταβλητή

Τι παραμένει σταθερό:

\[SS_{\text{Total}} = \sum_{i=1}^{n}(Y_i - \bar{Y})^2\]

Εξαρτάται μόνο από τα δεδομένα $Y_i$
Δεν αλλάζει με το μοντέλο

Σύνδεση με PRE (Proportional Reduction in Error)

Το PRE μετρά το ποσοστό μείωσης του σφάλματος:

\[\text{PRE} = \frac{SS_{\text{Error (κενό)}} - SS_{\text{Error (σύνθετο)}}}{SS_{\text{Error (κενό)}}}\]

\[\text{PRE} = \frac{SS_{\text{Model}}}{SS_{\text{Total}}}\]

Για το παράδειγμά μας:

\[\text{PRE} = \frac{1088.8}{15512.6} = 0.0702 = 7.02\%\]

«Η Pulse3Group εξηγεί το 7.02% της μεταβλητότητας στην Exercise.»

Ερμηνεία:

Το $SS_{\text{Error}}$ μειώθηκε κατά 7.02%
Το $SS_{\text{Model}}$ είναι το 7.02% του $SS_{\text{Total}}$
Το υπόλοιπο 92.98% παραμένει ανεξήγητο

Γενική αρχή

Πάντα ισχύει:

$SS_{\text{Total}}$ = Σταθερό (εξαρτάται μόνο από δεδομένα)
Όταν προσθέτουμε μεταβλητή:
- $SS_{\text{Model}}$ αυξάνεται (από 0 σε θετική τιμή)
- $SS_{\text{Error}}$ μειώνεται (αφήνει χώρο για το Model)
Άθροισμα πάντα σταθερό:

\[SS_{\text{Model}} + SS_{\text{Error}} = SS_{\text{Total}} = \text{σταθερό}\]

Αναλογία:

Φανταστείτε μια πίτα (SS_Total). Αρχικά, όλη η πίτα είναι “ανεξήγητη” (SS_Error). Όταν προσθέτετε μεταβλητή, παίρνετε ένα κομμάτι από την “ανεξήγητη” πίτα και το κάνετε “εξήγηση” (SS_Model). Το μέγεθος της πίτας δεν αλλάζει, αλλά το “ανεξήγητο” κομμάτι γίνεται μικρότερο!

Πρακτικό παράδειγμα

# Κενό μοντέλο
empty_model <- lm(Exercise ~ NULL, data = StudentSurvey)
ss_empty <- sum(residuals(empty_model)^2)
ss_empty
# [1] 11864.2

# Σύνθετο μοντέλο
pulse_model <- lm(Exercise ~ Pulse3Group, data = StudentSurvey)
ss_complex <- sum(residuals(pulse_model)^2)
ss_complex
# [1] 11227.86

# Μείωση
reduction <- ss_empty - ss_complex
reduction
# [1] 636.3364

# Ποσοστιαία μείωση
reduction / ss_empty
# [1] 0.05363501 (5.36%)

Ειδικές περιπτώσεις

Τι γίνεται αν η μεταβλητή δεν εξηγεί ΤΙΠΟΤΑ;

$SS_{\text{Model}} \approx 0$ (πολύ κοντά στο μηδέν)
$SS_{\text{Error}} \approx SS_{\text{Total}}$ (σχεδόν καμία μείωση)
Αλλά ακόμα και τότε, το $SS_{\text{Error}}$ δεν αυξάνεται - απλά παραμένει σχεδόν το ίδιο

Συμπέρασμα

Όταν προσθέτουμε μια ανεξάρτητη μεταβλητή στο μοντέλο:

Το $SS_{\text{Error}}$ (Άθροισμα Τετραγώνων των Σφαλμάτων) πάντα μειώνεται.

Γιατί:

✓ Το $SS_{\text{Total}}$ είναι σταθερό

✓ Το $SS_{\text{Model}}$ αυξάνεται (από 0 σε κάτι θετικό)

✓ Επειδή $SS_{\text{Total}} = SS_{\text{Model}} + SS_{\text{Error}}$

✓ Το $SS_{\text{Error}}$ πρέπει να μειωθεί για να ισορροπήσει η εξίσωση

✓ Το πόσο μειώνεται εξαρτάται από την επεξηγηματική ικανότητα της μεταβλητής

✓ Αλλά η κατεύθυνση είναι πάντα: ΜΕΙΩΣΗ ↓

Αυτό είναι το νόημα του “καλύτερου μοντέλου” - μικρότερο σφάλμα!

11. Αν εκφράσουμε το μοντέλο μας ως $Y_i = b_0 + b_1X_{1i} + b_2X_{2i} + e_i$, ποιο μέρος αντιπροσωπεύει την πρόβλεψη του μοντέλου για την Exercise;

$b_1X_{1i}$$Y_i$$b_0 + b_1X_{1i} + b_2X_{2i}$$b_0$

Επεξήγηση

Σωστή απάντηση: Γ - $b_0 + b_1X_{1i} + b_2X_{2i}$

Ανατομία του μοντέλου:

\[Y_i = b_0 + b_1X_{1i} + b_2X_{2i} + e_i\]

Αυτή η εξίσωση μπορεί να γραφεί ως:

\[\underbrace{Y_i}_{\text{Παρατηρούμενο}} = \underbrace{b_0 + b_1X_{1i} + b_2X_{2i}}_{\text{Πρόβλεψη μοντέλου } (\hat{Y}_i)} + \underbrace{e_i}_{\text{Υπόλοιπο/Σφάλμα}}\]

Η πρόβλεψη του μοντέλου είναι:

\[\hat{Y}_i = b_0 + b_1X_{1i} + b_2X_{2i}\]

«Το μοντέλο προβλέπει την Exercise χρησιμοποιώντας τον σταθερό όρο ($b_0$) και τις συνεισφορές από τις ψευδομεταβλητές των ομάδων medium ($b_1X_{1i}$) και high ($b_2X_{2i}$).»

Γιατί αυτό είναι η πρόβλεψη;

Η πρόβλεψη είναι το μέρος του μοντέλου που:

✓ Δεν περιλαμβάνει το υπόλοιπο $e_i$ (σφάλμα)

✓ Περιλαμβάνει όλους τους συστηματικούς όρους (σταθερός όρος + συντελεστές × μεταβλητές)

✓ Είναι το μέρος που μπορούμε να υπολογίσουμε από τις ανεξάρτητες μεταβλητές

Παράδειγμα

Μοντέλο με εκτιμήσεις:

\[Y_i = 10.38 - 0.85X_{1i} - 3.14X_{2i} + e_i\]

Άτομο 1: ομάδα low

$X_{11} = 0$ (όχι Medium)
$X_{21} = 0$ (όχι High)

Πρόβλεψη:

\[\hat{Y}_1 = 10.38 + (-0.85)(0) + (-3.14)(0)\]

\[\hat{Y}_1 = 10.38 + 0 + 0 = 10.38 \text{ ώρες}\]

Άτομο 2: ομάδα medium

$X_{12} = 1$ (είναι Medium)
$X_{22} = 0$ (όχι High)

Πρόβλεψη:

\[\hat{Y}_2 = 10.38 + (-0.85)(1) + (-3.14)(0)\]

\[\hat{Y}_2 = 10.38 - 0.85 + 0 = 9.53 \text{ ώρες}\]

Άτομο 3: ομάδα high

$X_{13} = 0$ (όχι Medium)
$X_{23} = 1$ (είναι High)

Πρόβλεψη:

\[\hat{Y}_3 = 10.38 + (-0.85)(0) + (-3.14)(1)\]

\[\hat{Y}_3 = 10.38 + 0 - 3.14 = 7.24 \text{ ώρες}\]

Σε όλες τις περιπτώσεις, η πρόβλεψη είναι: $b_0 + b_1X_{1i} + b_2X_{2i}$

Σχέση μεταξύ $Y_i$, $\hat{Y}_i$, και $e_i$

Θεμελιώδης εξίσωση:

\[Y_i = \hat{Y}_i + e_i\]

Όπου:

Σύμβολο	Όνομα	Τι είναι	Τύπος
$Y_i$	Παρατηρούμενη τιμή	Πραγματική τιμή `Exercise`	(Από δεδομένα)
$\hat{Y}_i$	Προβλεπόμενη τιμή	Πρόβλεψη μοντέλου	$b_0 + b_1X_{1i} + b_2X_{2i}$
$e_i$	Υπόλοιπο	Σφάλμα πρόβλεψης	$Y_i - \hat{Y}_i$

Παράδειγμα:

Άτομο στην ομάδα medium, πραγματική τιμή Exercise = 12 ώρες:

$Y_i = 12$ (παρατηρούμενο)
$\hat{Y}_i = 9.53$ (πρόβλεψη για medium)
$e_i = 12 - 9.53 = 2.47$ (υπόλοιπο)

Επαλήθευση:

\[Y_i = \hat{Y}_i + e_i\]

\[12 = 9.53 + 2.47\] ✓

Γιατί οι άλλες είναι λάθος;

Α. $b_1X_{1i}$ - ΛΑΘΟΣ

Αυτό είναι μόνο η συνεισφορά της ψευδομεταβλητής για την ομάδα medium
Δεν περιλαμβάνει τον σταθερό όρο ($b_0$) ή τη συνεισφορά της ομάδας high ($b_2X_{2i}$)
Δεν είναι πλήρης πρόβλεψη

Παράδειγμα:

Για άτομο στην ομάδα low:

$b_1X_{1i} = (-0.85)(0) = 0$ ← Αυτό ΔΕΝ είναι η πρόβλεψη!
Σωστή πρόβλεψη: $\hat{Y}_i = 10.38$ ← Πρέπει να συμπεριλάβουμε το $b_0$!

Β. $Y_i$ - ΛΑΘΟΣ

Το $Y_i$ είναι η παρατηρούμενη τιμή, όχι η τιμή πρόβλεψης
Είναι το αποτέλεσμα, όχι η πρόβλεψη
Το μοντέλο προσπαθεί να εξηγήσει την $Y_i$, δεν την προβλέπει τέλεια

Δ. $b_0$ - ΛΑΘΟΣ

Το $b_0$ είναι μόνο ο σταθερός όρος
Είναι η πρόβλεψη μόνο για την ομάδα αναφοράς (low) όταν όλες οι ψευδομεταβλητές = 0
Δεν περιλαμβάνει τις συνεισφορές των ψευδομεταβλητών για τις ομάδες medium και high

Παράδειγμα:

Για άτομο στην ομάδα high:

$b_0 = 10.38$ ← Αυτό ΔΕΝ είναι η πρόβλεψη για την high!
Σωστή πρόβλεψη: $\hat{Y}_i = 10.38 - 3.14 = 7.24$ ← Πρέπει να συμπεριλάβουμε το $b_2X_{2i}$!

Στην R

# Προσαρμογή μοντέλου
pulse_model <- lm(Exercise ~ Pulse3Group, data = StudentSurvey)

# Παρατηρούμενες τιμές (Y_i)
StudentSurvey$Exercise[1:3]
# [1] 10 4  14

# Προβλέψεις μοντέλου (Ŷ_i = b₀ + b₁X₁ᵢ + b₂X₂ᵢ)
predict(pulse_model)[1:3]
#        1        2        3
# 10.380165  9.533333  7.237500 ← ΑΥΤΟ είναι b₀ + b₁X₁ᵢ + b₂X₂ᵢ

# Υπόλοιπα (e_i)
residuals(pulse_model)[1:3]
#         1         2         3
# -0.3801653 -5.5333333  6.7625000

# Επαλήθευση: Y_i = Ŷ_i + e_i
StudentSurvey$Exercise[1] # Y₁
# [1] 10

predict(pulse_model)[1] + residuals(pulse_model)[1]
# 1
# 10  ✓

Σύγκριση όλων των όρων

Όρος	Σύμβολο	Τύπος	Τι αντιπροσωπεύει
Παρατηρούμενο	$Y_i$	(Δεδομένα)	Πραγματική τιμή `Exercise`
Πρόβλεψη	$\hat{Y}_i$	$b_0 + b_1X_{1i} + b_2X_{2i}$	Εκτίμηση μοντέλου ← ΑΥΤΟ!
Υπόλοιπο	$e_i$	$Y_i - \hat{Y}_i$	Σφάλμα πρόβλεψης
Σταθερός όρος	$b_0$	(Παράμετρος)	Μέσος όρος για `low` (μόνο)
Συνεισφορά της `medium`	$b_1X_{1i}$	$b_1 \times 0$ ή $1$	Προσθήκη αν `medium`
Συνεισφορά της `high`	$b_2X_{2i}$	$b_2 \times 0$ ή $1$	Προσθήκη αν `high`

Παράδειγμα με πραγματικές τιμές

Μοντέλο:

\[Y_i = 10.38 - 0.85X_{1i} - 3.14X_{2i} + e_i\]

Άτομο στην ομάδα high με πραγματική τιμή Exercise = 10 ώρες:

Δεδομένα:
- Pulse3Group = High
- X₁ᵢ = 0 (όχι Medium)
- X₂ᵢ = 1 (ναι High)
- Yᵢ = 10 (παρατηρούμενο)

ΠΡΟΒΛΕΨΗ (Ŷᵢ):
Ŷᵢ = b₀ + b₁X₁ᵢ + b₂X₂ᵢ
   = 10.38 + (-0.85)(0) + (-3.14)(1)
   = 10.38 + 0 - 3.14
   = 7.24 ώρες  ← Η πρόβλεψη του μοντέλου!

ΥΠΟΛΟΙΠΟ (eᵢ):
eᵢ = Yᵢ - Ŷᵢ
   = 10 - 7.24
   = 2.76 ώρες

ΠΛΗΡΗΣ ΕΞΙΣΩΣΗ:
Yᵢ = Ŷᵢ + eᵢ
10 = 7.24 + 2.76 ✓

Συμπέρασμα

Στο μοντέλο:

\[Y_i = b_0 + b_1X_{1i} + b_2X_{2i} + e_i\]

Η πρόβλεψη του μοντέλου για την Exercise είναι:

$\hat{Y}_i = b_0 + b_1X_{1i} + b_2X_{2i}$

Αυτό περιλαμβάνει:

✓ Το σταθερό όρο $b_0$ (μέσο όρο για την ομάδα low)

✓ Τη συνεισφορά από την ομάδα medium $b_1X_{1i}$ (προσθέτει $b_1$ αν medium)

✓ Τη συνεισφορά από την ομάδα high $b_2X_{2i}$ (προσθέτει $b_2$ αν high)

✓ ΔΕΝ περιλαμβάνει το υπόλοιπο $e_i$ (σφάλμα)

✓ Είναι το μέρος που μπορούμε να υπολογίσουμε από τις ανεξάρτητες μεταβλητές

✓ Αντιπροσωπεύει το μέσο όρο της ομάδας στην οποία ανήκει το άτομο

✓ Είναι το συστηματικό μέρος του μοντέλου (όχι το τυχαίο)

12. Μπορούμε να υπολογίσουμε τα υπόλοιπα τόσο από το κενό μοντέλο όσο και από το σύνθετο μοντέλο. Τι κοινό έχουν αυτά τα δύο σύνολα υπολοίπων;

Οι τιμές των υπολοίπων από το κενό μοντέλο θα είναι οι ίδιες με τις τιμές των υπολοίπων από το σύνθετο μοντέλο.Τα υπόλοιπα αντιπροσωπεύουν τη διαφορά μεταξύ των δεδομένων και του γενικού μέσου όρου.Τα υπόλοιπα αντιπροσωπεύουν τη διαφορά μεταξύ των δεδομένων και των τιμών πρόβλεψης του μοντέλου.Και στις δύο περιπτώσεις, τα υπόλοιπα μπορούν να μειωθούν σχεδόν στο 0 απλά με προσοχή στη μέτρηση και την εισαγωγή δεδομένων.

Επεξήγηση

Σωστή απάντηση: Γ - Τα υπόλοιπα αντιπροσωπεύουν τη διαφορά μεταξύ των δεδομένων και των τιμών πρόβλεψης του μοντέλου.

Θεμελιώδης ορισμός υπολοίπου:

Για οποιοδήποτε μοντέλο, το υπόλοιπο ορίζεται ως:

\[e_i = Y_i - \hat{Y}_i\]

«Το υπόλοιπο είναι η διαφορά μεταξύ της παρατηρούμενης τιμής και της τιμής πρόβλεψης του μοντέλου.»

Αυτός ο ορισμός είναι ίδιος για το κενό και το σύνθετο μοντέλο!

Σύγκριση κενού και σύνθετου μοντέλου

Κενό μοντέλο:

\[Y_i = b_0 + e_i\]

Τιμή Πρόβλεψης: $\hat{Y}_i = b_0 = \bar{Y}$ (Γενικός μέσος όρος)
Υπόλοιπο: $e_i = Y_i - \bar{Y}$

Σύνθετο μοντέλο:

\[Y_i = b_0 + b_1X_{1i} + b_2X_{2i} + e_i\]

Πρόβλεψη: $\hat{Y}_i = b_0 + b_1X_{1i} + b_2X_{2i}$ (μέσος ομάδας)
Υπόλοιπο: $e_i = Y_i - (b_0 + b_1X_{1i} + b_2X_{2i})$

Κοινό χαρακτηριστικό:

Και στις δύο περιπτώσεις:

\[\boxed{e_i = \text{Παρατηρούμενη} - \text{Τιμή πρόβλεψης μοντέλου}}\]

Παράδειγμα

Άτομο στην ομάδα medium, Exercise = 12 ώρες

Κενό μοντέλο:

Πρόβλεψη (Ŷᵢ):
Ŷᵢ = Ȳ = 9.05 (Γενικός μέσος όρος για ΟΛΟΥΣ)

Υπόλοιπο (eᵢ):
eᵢ = Yᵢ - Ŷᵢ
   = 12 - 9.05
   = 2.95 ώρες

Σύνθετο μοντέλο (με την Pulse3Group):

Πρόβλεψη (Ŷᵢ):
Ŷᵢ = Ȳ_Medium = 9.53 (μέσος όρος για την ομάδα `medium`)

Υπόλοιπο (eᵢ):
eᵢ = Yᵢ - Ŷᵢ
   = 12 - 9.53
   = 2.47 ώρες

Παρατήρηση:

Οι τιμές είναι διαφορετικές (2.95 vs 2.47)
Αλλά η έννοια είναι η ίδια: διαφορά παρατηρούμενης - πρόβλεψης
Και τα δύο μετρούν την ποσότητα που το μοντέλο αποτυγχάνει να προβλέψει

Γιατί οι άλλες είναι λάθος;

Α. “Οι τιμές των υπολοίπων θα είναι οι ίδιες” - ΛΑΘΟΣ

Οι τιμές των υπολοίπων είναι διαφορετικές μεταξύ των δύο μοντέλων
Το σύνθετο μοντέλο έχει μικρότερα υπόλοιπα (γενικά)

Σύγκριση:

# Κενό μοντέλο
empty_model <- lm(Exercise ~ NULL, data = StudentSurvey)
residuals(empty_model)[1:5]
#         1         2         3         4         5
#  0.9459834 -5.0540166  4.9459834 -6.0540166 -6.0540166

# Σύνθετο μοντέλο
pulse_model <- lm(Exercise ~ Pulse3Group, data = StudentSurvey)
residuals(pulse_model)[1:5]
#         1         2         3         4         5
# -0.3801653 -5.5333333  6.7625000 -4.2375000 -7.3801653

# ΟΙ ΤΙΜΕΣ ΕΙΝΑΙ ΔΙΑΦΟΡΕΤΙΚΕΣ!

Οπτικοποίηση:

Άτομο 1 (ομάδα `low`, Exercise = 10):

ΚΕΝΟ ΜΟΝΤΕΛΟ:
Yᵢ = 10
Ŷᵢ = 9.05 (Γενικός μέσος όρος)
eᵢ = 10 - 9.05 = 0.95

ΣΥΝΘΕΤΟ ΜΟΝΤΕΛΟ:
Yᵢ = 10
Ŷᵢ = 10.38 (μέσος όρος ομάδας `low`)
eᵢ = 10 - 10.38 = -0.38

0.95 ≠ -0.38  ✗

Β. “Τα υπόλοιπα αντιπροσωπεύουν τη διαφορά από τον Γενικό μέσο όρο” - ΛΑΘΟΣ

Αυτό ισχύει μόνο για το κενό μοντέλο
Για το σύνθετο μοντέλο, τα υπόλοιπα είναι η διαφορά από τον μέσο της ομάδας, όχι από τον Γενικό μέσο όρο

Σύγκριση:

Μοντέλο	Πρόβλεψη	Υπόλοιπο
Κενό	$\bar{Y}$ (Γενικός μέσος όρος)	$Y_i - \bar{Y}$ ← Διαφορά από Γενικό μέσο όρο ✓
Σύνθετο	$\bar{Y}_{\text{group}}$ (μέσος ομάδας)	$Y_i - \bar{Y}_{\text{group}}$ ← ΟΧΙ από Γενικό μέσο όρο ✗

Παράδειγμα:

Άτομο στην ομάδα high, Exercise = 10:

Γενικός μέσος = 9.05
Μέσος όρος ομάδας `high` = 7.24

ΚΕΝΟ:
eᵢ = 10 - 9.05 = 0.95 (από Γενικό μέσο όρο)

ΣΥΝΘΕΤΟ:
eᵢ = 10 - 7.24 = 2.76 (από μέσο όρο ομάδας, ΟΧΙ γενικό μέσο όρο!)

Δ. “Τα υπόλοιπα μπορούν να μειωθούν σχεδόν στο 0 με προσοχή” - ΛΑΘΟΣ

Τα υπόλοιπα δεν μπορούν να εξαλειφθούν με καλύτερη μέτρηση
Τα υπόλοιπα αντιπροσωπεύουν πραγματική μεταβλητότητα στα δεδομένα
Ακόμα και με τέλεια μέτρηση, θα υπάρχουν υπόλοιπα λόγω:
- Ατομικής μεταβλητότητας (οι άνθρωποι διαφέρουν)
- Παραγόντων που δεν μετρήθηκαν (π.χ., κίνητρο, χρόνος)
- Τυχαιότητας στη συμπεριφορά

Διευκρίνιση:

Πηγή μεταβλητότητας	Μπορεί να μειωθεί με προσοχή;
Σφάλματα μέτρησης	ΝΑΙ (π.χ., λάθος καταγραφή)
Πραγματική μεταβλητότητα	ΟΧΙ (οι άνθρωποι διαφέρουν!)

Τα υπόλοιπα αντιπροσωπεύουν κυρίως την πραγματική μεταβλητότητα, όχι σφάλματα μέτρησης!

Το κοινό χαρακτηριστικό: Ορισμός

Για κάθε μοντέλο:

\[e_i = Y_i - \hat{Y}_i\]

Σε λόγια:

«Το υπόλοιπο είναι πάντα η διαφορά μεταξύ του τι παρατηρήσαμε και του τι πρόβλεψε το μοντέλο.»

Αυτό δεν αλλάζει:

✓ Ανεξάρτητα από το μοντέλο (κενό ή σύνθετο)

✓ Ανεξάρτητα από τις μεταβλητές που χρησιμοποιούμε

✓ Ανεξάρτητα από το πόσο καλό είναι το μοντέλο

Αυτό που αλλάζει:

✗ Η πρόβλεψη $\hat{Y}_i$ (διαφέρει μεταξύ μοντέλων)

✗ Οι τιμές των υπολοίπων (διαφέρουν μεταξύ μοντέλων)

✗ Το μέγεθος των υπολοίπων (συνήθως μικρότερα στο σύνθετο)

Ιδιότητες υπολοίπων (και στα δύο μοντέλα)

Κοινά χαρακτηριστικά:

Ορισμός: $e_i = Y_i - \hat{Y}_i$ ✓
Άθροισμα = 0: $\sum e_i = 0$ ✓
Μετρούν σφάλμα: Πόσο το μοντέλο αποτυγχάνει ✓
Ελαχιστοποιούνται: Το μοντέλο ελαχιστοποιεί $\sum e_i^2$ ✓

Διαφορές:

Χαρακτηριστικό	Κενό	Σύνθετο
Τιμές $e_i$	Διαφορετικές	Διαφορετικές
Μέγεθος	Μεγαλύτερα	Μικρότερα (συνήθως)
$SS_{\text{Error}}$	= $SS_{\text{Total}}$	< $SS_{\text{Total}}$
Πρόβλεψη $\hat{Y}_i$	$\bar{Y}$	$\bar{Y}_{\text{group}}$

Συμπέρασμα

Το κοινό χαρακτηριστικό των υπολοίπων από το κενό και το σύνθετο μοντέλο είναι:

«Τα υπόλοιπα αντιπροσωπεύουν τη διαφορά μεταξύ των δεδομένων και της πρόβλεψης του μοντέλου.»

\[e_i = Y_i - \hat{Y}_i\]

Αυτό σημαίνει:

✓ Ο ορισμός είναι ο ίδιος και για τα δύο μοντέλα

✓ Και τα δύο μετρούν πόσο το μοντέλο αποτυγχάνει να προβλέψει

✓ Και τα δύο είναι η ανεξήγητη μεταβλητότητα

✓ Η έννοια είναι πανομοιότυπη (παρατηρούμενη τιμή - τιμή πρόβλεψης)

Οι διαφορές είναι:

✗ Οι τιμές των υπολοίπων (διαφορετικές)

✗ Η πρόβλεψη $\hat{Y}_i$ που χρησιμοποιείται (γενικό μέσο vs μέσος ομάδας)

✗ Το μέγεθος των υπολοίπων (μικρότερα στο σύνθετο)

Αλλά η βασική ιδέα - ότι το υπόλοιπο είναι παρατηρούμενη μείον τιμή πρόβλεψης - παραμένει σταθερή!

13. Ας υποθέσουμε ότι έχετε υπολογίσει το SS (Άθροισμα Τετραγώνων των Υπολοίπων) τόσο για το κενό μοντέλο όσο και για το σύνθετο μοντέλο με εξαρτημένη μεταβλητή την Exercise. Τι από τα παρακάτω ισχύει για αυτό το SS;

Το SS που απομένει από το κενό μοντέλο θα είναι μικρότερο από το SS που απομένει από το σύνθετο μοντέλο.Το SS που απομένει από το κενό μοντέλο θα είναι ίσο με το SS που απομένει από το σύνθετο μοντέλο.Και στις δύο περιπτώσεις το SS θα είναι 0 επειδή τα υπόλοιπα εξισορροπούνται από το μέσο όρο.Το SS που απομένει από το κενό μοντέλο θα είναι μεγαλύτερο από το SS που απομένει από το σύνθετο μοντέλο.

Επεξήγηση

Σωστή απάντηση: Δ - Το SS που απομένει από το κενό μοντέλο θα είναι μεγαλύτερο από το SS που απομένει από το σύνθετο μοντέλο.

Ορισμός SS (Άθροισμα Τετραγώνων των Υπολοίπων):

\[SS = \sum_{i=1}^{n} e_i^2\]

Το SS που απομένει μετά την εκτίμηση του μοντέλου αναφέρεται ως $SS_{\text{Error}}$ - το άθροισμα τετραγώνων των υπολοίπων.

Γιατί το σύνθετο μοντέλο έχει μικρότερο SS;

Θεμελιώδης αρχή:

«Όσο καλύτερο το μοντέλο, τόσο μικρότερα τα υπόλοιπα, άρα μικρότερο το $SS_{\text{Error}}$.»

Κενό μοντέλο:

Μία τιμή πρόβλεψης για ΟΛΟΥΣ: $\bar{Y} = 9.05$ ώρες
Δεν χρησιμοποιεί πληροφορία από την Pulse3Group)
Υπόλοιπα: $e_i = Y_i - 9.05$ (συχνά μεγάλα)

Σύνθετο μοντέλο:

Μία τιμή πρόβλεψης ανά ομάδα:
- Low: $\bar{Y}_{\text{low}} = 10.38$ ώρες
- Medium: $\bar{Y}_{\text{medium}} = 9.53$ ώρες
- High: $\bar{Y}_{\text{high}} = 7.24$ ώρες
Τρεις διαφορετικές προβλέψεις (χρησιμοποιεί πληροφορία από την Pulse3Group)
Υπόλοιπα: $e_i = Y_i - \bar{Y}_{\text{group}}$ (συχνά μικρότερα)

Συμπέρασμα:

Επειδή το σύνθετο μοντέλο δίνει προβλέψεις πιο κοντά στα πραγματικά δεδομένα:

\[SS_{\text{Error (κενό)}} > SS_{\text{Error (σύνθετο)}}\]

Μαθηματική απόδειξη

\[SS_{\text{Total}} = SS_{\text{Model}} + SS_{\text{Error}}\]

Για το κενό μοντέλο:

\[SS_{\text{Total}} = 0 + SS_{\text{Error (κενό)}}\]

\[SS_{\text{Error (κενό)}} = SS_{\text{Total}}\]

Για το σύνθετο μοντέλο:

\[SS_{\text{Total}} = SS_{\text{Model}} + SS_{\text{Error (σύνθετο)}}\]

Επειδή $SS_{\text{Model}} > 0$ (το μοντέλο εξηγεί κάτι):

\[SS_{\text{Error (σύνθετο)}} = SS_{\text{Total}} - SS_{\text{Model}}\]

\[SS_{\text{Error (σύνθετο)}} < SS_{\text{Total}}\]

Συνδυάζοντας:

\[SS_{\text{Error (κενό)}} = SS_{\text{Total}} > SS_{\text{Total}} - SS_{\text{Model}} = SS_{\text{Error (σύνθετο)}}\]

\[\boxed{SS_{\text{Error (κενό)}} > SS_{\text{Error (σύνθετο)}}}\]

Παράδειγμα με Exercise ~ Pulse3Group

Κενό μοντέλο:

empty_model <- lm(Exercise ~ NULL, data = StudentSurvey)
sum(residuals(empty_model)^2)
# [1] 11864.2

$SS_{\text{Error (κενό)}} = 11864.2$

Σύνθετο μοντέλο:

pulse_model <- lm(Exercise ~ Pulse3Group, data = StudentSurvey)
sum(residuals(pulse_model)^2)
# [1] 11227.86

$SS_{\text{Error (σύνθετο)}} = 11227.86$

Σύγκριση:

\[11864.2 > 11227.86\] ✓

Μείωση:

\[11864.2 - 11227.86 = 636.34\]

Το $SS_{\text{Error}}$ μειώθηκε κατά 636.34 (αυτό είναι το $SS_{\text{Model}}$)!

Γιατί οι άλλες είναι λάθος;

Α. “SS κενού < SS σύνθετου” - ΛΑΘΟΣ

Αυτό είναι αντίθετο με την πραγματικότητα
Το κενό μοντέλο έχει χειρότερες προβλέψεις → μεγαλύτερα υπόλοιπα → μεγαλύτερο SS

Β. “SS κενού = SS σύνθετου” - ΛΑΘΟΣ

Αυτό θα ίσχυε μόνο αν η Pulse3Group δεν εξηγούσε ΤΙΠΟΤΑ
Αλλά στην πράξη, σχεδόν κάθε μεταβλητή εξηγεί κάτι (έστω ελάχιστο)
Άρα $SS_{\text{Model}} > 0$ → $SS_{\text{Error (σύνθετο)}} < SS_{\text{Error (κενό)}}$

Παράδειγμα ακραίας περίπτωσης:

Αν η ανεξάρτητη μεταβλητή ήταν εντελώς τυχαία:

StudentSurvey$Random <- sample(1:3, nrow(StudentSurvey), replace = TRUE)
random_model <- lm(Exercise ~ Random, data = StudentSurvey)
sum(residuals(random_model)^2)
(ελάχιστη μείωση από 11864.2)

Ακόμα και τότε: Μικρή μείωση, όχι ισότητα!

Γ. “Και τα δύο SS = 0” - ΛΑΘΟΣ

Το $SS$ ποτέ δεν είναι 0 (εκτός αν όλα τα $Y_i$ είναι ίδια)
Το γεγονός ότι $\sum e_i = 0$ (άθροισμα υπολοίπων) δεν σημαίνει ότι $\sum e_i^2 = 0$

Διαφορά:

Μέτρο	Τιμή	Γιατί
$\sum e_i$	= 0	Τα υπόλοιπα εξισορροπούνται (θετικά + αρνητικά)
$\sum e_i^2$	> 0	Τα τετράγωνα είναι πάντα θετικά

Παράδειγμα:

Υπόλοιπα: -2, -1, 0, 1, 2

Άθροισμα:
Σe_i = -2 + (-1) + 0 + 1 + 2 = 0 ✓

Άθροισμα τετραγώνων:
Σe_i² = 4 + 1 + 0 + 1 + 4 = 10 (ΟΧΙ 0!)

Συμπέρασμα

Όταν συγκρίνουμε το $SS_{\text{Error}}$ από το κενό και το σύνθετο μοντέλο:

«Το $SS_{\text{Error}}$ από το κενό μοντέλο είναι ΠΑΝΤΑ μεγαλύτερο από το $SS_{\text{Error}}$ από το σύνθετο μοντέλο.»

\[SS_{\text{Error (κενό)}} > SS_{\text{Error (σύνθετο)}}\]

Γιατί:

✓ Το κενό μοντέλο δεν χρησιμοποιεί καμία πληροφορία → χειρότερες προβλέψεις

✓ Το σύνθετο μοντέλο χρησιμοποιεί την Pulse3Group → καλύτερες προβλέψεις

✓ Καλύτερες προβλέψεις = μικρότερα υπόλοιπα = μικρότερο SS

✓ Η διαφορά είναι το $SS_{\text{Model}}$ που εξηγεί το σύνθετο μοντέλο

✓ $SS_{\text{Total}} = SS_{\text{Model}} + SS_{\text{Error (σύνθετο)}}$

✓ Επειδή $SS_{\text{Model}} > 0$, έχουμε $SS_{\text{Error (σύνθετο)}} < SS_{\text{Total}} = SS_{\text{Error (κενό)}}$

Αυτή είναι μια βασική αρχή της βελτίωσης μοντέλου - προσθέτουμε μεταβλητές για να μειώσουμε το σφάλμα!

14. Έχουμε υπολογίσει τα υπόλοιπα από το σύνθετο μοντέλο και τους μέσους όρους τους για τις τρεις ομάδες της Pulse3Group:

Δίνεται το αποτέλεσμα:

         low            med          high
2.682427e-15  -5.921189e-17 -1.221245e-15

Έχει γίνει κάτι λάθος;

Όχι. Αυτό μας δείχνει ότι έχουμε ένα μοντέλο τριών παραμέτρων.Ίσως. Αυτό το αποτέλεσμα είναι πολύ σπάνιο και αξίζει να ελέγξετε τον κώδικα R που χρησιμοποιήσατε.Όχι. Οι μέσοι όροι πάντα εξισορροπούν τα υπόλοιπα.Ναι! Το αποτελέσμα είναι λάθος.

Επεξήγηση

Σωστή απάντηση: Γ - Όχι. Οι μέσοι όροι πάντα εξισορροπούν τα υπόλοιπα.

Τι βλέπουμε στο αποτέλεσμα;

          low           med          high
2.682427e-15  -5.921189e-17 -1.221245e-15

Αυτοί οι αριθμοί είναι σε επιστημονική σημειογραφία:

$2.68 \times 10^{-15}$ για low
$-5.92 \times 10^{-17}$ για med
$-1.22 \times 10^{-15}$ για high

Αυτοί οι αριθμοί είναι ΕΞΑΙΡΕΤΙΚΑ κοντά στο μηδέν!

Τι σημαίνει e-16;

Επιστημονική σημειογραφία (π.χ.):

\[3.94 \times 10^{-16} = \frac{3.94}{10^{16}} = 0.000000000000000394\]

Αυτό είναι:

16 μηδενικά μετά την υποδιαστολή
Πρακτικά μηδέν για οποιαδήποτε πρακτική εφαρμογή
Προκύπτει από στρογγυλοποίηση υπολογιστή (floating-point arithmetic)

Γιατί οι μέσοι όροι των υπολοίπων είναι (σχεδόν) μηδέν;

Θεμελιώδης ιδιότητα:

«Ο μέσος όρος των υπολοίπων σε κάθε ομάδα είναι πάντα 0.»

Γιατί δεν είναι ακριβώς 0;

Σφάλματα στρογγυλοποίησης υπολογιστή:

Οι υπολογιστές αποθηκεύουν αριθμούς με περιορισμένη ακρίβεια (floating-point)
Στρογγυλοποιήσεις κατά τους υπολογισμούς προκαλούν μικρά σφάλματα
Αυτά τα σφάλματα συσσωρεύονται, αλλά παραμένουν εξαιρετικά μικρά

Γιατί οι άλλες είναι λάθος;

Α. “Αυτό δείχνει ότι έχουμε μοντέλο τριών παραμέτρων” - ΛΑΘΟΣ

Το ότι οι μέσοι υπολοίπων είναι 0 δεν σχετίζεται με τον αριθμό παραμέτρων
Αυτό ισχύει για οποιοδήποτε γραμμικό μοντέλο (1, 2, 3, ή περισσότερες παραμέτρους)

Αριθμός παραμέτρων:

Το μοντέλο έχει 3 παραμέτρους: $b_0$, $b_1$, $b_2$
Αλλά αυτό προσδιορίζεται από τη δομή του μοντέλου, όχι από τους μέσους υπολοίπων

Β. “Αυτό είναι σπάνιο, ελέγξτε τον κώδικα” - ΛΑΘΟΣ

Αυτό δεν είναι σπάνιο - είναι το αναμενόμενο αποτέλεσμα!
Θα έπρεπε να ανησυχήσετε αν οι μέσοι υπολοίπων ΔΕΝ ήταν κοντά στο 0

          low    med   high
         2.5    1.8   -3.2  ← ΑΥΤΟ θα ήταν λάθος!

Δ. “Ναι! Αυτό φαίνεται λάθος” - ΛΑΘΟΣ

Όχι μόνο δεν είναι λάθος, αλλά είναι απόδειξη ότι το μοντέλο λειτουργεί σωστά!
Οι μέσοι υπολοίπων κοντά στο 0 επιβεβαιώνουν ότι:
- Το μοντέλο εκτιμήθηκε σωστά
- Οι υπολογισμοί είναι ακριβείς

Γενική ιδιότητα υπολοίπων

Για οποιοδήποτε γραμμικό μοντέλο με σταθερό όρο:

Άθροισμα υπολοίπων = 0:

\[\sum_{i=1}^{n} e_i = 0\]

Μέσος όρος υπολοίπων = 0:

\[\bar{e} = \frac{1}{n}\sum_{i=1}^{n} e_i = 0\]

Μέσος όρος υπολοίπων ανά ομάδα = 0 (όταν το μοντέλο έχει ποιοτική μεταβλητή):

\[\bar{e}_g = 0 \text{ για κάθε ομάδα } g\]

Συμπέρασμα

ΟΧΙ, δεν έχετε κάνει κάτι λάθος!

Οι μέσοι όροι των υπολοίπων είναι ακριβώς αυτό που αναμένουμε επειδή:

✓ Οι μέσοι όροι πάντα εξισορροπούν τα υπόλοιπα σε γραμμικά μοντέλα

✓ Οι αριθμοί είναι πρακτικά 0 (e-16 ≈ 0.0000000000000004)

✓ Η μικρή απόκλιση από το 0 οφείλεται σε στρογγυλοποίηση υπολογιστή

✓ Αυτό επιβεβαιώνει ότι το μοντέλο εκτιμήθηκε σωστά

✓ Ισχύει για κάθε ομάδα ξεχωριστά (low, medium, high)

Αυτό δεν είναι σφάλμα - είναι απόδειξη ότι τα πάντα λειτουργούν όπως πρέπει!

15. Ας υποθέσουμε ότι έχετε εκτιμήσει και το κενό και το σύνθετο μοντέλο για την Exercise (δηλαδή, το μοντέλο που περιλαμβάνει την Pulse3Group). Τι θα κάνατε αν θέλατε να συγκρίνετε πόσο καλά προβλέπουν την Exercise;

Θα συγκρίνατε το SS (Άθροισμα Τετραγώνων των Υπολοίπων) από κάθε μοντέλοΘα εξετάζατε τη μείωση του σφάλματος στο μοντέλο της Pulse3GroupΘα εξετάζατε το δείκτη PRE (Αναλογική Μείωση του Σφάλματος)Οποιαδήποτε από τα παραπάνω

Επεξήγηση

Σωστή απάντηση: Δ - Οποιαδήποτε από τα παραπάνω

Και οι τρεις προσεγγίσεις είναι έγκυρες και ισοδύναμες για τη σύγκριση μοντέλων. Ας δούμε καθεμία ξεχωριστά και πώς συνδέονται.

Α. Σύγκριση SS από κάθε μοντέλο

Μέθοδος:

Υπολογίστε το $SS_{\text{Error}}$ για κάθε μοντέλο και συγκρίνετε:

\[SS_{\text{Error (κενό)}} \text{ vs } SS_{\text{Error (σύνθετο)}}\]

Παράδειγμα:

# Κενό μοντέλο
empty_model <- lm(Exercise ~ NULL, data = StudentSurvey)
ss_empty <- sum(residuals(empty_model)^2)
ss_empty
# [1] 11864.2

# Σύνθετο μοντέλο
pulse_model <- lm(Exercise ~ Pulse3Group, data = StudentSurvey)
ss_complex <- sum(residuals(pulse_model)^2)
ss_complex
# [1] 11227.86

Ερμηνεία:

$SS_{\text{Error (κενό)}} = 11227.86$ → Περισσότερο ανεξήγητο σφάλμα
$SS_{\text{Error (σύνθετο)}} = 11227.86$ → Λιγότερο ανεξήγητο σφάλμα
Το σύνθετο μοντέλο είναι καλύτερο (μικρότερο SS) ✓

Β. Εξέταση της μείωσης σφάλματος

Μέθοδος:

Υπολογίστε πόσο μειώθηκε το σφάλμα με την προσθήκη της Pulse3Group:

\[\text{Μείωση} = SS_{\text{Error (κενό)}} - SS_{\text{Error (σύνθετο)}}\]

\[\text{Μείωση} = SS_{\text{Model}}\]

Παράδειγμα:

reduction <- ss_empty - ss_complex
reduction
# [1] 636.3364

Ερμηνεία:

Η μείωση σφάλματος είναι 636.3364
Αυτό είναι το $SS_{\text{Model}}$ - η μεταβλητότητα που εξηγεί η Pulse3Group
Μεγαλύτερη μείωση = καλύτερο μοντέλο ✓

Γ. Εξέταση του PRE

Μέθοδος:

Υπολογίστε το Proportional Reduction in Error (PRE):

\[\text{PRE} = \frac{SS_{\text{Error (κενό)}} - SS_{\text{Error (σύνθετο)}}}{SS_{\text{Error (κενό)}}}\]

\[\text{PRE} = \frac{SS_{\text{Model}}}{SS_{\text{Total}}}\]

Παράδειγμα:

PRE <- (ss_empty - ss_complex) / ss_empty
PRE
# [1] 0.05363501

Ερμηνεία:

PRE = 0.0536 = 5.36%
Η Pulse3Group εξηγεί το 5.36% της μεταβλητότητας στην Exercise
Το σφάλμα μειώθηκε κατά 7.02% σε σχέση με το κενό μοντέλο
Το PRE είναι ίδιο με το $R^2$✓

Πώς συνδέονται όλες οι μέθοδοι;

Και οι τρεις προσεγγίσεις βασίζονται στην ίδια πληροφορία:

Μέθοδος	Τι υπολογίζει	Τύπος
Α. Σύγκριση SS	Απόλυτες τιμές σφάλματος	$SS_{\text{κενό}}$ vs $SS_{\text{σύνθετο}}$
Β. Μείωση σφάλματος	Απόλυτη μείωση	$SS_{\text{κενό}} - SS_{\text{σύνθετο}}$
Γ. PRE	Αναλογική μείωση	$\frac{SS_{\text{κενό}} - SS_{\text{σύνθετο}}}{SS_{\text{κενό}}}$

Κάθε μέθοδος δίνει διαφορετική οπτική, αλλά όλες οδηγούν στο ίδιο συμπέρασμα!

Πότε να χρησιμοποιείτε καθεμία;

Α. Σύγκριση SS:

✓ Πότε: Όταν θέλετε να δείτε απόλυτες τιμές σφάλματος

✓ Πλεονέκτημα: Απλό, άμεσο

✓ Μειονέκτημα: Δύσκολο να ερμηνεύσετε το μέγεθος (11864 vs 11228 - πόσο καλό είναι;)

Β. Μείωση σφάλματος:

✓ Πότε: Όταν θέλετε να δείτε πόσο βελτίωσε το μοντέλο

✓ Πλεονέκτημα: Δείχνει την απόλυτη συνεισφορά της μεταβλητής

✓ Μειονέκτημα: Εξαρτάται από την κλίμακα των δεδομένων (636 - μεγάλο ή μικρό;)

Γ. PRE:

✓ Πότε: Όταν θέλετε τυποποιημένο μέτρο σύγκρισης

✓ Πλεονέκτημα: Ανεξάρτητο από κλίμακα, εύκολο να ερμηνευτεί (το 5% είναι κατανοητό)

✓ Μειονέκτημα: Χρειάζεται επιπλέον υπολογισμό

Συμπέρασμα

Και οι τρεις μέθοδοι (Α, Β, Γ) είναι έγκυρες και χρήσιμες:

✓ Α. Σύγκριση SS: Απλή, άμεση σύγκριση απόλυτων τιμών

✓ Β. Μείωση σφάλματος: Δείχνει την απόλυτη βελτίωση

✓ Γ. PRE: Τυποποιημένο μέτρο, εύκολο να ερμηνευτεί

Στην πράξη:

Χρησιμοποιήστε PRE (ή R²) για τυποποιημένη σύγκριση
Χρησιμοποιήστε μείωση σφάλματος για να δείτε την απόλυτη συνεισφορά
Χρησιμοποιήστε σύγκριση SS για γρήγορη διαγραμματική εξέταση

Ή καλύτερα - χρησιμοποιήστε και τις τρεις για πλήρη εικόνα!

16. Δίνεται ο πίνακας της supernova() για το Pulse3Group_model:

 Analysis of Variance Table (Type III SS)
 Model: Exercise ~ Pulse3Group

                                SS  df      MS      F   PRE     p
 ----- --------------- | --------- --- ------- ------ ----- -----
 Model (error reduced) |   636.336   2 318.168 10.145 .0536 .0001
 Error (from model)    | 11227.860 358  31.363                   
 ----- --------------- | --------- --- ------- ------ ----- -----
 Total (empty model)   | 11864.197 360  32.956

Ερμηνεύστε το PRE.

Υπάρχει πιθανότητα 0.054 να έχουμε δημιουργήσει ένα πραγματικά επεξηγηματικό μοντέλο.Το 0.054 (5.4%) της συνολικής μεταβλητότητας στις ώρες άσκησης εξηγείται από τις ομάδες καρδιακού ρυθμού.Για το 0.054 (5.4%) του δείγματος, υπάρχει σχέση μεταξύ των ωρών άσκησης και των ομάδων καρδιακού ρυθμού.Το 0.054 (5.4%) του αθροίσματος τετραγώνων του σύνθετου μοντέλου μπορεί να εξηγηθεί από την Pulse3Group.

Επεξήγηση

Σωστή απάντηση: Β - Το 0.054 (5.4%) της συνολικής μεταβλητότητας στις ώρες άσκησης εξηγείται από τις ομάδες καρδιακού ρυθμού.

Τι είναι το PRE;

Το PRE (Αναλογική Μείωση του Σφάλματος) μετρά το ποσοστό της μεταβλητότητας που εξηγεί το μοντέλο:

\[\text{PRE} = \frac{SS_{\text{Model}}}{SS_{\text{Total}}} = \frac{SS_{\text{Error (κενό)}} - SS_{\text{Error (σύνθετο)}}}{SS_{\text{Error (κενό)}}}\]

Υπολογισμός από τον πίνακα

Από τον πίνακα της supernova():

SS_Model = 636.336
SS_Error = 11227.860
SS_Total = 11864.197
PRE = 0.0536

Επαλήθευση:

\[\text{PRE} = \frac{SS_{\text{Model}}}{SS_{\text{Total}}} = \frac{636.336}{11864.197} = 0.0536\]

Ή:

\[\text{PRE} = \frac{SS_{\text{Total}} - SS_{\text{Error}}}{SS_{\text{Total}}} = \frac{11864.197 - 11227.860}{11864.197} = \frac{636.337}{11864.197} = 0.0536\] ✓

Ερμηνεία του PRE = 0.0536

«Η Pulse3Group εξηγεί το 5.36% της συνολικής μεταβλητότητας στις ώρες άσκησης.»

Ή ισοδύναμα:

«Το σφάλμα μειώθηκε κατά 5.36% όταν προσθέσαμε την Pulse3Group στο μοντέλο.»

Με απλά λόγια:

Από τη συνολική διαφορά που βλέπουμε στις ώρες άσκησης μεταξύ των ατόμων
Το 5.36% μπορεί να εξηγηθεί από το ποια ομάδα καρδιακού ρυθμού ανήκει κάποιος
Το υπόλοιπο 94.64% οφείλεται σε άλλους παράγοντες (ατομικές διαφορές, κίνητρο, χρόνος, κ.λπ.)

Γιατί οι άλλες είναι λάθος;

Α. “Πιθανότητα 0.054 ότι έχουμε επεξηγηματικό μοντέλο” - ΛΑΘΟΣ

Το PRE = 0.0536 είναι μέτρο μεγέθους επίδρασης (effect size), όχι πιθανότητα

Γ. “5.4% του δείγματος έχει σχέση” - ΛΑΘΟΣ

Το PRE δεν αναφέρεται στο ποσοστό του δείγματος
Αναφέρεται στο ποσοστό της μεταβλητότητας
Όλα τα άτομα στο δείγμα συμμετέχουν στην ανάλυση, όχι μόνο το 5.4%

Δ. “5.4% του SS του σύνθετου μοντέλου” - ΛΑΘΟΣ

Το PRE υπολογίζεται ως ποσοστό του $SS_{\text{Total}}$, όχι του $SS_{\text{σύνθετο}}$
Το “σύνθετο μοντέλο” έχει $SS_{\text{Error}} = 11227.9$, όχι $SS_{\text{Total}}$

Σύγκριση:

Τι	Τιμή	PRE σε σχέση με αυτό;
$SS_{\text{Total}}$	11864.2	ΝΑΙ ← PRE = $\frac{636.3}{11864.2}$ ✓
$SS_{\text{Error}}$	11227.9	ΟΧΙ ← Αυτό είναι το ανεξήγητο μέρος ✗
$SS_{\text{Model}}$	636.3	ΟΧΙ ← Αυτό είναι ο αριθμητής, όχι το παρονομαστής ✗

Αν υπολογίζαμε λάθος:

\[\frac{SS_{\text{Model}}}{SS_{\text{Error}}} = \frac{636.3}{11227.9} = 0.0567\] ← Λάθος τύπος!

Πλήρης διάσπαση της μεταβλητότητας

Από τον πίνακα:

SS_Total = SS_Model + SS_Error
11864.197 = 636.336 + 11227.860 ✓

PRE = SS_Model / SS_Total
    = 636.336 / 11864.197
    = 0.0536
    = 5.36%

Εξηγούμενη:   636.3 (5.36%)
Ανεξήγητη:  11227.9 (94.64%)
─────────────────────────────
Συνολική    11864.2 (100%)

Σύνδεση με R²

Το PRE είναι ίδιο με το R²:

\[\text{PRE} = R^2 = \frac{SS_{\text{Model}}}{SS_{\text{Total}}} = 0.0536\]

summary(Pulse3Group_model)$r.squared
# [1] 0.0536  ✓

Και τα δύο ερμηνεύονται ως:

«Το ποσοστό της μεταβλητότητας της εξαρτημένης μεταβλητής που εξηγείται από το μοντέλο.»

Πρακτική ερμηνεία

PRE = 0.0536 σημαίνει:

1. Σε όρους εξήγησης:

«Αν γνωρίζω σε ποια ομάδα καρδιακού ρυθμού ανήκει κάποιος, μπορώ να εξηγήσω το 5.4% της μεταβλητότητας στις ώρες άσκησης του.»

2. Σε όρους πρόβλεψης:

«Το μοντέλο της Pulse3Group κάνει 5.4% καλύτερες προβλέψεις από το κενό μοντέλο που χρησιμοποιεί μόνο το γενικό μέσο όρο.»

3. Σε όρους μείωσης σφάλματος:

«Το σφάλμα πρόβλεψης μειώθηκε κατά 5.4% όταν προσθέσαμε την Pulse3Group.»

4. Σε όρους ανεξήγητης μεταβλητότητας:

«Το 94.6% της μεταβλητότητας παραμένει ανεξήγητο - οφείλεται σε άλλους παράγοντες πέρα από την Pulse3Group.»

Είναι το 5.4% καλό;

Εξαρτάται από το πλαίσιο:

Στις κοινωνικές επιστήμες:

5.4% θεωρείται μικρό έως μέτριο μέγεθος επίδρασης
Αλλά μπορεί να είναι στατιστικά και πρακτικά σημαντικό

Συμπέρασμα

Το PRE = 0.0536 ερμηνεύεται ως:

«Το 5.36% της συνολικής μεταβλητότητας στις ώρες άσκησης εξηγείται από τις ομάδες καρδιακού ρυθμού (Pulse3Group).»

Με άλλα λόγια:

✓ Από τη συνολική διαφορά στις ώρες άσκησης μεταξύ ατόμων

✓ Το 5.4% οφείλεται στο ποια ομάδα καρδιακού ρυθμού ανήκουν

✓ Το 94.6% οφείλεται σε άλλους παράγοντες

✓ Η Pulse3Group βελτιώνει την πρόβλεψη σε σχέση με το κενό μοντέλο

✓ Αλλά υπάρχει πολύ μεγάλο περιθώριο για βελτίωση (94.6% ανεξήγητο!)

Το PRE μετρά ΠΑΝΤΑ το ποσοστό της μεταβλητότητας που εξηγείται, όχι πιθανότητα, ποσοστά δείγματος, ή άλλα μεγέθη!

17. Αποδεικνύει αυτή η ανάλυση ότι η καρδιαγγειακή υγεία (δηλαδή, το να ανήκει κάποιος σε χαμηλότερη ομάδα καρδιακού ρυθμού ηρεμίας) οδηγεί τους φοιτητές στο να ασκούνται περισσότερο;

Όχι, αυτή η ανάλυση στην πραγματικότητα δείχνει ότι η περισσότερη άσκηση προκαλεί χαμηλότερο καρδιακό ρυθμό ηρεμίας.Ναι, επειδή έχουμε εντοπίσει τις καλύτερες εκτιμήσεις παραμέτρων.Όχι, δεν μπορούμε να αποδείξουμε αιτιότητα από μια συσχετιστική μελέτη.Ναι, επειδή το στατιστικό F είναι αρκετά μεγάλο (περίπου 10.14), και το PRE είναι πρακτικά σημαντικό.

Επεξήγηση

Σωστή απάντηση: Γ - Όχι, δεν μπορούμε να αποδείξουμε την ύπαρξης αιτιότητας από μια συσχετιστική μελέτη.

Η ανάλυση μας δείχνει ότι υπάρχει σχέση (association) μεταξύ Pulse3Group και Exercise, αλλά όχι ότι η μία μεταβλητή προκαλεί την άλλη.

Τι είδους μελέτη είναι αυτή;

Μελέτη παρατήρησης/Συσχετιστική μελέτη (Observational/Correlational Study):

Περιλαμβάνει μέτρηση μεταβλητών
ΟΧΙ χειρισμό/παρέμβαση (manipulation)
ΟΧΙ τυχαία ανάθεση υποκειμένων (random assignment)
Δεν ελέγχονται συγχυτικοί παράγοντες (confounders)

Συγκεκριμένα, στη μελέτη:

Ρωτήσαμε φοιτητές πόσες ώρες ασκούνται
Μετρήσαμε τον καρδιακό τους ρυθμό ηρεμίας
Βρήκαμε σχέση μεταξύ τους
Αλλά ΔΕΝ ελέγξαμε άλλους παράγοντες μέσω κάποιας παρέμβασης

Γιατί δεν μπορούμε να αποδείξουμε αιτιότητα;

Υπάρχουν τρία πιθανά σενάρια:

1. Χαμηλός ρυθμός → Περισσότερη άσκηση (αιτιώδης κατεύθυνση Α)

«Άτομα με καλή καρδιαγγειακή υγεία (χαμηλός ρυθμός) έχουν περισσότερη ενέργεια και ασκούνται περισσότερο.»

2. Περισσότερη άσκηση → Χαμηλός ρυθμός (αιτιώδης κατεύθυνση Β)

«Άτομα που ασκούνται περισσότερο αναπτύσσουν καλύτερη καρδιαγγειακή υγεία και χαμηλότερο ρυθμό.»

3. Τρίτη μεταβλητή → Και τα δύο οφείλονται σε κάποιον τρίτο, συγχυτικό παράγοντα)

«Κάποιος άλλος παράγοντας (π.χ., γενετική, κοινωνικοοικονομική κατάσταση) επηρεάζει και τον καρδιακό ρυθμό ηρεμίας και τα επίπεδα άσκησης.»

Η συσχετιστική μελέτη ΔΕΝ μπορεί να διακρίνει μεταξύ αυτών των σεναρίων!

Τι θα χρειαζόταν για αιτιότητα;

Για να αποδείξουμε αιτιότητα, χρειαζόμαστε:

1. Πειραματικό σχεδιασμό (Experimental Design):

Τυχαία ανάθεση (random assignment) υποκειμένων σε ομάδες
Χειρισμός της ανεξάρτητης μεταβλητής
Έλεγχος άλλων παραγόντων

Παράδειγμα πειραματικού σχεδιασμού:

1. Παίρνουμε 300 άτομα με παρόμοια επίπεδα φυσικής κατάστασης

2. Τυχαία ανάθεση σε 3 ομάδες:
   - Ομάδα Α: 0 ώρες άσκησης/εβδομάδα (ομάδα ελέγχου)
   - Ομάδα Β: 5 ώρες άσκησης/εβδομάδα
   - Ομάδα Γ: 10 ώρες άσκησης/εβδομάδα

3. Παρακολούθηση για 6 μήνες

4. Μέτρηση καρδιακού ρυθμού ηρεμίας στο τέλος

5. Αν Β και Γ έχουν σημαντικά χαμηλότερο ρυθμό από Α:
   → Μπορούμε να ισχυριστούμε ότι έχουμε ενδείξεις ότι η άσκηση ΠΡΟΚΑΛΕΙ χαμηλότερο καρδιακό ρυθμό

2. Κριτήρια για αιτιότητα:

Χρονική προτεραιότητα: Η αιτία πρέπει να προηγείται του αποτελέσματος
Ισχύς σχέσης: Ισχυρότερη σχέση = πιο πιθανή αιτιότητα
Σχέση δόσης-απόκρισης: Περισσότερη αιτία = περισσότερο αποτέλεσμα
Συνέπεια: Μπορεί να αναπαραχθεί σε διαφορετικές μελέτες
Βιολογική σχέση: Υπάρχει μηχανισμός που εξηγεί τη σχέση;
Εναλλακτικές εξηγήσεις: Έχουν αποκλειστεί;

Η συγκεκριμένη μελέτη ΔΕΝ πληροί αυτά τα κριτήρια!

Γιατί οι άλλες είναι λάθος;

Α. “Η ανάλυση δείχνει ότι η άσκηση προκαλεί χαμηλό ρυθμό” - ΛΑΘΟΣ

Αυτό επίσης δεν αποδεικνύεται από τη συσχετιστική μελέτη
Η επιλογή Α απλά αντιστρέφει την αιτιώδη κατεύθυνση, αλλά εξακολουθεί να είναι λάθος
Κανένα από τα δύο σενάρια δεν αποδεικνύεται

Διευκρίνιση:

Ενώ είναι πιο πιθανό (βάσει βιολογίας) ότι η άσκηση προκαλεί χαμηλό καρδιακό ρυθμό ηρεμίας, η συσχετιστική μελέτη δεν το αποδεικνύει.

Β. “Ναι, επειδή έχουμε τις καλύτερες εκτιμήσεις παραμέτρων” - ΛΑΘΟΣ

Οι εκτιμήσεις παραμέτρων του μοντέλου ($b_0$, $b_1$, $b_2$) περιγράφουν τη σχέση
ΟΧΙ την αιτιότητα

Δ. “Ναι, επειδή το πηλίκο F είναι μεγάλο και το PRE πρακτικά σημαντικό” - ΛΑΘΟΣ

Το πηλίκο F δείχνει ότι η σχέση είναι στατιστικά σημαντική (περισσότερα σε επόμενο κεφάλαιο)
Ο δείκτης PRE δείχνει το μέγεθος της σχέσης
Κανένας από τους δύο δείκτες δεν δείχνει αιτιότητα

Τι ΜΠΟΡΟΥΜΕ να ισχυριστούμε από αυτή τη μελέτη;

Ασφαλείς δηλώσεις:

✓ «Υπάρχει σχέση μεταξύ καρδιακού ρυθμού ηρεμίας και ωρών άσκησης.»

✓ «Άτομα με χαμηλό καρδιακό ρυθμό τείνουν να ασκούνται περισσότερο κατά μέσο όρο.»

✓ «Άτομα με υψηλό καρδιακό ρυθμό τείνουν να ασκούνται λιγότερο κατά μέσο όρο.»

✓ «Η Pulse3Group εξηγεί το 5% της μεταβλητότητας στην Exercise.»

Μη ασφαλείς δηλώσεις (χωρίς πειραματικό σχεδιασμό):

✗ «Χαμηλός ρυθμός προκαλεί περισσότερη άσκηση.»

✗ «Η άσκηση προκαλεί χαμηλό καρδιακό ρυθμό ηρεμίας.»

✗ «Αν βελτιώσεις την καρδιαγγειακή σου υγεία, θα ασκηθείς περισσότερο.»

✗ «Αν ασκηθείς περισσότερο, θα έχεις χαμηλότερο ρυθμό ηρεμίας.»

Παράδειγμα με πιθανούς συγχυτικούς παράγοντες

Πιθανές τρίτες μεταβλητές που επηρεάζουν και τα δύο:

1. Ηλικία:

Νεότεροι άνθρωποι: χαμηλότερος ρυθμός + περισσότερη άσκηση
Μεγαλύτεροι άνθρωποι: υψηλότερος ρυθμός + λιγότερη άσκηση

2. Γενετική προδιάθεση:

Κάποιοι γεννιούνται με καλύτερο μεταβολισμό → χαμηλότερος ρυθμός + περισσότερη ενέργεια για άσκηση

3. Κοινωνικοοικονομική κατάσταση:

Υψηλότερο εισόδημα → πρόσβαση σε γυμναστήρια, διατροφολόγους → καλύτερη υγεία + περισσότερη άσκηση

4. Stress:

Χαμηλό stress → χαμηλότερος ρυθμός + περισσότερος χρόνος για άσκηση
Υψηλό stress → υψηλότερος ρυθμός + λιγότερος χρόνος για άσκηση

5. Ύπνος:

Καλός ύπνος → χαμηλότερος ρυθμός + περισσότερη ενέργεια για άσκηση

Χωρίς έλεγχο αυτών των παραγόντων, δεν μπορούμε να ξεχωρίσουμε την αιτία!

Σύγκριση σχεδιασμών μελέτης

Χαρακτηριστικό	Μελέτη Παρατήρησης	Πειραματική
Τυχαία ανάθεση	ΟΧΙ	ΝΑΙ
Χειρισμός μεταβλητής	ΟΧΙ	ΝΑΙ
Έλεγχος συγχυτικών παραγόντων	ΟΧΙ	ΝΑΙ
Μπορεί να δείξει σχέση	ΝΑΙ	ΝΑΙ
Μπορεί να δείξει αιτιότητα	ΟΧΙ	ΝΑΙ
Παράδειγμα	Ερωτηματολόγιο	Τυχαιοποιημένο πείραμα

Η μελέτη μας είναι συσχετιστική ή παρατήρησης → ΔΕΝ μπορεί να αποδείξει αιτιότητα!

Συμπέρασμα

ΟΧΙ, αυτή η ανάλυση ΔΕΝ αποδεικνύει αιτιότητα.

Γιατί;

«Δεν μπορούμε να αποδείξουμε αιτιότητα από μια συσχετιστική μελέτη.»

Τι έχουμε:

✓ Συγχρονική μελέτη δεδομένα παρατήρησης (ερωτηματολόγιο)

✓ Στατιστικά σημαντική σχέση (F = 18.9, p < 0.001)

✓ Μέτριο μέγεθος επίδρασης (PRE = 5%)

Τι ΔΕΝ έχουμε:

✗ Τυχαία ανάθεση σε ομάδες

✗ Χειρισμό της ανεξάρτητης μεταβλητής

✗ Έλεγχο συγχυτικών παραγόντων (confounders)

✗ Χρονική προτεραιότητα (ποια έρχεται πρώτη;)

Πιθανές εξηγήσεις:

Χαμηλός ρυθμός → Περισσότερη άσκηση
Περισσότερη άσκηση → Χαμηλός ρυθμός (πιο πιθανό βιολογικά)
Τρίτη μεταβλητή → Και τα δύο (π.χ., γενετική, ηλικία, κοινωνικοοικονομικό επίπεδο)

Χωρίς πειραματικό σχεδιασμό, δεν μπορούμε να διακρίνουμε μεταξύ αυτών!

Για να αποδείξουμε αιτιότητα, θα χρειαζόμασταν:

Τυχαιοποιημένη Ελεγχόμενη Δοκιμική (RCT)
Διαχρονική μελέτη
Ημι-πειραματικό σχεδιασμό με προσεκτικό έλεγχο συγχυτικών παραγόντων

Μέχρι τότε, μπορούμε μόνο να πούμε: “Υπάρχει σχέση, όχι απαραίτητα αιτιότητα.”

18. Ας υποθέσουμε ότι μας ενδιαφέρει αν οι ομάδες καρδιακού ρυθμού ηρεμίας (μεταβλητή Pulse3Group) εξηγούν κάποια από τη μεταβλητότητα στον αριθμό των piercing που έχουν οι φοιτητές στο σώμα τους (μεταβλητή Piercings). Δίνεται ο πίνακας της supernova() για το συγκεκριμένο μοντέλο:

 Analysis of Variance Table (Type III SS)
 Model: Piercings ~ Pulse3Group

                               SS  df     MS     F   PRE     p
 ----- --------------- | -------- --- ------ ----- ----- -----
 Model (error reduced) |   40.999   2 20.499 4.425 .0241 .0126
 Error (from model)    | 1658.431 358  4.632                  
 ----- --------------- | -------- --- ------ ----- ----- -----
 Total (empty model)   | 1699.429 360  4.721

Γιατί αυτός ο πίνακας έχει μικρότερο SS Total (1699) από αυτό στον πίνακα της supernova() για την Exercise που εξηγείται από την Pulse3Group (11864);

Το SS Total δεν πρέπει ποτέ να αλλάζει. Αυτό πρέπει να είναι σφάλμα στον κώδικα.Το SS Total εξαρτάται από τη μεταβλητότητα στην ανεξάρτητη μεταβλητή. Η Piercings είναι διαφορετική ανεξάρτητη μεταβλητή, οπότε έχει διαφορετικό SS Total.Το SS Total θα διαφέρει πάντα. Δεν πρέπει ποτέ να περιμένουμε να έχει ακριβώς την ίδια τιμή.Το SS Total εξαρτάται από τη μεταβλητότητα στην εξαρτημένη μεταβλητή. Η Piercings είναι διαφορετική εξαρτημένη μεταβλητή, οπότε έχει διαφορετικό SS Total.

Επεξήγηση

Σωστή απάντηση: Δ - Το SS Total εξαρτάται από τη μεταβλητότητα στην εξαρτημένη μεταβλητή. Η Piercings είναι διαφορετική εξαρτημένη μεταβλητή, οπότε έχει διαφορετικό SS Total.

Τι είναι το $SS_{\text{Total}}$;

\[SS_{\text{Total}} = \sum_{i=1}^{n}(Y_i - \bar{Y})^2\]

«Το $SS_{\text{Total}}$ μετρά τη συνολική μεταβλητότητα στην εξαρτημένη μεταβλητή, ανεξάρτητα από οποιαδήποτε ανεξάρτητη μεταβλητή.»

Σύγκριση των δύο μοντέλων

Μοντέλο 1: Exercise ~ Pulse3Group

SS_Total = 11864.197

Εξαρτημένη μεταβλητή: Exercise (ώρες άσκησης/εβδομάδα)
Ανεξάρτητη μεταβλητή: Pulse3Group
$SS_{\text{Total}} = \sum(\text{Exercise}_i - \overline{\text{Exercise}})^2$

Μοντέλο 2: Piercings ~ Pulse3Group

SS_Total = 1699.429

Εξαρτημένη μεταβλητή: Piercings (αριθμός piercing)
Ανεξάρτητη μεταβλητή: Pulse3Group (ίδια!)
$SS_{\text{Total}} = \sum(\text{Piercings}_i - \overline{\text{Piercings}})^2$

Διαφορά:

Η ανεξάρτητη μεταβλητή είναι η ίδια (Pulse3Group), αλλά η εξαρτημένη μεταβλητή είναι διαφορετική (Exercise vs Piercings).

Γιατί το $SS_{\text{Total}}$ διαφέρει;

Το $SS_{\text{Total}}$ μετρά τη μεταβλητότητα στην Y (εξαρτημένη):

\[SS_{\text{Total}} = \sum_{i=1}^{n}(Y_i - \bar{Y})^2\]

Για την Exercise:

Μέσος όρος: $\bar{\text{Exercise}} \approx 9.05$ ώρες
Εύρος: από 0 έως ~40 ώρες (μεγάλη διασπορά)
Διακύμανση: $s^2 \approx 32.96$
$SS_{\text{Total}} = 11864.2$ (μεγάλο)

Για την Piercings:

Μέσος όρος: $\bar{\text{Piercings}} \approx 1.7$ piercing
Εύρος: από 0 έως ~10 piercing (μικρότερη διακύμανση)
Διακύμανση: $s^2 \approx 4.72$
$SS_{\text{Total}} = 1699.4$ (μικρότερο)

Συμπέρασμα:

H Exercise έχει μεγαλύτερη μεταβλητότητα από την Piercings → μεγαλύτερο $SS_{\text{Total}}$!

Μαθηματική εξήγηση

Σχέση SS Total με διακύμανση:

\[SS_{\text{Total}} = (n-1) \times s^2\]

Όπου:

$n$ = αριθμός παρατηρήσεων
$s^2$ = διακύμανση (variance)

Για την Exercise:

\[SS_{\text{Total}} = 360 \times 32.956 = 11864.2\] ✓

Για την Piercings:

\[SS_{\text{Total}} = 360 \times 4.721 = 1699.4\] ✓

Επειδή η Exercise έχει μεγαλύτερη διακύμανση ($s^2 = 32.96$ vs $4.72$), έχει μεγαλύτερο $SS_{\text{Total}}$!

Γιατί οι άλλες είναι λάθος;

Α. “Το SS Total δεν πρέπει ποτέ να αλλάζει - σφάλμα κώδικα” - ΛΑΘΟΣ

Το $SS_{\text{Total}}$ αλλάζει όταν αλλάζει η εξαρτημένη μεταβλητή
Είναι φυσιολογικό να είναι διαφορετικό για Exercise vs Piercings
Δεν υπάρχει σφάλμα!

Τι παραμένει σταθερό:

Το $SS_{\text{Total}}$ παραμένει σταθερό μόνο για την ίδια εξαρτημένη μεταβλητή, ανεξάρτητα από το μοντέλο:

Μοντέλο	$SS_{\text{Total}}$
`Exercise ~ NULL`	11864.2
`Exercise ~ Pulse3Group`	11864.2 ✓ (ίδιο)
`Exercise ~ Gender`	11864.2 ✓ (ίδιο)
`Piercings ~ Pulse3Group`	1699.4 ✗ (διαφορετικό Y!)

Β. “Το SS Total εξαρτάται από την ανεξάρτητη μεταβλητή” - ΛΑΘΟΣ

Το $SS_{\text{Total}}$ ΔΕΝ εξαρτάται από την ανεξάρτητη μεταβλητή (X)
Εξαρτάται ΜΟΝΟ από την εξαρτημένη μεταβλητή (Y)

Απόδειξη:

\[SS_{\text{Total}} = \sum(Y_i - \bar{Y})^2\]

Δεν υπάρχει X σε αυτόν τον τύπο! Μόνο Y!

Παράδειγμα:

# `Exercise` με διαφορετικές ανεξάρτητες μεταβλητές
model1 <- lm(Exercise ~ Pulse3Group, data = StudentSurvey)
model2 <- lm(Exercise ~ Gender, data = StudentSurvey)
model3 <- lm(Exercise ~ Year, data = StudentSurvey)

# Όλα έχουν το ΙΔΙΟ `SS_Total`!
sum(residuals(lm(Exercise ~ NULL))^2)
# [1] 11864.197  ← Πάντα το ίδιο για την `Exercise`!

Γ. “Το SS Total είναι πάντα διαφορετικό” - ΛΑΘΟΣ

Αυτό είναι υπερβολικά γενικό και ανακριβές
Το $SS_{\text{Total}}$ είναι το ίδιο για την ίδια εξαρτημένη μεταβλητή
Είναι διαφορετικό μόνο όταν αλλάζει η εξαρτημένη μεταβλητή

Σωστή δήλωση:

«Το $SS_{\text{Total}}$ είναι μοναδικό για κάθε εξαρτημένη μεταβλητή, αλλά σταθερό για την ίδια εξαρτημένη μεταβλητή ανεξάρτητα από το μοντέλο.»

Συμπέρασμα

Το $SS_{\text{Total}}$ είναι μικρότερο για την Piercings (1699) από ό,τι για την Exercise (11864) επειδή:

«Το $SS_{\text{Total}}$ εξαρτάται από τη μεταβλητότητα στην εξαρτημένη μεταβλητή. Η Piercings είναι διαφορετική εξαρτημένη μεταβλητή, οπότε έχει διαφορετικό $SS_{\text{Total}}$.»

Συγκεκριμένα:

✓ Η Exercise έχει μεγαλύτερη μεταβλητότητα ($s^2 = 32.96$)

✓ Η Piercings έχει μικρότερη μεταβλητότητα ($s^2 = 4.72$)

✓ Άρα: $SS_{\text{Total (`Exercise`)}} > SS_{\text{Total (Piercings)}}$

✓ Η ανεξάρτητη μεταβλητή (Pulse3Group) είναι ίδια και στα δύο

✓ Αλλά η εξαρτημένη μεταβλητή είναι διαφορετική

✓ Το $SS_{\text{Total}}$ καθορίζεται μόνο από το Y, όχι από το X

Γενικός κανόνας:

\[SS_{\text{Total}} = \sum(Y_i - \bar{Y})^2 = (n-1) \times s_Y^2\]

Διαφορετικό Y → Διαφορετική διακύμανση → Διαφορετικό $SS_{\text{Total}}$!

Μελετήστε τους δύο πίνακες της supernova() που ακολουθούν. Με βάση αυτούς τους πίνακες, θα μπορούσαμε να υποστηρίξουμε ότι η Pulse3Group εξηγεί μεγαλύτερο μέρος της μεταβλητότητας στην Exercise παρά στην Piercings. Εξηγήστε γιατί.

 Analysis of Variance Table (Type III SS)
 Model: Exercise ~ Pulse3Group

                                SS  df      MS      F   PRE     p
 ----- --------------- | --------- --- ------- ------ ----- -----
 Model (error reduced) |   636.336   2 318.168 10.145 .0536 .0001
 Error (from model)    | 11227.860 358  31.363                   
 ----- --------------- | --------- --- ------- ------ ----- -----
 Total (empty model)   | 11864.197 360  32.956       

 Analysis of Variance Table (Type III SS)
 Model: Piercings ~ Pulse3Group

                               SS  df     MS     F   PRE     p
 ----- --------------- | -------- --- ------ ----- ----- -----
 Model (error reduced) |   40.999   2 20.499 4.425 .0241 .0126
 Error (from model)    | 1658.431 358  4.632                  
 ----- --------------- | -------- --- ------ ----- ----- -----
 Total (empty model)   | 1699.429 360  4.721

20. Μπορούμε να χρησιμοποιήσουμε το άθροισμα τετραγώνων για να υποστηρίξουμε ότι η μεταβλητή Pulse3Group εξηγεί μεγαλύτερη μεταβλητότητα στην Exercise σε σχέση με την Piercings; Γιατί ναι ή γιατί όχι;

Ναι, επειδή το SS Model για την Exercise (636.336) είναι μεγαλύτερο από το SS Model για την Piercings (40.999).Όχι, επειδή το SS Model εξαρτάται από το SS Total κάθε μεταβλητής. Πρέπει να χρησιμοποιήσουμε το PRE για να συγκρίνουμε το ποσοστό εξηγούμενης μεταβλητότητας.Ναι, αλλά μόνο αν διαιρέσουμε το SS Model με τους βαθμούς ελευθερίας.Όχι, επειδή το SS Total είναι διαφορετικό για τις δύο μεταβλητές και δεν μπορούμε να συγκρίνουμε τίποτα.

Επεξήγηση

Σωστή απάντηση: Β - Όχι, επειδή το SS Model εξαρτάται από το SS Total κάθε μεταβλητής. Πρέπει να χρησιμοποιήσουμε το PRE για να συγκρίνουμε το ποσοστό εξηγούμενης μεταβλητότητας.

Γιατί όχι το SS Model;

Το SS Model δεν είναι συγκρίσιμο μεταξύ διαφορετικών εξαρτημένων μεταβλητών:

Από τους πίνακες:

Exercise:  SS Model = 636.336
Piercings: SS Model =  40.999

Αν και το 636.336 > 40.999, αυτό ΔΕΝ σημαίνει ότι η Pulse3Group εξηγεί περισσότερη μεταβλητότητα στην Exercise!

Οι τρεις λόγοι

1. Διαφορετικό SS Total

Τα δύο μοντέλα έχουν εντελώς διαφορετικά SS Total:

Exercise:  SS Total = 11864.197
Piercings: SS Total =  1699.429

Το SS Model πρέπει να κρίνεται σε σχέση με το SS Total:

636 από 11864 είναι μικρό κομμάτι (5.36%)
41 από 1699 είναι ακόμα μικρότερο κομμάτι (2.41%)

2. Διαφορετικές κλίμακες μέτρησης

Οι μεταβλητές μετριούνται σε διαφορετικές κλίμακες:

Exercise: Ώρες ανά εβδομάδα (εύρος: 0-40 περίπου)
Piercings: Αριθμός piercing (εύρος: 0-10 περίπου)

Το SS εξαρτάται από την κλίμακα και τη διασπορά της μεταβλητής. Μια μεταβλητή που μετριέται σε μεγαλύτερη κλίμακα θα έχει φυσικά μεγαλύτερο SS.

3. Διαφορετική διακύμανση (variance)

Exercise:  Variance (MS Total) = 32.956 → Μεγάλη διασπορά
Piercings: Variance (MS Total) =  4.721 → Μικρή διασπορά

Σχέση με SS Total:

\[SS_{\text{Total}} = (n-1) \times s^2\]

Για την Exercise:

\[SS_{\text{Total}} = 360 \times 32.956 = 11864.2\]

Για την Piercings:

\[SS_{\text{Total}} = 360 \times 4.721 = 1699.4\]

Μεταβλητές με μεγαλύτερη διακύμανση θα έχουν φυσικά μεγαλύτερα SS, ανεξάρτητα από το πόσο καλά εξηγούνται από το μοντέλο!

Η σωστή μέτρηση: PRE (ή R²)

Αντί για το SS Model, χρησιμοποιούμε το PRE:

\[\text{PRE} = \frac{SS_{\text{Model}}}{SS_{\text{Total}}}\]

Το PRE είναι τυποποιημένο μέτρο (0-1) που:

✓ Κανονικοποιεί ως προς το SS Total κάθε μεταβλητής

✓ Επιτρέπει τη σύγκριση μεταξύ διαφορετικών εξαρτημένων μεταβλητών

✓ Απαντά στην ερώτηση: “Τι ποσοστό της μεταβλητότητας εξηγείται;”

Για την Exercise:

\[\text{PRE} = \frac{636.336}{11864.197} = 0.0536 = 5.36\%\]

Για την Piercings:

\[\text{PRE} = \frac{40.999}{1699.429} = 0.0241 = 2.41\%\]

Τώρα βλέπουμε ξεκάθαρα: 5.36% > 2.41%

Η Pulse3Group εξηγεί περισσότερο από διπλάσιο ποσοστό μεταβλητότητας στην Exercise!

Σύγκριση δίπλα-δίπλα

Μέτρηση	`Exercise`	`Piercings`	Συγκρίσιμο;
SS Model	636.336	40.999	ΟΧΙ ✗
SS Total	11864.197	1699.429	ΟΧΙ ✗
PRE	0.0536 (5.36%)	0.0241 (2.41%)	ΝΑΙ ✓
Variance	32.956	4.721	ΟΧΙ ✗

Μόνο το PRE είναι συγκρίσιμο μεταξύ διαφορετικών εξαρτημένων μεταβλητών!

Γιατί οι άλλες είναι λάθος;

Α. “Ναι, επειδή SS Model για Exercise (636.336) > SS Model για Piercings (40.999)” - ΛΑΘΟΣ

Αυτό αγνοεί το διαφορετικό SS Total
Τα απόλυτα SS δεν είναι συγκρίσιμα μεταξύ διαφορετικών μεταβλητών
Είναι σαν να συγκρίνουμε €1000 στα €20,000 με €500 στα €2,000

Γ. “Ναι, αλλά μόνο αν διαιρέσουμε το SS Model με τους βαθμούς ελευθερίας” - ΛΑΘΟΣ

Η διαίρεση με df δίνει το MS Model (Mean Square)
Αλλά και το MS Model δεν είναι συγκρίσιμο μεταξύ διαφορετικών μεταβλητών
Εξακολουθεί να εξαρτάται από την κλίμακα και τη διακύμανση της εξαρτημένης μεταβλητής

Υπολογισμός:

MS Model (`Exercise`)  = 636.336 / 2 = 318.168
MS Model (`Piercings`) =  40.999 / 2 =  20.499

Και πάλι, 318 vs 20 δεν είναι συγκρίσιμα χωρίς να λάβουμε υπόψη το SS Total!

Δ. “Όχι, επειδή το SS Total είναι διαφορετικό και δεν μπορούμε να συγκρίνουμε τίποτα” - ΛΑΘΟΣ

Αυτό είναι υπερβολικά απαισιόδοξο
Μπορούμε να συγκρίνουμε, αλλά όχι με το SS Model
Χρησιμοποιούμε το PRE που κανονικοποιεί ως προς το SS Total

Συμπέρασμα

Όχι, δεν μπορούμε να χρησιμοποιήσουμε το SS Model για τη σύγκριση, επειδή:

✗ Τα SS Total είναι διαφορετικά (11864 vs 1699)

✗ Οι κλίμακες μέτρησης είναι διαφορετικές (ώρες vs αριθμός)

✗ Οι διακυμάνσεις είναι διαφορετικές (32.96 vs 4.72)

✗ Τα απόλυτα SS δεν είναι συγκρίσιμα μεταξύ διαφορετικών μεταβλητών

✓ Πρέπει να χρησιμοποιήσουμε το PRE (ή R²) που είναι τυποποιημένο μέτρο

✓ Το PRE κανονικοποιεί ως προς το SS Total κάθε μεταβλητής

✓ Το PRE μας επιτρέπει να συγκρίνουμε το σχετικό ποσοστό εξηγούμενης μεταβλητότητας

Σωστή δήλωση:

“Η Pulse3Group εξηγεί μεγαλύτερο ποσοστό της μεταβλητότητας στην Exercise (PRE = 5.36%) παρά στην Piercings (PRE = 2.41%), όπως φαίνεται από τη σύγκριση των PRE, όχι των SS Model.”

Γενικός κανόνας:

Για να συγκρίνουμε την επεξηγηματική ικανότητα ενός μοντέλου σε διαφορετικές εξαρτημένες μεταβλητές, χρησιμοποιούμε ΠΑΝΤΑ το PRE (ή R²), ΠΟΤΕ το SS Model.

Μοντέλο	Τιμή πρόβλεψης	Υπόλοιπο (\(e_i\))
Κενό	\(\bar{Y}\) (Γενικός μέσος όρος)	\(Y_i - \bar{Y}\)
Σύνθετο	\(\bar{Y}_{\text{group}[i]}\)	\(Y_i - \bar{Y}_{\text{group}[i]}\)

9 Κεφάλαιο: Εμβαθύνοντας στα Mοντέλα Oμάδων

9.1 Επέκταση σε Μοντέλο Τριών Ομάδων

Ένα Νέο Μοντέλο Δύο Ομάδων

Ένα Μοντέλο Τριών Ομάδων

9.2 Προσαρμογή και Ερμηνεία του Μοντέλου Τριών Ομάδων

Προσαρμογή του Μοντέλου της `Height3Group`

Ερμηνεία του Μοντέλου της `Height3Group`

9.3 Σύγκριση της Προσαρμογής των Μοντέλων Δύο και Τριών Ομάδων

Εξέταση της Προσαρμογής του Μοντέλου Τριών Ομάδων

Μοντέλο της `Height2Group`

Μοντέλο της `Height3Group`

Βελτίωση Μοντέλων με την Προσθήκη Παραμέτρων

9.4 Το πηλίκο `F`

Βαθμοί Ελευθερίας (`df`)

Μέσα Αθροίσματα Τετραγώνων (`MS`)

Το πηλίκο `F`

Ένας Εναλλακτικός Τρόπος Έκφρασης του Πηλίκου `F`

9.5 Μέτρα Μεγέθους Επίδρασης

Επανεξέταση της Μελέτης του Φιλοδωρήματος

Διαφορά Μέσων Όρων (ή \(b_1\))

R: Η Συνάρτηση `b1()`

PRE

R: Η Συνάρτηση `pre()`

Ο δείκτης d του Cohen

Υπολογισμός του d του Cohen: Ποια Τυπική Απόκλιση να Χρησιμοποιήσουμε;

R: Η Συνάρτηση `cohensD()`

9.6 Μοντελοποίηση της ΔΠΔ

Σκέψεις για τη ΔΠΔ των Φιλοδωρημάτων

Μοντελοποίηση των Δεδομένων

Σύγκριση Δύο Μοντέλων της ΔΠΔ

9.7 Χρήση του Τυχαίου Ανακατέματος για Σύγκριση Μοντέλων της ΔΠΔ

Προσομοίωση του Κενού Μοντέλου με τη `shuffle()`

Χρήση Προσομοιωμένων \(b_1\) για Καλύτερη Κατανόηση των Δεδομένων

9.8 Ασκήσεις Επανάληψης Κεφαλαίου 9

Μοντέλο	Παράμετροι \((k)\)	Παρατηρήσεις \((n)\)	df Error
Κενό μοντέλο	1 (\(b_0\))	157	\(157 - 1 = 156\)
Height2Group	2 (\(b_0, b_1\))	157	\(157 - 2 = 155\)
Height3Group	3 (\(b_0, b_1, b_2\))	157	\(157 - 3 = 154\)

9.1 Επέκταση σε Μοντέλο Τριών Ομάδων

Ένα Νέο Μοντέλο Δύο Ομάδων

Ένα Μοντέλο Τριών Ομάδων

9.2 Προσαρμογή και Ερμηνεία του Μοντέλου Τριών Ομάδων

Προσαρμογή του Μοντέλου της Height3Group

Ερμηνεία του Μοντέλου της Height3Group

9.3 Σύγκριση της Προσαρμογής των Μοντέλων Δύο και Τριών Ομάδων

Εξέταση της Προσαρμογής του Μοντέλου Τριών Ομάδων

Μοντέλο της Height2Group

Μοντέλο της Height3Group

Βελτίωση Μοντέλων με την Προσθήκη Παραμέτρων

9.4 Το πηλίκο F

Βαθμοί Ελευθερίας (df)

Μέσα Αθροίσματα Τετραγώνων (MS)

Το πηλίκο F

Ένας Εναλλακτικός Τρόπος Έκφρασης του Πηλίκου F

9.5 Μέτρα Μεγέθους Επίδρασης

Επανεξέταση της Μελέτης του Φιλοδωρήματος

Διαφορά Μέσων Όρων (ή \(b_1\))

R: Η Συνάρτηση b1()

PRE

R: Η Συνάρτηση pre()

Ο δείκτης d του Cohen

Υπολογισμός του d του Cohen: Ποια Τυπική Απόκλιση να Χρησιμοποιήσουμε;

R: Η Συνάρτηση cohensD()

9.6 Μοντελοποίηση της ΔΠΔ

Σκέψεις για τη ΔΠΔ των Φιλοδωρημάτων

Μοντελοποίηση των Δεδομένων

Σύγκριση Δύο Μοντέλων της ΔΠΔ

9.7 Χρήση του Τυχαίου Ανακατέματος για Σύγκριση Μοντέλων της ΔΠΔ

Προσομοίωση του Κενού Μοντέλου με τη shuffle()

Χρήση Προσομοιωμένων \(b_1\) για Καλύτερη Κατανόηση των Δεδομένων

9.8 Ασκήσεις Επανάληψης Κεφαλαίου 9

Προσαρμογή του Μοντέλου της `Height3Group`

Ερμηνεία του Μοντέλου της `Height3Group`

Μοντέλο της `Height2Group`

Μοντέλο της `Height3Group`

9.4 Το πηλίκο `F`

Βαθμοί Ελευθερίας (`df`)

Μέσα Αθροίσματα Τετραγώνων (`MS`)

Το πηλίκο `F`

Ένας Εναλλακτικός Τρόπος Έκφρασης του Πηλίκου `F`

R: Η Συνάρτηση `b1()`

R: Η Συνάρτηση `pre()`

R: Η Συνάρτηση `cohensD()`

Προσομοίωση του Κενού Μοντέλου με τη `shuffle()`